Modern and Traditional Methods for Measuring Money Supply: The Case of Saudi Arabia
Abstract
:1. Introduction
“A monetary aggregate that is an unweighted sum of components has the advantage of simplicity, but a monetary aggregate with weighted components may be expected to exhibit a stronger link to aggregate spending in an economy. By weighting the monetary components, a Divisia Money formulation takes account of the trade-off between the medium-of-exchange and store-of-value functions of holding of money components.”
2. Monetary Aggregation Theory and Statistical Index Numbers
3. Data Descriptions and Sources
4. Constructing New Monetary Aggregates for Saudi Arabia
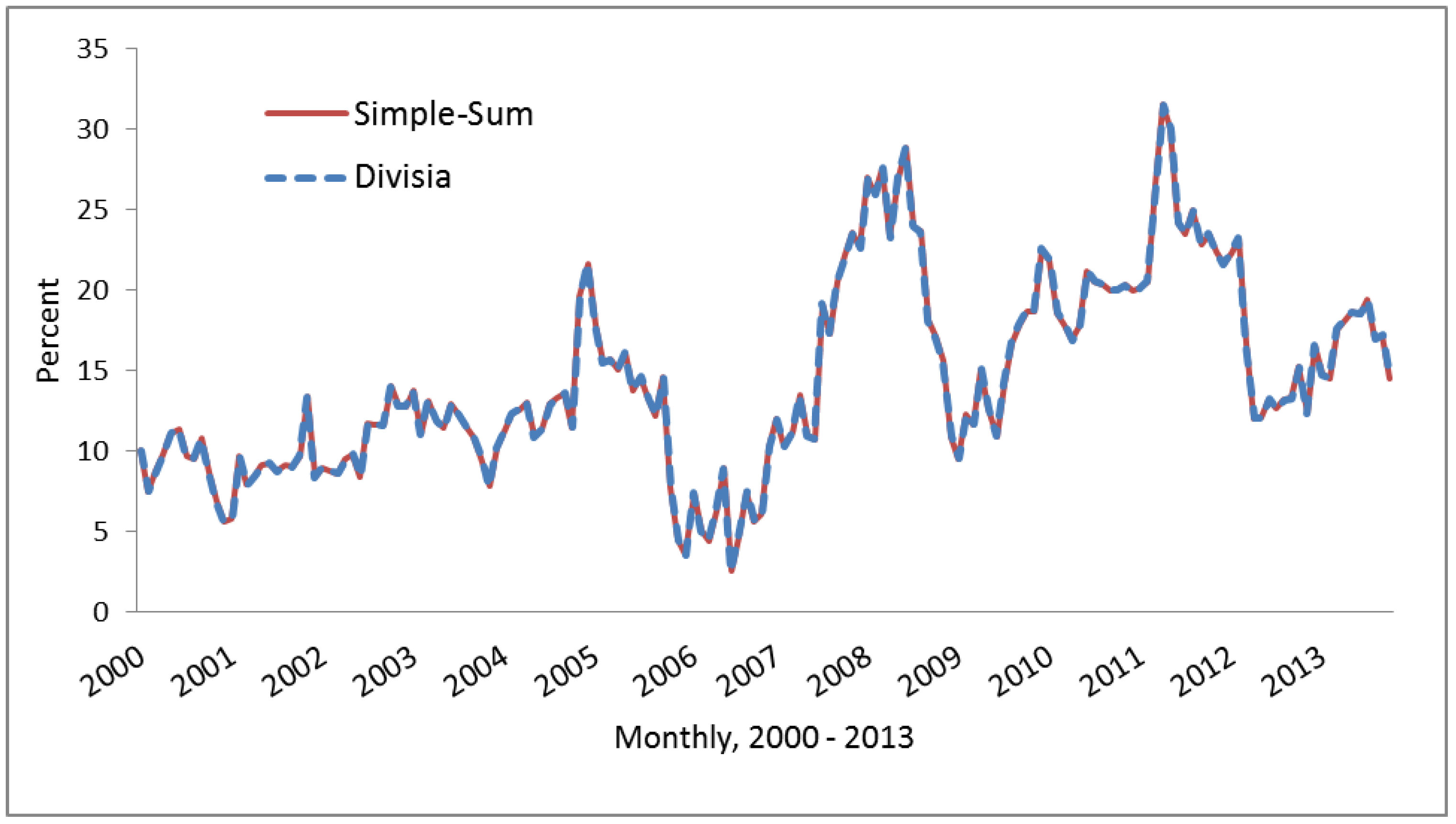
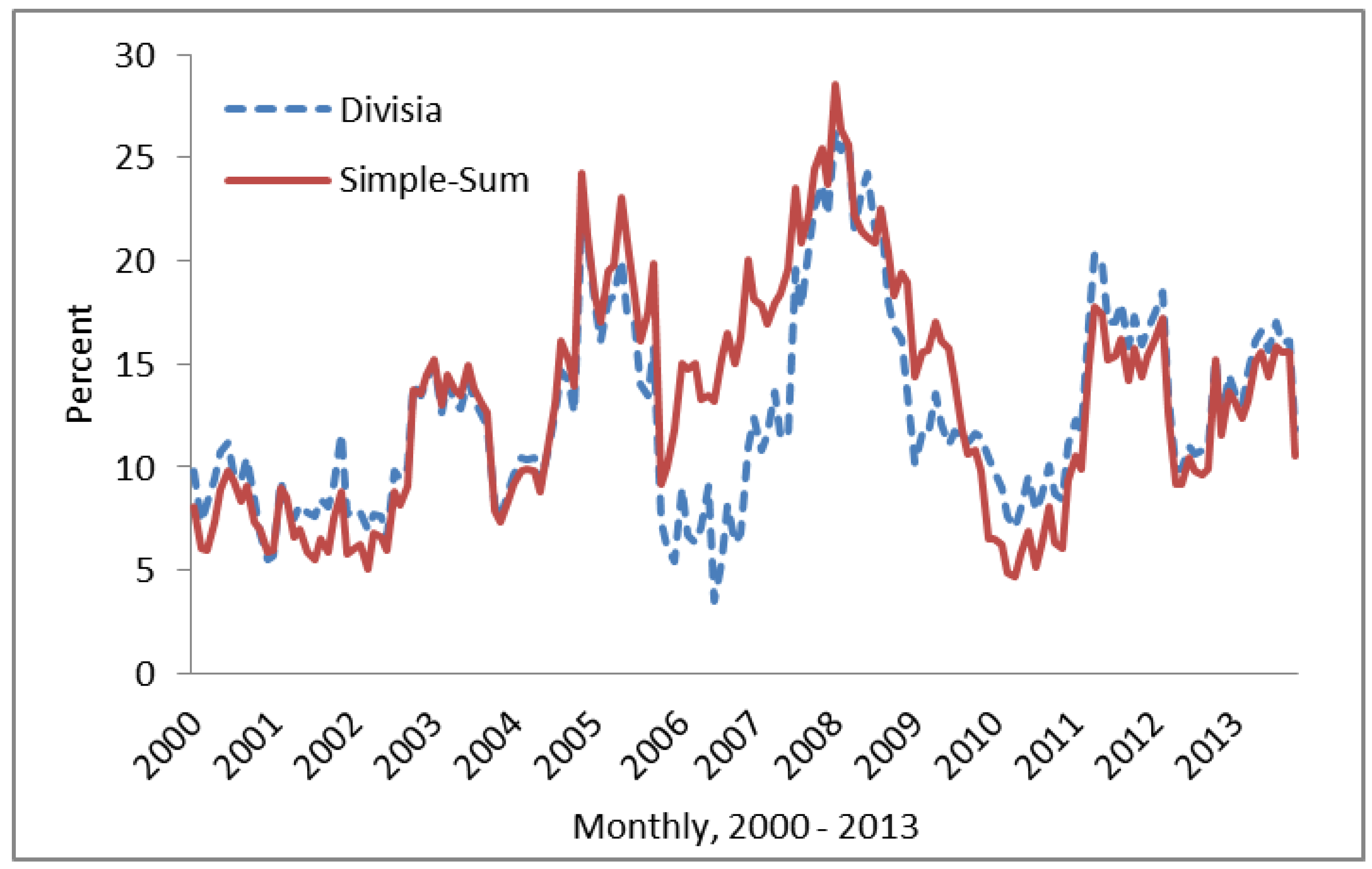
5. Conclusions
Author Contributions
Conflicts of Interest
References
- W.A. Barnett. “The User Cost of Money.” Econ. Lett. 1 (1978): 145–149. [Google Scholar] [CrossRef]
- W.A. Barnett. “Economic Monetary Aggregates: An Application of Index Number and Aggregation Theory.” J. Econom. 14 (1980): 11–48. [Google Scholar] [CrossRef]
- W.A. Barnett. “The New Monetary Aggregates: A Comment.” J. Money Credit Bank. 13 (1981): 485–489. [Google Scholar] [CrossRef]
- W.A. Barnett. Getting It Wrong: How Faulty Monetary Statistics Undermine the Fed, the Financial System, and the Economy. Boston, MA, USA: MIT Press, 2012. [Google Scholar]
- W.A. Barnett, and A. Serletis. Functional Structure Inference. Cambridge, MA, USA: Elsevier, 2007. [Google Scholar]
- R.M. Alkhareif, and W.A. Barnett. “Divisia Monetary Aggregates for the GCC Countries.” In Recent Developments in Alternative Finance: Empirical Assessments and Economic Implications. Edited by W.A. Barnett and F. Jawadi. West Yorkshire, UK: Emerald Press, 2012, pp. 1–37. [Google Scholar]
- W.A. Barnett. “The Microeconomic Theory of Monetary Aggregation.” In New Approaches to Monetary Economics. Cambridge, UK: Cambridge University Press, 1987. [Google Scholar]
- A. Serletis, and P. Gogas. “Divisia Monetary Aggregates, the Great Ratios, and Classical Money Demand Functions.” J. Money Credit Bank. 46 (2014): 229–241. [Google Scholar] [CrossRef]
- R.M. Alkhareif, and W.A. Barnett. Advances in Monetary Policy Design. Newcastle upon Tyne, UK: Cambridge Scholars Publishing, 2013. [Google Scholar]
- W.E. Diewert. “Exact and Superlative Index Numbers.” J. Econom. 4 (1976): 115–145. [Google Scholar] [CrossRef]
- W.A. Barnett. “The Optimal Level of Monetary Aggregation.” J. Money Credit Bank. 14 (1982): 687–710. [Google Scholar] [CrossRef]
- R.M. Alkhareif. Essays in Divisia Monetary Aggregation: Applications to the Gulf Monetary Union. Ann Arbor, MI, USA: ProQuest Dissertation Publishing, 2013. [Google Scholar]
- B. Klein. “Competitive Interest Payments on Bank Deposits and the Long-Run Demand for Money.” Am. Econ. Rev. 64 (1974): 931–949. [Google Scholar]
- R. Startz. “Implicit Interest on Demand Deposits.” J. Monet. Econ. 5 (1979): 515–534. [Google Scholar] [CrossRef]
- H. Theil. Economics and Information Theory. Amsterdam, The Netherlands: Elsevier, 1967. [Google Scholar]
- W.A. Barnett. “The Joint Allocation of Leisure and Goods Expenditure.” Econometrica 47 (1979): 539–563. [Google Scholar] [CrossRef]
- 1Divisia indexes were proposed and analyzed formally by François Divisia in 1926, and discussed in related 1925 and 1928 works. Barnett linked aggregation theory to monetary economics and accordingly produced the Divisia monetary indexes. See Barnett [3,4] and Barnett and Serletis [5] for more details.
- 2While aggregation and index number theory are highly developed in the fields of consumer demand theory and production theory, they were not applied to monetary theory until Barnett [1,2] derived the correct formula of the price (user cost) of monetary assets and thereby produced a connection between monetary economics and index number theory. Alkhareif and Barnett [6] provide a formal derivation of the user cost formula.
- 3BoE has published Divisia money series since 1993. The Center for Financial Stability (CFS) in New York City provides a directory on the literature pertaining to Divisia monetary aggregations for over 40 countries throughout the world. For more information on Divisia monetary aggregates, visit the CFS website at www.centerforfinancialstability.org/amfm.php.
- 4The complete dataset used in this study is available as an Excel workbook. For more information, contact the authors at: alkhareif@gmail.com.
- 5For a more detailed discussion of aggregation theory and statistical index number theory, see Barnett [11].
- 6Statistical index number theory offers parameter-free approximations to aggregator functions.
- 7Some papers impute an implicit rate of return on demand deposits (see, e.g., Klein [13] and Startz [14]). Nevertheless, given the fact that there is neither public data nor solid evidence on such an imputation, we exclude implied interest rates on demand deposits. In addition, Saudis are relatively insensitive to interest rates paid on their personal banking deposits, as a result of religious and cultural reasons. The ubiquitous prevalence of gold and platinum debit cards, which entitle the holders to special services at the bank branches, suggests that Saudis prefer these services in lieu of receiving interest on their demand deposits. It should be noted that there are no explicit legal prohibitions to the paying of interest.
- 8Perfect substitutability among assets exists, if and only if, all assets within an aggregate offer the same rate of return.
- 9The stock market decline in 2006 was the case of a classical asset bubble caused by a flood of oil money. The boom-bust cycle was exacerbated by retail investors who drove the average P/E ratio to a value higher than 50 at one point. The 2008 spike of the Divisia growth rate was likely driven by the high oil prices that prevailed in early to mid-2008.
- 10See Alkhareif and Barnett [9] for a more complete discussion pertaining to the user-cost subject.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barnett, W.A.; Alkhareif, R.M. Modern and Traditional Methods for Measuring Money Supply: The Case of Saudi Arabia. Int. J. Financial Stud. 2015, 3, 49-55. https://doi.org/10.3390/ijfs3010049
Barnett WA, Alkhareif RM. Modern and Traditional Methods for Measuring Money Supply: The Case of Saudi Arabia. International Journal of Financial Studies. 2015; 3(1):49-55. https://doi.org/10.3390/ijfs3010049
Chicago/Turabian StyleBarnett, William A., and Ryadh M. Alkhareif. 2015. "Modern and Traditional Methods for Measuring Money Supply: The Case of Saudi Arabia" International Journal of Financial Studies 3, no. 1: 49-55. https://doi.org/10.3390/ijfs3010049
APA StyleBarnett, W. A., & Alkhareif, R. M. (2015). Modern and Traditional Methods for Measuring Money Supply: The Case of Saudi Arabia. International Journal of Financial Studies, 3(1), 49-55. https://doi.org/10.3390/ijfs3010049





