Abstract
The global economy frequently experiences cycles of rapid growth followed by abrupt crashes, challenging economists and analysts in forecasting and risk management. Crashes like the dot-com bubble crash and the 2008 global financial crisis caused huge disruptions to the world economy. These crashes have been found to display somewhat similar characteristics, like rapid price inflation and speculation, followed by collapse. In search of these underlying patterns, the Log-Periodic Power-Law (LPPL) model has emerged as a promising framework, capable of capturing self-reinforcing dynamics and log-periodic oscillations. However, while log-periodic structures have been tested in developed and stable markets, they lack validation in volatile and developing markets. This study investigates the applicability of the LPPL framework for modeling financial crashes in the Brazilian stock market, which serves as a representative case of a volatile market, particularly through the Bovespa Index (IBOVESPA). In this study, daily data spanning 1993 to 2025 is analyzed to model pre-crash oscillations and speculative bubbles for five major market crashes. In addition to the traditional LPPL model, autoregressive residual analysis is incorporated to account for market noise and improve predictive accuracy. The results demonstrate that the enhanced LPPL model effectively captures pre-crash oscillations and critical transitions, with low error metrics. Eigenstructure analysis of the Hessian matrices highlights stiff and sloppy parameters, emphasizing the pivotal role of critical time and frequency parameters. Overall, these findings validate LPPL-based nonlinear modeling as an effective approach for anticipating speculative bubbles and crash dynamics in complex financial systems.
1. Introduction
Financial markets have always attracted the attention of researchers and investors due to their complex and dynamic nature, along with their potential for profit (Sarda et al., 2010, 2019). With proper knowledge and understanding, investors can book profits at prosperous times. However, in contrast to making profits, they may incur losses during market crashes. These market crashes are abrupt and can occur due to numerous reasons. Nevertheless, there may be structural consistency among all the crashes that can provide useful information about an impending crash. Hence, there is a need to generalize this structural consistency by finding enough evidence in the context of different markets and crashes. Researchers suggests some that precursory patterns, aftershock signals, and distinctive oscillations occur during crash periods (Sornette et al., 1995). The major reason behind crashes is the bursting of market bubbles that are formed due to various reasons, including herding behavior (Investopedia, 2022; Sarda et al., 2010; Sornette & Johansen, 1997), positive feedback loops, and easy credit. These factors lead to overpricing of stocks to a value much more than their original value (Investopedia, 2022). Figure 1 highlights various reasons for bubble formation and bubble bursting. Eventually, when there is a market correction, these bubbles burst, resulting in a sudden drop in the value of stock and asset prices (Jacobsson, 2009). These devaluations result in substantial losses to investors. This graphical interpretation of the crashes has been linked with a specific type of oscillation known as log-periodic oscillations (Sornette & Johansen, 2001). The term log-periodicity is a mathematical concept that is particularly useful in the study of financial markets during crash conditions (Jacobsson, 2009; Sarda et al., 2010). Price fluctuations at the time of market crashes exhibit log-periodic oscillations, which are characterized by an increase in frequency along with a decrease in amplitude (Brée et al., 2013; Dai et al., 2018).
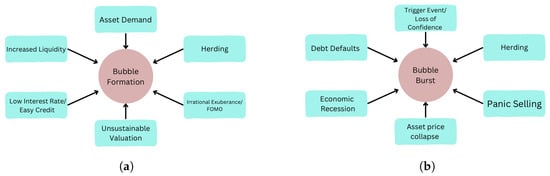
Figure 1.
Factors driving the formation and collapse of financial bubbles in stock markets. (a) Factors driving bubble formation; (b) factors driving bubble collapse.
Various markets around the world have suffered numerous financial crashes in recent history. Some of them were significant enough to affect the whole world at once. For instance, the 2008 global financial crisis, triggered by the collapse of the US housing bubble and the subsequent failure of major financial institutions, sent shockwaves across the global markets (Baily et al., 2008). Many researchers have studied this crash and have found log-periodic structures prior to the 2008 crash (Brée et al., 2013; Clark, 2004). Similarly, researchers have investigated major crashes like the 1929 and the 1987 crashes, which are the largest financial crashes in history (Sornette & Johansen, 1997). Moreover, the applicability of log-periodicity has been tested over crashes from developed and steady markets like China and the US (Jiang et al., 2010; Zhou & Sornette, 2003). Researchers have sought to improve the traditional LPPL model by incorporating various theories and optimization techniques. For instance, a modified LPPL model was proposed, using mathematical physics, behavioral finance, and economic theories (Jiang et al., 2010). It was able to predict the market crashes in China between 2005 and 2009. Moreover, a conclusion was drawn that speculative bubbles precede market crashes and that these bubbles are characterized by power-law acceleration and log-periodic oscillations (Sarda et al., 2021, 2010). More attempts to refine the model include the proposal by Geraskin and Fantazzini (2013), where they proposed alternative methodologies and diagnostic tests to model real-time financial bubbles (Geraskin & Fantazzini, 2013). On the other hand, Jacobsson (2009) suggested that a Genetic algorithm should be used to estimate the parameters of the LPPL model and demonstrated its predictive capabilities for the 2008 financial crisis (Jacobsson, 2009). In addition, Vandewalle et al. (1999) introduced an envelope function technique to visualize log-periodic crash patterns. Furthermore, Oświęcimka et al. (2010) suggested a Weierstrass-type function that allows predictive modeling of crashes using the oscillations that precede the crash. In addition, Dos Santos Maciel (2023) established a correlation between lower efficiency and higher predictability of the stock market, further contributing to the potential of log-periodic models. Chang and Feigenbaum (2008) found log-periodic variations in S&P 500 returns but noted some inconsistencies with the Johansen–Ledoit–Sornette (JLS) model. Chang and Feigenbaum (2006) later proposed a refinement by including Bayesian testing of log-periodicity. Further improvements include alternative methodologies for parameter tuning by Cajueiro et al. (2009), and application of machine learning models like Lasso, Elastic Net, and Ridge regression for crash prediction by Gupta et al. (2024).
Several studies have also explored the applicability and predictive power of log-periodic models in the financial markets. Matsushita et al. (2006) demonstrated that one and two harmonic equations can model bubbles but fail in the case of anti-bubbles. Their suggested improvement was the use of three harmonic equations that can effectively fit both. Two and three harmonic equations add another set of oscillation component in the main LPPL function. Other advancements in the prediction models include the proposition of nonlinear models, particularly the Log-Periodic Gaussian processes by Demirer et al. (2024), which effectively anticipated downward-moving trends. Similarly, Gupta et al. (2025) emphasized the strong predictability of volatility across markets, including the influence of positive bubbles and feedback loops among G7 stock market volatility. Furthermore, Burks et al. (2021) demonstrated that the LPPL model effectively captures the lifecycle of asset bubbles, highlighting its applicability in detecting volatility-driven market anomalies. Other researchers have tried to expand the applicability of LPPL beyond the equity markets. Wosnitza and Denz (2013) found LPPL patterns to be evident in Credit Default Swap (CDS) spreads during the late 2000s crisis. They supported the hypothesis of discrete scale variance that governs financial markets. Moreover, Ghosh et al. (2022) applied the LPPL model to carbon credit markets during the COVID-19 pandemic, finding that their growth patterns consistently followed log-periodic structures indicative of social bubble behavior. Furthermore, Clark (2004) confirmed that the Aaa and Baa spreads (United States corporate bond spread) also adhere to log-periodicity. In addition, Wosnitza and Sornette (2015) further strengthened the above adherence by confirming the appearance of LPPL patterns in credit risk data. However, log-periodic structures were found to be ineffective in the case of Indian realty markets, calling into question the applicability of log-periodicity in certain situations (Sarda et al., 2019). Additionally, Brée et al. (2013) illustrated that LPPL functions are difficult to fit into time series data.
In order to validate or generalize the applicability of log-periodicity over volatile and unsteady markets, there is a need to test the pre-crash signals over such a market. Among developing countries, Brazil has been selected as the country of interest for this study. Being the largest economy in South America and one of the largest emerging markets in the world, the country has a mixed economy that includes manufacturing, mining, tourism, agriculture, and services (Gabriel et al., 2025). Brazil is also a part of an intergovernmental organization known as BRICS (Brazil, Russia, India, China, and South Africa). This highlights the role of this country in the global economy. This study will use the Bovespa Index (IBOVESPA), a benchmark of the Brazilian stock market, which accounts for the most liquid and traded stocks in the country (Castro et al., 2018). It serves as a key indicator of investor sentiment and economic health in Brazil. However, the country faces challenges such as economic inequality, inflation, and political instability, which impact its economic growth, making it essential to study bubbles and crashes present in the market. Some studies have been conducted on the Brazilian stock market. Nyasha and Odhiambo (2013) talks about the origin of and reforms introduced in the Brazilian stock market. They also elaborate on BM&FBOVESPA (the main stock exchange in Brazil, formed by the merger of BM&F and BOVESPA), along with the formation of regulatory bodies and newly amended laws, which lead to significant development of the market. Other studies, like Fondaik et al. (2024), have investigated the impact of COVID-19 on Brazilian stocks, revealing that socially responsible and less leveraged companies faced fewer negative impacts. Zhang et al. (2024) analyzed herding behavior in the BRICS stock market, showing an increase during market stress, challenging the benefits of diversification.
Despite extensive research on financial markets, the applicability and predictive power of LPPL modeling in cases of emerging markets remain uncertain. Since Brazil is an emerging market and a dynamic economy compared to developed markets, the application of log-periodicity in the Bovespa index needs thorough investigation. This study aims to investigate the applicability of log-periodicity to the Bovespa index of the Brazilian stock market. After going through various optimization techniques and models in previous studies, like Chang and Feigenbaum (2006); Jacobsson (2009); Jiang et al. (2010), this research seeks to address the following questions: (1) How can the Log-Periodic Power-Law (LPPL) model, when integrated with autoregressive residual analysis, enhance the understanding of financial crash dynamics in emerging markets like Brazil? (2) What insights into market sensitivity and parameter interdependence can be drawn from the eigenstructure analysis of the LPPL model applied to major Brazilian stock market crashes? Table 1 summarizes the main findings of previous research studies.

Table 1.
Summary of literature review.
This paper is structured as follows: The current section discuss the literature review, followed by a discussion of log-periodicity as a measure of crash predictability. The subsequent section gives an overview of the data used, followed by the methodology adopted for the analysis, the empirical findings, and the eigenvalue analysis of different crashes in the Brazilian stock market. The final section presents our conclusions, discusses the implications of the results, and outlines directions for future research.
2. Data and Research Methods
2.1. Data
For this research, a dataset was collected comprising daily observations of the Bovespa index, spanning from 27 April 1993 to 6 March 2025. Based on public availability, the historical data was downloaded from Yahoo Finance for the above-mentioned dates. The dataset contains a total of 7889 entries, including various indicators such as Date, Open, Close, High, Low, and Volume traded. Table 2 provides the first and last five rows of the dataset used for the research work. Non-trading days, including weekends and official public holidays, were naturally excluded from the dataset as no market activity occurs on these days.

Table 2.
Historical data of Bovespa Index, including price and trading volume.
Figure 2 illustrates a time series plot of the daily closing prices over the span of 32 years of the Bovespa index. As seen in the figure, the index exhibits a nonlinear upward trend across the given period, including some downturns, depicting crashes. These visible drops correspond to major financial crashes or periods of economic stress, and form the empirical foundation for subsequent modeling and analysis using the LPPL framework.
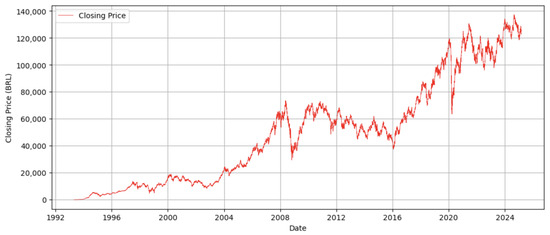
Figure 2.
Daily closing prices of the Bovespa Index (IBOVESPA) from 1993 to 2025.
2.2. LPPL Model
Log-periodic patterns signify self-similar oscillatory structures that scale according to the logarithmic function (Sarda et al., 2010). In terms of finance, it is attributed to the LPPL model, which fundamentally describes asset price dynamics preceding a crash (Geraskin & Fantazzini, 2013). It describes how market prices accelerate super-exponentially, followed by a specific oscillatory pattern that is observed during negative price fluctuations, and follows a power-law behavior, and can be seen as a warning signal of an impending crash (Sornette & Johansen, 2001). The LPPL model assumes two fundamental steps: there is (1) a super-exponential growth phase which is driven by investor behavior, and (2) a market downturn marked by log-periodic oscillations with increasing frequency and decreasing amplitude. The LPPL model can be mathematically expressed by the following expression, as given by Sornette and Johansen (2001):
Equation (1) represents the LPPL formula, which is known to have the ability to model financial bubbles and their subsequent crashes. Sornette and Johansen (2001) discusses the various parts and parameters involved in the LPPL formula. In a single expression, this formula captures the above-mentioned fundamental assumptions of the LPPL model. The initial part of the formula, , captures the power-law acceleration prior to the crash, also known as the super-exponential growth. The second part of the formula, the log-periodic component, , is responsible for decorating the power-law trend, with oscillations that become more frequent as t reaches . is the predicted price of the asset at time t. Here, A denotes the baseline price level at the critical time, while B controls the magnitude of power-law growth. The parameter represents the critical time at which the bubble is expected to burst. Within this formula, the power-law exponent, controls the rate of growth of the price. The coefficient C represents the amplitudes of the oscillations, while is the angular frequency of the log-periodic oscillations. Finally, defines the phase shift of these oscillations. In essence, the LPPL model uses these components to characterize a bubble’s trajectory as an accelerating trend followed by rapid oscillations, providing a framework for identifying unsustainable market behavior. This model has immense abilities to capture investor behavior and herding effects, which result in price distortions (Sarda et al., 2010). Despite challenges in their practical application, the continued refinement of log-periodic models within a nonlinear stochastic framework, along with integration of other prediction and statistical approaches, holds significant value for risk assessment and market forecasting (Brée et al., 2013; Chang & Feigenbaum, 2006; Geraskin & Fantazzini, 2013).
However, due to computational constraints and data availability limitations, this study does not include a comparative analysis against alternative crash prediction models (GARCH, ARIMA, and LSTM neural networks) or formal cross-validation procedures. Comparative studies in the crash prediction literature reveal mixed performance across different model types. Sornette and Zhou (2006) demonstrated that LPPL models outperformed traditional econometric approaches in identifying bubble periods, while Geraskin and Fantazzini (2013) noted that LPPL effectiveness varies significantly with market conditions. Nevertheless, the absence of direct benchmarking in this study prevents quantitative assessment of the performance of the LPPL model over alternative approaches for Brazilian market crash prediction.
2.3. Modeling Process
The methodology of this research follows a quantitative approach under a nonlinear stochastic framework to assess the applicability of the LPPL model in modeling financial crashes in the Brazilian stock market. The application of LPPL in emerging markets builds on earlier empirical studies that have tested the model in emerging-market contexts. Prior work has shown that LPPL structures can be identified in Indian stock market crashes (Sarda et al., 2014, 2010), as well as in the South African market during the 2003–2006 speculative bubble (Zhou & Sornette, 2009). More recently, Ghosh et al. (2021) provided evidence that the LPPL framework captures the nonlinear dynamics of financial bubbles in an emerging-market setting. On the other hand, only a few studies, such as Sarda et al. (2019), suggest that LPPL is not applicable in contexts like the Indian realty market. Therefore, the LPPL model can offer meaningful explanatory and predictive insights in markets that share structural similarities with Brazil, thereby supporting its adoption for the present analysis. The primary goal is to identify and understand pre-crash dynamics through data-driven modeling and time series analysis. Although Brée et al. (2013) states that time series modeling is inherently complex, its application is essential in studying speculative bubbles and anticipating market downturns. The study uses Python-3.12 as the primary computational tool and programming framework, integrating libraries such as Pandas and NumPy for data handling, Matplotlib-3.8.4 and Seaborn-0.13.2 for visualization, SciPy-1.13.1 for optimization, and Statsmodels for time series analysis. The first step involves data preprocessing, where missing values are handled, and time formats are standardized. A logarithmic transformation is applied to normalize price distributions:
In the above equation, denotes the natural logarithm of the closing price of a financial asset at time t, where represents the actual closing price of the asset at time t. Following this, Exploratory Data Analysis (EDA) is conducted in order to analyze the features present in the data. This includes plotting the log-transformed price series, rolling means, correlation heatmap, and scatter plot. These steps are foundational in identifying preliminary patterns that may resemble LPPL behavior. Historical financial data is analyzed in order to identify five major crash periods in Brazil:
- The 1999 Brazil currency crisis;
- The 2008 global financial crisis;
- The 2015 Brazilian economic recession;
- The 2020 COVID-19 crash;
- The 2022 presidential election volatility.
These periods serve as experimental windows for LPPL fitting and validation. The LPPL model is fitted using a constrained nonlinear least-squares approach, minimizing the residual sum of squares between observed prices and the LPPL fit. The objective function is
In this equation, RSS stands for the residual sum of squares, which measures the total squared difference between the observed and predicted values. Specifically, denotes the actual price of the asset at time t, while represents the price predicted by the model at the same time. To ensure the stability and interpretability of the LPPL model, parameter bounds are added based on empirical findings in prior studies. The power-law exponent is constrained within the range , which has been shown to be stable across various market crashes by Sornette and Johansen (2001). The oscillation amplitude C is bounded between and 1 to maintain numerical stability and to reduce the risk of overfitting due to excessive oscillatory behavior (Geraskin & Fantazzini, 2013). Additionally, the angular frequency is typically observed to be in the range of 6 to 15 in historical bubbles (Geraskin & Fantazzini, 2013).
Post-fitting, the residuals , which are defined as the differences between actual and predicted prices, are extracted using Equation (4):
To account for short-term dependencies in the residuals, an autoregressive model of order 5 (AR(5)) is fitted using the AutoReg module in Statsmodels (Seabold & Perktold, 2010). The AR-based residuals are then added back to the LPPL predictions to refine the overall model fit and enhance short-term accuracy. The AR(5) order was chosen to capture potential dependencies in Brazilian market residuals, representing a compromise between model complexity and computational feasibility. This specification was not validated through formal model selection criteria due to computational constraints, which limits the optimality of the chosen order.
In this equation, represents the residual at time t, modeled as a linear combination of its past five values to , with corresponding coefficients to , and an added white noise error term . Model accuracy is assessed using standard error metrics such as the Mean Absolute Error (MAE), Mean-Squared Error (MSE) and Root-Mean-Squared Error (RMSE):
In these equations, n represents the total number of data points used. The variable i acts as the index for each observation, running from 1 to n. denotes the actual observed value at the i-th position, while indicates the corresponding predicted value produced by the model. To understand model dependency over the parameters, the Hessian matrix of second-order partial derivatives of the loss function is calculated. The eigenvalues and eigenvectors of this matrix are then analyzed to interpret the parameter interdependencies and model stability. This methodology is visually summarized in Figure 3, illustrating an overview of the progression from raw data to predictive modeling and interpretation.
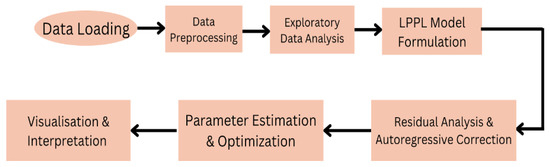
Figure 3.
Schematic overview of the progression from raw data to predictive modeling and interpretation.
Additionally, this study focuses exclusively on five crash episodes without systematic testing during calm market periods. The analysis does not validate the model’s ability to avoid false positive signals during conditions when crashes are not imminent. Due to computational limitations, systematic robustness testing across non-crisis periods was not implemented, representing a methodological constraint that limits assessment of the model’s discriminatory power.
3. Results and Discussion
3.1. Graphical Analysis
The EDA resulted in two plots, including a heatmap showing the correlation among the variables and a scatter plot visualizing the relation between closing price and trading volume. Figure 4a highlights the correlation between the data fields and indicates that the fields Close, High, Low, and Open have strong positive correlations (close to 1.00) with each other. This reflects that they are closely related to each other in the dataset. The calculated variables, Log_Close and Rolling_Close, also show high correlations with other variables. On the other hand, Volume shows a very weak correlation with all the other features, suggesting that it is not linearly related to any other feature. This suggests that price features are highly interdependent, whereas volume is independent. Furthermore, Figure 4b reinforces the deduction from the heatmap. The scatter plot shows a wide distribution of points, which indicates that there is no linear relationship between trading volume and closing price. There are instances where some data points have extremely high trading volumes, but they do not correspond to higher or lower closing prices. These data points are suggested to be potential outliers or periods of unusual market activity, highlighting other intangible factors. These results imply that adding all the price-related features would not be necessary due to their high correlation. Although Volume does not have a high correlation with the other factors, it can help to understand market sentiment and volatility.
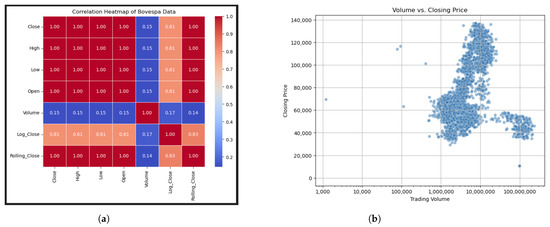
Figure 4.
Correlation heatmap and scatter plot illustrating relationships between variables and feature selection. (a) Heatmap. (b) Volume over closing price.
The initial fitting (Figure 5) attempt produced an almost horizontal line that represents an unreliable fit, likely converging to a local minimum, and failing to identify the correct parameters required to represent the crashes. After applying parameter bounds, optimizing the fit, and adjusting the model by incorporating AR(5) residuals, Figure 6a was obtained. It demonstrates the ability of the model to track noisy financial time series. The green curve represents the LPPL signal with AR(5) noise, while the yellow line represents the LPPL fit to this series. On the other hand, Figure 6b presents the comparison between the predicted and actual crash dates, which overlap with each other. It shows five major financial crashes in the Brazilian stock market between 1993 and 2025. The dotted black lines indicate actual crash dates, whereas the dashed yellow lines are coincident with the black ones. The close alignment between the lines suggests that the LPPL model, when used with residual modeling, can effectively trace financial crashes.
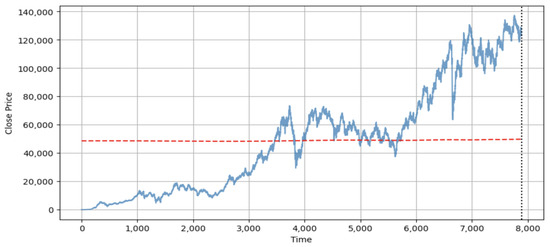
Figure 5.
Initial LPPL model fit to the closing price time series, converging at a local minimum.
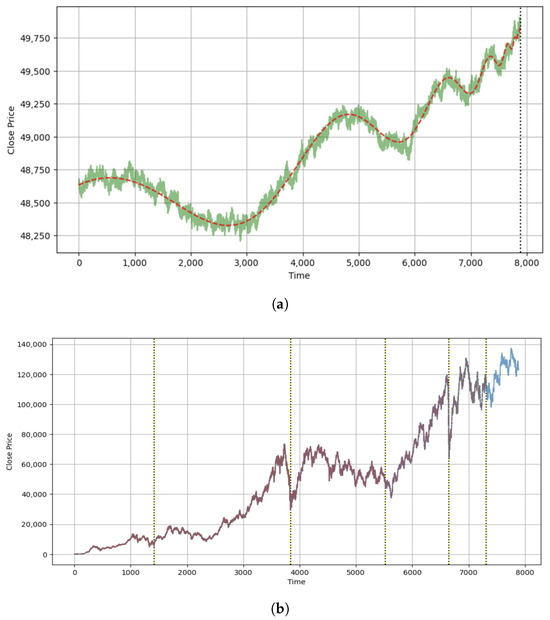
Figure 6.
(a) Fitted LPPL model applied to the Bovespa index with AR(5) noise added to the residuals, and (b) The LPPL model with AR(5) residuals, showing fitted regimes and predicted crash points.
3.2. Eigenstructure Analysis
The examination of the eigenvalues and eigenvectors of the Hessian matrix provides a structural view into the stability and identifiability of LPPL parameters. Specifically, eigenvalue magnitudes help distinguish between stiff directions, where small parameter changes strongly affect model behavior, and sloppy directions, where many parameter combinations yield similar fits (Brée et al., 2013). This analysis not only quantifies parameter sensitivity, but also clarifies the extent to which crash time () and oscillatory components can be identified. Such an approach is therefore essential to evaluate the reliability of the LPPL model.
After finding the optimal fit, the parameters and the eigenstructures for each of the five crashes are found. The following tables represent the eigenvalues and eigenvectors, which are calculated using the Hessian matrix from predictions of past crashes. Table 3 indicates the eigenvalues and eigenvectors of the first crash of 1999.

Table 3.
Eigenvalues () corresponding to eigenvectors in the 1999 crash.
The largest eigenvalue in Table 3 is , while the smallest is , which represents a separation of 13 orders of magnitude. As per Brée et al. (2013); Brown and Sethna (2003), this confirms the presence of sloppiness among the parameters. Brée et al. (2013) suggests that parameter combinations associated with large eigenvalues are referred to as stiff, meaning that even small changes in these combinations significantly affect the function. In contrast, combinations linked to small eigenvalues are called sloppy, as variations in these have little impact on the value of the function. Based on the above chronology, the expected crash time parameter () appears in multiple eigenvectors, particularly in the most sloppy directions, indicating its presence in directions where changes in parameters cause very little change in model behavior. In particular, the magnitude of the () component is consistently very small in the eigenvectors associated with the smaller eigenvalues, typically the last few rows of the table. In the eigenvectors associated with the smallest eigenvalues, representing the sloppiest directions in the parameter space, () is not in isolation but appears in combination with other parameters, particularly with and (Gutenkunst et al., 2007). This indicates that accurately estimating the crash time is difficult due to its high correlation with (log-periodic frequency) and (phase shift). As documented by Brée et al. (2013), exhibits high interdependency with angular frequency () and phase shift (), creating parameter “sloppiness”. This structural dependency makes the least stable parameter and compromises the precision of crash timing predictions. This challenge reflects a fundamental limitation of the LPPL model, as the steep decay of the eigenvalues confirms that only a small subset of parameter combinations drive model sensitivity. While advanced methods such as Bayesian calibration, credible interval estimation, and dimension-reduction approaches like PCA and sensitivity analysis have been proposed to address this issue (Chang & Feigenbaum, 2008; Geraskin & Fantazzini, 2013), their computational requirements place them beyond the scope of the present study. Advanced uncertainty quantification techniques (bootstrap, Monte Carlo) were similarly not implemented due to computational constraints. Recognizing this limitation is crucial, since the inherent uncertainty in parameter estimation, most notably in , translates into reduced confidence in both the predictive accuracy and structural reliability of LPPL-based crash modeling.
Parameters A and B add minor adjustments to the flat regions of the parameter space. Other parameters, like C, and , moderately contribute across various modes and are involved in controlling oscillatory behavior (Sornette, 2003).
The tables presented above summarize the eigenstructures of the major financial crashes in the Brazilian stock market for the crashes of 2008, 2015, 2020, and 2022. Table 4 shows the eigenstructures of the 2008 crash in the Brazilian market, which was triggered by the global financial crisis. Table 5 illustrates the eigenstructure associated with the Brazilian economic recession of 2015. Furthermore, Table 6 presents the corresponding analysis for the 2020 crash, which resulted from the COVID-19 recession. Lastly, Table 7 highlights the eigenstructures of the 2022 crash, driven by market volatility during the Brazilian presidential elections. They reveal strikingly consistent patterns that align with the theoretical structure of the LPPL model (Brée et al., 2013; Sornette, 2003). The eigenstructure of these parameter spaces varies dramatically in different directions, revealing a highly anisotropic curvature structure. The eigenvalue spectrums highlight sharp decay after the first two eigenvalues, indicating that the sensitivity of the system is mainly governed by two or at most three directions, and that the remaining directions exhibit negligible curvature.

Table 4.
Eigenvalues () corresponding to eigenvectors in 2008 crash.

Table 5.
Eigenvalues () corresponding to eigenvectors in 2015 crash.

Table 6.
Eigenvalues () corresponding to eigenvectors in 2020 crash.

Table 7.
Eigenvalues () corresponding to eigenvectors in the 2022 crash.
Across all crashes, a common observation is the presence of a leading eigenvalue (of the order ), which is significantly higher than the subsequent eigenvalues. This steep decline indicates that the model’s sensitivity is governed primarily by one or two stiff directions in parameter space, while the remaining directions are “sloppy”, contributing marginally to the model’s output (Brée et al., 2013). In financial terms, this reflects strong collective market behavior, also known as herding, which is a key feature of bubble dynamics of the LPPL framework, followed by a sharp decay in the following eigenvalues (Sornette, 2003). The parameters A (baseline price level) and B (magnitude of the power-law component) typically exhibit minimal values in the sloppier directions, but show significant contributions in the dominant eigenvector. This transition reflects the increasing dominance of the power-law term, as the system approaches the critical crash phase, a hallmark of LPPL-based dynamics (Sornette, 2003).
The eigenvectors associated with the dominant eigenvalues (i.e., the stiff directions) highlight how sensitive the LPPL model is to certain parameter combinations. In particular, the component corresponding to in these eigenvectors often has a relatively large magnitude, implying that variations in substantially influence the model’s output. This reinforces the theoretical role of in the LPPL model, where ensures power-law acceleration characteristic of speculative bubbles (Sornette, 2003). While eigenvector components are not constrained by model parameter bounds and do not represent parameter values directly, their relative magnitudes indicate the importance of the parameters in shaping the model’s dynamics (Transtrum et al., 2011). Additionally, the oscillatory amplitude C frequently appears with negative or near-zero components in the eigenvectors. This reflects the need for phase adjustment in the oscillatory term (Sornette & Zhou, 2006). The value of the angular log-frequency is often found to be close to 1 in the eigenvector components of stiff directions, consistent with long-period oscillations that emerge before crashes, a hallmark of log-periodic structures (Huang et al., 2000). Lastly, the components associated with the phase parameter remain small in most dominant eigenvectors, indicating that it has less effect on the LPPL function compared to stiff parameters (Brée et al., 2013).
3.3. Parameter Analysis
Table 8 presents the LPPL parameters for the five significant market crashes in the Brazilian stock market, offering deep insights into the evolution of financial bubbles and their impending breakdowns over time. The parameter A (baseline price) clearly exhibits an increasing trend, with its value increasing from 5751.09 in 1999 to 44,242.48 in 2022, highlighting the overall growth of market capitalization over this period of time. Moreover, the parameter B remains negative throughout all crashes, which aligns with the theory of market correction after bubble formation. Parameter B remains consistently negative across all crash periods (ranging from −927.87 to −986.46), which aligns with theoretical expectations that B < 0 highlights super-exponential growth (Sornette, 2003). The power-law exponent , associated with the acceleration of prices before a crash, increases from 0.1321 in 1999 to 0.2725 in 2022. This indicates a rising intensity of speculative growth and suggests that recent market bubbles escalate more sharply in their final phases (Sornette & Johansen, 1997).

Table 8.
Crash years and corresponding parameters.
The parameter C, representing the amplitude of log-periodic oscillations, fluctuates across crashes, reflecting varying market sentiments and investor behavior during different periods (Sornette et al., 1995). Meanwhile, the angular frequency (), which governs the frequency of oscillations, remains stable across all crashes, ranging between 9 and 11. This consistency indicates that there is a structural regularity in the speculation dynamics regardless of the crash year (Sornette, 2003). Finally, the phase parameter , which captures the alignment of log-periodic oscillations, exhibits minor variation, ranging from −0.0357 to 0.1520. This suggests that while the frequency of oscillations is stable, the exact positioning of the crash within those oscillations differs, potentially due to differing external triggers or market structures (Johansen & Sornette, 2001). Overall, these results not only validate the theoretical explanations of the LPPL model, but also highlight its practical applicability to capture pre-crash dynamics in the context of the Brazilian stock market, which is an emerging market. The presence of dominant eigenvalues, stable power-law exponents, clear log-periodic oscillations, and the interdependency of critical parameters across multiple crashes emphasize the robustness of the LPPL model in modeling financial bubbles and crashes. In addition to this, parameter trends highlight that while certain characteristics, such as oscillation frequency, have remained stable, others, such as bubble amplitude and growth acceleration, have intensified over time, emphasizing the increasing complexity and volatility of modern financial markets.
While the fitted parameters capture the dynamics of the studied crashes, it is important to note that the present analysis does not include formal measures of uncertainty, such as confidence intervals or credible regions for parameter estimates. As a result, the statistical significance of the numerical results cannot be formally assessed due to infeasible computational requirements and unavailability of data. In addition to its predictive application, the LPPL framework has implications for preventive market regulation. Since parameter sloppiness and instability reduce the reliability of precise crash timing forecasts, regulators should not rely solely on point predictions, but also monitor early-warning indicators of accelerating log-periodic oscillations.
3.4. Limitations
The application of the Log-Periodic Power-Law (LPPL) framework to financial crash dynamics is constrained by significant methodological limitations, primarily centered on parameter sloppiness and the absence of uncertainty quantification. The LPPL model suffers from structural dependency where multiple parameter combinations can yield nearly identical fits, an issue confirmed by the eigenstructure analysis, which shows that the critical time () is highly correlated with oscillatory parameters ( and ). This lack of unique identifiability compromises the stability of parameter estimation and calls into question the precision of crash timing predictions.
Additionally, the study’s omission of formal uncertainty measures, such as confidence intervals or credible regions, prevents a formal assessment of the statistical significance and reliability of the parameter estimates. Furthermore, the exclusion of robustness checks like bootstrapping and Monte Carlo simulations, mainly due to computational constraints, increases the risk of overfitting and limits the generalizability of findings across different market regimes.
Another important limitation is that testing took place during tranquil market periods. Since the current analysis focuses on historical crash periods, it does not account for simulations in calm periods using artificial data. In addition, the residual noise component was modeled using an AR(5) process chosen on empirical grounds rather than through formal selection criteria, which limits the optimality of our results and highlights the need for future validation using information-theoretic measures or alternative stochastic models. Taken together, these constraints collectively reduce the interpretative power and predictive reliability of the LPPL analysis, underscoring the necessity for future research to incorporate advanced techniques like Bayesian calibration and dimension-reduction approaches to enhance model robustness.
Lastly, although studies in the literature have tested the LPPL model in emerging markets like India and South Africa and found it applicable in most cases, a few cases have been unsuccessful.
4. Conclusions
This research successfully demonstrates the applicability of the Log-Periodic Power-Law (LPPL) model to financial crashes in a developing market like the Brazilian stock market. By analyzing five major crashes in the Bovespa index data, the presence of log-periodic structures and pre-crash oscillations is validated. The integration of AR(5) residual analysis strengthens the capacity of the model by capturing short-term fluctuations, offering a more refined understanding of market behavior. The eigenstructures derived from the Hessian matrices within our nonlinear stochastic framework reveal the influence of various parameters on the model, especially , B, and , in capturing market behavior in the pre-crash phase. The presence of herding behavior is evident in all crashes, as indicated by the significantly greater value of the largest eigenvalue () compared to the others. The consistency in the parameters and B indicates that all crashes are characterized by super-exponential price growth leading to the crash. Moreover, the values of and in the crashes highlight the presence of log-periodic oscillations. , being the most sloppy parameter, is highly interdependent within the model framework. Its strong correlation with and makes independent estimation challenging and implies that the accuracy of the prediction of the timing of the crash is significantly influenced by the other two. The model accuracy metrics (MAE = 0.997, MSE = 0.994, RMSE = 0.997) further confirm the robustness of the LPPL framework in capturing market behavior. The low error values validate the performance of the model, affirming its suitability for analyzing real-world financial data, even in the context of emerging markets such as Brazil. Thus, it can be inferred that the LPPL model with AR(5) may be used to predict crashes in the Brazilian stock market. Further studies may be conducted that include systematic comparisons with old time series from BRICS countries to test and validate the model’s robustness and validity.
Author Contributions
Conceptualization, A.S., A.K.G., R.M. and V.S.; methodology, A.S., R.M. and V.S.; software, A.S., R.M. and V.S.; validation, A.S. and V.S.; formal analysis, A.S., R.M. and V.S.; investigation, A.K.G., R.M. and V.S.; resources, A.K.G., R.M. and V.S.; writing—original draft preparation, A.S., A.K.G., R.M. and V.S.; writing—review and editing, A.K.G., R.M. and V.S.; supervision, A.K.G., R.M. and V.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions of this study are included in the article. Further inquiries can be directed to the corresponding authors (A.K.G. and V.S.).
Acknowledgments
The authors express their gratitude to Manipal Academy of Higher Education, India, for providing research facilities and support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Baily, M. N., Johnson, M. S., & Litan, R. E. (2008). The origins of the financial crisis. The Brookings Institution. Available online: https://www.brookings.edu/articles/the-origins-of-the-financial-crisis/ (accessed on 17 March 2025).
- Brée, D. S., Challet, D., & Peirano, P. P. (2013). Prediction accuracy and sloppiness of log-periodic functions. Quantitative Finance, 13(2), 275–280. [Google Scholar] [CrossRef]
- Brown, K. S., & Sethna, J. P. (2003). Statistical mechanical approaches to models with many poorly known parameters. Physical Review E, 68(2), 021904. [Google Scholar] [CrossRef] [PubMed]
- Burks, N., Fadahunsi, A., & Hibbert, A. M. (2021). Financial contagion: A tale of three bubbles. Journal of Risk and Financial Management, 14(5), 229. [Google Scholar] [CrossRef]
- Cajueiro, D. O., Tabak, B. M., & Werneck, F. K. (2009). Can we predict crashes? The case of the Brazilian stock market. Physica A: Statistical Mechanics and Its Applications, 388(8), 1603–1609. [Google Scholar]
- Castro, F. H., Eid Junior, W., Santana, V. F., & Yoshinaga, C. E. (2018). Fifty-year history of the ibovespa. Revista Brasileira de Finanças, 16(2), 205–240. [Google Scholar] [CrossRef]
- Chang, G., & Feigenbaum, J. (2006). A Bayesian analysis of log-periodic precursors to financial crashes. Quantitative Finance, 6(1), 15–36. [Google Scholar] [CrossRef]
- Chang, G., & Feigenbaum, J. (2008). Detecting log-periodicity in a regime-switching model of stock returns. Quantitative Finance, 8(7), 723–738. [Google Scholar] [CrossRef]
- Clark, A. (2004). Evidence of log-periodicity in corporate bond spreads. Physica A: Statistical Mechanics and Its Applications, 338(3–4), 585–595. [Google Scholar] [CrossRef]
- Dai, B., Zhang, F., Tarzia, D., & Ahn, K. (2018). Forecasting financial crashes: Revisit to log-periodic power law. Complexity, 2018(1), 4237471. [Google Scholar] [CrossRef]
- Demirer, R., Gabauer, D., Gupta, R., & Nielsen, J. (2024). Gold, platinum and the predictability of bubbles in global stock markets. Resources Policy, 90, 104808. [Google Scholar] [CrossRef]
- Dos Santos Maciel, L. (2023). Brazilian stock-market efficiency before and after COVID-19: The roles of fractality and predictability. Global Finance Journal, 58, 100887. [Google Scholar] [CrossRef]
- Fondaik, N. P., Brum, J. A., Roma, C. M. d. S., & Iquiapaza, R. A. (2024). Brazilian stock market reaction to the COVID-19 pandemic and firm characteristics. RAM. Revista de Administração Mackenzie, 25, eRAMF240002. [Google Scholar] [CrossRef]
- Gabriel, L. F., de Santana Ribeiro, L. C., & Filho, J. F. S. (2025). Structural change and productive interdependence: An analysis for Brazil. Structural Change and Economic Dynamics, 72, 256–274. [Google Scholar] [CrossRef]
- Geraskin, P., & Fantazzini, D. (2013). Everything you always wanted to know about log-periodic power laws for bubble modeling but were afraid to ask. The European Journal of Finance, 19(5), 366–391. [Google Scholar] [CrossRef]
- Ghosh, B., Kenourgios, D., Francis, A., & Bhattacharyya, S. (2021). How well the log periodic power law works in an emerging stock market? Applied Economics Letters, 28(14), 1174–1180. [Google Scholar] [CrossRef]
- Ghosh, B., Papathanasiou, S., Dar, V., & Gravas, K. (2022). Bubble in carbon credits during COVID-19: Financial instability or positive impact (“Minsky” or “Social”)? Journal of Risk and Financial Management, 15(8), 367. [Google Scholar] [CrossRef]
- Gupta, R., Nel, J., Nielsen, J., & Pierdzioch, C. (2025). Stock market volatility and multi-scale positive and negative bubbles. The North American Journal of Economics and Finance, 75, 102300. [Google Scholar] [CrossRef]
- Gupta, R., Nielsen, J., & Pierdzioch, C. (2024). Stock market bubbles and the realized volatility of oil price returns. Energy Economics, 132, 107432. [Google Scholar] [CrossRef]
- Gutenkunst, R. N., Waterfall, J. J., Casey, F. P., Brown, K. S., Myers, C. R., & Sethna, J. P. (2007). Universally sloppy parameter sensitivities in systems biology models. PLoS Computational Biology, 3(10), e189. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y., Johansen, A., Lee, M., Saleur, H., & Sornette, D. (2000). Artifactual log-periodicity in finite size data: Relevance for earthquake aftershocks. Journal of Geophysical Research: Solid Earth, 105(B11), 25451–25471. [Google Scholar] [CrossRef]
- Investopedia. (2022). What is an economic bubble and how does it work, with examples. Available online: https://www.investopedia.com/terms/b/bubble.asp (accessed on 13 March 2025).
- Jacobsson, E. (2009). How to predict crashes in financial markets with the Log-Periodic Power Law [Master’s thesis, Stockholm University]. [Google Scholar]
- Jiang, Z. Q., Zhou, W. X., Sornette, D., Woodard, R., Bastiaensen, K., & Cauwels, P. (2010). Bubble diagnosis and prediction of the 2005–2007 and 2008–2009 Chinese stock market bubbles. Journal of Economic Behavior & Organization, 74(3), 149–162. [Google Scholar] [CrossRef]
- Johansen, A., & Sornette, D. (2001). Finite-time singularity in the dynamics of the world population, economic and financial indices. Physica A: Statistical Mechanics and Its Applications, 294(3–4), 465–502. [Google Scholar] [CrossRef]
- Matsushita, R., Da Silva, S., Figueiredo, A., & Gleria, I. (2006). Log-periodic crashes revisited. Physica A: Statistical Mechanics and Its Applications, 364, 331–335. [Google Scholar] [CrossRef]
- Nyasha, S., & Odhiambo, N. (2013). The Brazilian stock market development: A critical analysis of progress and prospects during the past 50 years. Risk Governance and Control: Financial Markets & Institutions, 3(3), 7–15. [Google Scholar] [CrossRef]
- Oświęcimka, P., Drożdż, S., Kwapień, J., & Górski, A. (2010). Fractals, log-periodicity and financial crashes. Acta Physica Polonica A, 117(4), 637–639. [Google Scholar] [CrossRef]
- Sarda, V., Karmarkar, Y., & Lakhotia, N. (2014). An empirical study applying chart patterns to Indian stock market crashes. Pacific Business Review International, 6(11), 24–27. [Google Scholar]
- Sarda, V., Karmarkar, Y., & Lakhotia, N. (2021). An Empirical study applying log periodic structures for prediction of crashes in Indian stock market. Finance India, 35(4), 1299–1312. [Google Scholar]
- Sarda, V., Karmarkar, Y., Lakhotia, N., & Sen, P. (2010). What can the log-periodic power law tell about stock market crash in India? Applied Economics Journal, 17(2), 45–54. [Google Scholar]
- Sarda, V., Karmarkar, Y., & Sarda, N. L. (2019). An empirical study applying log periodic structures for prediction of realty market crashes in India. Vision, 23(4), 357–363. [Google Scholar] [CrossRef]
- Seabold, S., & Perktold, J. (2010, June 28–July 3). Statsmodels: Econometric and statistical modeling with Python. 9th Python in Science Conference, Austin, TX, USA. [Google Scholar]
- Sornette, D. (2003). Why stock markets crash: Critical events in complex financial systems. Princeton University Press. [Google Scholar]
- Sornette, D., & Johansen, A. (1997). Large financial crashes. Physica A: Statistical Mechanics and Its Applications, 245(3–4), 411–422. [Google Scholar] [CrossRef]
- Sornette, D., & Johansen, A. (2001). Significance of log-periodic precursors to financial crashes. Quantitative Finance, 1(4), 452. [Google Scholar] [CrossRef]
- Sornette, D., Johansen, A., & Bouchaud, J.-P. (1995). Stock market crashes, precursors and replicas. Journal de Physique I, 6, 167–175. [Google Scholar] [CrossRef]
- Sornette, D., & Zhou, W.-X. (2006). Predictability of large future changes in major financial indices. International Journal of Forecasting, 22(1), 153–168. [Google Scholar] [CrossRef]
- Transtrum, M. K., Machta, B. B., & Sethna, J. P. (2011). Geometry of nonlinear least squares with applications to sloppy models and optimization. Physical Review E, 83(3), 036701. [Google Scholar] [CrossRef]
- Vandewalle, N., Ausloos, M., Boveroux, P., & Minguet, A. (1999). Visualizing the log-periodic pattern before crashes. The European Physical Journal B-Condensed Matter and Complex Systems, 9, 355–359. [Google Scholar] [CrossRef]
- Wosnitza, J. H., & Denz, C. (2013). Liquidity crisis detection: An application of log-periodic power law structures to default prediction. Physica A: Statistical Mechanics and Its Applications, 392(17), 3666–3681. [Google Scholar] [CrossRef]
- Wosnitza, J. H., & Sornette, D. (2015). Analysis of log-periodic power law singularity patterns in time series related to credit risk. The European Physical Journal B, 88, 97. [Google Scholar] [CrossRef]
- Zhang, Y., Zhou, L., Liu, Z., & Wu, B. (2024). Herding behaviour towards high order systematic risks and the contagion effect evidence from BRICS stock marke. The North American Journal of Economics and Finance, 74, 102219. [Google Scholar] [CrossRef]
- Zhou, W.-X., & Sornette, D. (2003). Testing the stability of the 2000–2003 US stock market “antibubble”. arXiv, arXiv:cond-mat/0310092. [Google Scholar] [CrossRef]
- Zhou, W.-X., & Sornette, D. (2009). A case study of speculative financial bubbles in the South African stock market 2003–2006. Physica A: Statistical Mechanics and Its Applications, 388(6), 869–880. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).