Abstract
The aim of this study is to enhance the understanding of volatility dynamics in commodity returns, such as gold and cocoa, as well as the financial market index S&P500. It provides a comprehensive overview of each model’s efficacy in capturing volatility clustering, asymmetry, and long-term memory effects in asset returns. By employing models like sGARCH, eGARCH, gjrGARCH, and FIGARCH, the research offers a nuanced understanding of volatility evolution and its impact on asset returns. Using the Skewed Generalized Error Distribution (SGED) in model optimization shows how important it is to understand asymmetry and fat-tailedness in return distributions, which are common in financial data. Key findings include the sGARCH model being the preferred choice for Gold Futures due to its lower AIC value and favorable parameter estimates, indicating significant volatility clustering and a slight positive skewness in return distribution. For Cocoa Futures, the FIGARCH model demonstrates superior performance in capturing long memory effects, as evidenced by its higher log-likelihood value and lower AIC value. For the S&P500 Index, the eGARCH model stands out for its ability to capture asymmetry in volatility responses, showing superior performance in both log-likelihood and AIC values. Overall, identifying superior modeling approaches like the FIGARCH model for long memory effects can enhance risk management strategies by providing more accurate estimates of Value-at-Risk (VaR) and Expected Shortfall (ES). Additionally, the out-of-sample evaluation reveals that Support Vector Regression (SVR) outperforms traditional GARCH models for short-term forecasting horizons, indicating its potential as an alternative forecasting tool in financial markets. These findings underscore the importance of selecting appropriate modeling techniques tailored to specific asset classes and forecasting horizons. Furthermore, the study highlights the potential of advanced techniques like SVR in enhancing forecasting accuracy, thus offering valuable implications for portfolio management and risk assessment in financial markets.
1. Introduction
Geopolitical conflicts significantly impact the level of risk associated with commodity market volatility. Several events, such as the COVID-19 pandemic, the conflict between Russia and Ukraine, and the war between Israel and Hamas, have already caused significant economic and financial disruptions. These disruptions have led to a sharp increase in commodity prices (Fang and Shao 2022). However, the latest Israel–Hamas war has had a limited but noticeable impact on specific commodity prices, particularly energy and agricultural commodities, while impacting Gold and Cocoa Futures differently (Kim and Fortner 2023; Mintec.com 2023). Research on commodity futures markets like cocoa suggests that speculators react quickly to new information, leading to efficient price discovery mechanisms (Nardella 2006). In contrast, even earlier studies on armed conflicts like the Israeli military offensive in Gaza show that conflicts can affect capital markets negatively, causing declines in asset prices during escalations in violence (Kollias et al. 2010). Therefore, while the efficiency of price discovery in cocoa market prices remains intact despite speculator activity, armed conflicts like the Israel–Hamas war can lead to adverse effects on asset prices in capital markets, including gold prices (Baur and McDermott 2010, 2012), due to increased uncertainty and risk aversion among investors.
Modeling volatility is a crucial aspect of assessing risk management strategies. Given the highly volatile environment following recent conflicts, it is necessary to determine the volatility of commodities compared to financial stock markets. Commodity prices have shown significant fluctuations over the last few years, and their behavior is raising concerns about overall economic market stability. For example, according to research by Baur and McDermott (2010), gold prices exhibit unique behavior; unlike other asset classes, gold prices tend to respond positively to negative market shocks. This finding significantly contributes to understanding commodity markets and raises additional questions in forecasting their volatility.
In traditional econometric methods, the growth of volatility models has been a significant area of development since the initial study by Engle (1982), which introduced the autoregressive conditional heteroscedastic (ARCH) class of models. Building on Engle’s earlier work, Bollerslev (1986) presented the generalized autoregressive conditional heteroscedastic (GARCH) model. Over time, GARCH models have emerged as the most commonly used method for estimating volatility. According to the literature, various authors have utilized different GARCH models to assess the volatility of financial markets and cryptocurrencies (see Alfeus and Nikitopoulos 2022; Ampountolas 2022, 2023; Bakas and Triantafyllou 2019; Iftikhar et al. 2023; Mensi et al. 2022; Nguyen and Walther 2020; Takaishi 2020). Therefore, it is crucial to identify the most suitable technique for predicting the volatility of commodities and overall financial assets. This question is becoming increasingly vital as predicting the future volatility of the commodities marketplace greatly influences managing price risk for both commodity producers and consumers.
Therefore, our focus has shifted towards the commodity markets due to their recent increasing importance in financial and economic news. Specifically, we are paying attention to gold and cocoa, which have experienced substantial price increases over the past few months. Of particular note is cocoa, which has seen a significant fivefold rise from 2023 to 2024, as presented in Figure 1. Our research contributes to the growing literature in several ways. While building on previous studies, we distinguish our work by examining the significance of capturing the volatility of commodity markets during periods of conflict. Our primary aim is to explore the importance of volatility in the daily dynamics of commodity markets by employing various GARCH models such as standard GARCH, eGARCH, and gjrGARCH, as well as long memory models like FIGARCH. Additionally, our study provides an empirical analysis of price forecasts by considering five forecasting models, including the Support Vector Regression (SVR) model and the GARCH family models, to determine the preferred method for price forecasting in the commodities market. Thus, we aim to evaluate the accuracy of predicting commodities market volatility dynamics beyond the observed data sample at various future time horizons. Furthermore, this study investigates the reliability of conditional heteroscedasticity models and distributional assumptions to effectively describe commodities’ price volatility. We use the Diebold and Mariano test (Diebold and Mariano 1995) to conduct pairwise model comparisons and determine the best set of models. Our evaluation of the models is based on three loss functions: mean absolute error (MAE), mean square error (MSE), and the root mean square error (RMSE). Finally, the Value-at-Risk (VaR) model estimates market risk. To be more precise, a Cornish–Fisher expansion (CFVaR), which is a four-moment modified VaR, is used to consider both mean and variance and skewness and kurtosis. The two-moment VaR is considered less accurate than the CFVaR approach (Ali et al. 2021; Favre and Galeano 2002).
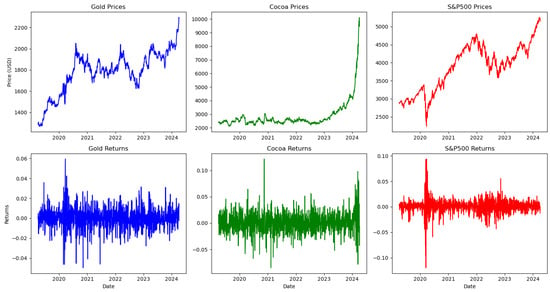
Figure 1.
Assets’ price and returns trajectory—period 2019–2024.
The following section briefly summarizes the relevant literature, and Section 3 highlights the employed techniques and analyzes the data. Finally, Section 4 examines the study’s findings, emphasizing the methods used, and Section 5 summarizes the paper’s conclusions and directions for future research.
2. Research Background
The commodity price forecasting literature has advanced significantly in recent years. Recent studies have drawn attention to the importance of commodity assets for asset allocation and portfolio diversification (Alfeus and Nikitopoulos 2022; Degiannakis and Filis 2018; Gkillas et al. 2020; Klein 2017). Additionally, research has affirmed the potential of commodity assets to act as safe havens and hedges (Rubbaniy et al. 2022). Authors have emphasized the significant influence of macroeconomic news (Smales 2017, 2022), macroeconomic factors, such as industrial production and inflation (Bakas and Triantafyllou 2019; Karali and Power 2013), economic uncertainty (Bakas and Triantafyllou 2019; Fang et al. 2019), and financial drivers like the VIX measure (Baur and Smales 2020), the default return spread, bond markets, and the Treasury–Eurodollar spread (Prokopczuk et al. 2017), in forecasting commodity prices.
Gargano and Timmermann (2014) study utilized a broad array of commodity prices to evaluate the out-of-sample predictability of commodity prices based on financial and macroeconomic variables. Commodity currencies were found to be able to predict short-term forecast horizons, while economic growth and the investment-capital ratio were found to have the ability to predict relatively longer horizons.
Other research has utilized a Bayesian method to create stochastic models. For example, Kostrzewski and Kostrzewska (2019) compared the Bayesian approach with non-Bayesian individual autoregressive models and three averaging methods for predicting spot prices. They determined that the Bayesian stochastic volatility model outperformed the others because it takes into account time-varying parameters, latent volatility, and jumps.
The Foroutan and Lahmiri (2024) study examined the connectedness between the ten most traded cryptocurrencies and the gold and crude oil markets before and during the COVID-19 pandemic. The authors utilized various statistical techniques, such as cointegration tests, vector error correction models, vector autoregressive models, Granger causality analyses, and the autoregressive distributed lag models, to investigate the relationship between these markets and to evaluate the safe haven properties of gold and crude oil for cryptocurrencies. The results indicate that during the COVID-19 pandemic, gold serves as a solid safe haven for Bitcoin, Litecoin, and Monero while showing a weaker safe haven potential for Bitcoin Cash, EOS, Chainlink, and Cardano. In contrast, gold only demonstrates a robust safe haven characteristic for Litecoin and Monero before the pandemic.
Alfeus and Nikitopoulos (2022) investigated the fluctuations in volatility within commodity markets using three standard long memory models: the fractional integrated generalized autoregressive conditional heteroscedastic (FIGARCH), fractional stochastic volatility (FSV), and heterogeneous autoregressive (HAR) models. The results indicated that commodity market volatility is characterized by roughness, with volatility components across different time frames being economically and statistically significant. Anti-persistent long memory was observed across all commodities, with weekly volatility prevailing in most commodity markets and daily volatility dominating the oil and gold markets. Moreover, HAR models demonstrated superior forecasting performance for short time frames compared to the other two, while fractional volatility models produced comparatively more accurate forecasts over more extended time frames.
Nguyen and Walther (2020) examined the changing volatility patterns of major commodities and the potential factors influencing their long-term volatility. The study utilizes a recently developed approach that combines generalized autoregressive conditional heteroscedasticity with mixed data sampling (GARCH-MIDAS). The research used commodity futures for crude oil (WTI and Brent), gold, silver, platinum, and a commodity index. The findings highlight the importance of distinguishing between short-term and long-term components when modeling and predicting commodity volatility. They also suggest that long-term volatility is significantly influenced by real global economic activity, changes in consumer sentiment, industrial production, and monetary policy uncertainty.
The use of traditional time series models for forecasting commodity prices has been widespread for a long time. For example, in their study, Dooley and Lenihan (2005) employed a time series ARIMA model and lagged-forward price modeling to predict future metals prices, demonstrating the high effectiveness of the ARIMA model. However, recent studies have proposed adopting stochastic models for price forecasting (Lee et al. 2017). According to Ben Ameur et al. (2023), a stochastic model with time-varying specificity and non-Gaussian distribution can account for the time dependency of commodity markets. They discovered that its asymmetric distribution could outperform traditional time series models. The study of Idilbi-Bayaa and Qadan (2021) examined the effectiveness of the yield curve on US government bonds in predicting the future movements in the prices of commodities. They analyzed the monthly prices of nine commodities over more than 30 years. Their results suggest that the predictive power changes over time. In the earlier years, the yield curve effectively forecasted monthly changes in commodity prices, but this effectiveness declined in the subsequent period.
In addition, during the last decade, the literature on forecasting commodity prices has focused on utilizing operational research tools such as artificial intelligence (AI), machine learning (ML), and deep learning (DL) systems. Panella et al. (2012) used an ML approach, specifically neural networks, to forecast crude oil, coal, natural gas, and electricity prices. They found that a mixture of Gaussian neural network algorithms was optimal and could be identified using a hierarchical constructive procedure.
Narayan et al. (2013) showed that their proposed model for predicting future oil prices was simple and accurate. It was based on a regime-switching framework and used hidden Markov filtering algorithms. However, only some studies have utilized DL models for commodity price forecasting. For example, Kamdem et al. (2020) applied DL models, specifically the Long Short-Term Memory (LSTM) model, to forecast commodity prices during the COVID-19 pandemic crisis. Their results showed that the LSTM model accurately predicted commodity prices.
As such, various studies have demonstrated that both traditional time series models and modern machine learning techniques, including Bayesian and deep learning approaches, offer valuable insights for forecasting. Moreover, the research highlights the significant roles of macroeconomic factors, financial drivers, and advanced stochastic models in predicting commodity prices. The evolving methodologies and findings underscore the dynamic nature of commodity markets and the continual need for robust forecasting models to navigate economic uncertainties and market volatilities effectively.
3. Data and Methodology
3.1. Data Analysis
This study evaluates the daily commodity prices of GC=F and CC=F and the GSPC (S&P500) index. The prices dataset was sourced from the Yahoo Finance site from 3 April 2019 to 4 April 2024.1 To assess the forecasting models’ performance and the asset indices’ fluctuations, we divided the dataset into a training and a test set at a ratio of 80:20, which is a good rule of thumb (Kuhn et al. 2013). Moreover, ensuring data are stationary is imperative for evaluating the proposed models. Thus, we calculated the log returns and conducted the Augmented Dickey–Fuller (ADF) test to examine the unit root null hypothesis. In addition, the Jarque–Bera test will determine whether the financial assets dataset displays skewness and kurtosis consistent with a normal distribution.
We employed the formula to compute the returns of both commodities and the S&P500 index. Furthermore, we defined , where denoted the assets’ closing price at time t. To ensure that our analyzed models utilized stationary data, we first determined data stationarity using the Dickey–Fuller (ADF) coefficient test for detecting non-seasonal unit roots (Dickey and Fuller 1979). After calculating the log returns, we performed the Augmented Dickey–Fuller (ADF) test to confirm the absence of unit roots. The outcomes of the unit root tests indicated that the null hypothesis was rejected at a 0.001 level for the analyzed financial assets’ returns (refer to Table 1). In addition, we conducted the Jarque–Bera Test, which assesses whether a given dataset adheres to the normal distribution by assessing the skewness and kurtosis (Jarque and Bera 1987). The test’s statistical expression incorporates skewness and kurtosis, which is expressed as where n denotes the number of data values. Here, S denotes the sample skewness, indicating the degree to which the data deviates from the mean, and K pertains to the sample kurtosis, which reflects the thickness of the distribution’s tails. The Akaike information criterion (AIC) also ranks the models in a specific order.

Table 1.
Summary statistics for the assets’ returns.
Figure 1 displays the commodities index dataset’s daily closing prices and returns trajectory. Upon initial observation, significant upward trends are noticeable. A sudden shift occurred when the Israel–Hamas war began in October 2023, impacting the gold market. Interestingly, the gold index yielded to the pre-crash levels after a short period of outbreak and financial market crashes. The increase was significant, and the commodities market responded positively and rapidly after a few trading days. Additionally, the cocoa commodity price exhibited a significant clear upward pattern. Hence, after a challenging bear market, the market demonstrated a robust recovery, resulting in a shift in market momentum and a return to its upward movement following the prior shift in market dynamics. We observe the same trend, similar to the gold index, in the S&P500 index.
Table 1 reports a breakdown of the commodities’ returns during the study period. We observe that the Gold Futures (GC=F) returns have relatively low volatility compared to Cocoa Futures (CC=F) and the S&P500 Index (GSPC). Additionally, the Sharpe Ratio (SR) for gold stands at 0.815, indicating favorable risk-adjusted performance; Cocoa Futures show a slightly higher Sharpe Ratio of 1.131, and the S&P 500 Index displays a mean return of 0.06% with a standard deviation (SD) of 1.3%, indicating moderate volatility. Their return distributions were right-skewed with heavier tails, shown by positive kurtosis, while skewness values vary, suggesting different degrees of asymmetry. The time series were also stationary, highly negative, and had significant Augmented Dickey–Fuller (ADF) unit root test statistics. Finally, neither time series followed a normal distribution, as evidenced by highly significant Jarque–Bera test statistics. Gold and Cocoa Futures exhibit a positive correlation of 0.07, indicating a modest association between these commodity markets. Conversely, the S&P500 Index shows weak correlations with Gold Futures (0.09) and Cocoa Futures (0.11), suggesting that the correlations with stocks are low, which has also been seen in other studies (Hollstein et al. 2021).
3.2. Model Specifications
3.2.1. GARCH Model
The generalized autoregressive conditional heteroscedasticity (GARCH) model extends the autoregressive conditional heteroscedasticity (ARCH) model. It facilitates the conditional variance to change over time based on past errors while keeping a constant unconditional variance (Bollerslev 1986). These models have been widely employed in financial modeling to predict the volatility of financial returns. Financial returns are susceptible to major shocks such as the war in Ukraine and the Middle East and, earlier, the coronavirus pandemic, so they often create outliers (see Figure 1). These shocks can present challenges to the volatility estimation models employed by GARCH-type models.
Much research has focused on studying volatility models because volatility is more consistent than price in financial markets. Therefore, volatility is mathematically defined as follows:
where the volatility is denoted by , the mean log return is denoted by , the log return at a specific time i is denoted by , and the total number of log return observations is denoted by n.
When parameterizing GARCH models, various error distributions can be utilized better to capture the characteristics of financial time series data. Common error distributions include, for example, the normal, Student’s t, GED, skew GED, normal inverse Gaussian, generalized hyperbolic, and Johnson’s reparameterized SU innovation distributions (Ghalanos 2015). In this research, the skew GED was used to parameterize the distributions of the GARCH-type models.
The standard GARCH model suggests positive and negative error terms impact volatility equally. This means that both positive and negative news have the same influence on volatility. Nevertheless, this assumption does not hold in the financial assets market. In reality, negative news tends to have a more noticeable effect on volatility than positive news, known as the leverage effect. Asymmetric GARCH models have been developed to address this issue of asset returns. Therefore, this research evaluated commodities’ volatility using standard GARCH and asymmetric GARCH models. The following sections briefly describe the EGARCH, GJR-GARCH, long memory volatility process, and FIGARCH models. We selected the best model (p and q) based on the Akaike information criterion (AIC).
3.2.2. Standard GARCH (sGARCH) Model
The GARCH model, an extension of the ARCH model, was introduced in Bollerslev’s work (Bollerslev 1986). It can be expressed as follows:
where represents the observed time series value at time t and is the time-varying conditional mean, typically expressed as , where is a parameter vector of dimensions that needs to be estimated, and is a vector of stochastic covariates. In addition, is the error term at time t, the denotes the conditional variance at time t, and the represents the error term, which follows an independent and identically distributed (i.i.d.) standard normal distribution.
The conditional variance is modeled as: is the constant term and represents the lagged squared residual from the mean equation, capturing the impact of past shocks on current volatility. Finally, is the lagged conditional variance, capturing the persistence of volatility over time. Certain conditions must be met by the parameters , , and , with the additional constraint that .
3.2.3. EGARCH Model
Financial instruments and commodities’ volatility is often involved using GARCH-class models due to their effectiveness in capturing volatility clustering and leptokurtosis. Typically, a maximum likelihood (ML) estimator is used to estimate these models’ vector of unstructured parameters. However, while symmetric ARCH and GARCH models are adept at modeling volatility clustering, they do not account for the asymmetric relationship between asset returns and volatility changes.
Nelson (1991) proposed the exponential generalized autoregressive conditional heteroscedasticity (EGARCH) model to address this limitation, a more rigorous parametric form. He employed the natural logarithm of the conditional variance to ensure non-negativity. The logarithmic form of the conditional variance in the EGARCH model is given by:
where represents the conditional variance at time t and is a constant term. captures the magnitude effect, representing the impact of the size of past standardized residuals on current volatility. captures the sign effect, representing the impact of past standardized residuals’ direction (sign) on current volatility, and is the GARCH coefficient, typically close to 1, indicating the persistence of volatility. The term is known as the magnitude effect, highlighting how past absolute standardized innovations influence current volatility. Meanwhile, is the sign effect, indicating that if , negative shocks (or news) increase volatility more than positive shocks of the same size. Additionally, the logarithmic adjustment of the volatility specification suggests that the model’s parameters allow for negative values of the parameters.
3.2.4. GJR-GARCH Model
The GJR-GARCH model, namely the Glosten–Jagannathan–Runkle Generalized Autoregressive Conditional Heteroscedasticity, was developed by Glosten et al. (1993) as an alternative to model volatility asymmetry. This approach has gained popularity among researchers because it assumes a specific parametric form for conditional heteroscedasticity. One of the advantages of using GJR-GARCH over other similar models, such as EGARCH, is that it is easier to execute in practice since the variance is explicitly represented instead of using the natural logarithm (Choi 2002).
where the impact of the unexpected return relies on its sign:
The parameters are typically subject to certain restrictions, such that they are all greater than zero. The GARCH model is essentially a more limited version of the GJR-GARCH, where the value of is fixed at zero. By testing the hypothesis that , you might determine whether the current and past squared returns have an asymmetric effect on volatility.
3.2.5. FIGARCH
The FIGARCH model, an advancement of the integrated GARCH (IGARCH) model by Baillie et al. (1996), addresses long memory in the autocorrelations of squared returns of various financial assets (Baillie 1996; Bollerslev and Mikkelsen 1996). Distinct from the traditional GARCH model, where shocks decay exponentially, or the IGARCH model, where shocks persist indefinitely, the FIGARCH model involves shocks that decay at a slower, hyperbolic rate. Let be an independently and identically distributed random variable for , with , and represents the information set containing all information up to time t. The observation errors are defined as:
where , for , denotes the conditional variance series.
The FIGARCH model expands the standard GARCH model by incorporating the fractional differencing operator . This operator is defined using the hypergeometric function and expressed as an ARMA process in :
where , , , and . Here, L is the lag operator with the fractional difference parameter d, and denotes the Gamma function. The long memory property of conditional variance time series captures the effect of shocks decaying at a hyperbolic rate, which is slower than exponential. The parameter d indicates the characteristics of the long memory of the volatility. Specifically, indicates a stationary series with an exponentially decaying autocorrelation function, while indicates a series with a unit root and a non-decaying autocorrelation function. The autocorrelation function exhibits hyperbolic decay for . Thus, the parameter d indicates the long memory characteristics of the volatility.
FIGARCH is a suitable method to represent volatility through high-frequency commodity data, as stated by Bollerslev (1996) in his work on modeling. It is an infinite-order ARCH process.
where the constant intercept, represented by , signifies the long-term baseline of the volatility dynamics. The observationally infinite-order ARCH representation has two parameters, and , and a polynomial on the lag operator, , where can be written in relation to the ARCH parameters as and . According to Bollerslev (1996), the FIGARCH model’s conditional variance is non-negative when , , and .
The quasi-maximum likelihood method, assuming normality for , is employed to estimate the parameters of the FIGARCH model. The likelihood function for a FIGARCH approach is based on the sample data , with parameters .
3.2.6. Support Vector Regression (SVR) Model
The SVM and its variations, like SVR, have been extensively employed in machine learning due to their ease of use (Clarkson et al. 2012). The SVM approach enables the application of the support vector classifier in a space with a higher number of dimensions (Drucker et al. 1999). The mapping function (kernel) is utilized to achieve this adaptation in a higher-dimensional space. Kernels such as radial-basis, polynomials, and linear functions can transform data into a higher-dimensional space.
The dataset comprises , where and . Here, represents the features and represents the label, both normalized to . The classifier classifies the data based on the labels. Therefore, a hyperplane must be created to separate the data. Given the nature of the data, many hyperplanes can be categorized into the same dataset. The selected hyperplane should maximize the margin, defined by the nearest points to the margin, known as support vectors. The margin can be either hard or soft. Generally, soft SVMs are preferred because they allow for outliers and misclassified samples, providing a more practical approach.
Hence, Smola and Schölkopf (2004) defined the SVM formula as:
Subjected to
where the margin width is denoted by w, whereas b represents the bias. The slack variable is related to the soft SVM and allows some values to fall within the margin. C represents the trade-off margin width.
3.2.7. Assessment Indicators
This study presents a comprehensive analysis of the forecasting accuracy of various loss functions, including the commonly used Mean Absolute Error (MAE), as well as the Mean Square Error (MSE) and Root Mean Square Error (RMSE). As such, we conducted multiple robustness tests and have presented the results for each accuracy metric.
where indicates the model’s forecast at time t. refers to the dataset actual values, h to the forecasting horizon, and finally, j indicates the number of historical observations.
In addition to that, we employed the predictive accuracy test proposed by Diebold and Mariano (1995) to evaluate the statistical significance of improvements in forecast accuracy. This test is widely used to compare the predictive power of different models and determine whether the differences in accuracy are statistically significant.
where refers to the mean of the loss differential series and represents the difference between the loss from the first model and the loss from the second model. T represents the number of observations and indicates an estimate of the variance of .
3.3. Value-at-Risk (VaR)—Downside Risk
Value at Risk (VaR) is a statistical tool that has become increasingly popular in market risk analysis, used to assess the volatility of financial indexes (Favre and Galeano 2002). Given a particular confidence level, it calculates the maximum potential loss of financial assets over a specified period. If returns follow a normal distribution, a two-moment VaR, which considers the mean and standard deviation of returns, can be used to assess downside risk. The definition of VaR is:
where and represent the portfolio’s mean daily returns and standard deviation. Additionally, denotes a standard normal distribution’s quantile. To highlight the differences, our study includes the typical values for , generally reported as 90%, 95%, and 99%. As such, during periods of market instability, returns may not follow a normal distribution. In such cases, a modified VaR approach that considers four statistical moments incorporating skewness and excess kurtosis provides more reliable estimates of potential losses a portfolio could experience. Higher statistical moments simulate potential diversification benefits across different financial assets being evaluated to determine the downside risk.
To this point, using VaR calculation may lead to inaccurate results, as the log returns of financial assets are often skewed and, therefore, not distributed normally. To address this, a viable alternative is a Cornish–Fisher expansion (Cornish and Fisher 1938) used to calculate quantiles of a non-normal distribution (Favre and Galeano 2002).
The conversion of a conventional Gaussian variable z into a non-Gaussian random variable Z can be achieved through the Cornish–Fisher expansion. This expansion employs four moments and can be described by the following equation:
where indicates the critical value for probability (1 − ). The parameter S represents skewness, while K represents excess kurtosis. It is essential to consider that S and K are parameters, meaning they might differ significantly from the actual skewness and excess kurtosis of the obtained distribution after applying the Cornish–Fisher expansion.
where the variable W represents the portfolio’s exposure to risk, while is the annual standard deviation.
4. Results and Discussions
This study aims to analyze the volatility dynamics of commodities’ returns such as gold, cocoa, and the financial market index S&P500 by applying different GARCH models, namely sGARCH, eGARCH, gjrGARCH, and FIGARCH. We used the Akaike information criterion (AIC) to determine the best model. In addition, we optimized each model with the Skewed Generalized Error Distribution (SGED), and the autoregressive parameters of the mean model are GC=F: ARFIMA (0, 0, 0), CC=F: ARFIMA (1, 0, 0), and GSPC: ARFIMA (3, 0, 2), respectively.
More specifically, for Gold Futures (GC=F), the study’s findings are presented in Table 2, which includes the maximum likelihood estimates of these models. Among the GARCH models considered for modeling Gold Futures (GC=F) returns, the sGARCH model appears to have generated better results based on Akaike’s information criterion (AIC) and the overall pattern of parameter estimates. The sGARCH model exhibits the lowest AIC value (−6.4802), indicating a favorable balance between model fit and complexity compared to the other models. Additionally, the parameter estimates in the sGARCH model suggest significant volatility clustering, as evidenced by the relatively high value of (0.057106) and the corresponding low value of (0.883539). This implies that past volatility shocks persistently impact current volatility levels, a characteristic often observed in financial time series data. The skewness parameter (Skew) is estimated at 0.929098, indicating a slight positive skewness in the return distribution.

Table 2.
Maximum likelihood estimates of the GARCH models for Gold Future.
While the eGARCH model also demonstrates volatility clustering, its AIC value is slightly higher (−6.4793) than that of the sGARCH model, suggesting a somewhat inferior fit. In the eGARCH model, the estimated parameters show a similar pattern of volatility persistence, with (0.038442) and (0.965718), indicating significant volatility clustering. The gjrGARCH model, which incorporates asymmetry in volatility responses to positive and negative shocks, does not show substantial evidence of asymmetry based on the estimated parameter (−0.054843). The other parameters and suggest similar levels of volatility persistence compared to the sGARCH and eGARCH models.
Lastly, the FIGARCH model, which accounts for long memory dependence in volatility, indicates strong evidence of long memory effects based on the estimated fractional integration parameter (0.999998), which is close to 1. However, the FIGARCH model’s AIC value (−6.4678) is higher than the sGARCH model’s, indicating a less favorable trade-off between model fit and complexity. Therefore, considering the lower AIC value and the favorable pattern of parameter estimates indicating volatility clustering, the sGARCH model is likely to have generated better results for modeling Gold Futures returns.
Table 3 presents the maximum likelihood estimates of the study’s GARCH models for Cocoa Futures and compares the performance in estimating the volatility dynamics. The results indicate that the sGARCH model has limitations in accurately capturing these dynamics, as evidenced by its lower log-likelihood value of and AIC value of compared to other models. Moreover, while the estimated parameters are statistically significant, they may not fully account for the asymmetry and leverage effects present in the data. Finally, the absence of fractional integration may limit its ability to capture long-memory properties related to volatility.

Table 3.
Maximum likelihood estimates of the GARCH models for Cocoa Futures.
The eGARCH model attempts to address volatility’s asymmetric response to shocks. However, its performance seems subpar compared to other models, with a log-likelihood value of and an AIC value of . Although some model parameters are statistically significant, the presence of relatively high standard errors and the negative estimate for the constant term () raise concerns about the model’s stability and reliability in capturing Cocoa Futures’ volatility dynamics. The gjrGARCH model incorporates a leverage effect, enabling asymmetric responses to positive and negative shocks. However, its performance, with a log-likelihood value of and an AIC value of , is similar to that of the sGARCH and eGARCH models. Notably, the estimated parameters for the gjrGARCH model include (standard error ), (standard error ), and (standard error ). While some parameters are statistically significant, the absence of fractional integration might limit its ability to capture long memory effects in volatility, potentially leading to suboptimal model fit.
In contrast, the FIGARCH model is the most promising model for estimating Cocoa Futures’ volatility dynamics. It achieves the highest log-likelihood value of and the lowest AIC value of among all models, indicating superior model fit. These findings confirm the results shown in the study by Alfeus and Nikitopoulos (2022), where the FIGARCH model successfully detected the long-memory characteristics of commodity markets. The statistically significant parameter estimates, including the fractional differencing parameter (), (standard error ), suggest that the model effectively captures the autocorrelation and volatility clustering in Cocoa Futures’ returns. Additionally, including skewness and shape parameters enhances the model’s ability to capture the distributional characteristics of the data.
Table 4 presents the evaluation results of GARCH models for the S&P500 financial index. Regarding model fit, the eGARCH model demonstrates superior performance, boasting the highest log-likelihood value and the lowest AIC value among all models. The eGARCH’s log-likelihood value of and AIC value of suggest it best compromises between model complexity and goodness of fit. This implies that the eGARCH model effectively captures the volatility dynamics of the GSPC index compared to the other analyzed models. Furthermore, the parameter estimates for the eGARCH model, including , , and , indicate robustness and reliability in estimation.

Table 4.
Maximum likelihood estimates of the GARCH models for GSPC.
Despite the eGARCH model’s superiority, the gjrGARCH model also demonstrates strong performance in model fit, with log-likelihood and AIC values comparable to those of the eGARCH model. The gjrGARCH model’s log-likelihood value of and AIC value of suggest that it captures the volatility dynamics of the GSPC index effectively, albeit slightly less optimally than the eGARCH model. The parameter estimates for the gjrGARCH model, including , , and , further reinforce its robustness and reliability in estimation. Conversely, while the sGARCH model provides some insights into the volatility dynamics of the GSPC index, its limitations become apparent regarding model fit. The sGARCH model’s log-likelihood value of and AIC value of indicate that it captures volatility dynamics less effectively than the eGARCH and gjrGARCH models. Additionally, the sGARCH model’s parameter estimates, including , , and , suggest limitations in capturing asymmetry and long memory effects in volatility.
Finally, the FIGARCH model exhibits promising performance in log-likelihood but faces challenges related to estimation precision. Although the FiGARCH model’s log-likelihood value of suggests that it captures volatility dynamics reasonably well, its relatively higher AIC value of compared to the eGARCH and gjrGARCH models raises concerns. Moreover, the FIGARCH model’s parameter estimates, particularly the relatively high standard errors for some parameters (e.g., and ), indicate potential issues with estimation precision, which could affect the reliability of the model’s predictions.
The study presents experimental results in Table 5 analyzing h-step-ahead forecasting performance for gold, cocoa, and S&P500 using sGARCH (1,1), eGARCH (1,1), GJR-GARCH (1,1), FIGARCH (1,1), and the SVR model. For a robust comparison, we applied three loss functions and adaptive forecasting with a 252 market days rolling window for testing over a recursive one. This approach was more robust to time-varying parameters. To evaluate the sensitivity of their volatility prediction for financial assets time series return data, we investigated three horizons (h) of 1, 5, and 20 market days, covering both short-term and long-term intervals. As demonstrated in Table 5, the forecasting performance depends on the horizon, with significantly reduced forecast losses under each metric over longer forecast horizons for all assets. The GARCH-type models, particularly sGARCH, eGARCH, and GJR-GARCH, show effective volatility forecasting capabilities across different assets and forecast horizons according to the loss function analysis. However, the SVR model displays relatively lower accuracy.

Table 5.
Out-of-sample evaluation of the model forecasts.
More specifically, across all forecasting horizons, the accuracy of the gold performance was measured using GARCH models, particularly the sGARCH and grjGARCH models, which consistently demonstrated superior forecasting accuracy compared to the support vector regression (SVR) model. In the short term (1-day horizon), the sGARCH model exhibited the lowest MAE, MSE, and RMSE values (MAE: 0.003863, MSE: 0.000015, and RMSE: 0.003863), indicating its ability to provide more accurate forecasts of Gold Futures prices. The SVR model showed promising results at longer horizons with considerable improvement compared to the 1-day horizon. Thus, the SVR model consistently outperforms the others in terms of forecasting accuracy for 5 and 20 trading days. The SVR demonstrates the lowest accuracy measures, indicating advanced predictive capability compared to traditional GARCH-based models, suggesting that SVR effectively captures the underlying patterns and dynamics in asset returns. Finally, the grjGARCH, followed by the eGARCH model, exhibited moderate accuracy in all horizons. Overall, the results highlight the potential of SVR as a superior alternative to traditional GARCH-based models for accurate and reliable asset return forecasting over extended time horizons.
Table 5 also provides a comprehensive overview of the accuracy metrics for Cocoa Futures (CC=F), confirming the superior performance of the Support Vector Regression (SVR) model over traditional GARCH-based models. Across all three forecasting horizons, SVR consistently outperforms the GARCH models, as evidenced by the accuracy metrics. For example, for the 1-day horizon, SVR yields an MAE of approximately 0.023759, significantly lower than the values obtained by the GARCH models, which range from 0.036262 to 0.037242. Similarly, SVR consistently demonstrates superior accuracy for the 5-day and 20-day horizons, with lower MAE, MSE, and RMSE values than the GARCH models. As such, these results highlight SVR’s capability to capture the underlying dynamics of Cocoa Futures returns more effectively than traditional GARCH models. However, these findings differ somewhat from those observed in gold forecasting, where SVR exhibited greater accuracy over longer horizons than shorter ones. Despite this discrepancy, SVR remains the preferred choice for Cocoa Futures forecasting, offering precise predictions across various forecasting horizons. Finally, while SVR consistently demonstrates superior accuracy, the performance of the grjGARCH and FIGARCH models also deserves attention. These traditional GARCH-based models exhibit competitive results, especially for shorter forecasting horizons. However, as the forecasting horizon extends, the performance gap between the SVR and the GARCH models becomes more pronounced. Despite some variability, the grjGARCH and FIGARCH models may still offer viable alternatives to SVR. Nevertheless, according to the results, the SVR’s consistently superior performance makes it the preferred choice for capturing the intricate dynamics of Cocoa Futures returns across different forecasting horizons.
The analysis of various forecasting models for the S&P500 Index (GSPC) shows that Support Vector Regression (SVR) outperforms traditional GARCH-based models by a significant margin. At a 1-day forecast horizon, SVR exhibits remarkable accuracy with a low mean absolute error (MAE) of around 0.002960, which is substantially lower compared to the MAE values obtained by the sGARCH (MAE: 0.005662), eGARCH (MAE: 0.006091), grjGARCH (MAE: 0.005364), and FIGARCH (MAE: 0.005437) models. This substantial difference in MAE values confirms SVR’s superior capability in short-term forecasting, similar to cocoa forecasting. As the forecast horizon extends to 5 days, SVR maintains its dominance, although with a slight increase in error metrics. Even in this scenario, SVR (MAE: 0.003775) outperforms traditional GARCH models, including sGARCH (MAE: 0.010252), eGARCH (MAE: 0.010534), grjGARCH (MAE: 0.009940), and FIGARCH (MAE: 0.010081), by a significant margin. Similarly, at the 20-day horizon, SVR exhibits better accuracy, although with a slightly higher MAE compared to the shorter horizons. Nonetheless, SVR’s MAE, MSE, and RMSE values remain significantly lower than those of the GARCH models across all forecasting horizons, reaffirming its consistent performance superiority. These results highlight SVR’s reliability and effectiveness as a forecasting tool for the S&P500 Index. In addition, traditional GARCH models may need help to capture the index’s intricate volatility dynamics over longer timeframes. Therefore, the study underlines the importance of using advanced modeling approaches like SVR to improve forecasting accuracy and reliability in financial markets.
The Diebold–Mariano test results from Table 6 present the comparative forecast accuracy of various forecasting models for Gold Futures (GC=F), Cocoa Futures (CC=F), and the S&P500 index (GSPC). Overall, significant differences in forecast accuracy are observed across different sets of comparisons. Based on the results in Set 1, the sGARCH model does not perform as well as the eGARCH, gjrGARCH, and FIGARCH models for Gold Futures. However, its performance varies for Cocoa Futures and the S&P500 index. In Set 2, the eGARCH model outperforms the gjrGARCH model for Gold Futures but falls short compared to the FIGARCH model for the same asset. In addition, for the S&P500 index, the eGARCH model does not perform as well as the FIGARCH model. Moving on to Set 3, the gjrGARCH model consistently outperforms the FIGARCH model across all assets, indicating its superior forecast accuracy. Lastly, Set 4 demonstrates that the FIGARCH model outperforms the SVR model significantly for all assets, highlighting the effectiveness of the FIGARCH model in forecasting.

Table 6.
Diebold–Mariano results of the forecasting models.
Table 7 displays estimations of Value at Risk (VaR) and Cornish–Fisher expansion (CFVaR) for various financial instruments over the period spanning 4 April 2019 to 4 April 2024. VaR represents the maximum potential loss at a specific confidence level, while CFVaR offers a modified VaR considering higher moments of the return distribution. For Gold Futures (GC=F), the VaR and CFVaR estimates increase as the confidence level increases, indicating more significant potential losses. Similar patterns are observed for Cocoa Futures (CC=F), with both VaR and CFVaR estimates showing an upward trend as the confidence level rises. However, it is worth noting that the CFVaR estimates tend to be slightly lower than the VaR estimates for Cocoa Futures across all confidence levels, suggesting a potential smoothing effect introduced by the Cornish–Fisher expansion. For the S&P500 index (GSPC), the VaR and CFVaR estimates show more variability than the other instruments, particularly at higher confidence levels. Interestingly, at the 90% confidence level, the CFVaR estimate for the S&P500 index is notably higher than the corresponding VaR estimate, indicating a more conservative risk assessment considering higher moments of the return distribution.

Table 7.
Value at Risk (VaR) and Cornish–Fisher expansion (CFVaR) estimations.
5. Conclusions
This study aims to provide a better understanding of the volatility patterns in commodity returns such as gold and cocoa, as well as the financial market index S&P500. We employed various GARCH models to achieve this and evaluated their effectiveness using Akaike’s information criterion (AIC) and maximum likelihood estimates. The study found that these findings could have significant implications for financial practitioners and researchers. To develop accurate forecasting models, we must understand the underlying dynamics of commodity returns.
Therefore, the study provides an overview of each model’s effectiveness in capturing volatility clustering, asymmetry, and long-term memory effects in the respective asset returns. By employing models like sGARCH, eGARCH, gjrGARCH, and FIGARCH, researchers gain a nuanced understanding of how volatility evolves over time and its impact on asset returns. Moreover, incorporating Skewed Generalized Error Distribution (SGED) in model optimization underscores the significance of capturing asymmetry and fat-tailedness in return distributions, standard features in financial data.
The analysis reveals several key findings regarding the performance of GARCH models in modeling the volatility of different assets. For Gold Futures (GC=F), the sGARCH model emerges as the preferred choice due to its lower AIC value and favorable parameter estimates, indicating significant volatility clustering and a slight positive skewness in return distribution. Conversely, while other models like eGARCH, gjrGARCH, and FIGARCH exhibit some strengths in capturing certain aspects of volatility dynamics, they generally show inferior performance compared to sGARCH in model fit and complexity.
Similarly, for Cocoa Futures (CC=F), the FIGARCH model demonstrates the best performance in capturing volatility dynamics, as evidenced by its higher log-likelihood value and lower AIC value than other models. The results suggest that the FIGARCH model effectively captures long-memory effects in Cocoa Futures returns, providing more reliable forecasts over various forecasting horizons.
In the case of the S&P500 Index (GSPC), the eGARCH model stands out as the most effective in modeling volatility dynamics, exhibiting superior performance in both log-likelihood and AIC values compared to other models. The eGARCH model’s ability to capture asymmetry in volatility responses contributes to its robust forecasting capabilities for the S&P500 Index.
Overall, identifying superior modeling approaches, such as the FIGARCH model for capturing long memory effects in volatility, can enhance risk management strategies by providing more accurate estimates of Value-at-Risk (VaR) and Expected Shortfall (ES).
Furthermore, the out-of-sample evaluation of forecasting models reveals that Support Vector Regression (SVR) outperforms traditional GARCH models, particularly for short-term forecasting horizons, across all analyzed assets. SVR consistently accurately predicts asset returns, indicating its potential as an alternative forecasting tool in financial markets.
Limitations and Future Research
While the study provides valuable insights into volatility modeling and forecasting accuracy in financial markets and, more specifically, in commodities, several limitations should be considered when interpreting the results, similar to many other studies. It is essential to acknowledge that several factors may limit the generalization of the findings. Firstly, the analysis is primarily focused on specific assets, so it may not be possible to extrapolate the results to other asset classes or different market conditions. Different assets may exhibit unique volatility dynamics influenced by factors such as sector-specific news, geopolitical events, or macroeconomic trends, which are not fully captured in the study’s analysis. Moreover, the study’s comparison of forecasting accuracy between GARCH models and SVR may be subject to methodological biases. For example, selecting specific SVR parameters or kernel functions could influence the comparative performance results.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are publicly available.
Conflicts of Interest
The authors declare no conflicts of interest.
Note
| 1 | The data are publicly available at https://www.finance.yahoo.com (accessed on 10 April 2024) in the Eastern Daylight Time (EDT) zone. |
References
- Alfeus, Mesias, and Christina Sklibosios Nikitopoulos. 2022. Forecasting volatility in commodity markets with long-memory models. Journal of Commodity Markets 28: 100248. [Google Scholar] [CrossRef]
- Ali, Fahad, Yuexiang Jiang, and Ahmet Sensoy. 2021. Downside risk in dow jones islamic equity indices: Precious metals and portfolio diversification before and after the COVID-19 bear market. Research in International Business and Finance 58: 101502. [Google Scholar] [CrossRef]
- Ampountolas, Apostolos. 2022. Cryptocurrencies intraday high-frequency volatility spillover effects using univariate and multivariate garch models. International Journal of Financial Studies 10: 51. [Google Scholar] [CrossRef]
- Ampountolas, Apostolos. 2023. The effect of COVID-19 on cryptocurrencies and the stock market volatility: A two-stage dcc-egarch model analysis. Journal of Risk and Financial Management 16: 25. [Google Scholar] [CrossRef]
- Baillie, Richard T. 1996. Long memory processes and fractional integration in econometrics. Journal of Econometrics 73: 5–59. [Google Scholar] [CrossRef]
- Baillie, Richard T., Tim Bollerslev, and Hans Ole Mikkelsen. 1996. Fractionally integrated generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 4: 3–30. [Google Scholar] [CrossRef]
- Bakas, Dimitrios, and Athanasios Triantafyllou. 2019. Volatility forecasting in commodity markets using macro uncertainty. Energy Economics 81: 79–94. [Google Scholar] [CrossRef]
- Baur, Dirk G., and Lee A. Smales. 2020. Hedging geopolitical risk with precious metals. Journal of Banking & Finance 117: 105823. [Google Scholar]
- Baur, Dirk G., and Thomas K. McDermott. 2010. Is gold a safe haven? international evidence. Journal of Banking & Finance 34: 1886–98. [Google Scholar]
- Baur, Dirk G., and Thomas KJ McDermott. 2012. Safe Haven Assets and Investor Behaviour Under Uncertainty. Dublin: Institute for International Integration Studies. [Google Scholar]
- Ben Ameur, Hachmi, Sahbi Boubaker, Zied Ftiti, Wael Louhichi, and Kais Tissaoui. 2023. Forecasting commodity prices: Empirical evidence using deep learning tools. Annals of Operations Research: 1–19. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bollerslev, Tim, and Hans Ole Mikkelsen. 1996. Modeling and pricing long memory in stock market volatility. Journal of Econometrics 73: 151–84. [Google Scholar] [CrossRef]
- Choi, In. 2002. Econometrics: By fumio hayashi, princeton university press, 2000. Econometric Theory, 18. [Google Scholar] [CrossRef]
- Clarkson, Kenneth L., Elad Hazan, and David P. Woodruff. 2012. Sublinear optimization for machine learning. Journal of the ACM (JACM) 59: 1–49. [Google Scholar] [CrossRef]
- Cornish, Edmund A., and Ronald A. Fisher. 1938. Moments and cumulants in the specification of distributions. Revue de l’Institut International de Statistique 5: 307–20. [Google Scholar] [CrossRef]
- Degiannakis, Stavros, and George Filis. 2018. Forecasting oil prices: High-frequency financial data are indeed useful. Energy Economics 76: 388–402. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Diebold, Francis X., and Roberto S. Mariano. 1995. Comparing predictive accuracy. Journal of Business & Economic Statistics 13: 253–63. [Google Scholar]
- Dooley, Gillian, and Helena Lenihan. 2005. An assessment of time series methods in metal price forecasting. Resources Policy 30: 208–17. [Google Scholar] [CrossRef]
- Drucker, Harris, Donghui Wu, and Vladimir N. Vapnik. 1999. Support vector machines for spam categorization. IEEE Transactions on Neural Networks 10: 1048–54. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive conditional heteroscedasticity with estimates of the variance of united kingdom inflation. Econometrica: Journal of the Econometric Society 50: 987–1007. [Google Scholar] [CrossRef]
- Fang, Libing, Elie Bouri, Rangan Gupta, and David Roubaud. 2019. Does global economic uncertainty matter for the volatility and hedging effectiveness of bitcoin? International Review of Financial Analysis 61: 29–36. [Google Scholar] [CrossRef]
- Fang, Yi, and Zhiquan Shao. 2022. The russia-ukraine conflict and volatility risk of commodity markets. Finance Research Letters 50: 103264. [Google Scholar] [CrossRef]
- Favre, Laurent, and José-Antonio Galeano. 2002. Mean-modified value-at-risk optimization with hedge funds. Journal of Alternative Investments 5: 21–25. [Google Scholar] [CrossRef]
- Foroutan, Parisa, and Salim Lahmiri. 2024. Connectedness of cryptocurrency markets to crude oil and gold: An analysis of the effect of COVID-19 pandemic. Financial Innovation 10: 68. [Google Scholar] [CrossRef]
- Gargano, Antonio, and Allan Timmermann. 2014. Forecasting commodity price indexes using macroeconomic and financial predictors. International Journal of Forecasting 30: 825–843. [Google Scholar] [CrossRef]
- Ghalanos, Alexios. 2015. The Rmgarch Models: Background and Properties. (Version 1.3-0). Available online: https://bioconductor.statistik.tu-dortmund.de/cran/web/packages/rmgarch/vignettes/The_rmgarch_models.pdf (accessed on 14 April 2024).
- Gkillas, Konstantinos, Rangan Gupta, and Christian Pierdzioch. 2020. Forecasting realized oil-price volatility: The role of financial stress and asymmetric loss. Journal of International Money and Finance 104: 102137. [Google Scholar] [CrossRef]
- Glosten, Lawrence R., Ravi Jagannathan, and David E. Runkle. 1993. On the relation between the expected value and the volatility of the nominal excess return on stocks. The Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Hollstein, Fabian, Marcel Prokopczuk, Björn Tharann, and Chardin Wese Simen. 2021. Predictability in commodity markets: Evidence from more than a century. Journal of Commodity Markets 24: 100171. [Google Scholar] [CrossRef]
- Idilbi-Bayaa, Yasmeen, and Mahmoud Qadan. 2021. Forecasting commodity prices using the term structure. Journal of Risk and Financial Management 14: 585. [Google Scholar] [CrossRef]
- Iftikhar, Hasnain, Aimel Zafar, Josue E. Turpo-Chaparro, Paulo Canas Rodrigues, and Javier Linkolk López-Gonzales. 2023. Forecasting day-ahead brent crude oil prices using hybrid combinations of time series models. Mathematics 11: 3548. [Google Scholar] [CrossRef]
- Jarque, Carlos M., and Anil K. Bera. 1987. A test for normality of observations and regression residuals. International Statistical Review/Revue Internationale de Statistique 55: 163–72. [Google Scholar] [CrossRef]
- Kamdem, Jules Sadefo, Rose Bandolo Essomba, and James Njong Berinyuy. 2020. Deep learning models for forecasting and analyzing the implications of COVID-19 spread on some commodities markets volatilities. Chaos, Solitons & Fractals 140: 110215. [Google Scholar]
- Karali, Berna, and Gabriel J. Power. 2013. Short-and long-run determinants of commodity price volatility. American Journal of Agricultural Economics 95: 724–38. [Google Scholar] [CrossRef]
- Kim, Shinwoo, and Jackie Fortner. 2023. The Impact of the Israel-Hamas War on Oil Prices. T.RowePrice. troweprice.com. Available online: https://www.troweprice.com/financial-intermediary/us/en/insights/articles/2023/q4/the-impact-of-the-israel-hamaswar-on-oil-prices.html (accessed on 10 May 2024).
- Klein, Tony. 2017. Dynamic correlation of precious metals and flight-to-quality in developed markets. Finance Research Letters 23: 283–90. [Google Scholar] [CrossRef]
- Kollias, Christos, Stephanos Papadamou, and Apostolos Stagiannis. 2010. Armed conflicts and capital markets: The case of the israeli military offensive in the gaza strip. Defence and Peace Economics 21: 357–65. [Google Scholar] [CrossRef]
- Kostrzewski, Maciej, and Jadwiga Kostrzewska. 2019. Probabilistic electricity price forecasting with bayesian stochastic volatility models. Energy Economics 80: 610–20. [Google Scholar] [CrossRef]
- Kuhn, Max, and Kjell Johnson. 2013. Applied Predictive Modeling. New York: Springer. [Google Scholar]
- Lee, Eunhee, Doo Bong Han, and Rodolfo M. Nayga, Jr. 2017. A common factor of stochastic volatilities between oil and commodity prices. Applied Economics 49: 2203–15. [Google Scholar] [CrossRef]
- Mensi, Walid, Xuan Vinh Vo, and Sang Hoon Kang. 2022. COVID-19 pandemic’s impact on intraday volatility spillover between oil, gold, and stock markets. Economic Analysis and Policy 74: 702–15. [Google Scholar] [CrossRef]
- Mintec.com. 2023. The Israel-Palestine Impact on Commodities. mintecglobal.com. Available online: https://www.mintecglobal.com/top-stories/theisrael-palestine-impact-on-commodities (accessed on 10 May 2024).
- Narayan, Paresh Kumar, Seema Narayan, and Susan Sunila Sharma. 2013. An analysis of commodity markets: What gain for investors? Journal of Banking & Finance 37: 3878–89. [Google Scholar]
- Nardella, Michele. 2006. Price efficiency and speculative trading in cocoa futures markets. Research Papers in Economics. [Google Scholar] [CrossRef]
- Nelson, Daniel B. 1991. Conditional heteroskedasticity in asset returns: A new approach. Econometrica: Journal of the Econometric Society 59: 347–70. [Google Scholar] [CrossRef]
- Nguyen, Duc Khuong, and Thomas Walther. 2020. Modeling and forecasting commodity market volatility with long-term economic and financial variables. Journal of Forecasting 39: 126–42. [Google Scholar] [CrossRef]
- Panella, Massimo, Francesco Barcellona, and Rita L D’ecclesia. 2012. Forecasting energy commodity prices using neural networks. Advances in Decision Sciences 2012: 289810. [Google Scholar] [CrossRef]
- Prokopczuk, Marcel, Lazaros Symeonidis, and Chardin Wese Simen. 2017. Variance risk in commodity markets. Journal of Banking & Finance 81: 136–49. [Google Scholar]
- Rubbaniy, Ghulame, Ali Awais Khalid, Konstantinos Syriopoulos, and Aristeidis Samitas. 2022. Safe-haven properties of soft commodities during times of COVID-19. Journal of Commodity Markets 27: 100223. [Google Scholar] [CrossRef]
- Smales, Lee A. 2017. Commodity market volatility in the presence of us and chinese macroeconomic news. Journal of Commodity Markets 7: 15–27. [Google Scholar] [CrossRef]
- Smales, Lee A. 2022. Trading behavior in agricultural commodity futures around the 52-week high. Commodities 1: 3–17. [Google Scholar] [CrossRef]
- Smola, Alex J., and Bernhard Schölkopf. 2004. A tutorial on support vector regression. Statistics and Computing 14: 199–222. [Google Scholar] [CrossRef]
- Takaishi, Tetsuya. 2020. Rough volatility of bitcoin. Finance Research Letters 32: 101379. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).