Abstract
This study investigates the distinctive modeling of regret utility when compared with common utility. I also introduce the interplay between common utility and regret utility. Using this model, I examine the differences in decision making, which encompasses issues such as risk sharing and principal–agent dilemmas. Regret utility is set so that its risk aversion shows common utility’s prudence (i.e., downside risk aversion). This paper reveals, both qualitatively and quantitively and with a concrete model, that regret utility leads to a more balanced and optimal ratio of agent payouts to outputs compared with common utility, meaning when major outputs are kept by principal, there are relatively larger agent payouts, and when major outputs are kept by the agent, there are relatively smaller agent payouts. This means that regret makes a more balanced distribution, and regret utility is more conservative (not biased). In addition, preliminary empirical research was performed in which people were asked risk preference or averseness questions, and their risk averseness was calculated by using the CRRA (Constant Relative Risk Aversion) utility function. The regret condition leads to a more conservative attitude. Furthermore, the regret model can be used in other areas, like in conservative investment portfolio optimization.
1. Introduction
Regret constitutes an essential characteristic of human nature. Several studies have explored the regret theory as an enhancement to the widely used von Neumann–Morgenstern expected utility, which is referred to as common utility in this paper. These studies have sought to provide innovative explanations for phenomena that were previously unexplained. Remarkably, Camille et al. (2004) found that patients with orbitofrontal cortical lesions did not report experiencing regret, although individuals without this impairment relied on regret in decision making. This suggests that these patients adhere to the standard theory of decision making, which proposes that emotions related to experiencing gains or losses are independent of the decision-making process. I explore the concept of regret utility, and I conduct investigations within the framework of risk sharing and principal–agent problems, as articulated in the studies by Holmstrom and Milgrom (1987) and Cvitanić and Zhang (2013).
The regret theory was originally proposed by Bell (1982) and further developed by Loomes and Sugden (1982). It eventually received formal axiomatization based on the works by Sugden (1993) and Quiggin (1994). The theory defined regret as disutility associated with not having chosen the ex-post optimal alternative. The practical formulation of regret, as employed by Braun and Muermann (2004), with some arrangement, is as follows: a regret utility function is defined as , where is a common utility function of a variable outcome, x, with a reference outcome . This formulation extends to encompass the experience of regret when and joy when . In their work, they examine optimal insurance purchase decisions of individuals who exhibit behavior consistent with the regret theory, and they predict that individuals with regret theory preferences deviate from the extreme choices of either full insurance or no insurance coverage, which is something that the traditional utility theory would not suggest. The model presented in this study commences with an examination of the characteristics of the regret utility function, employing the following assumptions and methodologies:
- -
- It establishes regret utility using constant relative risk averse (CRRA) utility and through insights between common utility and regret utility.
- -
- It examines the specific regret utility within the context of risk sharing in the Holmstrom–Milgrom problem.
- -
- It applies the risk-sharing framework to the dynamic stochastic principal–agent problem.
- -
- It summarizes that regret utility is set so that it has a particular relationship with common utility.
The regret model in this paper is more concreating and reasonable compared to the original and related models. Related studies include those by Cvitanić and Zhang (2013) and Sannikov (2008), both of which explore the static and dynamic stochastic models of the Holmstrom–Milgrom problem. This study’s contribution lies in its exploration of the distinctions and tendencies between regret utility and common utility concerning the Holmstrom–Milgrom problem.
The rest of this paper is structured as follows: Section 2 describes the models regarding regret utility. Section 3 provides examples of risk sharing within the Holmstrom–Milgrom model and the dynamic stochastic principal–agent problem, including numerical illustrations highlighting the differences between regret utility and common utility. Section 4 describes preliminary empirical research, and Section 5 is dedicated to discussions. Section 6 concludes this paper.
2. Model Setup for Regret
2.1. Regret Utility
Eeckhoudt and Schlesinger (2006) defined prudence as “downside risk aversion” (if one is risk-averse for both upward and downward movements, being more concerned about downside risk is the issue) and temperance as “outer risk aversion” (the concern here is extreme negative results on the downside). Independently, the regret theory has been successfully employed to explain some actual phenomena that violate the expected utility theory by penalizing utility because of an inferior result versus the benchmark result, which usually means the outcome is lower than the benchmark. In this sense, regret aversion expresses lower outcome aversion, which is usually prudence. In addition, regret prudence dives deeper into the fear of the outcome of a fat lower tail distribution.
In addition, Menegatti (2014) explains risk aversion, prudence, and temperance as follows:
“… Prudence: This concept was originally introduced in the precautionary saving (see Kimball 1990; Leland 1968; Sandmo 1970); it reflects the desire to increase savings in the face of income risk. According to utility theory, it is considered prudent if and imprudent if .
Temperance: This concept was introduced by Kimball (1992) in their study on the effect of labor income risk on the fraction of savings devoted to risky investment, and is defined as moderation in accepting independent risks. In utility theory, it is considered frugal if and intemperate if .
Risk aversion: Originally introduced by Pratt (1964), this refers to an affinity or aversion to risk. For utility function u, a person is considered risk averse if and risk-loving if . …” (The description is from Yamashita (2024))
In the end, under plausible assumptions regarding the utility function, prudence implies regret utility’s risk aversion (imprudence implies risk loving), and temperance implies regret utility’s prudence (intemperance implies imprudence). As shown in Table 1, in this particular context, the regret utility function exhibits risk aversion analogous to common utility’s downside risk aversion, while the regret utility function demonstrates prudence similar to common utility’s outer risk aversion. In both cases, the regret utility function delves deeper into assessing and addressing risk compared to the common utility function.

Table 1.
Relationship between common utility and ambiguity utility.
However, based on Braun and Muermann (2004), with some extension, regret utility is defined as follows:
where is a common utility function (see above) for a variable outcome x with a reference outcome . Notably, , , , and —at least with —is a scalar function. I set as CRRA utility, which means, for example, that the pain of loss of 0.01 out of 1 and that of 1 out of 100 are the same, because 0.01/1 = 1/100, and it is very natural in common utility (additionally, I set k as 1 without losing generality). From the above discussion of the equations are as follows (Appendix A):
where is a constant. The common utility is set as shown below.
if γ ≠ 1,
if γ = 1 (γ: a relative risk aversion parameter).
Equations (1) and (2) and Equations (1) and (4) reveal Equations (5) and (6), respectively, with the natural condition as follows:
If γ ≠ 1; ,
If γ = 1; ,
Not only do the common utility and regret utility functions (with affine transformation) align with the power utility of and , respectively (meaning that common utility exhibits a relative risk aversion of 1, while regret utility demonstrates a relative risk aversion of 2), but also, as indicated in Table 1, the second and the third derivatives of the regret utility function correspond to the third and fourth derivatives of the common utility function. Risk aversion, prudence, and temperance are therefore concepts that pertain to different aspects of the agent’s attitude toward risk, and they are related to three derivatives of different orders of the utility function.
In addition, just in case, by supposing that the CRRA utility and by finding of the regret utility as , the below can be obtained:
However, generally speaking, finding from does not work because no appropriate can be found.
2.2. Difference between Regret and Common Utilities
Based on Equation (6), I set as 1 for the numerical analysis. Figure 1 illustrates the difference between regret utility and common utility, described as and . Since the reference level is = 1, values where illustrate regret, whereas values where indicate joy.
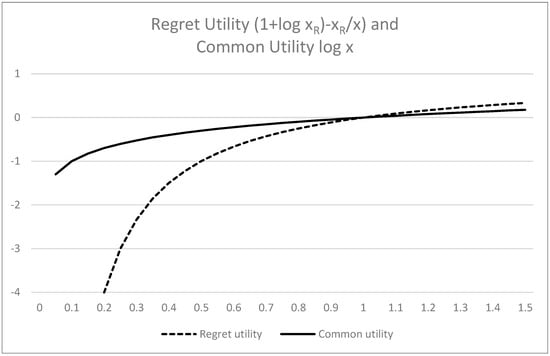
Figure 1.
Difference between regret utility and common utility log when = 1.
3. Regret Application to Holmstrom–Milgrom’s Principal–Agent Problem
3.1. Risk-Sharing Problem
By following the description and methodology presented by Cvitanić and Zhang (2013), I delve into the risk-sharing problem, also called the “first best scenario.” In this case, the principal and the agent share the same information and must agree on how to share the risk (total X) between them (principal: X − C; agent: C). The problem is expressed as follows:
where is the principal’s utility, is the agent’s utility, X is the output of this Holmstrom–Milgrom principal–agent problem (also a stochastic variable), and C is the payout from the principal to the agent (also a stochastic variable). The choice of action is denoted by . I omit the agent’s cost because of the risk-sharing setting. Mathematically, the problem becomes a stochastic control problem for a single individual (the principal) who chooses both the contract and the actions (payout to the agent). The first-order condition is known as the Borch rule (Borch 1962; Cvitanić and Zhang 2013) and it takes the following form, with representing the Lagrange multiplier for the individual participation constraint:
3.2. Numerical Example of Risk-Sharing Problem
I also assume , and that common utility is while its responding regret utility is , where serves as a regret reference level for both the principal and the agent. I then examine various cases involving different values for both the principal and the agent. I investigate two scenarios; in the first, both are common utility, and in the second, both are regret utility. The outcomes of the risk-sharing problem in the Holmstrom–Milgrom model are summarized below, with their numerical illustration presented in Figure 2. (See Appendix B).
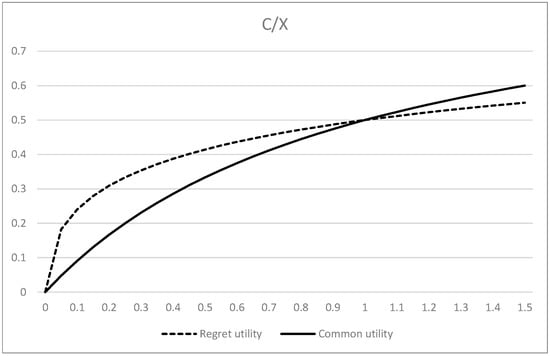
Figure 2.
C/X simulation with λ on horizontal axis.
For the common utility case, .
For the regret utility case, .
Figure 2 demonstrates that the regret utility model leads the principal to pay the agent more money than the common utility case when , where major outputs are kept by the principal. When , the regret utility leads the principal to pay the agent less money than the common utility case, where major outputs are kept by the agent. This means that regret makes a more balanced distribution than the common case, and the meaning is not biased nor deviated.
3.3. Dynamic Stochastic Principal–Agent Problem
I extend the analysis to the dynamic stochastic principal–agent problem based on the study by Cvitanić and Zhang (2013). Suppose that the agent is paid an amount once at the end time, T. This payment is influenced by the stochastic process of the output X, and the objective is to collectively maximize the expectation while considering as follows:
where represents the Lagrange multiplier, and is a Brownian motion process that generates the information filtration on the probability space. Processes and are adapted to that filtration, with being the interest rate process (given), while signifies the volatility process controlled by the agent, and is a fixed constant. As Cvitanić and Zhang (2013) described, this setup mirrors the dynamics of the wealth process of a portfolio, which holds the amount of dollars at time T in a risky asset with volatility σ and risk premium α, and it holds [] dollars in a risk-free asset, from which one can borrow and lend at the short-term interest rate .
By introducing a risk-neutral density process and using the martingale representation theorem, Cvitanić and Zhang (2013) demonstrated that
where = and = , , and λ and z are Lagrange multipliers. (Details are shown in Appendix B).
3.4. Numerical Example of Dynamic Stochastic Principal–Agent Problem
Assuming , and the common utility is while its responding regret utility is , serves as a regret reference level for both the principal and the agent. The results of the dynamic stochastic principal–agent problem are summarized below and illustrated in Figure 3. (Details are shown in Appendix B).
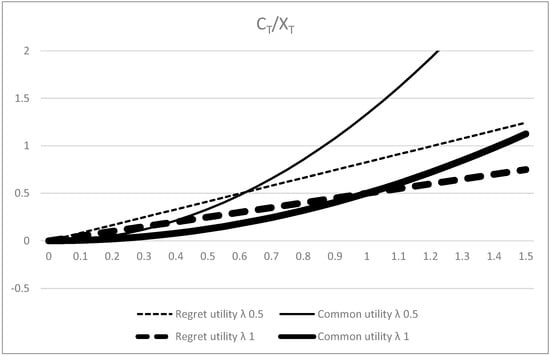
Figure 3.
numerical example with z on horizontal axis. λ is set to 0.5 or 1.
For the common utility case, .
For the regret utility case, .
By comparing the results of the regret utility model with those of the common utility model, it can be seen that the numerical example indicates that regret leads the principal to pay the agent more money when a major part of the outcome is kept with the principal, and it leads the principal to pay the agent less money when a major part of the outcome is kept with the agent, as illustrated in Figure 3.
In the case where is the reference point for the principal and is the reference point for the agent, the following results are found:
Risk-sharing case:
Common utility case: ,
Regret utility case: .
Dynamic stochastic case:
Common utility case: ,
Regret utility case: .
The previous tendency seems to be true and, in other words, as shown in Section 3.2, regret makes a more balanced distribution than the common case, and the meaning is not biased nor deviated.
4. Preliminary Empirical Research
4.1. Data and Questionnaire
The empirical research was based on the work by Camerer and Loewenstein (2003) and the materials quoted there. The data represent risk averseness and averseness with regret for 43 university students, who are supposed to be unbiased regarding questionnaires. Based on those data, everyone’s averseness is calculated by setting the CRRA utility as . (See details of the sample, questionnaire, and calculation in Appendix C). There are five questions. The first two (1.a. and 1.b.) are used to calculate risk averseness with a small or large probability for a small amount, and the next two (2.a. and 2.b.) are used for a large amount with small or larger probability. The fifth question (3.) is used for regret aversion. (Two previous people received the prize, so it is a shame if the next person fails to win). See Table 2.

Table 2.
Intentions of questions’ in questionnaire.
Regret Condition means that previous two people rolled the dice and won (received) the prizes. Note that the use of dice is fair.
Averseness is usually represented by positive figures, and in case that averseness is negative, this means there is risk preference.
4.2. Respondent Data Analysis
Table 3 shows each question’s basic statistics. There might be some differences among the probability to win, so there is also a difference among prize sizes.

Table 3.
γ distribution characteristics for all participants.
Additional details are shown in Appendix C. The last column’s t-value is 0.42. However, its distribution is widespread.
For risk-averse people, is positive, and a larger value means more averseness. For risk lovers, it is negative, and a larger magnitude means a higher preference for risk. The followings show comparison of values.
Average figures are affected by extreme samples, so by comparing the mode with a probability of 0.17 and a prize of JPY 1000 (1.a.), most of the samples are risk averse, but to some extent, there are risk lovers. Comparisons can be made as bellows:
- -
- When comparing 1.a. and 1.b., regarding the probability difference, there is not so much difference (t-value 0.45). (The results are almost the same when comparing 2.a. and 2.b. (t-value 0.79)).
- -
- When comparing 1.a. and 2.a., regarding the prize amount difference, there is not so much difference (t-value 0.71). (The results are almost the same when comparing 1.b. and 2.b. (t-value 0.37)).
- -
- When comparing 2.a. and 3., regarding the difference among four normal risk aversion cases and regret cases, the regret cases showed more risk averseness. There wasn’t 1% significance for the rejection of the null hypothesis, and 43 participants’ figures were distributed in a wide range (see Appendix C), where half of them showed equal or more risk aversion in the regret situation.
5. Discussion
The following are discussions based on the above research:
- Regarding principal–agent-type risk sharing, this mathematical model easily reveals that, usually, among regret utility persons, the principal tends to share the risk with the agent relatively equally. This tendency can be used for insurance-type risk-sharing pool consideration. Regret makes participants share the risk with each other more, so setting a regret condition will be important for better risk-sharing pool management.
- The model can be expanded into areas other than insurance, like investment. Investment portfolio suiting for regret persons (persons with regret utility) can be modeled using regret utility optimization. The model in this paper is concrete, and an optimal portfolio can be obtained with more conservative characteristics.
- The regret utility characteristic can also be used to determine how to care about persons in regret situations. For example, managing downside risk is effective for a person with a regret tendency.
- Regret makes people require a higher premium for risk, which means their shame is mitigated in case they fail or lose. In particular, preliminary empirical research shows that, as the model reveals, regret increases risk aversion, with the magnitude of incrementation of the risk averse parameter being around 0.1 to 0.2, which is smaller than the expected size of 1. The regret condition of the preliminary empirical research could be insufficient, and there might be room for improvement.
Future challenges involve constructing more appropriate regret conditions in empirical research.
6. Conclusions
In this study, I examined how regret utility deviates from common utility, and by using this result, I calculated the solution of the Holmstrom–Milgrom problem by encompassing the risk-sharing and principal–agent problems. The specific case explored in this study revealed that regret theory utility encourages conservative actions, meaning that, compared with the common utility case, the principal pays the agent more money when a major part of the outcomes is kept with the principal, and the principal pays less money when a major part of the outcomes are kept with the agent, meaning regret causes a more balanced distribution than the common case, meaning it is not biased nor deviated.
In addition, preliminary empirical research shows that regret causes more risk aversion than the common case, but the magnitude of the difference is not large enough and has less significance.
The regret utility characteristic modeled in this paper can be used to determine how to care for persons in regret situations, as well as for insurance (risk sharing) and finance (optimal investment portfolio) issues. For example, managing downside risk is effective for a person with regret tendencies.
Funding
Funded by Toyo University ordinary budget FY2024.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Dataset available on request from the author.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A
I solved and searched the function using (: constant) and not nor , because using only treats and not nor , making the equation easier to solve.
When , , and by setting k = 1, I obtain the following:
By setting = y, the below can be obtained.
Based on the work by Braun and Muermann (2004), where , is 0, and , I obtained the below.
When , , and in the same way as the above case, I obtained the below.
Just in case, by chance, “not but ,” the solution is discussed below. (In that case, g( ) is meaningless).
By denoting , are calculated. (k is set as 1).
When , the below can be obtained.
When ,
Obviously, < 0, and in these cases, modeling regret is not appropriate.
Appendix B
Regarding the risk-sharing problem and dynamic stochastic principal–agent problem, Cvitanić and Zhang (2013) show the below solution, as described in Section 3.1 and Section 3.3.
In the case of risk-sharing,
In this condition, is the principal’s utility, is the agent’s utility, X is the output of this Holmstrom–Milgrom principal–agent problem (also a stochastic variable), and C is the payout from the principal to the agent (also a stochastic variable). The choice of action is denoted by .
For the common utility case, by applying to , , is obtained. For the regret utility case, by applying to , , is obtained.
In the case of the dynamic stochastic principal–agent problem, the setting and the solutions are shown below, as described in Section 3.3. Suppose that the agent is paid an amount once at the end time, T. This payment is influenced by the stochastic process of the output X, and the objective is to collectively maximize the expectation while considering as follows:
where represents the Lagrange multiplier, and is a Brownian motion process that generates the information filtration on the probability space with volatility . Processes and are adapted to that filtration, with being the interest rate process (given), while signifies the volatility process controlled by the agent, and is a fixed constant.
Cvitanić and Zhang (2013) solved the problem in an efficient way. If the following risk-neutral density process is introduced,
which satisfies the dynamics
the process satisfies, by Itô’s rule,
This is thus a local martingale, and since there is a budget constraint, the maximization problem becomes the following:
where the martingale representation theorem, the below, is used, and z is the Lagrange multiplier for the budget constraint.
By solving this, the solutions are as follows:
where = and = . and z represent the Lagrange multipliers.
Using a specific function, the solutions of the case of the regret utility can be obtained, where both and are set as (common utility) or (regret utility, ). The results are below.
Risk-sharing:
For the common utility case: .
For the regret utility case: .
Dynamic stochastic principal–agent problem:
For the common utility case: .
For the regret utility case: .
Appendix C
- -
- Aim and Methods
In order to research how risk averse they are in several situations, including the regret condition, voluntarily, university students were asked the below questions. The empirical research was based on Camerer and Loewenstein (2003) and the materials quoted there. The data represent risk averseness and averseness with regret using the utility function model. The number of university students who answered was 43, and their ages ranged from 20 to 22; they are supposed to be unbiased with almost the same gender ratio.
Based on the effective size discussion by Ellis (2010), the sample size of 43 is meaningful (for instance, 5% z score^2*standard deviation^2/margin of error^2~(1.645*0.3/0.1)^2=25).
- -
- Calculation
Using the utility function , regarding the case of gaining L by certain probability p, the price is calculated as . This leads to .
- -
- Questionnaire
The structure is as follows: There are five questions. The first two (1.a. and 1.b.) are used to calculate risk averseness with a small or large probability for a small amount, and the next two (2.a. and 2.b.) are used for a large amount with small or larger probability. The fifth question (3.) is about regret aversion. (Two previous people received the prize, so it is a shame if the next person fails to win).
The questionnaire asked the following questions (supposing 1/6 = 0.1700):
1. You are going to bet “to get the prize Yen 1000 (around $7) or nothing” lottery.
a. Based on rolling a fair dice and in case #1 of the dice appears, you get the prize. (Probability 1/6).
In case other numbers shows up, you get nothing. In that situation, how much at most you pay to do the bet? Or how much at least the payment should be?
b. Based on rolling a fair dice and in case #1, #3, or #5 of the dice appears, you get the prize. (Probability 3/6).
In case other numbers shows up, you get nothing. In that above situation, how much at most you pay to do the bet? Or how much at least the payment should be?
2. You are going to bet “to get the prize Yen 10,000 (around $70) or nothing” lottery.
a. Based on rolling a fair dice and in case #1 of the dice appears, you get the prize. (Probability 1/6).
In case other numbers shows up, you get nothing. In that situation, how much at most you pay to do the betting? Or how much at least the payment should be?
b. Based on rolling a fair dice and in case #1, #3, or #5 of the dice appears, you get the prize. (Probability 3/6).
In case other numbers shows up, you get nothing. In that situation, how much at most you pay to do the betting? Or how much at least the payment should be?
3. You are going to bet “to get the prize Yen 10,000 (around $70) or nothing” lottery.
Based on rolling a fair dice and in case #1 of the dice appears, you get the prize. (Probability 1/6).
In case other numbers shows up, you get nothing. Two people have tried before you do and they all get the prize with both paying Yen 1700. In that situation, how much at most you pay to do the betting? Or how much at least the payment should be?
- -
- Distribution (Histogram)
Most respondents were risk averse, but to some extent, there were risk lovers. Figure A1, Figure A2, Figure A3 and Figure A4 show general information. The number of regret cases is 3 and Figure A5 includes the regret case.
The left figure in Figure A1 compares 1.a. and 1.b. regarding the probability difference, and there is not much difference. The right figure shows the distribution of each person’s difference between 1.a and 1.b. (The same is shown for the following figures). Figure A2 shows a different amount of cases compared to Figure A1. Figure A3 is a comparison regarding the amount of difference with the same probability compared to Figure A1. Figure A4 is a comparison of different probability compared to Figure A3. Figure A5 compares the common case (2.a.) and regret case (3.).
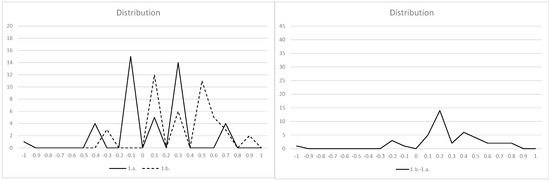
Figure A1.
(Left) Distribution of 1.a. and 1.b. (Right) Distribution of difference between 1.a. and 1.b.
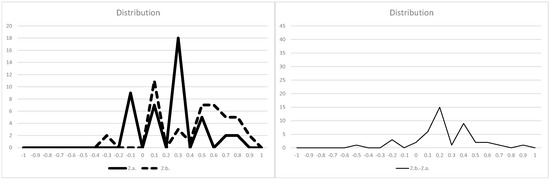
Figure A2.
(Left) Distribution of 2.a. and 2.b. (Right) Distribution of difference between 2.a. and 2.b.
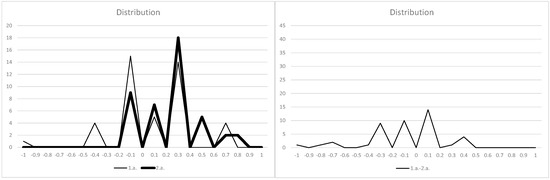
Figure A3.
(Left) Distribution of 1.a. and 2.a. (Right) Distribution of difference between 1.a. and 2.a.
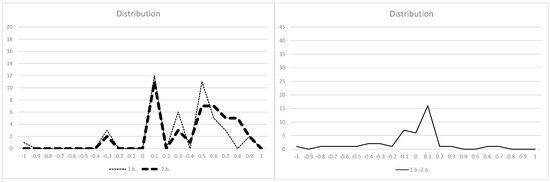
Figure A4.
(Left) Distribution of 1.b. and 2.b. (Right) Distribution of difference between 1.b. and 2.b.
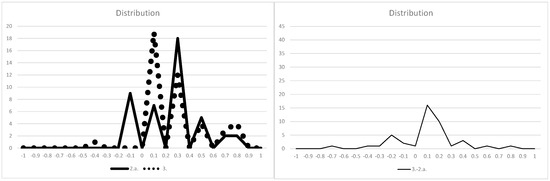
Figure A5.
(Left) Distribution of 2.a. and 3. (Right) Distribution of difference between 2.a. and 3.
In all figures, the vertical axis shows the number of samples, and the horizontal axis shows the γ ranges.
References
- Bell, David E. 1982. Regret in decision making under uncertainty. Operations Research 30: 961–81. [Google Scholar] [CrossRef]
- Borch, Karl. 1962. Equilibrium in a reinsurance market. Econometrica 30: 424–44. [Google Scholar] [CrossRef]
- Braun, Michael, and Alexander Muermann. 2004. The impact of regret on the demand for insurance. Journal of Risk and Insurance 71: 737–67. [Google Scholar] [CrossRef]
- Camerer, Colin, and George Loewenstein. 2003. Behavioral Economics: Past, Present, Future. In Advances in Behavioral Economics. Edited by Colin F. Camerer, George Loewenstein and Matthew Rabin. Princeton: Princeton University Press. [Google Scholar]
- Camille, Nathalie, Giorgio Coricelli, Jerome Sallet, Pascale Pradat-Diehl, Jean-René Duhamel, and Angela Sirigu. 2004. The involvement of the orbitofrontal cortex in the experience of regret. Science 304: 1167–70. [Google Scholar] [CrossRef] [PubMed]
- Cvitanić, Jakša, and Jianfeng Zhang. 2013. Contract Theory in Continuous-Time Models. Berlin/Heidelberg: Springer. [Google Scholar]
- Eeckhoudt, Louis, and Harris Schlesinger. 2006. Putting risk in its proper place. American Economic Review 96: 280–89. [Google Scholar] [CrossRef]
- Ellis, Paul D. 2010. The Essential Guide to Effect Sizes: Statistical Power, Meta-Analysis, and the Interpretation of Research Results. Cambridge: Cambridge University Press. [Google Scholar]
- Holmstrom, Bengt, and Paul Milgrom. 1987. Aggregation and linearity in the provision of intertemporal incentives. Econometrica 55: 303–28. [Google Scholar] [CrossRef]
- Kimball, Miles S. 1990. Precautionary savings in the small and in the large. Econometrica 58: 53–57. [Google Scholar] [CrossRef]
- Kimball, Miles S. 1992. Precautionary motives for holding assets. In The New Palgrave Dictionary of Money and Finance. Edited by Peter Newman, Murray Milgate and John Eatwell. New York: Stockton Press, pp. 158–61. [Google Scholar]
- Leland, Hayne E. 1968. Saving and uncertainty: The precautionary demand for saving. The Quarterly Journal of Economics 82: 465–73. [Google Scholar] [CrossRef]
- Loomes, Graham, and Robert Sugden. 1982. Regret theory: An alternative theory of rational choice under uncertainty. The Economic Journal 92: 805–24. [Google Scholar] [CrossRef]
- Menegatti, Mario. 2014. New results on the relationship among risk aversion, prudence and temperance. European Journal of Operational Research 232: 613–17. [Google Scholar] [CrossRef]
- Pratt, John W. 1964. Risk aversion in the Small and in the Large. Econometrica 32: 122–36. [Google Scholar] [CrossRef]
- Quiggin, John. 1994. Regret theory with General Choice sets. Journal of Risk and Uncertainty 8: 153–65. [Google Scholar] [CrossRef]
- Sandmo, A. 1970. The effect of uncertainty on saving decisions. The Review of Economic Studies 37: 353–60. [Google Scholar] [CrossRef]
- Sannikov, Yuliy. 2008. A continuous- time version of the principal: Agent problem. The Review of Economic Studies 75: 957–84. [Google Scholar] [CrossRef]
- Sugden, Robert. 1993. An axiomatic foundation of regret. Journal of Economic Theory 60: 159–80. [Google Scholar] [CrossRef]
- Yamashita, Miwaka. 2024. Quantum Mechanics Approach for Risk Aversion, Prudence, and Temperance. Journal of Mathematical Finance 14: 130–42. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).