Abstract
In this study, the dependence between Bitcoin (BTC) and economic policy uncertainty (EPU) of USA and China is estimated by applying the latest methodology of quantile cross-spectral dependence. Daily data comprising a total of 1947 observations and covering the period of 1 October 2013 to 31 January 2019 are used in this study. The findings indicate that a positive return interdependence between BTC and EPU is high in the short term, and this dependence decreases as investment horizons increase from weekly to yearly. The information on the time-varying and time–frequency structure of interdependence is also extracted by applying wavelet coherence analysis. The estimated results of wavelet coherence suggest that the correlation between BTC and EPU is positive during a short-term investment horizon. Finally, the frequency domain Breitung and Candelon causality test is applied, and results show the evidence of insignificant causality between Bitcoin and EPU. Overall, the findings highlight the diversification benefits of Bitcoin during the period of uncertainty.
Keywords:
Bitcoin; economic policy uncertainty; spillover; wavelet coherence analysis; quantile cross-spectral dependence JEL Classification:
C58; D80; G11
1. Introduction
In the context of extreme uncertainty regarding economic policy measures and the loss of confidence in the existing international financial system, Nakamoto (2008) introduced a new digital currency, i.e., Bitcoin, a fully decentralized cryptocurrency without any control from a central authority. Since its introduction, the Bitcoin price has increased dramatically from USD 0.09 on 18 July 2010 to USD 48,767 on 23 August 2021. The dramatic change in the price of Bitcoin has motivated academicians and practitioners to explore the economic and financial factors which may affect the Bitcoin price (Demir et al. 2018), since the behavior of this digital currency seems to be independent of economic and financial development (Kristoufek 2015). Some studies argue that the attractiveness of Bitcoin increases during the period of financial distress and economic uncertainty (Bouri et al. 2017; Demir et al. 2018; Fang et al. 2019). With this backdrop, it is stated that Bitcoin offers significant diversification benefits to investors during the times of extreme economic uncertainty (Cheng and Yen 2020; Guesmi et al. 2019; Kang et al. 2020; Mokni et al. 2020; Paule-Vianez et al. 2020; Wang et al. 2019). However, there are several studies that criticized the role and suitability of Bitcoin in financial markets by analyzing its speculative nature (Corbet et al. 2018; Eom et al. 2019), high price volatility (Aalborg et al. 2019; Shi et al. 2020; Elsayed et al. 2022), bubble formation tendencies (Baur et al. 2018; Eom et al. 2019; Bouri et al. 2019), legal regulations (Spaeth and Peráček 2022), and market efficiency (Al-Yahyaee et al. 2020; Choi et al. 2022; Mensi et al. 2019).
No doubt, government’s economic policies, namely, fiscal and monetary policies, significantly impact the entire economy. Specifically, during the period of recession/distress, direct government intervention significantly impacts financial markets. Frequent interventions after global financial turmoil have aroused scholars’ interest in such issues. In this regard, Baker et al. (2016) introduced the economic policy uncertainty (EPU) index to measure the uncertainties that arise due to government intervention and policies. Following that, recent studies have analyzed that such policy uncertainties have considerable impact on real economic systems and financial markets (Arreola Hernandez et al. 2022; Baker et al. 2016; Nguyen et al. 2020; Darsono et al. 2022; Mensi et al. 2021).
The interest in investigating the impact of EPU on the cryptocurrency market is fairly recent. Bouri et al. (2017), Bouri and Gupta (2019), Fang et al. (2020), and Colon et al. (2021) found that EPU is a significant predictor of volatility in the cryptocurrency market, especially in the Bitcoin market. Demir et al. (2018), Mokni et al. (2020), Mokni (2021), and Rubbaniy et al. (2021) reported that EPU significantly impacts Bitcoin returns and that Bitcoin acts as a potential hedging tool against economic uncertainty. On the contrary, Cheema et al. (2020) and Hasan et al. (2022) noted that cryptocurrencies do not act as a hedge or safe-haven during risky periods. Shaikh (2020) found that EPU in the US and Japan are negatively associated with the Bitcoin market whereas EPU in China is positively associated. Cheng and Yen (2020) found a positive correlation between Chinese EPU and the cryptocurrency market, while Yen and Cheng (2021) showed a negative correlation between Chinese EPU and the cryptocurrency market. Jiang et al. (2021) demonstrated that cryptocurrencies act as a hedge for higher EPU but not in moderate or low EPU. Furthermore, Haq et al. (2021) conducted a systematic review of empirical literature based on the cryptocurrency market and discovered the mixed connectedness pattern of cryptocurrency with all national EPU. This heterogenous correlation patterns suggest future research avenues in the cryptocurrency market.
Accordingly, this study explores the linkage between Bitcoin returns and EPU indices of USA and China developed by Baker et al. (2016). More precisely, the dependence structure between Bitcoin and EPU is measured using the latest methodology of quantile cross-spectral (QS) analysis proposed by Baruník and Kley (2019). Our research has the following three contributions. First, prior studies (e.g., Demir et al. 2018; Wang et al. 2019; Shaikh 2020) have ignored the quantile interdependence across varied frequencies in describing the interrelationship between Bitcoin and EPU. Our study captures the interdependencies at various market conditions across and at different investment horizons. This is important because money market correlation increases during uncertain periods (Longin and Solnik 2001). Second, to enrich our results with respect to interdependence between Bitcoin and EPU across time frequencies, we have applied wavelet coherence analysis. Indeed, it is important to recognize the behavior of Bitcoin across various frequencies because the driving forces behind Bitcoin pricing are not constant since its inception in the global market (Maghyereh and Abdoh 2021). Third, Breitung and Candelon’s (2006) Granger causality test is applied to investigate the causality between BTC and EPU at various frequency domains.
The general outcomes of the study estimated by applying quantile cross-spectral (QS) methodology indicate that EPU does not affect Bitcoin returns over long terms. Furthermore, the dependence between BTC and EPU decreases with the increase in frequency from weekly to yearly. Breitung and Candelon’s (2006) Granger causality test shows evidence of an insignificant bidirectional causality between Bitcoin and USA-EPU at long-term frequencies. Moreover, the weak dependence and insignificant causality between Bitcoin and USA-EPU suggest the better diversification benefits of Bitcoin and USA-EPU.
2. Data and Empirical Analysis Methods
2.1. Data
The daily data comprising a total of 1947 observations and covering the period 1 October 2013 to 31 January 2019 was used for empirical investigation. The price data on Bitcoin (BTC) denominated in USD was gathered from the website: https://bitcoincharts.com (accessed on 3 March 2019). The data of the EPU index of USA (USA-EPU) and EPU index of China (CHN-EPU) was obtained from the website: https://www.policy uncertainty.com (accessed on 3 March 2019).
The statistical properties of BTC and EPU indices are reported in Table 1. It is shown from Table 1 that BTC has the highest mean value of 2491.5, followed by CHN-EPU with a value equal to 129.3. The standard deviation of BTC is the highest, whereas the standard deviation of USA-EPU is the lowest. All variables are skewed to the right as demonstrated by the positive value of skewness. Furthermore, the calculated values of kurtosis statistics are high, implying a wider distribution than normal distribution. The values of the Jarque–Bera test statistic suggest that the distribution of selected variables is not normal.

Table 1.
Descriptive analysis.
2.2. Empirical Analysis Methods
In this study, the dependence structure between BTC and EPU is measured by applying quantile cross-spectral (QS) analysis. This method can capture the extreme period of interrelationship between variables in the frequency domain. This technique is independent of the conditional variances of the distribution in recognizing the co-movement of BTC and EPU at different quantiles. Thus, with the application of this technique, we can elucidate the interrelationship between BTC and EPU at varying frequencies as well as identify the dynamic correlation between these variables under changing market conditions.
In the next step, we have applied the wavelet coherence analysis to measure the strength of co-movement between time-series of BTC and EPU across frequencies and time scales. This technique has the ability to control for non-linearities, non-stationarity, structural breaks, and any seasonality in the linkage between time-series (Roueff and Von Sachs 2011). Cross-wavelet transformation is used to estimate wavelet coherence following the approach of Reboredo et al. (2017). Finally, Breitung and Candelon’s (2006) Granger causality test is applied for further clarification of results.
2.2.1. QS Approach
Following Baruník and Kley (2019), has two components and represents two strictly stationary processes of . Thus, the quantile coherency between these two processes can be written as:
where and . QS density and quantile spectral densities of and are represented by , , and , respectively. These densities can be obtained from the Fourier transform of the matrix of quantile-cross covariance kernels,
where , and is the indicator function of event . The information about the serial dependence is denoted by the m value. Further information about cross-section dependence can be obtained by choosing . In the frequency domain, this yields the matrix of QS density kernels,
Then, quantile coherency can be estimated by the smoothed quantile cross-periodograms as
where shows the rank-based copula cross-periodograms matrix and describes the sequence of weight functions. Then, the estimators for the quantile coherency can be computed by
The coherency matrix for three quantiles (lower 0.05, medium 0.5, and upper 0.95) and the combination of quantile levels of joint distribution (0.05|0.05, 0.5|0.5, and 0.95|0.95) are estimated in this paper.
2.2.2. Wavelet Coherence
The cross-wavelet of two time-series and is written as:
where represents the position index and denotes the scale.
According to Torrence and Webster (1999), the co-movement between and over time and across frequencies can be estimated using wavelet coherence, which can be written as:
In the above equation, is the squared wavelet coherence coefficient and is the smoothing operator in both time and frequency. The value of lies between ‘0’ and ‘1’ in the time–frequency space. The value of close to zero indicates weak correlation between time-series and a value close to 1 indicates a strong correlation. Monte Carlo simulations with statistical significance at 5% is used to examine statistical significance of coherence (Torrence and Compo 1998).
2.2.3. Granger Causality Test
The dependence structure between Bitcoin and EPU is further explored by applying Breitung and Candelon’s (2006) Granger causality test in the frequency domain. This test is based on the fact that causality between two stationary time-series can vary along the time-scale as well as over different frequencies.
Breitung and Candelon (2006) used the bivariate vector autoregressive (VAR) model to show the relationship between and variables. The model takes the following form:
where and are coefficients and is the error term. The null hypothesis of Granger causality from to at frequency is tested by , which is equivalent to the null linear restriction:
where is the vector of the coefficients and
-statistics are used to test the null hypothesis in the frequency interval, .
3. Results of Empirical Analysis
3.1. Results of Quantile Coherency Estimation
The quantile coherency results estimated by applying the QS approach are displayed in Figure 1. The plots show the real and unreal parts of the quantile coherency estimates across various frequencies and different quantiles (lower 0.05|0.05, middle 0.5|0.5, upper 0.95|0.95) in their joint distribution. The lower label of the horizontal axis shows the daily cycles, while the upper label illustrates the frequency cycles. The vertical axis displays the interdependence between BTC and EPU. The visual inspection of plots shows that return quantiles of BTC and USA-EPU, and BTC and CHN-EPU are strongly connected in short-term frequency as compared to long-term frequency. Indeed, a strong dependence between BTC and EPU indices is shown in the case of the short-term horizon, i.e., weekly frequency. Moreover, the dependence between BTC and EPU decreases with the increase in frequency from weekly to yearly. Overall, the estimates indicate that the irregularity in the interdependence structure between BTC and EPU depends upon market conditions and investment time horizons.
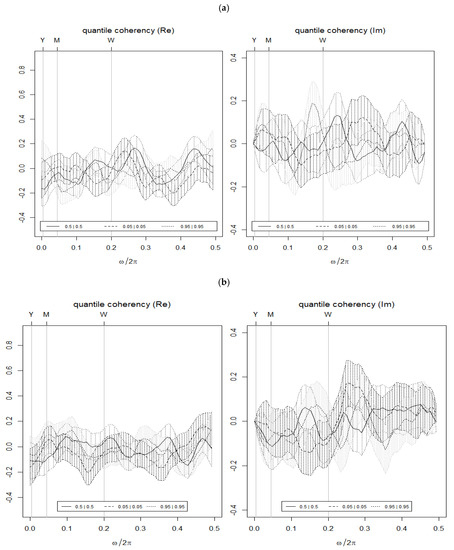
Figure 1.
Quantile coherence estimates. (a) BTC vs. USA-EPU. (b) BTC vs. CHN-EPU. Notes: (i) BTC = Bitcoin; CHN_EPU = Chinese economic policy uncertainty index; USA_EPU = USA economic policy uncertainty index. (ii) The plots report the real (left) and unreal (right) parts of the quantile coherency estimates for the different lower, middle, and upper quantiles (0.05|0.05, 0.5|0.5, and 0.95|0.95) of the joint distribution across the different frequencies. The daily cycles over the intervals [0, 0.5] are shown on the horizontal axis, whereas the vertical axis measures the co-dependence of two time series. The frequency cycles in the upper label of the horizontal axis show how yearly (Y), monthly (M), and weekly (W) frequencies are connected across the joint-distribution quantiles.
With respect to weekly frequency, it can be noted that the dependence of the BTC high return quantile on CHN-EPU is slightly highest with a value of 0.25 as compared to USA-EPU with a value of 0.20. Overall, the findings indicate that short-term fluctuation can explain well the positive return portfolio of BTC and EPU. The findings are consistent with the study of Cheng and Yen (2020) that CHN-EPU can better predict the BTC monthly returns than USA-EPU.
By using the QS approach, the dependence of the joint distribution between 0.05|0.95 quantiles can also be measured. In particular, we can examine the positive return of BTC (0.95 quantile) and a negative effect of EPU (0.05 quantile) by using the QS approach. The plots of Figure 2 show that the extreme return quantiles are weak for BTC with respect to USA-EPU and dependence displays the lowest level at a monthly frequency. However, the extreme return quantiles are strong for BTC and CHN-EPU. This result explains that greater uncertainty in the economic policies of China leads to asymmetric information in the market and, in turn, leads to asymmetric investors’ expectations (Akerlof 1970). This evidence supports the conclusion of Fang et al. (2019) and Paule-Vianez et al. (2020) that Bitcoin is an investment asset like gold and not just a means of exchange.
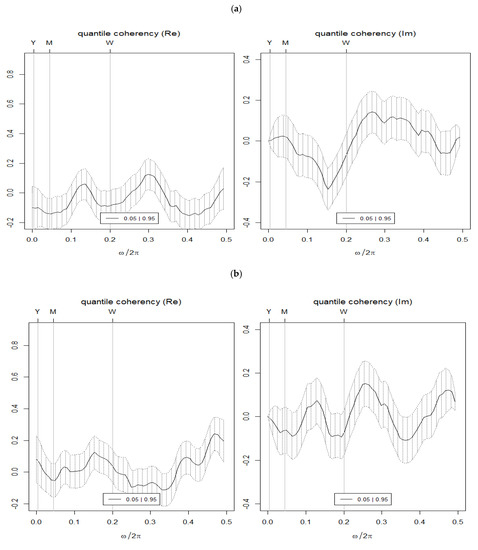
Figure 2.
Interdependence between the 0.05|0.95 quantiles of joint distribution. (a) BTC vs. USA-EPU. (b) BTC vs. CHN-EPU. Note: (i) BTC = Bitcoin; CHN_EPU = Chinese economic policy uncertainty index; USA_EPU = USA economic policy uncertainty index. (ii) The plots measure the interdependence between the 0.05|0.95 quantiles of joint distribution. The daily cycles over the intervals [0, 0.5] are shown on the horizontal axis, whereas the vertical axis measures the co-dependence of two time series. The frequency cycles in the upper label of the horizontal axis show how yearly (Y), monthly (M), and weekly (W) frequencies are connected across the joint-distribution quantiles.
3.2. Results of Wavelet Coherence Analysis
Next, we have applied wavelet coherence and phase difference to investigate the correlation and causality between BTC and EPU over time and frequency domains. Figure 3 shows the outcomes of wavelet coherence and phase difference for pairs of BTC and EPU from 2 days to 512 days (approximately two years). The horizontal axis displays the time-scale, whereas the vertical axis measures the frequencies. Higher frequencies relate to a short-term investment horizon, whereas the lowest frequencies relate to a long-term investment horizon. The direction of arrows signifies the phase differences between BTC and EPU. Arrows pointing right and left indicate that both time-series are in phase and out of phase, respectively. An upward direction of an arrow indicates that BTC returns were leading during economic uncertainty, whereas a downward direction of an arrow indicates that BTC returns were lagging during uncertainty.
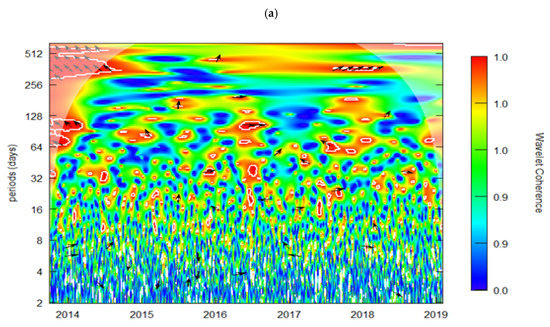
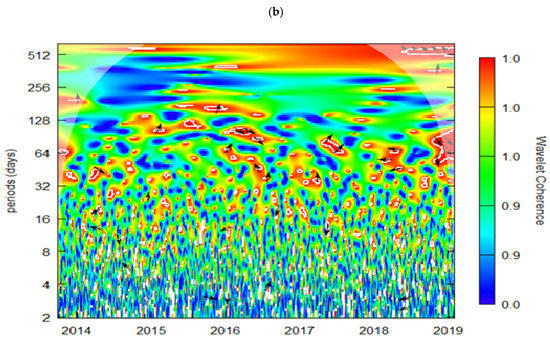
Figure 3.
Wavelet coherence. (a) BTC vs. USA-EPU. (b) BTC vs. CHN-EPU. Notes: (i) BTC = Bitcoin; CHN_EPU = Chinese economic policy uncertainty index; USA_EPU = USA economic policy uncertainty index. (ii) The plots show the estimated wavelet coherence for pairs of Bitcoin and the EPU. Lower scales are associated with the long-term investment horizon, whereas higher scales are associated with the short-term investment horizon. The horizontal axis shows the time; the leftmost reflects the start of the data interval and the rightmost reflects the end of the data interval. Warm colors such as red represent high coherence (or correlation) and cold colors such as blue represent low coherence. A thick black line represents statistically significant areas of coherence. The direction of the black arrows displays two things: the sign of correlation and the lead–lag phase relations between the two series.
The panel (a) of Figure 3 demonstrates the significant and strong interdependence between BTC and USA-EPU for the 2013–2015 period during a short-term investment horizon, i.e., a 280–512 day frequency band, with Bitcoin returns leading during the period of economic uncertainty. Some evidence of relatively strong and significant coherence is also observed during the 2013–2014 period and a 64–128 day frequency band with leading Bitcoin returns. The evidence of weak and negative coherence is observed at a long-term investment horizon and a 2–6 day frequency cycle throughout the sample period where Bitcoin returns are lagging during uncertainty. These outcomes support the short-run effectiveness of the hedge/diversification benefits of Bitcoin during uncertainty such as the European Sovereign debt. Our findings corroborate the conclusion of Cheng and Yen (2020), Mokni et al. (2020), and Paule-Vianez et al. (2020).
The panel (b) of Figure 3 explains that the strong coherence between BTC and CHN-EPU is observed from a 16–512 day frequency cycle during the mid-2016–2019 period. At the long-term investment horizon, the co-movement between BTC and CHN-EPU becomes weak and insignificant. The evidence of strong coherence from mid-2016–2019 supports the conclusion of Cheng and Yen (2020) that the trade ban announced by the Chinese government in 2017 increased the predictive ability of the CHN-EPU index for BTC returns.
Overall, the findings of this section support the previous analysis that coherence between BTC and EPU is strong during short-term and medium-term scales and future returns of Bitcoin increase during uncertainty that justify the role of Bitcoin as a hedging instrument during crisis periods.
3.3. Result of Additional Test
We have applied the Breitung and Candelon’s (2006) Granger causality test to further investigate the interdependence structure between BTC and EPU in the frequency domain. The advantage of this test is that it explains causality between two stationary time-series at various time-scales and across varying frequencies by imposing linear restriction on the autoregressive parameters in a VAR model.
However, prior to the application of Breitung and Candelon’s (2006) Granger causality test, we have applied the Toda–Yamamoto (TY) causality test, as shown in Table 2. This test is a modified version of the Granger causality test and does not depend on stationary properties of a time-series. The outcomes show clear evidence of a unidirectional causal relationship from CHN-EPU to BTC. In contrast, we cannot find evidence to prove causality either bidirectionally or unidirectionally between USA-EPU and BTC. This evidence indicates that Bitcoin returns are independent of the changes of EPU and can be used as a safe-haven or a diversifier in conditions of extreme EPU shocks. In other words, Bitcoin can be a safe-haven, like gold, and allows investors to consider this cryptocurrency as a tool to protect their savings in times of economic uncertainty. The role played by Bitcoin in uncertainty is found to be relevant in the formation of investment portfolios, because this cryptocurrency can contribute to the construction of better diversified portfolios. This result supports the findings of Wang et al. (2019).

Table 2.
TY Granger causality test.
Unfortunately, Toda–Yamamoto causality cannot identify the evidence of causality across different frequency bands, and that was why we applied Breitung and Candelon’s (2006) Granger causality approach. Figure 4 illustrates that CHN-EPU Granger cause BTC at short-term frequencies, whereas BTC does not show Granger causality with CHN-EPU at any frequency level. Granger causality from USA-EPU to BTC is significant at an intermediate level of frequency; however, we cannot find evidence of causality from BTC to USA-EPU. Finally, the causality from CHN-EPU to BTC is more significant than USA-EPU to BTC.
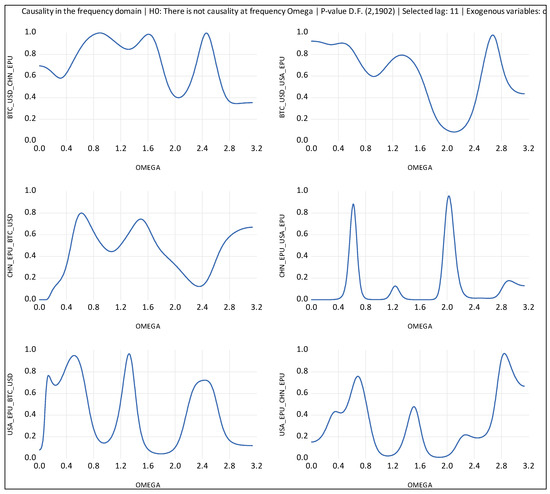
Figure 4.
Breitung and Candelon’s (2006) Granger causality test. Notes: (i) BTC = Bitcoin; CHN_EPU = Chinese economic policy uncertainty index; USA_EPU = USA economic policy uncertainty index. (ii) Breitung and Candelon’s (2006) Granger causality test measures the causality in the frequency domain.
4. Conclusions
This study investigates the dependence structure between BTC and EPU indices of USA and China by applying the latest QS dependence approach and wavelet coherence analysis. The findings estimated using daily data covering the period of 1 October 2013 to 31 January 2019 demonstrate that (i) the positive return quantile of BTC and EPU is higher in the short term rather than in the long term, (ii) a strong dependence between BTC and EPU indices is observed during the short-term horizon, i.e., weekly frequency, (iii) the correlation between BTC and EPU is found to be significant and strong during the 2013–2015 period and the short-term investment horizon, i.e., 280–512 day frequency cycle, (iv) the frequency domain causality test shows the evidence of a significant causal relationship running from CHN-EPU to BTC at short-term frequencies. Overall, the results suggest that prevalence of EPU over the long run do not affect BTC returns and BTC provides more diversification benefits during USA-EPU due to its weak dependence and insignificant causality with BTC.
From a policy perspective, our findings are useful to researchers and Bitcoin market participants to understand the diversification benefit of Bitcoin and in making better risk management decisions in terms of portfolio optimization since uncertainty is an important factor driving investor behavior in financial markets. Furthermore, the announcement of the ban on crypto-trading by the Chinese government to curtail financial losses and prevent economic instability is not the right solution because the ban on crypto-trading has no significant impact on the predictive power of the CHN-EPU for the volatility of Bitcoin. The need of the hour is to develop a more comprehensive regulatory framework for Bitcoin exchange that will protect investors and firms alike. The security risks and financial losses call for risk management approaches and insurance of the individual users of cryptocurrencies. Finally, the hedging quality and diversification benefits of Bitcoin demand the acceleration and prioritization of the development of Blockchain technology (see also Čajková and Čajka (2021) on the sustainability of China’s socio-economic development).
Although the findings of this study are relevant to the literature on the role played by Bitcoin in the face of uncertainty, it is not without limitations. In this study, for the measurement of economic policy uncertainty, we used the daily CHN-EPU and US-EPU indices developed by Baker et al. (2016), and the prices of Bitcoin are dominated by USD. In the future, our research can be extended to examine whether our results are sensitive to the use of other uncertainty measures and Bitcoin data dominated in other currencies.
Author Contributions
All the authors contributed to the entire process of writing this paper. S.N., A.K.T., Z.J. and S.-M.Y. conceived the idea and designed the structure of this paper; S.N. and A.K.T. collected and examined the data and devised the methodology; S.N. and A.K.T. wrote the draft of Section 2 and Section 3; Z.J. wrote Section 1 and Section 4; S.-M.Y. wrote Section 1 and Section 4; and Z.J. and S.-M.Y. performed a final revision of the entire paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea (NRF-2020S1A5B8103268).
Data Availability Statement
The price data on Bitcoin (BTC) denominated in USD, that supports the findings of this study, are openly available on the website: https://bitcoincharts.com (accessed on 3 March 2019). And the data of the EPU index of USA (USA-EPU) and EPU index of China (CHN-EPU) that support the findings of this study are openly available on the website: https://www.policy uncertainty.com (accessed on 3 March 2019).
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Aalborg, Halvor Aarhus, Peter Molnar, and Jon Erik de Vries. 2019. What can explain the price, volatility and trading volume of Bitcoin? Finance Research Letters 29: 255–65. [Google Scholar] [CrossRef]
- Akerlof, George A. 1970. The market for “lemons”: Quality uncertainty and the market mechanism. Quarterly Journal of Economics 84: 488–500. [Google Scholar] [CrossRef]
- Al-Yahyaee, Khamis Hamed, Walid Mensi, Hee-Un Ko, Seong-Min Yoon, and Sang Hoon Kang. 2020. Why cryptocurrency markets are inefficient: The impact of liquidity and volatility. North American Journal of Economics and Finance 52: 101168. [Google Scholar] [CrossRef]
- Arreola Hernandez, Jose, Sang Hoon Kang, Zhuhua Jiang, and Seong-Min Yoon. 2022. Spillover network among economic sentiment and economic policy uncertainty in Europe. Systems 10: 93. [Google Scholar] [CrossRef]
- Baker, Scott R., Nicholas Bloom, and Steven J. Davis. 2016. Measuring economic policy uncertainty. Quarterly Journal of Economics 131: 1593–636. [Google Scholar] [CrossRef]
- Baruník, Jozef, and Tobias Kley. 2019. Quantile coherency: A general measure for dependence between cyclical economic variables. Econometrics Journal 22: 131–52. [Google Scholar] [CrossRef] [Green Version]
- Baur, Dirk G., Kihoon Hong, and Adrian D. Lee. 2018. Bitcoin: Medium of exchange or speculative assets? Journal of International Financial Markets, Institutions and Money 54: 177–89. [Google Scholar] [CrossRef]
- Bouri, Elie, and Rangan Gupta. 2019. Predicting Bitcoin returns: Comparing the roles of newspaper- and internet search-based measures of uncertainty. Finance Research Letters 38: 101398. [Google Scholar] [CrossRef] [Green Version]
- Bouri, Elie, Rangan Gupta, Aviral Kumar Tiwari, and David Roubaud. 2017. Does Bitcoin hedge global uncertainty? Evidence from wavelet-based quantile-in-quantile regressions. Finance Research Letters 23: 87–95. [Google Scholar] [CrossRef] [Green Version]
- Bouri, Elie, Syed Jawad Shahzad, and David Roubaud. 2019. Co-explosivity in the cryptocurrency market. Finance Research Letters 29: 178–83. [Google Scholar] [CrossRef]
- Breitung, Jörg, and Bertrand Candelon. 2006. Testing for short- and long-run causality: A frequency-domain approach. Journal of Econometrics 132: 363–78. [Google Scholar] [CrossRef]
- Čajková, Andrea, and Peter Čajka. 2021. Challenges and sustainability of China’s socio-economic stability in the context of its demographic development. Societies 11: 22. [Google Scholar] [CrossRef]
- Cheema, Muhammad A., Kenneth Szulczuk, and Elie Bouri. 2020. Predicting cryptocurrency returns based on economic policy uncertainty: A multicountry analysis using linear and quantile-based models. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Cheng, Hui-Pei, and Kuang-Chieh Yen. 2020. The relationship between the economic policy uncertainty and the cryptocurrency market. Finance Research Letters 35: 101308. [Google Scholar] [CrossRef]
- Choi, Ki-Hong, Sang Hoon Kang, and Seong-Min Yoon. 2022. Herding behaviour in Korea’s cryptocurrency market. Applied Economics 54: 2795–809. [Google Scholar] [CrossRef]
- Colon, Francisco, Chaehyun Kim, Hana Kim, and Wonjoon Kim. 2021. The effect of political and economic uncertainty on the cryptocurrency market. Finance Research Letters 39: 101621. [Google Scholar] [CrossRef]
- Corbet, Shaen, Brian Lucey, and Larisa Yarovaya. 2018. Datestamping the Bitcoin and Ethereum bubbles. Finance Research Letters 26: 81–88. [Google Scholar] [CrossRef] [Green Version]
- Darsono, Susilo Nur Aji Cokro, Wing-Keung Wong, Tran Thai Ha Nguyen, and Dyah Titis Kusuma Wardani. 2022. The economic policy uncertainty and its effect on sustainable investment: A panel ARDL approach. Journal of Risk and Financial Management 15: 254. [Google Scholar] [CrossRef]
- Demir, Ender, Giray Gozgor, Chi Keung Marco Lau, and Samuel A. Vigne. 2018. Does economic policy uncertainty predict the Bitcoin returns? An empirical investigation. Finance Research Letters 26: 145–49. [Google Scholar] [CrossRef] [Green Version]
- Elsayed, Ahmed H., Giray Gozgor, and Chi Keung Marco Lau. 2022. Causality and dynamic spillovers among cryptocurrencies and currency markets. International Journal of Financial Economics 22: 2026–40. [Google Scholar] [CrossRef]
- Eom, Cheoljun, Taisei Kaizoji, Sang Hoon Kang, and Lukas Pichl. 2019. Bitcoin and investor sentiment: Statistical characteristics and predictability. Physica A: Statistical Mechanics and its Applications 514: 511–21. [Google Scholar] [CrossRef]
- Fang, Libing, Elie Bouri, Rangan Gupta, and David Roubaud. 2019. Does global economic uncertainty matter for the volatility and hedging effectiveness of Bitcoin? International Review of Financial Analysis 61: 29–36. [Google Scholar] [CrossRef]
- Fang, Tong, Zhi Su, and Libo Yin. 2020. Economic fundamentals or investor perceptions? The role of uncertainty in predicting long-term cryptocurrency volatility. International Review of Financial Analysis 71: 101566. [Google Scholar] [CrossRef]
- Guesmi, Khaled, Samir Saadi, Ilyes Abid, and Zied Ftiti. 2019. Portfolio diversification with virtual currency: Evidence from bitcoin. International Review of Financial Analysis 63: 431–37. [Google Scholar] [CrossRef]
- Haq, Inzamam Ul, Apichit Maneengam, Supat Chupradit, Wanich Suksatan, and Chunhui Huo. 2021. Economic policy uncertainty and cryptocurrency market as a risk management avenue: A systematic review. Risks 9: 163. [Google Scholar] [CrossRef]
- Hasan, Md. Bokhtiar, Kabir K. Hassan, Zulkefly Abdul Karim, and Md. Mamunur Rashid. 2022. Exploring the hedge and safe haven properties of cryptocurrency in policy uncertainty. Finance Research Letters 46: 102272. [Google Scholar] [CrossRef]
- Jiang, Yonghong, Lanxin Wu, Gengyu Tian, and He Nie. 2021. Do cryptocurrencies hedge against EPU and the equity market volatility during COVID-19?—New evidence from quantile coherency analysis. Journal of International Financial Markets, Institutions and Money 72: 101324. [Google Scholar] [CrossRef]
- Kang, Sang Hoon, Seong-Min Yoon, Stelios Bekiros, and Gazi S. Uddin. 2020. Bitcoin as hedge or safe haven: Evidence from stock, currency, bond and derivatives markets. Computational Economics 56: 529–45. [Google Scholar] [CrossRef]
- Kristoufek, Ladislav. 2015. What are the main drivers of the Bitcoin price? Evidence from wavelet coherence analysis. PLoS ONE 10: e0123923. [Google Scholar] [CrossRef]
- Longin, Francois, and Bruno Solnik. 2001. Extreme correlation of international equity markets. Journal of Finance 56: 649–76. [Google Scholar] [CrossRef]
- Maghyereh, Aktham, and Hussein Abdoh. 2021. Time–frequency quantile dependence between Bitcoin and global equity markets. North American Journal of Economics and Finance 56: 101355. [Google Scholar] [CrossRef]
- Mensi, Walid, Yun-Jung Lee, Khamis Hamed Al-Yahyaee, Ahmet Sensoy, and Seong-Min Yoon. 2019. Intraday downward/upward multifractality and long memory in Bitcoin and Ethereum markets: An asymmetric multifractal detrended fluctuation analysis. Finance Research Letters 31: 19–25. [Google Scholar] [CrossRef]
- Mensi, Walid, Yun-Jung Lee, Xuan Vinh Vo, and Seong-Min Yoon. 2021. Quantile connectedness among gold, gold mining, silver, oil and energy sector uncertainty indexes. Resources Policy 74: 102450. [Google Scholar] [CrossRef]
- Mokni, Khaled. 2021. When, where, and how economic policy uncertainty predicts Bitcoin returns and volatility? A quantiles-based analysis. Quarterly Review of Economics and Finance 80: 65–73. [Google Scholar] [CrossRef]
- Mokni, Khaled, Ahdi Noomen Ajmi, Elie Bouri, and Xuan Vinh Vo. 2020. Economic policy uncertainty and the Bitcoin-US stock nexus. Journal of Multinational Financial Management 57–58: 100656. [Google Scholar] [CrossRef]
- Nakamoto, Satoshi. 2008. Bitcoin: A peer-to-peer electronic cash system. Decentralized Business Review, 21260. [Google Scholar]
- Nguyen, Ha, Bin Liu, and Nirav Y. Parikh. 2020. Exploring the short-term momentum effect in the cryptocurrency market. Evolutionary and Institutional Economics Review 17: 425–43. [Google Scholar] [CrossRef]
- Paule-Vianez, Jessica, Camilo Prado-Román, and Raúl Gómez-Martínez. 2020. Economic policy uncertainty and Bitcoin. Is Bitcoin a safe-haven asset? European Journal of Management and Business Economics 29: 347–63. [Google Scholar] [CrossRef] [Green Version]
- Reboredo, Juan C., Miguel A. Rivera-Castro, and Andrea Ugolini. 2017. Wavelet-based test of co-movement and causality between oil and renewable energy stock prices. Energy Economics 61: 241–52. [Google Scholar] [CrossRef]
- Roueff, François, and Rainer Von Sachs. 2011. Locally stationary long memory estimation. Stochastic Processes and Their Applications 121: 813–44. [Google Scholar] [CrossRef] [Green Version]
- Rubbaniy, Ghulame, Ali Awais Khalid, and Aristeidis Samitas. 2021. Are cryptos safe-haven assets during COVID-19? Evidence from wavelet coherence analysis. Emerging Markets Finance and Trade 57: 1741–56. [Google Scholar] [CrossRef]
- Shaikh, Imlak. 2020. Policy uncertainty and Bitcoin returns. Borsa Istanbul Review 20: 257–68. [Google Scholar] [CrossRef]
- Shi, Yongjing, Aviral Kumar Tiwari, Giray Gozgor, and Zhou Lu. 2020. Correlations among cryptocurrencies: Evidence from multivariate factor stochastic volatility model. Research in International Business and Finance 53: 101231. [Google Scholar] [CrossRef]
- Spaeth, Walter, and Tomáš Peráček. 2022. Cryptocurrencies, electronic securities, security token offerings, non fungible tokens: New legal regulations for ‘crypto securities’ and implications for issuers and investor and consumer protection. In Developments in Information & Knowledge Management for Business Applications. Edited by Natalia Kryvinska and Aneta Poniszewska-Marańda. Cham: Springer, pp. 217–38. [Google Scholar]
- Torrence, Christopher, and Gilbert P. Compo. 1998. A practical guide to wavelet analysis. Bulletin of the American Meteorological Society 79: 61–78. [Google Scholar] [CrossRef] [Green Version]
- Torrence, Christopher, and Peter J. Webster. 1999. Interdecadal changes in the ENSO–monsoon system. Journal of Climate 12: 2679–90. [Google Scholar] [CrossRef] [Green Version]
- Wang, Gang-Jin, Chi Xie, Danyan Wen, and Longfeng Zhao. 2019. When Bitcoin meets economic policy uncertainty (EPU): Measuring risk spillover effect from EPU to Bitcoin. Finance Research Letters 31: 489–97. [Google Scholar] [CrossRef]
- Yen, Kuang-Chieh, and Hui-Pei Cheng. 2021. Economic policy uncertainty and cryptocurrency volatility. Finance Research Letters 38: 101428. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).