Market Manipulation around Seasoned Equity Offerings: Evidence Prior to the Global Financial Crisis of 2007–2009

Abstract

Since the adoption of the SEC’s Rule 10b-21 in 1988, many researchers have been concerned over the effectiveness of short sales constraints in preventing manipulative trading in the derivatives market. We analyze whether options can be used as synthetic short sale instruments to manipulate stock prices before a seasoned equity offer. Due to the existence of strict short sales constraints in the equity market and market makers’ anticipation of manipulative trading, it would be very costly for a manipulator to drive stock prices down artificially either by short selling in the equity market or by using synthetic short sales in the options market. Using a sample of 237 firms that issued SEOs on the NYSE and had options listed on any U.S. options exchange from April 2002 to December 2004, we show that potential manipulators in the options market tend to use put options as a trading vehicle during the SEO’s pre-offer period. The results of our empirical tests support the predictions of our model.

1. Introduction

Prior to the SEC’s adoption of Rule 10b-21, it was popularly believed that some investors could manipulate the stock price through short selling during the pre-offer period. Market participants assumed that informed investors with favorable private information on the issuers would trade contrary to their private information to drive the open market price down. Because the prices of new offers are typically based on the closing price prior to the pricing, such manipulative conduct distorts the market price for the security, inhibiting the stock market from functioning as an independent pricing mechanism and eroding the fairness of the offer price.

In 1988, the SEC adopted Rule 10b-21, which prohibited a short seller from covering short positions established after the announcement of new issues with offering securities from participants in the offerings. The rationale of this rule is to protect the issuers from manipulative short sales immediately prior to the pricing of an offer. However, researchers suspect that the development of the derivative securities market provides potential manipulators more ways to circumvent Rule 10b-21′s restrictions on short sales.1

Many scholars have studied investors’ strategies when faced with short sales constraints and suggested that options can be the substitutes for short sales. They criticize that although Rule 10b-21 can curb the direct short sales in the stock market, it cannot avoid the synthetic short sales in the options market (Safieddine and Wilhelm 1996). Diamond and Verrecchia (1987) suggest that the introduction of options can “reduce the cost of establishing what is effectively a short position.” Danielsen and Sorescu (2001) find that the option’s introduction can effectively mitigate short sale constraints and abate the overvaluation of stock prices. Having observed abnormally high levels of options’ open interest during the several days preceding the offer date and a subsequent sharp drop after the offer, Safieddine and Wilhelm (1996) report a shift from direct short sales in the equity market to synthetic short sales via the options market after the adoption of Rule 10b-21.

In this paper, we extend Easley et al.’s (1998) trading venue model to analyze the manipulators’ trading strategies in the framework of both the equity and options markets. The objective of this study is to analyze whether options can be a perfect synthetic short sale used to manipulate stock prices in the secondary market and whether the options market can be a venue for informed traders with favorable private information to disseminate fake, unfavorable information to the public. To do so, we set up a simple model to simulate the trading strategies of potential manipulators, other informed traders, and uninformed traders. We also incorporate into the model the market makers’ rational response to the observed transactions in both the equity and options markets. Our model predicts that due to the existence of short sales constraints in the spot market and market makers’ rational anticipation of manipulation, it will be very costly for potential manipulators to distort stock prices, whether through direct short sales or through synthetic short sales. We investigate the predictions of our model for the trading strategies of manipulators who hold favorable information and informed traders with unfavorable information.

Easley et al. (1998) do not include informed traders who are manipulators in their study. However, as a contribution of our paper, we have included them. We add to the existing literature on market manipulation by going beyond simple manipulative trading strategies in the equity market to investigating the actions of informed traders in the options market. We find that the trading volume and open interest increase substantially in the pre-offer options market. These results are consistent with the findings of Safieddine and Wilhelm (1996). We also find that, compared with the calls market, the puts market attracts more trading activities that spill over from the equity market. After dividing our sample into two subsamples that consist of firms with unfavorable and favorable information, conditioned on the signing of a 21-day post-offer CAR, CAR [0, 20], where CAR refers to the Cumulative Abnormal Returns, we observe that the abnormally large increases in the open interest of the puts are more likely due to the trading activities of manipulators.2 We also find that the pre-offer and post-offer CARs are significant and negatively correlated only in the category with the highest rises in the puts’ open interest. This reveals that manipulators must acting contrary to their private information to accomplish their goals.

While our findings pertain primarily to market manipulation prior to the Global Financial Crisis of 2007–2009, the implications of our results continue to stand as evidenced by the findings of more recent studies (e.g., Cumming et al. 2020; Griffin and Shams 2018; Horst and Naujokat 2011; Jarrow et al. 2018; Nyström and Parviainen 2017). For example, Jarrow et al. (2018) find that large traders’ option positions have an impact on the underlying asset’s price and that they can generate significantly positive alphas from trading options. They attribute the abnormal returns to strategic trading and cross-market manipulation.

The remainder of this paper is organized as follows. In Section 2, we review the previous studies on the information flow between the equity and options markets, and studies on the manipulative conduct in equity or derivative markets. In Section 3, we develop our model of multi-market transactions and analyze the trading strategies of different types of traders in the equity market and options market. We also derive the conditions that induce the informed traders to perform manipulative conduct. We describe the data in Section 4 and empirically investigate the predictions of our model in Section 5. We conclude our study in Section 6.

2. Literature Review

The direction of the information flow between the equity and options markets is very important to a manipulator in the secondary market. If stock prices do not respond to the trading volume or trading direction in the options market or if the response is immaterial, it has no meaning for the trader to trade contrary to his private information in the options market.

Previous studies show that the information flow between the equity market and options market is bidirectional, and under certain conditions, the options market leads the equity market. Mayhew et al. (1995) analyze the impact of the change in the equity–option margin and find that the margin plays a very important role in the allocation of informed trading across related markets. Easley et al. (1998) model the informed traders’ choice of a trading venue and reason that when the leverage on an option trade is higher or when the options market is more liquid, the options trades convey more information than do stock trades. Chan et al. (2002) further demonstrate that it is quote revisions, not trades in the options market, that contain information on the market. Amin and Lee (1997) observe the trading activities in both markets before quarterly earnings announcements and find that options traders trade on their private information prior to the earnings announcements. Cao et al. (2005) examine the information content in both markets prior to takeovers.3 They find that the call volume imbalance has more prediction powers regarding the next day’s stock returns and further conclude that the options market contributes more to price discovery in the presence of a pending extreme information event.

The two-way information flow creates the necessary conditions for manipulative conduct in the options market. However, only when the loss incurred by manipulators in the options market can be totally compensated by the profits gained from the issuing market do they have the incentive to perform manipulative trading. Safieddine and Wilhelm (1996) argue that if arbitrage links the options and equity markets together, based on the put–call parity, buying the put or selling the call will drive the stock prices down, so investors can depress stock prices through trading in the options market easily. However, the true story is not so simple. Ofek et al. (2004) indicate that due to the existence of short sales constraints, the arbitrage between the equity and options markets is asymmetrically violated, and thus stock prices are more likely to exceed the upper bound implied by the prices of puts or calls. Furthermore, due to the market makers’ rational expectation of the potential existence of manipulation, it is less likely for the market makers to adjust the quotes’ downside when they observe the bear signals, such as selling stocks, writing calls, or buying puts. In other words, if a manipulator attempts to mimic the trading behavior of informed traders with unfavorable information, they must increasingly trade contrary to their information, which makes them incur more losses in the options transactions. In sum, both the rational expectations of the market makers and the asymmetric violation of put–call parity would largely enhance the difficulties of manipulating stock prices through the options market.

Many papers have examined theoretically or empirically the feasibility of manipulation in different kinds of settings. Some papers investigate the manipulative behaviors in the equity market. Aggarwal and Wu (2006) demonstrate that a manipulator can achieve their scheme in the presence of information seekers, who play a vital role in sustaining manipulation. Mei et al. (2004) study manipulation cases in the framework of behavioral finance. They find that when investors are irrational and arbitrages are limited, manipulators can profit from “pump-to-dump” strategies, i.e., buying many stocks to drive the price up and then selling them at a high price.

Some other papers study the cases of manipulation by linking the equity market and derivative market together. Kumar and Seppi (1992) model the possibility of manipulations with “cash settlements” in the futures market. They suggest that uninformed traders can earn profits by establishing a futures position and then manipulating the spot price by trading in the spot market. In the framework of their analysis, informed traders only trade in the spot market, and the futures market is only the venue of hedging. However, they further point out that the profit earned from such a trading strategy cannot be guaranteed because when more investors trade in this way, the profits from manipulation fall to zero. Jarrow (1994) reasons how to manipulate the stock market through trading derivative securities to corner the market. They argue that when the stock market and derivative market are closely linked, it is not likely for a large trader to manipulate the stock prices.

Similar to the setting of our model, Gerard and Nanda (1993) study the potential for manipulation prior to seasoned equity offerings. Their model predicts that the more likely an informed trader is to be allocated many new shares or the less the manipulative conduct is identified by market makers, the more incentive they have to manipulate the stock price. However, our study differs from Gerard and Nanda’s (1993) model in several aspects. Firstly, Gerard and Nanda’s (1993) study is based on the assumption that there exist no constraints on short sales, while in our model, short sales are strictly restricted prior to the pricing of offers. Secondly, Gerard and Nanda’s (1993) model is only in the framework of a unitary equity market. We introduce the options market into the analysis of the manipulation potential in this study. Thirdly, Gerard and Nanda (1993) analyze a manipulator’s trading strategies independently. In their model, they assume that the other traders’ trading directions are given and analyze the behavior of an individual manipulator’s trading strategy based on their observation of others’ actions. Compared with their static game, we design a sequential model which focuses on the interactions between manipulators, non-manipulators, and market makers. In our model, each of the market participants can observe the other participants’ actions and adjust their own action corresponding to their observation. The design of our model ameliorates Gerard and Nanda (1993)’s setting and makes the framework of analysis more in line with the real situation in the security markets around seasoned equity offerings.

More recent studies, such as Cumming et al. (2020), find that end-of-day stock price manipulation is generally associated with short-termism, long-term damage to equity values, and reduced incentives for employees to innovate. Interestingly, they highlight that market manipulation is likely to affect firm insiders on days when options expire. Griffin and Shams (2018), in their study of S&P 500 Index options, report that at the settlement time of the VIX Volatility Index, trading volume in out-of-the-money S&P 500 Index options sharply increases. They investigate alternative explanations of hedging and coordinated liquidity trading by utilizing differences in put and call options and report results that are consistent with market manipulation.

3. The Model

3.1. Market Participants

In this section, we set up our model of multi-market trading in the spirit of Easley et al. (1998). We assume three types of investors in our model. First, there are a group of traders who have knowledge of stock values in the future and choose how to trade based on their private information. For simplicity, we also assume the future value follows a binomial distribution. With probability δ, the future stock value is low, $\underset{\_}{V}$, and with probability (1 − δ), the future value is high, $\overline{V}$. It is necessary to clarify here that in our model, some informed traders obtain information through their analyses of publicly available sources, rather than directly from insiders. Therefore, their trading should not be prohibited by regulation.

Second, among the informed traders with favorable private information about the future performance of the issuers, there are one or more potential manipulators who plan to buy many new shares in the issuing market. These informed traders have the potential to trade contrary to their private information. That is, despite their favorable private information, they try to confuse market makers by mimicking the trading behavior of informed traders with unfavorable information, such as selling stocks in the equity market, writing calls, or buying puts in the options market. The actions of these manipulators may reduce the informativeness of stock prices and drive the stock prices below their true values.

Third, there are also many uninformed traders in the market. These traders are assumed to be liquidity traders. The propensity of uninformed traders to buy or sell stocks or options is exogenous. It is assumed that their propensities of buying stocks, selling stocks, buying puts, writing puts, buying calls, writing calls are a, b, c, d, e, and f, respectively. The existence of numerous uninformed traders sustains the trading of “regular” informed traders. The uninformed transactions improve the depth of financial markets, thus increasing market liquidity and making informed trading hard to be detected. The dilution effects of these liquidity transactions, however, increase the difficulty of manipulation to mislead market makers.

Besides these three types of investors, market makers also play an important role in the pricing mechanism. In our model, market makers are assumed to be risk-neutral and competitive. They are also rational traders and have rational expectations of the existence of manipulators. Market makers quote bid and ask prices based on their observation of the trading in both the equity market and options market. Due to the competition among market makers across markets and the homogeneity of the information they hold, there is no arbitrage between the equity market and options market. This means that the call–put parity should hold if there are no additional restrictions.

3.2. Market Transactions, Market Makers’ Rational Expectations, and Manipulators’ Trading Strategies

As discussed earlier, manipulators distort market prices by confusing market makers with trading activities characterized by negative private information. Figure 1 shows the trading propensities of uninformed and informed traders in both the equity and options markets prior to a seasoned equity offering (SEO). We denote by µ and 1 − µ the percentage of informed and uninformed traders, respectively, which will be viewed as an exogenous factor in the following sections. We also denote by ${\alpha }_{\underset{\_}{V}},{\alpha }_{\overline{V}},{\alpha }_m$ an investor’s propensity to trade in the equity market given that they are an informed trader with unfavorable information, a “regular” informed trader with favorable information, or a manipulator, respectively. Similarly, ${\beta }_{\underset{\_}{V}},{\beta }_{\overline{V}},{\beta }_m$ denote an option trader’s propensity to trade calls in the options market if they are an informed trader with unfavorable information, a “regular” informed trader with favorable information, or a manipulator, respectively. κ denotes the anticipated percentage of manipulators (i.e., informed traders with favorable information who trade contrary to their private information) by market makers.

Do market makers price stocks and options based only on trading activities observed in the financial markets? The answer is no. Market makers are rational traders, and they have rational anticipation regarding the existence of manipulators. They ex ante estimate the propensity of an informed trader with favorable information to trade contrary to their information and incorporate this anticipation into the pricing of stocks. Having considered the possibility of manipulation, the market makers will lower their estimation of the probability of low firm values when they observe the “bear” signals.

Figure 1. Market makers’ anticipation of the existence of manipulators.

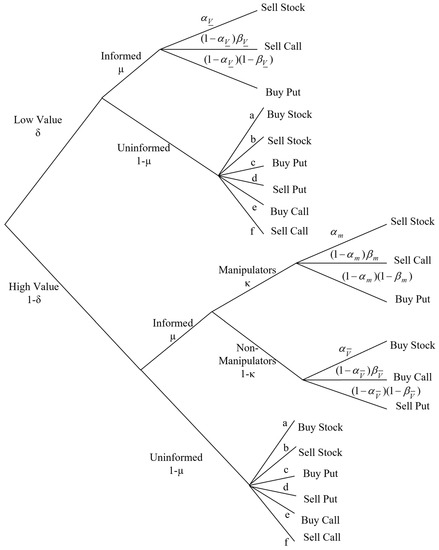
Figure 1. Market makers’ anticipation of the existence of manipulators.

The diagram displays trading strategies of informed and uninformed traders. With the probability δ, the future stock value is low, $\underset{\_}{V}$, and with the probability (1 − δ), the future value is high, $\overline{V}$. µ and 1 − µ denote the percentage of informed and uninformed traders, respectively. ${\alpha }_{\underset{\_}{V}},{\alpha }_{\overline{V}},{\alpha }_m$ denote an investor’s propensity to trade in the equity market given that they are an informed trader with unfavorable information, a “regular” informed trader with favorable information, or a manipulator, respectively. ${\beta }_{\underset{\_}{V}},{\beta }_{\overline{V}},{\beta }_m$ denote an option trader’s propensity to trade calls in the options market if they are an informed trader with unfavorable information, a “regular” informed trader with favorable information, or a manipulator, respectively. κ denotes the anticipated percentage of manipulators by market makers.

3.3. Equilibrium Prices in the Options and Equity Markets in the Presence of Manipulators

Easley et al. (1998) deduce the equilibrium quotes in the options and equity markets in the absence of manipulators. In this section, we will analyze the impact of the existence of manipulators on the equilibrium quotes.

Equilibrium requires the prices set by the market makers to be equal to their expectation of the stock value based on the received orders’ trading directions. We use b_s, a_s, b_c, a_c, b_p, and a_p to denote the bid and ask quotes of stocks, calls, and puts, respectively. We also assume that the number of shares controlled by the option is θ, while that of the stock is γ.

We first determine the quotes for stocks. According to the conditions of equilibrium, the bid quote set for a stock should be equal to its conditional expected value given that a trader sells the stock.4 From Figure 1, we can know that when a trader chooses to sell stock, the probability that the future firm value is low and high is $\delta \left[\mu {\alpha }_{\underset{\_}{V}}+\left(1-\mu \right)b\right]$ and $\left(1-\delta \right)\left(\mu \kappa {\alpha }_m+\left(1-\mu \right)b\right)$, respectively. Therefore,

$$b_s=E[V|Sell\_Stock]=\frac{\underset{\_}{V}\delta \left(\mu {\alpha }_{\underset{\_}{V}}+\left(1-\mu \right)b\right)+\overline{V}\left(1-\delta \right)\left(\mu \kappa {\alpha }_m+\left(1-\mu \right)b\right)}{\delta \mu {\alpha }_{\underset{\_}{V}}+\left(1-\delta \right)\mu \kappa {\alpha }_m+\left(1-\mu \right)b}$$

(1)

Similarly,

$$a_s=E[V|Buy\_Stock]=\frac{\underset{\_}{V}\delta \left(1-\mu \right)a+\overline{V}\left(1-\delta \right)\left[\mu \left(1-\kappa \right){\alpha }_{\overline{V}}+\left(1-\mu \right)a\right]}{\left(1-\delta \right)\mu \left(1-\kappa \right){\alpha }_{\overline{V}}+\left(1-\mu \right)a}$$

(2)

Calculating the first order differentiation coefficient of the bid and ask quotes with respect to κ, we obtain

$$\frac{\partial b_s}{\partial \kappa }=\frac{\left(\overline{V}-\underset{\_}{V}\right)\left(1-\delta \right)\mu {\alpha }_m\delta \left(\mu {\alpha }_{\underset{\_}{V}}+\left(1-\mu \right)b\right)}{{[\delta \mu {\alpha }_{\underset{\_}{V}}+\left(1-\delta \right)\mu \kappa {\alpha }_m+\left(1-\mu \right)b]}^2}>0\mathrm{and}$$

$$\frac{\partial a_s}{\partial \kappa }=\frac{\left(\underset{\_}{V}-\overline{V}\right)\delta \left(1-\mu \right)a}{{[\left(1-\delta \right)\mu \left(1-\kappa \right){\alpha }_{\overline{V}}+\left(1-\mu \right)a]}^2}<0$$

The positive (negative) relationship between κ and b_s (a_s) means that the increase in κ leads to the increase in b_s (decrease in a_s). Therefore, when market makers believe there are manipulators in the market, they will narrow the bid–ask spread because the manipulators’ reverse trading brings no adverse effects but benefits market makers.

The requirement of equilibrium is also applied to the options market. An option is a contingent contract that generates either positive or zero payoff, depending on whether the option will be in or out of the money. Hence, the current value of the option is just the expected value of this positive payoff. We now extend this basic concept to determine the bid and ask prices of call and put options.

Let us first consider the bid price of a call with a strike price Y, where Y is higher than $\underset{\_}{V}$ and less than $\overline{V}$. In the order-driven market, an order that hits the bid price must be a sell order. The knowledge on the sell order allows the market maker to reassess the probability of the high value of the underlying asset conditioned on the sell order. Therefore, the bid value of a call contract with θ units of the underlying asset is equal to the positive payoff, $\left(\overline{V}-Y\right)\theta$, multiplied by the conditional probability of $\overline{V}$ given the sell order. Mathematically,

$$b_c=\left(\overline{V}-Y\right)\theta \frac{\left(1-\delta \right)\left[\mu \kappa \left(1-{\alpha }_m\right){\beta }_m+\left(1-\mu \right)f\right]}{\delta \mu \left(1-{\alpha }_{\underset{\_}{V}}\right){\beta }_{\underset{\_}{V}}+\left(1-\delta \right)\mu \kappa \left(1-{\alpha }_m\right){\beta }_m+\left(1-\mu \right)f}$$

(3)

The ask value of a call contract is like the bid value except for the probability of $\overline{V}$, which is now conditioned on the buy order. Mathematically,

$$a_c=\left(\overline{V}-Y\right)\theta \frac{\left(1-\delta \right)\left[\mu \left(1-\kappa \right)\left(1-{\alpha }_{\overline{V}}\right){\beta }_{\overline{V}}+\left(1-\mu \right)e\right]}{\left(1-\delta \right)\mu \left(1-\kappa \right)\left(1-{\alpha }_{\overline{V}}\right){\beta }_{\overline{V}}+\left(1-\mu \right)e}$$

(4)

Further examining the impact of κ on a_c and b_c, we get

$$\frac{\partial b_c}{\partial \kappa }=\left(\overline{V}-Y\right)\theta \frac{\left(1-\delta \right)\delta \mu \left(1-{\alpha }_m\right){\beta }_m\left[\mu \left(1-{\alpha }_{\underset{\_}{V}}\right){\beta }_{\underset{\_}{V}}+\left(1-\mu \right)f\right]}{{[\delta \mu \left(1-{\alpha }_{\underset{\_}{V}}\right){\beta }_{\underset{\_}{V}}+\left(1-\delta \right)\mu \kappa \left(1-{\alpha }_m\right){\beta }_m+\left(1-\mu \right)f]}^2}>0\mathrm{and}$$

$$\frac{\partial a_c}{\partial \kappa }=\left(\overline{V}-Y\right)\theta \frac{-\left(1-\delta \right)\delta \mu \left(1-{\alpha }_{\overline{V}}\right){\beta }_{\overline{V}}\left(1-\mu \right)e}{{[\left(1-\delta \right)\mu \left(1-\kappa \right)\left(1-{\alpha }_{\overline{V}}\right){\beta }_{\overline{V}}+\left(1-\mu \right)e]}^2}<0$$

The differentiation coefficient of (3) shows that the bid quote increases with the market makers’ estimation of the percentage of manipulators, κ. Similarly, the differentiation coefficient of (4) shows that the ask quote moves inversely with the estimated proportion of manipulators. Therefore, the market makers in the options are also expected to narrow the bid–ask spreads because of the contribution by manipulators.

For a put option with a strike price X, where X is higher than $\underset{\_}{V}$ and less than $\overline{V}$, the put will be in the money only when the future price of the asset is equal to $\underset{\_}{V}$. The bid value and the ask value of a put contract with θ units of the underlying asset are equal to the positive payoff, $\left(X-\underset{\_}{V}\right)\theta$, multiplied by the conditional probabilities of $\underset{\_}{V}$ given the sell order and the buy order, respectively. Mathematically,

$$b_p=\left(X-\underset{\_}{V}\right)\theta \frac{\delta \left(1-\mu \right)d}{\left(1-\delta \right)\mu \left(1-\kappa \right)\left(1-{\alpha }_{\overline{V}}\right)\left(1-{\beta }_{\overline{V}}\right)+\left(1-\mu \right)d}$$

(5)

$$a_p=\left(X-\underset{\_}{V}\right)\theta \frac{\delta \mu \left(1-{\alpha }_{\underset{\_}{V}}\right)\left(1-{\beta }_{\underset{\_}{V}}\right)+\delta \left(1-\mu \right)c}{\delta \mu \left(1-{\alpha }_{\underset{\_}{V}}\right)\left(1-{\beta }_{\underset{\_}{V}}\right)+\left(1-\delta \right)\mu \kappa \left(1-{\alpha }_m\right)\left(1-{\beta }_m\right)+\left(1-\mu \right)c}$$

(6)

Further examining the impact of κ on a_p and b_p, we get

$$\frac{\partial b_p}{\partial \kappa }=\left(X-\underset{\_}{V}\right)\theta \frac{\delta \mu \left(1-\mu \right)d\left(1-\delta \right)\left(1-{\alpha }_{\overline{V}}\right)\left(1-{\beta }_{\overline{V}}\right)}{{[\left(1-\delta \right)\mu \left(1-\kappa \right)\left(1-{\alpha }_{\overline{V}}\right)\left(1-{\beta }_{\overline{V}}\right)+\left(1-\mu \right)d]}^2}>0\mathrm{and}$$

$$\frac{\partial a_p}{\partial \kappa }=-\left(X-\underset{\_}{V}\right)\theta \frac{\left[\delta \mu \left(1-\alpha \underset{\_}{V}\right)\left(1-\beta \underset{\_}{V}\right)+\delta \left(1-\mu \right)c\right]\left(1-\delta \right)\mu \left(1-{\alpha }_m\right)\left(1-{\beta }_m\right)}{{[\delta \mu \left(1-\alpha \underset{\_}{V}\right)\left(1-\beta \underset{\_}{V}\right)+\left(1-\delta \right)\mu \kappa \left(1-{\alpha }_m\right)\left(1-{\beta }_m\right)+\left(1-\mu \right)c]}^2}<0$$

Like other markets, the bid quote increases, while the ask quote decreases due to the existence of manipulation, leading to narrowed bid–ask spreads.

3.4. The Profits and Losses of Informed Traders

Given the anticipation of the existence of manipulative trading prior to an offer, market makers become less pessimistic when they observe “bear” signals, such as selling stocks, writing calls, or buying puts. The market makers’ optimism regarding future stock values benefits informed traders with unfavorable private information because they can trade stocks or options at better prices. Furthermore, the market makers’ response towards “bear” signals increases the difficulty of manipulating stock prices.

3.4.1. Profits of Informed Traders with Unfavorable Information

If an informed trader knows that a future stock value is low, they will choose to either sell stocks, write calls, or buy puts. Their expected profit from selling stocks in the equity market is $\left(b_s-\underset{\_}{V}\right)\gamma$. Specifically, their profit is:

$$P_{uf\_stock}=\left(b_s-\underset{\_}{V}\right)\gamma =\left(\overline{V}-\underset{\_}{V}\right)\left(1-\delta \right)\gamma \frac{\mu \kappa {\alpha }_m+\left(1-\mu \right)b}{\delta \mu {\alpha }_{\underset{\_}{V}}+\left(1-\delta \right)\mu \kappa {\alpha }_m+\left(1-\mu \right)b}$$

(7)

The expected profit from writing calls is

$$P_{uf\_call}=b_c=\left(\overline{V}-Y\right)\left(1-\delta \right)\theta \frac{\mu \kappa \left(1-{\alpha }_m\right){\beta }_m+\left(1-\mu \right)f}{\delta \mu \left(1-{\alpha }_{\underset{\_}{V}}\right){\beta }_{\underset{\_}{V}}+\left(1-\delta \right)\mu \kappa \left(1-{\alpha }_m\right){\beta }_m+\left(1-\mu \right)f}$$

(8)

and the expected profit from buying puts is

$$P_{uf\_put}=-a_p+\left(X-\underset{\_}{V}\right)\theta =\left(X-\underset{\_}{V}\right)\theta \left(1-\delta \right)\frac{\mu \kappa \left(1-{\alpha }_m\right)\left(1-{\beta }_m\right)+\left(1-\mu \right)c}{\delta \mu \left(1-{\alpha }_{\underset{\_}{V}}\right){\beta }_{\underset{\_}{V}}+\left(1-\delta \right)\mu \kappa \left(1-{\alpha }_m\right)\left(1-{\beta }_m\right)+\left(1-\mu \right)c}$$

(9)

Corollary 1.

The profits of informed traders with unfavorable information increase with the market makers’ anticipated probability of manipulation.

$$\left(\frac{\partial P_{uf\_stock}}{\partial \kappa }>0,\frac{\partial P_{uf\_call}}{\partial \kappa }>0,\frac{\partial P_{uf\_put}}{\partial \kappa }>0\right)$$

As indicated earlier, the market makers become more optimistic about a stocks’ future value if they anticipate that some of the “bear” signals are tricks, and this behavior benefits the informed traders with adverse news.

3.4.2. Profits of Non-Manipulative Informed Traders with Favorable Information

For a non-manipulative trader, when they know a future stock value is high, they should choose to trade by buying stocks, buying calls, or writing puts.

If the investor chooses to buy stocks, their expected profit is

$$P_{f\_stock}=\left(-a_s+\overline{V}\right)\gamma =\left(\overline{V}-\underset{\_}{V}\right)\delta \gamma \frac{\left(1-\mu \right)a}{\left(1-\delta \right)\mu \left(1-\kappa \right){\alpha }_{\overline{V}}+\left(1-\mu \right)a}$$

(10)

If they chooses to buy calls, the expected profit they will earn is

$$P_{f\_call}=-a_c+\left(\overline{V}-Y\right)\theta =\left(\overline{V}-Y\right)\delta \theta \frac{\left(1-\mu \right)e}{\left(1-\delta \right)\mu \left(1-\kappa \right)\left(1-{\alpha }_{\overline{V}}\right){\beta }_{\overline{V}}+\left(1-\mu \right)e}$$

(11)

while if they choose to write puts, the expected profit is

$$P_{f\_put}=b_p=\left(X-\underset{\_}{V}\right)\delta \theta \frac{\left(1-\mu \right)d}{\left(1-\delta \right)\mu \left(1-\kappa \right)\left(1-{\alpha }_{\overline{V}}\right)\left(1-{\beta }_{\overline{V}}\right)+\left(1-\mu \right)d}$$

(12)

Corollary 2.

The profits of non-manipulative informed traders with favorable information increase with the market makers’ anticipated probability of manipulation.

$$\left(\frac{\partial P_{f\_stock}}{\partial \kappa }>0,\frac{\partial P_{f\_call}}{\partial \kappa }>0,\frac{\partial P_{f\_put}}{\partial \kappa }>0\right)$$

In the presence of market makers’ anticipation of manipulation, informed traders that trade on private information earn more. Moreover, the profits earned by these informed traders increase with the market makers’ anticipation of κ. The reason is that the reverse trading of manipulators reduces the true information incorporated into the stock prices, and thus these “regular” informed traders can buy stocks and calls at relatively lower prices or write puts at relatively higher prices.

3.4.3. Losses of Manipulators in the Secondary Markets

In a continuous market, no informed trader would trade contrary to their private information, as losses will be incurred by doing so. However, if such a trader can purchase many new shares from the issuing market, they may choose to disguise their information by trading in the opposite direction.

The expected loss of manipulators if they sell stocks is

$$P_{m\_stock}=\left(b_s-\overline{V}\right)\gamma =\left(\overline{V}-\underset{\_}{V}\right)\delta \gamma \frac{-\mu {\alpha }_{\underset{\_}{V}}-\left(1-\mu \right)b}{\delta \mu {\alpha }_{\underset{\_}{V}}+\left(1-\delta \right)\mu \kappa {\alpha }_m+\left(1-\mu \right)b}$$

(13)

The expected loss of writing calls is

$$P_{m\_call}=b_c-\left(\overline{V}-Y\right)\delta \theta =\left(\overline{V}-Y\right)\delta \theta \frac{-\mu \left(1-{\alpha }_{\underset{\_}{V}}\right){\beta }_{\underset{\_}{V}}-\left(1-\mu \right)f}{\delta \mu \left(1-{\alpha }_{\underset{\_}{V}}\right){\beta }_{\underset{\_}{V}}+\left(1-\delta \right)\mu \kappa \left(1-{\alpha }_m\right){\beta }_m+\left(1-\mu \right)f}$$

(14)

and the expected loss of buying puts is

$$P_{m\_put}=-a_p=\left(X-\underset{\_}{V}\right)\delta \theta \frac{-\mu \left(1-{\alpha }_{\underset{\_}{V}}\right)\left(1-{\beta }_{\underset{\_}{V}}\right)-\left(1-\mu \right)c}{\delta \mu \left(1-{\alpha }_{\underset{\_}{V}}\right)\left(1-{\beta }_{\underset{\_}{V}}\right)+\left(1-\delta \right)\mu \kappa \left(1-{\alpha }_m\right)\left(1-{\beta }_m\right)+\left(1-\mu \right)c}$$

(15)

Corollary 3.

The losses incurred by manipulators decrease with the market makers’ anticipated probability of manipulation.

$$\left(\frac{\partial P_{m\_stock}}{\partial \kappa }<0,\frac{\partial P_{m\_call}}{\partial \kappa }<0,\frac{\partial P_{m\_put}}{\partial \kappa }<0\right)$$

From Corollary 3, we know that the anticipation of manipulation reduces the manipulators’ losses caused by converse trading. However, this is not good news to manipulators because their objective is to drive the stock price down and recoup losses through purchasing shares at a reduced offer price. The reduced losses reflect that it is more difficult for manipulators to distort the stock market through converse trading if their incentives are anticipated. Therefore, it is predicted that the rational anticipation of market makers can to some extent inhibit manipulative behaviors.

3.5. The Trading Strategies of Different Types of Traders

Having known the expected profits and losses of informed traders in the equity, calls, and puts markets, in this section, we try to find the equilibrium of the propensity of each type of trader to choose a trading vehicle. Equilibrium requires that the expected profits of a trader to trade in any of the three markets are the same. Specifically, we need to find the values of ${\alpha }_{\underset{\_}{V}},{\alpha }_{\overline{V}},{\alpha }_m$ and ${\beta }_{\underset{\_}{V}},{\beta }_{\overline{V}},{\beta }_m$ to make Equation (7) = (8) = (9), (10) = (11) = (12), and (13) = (14) = (15) simultaneously satisfied. For simplicity, we assume the strike prices of puts and calls are the same, i.e., X = Y.

3.5.1. Trading Strategies of Informed Traders

Proposition 1.

Given the constant anticipation of the percentage of manipulators, κ, the values of${\alpha }_{\underset{\_}{V}},{\alpha }_{\overline{V}},{\alpha }_m$and${\beta }_{\underset{\_}{V}},{\beta }_{\overline{V}},{\beta }_m$required by the multi-market equilibrium are as follows:

(a) 

${\alpha }_{\overline{V}}=\frac{a\left[\left(d+e\right)\left(1-\mu \right)\left(\gamma -\theta \right)+\gamma \left(1-\delta \right)\mu \left(1-\kappa \right)\right]}{\left(1-\delta \right)\mu \left[\left(d+e\right)\theta +\gamma a\right]\left(1-\kappa \right)}$

(b) 

${\alpha }_{\underset{\_}{V}}=\frac{\left[\mu +\left(1-\mu \right)\left(b+c+f\right)\right]\kappa {\alpha }_m+\left(1-\kappa \right)\left(1-\mu \right)b}{\mu \kappa +\left(1-\mu \right)\left(b+c+f\right)}$

(c) 

${\beta }_m=0$

(d) 

${\beta }_{\overline{V}}=\frac{e}{d+e}$

(e) 

${\beta }_{\underset{\_}{V}}=\frac{\left(1-\mu \right)f\left[\left(1-{\alpha }_{\underset{\_}{V}}\right)-\kappa \left(1-{\alpha }_m\right)\right]}{\left[\mu \kappa \left(1-{\alpha }_m\right)+\left(1-\mu \right)\left(c+f\right)\right]\left(1-{\alpha }_{\underset{\_}{V}}\right)}$

Condition (a) suggests an equilibrium propensity of informed traders with favorable information to trade in the equity market. Increase in the relative leverage in the options market, (γ−θ), induces more informed traders with favorable information to trade in the options market. However, the increase in market makers’ anticipation of the presence of manipulators drives more such informed traders to trade in the equity market. The informed traders’ movement from the options market to the equity market is due to the asymmetric impacts of manipulative trading in the equity and options markets. The manipulation in the equity market not only affects market makers’ estimation of the probability of low future stock value, δ, but also directly improves the supply in the equity market, which drives the stock price down. As discussed in the last section, the informed traders with favorable information benefit from manipulative trading. The distortion effects of manipulation through equity trading are more direct and effective than those through options trading. Therefore, informed traders move to the equity market to enjoy more benefits from manipulation.

Condition (b) shows how the manipulators’ propensity to trade in the equity market relates to that of informed traders with bad information. It is easily seen that ${\alpha }_{\underset{\_}{V}}$ increases with $\kappa {\alpha }_m$. This is because informed traders with negative information can earn more by making themselves look more like manipulators. However, these informed traders would not exactly copy the strategies of manipulators; they will be able to make more profits by concealing their information in large volumes of uninformed trading. Therefore, the relative market depth, b/(b + c + f), is also a consideration for this type of informed trader.

Condition (c) tells us that all manipulators who trade in the options market will choose to manipulate the stock price by buying puts. This condition also accords with practice. When the future stock value is indeed high, the loss of buying a put is fixed while the loss of writing a call is infinite. In order to limit their losses in the options market, the optimal choice for manipulators is to buy puts. The important underlying assumption here is that call trading and put trading of the same volume have the same force in depressing stock prices.

Condition (d) shows that the propensity of informed traders with favorable information to select calls or puts is a function of the relative depth of the call and put markets. The informed traders are more likely to choose the market that has a larger trading volume or higher open interest. The high trading volume and open interest in the market increase its liquidity, which make the informed traders’ trading less likely to be detected by market makers. In addition, we can observe that such informed traders’ choices of trading venues are unaffected by the existence of manipulators.

Condition (e) indicates that as the anticipated percentage of manipulators increases, the informed traders with unfavorable information are less likely to trade through writing calls. Recall that in the last section, we report that, in the presence of manipulators, informed traders with unfavorable private information can profit more because when they trade on their information, it is difficult for market makers to distinguish their orders from those of manipulators. Therefore, it is advisable for such informed traders to try their best to mimic the trading strategies of manipulators, that is, by buying puts. However, unlike manipulators, informed traders are also concerned with their trading being detected by market makers. For this reason, besides simply following the strategies of manipulators, they also tend to trade in more liquid markets where they can easily hide in the crowds of uninformed traders. As Condition (d) shows, the relative increase in depth in the call market will attract more such informed trading.

3.5.2. The Trading Strategies of Uninformed Traders

In the preceding sections, the uninformed traders’ propensity to trade is assumed to be exogenous and constant. In fact, uninformed traders are also rational traders who adjust their trade strategies upon their anticipations and observations of each market. Like the market makers, the uninformed traders have a rational anticipation of the existence of manipulators. Without this anticipation, the uninformed would follow the informed traders to sell stocks, write calls, or buy puts when they perceive abnormal transactions. However, having anticipated the potential for manipulation, the uninformed view the “bear” signals more optimistically. They are more likely to trade against the transaction directions that they observe from the equity or options markets. Moreover, the higher the anticipated probability of manipulation, the less likely they follow the informed traders.

Based on this reasoning, during the pre-offer period, the uninformed are more likely to buy stocks, buy calls, and write puts. Specifically, over this period, a, d, and e are expected to increase, while b, c, and f are predicted to decrease. The actions of the uninformed play a role in supporting the stock price in the secondary market, making the manipulation more difficult to conduct correspondingly.

3.6. Mechanism of Distorting Stock Prices and Rational Anticipation of the Market Makers

In this section, we analyze under what situations an informed trader with favorable information will choose to trade by or against their private information. We further study whether market makers’ rational anticipation of the presence of manipulation would increase the difficulty of manipulative actions.

3.6.1. Manipulative Behavior in the Absence of Market Makers’ Anticipation

Before we study an informed trader’s potential to become a manipulator, it is necessary to make clear how a manipulator distorts stock prices. Market makers make judgments of the possibility of a low future stock value, δ, based on their observation of “bear” signals in both the equity and options markets. If they observe more “bear” signals in the markets, they will adjust their estimation of δ upward; if they observe more “bull” signals, they will decrease the estimation of δ. Manipulators mimic the trading of informed traders with bad information and send distorted signals to market makers, thus leading market makers to increase the estimated likelihood of low future stock values and depressing prices in the secondary market.

Assume a future stock price is high. When there is no informed trader who will take part in manipulation, market makers’ belief would be that δ = δ₀ where 0 < = δ₀ < = 1. Their belief would switch to δ = δ₁ where 0 < δ₀ < δ₁ < 1 when all the informed traders are manipulators. When the future stock price is high with a probability ρ, the informed traders will manipulate the stock prices, and the manipulative trading will lead market makers to believe that the possibility of low future values is δ₀ + ρ⋅(δ₁ − δ₀). It is worth noting that if there is no manipulator, the market makers can make accurate judgments about the future stock value. For further analysis, we assume that an informed trader with favorable information will be allocated λ shares in seasoned equity offerings. For simplicity, we also assume that offer prices are at the quote price and bid–ask spreads are immaterial relative to the stock price so that they can be ignored.

An informed trader determines whether to manipulate the stock price by comparing profits from trading against their private information. If the informed trader trades on their private information, the total expected profits from both the secondary market and the issuing market are

$$\left(-a_s+\overline{V}\right)\gamma +\left(\overline{V}-a_s\right)\lambda =\left(\overline{V}-\underset{\_}{V}\right){\delta }_0\left(\gamma +\lambda \right)\frac{\left(1-\mu \right)a}{\left(1-{\delta }_0\right)\mu {\alpha }_{\overline{V}}+\left(1-\mu \right)a}$$

(16)

Consider the total expected profits from trading if traders are informed with unfavorable information:

$$\left(b_s-\overline{V}\right)\gamma +\left(\overline{V}-b_s\right)\lambda =\left(\overline{V}-\underset{\_}{V}\right)\left[\left({\delta }_1-{\delta }_0\right)\rho +{\delta }_0\right]\left(\lambda -\gamma \right)\frac{\mu {\alpha }_{\underset{\_}{V}}+\left(1-\mu \right)b}{\left[\left({\delta }_1-{\delta }_0\right)\rho +{\delta }_0\right]\mu {\alpha }_{\underset{\_}{V}}+\left(1-\mu \right)b}$$

(17)

If λ is larger than γ, the total expected profits from manipulation increase with the propensity of manipulation, ρ. The maximum profits are

$$\left(\overline{V}-\underset{\_}{V}\right)\left(\lambda -\gamma \right){\delta }_1\frac{\mu {\alpha }_{\underset{\_}{V}}+\left(1-\mu \right)b}{{\delta }_1\mu {\alpha }_{\underset{\_}{V}}+\left(1-\mu \right)b}$$

when all informed traders choose to conduct converse trading. An informed trader will not manipulate the stock price only when the following condition is not satisfied.

$$\left(\gamma +\lambda \right){\delta }_0\frac{\left(1-\mu \right)a}{\left(1-{\delta }_0\right)\mu {\alpha }_{\overline{V}}+\left(1-\mu \right)a}<\left(\lambda -\gamma \right){\delta }_1\frac{\mu {\alpha }_{\underset{\_}{V}}+\left(1-\mu \right)b}{{\delta }_1\mu {\alpha }_{\underset{\_}{V}}+\left(1-\mu \right)b}$$

(18)

First, the more shares an informed trader, λ, is allocated, the more likely they will distort the stock prices. Second, market makers’ higher estimation of the probability of informed traders, µ, makes the manipulation relatively easier. Third, the higher the propensity of regular informed traders to trade on the equity market (${\alpha }_{\underset{\_}{V}}$ and ${\alpha }_{\overline{V}}$), the easier the manipulation will be. Lastly, the minimum and maximum estimations of the probability of low future values, δ₀ and δ₁, are also important factors. The lower value of δ₀ or the higher value of δ₁ facilitates the manipulative trading. The difference between δ₀ and δ₁ reflects the sensitivity of market makers to the “bear” signals.

3.6.2. Manipulative Trading with the Presence of Market Makers’ Anticipation

In Section 3.4, we analyze the profits and losses from trading in the presence of market makers’ rational anticipation of manipulators. From (13) to (15), we find that the rational expectation of market makers increases the difficulty of distorting stock prices by sending “bear” signals. In this section, we will further analyze the impacts of rational anticipation on informed traders’ manipulative actions.

Given the rational anticipation of market makers, κ, the total expected profits from trading on private information are

$$\left(-a_s+\overline{V}\right)\gamma +\left(\overline{V}-a_s\right)\lambda =\left(\overline{V}-\underset{\_}{V}\right){\delta }_0\left(\gamma +\lambda \right)\frac{\left(1-\mu \right)a}{\left(1-{\delta }_0\right)\mu \left(1-\kappa \right){\alpha }_{\overline{V}}+\left(1-\mu \right)a}$$

while the total expected profits from trading against private information are

$$\left(b_s-\overline{V}\right)\gamma +\left(\overline{V}-b_s\right)\lambda =\left(\overline{V}-\underset{\_}{V}\right)\left[\left({\delta }_1-{\delta }_0\right)\rho +{\delta }_0\right]\left(\lambda -\gamma \right)\frac{\mu {\alpha }_{\underset{\_}{V}}+\left(1-\mu \right)b}{\left[\left({\delta }_1-{\delta }_0\right)\rho +{\delta }_0\right]\mu {\alpha }_{\underset{\_}{V}}+\left(1-\left({\delta }_1-{\delta }_0\right)\rho -{\delta }_0\right)\mu \kappa {\alpha }_m+\left(1-\mu \right)b}$$

An informed trader determines to distort stock prices only when the following inequality holds.

$$\left(\gamma +\lambda \right){\delta }_0\frac{\left(1-\mu \right)a}{\left(1-{\delta }_0\right)\mu \left(1-\kappa \right){\alpha }_{\overline{V}}+\left(1-\mu \right)a}<\left(\lambda -\gamma \right){\delta }_1\frac{\mu {\alpha }_{\underset{\_}{V}}+\left(1-\mu \right)b}{{\delta }_1\mu {\alpha }_{\underset{\_}{V}}+\left(1-{\delta }_1\right)\mu \kappa {\alpha }_m+\left(1-\mu \right)b}$$

(19)

In addition to the specific implications stated in Section 5.1, we find that the increase in κ makes manipulation more costly but makes non-manipulative informed trading more profitable. Therefore, informed traders have less incentive to trade conversely in the presence of market makers’ rational expectations.

3.7. Short Sales Constraints and SEO Pre-Offer Market

3.7.1. Short Sales Constraints and Bid–Ask Spreads in Each Market

We first analyze the impacts on quotes when both manipulative trading and “informative” trading in the equity market are restricted. From Equation (1), we find that, differing from informed trading in the options market, informed trading in the equity market not only affects the market makers’ estimation of δ, but also drives the stock prices down directly by breaking the balancing of supply and demand. Therefore, it is predicted that although informed traders can circumvent the short sales constraints via options markets, the impact of such trading on market makers’ quote setting is smaller.

We anatomize the impacts of short sales constraints on the bid and ask quotes here. First, we examine the equity market. Recall from Equations (1) and (2) that the ask in the equity market is not affected by this constraint. However,

$$\frac{\partial b_s}{\partial {\alpha }_{\underset{\_}{V}}}=\frac{\left(\underset{\_}{V}-\overline{V}\right)\delta \mu \left(1-\delta \right)\left[\mu \kappa {\alpha }_m+\left(1-\mu \right)b\right]}{{[\delta \mu {\alpha }_{\underset{\_}{V}}+\left(1-\delta \right)\mu \kappa {\alpha }_m+\left(1-\mu \right)b]}^2}<0\mathrm{and}$$

$$\frac{\partial b_s}{\partial \kappa {\alpha }_m}=\frac{\left(\overline{V}-\underset{\_}{V}\right)\left(1-\delta \right)\mu \delta \left[\mu {\alpha }_{\underset{\_}{V}}+\left(1-\mu \right)b\right]}{{[\delta \mu {\alpha }_{\underset{\_}{V}}+\left(1-\delta \right)\mu \kappa {\alpha }_m+\left(1-\mu \right)b]}^2}>0$$

This means that the decrease in ${\alpha }_{\underset{\_}{V}}$ leads to the increase in $b_s$, narrowing the bid–ask spread. This is due to the informed traders moving out of the equity market. Conversely, the decrease in ${\alpha }_m$ drives the bid quotes down, widening bid–ask spreads. Manipulators trade against their private information, so their trading does no harm to market makers, but benefits them instead. Therefore, the bid–ask spread decreases when there is manipulation. When manipulation in the equity market is restricted, market makers should re-open the spread.

It is worth noting that when we compare the bid–ask spread during the pre-restricted period with the restricted period under Regulation M, we only need to consider the impacts of ${\alpha }_{\underset{\_}{V}}$ because, under the short sales constraints, there is no manipulator in both periods. The decreases in ${\alpha }_{\underset{\_}{V}}$ is associated with the narrowing of the bid–ask spread, so it is predicted that the bid–ask spread decreases during the restricted period under this regulation.

Second, we examine the calls market. From Equations (3) and (4), it is easy to observe that $\frac{\partial b_c}{\partial {\alpha }_{\underset{\_}{V}}}>0$, $\frac{\partial b_c}{\partial {\alpha }_m}<0$ while $\frac{\partial a_c}{\partial {\alpha }_{\underset{\_}{V}}}=\frac{\partial a_c}{\partial {\alpha }_m}=0$. These facts show that the ask quotes are unaffected by short sales constraints. However, decreases in ${\alpha }_{\underset{\_}{V}}$ lower bid quotes, widening the bid–ask spread, while decreases in ${\alpha }_m$ uplift bid quotes, narrowing the bid–ask spread.

Similarly, from Equations (5) and (6), we find that $\frac{\partial a_p}{\partial {\alpha }_{\underset{\_}{V}}}<0$, $\frac{\partial a_p}{\partial {\alpha }_m}>0$ while $\frac{\partial b_p}{\partial {\alpha }_{\underset{\_}{V}}}=\frac{\partial b_p}{\partial {\alpha }_m}=0$. In the put market, the restriction on ${\alpha }_{\underset{\_}{V}}$ uplifts the ask quotes and thus widens the bid–ask spread, while the restriction on ${\alpha }_m$ lowers the ask quotes and hence narrows the bid–ask spread.

The movement directions of the quotes and changes in the bid–ask spread in both the equity market and the options market are summarized in

Table 1. Effects of short sales constraints on bid–ask spreads.

	$\mathbf{Decrease}\mathbf{in}{\mathit{\alpha }}_{\underset{\_}{\mathit{V}}}$	$\mathbf{Decrease}\mathbf{in}{\mathit{\alpha }}_{\mathit{m}}$
$b_s$	Increase	Decrease
$a_s$	No change	No change
Bid–ask spread in the stock market	Decrease	Increase
$b_c$	Decrease	Increase
$a_c$	No change	No change
Bid–ask spread in the call market	Increase	Decrease
$b_p$	No change	No change
$a_p$	Increase	Decrease
Bid–ask spread in the put market	Increase	Decrease

The table summarizes the directions of changes in bid prices, ask prices, and bid–ask spreads in the equity market and the options market when the informed traders with unfavorable information and the manipulators decrease their propensity to trade. b_s, a_s, b_c, a_c, b_p, and a_p denote the bid and ask prices of the stock, the call, and the put. ${\alpha }_{\underset{\_}{V}}$ and ${\alpha }_m$ are the propensities to trade the stock by the informed traders with unfavorable information and the manipulators.

.

The market makers of the options markets widen the bid–ask spread because more informed traders are driven to the options market. However, anticipating that more manipulators may trade in the options market, market makers decrease the bid–ask spread correspondingly.

3.7.2. Short Sales Constraints and Venues of Informed Trading

When short sales are restricted in the equity market, both informed traders with unfavorable information and potential manipulators move to options markets to conduct synthetic short sales, such as writing calls or buying puts. It is intriguing to analyze whether the short sales constraint in the equity market has influence on the informed traders’ choice between puts markets and calls markets. For simplicity, we assume that the trading of both types of traders is completely prohibited by short sales constraints. Specifically, it is assumed that ${\alpha }_m=0$ and ${\alpha }_{\underset{\_}{V}}=0$ during the SEC rules’ restricted period.

Proposition 2.

With the existence of the strict short sales constraints in the equity market, and given the anticipation of a constant percentage of manipulators, κ, the values of ${\alpha }_{\overline{V}}$and${\beta }_{\underset{\_}{V}},{\beta }_{\overline{V}},{\beta }_m$required by the multi-market equilibrium are as follows:

(a) 

${\alpha }_{\overline{V}}=\frac{a\left[\left(d+e\right)\left(1-\mu \right)\left(\gamma -\theta \right)+\gamma \left(1-\delta \right)\mu \left(1-\kappa \right)\right]}{\left(1-\delta \right)\mu \left[\left(d+e\right)\theta +\gamma a\right]\left(1-\kappa \right)}$

(b) 

${\beta }_m=0$

(c) 

${\beta }_{\overline{V}}=\frac{e}{d+e}$

(d) 

${\beta }_{\underset{\_}{V}}=\frac{\left(1-\mu \right)f\left(1-\kappa \right)}{\mu \kappa +\left(1-\mu \right)\left(c+f\right)}$

Corollary 4.

Decrease in${\alpha }_{\underset{\_}{V}}$leads to an increase in${\beta }_{\underset{\_}{V}}$, while a decrease in${\alpha }_m$leads to a decrease in${\beta }_{\underset{\_}{V}}$. (Recall that${\beta }_{\underset{\_}{V}}=\frac{\left(1-\mu \right)f\left[\left(1-{\alpha }_{\underset{\_}{V}}\right)-\kappa \left(1-{\alpha }_m\right)\right]}{\left[\mu \kappa \left(1-{\alpha }_m\right)+\left(1-\mu \right)\left(c+f\right)\right]\left(1-{\alpha }_{\underset{\_}{V}}\right)}$when${\alpha }_{\underset{\_}{V}}\ne 0$.).

Comparing Proposition 2 with Proposition 1, we find that the short sales constraint has no effects on the choice of the informed with favorable information (Condition (a) and Condition (c)). Moreover, manipulators still tend to choose the put markets as their trading venue (Condition (b)).

However, the choice of informed traders with adverse information is little complicated by the existence of manipulators. On one hand, a decrease in ${\alpha }_m$ leads to a decrease in ${\beta }_{\underset{\_}{V}}$. As more manipulators shift to the puts market, more informed traders with unfavorable information choose to trade puts to earn profits by mimicking manipulators. On the other hand, the decrease in ${\alpha }_{\underset{\_}{V}}$ is associated with the increase in ${\beta }_{\underset{\_}{V}}$. The reason for the negative relation between ${\alpha }_{\underset{\_}{V}}$ and ${\beta }_{\underset{\_}{V}}$ is that if too many informed traders crowd in the put markets, the “bear” signaling is so powerful that both market makers and the uninformed tend to downgrade their estimation of stock value, which harms the informed traders with unfavorable information. Therefore, if too many informed traders are jammed in the puts market, some informed traders with bad information should move to the call markets.

3.7.3. Short Sales Constraints and Manipulative Conduct

Short Sales Constraints and Cost of Manipulation

Recall the inequality in Equation (18) in Section 3.6. This is the condition required to motivate an informed trader to distort stock price in the equity market. We can observe that if informed traders with negative news are barred from trading in the equity market, the value on the right of the inequality decrease. This means that it is more costly to conduct manipulation of stock prices through equity trading under the strict short sales constraints.

We investigate the difficulty of manipulation through options trading by considering the expected profits of options traders based on their private information:

$$b_p+\left(\overline{V}-a_s\right)\lambda =\left(\overline{V}-\underset{\_}{V}\right){\delta }_0\left[\theta \frac{\left(1-\mu \right)d}{\left(1-{\delta }_0\right)\mu \left(1-{\alpha }_{\overline{V}}\right)\left(1-{\beta }_{\overline{V}}\right)+\left(1-\mu \right)d}+\lambda \frac{\left(1-\mu \right)a}{\left(1-{\delta }_0\right)\mu {\alpha }_{\overline{V}}+\left(1-\mu \right)a}\right]$$

(20)

while the maximized expected profits from trading against private information in the options market is

$$-a_p+\left(\overline{V}-a_s\right)\lambda =\left(\overline{V}-\underset{\_}{V}\right){\delta }_1\left[-\theta \frac{\mu \left(1-{\alpha }_{\underset{\_}{V}}\right)\left(1-{\beta }_{\underset{\_}{V}}\right)+\left(1-\mu \right)c}{{\delta }_1\mu \left(1-{\alpha }_{\underset{\_}{V}}\right)\left(1-{\beta }_{\underset{\_}{V}}\right)+\left(1-\mu \right)c}+\gamma \frac{\left(1-\mu \right)a}{\left(1-{\delta }_1\right)\mu {\alpha }_{\overline{V}}+\left(1-\mu \right)a}\right]$$

(21)

Informed traders manipulate stock prices only when (20) < (21). We can see that the decrease in ${\alpha }_{\underset{\_}{V}}$ causes the value of the right-hand side to drop. Therefore, if short sales constraints drive more informed traders with negative information out of the equity market, manipulation of the options market will also be more difficult.

As discussed in Section 3.4, the impacts of informed trading via equity markets on the stock price are more direct and pronounced. Although informed trading in the options market may have influence on the stock prices, the impacts are less material. The mitigated influences bring more profits to informed traders with unfavorable private information and make the manipulators’ plan more difficult to realize. Therefore, while the strict short sales constraints in the equity market do not inhibit synthetic short sales via options transactions, they indirectly increase the cost of distorting stock prices, thus at least partially lessening the manipulation problem.

Short Sales Constraints and Market Makers’ Adjustments of Estimations

Besides making the manipulation more costly, short sale constraints may also make the manipulative trading more likely to be detected. An informed trader with unfavorable information can earn more from cheating market makers by camouflaging as a manipulator or hiding their trading in a market with many uninformed traders. Manipulators hope their transactions are mistaken by market makers as those of informed traders with unfavorable private information. Recall Condition (e) in Proposition 1; when stocks can be shorted freely in the equity market, ${\alpha }_{\underset{\_}{V}}$ and ${\alpha }_m$ are positively correlated, and both manipulators and informed traders with bad information are inclined to trade in the equity market. For manipulators, it is easier to drive the stock prices down when trading in the equity markets. For informed traders who predict low future stock values, the equity market is relatively more liquid, and thus it is easier to hide their trading. In other words, the trading strategies of manipulators and informed traders with unfavorable information are pooling, thus making it harder for market makers to distinguish between the two.

However, when the short sales in the equity market are restricted, the case is totally different. Due to strict short sales constraints in the equity markets, both manipulators and informed traders with bad information will move from equity markets to options markets. In the options market, manipulators tend to trade puts, and informed traders with bad information base their decision partly upon market liquidity. Therefore, when the call options market is relatively more liquid, informed traders are inclined to trade in the call options market, while manipulators are more likely to be put traders whose losses from converse trading are relatively small, and their trading is more likely to be mistaken as informed trading. Under this situation, the trading strategies of manipulators and informed traders are separating. The separation facilitates market makers to identify each trader’s type and makes manipulation more difficult.

For this reason, when the call market is more liquid, manipulators’ trading of put options is easier to be detected, which makes the manipulative effects of trading calls abated. Thus, it is reasonable to assume that the market makers’ estimation of the probability of low future stock values is adjusted to $\left(\eta {\delta }_1-{\delta }_0\right)\rho +{\delta }_0$. Here, η < 1. Under this situation, to earn more profits from trading against private information than trading on private information, the following inequality should be satisfied:

$${\delta }_0\left[\theta \frac{\left(1-\mu \right)d}{\left(1-{\delta }_0\right)\mu \left(1-{\alpha }_{\overline{V}}\right)\left(1-{\beta }_{\overline{V}}\right)+\left(1-\mu \right)d}+\lambda \frac{\left(1-\mu \right)a}{\left(1-{\delta }_0\right)\mu {\alpha }_{\overline{V}}+\left(1-\mu \right)a}\right]<{\delta }_1\left[\gamma \frac{\left(1-\mu \right)a}{\left(1-{\delta }_1\right)\mu {\alpha }_{\overline{V}}+\left(1-\mu \right)a}-\theta \frac{\mu \left(1-{\alpha }_{\underset{\_}{V}}\right)\left(1-{\beta }_{\underset{\_}{V}}\right)+\left(1-\mu \right)c}{\eta {\delta }_1\mu \left(1-{\alpha }_{\underset{\_}{V}}\right)\left(1-{\beta }_{\underset{\_}{V}}\right)+\left(1-\mu \right)c}\right]$$

(22)

η decreases the value of the right side of Equation (22), which implies an increase in the difficulty of manipulation. Based on the above analysis, we can learn that though the synthetic short sales are not directly restricted by Rule 10b-21, they would still be harnessed, especially when the call market is relatively more liquid.

4. Data

Our model predicts that if informed traders choose to manipulate the options market, they are more likely to select puts as a manipulating vehicle. In addition, it is very costly for manipulators to successfully distort stock prices under strict short sales constraints. In the following sections, we will empirically investigate the trading activities of different kinds of traders in the pre-offer market.

Our sample includes 237 firms that issued SEOs on the NYSE and had options listed on any U.S. options exchange from April 2002 to December 2004. The SEO sample is obtained from the Security Data Company (SDC). Units, rights, and closed-end funds are excluded from our sample. Following Safieddine and Wilhelm (1996) and Corwin (2003), we designate the day following the SDC offer date as the offer date if, on the day following the SDC offer date, the trading volume is more than twice the trading volume on the SDC offer date and more than twice the average daily trading volume over the 250 trading days before the offer.

The daily options data are collected from DeltaNeutral.com.5 The data provided by DeltaNeutral are for every optionable stock, index, and ETF in U.S. markets. They consist of the underlying stock symbols, underlying stock price, option symbol root, option extension, contract type, expiration date, quote date, strike, last transaction price, last bid price, last ask price, trading volume, and open interest. Intraday stock trading and quote data are from the Trade and Quote Database (TAQ), while stocks’ daily data, such as the daily stock price and daily trading volume are from the Center for Research in Security Prices (CRSP).

5. Empirical Results

5.1. Volume, Open Interest, and Spread for Calls, Puts around SEO Pricing

The analysis in Section 3 is based on a simple static equilibrium model (i.e., no time element). In actual market behavior, for example, informed traders and manipulators likely adjust their propensities to trade in response to changes in the bid and ask quotes set by market makers.6 After the implementation of Rule 10b-21, short sales are restricted in the equity market, so informed traders with unfavorable information and manipulators must move to the options market. We therefore expect that the trading volume and open interest in the options market will obviously increase prior to SEO pricing.

Table 2. Change in volume, open interest, and spread for calls, puts around SEO pricing.

Panel A: Calls
Day	Volume		Open Interest		Spread		Call/Stock (Volume)
	Level	Change	Level	Change	Level	Change	Level	Change
−5	724.26	0.3778 ***	23,340.38	0.0749 ***	0.1643	−0.0196	0.0334	0.1725 **
		(0.0000)		(0.0098)		(0.5064)		(0.0293)
−4	747.78	0.2532 ***	23,720.24	0.0574 *	0.1634	−0.0258	0.0305	0.0626
		(0.0026)		(0.0601)		(0.4186)		(0.4142)
−3	585.76	0.3220 ***	20,775.27	0.0564 *	0.1633	−0.0009	0.0294	0.0873
		(0.0001)		(0.0528)		(0.9783)		(0.2647)
−2	795.01	0.4099 ***	22,955.15	0.0458	0.1635	−0.0158	0.0353	0.1460 *
		(0.0000)		(0.1091)		(0.6217)		(0.0666)
−1	1124.57	0.5335 ***	22,397.54	0.0508 *	0.1618	−0.0025	0.0510	−0.0143
		(0.0000)		(0.0813)		(0.9445)		(0.8592)
0	1532.21	1.2263 ***	23,131.71	0.0794 ***	0.1687	0.0298	0.0191	−0.306 ***
		(0.0000)		(0.0038)		(0.3998)		(0.0002)
1	1063.74	0.8102 ***	23,507.88	0.1566 ***	0.1712	0.0302	0.0228	−0.0937
		(0.0000)		(0.0000)		(0.4108)		(0.2481)
2	915.78	0.4921 ***	23,877.86	0.1945 ***	0.1615	0.0022	0.0280	0.0071
		(0.0000)		(0.0000)		(0.9501)		(0.9293)
3	848.44	0.4220 ***	23,110.39	0.2012 ***	0.1724	0.0419	0.0277	0.0143
		(0.0000)		(0.0000)		(0.2804)		(0.8553)
4	576.92	0.3150 ***	23,153.83	0.2075 ***	0.1683	0.0261	0.0230	−0.0416
		(0.0006)		(0.0000)		(0.4908)		(0.6047)
5	746.23	0.2779 ***	23,187.22	0.2291 ***	0.1756	0.0329	0.0297	−0.0397
		(0.0051)		(0.0000)		(0.4220)		(0.6540)
Panel B: Puts.
Day	Volume		Open Interest		Spread		Put/Stock (Volume)
	Level	Change	Level	Change	Level	Change	Level	Change
−5	470.23	0.2795 ***	20,764.37	0.0868 **	0.2283	−0.0116	0.0218	0.1690 **
		(0.0008)		(0.0129)		(0.7175)		(0.0262)
−4	674.90	0.2887 ***	21,142.41	0.0885 ***	0.2321	−0.0125	0.0244	0.1751 **
		(0.0020)		(0.0098)		(0.7185)		(0.0443)
−3	686.08	0.4497 ***	19,151.21	0.0866 **	0.2278	−0.0204	0.0277	0.2829 ***
		(0.0000)		(0.0141)		(0.5288)		(0.0007)
−2	710.71	0.3569 ***	20,631.73	0.0998 ***	0.2267	−0.0236	0.0290	0.1864 **
		(0.0001)		(0.0069)		(0.4819)		(0.0276)
−1	717.73	0.3904 ***	20,313.36	0.1140 ***	0.2115	−0.100 ***	0.0223	0.0687
		(0.0001)		(0.0039)		(0.0058)		(0.4316)
0	1109.95	0.7084 ***	21,153.74	0.1429 ***	0.1979	−0.120 ***	0.0131	−0.280 ***
		(0.0000)		(0.0004)		(0.0016)		(0.0006)
1	884.60	0.4902 ***	21,492.04	0.1616 ***	0.1945	−0.118 ***	0.0143	−0.1292 *
		(0.0000)		(0.0001)		(0.0005)		(0.0915)
2	758.06	0.3671 ***	21,637.50	0.1840 ***	0.2075	−0.0884 **	0.0183	0.0794
		(0.0000)		(0.0000)		(0.0125)		(0.2834)
3	448.59	0.3230 ***	20,248.20	0.1686 ***	0.2134	−0.096 ***	0.0195	0.0887
		(0.0003)		(0.0001)		(0.0038)		(0.2766)
4	412.00	0.2692 ***	20,286.44	0.1919 ***	0.2141	−0.0752 **	0.0195	0.0764
		(0.0024)		(0.0000)		(0.0349)		(0.3478)
5	607.61	0.3063 ***	20,418.72	0.2153 ***	0.2196	−0.0696 *	0.0143	0.1232 *
		(0.0001)		(0.0000)		(0.0587)		(0.0727)

* Significant at the 10% level; ** Significant at the 5% level; *** Significant at the 1% level. Panel A (Panel B) of this table presents the change in the daily call (put) volume, open interests, relative bid–ask spread, and call–stock ratio (put–stock ratio) around SEO pricing (i.e., from day −5 to day 5) relative to the medians of the call (put) volume, open interests, relative bid–ask spread, and call–stock ratio (put–stock ratio) during the benchmark period (i.e., from day −40 to day −11). The call–stock ratio (put–stock ratio) is the daily number of calls (puts) traded relative to the number of stocks traded. The null hypothesis of no difference in the means between the benchmark period and event days is tested by using the t-test. The sample includes 237 firms that issued SEOs on the NYSE and had options listed on any U.S. options exchange from April 2002 to December 2004. The offer date is designated as day 0.

shows the level and the change in the volume, open interest, and relative bid–ask spread for calls and puts during the five trading days preceding an offer. The offer date is designated as day 0. The benchmark period is the 30 trading days ending 2 weeks before an offer, i.e., from day −40 to day −11. The changes in the trading volume, open interest, and spread, ∆Volume, ∆OI, and ∆Spread, are calculated, respectively, as follows:7

$$\mathsf{\Delta }Volum{e}_t=\log \left(\frac{Volum{e}_t}{Volum{e}_b}\right)$$

(23)

$$\mathsf{\Delta }O{I}_t=\log \left(\frac{O{I}_t}{O{I}_b}\right)$$

(24)

$$\Delta Sprea{d}_t=\log \left(\frac{Sprea{d}_t}{Sprea{d}_b}\right)$$

(25)

where $Volum{e}_b$, $O{I}_b$, and $Sprea{d}_b$ denote the median of the trading volume, open interest, and relative bid–ask spread in the benchmark period, respectively. t is from day −5 to day 5.

Further, we calculate the ratio of the trading volume in the calls (puts) market and in the stock market, as defined by Equation (26), and list both the value, $call/stoc{k}_t\left(put/stoc{k}_t\right)$_, and the change, $\mathsf{\Delta }call/stoc{k}_t\left(\mathsf{\Delta }put/stoc{k}_t\right)$, in Column 4 of Table 2.

$$call/stoc{k}_t\left(put/stoc{k}_t\right)=\frac{Volum{e}_{call,t}\left(Volum{e}_{put,t}\right)}{Volum{e}_{stock,t}}\times 100$$

Like ΔVolume, Δcall/stock (Δput/stock) is calculated as

$$\mathsf{\Delta }call/stoc{k}_t\left(\mathsf{\Delta }put/stoc{k}_t\right)=\log \left(\frac{call/stoc{k}_t\left(put/stoc{k}_t\right)}{call/stoc{k}_b\left(put/stoc{k}_b\right)}\right)$$

(26)

where $call/stoc{k}_b$ ($put/stoc{k}_b$) is the median of the ratios of the trading volume in the calls (puts) market and in the stock market.

Panel A of Table 2 shows that from day −5 to day −1, the trading volume in the calls market rises greatly. The changes during the pre-offer period are between 0.2532 and 0.5335, which are all significant at the 1% level. Open interest in the calls market also increases and the changes are mostly significant at the 10% level.

Similarly, from Panel B, we can observe that the increases in the trading volume in the puts market are also apparent, which are all significant at the 1% level. As for the open interest, during the five trading days before an offer, the puts market experiences more remarkable increases than the calls market. The rise in puts’ open interest is between 0.0866 and 0.1140, which are all significant at the 5% level, and especially, on day −4, day −2, and day −1, the increases are significant at the 1% level. Our finding of a rise in options’ open interest is consistent with Safieddine and Wilhelm (1996)’s finding.

The transfer of informed traders from the stock market to the options market can be more clearly observed from the change in the call–stock ratio (put–stock ratio), as shown in Column 4, Table 2. In the calls market, the trading volume grows steadily relative to the trading volume in the equity market. On day −5 and day −2, the change is 0.1725 and 0.1460, which are significant at the 5% level and the 10% level, respectively. In comparison, in the puts market, the changes in the trading volume relative to the stock market are more remarkable. From day −5 to day −2, the changes in the put–stock ratio relative to the benchmark period are between 0.1690 and 0.2829, which are all significant below the 5% level.

As summarized in Table 1, aware of the transfer of informed traders with unfavorable information to the options market, market makers in the options market will enlarge the bid–ask spread in order to avoid the loss of trading with those informed traders. However, if the informed traders moving to the options market are manipulators, market makers should decrease the spread accordingly. From Table 2, we can find that the relative bid–ask spread in the calls market changes slightly during the five trading days before an offer. In contrast, on day −1, the relative bid–ask spread in the puts market drops by about 0.1004, which is significant at the 1% level. The substantial decrease in the bid–ask spread in the puts market is likely due to the mass entry of manipulators into the puts market.

5.2. Change in Put–Call Ratio Prior to SEO Pricing

As suggested by Proposition 1 and Proposition 2, when private information is favorable, regardless of the existence of short sales constraints, manipulators trading in the options market tend to choose the puts market as their trading venue. Due to this reasoning, we expect that, prior to SEO pricing, the puts market should become more active than the calls market. Specifically, the rise in the trading volume and open interest in the puts market should be obviously higher than the rise in the calls market.

To compare the trading activity in the puts and calls market, we estimate the change in the put–call ratio prior to SEO pricing relative to the benchmark period. The values and changes in the put–call ratio for the volume, open interest, and relative bid–ask spread are presented in

Table 3. Put–call ratios around SEO pricing.

Change in Put-Call Ratio
	Volume		Open Interest		Spread
Day	Level	Change	Level	Change	Level	Change
−5	1.6066	7.5020 ***	0.9031	0.0264	3.1868	0.0355
		(0.0046)		(0.4009)		(0.5487)
−4	3.4564	20.1593 *	1.1845	0.0463	3.1719	0.0466
		(0.0636)		(0.1607)		(0.4383)
−3	3.4609	11.5715 ***	0.9438	0.0456	3.0164	−0.0105
		(0.0022)		(0.1574)		(0.8653)
−2	6.1027	11.9327 **	0.9742	0.0674 **	2.7370	0.0031
		(0.0317)		(0.0493)		(0.9585)
−1	2.1512	8.7328 ***	0.9719	0.0794 **	2.7284	−0.0879
		(0.0004)		(0.0224)		(0.1844)
0	0.9845	3.2992 ***	0.9627	0.0783 **	2.7685	−0.1310 *
		(0.0000)		(0.0271)		(0.0567)
1	1.2386	4.3561 ***	0.8055	0.0199	2.8055	−0.1080
		(0.0000)		(0.5979)		(0.1097)
2	1.3723	6.1316 ***	0.8709	0.0035	2.9589	−0.0630
		(0.0001)		(0.9279)		(0.3517)
3	2.4612	11.3684 **	0.8575	−0.0173	2.5806	−0.1408 **
		(0.0408)		(0.6472)		(0.0368)
4	1.2953	6.4719 ***	0.8706	−0.0003	2.5458	−0.1259 *
		(0.0005)		(0.9934)		(0.0650)
5	1.3354	5.1705 ***	0.8742	0.0033	2.7998	−0.1025
		(0.0000)		(0.9339)		(0.1583)

* Significant at the 10% level; ** Significant at the 5% level; *** Significant at the 1% level. This table presents the change in the daily put–call ratio for the volume, open interests, and relative bid–ask spread around SEO pricing (i.e., from day −5 to day 5) relative to the medians of the put–call ratios of volume, open interests, and relative bid–ask spread during the benchmark period (i.e., from day −40 to day −11). The null hypothesis of no difference in the means between the benchmark period and event days is tested by using the t-test. The sample includes 237 firms that issued SEOs on the NYSE and had options listed on any U.S. options exchange from April 2002 to December 2004.

.

Table 3 shows that the average change in the put–call ratio of the trading volume during the five trading days before an offer is between 7.50 and 20.16, which are significant at the 5% level.8 Moreover, the average change in the put–call ratio of the open interest grows gradually during the five trading days before an offer. On day −5, the change is only about 0.0264, which is not significant even at the 10% level, while on day −2 and day −1, the change reaches 0.0674 and 0.0794, respectively, which are both significant at the 5% level. The apparent increases in the put–call ratio of the volume and open interest in the pre-offer period corroborate our expectation that, due to the existence of potential manipulators, the puts market may attract relatively more trading activity.

This is an interesting finding. In almost all the literature studying the options market around an information event, regardless of whether it is a pre-scheduled one or not, the puts market plays a relatively minor role in disseminating private information compared with the calls market.9 This is because the trading volume and open interest in the calls market are usually higher, and informed traders tend to trade in a more liquid market. However, the manipulators before SEO pricing are informed traders who trade contrary to their private information. Their trading in the puts market out of a consideration of decreasing losses makes the relative role played by the puts market differ from its role around other information events.

The put–call ratio of the spread shows that the relative bid–ask spread of puts is about three times that of the spread of calls, and although the ratio decreases gradually during the five pre-offer trading days, the change is not so obvious. This is due to the fact that the effects of entry of different kinds of informed trading on the bid–ask spread are mixed. The changes in spreads depend on the balance of effects of both kinds of informed traders. We further study the change in the bid–ask spread under different situations.

5.3. Trading Activities upon Existence of Different Kinds of Information

As proposed in Proposition 1, sometimes informed trading with unfavorable information may follow the trading activities of manipulators to mislead market makers and uninformed traders and thus trade on better prices. Therefore, to differentiate the manipulators from those informed traders with favorable information, we divide our sample into two subsamples conditioned on the signing of a 21-day post-offer CAR. That is, if CAR [0, 20] is positive (negative), we assume that private information before an offer is favorable (unfavorable). We present the changes in the trading volume, open interest, and relative bid–ask spread of calls and puts for these two subsamples in

Table 4. Change in the volume, open interest, and spread for calls, puts around SEO pricing.

Panel A: Calls.
	Unfavorable Information (n = 123)				Favorable Information (n = 114)
	∆Volume	∆OI	∆Spread	∆Call/Stock	∆Volume	∆OI	∆Spread	∆Call/Stock
Day	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
−5	0.2119 *	0.0407	−0.0815 **	0.0050	0.5616 ***	0.1126 ***	0.0500	0.3580 ***
	(0.0675)	(0.3097)	(0.0346)	(0.9637)	(0.0000)	(0.0076)	(0.2644)	(0.0015)
−4	0.2360 **	0.0241	−0.0855 **	0.0682	0.2713 **	0.0922 **	0.0361	0.0568
	(0.0403)	(0.5676)	(0.0406)	(0.5097)	(0.0285)	(0.0378)	(0.4541)	(0.6197)
−3	0.2441 **	0.0463	−0.0575	0.0085	0.4083 ***	0.0675	0.0622	0.1746
	(0.0308)	(0.2425)	(0.1750)	(0.9363)	(0.0014)	(0.1180)	(0.2279)	(0.1329)
−2	0.2810 **	0.0497	−0.0816 *	0.0404	0.5552 ***	0.0413	0.0580	0.2650 **
	(0.0209)	(0.2063)	(0.0560)	(0.7079)	(0.0000)	(0.3228)	(0.2291)	(0.0249)
−1	0.4367 ***	0.0345	−0.0628	−0.0580	0.6387 ***	0.0683	0.0623	0.0333
	(0.0006)	(0.3436)	(0.1576)	(0.5995)	(0.0000)	(0.1399)	(0.2681)	(0.7770)
0	1.1037 ***	0.0551	0.0079	−0.3889 ***	1.3631 ***	0.1062 **	0.0543	−0.2141 **
	(0.0000)	(0.1283)	(0.8568)	(0.0016)	(0.0000)	(0.0111)	(0.3411)	(0.0437)
1	0.6980 ***	0.1214 ***	0.0005	−0.1559	0.9323 ***	0.1949 ***	0.0618	−0.0259
	(0.0000)	(0.0023)	(0.9918)	(0.1743)	(0.0000)	(0.0000)	(0.2778)	(0.8218)
2	0.4372 ***	0.1396 ***	−0.0210	0.0251	0.5519 ***	0.2538 ***	0.0263	−0.0125
	(0.0003)	(0.0010)	(0.6264)	(0.8245)	(0.0002)	(0.0000)	(0.6439)	(0.9125)
3	0.2810 ***	0.1418 ***	0.0415	−0.0671	0.5740 ***	0.2648 ***	0.0423	0.1022
	(0.0077)	(0.0010)	(0.3792)	(0.5041)	(0.0002)	(0.0000)	(0.4986)	(0.4046)
4	0.2494 **	0.1431 ***	0.0315	−0.0798	0.3881 ***	0.2789 ***	0.0201	0.0010
	(0.0307)	(0.0012)	(0.4752)	(0.4657)	(0.0077)	(0.0000)	(0.7509)	(0.9935)
5	0.1355	0.1543 ***	0.0612	−0.1562	0.4384 ***	0.3129 ***	0.0017	0.0917
	(0.2792)	(0.0008)	(0.2028)	(0.1718)	(0.0053)	(0.0000)	(0.9803)	(0.5052)
Panel B: Puts.
	Unfavorable Information (n = 123)				Favorable Information (n = 114)
	∆Volume	∆OI	∆Spread	∆Put/Stock	∆Volume	∆OI	∆Spread	∆Put/Stock
Day	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
−5	0.2376 **	0.0658	0.0413	0.1393	0.3263 ***	0.1100 **	−0.0696	0.2021 *
	(0.0344)	(0.1944)	(0.3679)	(0.1705)	(0.0093)	(0.0217)	(0.1220)	(0.0781)
−4	0.1951	0.0701	0.0518	0.1101	0.3872 ***	0.1077 **	−0.0798 *	0.2436 **
	(0.1404)	(0.1647)	(0.3281)	(0.3752)	(0.0034)	(0.0205)	(0.0723)	(0.0468)
−3	0.4752 ***	0.0888 *	0.0304	0.3093 ***	0.4212 ***	0.0841 *	−0.0765 *	0.2534 **
	(0.0002)	(0.0812)	(0.5263)	(0.0063)	(0.0019)	(0.0849)	(0.0753)	(0.0397)
−2	0.4842 ***	0.0893	0.0309	0.3214 ***	0.2134 *	0.1115 **	−0.0843 *	0.0342
	(0.0004)	(0.1028)	(0.5135)	(0.0096)	(0.0937)	(0.0231)	(0.0777)	(0.7632)
−1	0.3810 ***	0.0907	−0.0351	0.0759	0.4006 **	0.1392 ***	−0.1706 ***	0.0608
	(0.0045)	(0.1386)	(0.4971)	(0.5343)	(0.0107)	(0.0045)	(0.0008)	(0.6288)
0	0.9087 ***	0.1187 *	−0.0554	−0.1358	0.4865 ***	0.1696 ***	−0.1948 ***	−0.4404 ***
	(0.0000)	(0.0516)	(0.2827)	(0.1959)	(0.0044)	(0.0012)	(0.0005)	(0.0004)
1	0.5701 ***	0.1621 **	−0.1090 **	−0.0705	0.4026 ***	0.1611 ***	−0.1288 **	−0.1936 *
	(0.0001)	(0.0110)	(0.0179)	(0.5176)	(0.0036)	(0.0029)	(0.0121)	(0.0724)
2	0.4322 ***	0.1659 ***	−0.0952 **	0.1701	0.2956 **	0.2036 ***	−0.0807	−0.0202
	(0.0003)	(0.0095)	(0.0358)	(0.1048)	(0.0163)	(0.0002)	(0.1454)	(0.8467)
3	0.3616 ***	0.1367 **	−0.1036 **	0.1273	0.2814 **	0.2028 ***	−0.0869 *	0.0470
	(0.0082)	(0.0292)	(0.0179)	(0.3150)	(0.0143)	(0.0002)	(0.0828)	(0.6414)
4	0.2309 **	0.1701 **	−0.1033 **	0.0333	0.3119 **	0.2161 ***	−0.0434	0.1244
	(0.0491)	(0.0100)	(0.0257)	(0.7702)	(0.0215)	(0.0002)	(0.4324)	(0.2859)
5	0.4247 ***	0.1883 ***	−0.1323 ***	0.2435 **	0.1716	0.2455 ***	0.0023	−0.0136
	(0.0001)	(0.0047)	(0.0039)	(0.0111)	(0.1186)	(0.0000)	(0.9694)	(0.8898)

* Significant at the 10% level; ** Significant at the 5% level; *** Significant at the 1% level. Panel A (Panel B) of this table presents the change in the daily call (put) volume, open interests, relative bid–ask spread, and call–stock ratio (put–stock ratio) around SEO pricing (i.e., from day −5 to day 5) relative to the medians of call (put) volume, open interests, relative bid–ask spread, and call–stock ratio (put–stock ratio) during the benchmark period (i.e., from day −40 to day −11) of a subsample with private unfavorable information and a subsample with private favorable information. The call–stock ratio (put–stock ratio) is the daily number of calls (puts) traded relative to the number of stocks traded. Private information before an offer is assumed to be favorable (unfavorable) if CAR [0, 20] is positive (negative). The null hypothesis of no difference in means between the benchmark period and event days is tested by using the t-test.

.

For a firm with private unfavorable information, as shown in Column 4, the trading volume in the calls market only slightly changes relative to the equity market during the five trading days prior to an offer. The changes in the call–stock ratio are only between −0.0580 and 0.0682 and are all not significant at the 10% level. In comparison, the trading volume in the puts market increases remarkably relative to the equity market. During day −5 to day −2, the rises in the put–call ratio are above 11%. Especially on day −3 and day −2, the puts market experiences a soar in the put–stock ratio of the trading volume of 0.3093 and 0.3214, respectively, which are significant at the 1% level.

Furthermore, it can be observed from Column 3 that as more traders with unfavorable information choose puts as trading vehicles, the relative bid–ask spread in the calls market declines accordingly. On day −5 and day −4, bid–ask spreads decrease by more than 0.08 and are significant at the 5% level. In contrast, during day −5 to day −2, the bid–ask spread in the puts market increases slightly instead. All this evidence indicates that as expected by our proposition, before an offer, a small part of informed traders with unfavorable information tend to trade in the puts market like manipulators.

In comparison, Column 8 shows that, for a firm with private favorable information, both the trading volume in the calls market and the trading volume in the puts market relative to the equity market increases during the restricted period. Moreover, in the calls market, the open interest increases greatly during day −5 and day −4. The increases are about 0.1126 and 0.0922, respectively, which are significant at 5% level. In the meantime, the pre-offer puts market also experiences large increases in the open interest. It can be seen from Column 6, Table 4 that the increases in the open interest are between 0.0841 and 0.1392, which are all significant at the 10% level. Compared with the calls market, the increase in the open interest in the puts market is more remarkable.

We can also find from Column 7 that in the pre-offer period, the bid–ask spreads of calls increase slightly, while the bid–ask spreads of puts decrease substantially. During day −4 to day −1, the bid–ask spread in the puts market declines by more than 0.07. Especially on day −1, the decreases in the bid–ask spread reaches 0.1706, which is significant at the 1% level. The drops in the bid–ask spread, accompanied by the leaps in the trading volume and open interest, indicate that manipulators tend to trade in the puts market prior to an offer.

Notably, comparing Column 2 and Column 6, we can find that for a firm with unfavorable information, the open interest in the puts market only change slightly, while for a firm with private favorable information, the open interest of puts obviously rises. Recall Corollary 4: When there are strict short sales constraints in the equity market, ${\beta }_{\underset{\_}{V}}$ increases with the decline of ${\alpha }_{\underset{\_}{V}}$ because if too many informed traders are jammed in the put markets, the “bear” signaling will be too powerful. Therefore, it is advisable that some of these informed traders trade in the calls market. That is, although informed traders with unfavorable information also propend to trade puts in the pre-offer market, their propensities are mush weaker than those of manipulators.

5.4. Change in Open Interest and Change in Bid–Ask Spread

The summary of changes in the bid–ask spread in Table 1 expect that the entry of informed traders with unfavorable information will the increase bid–ask spread in the options market, while the entry of manipulators will lead to a decline in the bid–ask spread. Therefore, if with the increase in the open interest the bid–ask spread increases (decreases), this may indicate that compared with manipulators (informed traders), there are more informed traders (manipulators) trading in this market.

Table 5. Correlation between pre-offer CAR, change in open interest, and change in spread.

	CAR[−5, −1]	ΔOI_call−1	ΔSpread_call−1	ΔOI_put−1	Δspread_put−1
CAR[−5, −1]	1.0000	−0.0406	−0.3890 ***	−0.1484 **	0.3043 ***
		(0.5354)	(<0.0001)	(0.0229)	(<0.0001)
ΔOI_call−1	−0.0406	1.0000	0.0308	0.4616 ***	0.0035
	(0.5354)		(0.6454)	(<0.0001)	(0.9579)
Δspread_call−1	−0.3890 ***	0.0308	1.0000	0.1078	−0.4646 ***
	(<0.0001)	(0.6454)		(0.1061)	(<0.0001)
ΔOI_put−1	−0.1484 **	0.4616 ***	0.1078	1.0000	−0.1745 ***
	(0.0229)	(<0.0001)	(0.1061)		(0.0086)
Δspread_put−1	0.3043 ***	0.0035	−0.4646 ***	−0.1745 ***	1.0000
	(<0.0001)	(0.9579)	(<0.0001)	(0.0086)

** Significant at the 5% level; *** Significant at the 1% level. This table presents a Pearson correlation coefficient matrix. Pre-offer CAR, CAR[−5, −1], are five-day cumulative abnormal returns preceding the offer date of SEOs. The sample includes 237 firms that issued SEOs on the NYSE and had options listed on any U.S. options exchange from April 2002 to December 2004. Abnormal returns are calculated using the market model:

$$R_{it}=\widehat{\alpha }+\widehat{\beta }{R}_{mt},\mathrm{where}\mathrm{t}=-120,\dots ,-11$$

$$A{R}_{it}=R_{it}-\widehat{\alpha }-\widehat{\beta }{R}_{mt}$$

$$CAR\left[-5,-1\right]={\displaystyle \sum }_{t=-5}^{-1}A{R}_{it}$$

ΔOI_call₋₁, ΔSpread_call₋₁, ΔOI_put₋₁, and ΔSpread_put₋₁ denote the changes in calls’ open interests, calls’ bid–ask spread, puts’ open interests, and puts’ bid–ask spread on the day immediately prior to the offer date (i.e., day −1) relative to the median of calls’ open interests, calls’ bid–ask spreads, puts’ open interests, and puts’ bid–ask spreads during the benchmark period (i.e., day −40 to day −11), respectively.

displays the relationship between changes in the open interest and changes in the relative bid–ask spread.

Table 5 shows that the correlation between the changes in puts’ open interest and the changes in puts’ bid–ask spread is −0.1745, which is significant at the 1% level. This means the active trading in the puts market before an offer is more likely due to the entry of manipulators. However, in the calls market, the correlation between the change in the open interest and the change in the bid–ask spread is only 0.0308, which is not significant even at the 10% level. This indicates neither the informed traders nor the manipulators dominate the calls trading in the pre-offer market. These findings further support our proposition that in the pre-offer period, manipulators are inclined to choose puts as vehicles.

Moreover, the increase in puts’ open interest is also associated with the lower 5-day pre-offer cumulative abnormal return (CAR). In the puts market, the correlation between the change in the open interest and the 5-day pre-offer CAR is −0.1484, which is significant at the 5% level. In contrast, we find no obvious relationship between the change in the open interest and CAR in the calls market.

5.5. Change in Open Interest and 5-Day Pre-Offer CAR

We have shown in the previous sections that the abnormally high trading activities in the puts market are due to manipulative conduct. The manipulators try to depress stock price in the equity market by buying puts in the options market. However, the analysis in Section 3 proposes that under the short sales constraints in the equity market, it becomes much harder for a manipulator to drive the stock prices down. To gain their ends, they have to trade more puts and lose more money in the options market. Therefore, unless they can profit more in the issuing market, they will not carry out such manipulative trading.

In this section, we will check whether manipulators can succeed in depressing the stock price by such kinds of manipulative trading. The whole sample is divided into three categories equally by sorting changes in the open interest. Panel A and Panel B in

Table 6. Five-day Pre-offer CAR by Categories.

Panel A: CAR[−5, −1] for terciles of SEOs ranked by change in puts’ open interest.
		Five-day Pre-offer CAR
Change in Puts Open Interests	n	Mean	Std Dev	Median	Minimum	Q1	Q3	Maximum
Tercile 1 (Low)	78	0.6983	6.6865	−0.3165	−14.4529	−2.3216	2.0730	25.4722
Tercile 2 (Middle)	79	−2.1436	5.9128	−1.3526	−22.7571	−4.7246	0.5481	10.3906
Tercile 3 (High)	78	−2.9351	6.8017	−2.2004	−26.1788	−4.5232	1.6416	9.2187
Univariate Test across Categories for Pre-offer CAR
Wilcoxon Test					Median Test
Chi-Square	p-value				Chi-Square		p-value
8.7098	0.0128 **				5.4174		0.0666
Panel B: CAR[−5, −1] for terciles of SEOs ranked by change in calls’ open interest.
		Five-day Pre-offer CAR
Change in Calls Open Interests	n	Mean	Std Dev	Median	Minimum	Q1	Q3	Maximum
Tercile 1 (Low)	78	−1.0669	6.6177	−1.4275	−26.1788	−3.3268	1.1694	25.4722
Tercile 2 (Middle)	79	−1.5099	6.1611	−1.1619	−22.7571	−4.1977	1.4566	18.0239
Tercile 3 (High)	78	−1.8118	7.1597	−1.0669	−25.3441	−4.2608	2.1410	13.1235
Univariate Test across Categories for Pre-offer CAR
Wilcoxon Test					Median Test
Chi-Square	p-value				Chi-Square		p-value
0.0199	0.9901				1.1790		0.5546

** Significant at the 5% level.

list 5-day pre-offer CAR across categories of change in puts’ open interest and across categories of change in calls’ open interest, respectively.

Panel A (Panel B) of the table lists the mean five-day pre-offer CAR, CAR[−5, −1], for terciles of seasoned offers ranked according to ΔOI_put₋₁ (ΔOI_call₋₁). ΔOI_put₋₁ (ΔOI_call₋₁) is the change in puts’ (calls’) open interest on the day −1 relative to the median of puts’ (calls’) open interests during the restricted period (i.e., day −40 to day −11). The sample includes 237 firms that issued SEOs on the NYSE and had options listed on any U.S. options exchange from April 2002 to December 2004. Abnormal returns are calculated using the market model:

$$R_{it}=\widehat{\alpha }+\widehat{\beta }{R}_{mt},\mathrm{where}\mathrm{t}=-120,\dots ,-11$$

$$A{R}_{it}=R_{it}-\widehat{\alpha }-\widehat{\beta }{R}_{mt}$$

$$CAR\left[-5,-1\right]={\displaystyle \sum }_{t=-5}^{-1}A{R}_{it}$$

The null hypothesis of no difference in CAR[−5, −1] across terciles is tested by using the Wilcoxon and median tests.

From Panel A of Table 6, we observe that the 5-day pre-offer CAR decreases as the change in puts’ open interest increases. The pre-offer CARs across three categories are 0.6983, −2.1436, and −2.9351, respectively. The results of a non-parametric Wilcoxon test (p-value = 0.0128) and median test (p-value = 0.0666) show that the 5-day pre-offer CAR decreases with an increase in the puts market’s open interest.

In contrast, we do not find clear evidence of a relationship between the 5-day CAR and changes in the open interest of calls. The Wilcoxon and median tests show that the 5-day pre-offer CAR are almost equal across categories. All this evidence indicates that the puts market is related to manipulative trading.

5.6. Pre-Offer CAR and Post-Offer CAR

To check whether manipulators can distort stock prices successfully and how costly such manipulative conduct is, we estimate the correlation between the pre-offer CAR and post-offer CAR across three categories of change in the open interest in the options market. Kim and Shin (2004) suggest using the correlation between the pre-offer CAR and post-offer CAR to check whether the short selling before an offer is information-based or manipulative. Specifically, if the pre-offer CAR and post-offer CAR are negatively correlated, the price decline prior to SEO pricing is temporary, and the short selling can be inferred as manipulative; otherwise, the price decline is permanent, and the short selling is information-based.

The correlation between CAR[−5, −1] and CAR [0, 5] across three categories of change in puts’ open interest and across three categories of change in calls’ open interest are displayed in

Table 7. Correlation between pre-offer CAR and post-offer CAR by categories.

Panel A: Correlation between CAR[−5, −1] and CAR [0, 20] for terciles of SEOs ranked by change in puts’ open interest.
Change in Put/Call Ratio of Open Interest	n	Correlation (Pre-offer CAR, Post-offer CAR)
Tercile 1	78	−0.0899
		(0.4338)
Tercile 2	79	0.1960 *
		(0.0834)
Tercile 3	78	−0.2595 **
		(0.0218)
Panel B: Correlation between CAR[−5, −1] and CAR [0, 20] for terciles of SEOs ranked by change in calls’ open interest.
Change in Put/Call Ratio of Open Interest	n	Correlation (Pre-offer CAR, Post-offer CAR)
Tercile 1	78	−0.1254
		(0.2740)
Tercile 2	79	0.0715
		(0.5313)
Tercile 3	78	−0.0760
		(0.5083)

* Significant at the 10% level; ** Significant at the 5% level.

.

Panel A (Panel B) of this table lists the Pearson correlation coefficient between the pre-offer cumulative abnormal returns, CAR[−5, −1], and post-offer cumulative abnormal returns, CAR [0, 20], for terciles of seasoned offers ranked according to ΔOI_put₋₁ (ΔOI_call₋₁). ΔOI_put₋₁ (ΔOI_call₋₁) is the change in puts’ (calls’) open interest on day −1 relative to the median of puts’ (calls’) open interests during the restricted period (i.e., day −40 to day −11). The sample includes 237 firms that issued SEOs on the NYSE and had options listed on any U.S. options exchange from April 2002 to December 2004. Abnormal returns are calculated using the market model:

$$R_{it}=\widehat{\alpha }+\widehat{\beta }{R}_{mt},\mathrm{where}t=-120,\dots ,-11$$

$$A{R}_{it}=R_{it}-\widehat{\alpha }-\widehat{\beta }{R}_{mt}$$

$$CAR\left[-5,-1\right]={\displaystyle \sum }_{t=-5}^{-1}A{R}_{it}$$

$$CAR\left[0,20\right]={\displaystyle \sum }_{t=0}^{20}A{R}_{it}$$

Panel A of Table 7 shows that for the two categories with the lowest change in puts’ open interest, the correlation between CAR[−5, 0] and CAR [0, 5] is −0.0899, but this correlation is not significant, even at the 10% level. In the second category, where the change in the open interest is around zero, the correlation is equal to 0.1960, which is statistically significant at the 10% level, but the relationship is positive. Only in the category with the highest increase in the open interest in the puts market, where the minimum value of change in the open interest is 0.2317, the correlation is −0.2595, which is significant at the 5% level. This evidence reveals that although manipulative trading can drive the stock price down, the cost of such trading is very high because they must trade more puts to make their plan come through. For robustness, we further divide the sample into four and five groups, and both results show that only in the category with the highest change in puts’ open interest, the correlation between the pre-offer and post-offer CAR is significantly correlated (the results are not reported for reasons of parsimony).

In contrast, if we divide the sample into three categories by sorting changes in calls’ open interest, as shown in Panel B of Table 7, we cannot find a significant correlation in any of the categories. The results are robust regardless of the number of the categories. All of this evidence indicates that manipulators can succeed in distorting the stock price through trading in the puts market, but such trading is very costly.

Our findings have several practical implications to various groups of market participants. When market makers anticipate manipulative trading from the abnormally high buying of transactions in the puts market, they will narrow their bid and ask quotes in the equity and options markets accordingly. Uninformed traders who observe selling signals in the puts market will anticipate a rise in the stock price and choose to buy stock in the equity market instead. Since manipulation is costly, there is a limit to its occurrence. The reaction of market makers to the behavior of manipulators is a form of self-regulation. Thus, short-selling restrictions imposed by regulators may have limited usefulness.

6. Conclusions

In this paper, we analyze the trading strategies of potential manipulators, other informed traders, and uninformed traders before an offer in the framework of multiple markets. Our model predicts that due to short sales constraints imposed by Rule 10b-21, informed trading will be shifted to the options market. Furthermore, compared with other informed traders, manipulators are more likely to select puts as trading vehicles out of consideration for capping the losses incurred when distorting stock prices through the options market. Our empirical results prior to the GFC of 2007–2009 support these predictions. We observe a substantial increase in options’ trading volume and open interest during the pre-offer period. We also find that the increases in the volume and open interest in the puts market are much larger than the increases in the calls market, which partially reveals the existence of manipulators in the options market.

Through analyzing the setting of bid and ask quotes in both the equity and options market, we propose that market makers should widen the bid–ask spread when they expect the existence of informed traders and narrow the spread when they expect the existence of manipulators. Empirically, when dividing the whole sample into two subsamples with private favorable information and with private unfavorable information conditioned on the signing of a post-offer CAR, we find that for firms with private favorable information, the increase in puts’ open interest is associated with the decrease in the bid–ask spread in the puts market, which implies that manipulators tend to choose the puts market as a trading venue.

Our model also predicts that due to market makers’ rational expectations of the existence of manipulators in the options market and constraints on short sales imposed by Rule 10b-21, it will be very costly for a manipulator to distort stock prices whether through direct short sales in the equity market or through synthetic short sales in the options market. The empirical tests show that pre-offer CAR and post-offer CAR are significantly and negatively correlated only in the category with the highest increase in put options’ open interest, which indicates that manipulators must spend a large amount of money in depressing stock prices.

A limitation of this study is that our model does not include the time element. Trading tends to be dynamic in the actual market, with players such as market makers, informed traders, manipulators, and uninformed traders. Future research could investigate manipulative trading after the Global Financial Crisis and compare the results between the two periods to ascertain the efficacy of restrictive short selling across all economic conditions.