Abstract
Mean-variance optimization often leads to unreasonable asset allocations. This problem has forced scholars and practitioners alike to introduce portfolio constraints. The scope of our study is to verify which type of constraint is more suitable for achieving efficient performance. We have applied the main techniques developed by the financial community, including classical weight, flexible, norm-based, variance-based, tracking error volatility, and beta constraints. We employed panel data on the monthly returns of the sector indices forming the MSCI All Country World Index from January 1995 to December 2020. The assessment of each strategy was based on out-of-sample performance, measured using a rolling window method with annual rebalancing. We observed that the best strategies are those subject to constraints derived from the equal-weighted model. If the goal is the best compromise between absolute return, efficiency, total risk, economic sustainability, diversification, and ease of implementation, the best solution is a portfolio subject to no short selling and bound either to the equal weighting or to TEV limits. Overall, we found that constrained optimization models represent an efficient alternative to classic investment strategies that provide substantial advantages to investors.
1. Introduction
Mean-variance (MV) optimization often leads to unreasonable asset allocations, which are often highly unstable and show an excessive concentration, hindering diversification (Black and Litterman 1992; Michaud 1989). MV optimization is a deterministic approach that ignores the statistical uncertainty of inputs and, therefore, overweights (underweights) those assets that show positive (negative) estimated return errors and negative (positive) variance and covariance errors. Consequently, portfolios on the efficient frontier are characterized by a high distortion in out-of-sample performance, resulting in poor ex-post results in terms of risk and return (Basile and Ferrari 2016).
Furthermore, optimization input and output quality depend on the length and frequency of the time series employed to estimate the parameters. On the one hand, input estimates made with a limited sample are a poor representation of the true distribution of the population and show a low predictive ability, especially in the presence of outliers. On the other hand, a long-term horizon decreases this type of error but increases the likelihood of non-stationarity in parameters, meaning they may not be representative of true parameters in the following period (Broadie 1993).
In addition, estimated returns and correlations seem to be time-varying; that is, they frequently fluctuate with market conditions. For example, correlations appear to be higher in times of market stress (Lumholdt 2018). Estimates of parameters can often vary with up-to-date forecasts, resulting in a significant rebalancing of previously defined long-term portfolio allocations. This is due to the extreme sensitivity of portfolio allocations to even small variations in inputs, particularly in expected returns (Best and Grauer 1991). The techniques for the forecast of stock returns that have been proposed by scientific literature follow several approaches, as a unanimous consensus has yet to be reached: variance risk premium (Bollerslev et al. 2014), interest rates (Ang and Bekaert 2007), technical indicators (Dai et al. 2020), manager sentiment (Jiang et al. 2019), and short interest index (Rapach et al. 2016), among others.
Chopra and Ziemba (1993) show that errors in means have an impact that is 10–20 times larger than errors in standard deviations and covariances. At the same time, variance-covariance estimates are relatively stable over time and are therefore more reliable than expected returns (Merton 1980; Jorion 1985).
The scientific community has put forward two approaches to manage estimation error and limit its impact on portfolio construction. The first one is based upon the shrinkage of the covariance matrix (Ledoit and Wolf 2003; DeMiguel et al. 2009b; Kourtis et al. 2012) and regularization methods (Yen 2016). The second one is focused on robust optimization (Goldfarb and Iyengar 2003), but this model is subject to a severe computational complexity that has prevented its widespread use by the asset management industry. More recently, the integration of these methods into a unified approach has been investigated by Dai and Kang (2021). However, the extreme weights that are often present in efficient portfolios can also be related to the dominance of a single factor in the covariance matrix of returns. Therefore, their presence is not necessarily related to estimation error, but is intrinsic to the investment universe available to the investor (Green and Hollifield 1992).
Our study focuses on the implementation and evaluation of the choice of portfolio constraints. This methodology is closely related to the shrinkage approach and has gained widespread employment in both the academic and practitioner communities to manage the typical operational limits of MV optimization, deriving from the overfitting of input data of limited predictive value (Frost and Savarino 1988; Grauer and Shen 2000; Jagannathan and Ma 2003; Behr et al. 2013). From an operational point of view, the issue of portfolio constraints assumes great significance in the perspective of asset managers with the aim of creating more stable portfolios that are less subject to the effects of input estimation errors in the optimization process or to extreme weights, related to the dominance of a single factor in the covariance matrix. The main purpose of this study, therefore, is to compare different portfolio constraints in a realistic environment, with the aim of providing an evaluation of their performances and costs that is useful to asset managers seeking the most suitable approach to this crucial aspect of allocation.
The remainder of this paper is organized as follows. Section 2 reviews the solutions suggested by scientific literature to mitigate the impact of estimation errors and illustrates the role of portfolio constraints. Section 3 presents the methodology of our empirical analysis and describes the constrained optimization methods employed, while Section 4 presents the results of our analysis. Finally, Section 5 presents the main findings and conclusions.
2. Literature Review
Classic MV optimization is a deterministic approach that does not consider the randomness of asset prices. The use of inaccurate sample parameters and the tendency of MV optimization to maximize estimation errors often cause extreme and unreasonable investment strategies, with inconsistent ex-post results (Behr et al. 2013). Therefore, it is necessary to develop processes that manage sample errors and mitigate their harmful effects on portfolio allocation. The scientific literature proposes two classes of approaches: Bayesian and heuristic.
Bayesian approaches act on optimization inputs. They exploit estimation techniques to calculate better estimators other than the sample mean obtained from historical data. Heuristic approaches identify empirical criteria or methods to ensure that the optimization process produces desirable results from an investment perspective (Basile and Ferrari 2016). Among the latter, there is the imposition of additional weight constraints, which has gained wide popularity in the asset management industry (Amenc et al. 2011).
This method consists of integrating in MV optimization a minimum allocation bound (Lbi) and/or a maximum allocation bound (Ubi) for each asset i:
Lbi ≤ wi ≤ Ubi with Lbi ≤ Ubi.
These constraints can be set for each asset class, or they can be imposed simultaneously for every asset class through a single global constraint.
Under certainty, imposing constraints is counterintuitive and meaningless because it curbs the optimization potential. However, when the estimated parameters are subject to estimation errors, the method can ensure that the optimization algorithm fed with inputs of “dubious quality” does not generate unreasonable and extreme portfolio allocations. Essentially, the additional weight constraint method is a coercion of the Markowitz algorithm, which ensures a more diversified composition of optimal portfolios (Basile and Ferrari 2016).
The classic efficient frontier systematically dominates the constrained ones. Simultaneously, tightening of the constraints produces optimal ex-ante allocations that are less efficient. The difference in returns for the same level of risk between MV-efficient and constrained portfolios is the cost (in terms of reduced performance ex ante) of achieving more diversified portfolios (Eichhorn et al. 1998). From an asset management perspective, this improves the reasonability and feasibility of efficient portfolios.
Constraints reduce the negative effects of estimation errors in MV optimization and, at the same time, improve out-of-sample performance (Frost and Savarino 1988). However, when the estimated inputs are very close to the real ones, the inclusion of tight constraints can be counterproductive in terms of out-of-sample performance.
Another advantage of explicit portfolio constraints is the possibility of influencing the construction of portfolios through the imposition of stronger constraints on assets with poorly reliable estimates of inputs. Moreover, they allow managers to express their preferences for certain assets and comply with external regulatory limits.
Imposing weight constraints in the form of vectors of lower (Lb) and upper bounds (Ub) adjusts the covariance matrix in proportion to the relative Lagrange multiplier. Constraints, therefore, have a shrinkage-like effect that implicitly modifies the variance and covariance estimates of the considered assets.
To study this effect, consider the global minimum variance (GMV) portfolio defined by the unconstrained optimization problem:
where Σ is the sample covariance matrix and 1 a column vector of N ones.
s.t. w′1 = 1,
The following procedure is also valid for all other efficient portfolios (Roncalli 2014; Behr et al. 2013).
Let be the solution of the unconstrained optimization, and is the solution of the GMV optimization with the additional constraints:
wi ≥ Lbi, i = 1, …, N,
wi ≤ Ubi, i = 1, …, N.
We can identify a covariance matrix such that the constrained portfolio is obtained through the unconstrained optimization problem, that is, . Therefore, the goal is to analyze the constraint impact by studying the difference between Σ and .
The Lagrangian of the constrained optimization model is:
where λ,δ ≥ 0; λ = (λ1, …, λN)’ and δ = (δ1, …, δN)’ are the vectors of the Lagrange coefficients associated with the lower and upper bounds (3) and (4); Lb and Ub are the column vectors of the lower and upper bounds; λ0 is the multiplier for the budget constraint (2).
f(w; λ0; λ,δ) = w′Σw − λ0(1′w − 1) − λ′(w − Lb) − δ′(Ub − w),
Jagannathan and Ma (2003) prove that a constrained GMV portfolio constructed using the sample covariance matrix Σ is equivalent to an unconstrained GMV portfolio using in (1) the covariance matrix :
is symmetric and positive semidefinite. Because λ,δ ≥ 0, we can interpret as a covariance matrix after the penalization of its components.
With only lower bounds, the covariance matrix simplifies to = Σ − (λ1′ + 1λ′). The covariance between any i-th and j-th couple of assets undergoes a reduction of a positive quantity (λi + λj), while the respective variances decrease by the values 2λi and 2λj. The unconstrained optimization process tends to attribute negative weights to assets with high sample variances and covariances. Therefore, the matrix is constructed by shrinking the values of the most significant variances and covariances. Since high sample covariances and variances are likely derived from positive estimation errors, lower bounds reduce allocative inefficiencies related to these errors (Jagannathan and Ma 2003).
Similarly, upper bounds increase the variance of any i-th asset by a value equal to 2δi and its covariance with any j-th asset by a positive amount (δi + δj). Since assets with lower variances and covariances tend to take on high weights in the portfolios, the upward adjustment of matrix mainly concerns these assets.
As a result, constraints adjust the larger and smaller elements of matrix Σ, thus limiting their use by the optimizer and consequently decreasing the impact of estimation errors. This methodology is akin to shrinkage methods, whose goal is to limit estimation errors by narrowing the most extreme values. The difference is that the imposition of constraints implicitly causes a shrinkage effect (Jagannathan and Ma 2003; Behr et al. 2013).
Constraints only act on the sample covariance matrix, so their greatest impact is on the GMV portfolio. Regarding the other portfolios on the efficient frontier, the estimates of expected returns also affect their composition and out-of-sample performance. Therefore, even with the beneficial shrinkage effect of constraints on Σ, they remain significantly affected by the estimation errors of the expected returns. Hence, for these portfolios, it is appropriate to resort to more robust estimation methods for expected returns.
3. Data and Methodology
In this study, we analyze the most popular constrained optimization strategies and verify whether the inclusion of different types of constraints can improve the optimization results in a tangible way. We also identified the constraints that determine the best outcomes according to different evaluation criteria.
Our evaluation not only focuses on performance, but also on the ease of implementation, transaction costs, emotional sustainability, and temporal consistency of results. An out-of-sample approach stems from the possibility of measuring the actual performance achieved by considering both the joint effect of sample errors and the instability of return distributions, thus providing greater statistical robustness.
In our analysis, we employ a buy-and-hold strategy with annual rebalancing. First, we divide our strategy into in-sample and out-of-sample phases. Given a dataset of T monthly returns, we fix an in-sample estimation time window of length M = 60 months. Using the data collected in this time window, we identify the input parameters needed to determine the portfolio weights of each constrained strategy, and, with them, we calculate the portfolio returns over the next 12 months.
The rolling window procedure follows a periodic alternation between the in-sample and out-of-sample phases. At the end of the latter, we calculate the new composition of portfolios by shifting the time window of the in-sample estimation by the duration of the out-of-sample phase (12 months). Finally, we have a series of (T − M) out-of-sample monthly returns for each implemented strategy (DeMiguel et al. 2009a; Behr et al. 2013; Jacobs et al. 2014; Shi et al. 2020; Dai and Kang 2021).
This methodology is a compromise between the cases of no and extreme rebalancing. A monthly rebalancing could cause more costs than benefits, while no periodic intervention minimizes transaction costs, with the undesirable consequence of a deviation from the portfolio allocation defined by the optimization. Monthly rebalancing does not lead to significantly better results than annual rebalancing for the optimization models considered, but it substantially increases turnover and, therefore, transaction costs (DeMiguel et al. 2009a; Behr et al. 2013; Jacobs et al. 2014).
We use an in-sample time window of 60 months because we intend to consider an estimation period that includes different market phases. At the same time, a longer in-sample window is often inadequate, since older observations could have a lower predictive power than newer ones, or they could even be obsolete. In particular, Jacobs et al. (2014) found that estimations based on a rolling-window approach for 120 months did not produce a consistent improvement in MV optimization results.
3.1. Dataset
Our analysis employs the sector indices in the MSCI All Country World Index (ACWI) as asset classes. Table 1 lists these indices together with their main descriptive statistics for the period from January 1995 to December 2020, while Figure 1 illustrates their sample dynamics.

Table 1.
Descriptive statistics of the indices.
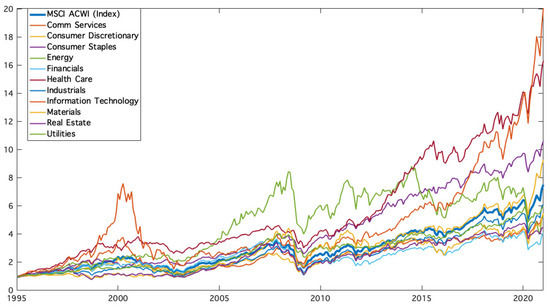
Figure 1.
Cumulative returns of MSCI indices.
Different sectors have generated heterogeneous performance in terms of mean returns and Sharpe ratios. Volatility also varies significantly among asset classes; for example, the standard deviation of the riskiest asset class is double that of the least risky asset class.
The sector characterized by the highest growth in terms of absolute returns is Information Technology. Health Care is also characterized by good growth and, at the same time, by low volatility. On the contrary, the Financials sector has the lowest mean return, mostly due to the 2007 financial crisis.
These asset classes cover the entire investment universe. Each one is composed of financial instruments that are as homogenous as possible and are exposed to distinct sources of systematic risk, such as macroeconomic and political factors. Moreover, these sectorial indices are very transparent and liquid, and they are characterized by greater internal coherence and better external differentiation than geographical ones, implying more dissimilar correlations (Basile et al. 2019).
The series of monthly gross total returns of each index was downloaded from Morningstar Direct. The sample period is from January 1995 to December 2020; thus, each series consists of 312 monthly returns. Since our methodology requires an in-sample period of 60 months to estimate the input parameters, the first portfolio is built at the beginning of January 2000 and the following ones annually, shifting the time window by 12 months. Thereafter, for every investment strategy, we obtain 21 portfolios defined by an optimization procedure that coincides with 21 years (252 months) of out-of-sample performance, including different business cycles and some major financial crises.
3.2. The Constrained Strategies Implemented
To construct the portfolios under study, we employ two different constrained optimization approaches, each characterized by a specific financial goal expressed through a mathematical function that is minimized or maximized, the GMV optimization (5) and the maximum Sharpe ratio (MSR) optimization (6):
s.t. w′1 = 1,
s.t. w′1 = 1.
In the financial literature, GMV optimization is preferred because it only depends on the sample covariance matrix, which is more stable and reliable over time than expected returns estimates. Consequently, GMV portfolios are less vulnerable in an out-of-sample context (Jagannathan and Ma 2003; DeMiguel et al. 2009a; Behr et al. 2013; Levy and Levy 2014). Nevertheless, we also employ MSR optimization, which is influenced by estimation errors in the means, because it is an interesting approach that aims to reach, ex-ante, the maximum efficiency between return and risk.
Depending on the model considered, the optimization is affected by the threshold value (α or δ) or by the lower and upper bounds. Therefore, the choice of reasonable values is fundamental, even though it is not possible to know their optimal level ex ante. On the one hand, excessively high thresholds push the optimization algorithm to converge to the unconstrained strategy and make the constraints ineffective. On the other hand, thresholds that are too low lead to a passive strategy that is strictly dependent on the imposed constraints. Moreover, the amplitude of the constraints can affect both the quantity of short positions and the extent of rebalancing.
We can set the constraints using a discretionary or statistical methodology. In the latter case, the thresholds are calibrated to achieve a precise ex-ante goal while avoiding overfitting. In this study, we define constraints using both methodologies. These constraints are discussed in the following subsections.
We also build two benchmark strategies. The first is the value-weighted (market) portfolio, represented by the MSCI ACWI GR USD index, while the second is the equal-weighted portfolio, which assigns the same weight to every sector index.
3.2.1. The Classical Constraints
The choice of classical constraints is not objective because the manager must determine their type and thresholds. Imposing constraints, in fact, is rather arbitrary, because there is no clear guidance for how these constraints should be imposed. Nevertheless, this is also an opportunity; thanks to their flexibility, a manager can impose constraints according to the investment strategy, and their simplicity makes it easy to report their use to investors.
As previously seen, we define lower and upper bounds as follows:
Lbi ≤ wi ≤ Ubi with Lbi ≤ Ubi.
We can use homogeneous individual constraints, which have identical lower and/or upper bounds for every asset class (Lbi = Lb and/or Ubi = Ub, ∀i), or we can use inhomogeneous individual constraints that differ for every asset class. It is also possible to impose group constraints that are lower and upper bounds defined not for a single, but for a set of asset classes (Lbi ≤ wgroup,i ≤ Ubi). Homogeneous constraints, however, do not take into account the fact that the standard deviations are not the same for each asset and, therefore, do not provide an equal contribution to portfolio risk.
A frequently used homogeneous individual constraint, that we analyze in this study, is represented by the no short selling constraint:
0 ≤ wi ≤ 1 ∀i, i = 1, …, N.
This constraint avoids allocations characterized by extreme weights due to short positions, as well as amounts higher than 100% invested in long positions.
Constraints can also be expressed according to the following formulation:
where k is a benchmark parameter to anchor the asset classes and α is the amount that signals the rigidity of this anchoring. In this study, we analyze two constraint strategies expressed in this way: the portfolio bound to the equal-weighted model (k = 1/N) and the portfolio bound to the market (k = wmarket,i).
|wi − k| ≤ α ∀i, i = 1, …, N,
In the first case, the goal is to find a portfolio in line with the equal-weighted portfolio, providing a simple procedure aimed at forcing diversification in a context without input parameters that are deemed sufficiently reliable. In this case, (7) becomes:
|wi − 1/N| ≤ α or 1/N − α ≤ wi ≤ 1/N + α.
In our analysis, we use the threshold α = 5%. Since we build our portfolio with 11 asset classes, 1/N = 9.09% and the minimum amount invested in an asset class is equal to 4.09%. Therefore, it is a long-only portfolio.
The portfolio bound to the market aims to obtain a strategic allocation consistent with the market itself. In particular, k = wmarket,i is the market weight of asset class i; that is, the capitalization of i divided by the total capitalization of the market. In this way, portfolio optimization is combined with the theory, consistent with the CAPM model, that a rational investor should hold risky assets in proportion to their market capitalization. In the formulation of constraints, we add or subtract an amount α that depends on the reliability of the input parameters. Hence, the lower the degree of reliability, the closer α is to 0 (Grauer and Shen 2000; Levy and Levy 2014).
In this analysis, we add a no short-selling constraint to the portfolio bound to the market, so the lower and upper bounds become:
Lbi = max(0, wmarket,i − α),
Ubi = min(1, wmarket,i + α).
Again, we use the threshold α = 5%.
3.2.2. The Flexible Portfolio Constraints
Behr et al. (2013) developed a constrained GMV strategy based on shrinkage, which employs flexible weight constraints.
As seen in Section 2, constraints ensure that optimized portfolios are not excessively affected by the sampling error of the covariance matrix Σ, and, at the same time, cause a loss of information on the sample by imposing a structural correction to Σ equal to (δ1′ + 1δ′) − (λ1′ + 1λ′). Therefore, the biased matrix is characterized by the presence of a systematic error. Generally, an estimator should be unbiased, but there are some situations in which, if adequately controlled, a biased estimator is advisable. Following Behr et al. (2013), we identify the weight constraints to reach an optimal compromise between the reduction of the estimation error in and the relative bias produced. In pragmatic terms, we deviate from the sample matrix Σ and accept the bias produced by weight constraints until the reduction in the variance of the estimator overcompensates for the introduced bias. To this end, the set of lower and upper bounds is calibrated to minimize the sum of the mean square errors (MSEs) of the entries of the covariance matrix . Behr et al. (2013) quantified the MSE using a quadratic measure of distance, according to the Frobenius norm, between and the true but unknown covariance matrix Σreal:
Taking expectations of this expression we obtain the following risk function:
The quantities in function (8) depend on the vectors of the Lagrange multipliers λ and δ. However, because their distribution cannot be determined in closed form, Behr et al. (2013) resort to bootstrapping techniques to obtain consistent estimates for Var(σi,j + (δi + δj) − (λi + λj)) and E((δi + δj) − (λi + λj)).
Starting from the actual sample returns matrix μ and repeating the bootstrap procedure K times, we obtain K matrices of resampled returns μk. For each of them, we estimate the covariance matrix Σ and compute the constrained GMV portfolio for a given set of portfolio weight constraints. From this procedure, we obtain the sample matrix estimate Σk for the k-th bootstrap sample, as well as the vector of Lagrange multipliers for the imposed upper and lower portfolio weight constraints, λk and δk. With these values, we can estimate Var(σi,j + (δi + δj) − (λi + λj)) and E((δi + δj) − (λi + λj)) as:
Inserting (10) and (9) into (8), we estimate the value of the risk function for the portfolio weight constraints. Because the risk function quantifies the sum of the MSEs of the entries in the biased covariance matrix , we set the lower () and upper bounds () for the GMV portfolio to minimize the function itself through the following nonlinear optimization problem:
The advantage of the approach by Behr et al. (2013) is its flexibility and ability to adapt itself to the available data without making any arbitrary choice by following a statistical method that finds the best trade-off between the imposed bias and the reduction in estimation errors of the sample covariance matrix. Moreover, this approach requires fewer hypotheses than classical shrinkage procedures that explicitly influence the sample covariance matrix, because there is no need to identify the parameter α, which can have a significant impact on the out-of-sample performance. In our analysis, we employ this strategy, but we do not allow short selling. For this reason, we changed the interval for the lower bound to 0 ≤ ≤ 1/N. This choice is coherent with the praxis followed by asset managers, due to usual regulatory constraints or investor specific constraints.
Following Behr et al. (2013), we randomly draw a certain block bi of consecutive returns from the in-sample returns matrix μ. The block size bi follows a geometric distribution with parameter q = 0.2, resulting in an average block size of = 1/q = 5. The drawn blocks are concatenated as {b1, b2,…} until the resampled time series contains 60 or more returns. In the latter case, the resampled time series is truncated after the 60th observation. These steps are repeated K = 100 times, so we obtain 100 bootstrap sample return matrices μk, from which we obtain the sample covariance matrix estimate Σk and the vector of Lagrange multipliers λk and δk. Finally, we minimize the risk function to determine the input parameters. This bootstrap procedure is repeated each time the GMV portfolio with flexible constraints is estimated.
3.2.3. The Norm-Based Constraints
The norm-constrained portfolio is the solution of the optimization problem subject to the additional constraint that the norm of the vector of portfolio-weights is smaller than a certain threshold δ; that is ‖w‖ ≤ δ (DeMiguel et al. 2009b). For δ→∞, the obtained portfolio is the one without limits to short selling.
Starting from the general case (‖w‖ ≤ δ), it is possible to show this type of constraint in different ways. The first case analyzed is the 1-norm constrained portfolio that imposes on optimization problems (5) and (6) the additional constraint:
which can be rewritten as:
where δ ≥ 1 and ℵ(w) = {i: wi < 0} represent the set of asset indices for which the corresponding portfolio weight is negative. The left-hand side of the inequation is the total proportion of wealth that is sold short, while the right-hand side is interpreted as the short-sale budget. If δ = 1, the solution of the 1-norm constrained optimization problem is a long-only portfolio. For δ > 1, this approach generates a class of portfolios that generalizes the portfolios with short-sale constraints. In this case, no specific constraints are given with respect to each asset, but the optimizer is left free to distribute these short sales globally to obtain the best possible result. This constraint, instead, limits the total amount of short selling in the portfolio and is therefore coherent with some strategies that are typical of the asset management industry, such as the “130–30” portfolios, where investors are long 130% and short 30% of their wealth.
In our analysis, we estimate parameter δ using a non-parametric cross-validation procedure to minimize the expected out-of-sample variance of the portfolio. This procedure is carried out as follows. Given an in-sample time window of τ = 60 sample returns (μτ×11), for each t between 1 and τ, we iteratively perform the following three phases. First, we remove the t-th vector of returns from μτ×11 and calculate the sample covariance matrix Σ(t) based on the remaining τ − 1 sample returns. Second, we determine the corresponding GMV or MSR portfolio subjected to the 1-norm constraint using a given threshold value θ = δ; that is, (wθ)(t). Then, we estimate the expected return in period t using the corresponding t-th vector of returns previously removed to calculate the optimal portfolio: (rθ)(t) = μt×11 × (wθ)(t). In this way, we obtain τ out-of-sample returns (rθ)τ×1 for every t = {1, …, τ} and use them to calculate the out-of-sample portfolio variance , with . Finally, we set the parameter δ = θ* that minimizes the expected out-of-sample variance (DeMiguel et al. 2009b).
Another case of a norm-constrained portfolio imposes a higher limit δ on the A-norm of the portfolio-weight vector; that is:
where A is positive-definite. If we set A equal to the identity matrix, we obtain the 2-norm constraint , which can be reformulated as follows:
‖w‖A ≤ δ with ‖w‖A = w’Aw.
From this expression, it emerges that the naïve portfolio is a special case of the 2-norm-constrained portfolio with δ = 1/N. For values of δ near 1/N, the 2-norm constraint tends to produce portfolios with weights that are relatively close to those of the equal-weighted portfolio, implying the absence of short positions. As shown in Shi et al. (2020), portfolio weights deriving from this approach coincide with those calculated with the covariance matrix estimator proposed by Ledoit and Wolf (2004) and Schatten 1-norm constrained portfolio weights.
In our analysis, we also construct a 2-norm-constrained portfolio. The parameter δ is calibrated to minimize the expected out-of-sample variance of the portfolio using the same cross-validation procedure employed for the 1-norm case. Obviously, in this case, the portfolio built in the cross-validation process is subject to the 2-norm constraint. This constraint allows short positions with a maximum amount that depends on the parameter δ.
The imposition of norm constraints on the optimization problem leads to a shrinkage effect on covariance matrix Σ. The 1-norm-constrained portfolio coincides with the solution of an unconstrained portfolio with covariance matrix Σ1norm = Σ − νn1′ − ν1n’, where ν ≥ 0 is the Lagrange multiplier for the non-linear 1-norm constraint, 1 is a column vector of ones, and n is a column vector whose i-th element takes a value of one if the weight assigned by the 1-norm-constrained portfolio to the i-th asset is negative and zero otherwise. It follows that the imposition of the 1-norm constraint implicitly reduces the covariance of each asset sold short by a constant value ν, and its variance by a value 2ν. This is the main difference in terms of the shrinkage effect with respect to the imposition of no short selling constraint through lower bounds; in this case, the shrinkage effect on the covariance matrix does not depend on a constant value, but on the corresponding Lagrange multipliers, which can assume different values.
Asset managers can opt for the 1-norm constraint if they aim to control the total amount of short sales that can be implemented in the optimal portfolio. Instead, they can resort to the 2-norm constraint if their focus is a suitable diversification, thus simultaneously granting the optimizer a certain degree of freedom. In addition to the aforementioned reasons, the inclusion of these constraints would also allow the portfolio to benefit from a reduction in the estimation error due to the shrinkage effect, thus favoring more consistent results from an out of sample perspective.
3.2.4. The Variance-Based Constraints
Levy and Levy (2014) suggested two extensions of the constrained optimization approach: variance-based constraints (VBC) and global variance-based constraints (GVBC) methods. These approaches assume that the estimation error of parameters is not equal for every asset class but is higher for those assets that present a higher sample variance.
The VBC method imposes an explicit weight constraint on each asset, which is inversely proportional to its standard deviation:
where σi is the standard deviation of asset i, and
is the average standard deviation of all assets. This equation implies that the higher the σi (relative to the average standard deviation), the tighter the constraint imposed on the weight of i. Note that if two assets have the same standard deviation, they are subject to the same constraint. The inclusion of heterogeneous standard deviations in the asset allocation process is an improvement compared to the homogeneous constraints approach. This model, however, does not take into account a relevant point: the relative contribution of each asset to the portfolio Sharpe ratio is not the same.
In our study, we find the parameter δ using the cross-validation method described in Section 3.2.3, replacing the 1-norm constraint with the VBC. This model allows for a short position when δ is high. In our case, short selling is admissible if δ is higher than 1/N = 9.09%. However, the precise value of δ that allows short selling varies for every asset class according to its volatility. However, this never occurred within our sample.
The GVBC is a single global constraint on the vector of portfolio weights, which implies that the sum of the squares of deviations of weights wi from the benchmark 1/N, weighted for the relative standard deviation, must be equal to or less than a given threshold δ:
Note that for every asset i, the higher the standard deviation σi, the more expensive the deviations from weight 1/N. Therefore, GVBC tends to restrict positions in assets that present higher standard deviations and presumably higher estimation errors.
The GVBC method tends to restrict extreme positions for highly volatile assets, such as the VBC method. However, in contrast to the VBC method, it also allows volatile assets to deviate significantly from 1/N. This happens when the returns of these assets more than compensate for their high volatility. Thus, in the GVBC method, the higher the mean of an asset, ceteris paribus, the higher the weight of the asset, allowing larger deviations from 1/N for the assets that contribute more to portfolio performance. As a consequence, unlike in the VBC approach, each asset gets a different share of the global constraint δ, depending on its contribution to the Sharpe ratio of the portfolio.
In our analysis, we calibrate δ to minimize the portfolio variance out-of-sample through the previously described cross-validation procedure. This constraint does not allow any short sale, unless δ is particularly high, a case that would negate the goal of the constraint.
3.2.5. The Tracking Error Volatility Constraint
Tracking error volatility (TEV) is the standard deviation of the difference between the portfolio return and its benchmark return. This is a relative risk measure that compares the relative return of an investment portfolio with respect to an index representing the whole market, assessing the level of managers’ activism. This measure provides an exhaustive assessment of the loyalty of the manager with respect to the selected benchmark. In analytical terms, in period T, the TEV is equal to:
with .
Even though TEV is frequently used as an ex-post measure of the level of activism, it can be used ex-ante as an additional constraint to the portfolio optimization problem. In this way, the key feature of passive management, that is, the tracking of market performance, is combined with the distinctive element of the active one, that is, the freedom of the optimizer to deviate from the benchmark according to a parameter α.
In our analysis, we set α equal to 2% monthly. In other words, we add the constraint TEV = α = 2%. This choice represents a compromise between the annualized TEV values within which active management is usually around 6% and 12%. Thus, the optimizer acts within a reasonable space to achieve the pre-established goal while simultaneously maintaining consistency with the reference market, represented by the MSCI ACWI. To this end, we also preclude short selling.
3.2.6. The Beta Constraint
Beta (β) is a relative risk measure that quantifies systematic risk in a portfolio. It originates from the Capital Asset Pricing Model and represents the sensitivity of the portfolio to variations of a benchmark, which is used as a proxy for the market, and whose scope is therefore similar to that of the TEV. The estimated value of β indicates whether a portfolio is neutral (β = 1), aggressive (β > 1), or defensive (0 < β < 1) with respect to the market. A portfolio can also move in the opposite direction relative to it (β < 0).
With that in mind, it is possible to add to the optimization problem a constraint that directs, according to an ex-ante target, the performance of the optimized portfolio with respect to the reference market by setting an appropriate value of α such that:
where β is the vector of the betas and w the vector of the percentage weights of the assets.
βportfolio = β’w = α,
In our analysis, we build a portfolio by imposing α = 0.5. The goal of this portfolio is to limit its sensitivity to the market while trying to exploit the advantages of the GMV or MSR portfolios. To make this possible, we allow for short sales without any limit.
3.2.7. Common Features of the Constraints
In some strategies, the MSR optimization is unable to converge according to the constraints and provide consistent results. These strategies, which we exclude from the analysis, are models with flexible constraints, with 1-norm constraints, and with market and beta constraints. We also exclude the MSR model with short selling because, although it shows consistency, it is characterized by extreme portfolio weights that rule out its use in a real context.
Table 2 briefly summarizes the analyzed portfolio models and the benchmarks, together with the abbreviations that will be used as a reference hereinafter.

Table 2.
List of portfolio models.
3.3. The Evaluation Criteria
Out-of-sample performance evaluation focuses on various criteria to reach an exhaustive judgment for each strategy. There are measures that quantify efficiency, overall riskiness, practical implementation, and sustainability. With them, we can establish whether any improvement introduced by constraints to portfolio optimization overcompensates the higher cost incurred by adding them.
The Sharpe ratio (SR) is the first measure we consider. It is an efficiency measure that summarizes the risk-return combination of the portfolio under assessment. This risk-adjusted performance assesses the out-of-sample excess return of a p-th portfolio per unit of total risk:
where μp is the difference between the average return of the portfolio and the risk-free rate, and σp is its standard deviation. We use the three-month Treasury Bill (T-Bill) as a proxy for risk-free asset.
SRp = μp/σp,
The second measure we consider is an absolute risk metric, the out-of-sample variance . For the GMV model, it also allows the evaluation of the effectiveness of the optimizer in reaching its goal.
We obtain an idea of the number of trades required to implement each strategy by computing the portfolio turnover, defined as the average percentage of wealth traded between asset classes at each rebalancing:
where h is the number of rebalancings, wp,t+ is the vector of portfolio weights after rebalancing, and wp,t is the vector of weights before it. In our analysis, these weight adjustments take place 20 times, that is, once a year, excluding the construction of the portfolio at the initial date. The only exception is the value-weighted portfolio because it is a passive buy-and-hold strategy and therefore has zero turnover. Given that transactions are subject to fees that influence portfolio performance, turnover provides a synthetic and approximate measure of transaction costs and allows the evaluation of the convenience of each portfolio strategy in practice.
TOp = ∑t|wp,t+ − wp,t|/h,
A more precise measure of performance adjusted for transaction costs is the certainty-equivalent excess return (CER) of each portfolio, defined as:
where γ is the risk-aversion coefficient and C is the transaction cost per trade. Following Shi et al. (2020), we set γ to be equal to 5 and C to be 50 basis points per trade. Given that turnover, like portfolio rebalancing, is annual, we calculated the annualized CER and then converted the result into a monthly frequency for a better comparability with the other performance and risk measures employed in this study.
The last measure we consider is the short interest (SI), which defines the average amount (in percentage) of wealth held in short positions throughout the valuation period:
In some strategies, portfolio optimization leads to short selling. However, if these positions are large and maintained for a long time, they can be economically expensive or technically difficult to achieve in practice. Therefore, short interest signals the practical feasibility of a strategy.
4. Results
We illustrate the monthly out-of-sample performance of the implemented optimization models and benchmarks in Table 3.

Table 3.
Sharpe ratios of portfolios.
The results of the GMV and MSR optimization strategies systematically outperformed those of the benchmark strategies. Overall, we found that constrained strategies generate a monthly Sharpe ratio between 26% and 76% and between 4% and 44% higher than the vw and 1n models, respectively. On average, the improvement was 49% compared to vw and 22% compared to 1n. Therefore, constrained models are empirically reasonable in terms of efficiency.
We also verified the statistical significance of the differences in Sharpe ratios between each constrained model and the benchmarks through a bootstrap procedure that is suitable when portfolio returns are not normal, independent, and identically distributed. We employed the studentized time series bootstrap procedure suggested by Ledoit and Wolf (2008), with average block size b = 5 and K = 1000 iterations, to calculate the bilateral p-value for the null hypothesis that the Sharpe ratio of strategy i is not statistically different from that of benchmark n, that is, H0: SRi − SRn = 0 (Behr et al. 2013; DeMiguel et al. 2009b). The p-values are listed in Table 3. The differences are considered statistically significant when the p-value is less than 0.1.
With respect to the vw benchmark, we found a consistent and statistically significant increase in the Sharpe ratio for most of the constrained strategies; only min-un, min-beta, maxsh-con, and maxsh-nc2 show p-values greater than 0.1. At the same time, the Sharpe ratios of the constrained strategies are always higher than that of the 1n model; however, in many cases, they cannot be considered significantly different.
The difference in the out-of-sample Sharpe ratios between optimization models and the benchmark strategies, not subject to estimation errors due to intrinsic characteristics, provides a general indication of the sampling error relevance in the former (DeMiguel et al. 2009a). The large mean difference that emerged seems to suggest a good ability to estimate input parameters, owing to an apparent limited estimation error. This is also confirmed by the fact that the performances obtained from the MSR portfolios are in line with those of the GMV portfolios, which are typically less subject to sampling errors than the former. This unusual situation may derive from the use of asset classes, characterized by a good representativity of the corresponding sector. If single stocks were used, the specific risk factors and the greater number of necessary estimates would have reduced the ex-post reliability of estimates.
The lower performance of the vw benchmark could be due to an excessive weighting of the value sectors at the expense of the growth sectors, which have shown better average performances in recent decades (e.g., the IT sector).
The main reason why the 1n benchmark tends to be dominated lies in the considerable disparity in performance of asset classes, as reported in the descriptive statistics of Table 1 and in Figure 1. In contrast, constrained optimization strategies consider these differences to take advantage of the trends in place. The constraints limit extreme situations, while the joint mathematical optimization procedure allows the active exploitation of inherent characteristics in the asset classes. Consequently, these strategies produce combinations that are more efficient in terms of risk-adjusted performance.
The empirical results in Table 4 show how the constrained GMV portfolios achieve substantial reductions in out-of-sample variance when compared to the benchmarks and MSR optimizations. In particular, the constrained GMV portfolios show an average reduction in volatility of 31% compared to the 1n strategy and 38% compared to the vw strategy. Therefore, the constrained GMV procedure is effective in generating portfolios that are consistent with the optimization goal. At the same time, the constrained MSR portfolios show volatility, on average, 10% and 19% lower than the 1n and vw portfolios, respectively.

Table 4.
Variance, turnover, and short interest of portfolios.
In this case, we also verified whether the out-of-sample variance of constrained portfolios is statistically different from that of the benchmarks. We tested the null hypothesis H0: and obtained the p-value using the bootstrap procedure of Ledoit and Wolf (2008) with an average block size b = 5 and K = 1000 iterations. Considering a significance level of 0.1, the differences between the out-of-sample variances of constrained optimizations and those of benchmarks are always statistically significant, except for the difference between the variances of the maxsh-con and 1n models. This confirms that the analyzed models generate less volatility.
To evaluate portfolio performance in real conditions, we considered the transaction costs of constrained optimizations. A high turnover implies a level of transaction costs that significantly reduces profitability and does not justify the implementation of the strategy from an economic point of view. Table 4 shows the turnover of each portfolio. In all cases, the turnovers of the optimization models are substantially higher than those of the 1n and vw portfolios. In particular, min-un, min-beta, maxsh-con, maxsh-nc2, and maxsh-tev models generate a very high average annual turnover, which hinders their implementation. At the same time, three strategies (min-un, min-beta, maxsh-nc2) are subject to an average share of short positions, measured by the short interest, which is unsustainable in real terms (83.5%, 67.6%, and 51.8%, respectively). For these reasons, we did not consider these five approaches. The other strategies with short positions (min-nc1, min-nc2) show acceptable short interests (7.4% and 3.8%) and turnover, which justifies their practical feasibility.
The CER provides a synthetic measure both of risk-adjusted performance and transaction costs (Table 4). Again, optimized portfolios are preferable to the benchmarks. In particular, norm-based constraints and TEV constraints appear to be the best models, while variance-based constraints only reach suboptimal results.
Figure 2 illustrates the cumulative returns of constrained portfolios. They behaved similarly to the 1n benchmark until 2012. Subsequently, there was a substantial increase in the performance of the constrained optimization models. Conversely, the vw benchmark always performs better than the other strategies.
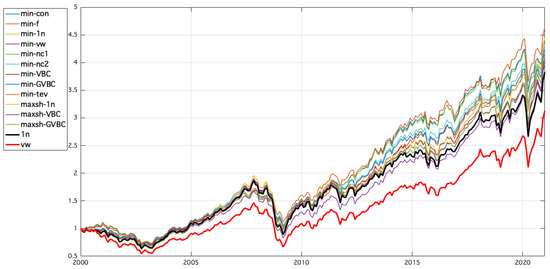
Figure 2.
Cumulative returns of portfolios.
Regarding drawdowns, there are no noticeable differences between the constrained portfolios and the 1n benchmark. However, optimization strategies register a considerable reduction in market decline with respect to the market portfolio (vw).
From the analysis of long-only portfolios, it emerges that both strategies are characterized by a strong concentration in few asset classes and well-diversified strategies. The box plots in Figure 3 allow an immediate identification of the distribution of portfolio weights through the representation of maximum, minimum, median, first, and third quartile values. The equal-weighted portfolio achieves the highest degree of diversification.
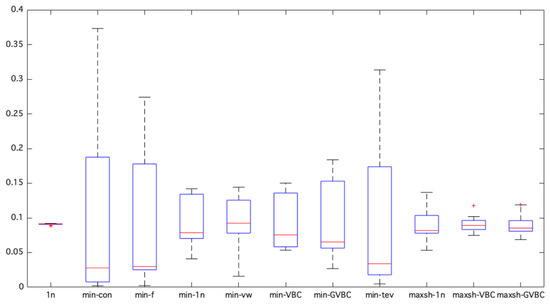
Figure 3.
Weights concentration of long-only strategies.
The average portfolio weights in the min-con, min-f, and min-tev models vary from very high to very low values (in all three cases, 50% of the asset classes have an average portfolio weight that is less than 4%), while the remaining models are characterized by more uniform average weights and, therefore, are more diversified. The insertion of tight constraints confirms the tendency to generate adequately diversified combinations.
Finally, we analyzed the constrained optimization models to identify the best ones in terms of performance, with reference to the previous findings and by resorting to Figure 4. The most efficient constrained optimization strategies are min-VBC, min-GVBC, min-1n, maxsh-VBC, maxsh-GVBC, and maxsh-1n. A common feature of these strategies is that they derive from the equal-weighted model; thus, they define the most appropriate deviation from the 1/N weight used as a benchmark for each asset class. This is an empirical confirmation of the goodness of the equal-weighted approach, despite its naïve formulation. These strategies combine the stability and absence of estimation errors of the equal-weighted model with the possibility of actively exploiting current trends with the result of enjoying a satisfactory diversification, low turnover costs, and good risk-adjusted performance.
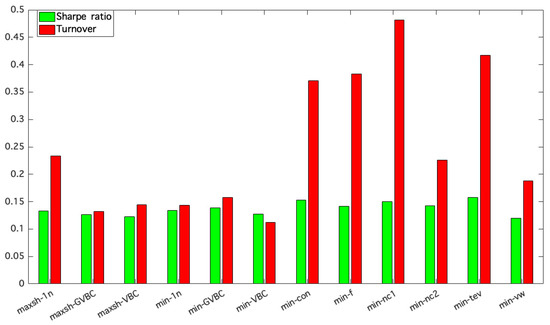
Figure 4.
Comparison among constrained optimization models.
5. Conclusions
In this study, we analyzed the role of the most common constraints in the scientific literature and evaluated their influence on portfolio optimization. The assessment of each strategy was based on out-of-sample performance, which was measured using a rolling window method with annual rebalancing. The issue of portfolio constraints deserves great attention in the asset management industry, with the aim of creating more stable portfolios and avoiding the presence of extreme allocations in a limited set of assets.
We found a positive and often significant increase in the performance of the constrained models compared to the most common strategies. We found improvements in terms of risk-adjusted performance and overall risk, without experiencing excessive turnover or significant short selling, thus validating the use of these strategies in practice. Moreover, in the presence of tighter constraints, these strategies can generate diversified portfolios. The choice of constraints was undoubtedly functional in outlining the properties and performance of each evaluated model.
We observed that the best strategies are those subject to constraints derived from the equal-weighted model. Moreover, the combination of this model with portfolio optimization provides improvements in various aspects.
We did not find substantial differences between the GMV and MSR optimization models. This could be attributed to the low estimation errors.
These results reflect our initial expectations. Nevertheless, they depend on dataset composition. The use of individual securities would probably have produced less significant results, limiting what we found in datasets composed of asset classes that are internally consistent, externally differentiated, and stable over time.
The empirical results show that all the assessed strategies provided appreciable solutions. Therefore, investors should choose the optimization model and constraints in accordance with their target. If the goal is a limited risk, GMV models are the best solution. If the targets are absolute performance and efficiency, GMV models with tracking error volatility (min-tev) and no short selling constraint (min-con) are a good choice. However, these strategies suffer from a non-negligible turnover. Therefore, the amount of transaction costs incurred by the investor plays a crucial role in the choice of these constraints. An extreme case is the maxsh-nc2, with the best performance but, at the same time, a high turnover and relevant short positions, which would prevent its use.
If the goal is the best compromise between absolute return, efficiency, total risk, economic sustainability, diversification, and ease of implementation, the best choice is a GMV or an MSR model, subject to no short selling and bound either to the equal weighting or to TEV limits. If attention to absolute risk is particularly relevant, it is appropriate to opt in favor of GMV models. Overall, we found that constrained optimization models represent an efficient alternative to classic investment strategies that provide substantial advantages to investors.
Author Contributions
Conceptualization, G.A. and P.F.; methodology, G.A. and P.F.; software, G.A.; validation, G.A., T.B. and P.F.; formal analysis, G.A.; investigation, G.A. and P.F.; resources, G.A. and P.F.; data curation, G.A.; writing—original draft preparation, G.A., T.B. and P.F.; writing—review and editing, G.A., T.B. and P.F.; visualization, G.A.; supervision, P.F.; project administration, G.A. and P.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in the Morningstar Direct database at https://www.morningstar.com/products/direct (accessed on 6 September 2021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Amenc, Noel, Felix Goltz, and Abraham Lioui. 2011. Practitioner Portfolio Construction and Performance Measurement: Evidence from Europe. Financial Analysts Journal 67: 39–50. [Google Scholar] [CrossRef]
- Ang, Andrew, and Geert Bekaert. 2007. Stock Return Predictability: Is it There? The Review of Financial Studies 20: 651–707. [Google Scholar] [CrossRef] [Green Version]
- Basile, Ignazio, and Pierpaolo Ferrari, eds. 2016. Asset Management and Institutional Investors. Cham: Springer. [Google Scholar] [CrossRef]
- Basile, Ignazio, Pierpaolo Ferrari, and Guido Abate. 2019. The Impact of Sectorial and Geographical Segmentation on Risk-based Asset Allocation Techniques. Investment Management and Financial Innovations 16: 260–74. [Google Scholar] [CrossRef]
- Behr, Patrick, Andre Guettler, and Felix Miebs. 2013. On Portfolio Optimization: Imposing the Right Constraints. Journal of Banking & Finance 37: 1232–42. [Google Scholar] [CrossRef]
- Best, Micheal J., and Robert R. Grauer. 1991. On the Sensitivity of Mean-Variance-Efficient Portfolios to Changes in Asset Means: Some Analytical and Computational Results. The Review of Financial Studies 4: 315–42. [Google Scholar] [CrossRef] [Green Version]
- Black, Fisher, and Robert Litterman. 1992. Global Portfolio Optimization. Financial Analysts Journal 48: 28–43. [Google Scholar] [CrossRef]
- Bollerslev, Tim, James Marrone, Lai Xu, and Hao Zhou. 2014. Stock Return Predictability and Variance Risk Premia: Statistical inference and International Evidence. Journal of Financial and Quantitative Analysis 49: 633–61. [Google Scholar] [CrossRef] [Green Version]
- Broadie, Mark. 1993. Computing Efficient Frontiers using Estimated Parameters. Annals of Operations Research: Special Issue on Financial Engineering 45: 21–58. [Google Scholar] [CrossRef]
- Chopra, Vijay K., and William T. Ziemba. 1993. The Effect of Errors in Means, Variances, and Covariances on Optimal Portfolio Choice. The Journal of Portfolio Management 19: 6–11. [Google Scholar] [CrossRef]
- Dai, Zhifeng, and Jie Kang. 2021. Some New Efficient Mean—Variance Portfolio Selection Models. International Journal of Finance and Economics 26: 1–13. [Google Scholar] [CrossRef]
- Dai, Zhifeng, Xiaodi Dong, Jie Kang, and Lianying Hong. 2020. Forecasting Stock Market Returns: New Technical Indicators and Two-step Economic Constraint Method. North American Journal of Economics and Finance 53: 101216. [Google Scholar] [CrossRef]
- DeMiguel, Victor, Lorenzo Garlappi, and Raman Uppal. 2009a. Optimal Versus Naive Diversification: How Inefficient Is the 1/N Portfolio Strategy? The Review of Financial Studies 22: 1915–53. [Google Scholar] [CrossRef] [Green Version]
- DeMiguel, Victor, Lorenzo Garlappi, Francisco J. Nogales, and Raman Uppal. 2009b. A Generalized Approach to Portfolio Optimization: Improving Performance by Constraining Portfolio Norms. Management Science 55: 798–812. [Google Scholar] [CrossRef] [Green Version]
- Eichhorn, David, Francis Gupta, and Eric Stubbs Eric. 1998. Using Constraints to Improve the Robustness of Asset Allocation. The Journal of Portfolio Management 24: 41–48. [Google Scholar] [CrossRef]
- Frost, Peter A., and James E. Savarino. 1988. For Better Performance: Constrain Portfolio Weights. The Journal of Portfolio Management 15: 29–34. [Google Scholar] [CrossRef]
- Goldfarb, Donald, and Garud Iyengar. 2003. Robust Portfolio Selection Problems. Mathematics of Operations Research 28: 1–38. [Google Scholar] [CrossRef] [Green Version]
- Grauer, Robert R., and Frederick C. Shen. 2000. Do Constraints Improve Portfolio Performance? Journal of Banking & Finance 24: 1253–74. [Google Scholar] [CrossRef]
- Green, Richard C., and Burton Hollifield. 1992. When Will Mean-Variance Efficient Portfolios Be Well Diversified? The Journal of Finance 47: 1785–809. [Google Scholar] [CrossRef]
- Jacobs, Heiko, Sebastian Müller, and Martin Weber. 2014. How Should Individual Investors Diversify? An Empirical Evaluation of Alternative Asset Allocation Policies. Journal of Financial Markets 19: 62–85. [Google Scholar] [CrossRef] [Green Version]
- Jagannathan, Ravi, and Tongshu Ma. 2003. Risk Reduction in Large Portfolios: Why Imposing the Wrong Constraints Helps. The Journal of Finance 58: 1651–83. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Fuwei, Joshua Lee, Xiumin Martin, and Guofu Zhou. 2019. Manager Sentiment and Stock Returns. Journal of Financial Economics 132: 126–49. [Google Scholar] [CrossRef]
- Jorion, Philippe. 1985. International Portfolio Diversification with Estimation Risk. The Journal of Business 58: 259–78. [Google Scholar] [CrossRef]
- Kourtis, Apostolos, George Dotsis, and Raphael N. Markellos. 2012. Parameter Uncertainty in Portfolio Selection: Shrinking the Inverse Covariance Matrix. Journal of Banking and Finance 36: 2522–31. [Google Scholar] [CrossRef]
- Ledoit, Olivier, and Michael Wolf. 2003. Improved Estimation of the Covariance Matrix of Stock Returns with an Application to Portfolio Selection. Journal of Empirical Finance 10: 603–21. [Google Scholar] [CrossRef] [Green Version]
- Ledoit, Olivier, and Michael Wolf. 2004. A Well-Conditioned Estimator for Large-Dimensional Covariance Matrices. Journal of Multivariate Analysis 88: 365–411. [Google Scholar] [CrossRef] [Green Version]
- Ledoit, Olivier, and Michael Wolf. 2008. Robust Performance Hypothesis Testing with the Sharpe Ratio. Journal of Empirical Finance 15: 850–59. [Google Scholar] [CrossRef] [Green Version]
- Levy, Haim, and Moshe Levy. 2014. The Benefits of Differential Variance-Based Constraints in Portfolio Optimization. European Journal of Operational Research 234: 372–81. [Google Scholar] [CrossRef]
- Lumholdt, Henrik. 2018. Strategic & Tactical Asset Allocation: An Integrated Approach. London: Palgrave Macmillan. [Google Scholar] [CrossRef]
- Merton, Robert C. 1980. On Estimating the Expected Return on the Market: An Exploratory Investigation. Journal of Financial Economics 8: 323–61. [Google Scholar] [CrossRef]
- Michaud, Richard O. 1989. The Markowitz Optimization Enigma: Is ‘Optimized’ Optimal? Financial Analysts Journal 45: 31–42. [Google Scholar] [CrossRef]
- Rapach, David E., Matthew C. Ringgenberg, and Guofu Zhou. 2016. Short interest and aggregate stock returns. Journal of Financial Economics 121: 46–65. [Google Scholar] [CrossRef]
- Roncalli, Thierry. 2014. Introduction to Risk Parity and Budgeting. Boca Raton: Chapman & Hall. [Google Scholar]
- Shi, Fangquan, Lianjie Shu, Aijun Yang, and Fangyi He. 2020. Improving Minimum-Variance Portfolios by Alleviating Overdispersion of Eigenvalues. Journal of Financial and Quantitative Analysis 55: 2700–31. [Google Scholar] [CrossRef]
- Yen, Yu-Min. 2016. Sparse Weighted-Norm Minimum Variance Portfolios. Review of Finance 20: 1259–87. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).