Abstract
Terrorist incidents exert a negative, albeit usually short-lived, impact on markets and equity returns. Given the integration of global financial markets, mega-terrorist events also have a high contagion potential with their shock waves being transmitted across countries and markets. This paper investigates the cross-market transmission of the London Stock Exchange’s reaction to the terrorist attacks of 2005. It focuses on how this reaction was transmitted to two other major European stock exchanges: Frankfurt and Paris. To this effect, high frequency intraday data are used and multivariate Genralised Autorgressive Conditional Heteroskedasticity (GARCH) models are employed. This type of data help reveal a more accurate picture of markets’ reaction to exogenous shocks, such as a terrorist attack, and thus allow more reliable inferences. Findings reported herein indicate that the volatility of stock market returns is increased in all cases examined.
JEL Code:
G14; G21
1. Introduction
The high velocity, with which the shock waves from major financial episodes, irrespective of the source that has generated them, travel across markets and countries, has attracted increasing attention in the relevant financial literature. A plethora of studies, a survey of which can be found in Pericoli and Sbracia [1], have examined both on a theoretical as well as empirical level the mechanisms and the channels through which financial shocks that occur in one country are transmitted and affect markets in another or indeed, have a major international impact on global markets and economic sentiment (inter alia: Goetzmann, et al. [2]; Saleem [3]; Meric and Meric [4]; Asimakopoulos et al. [5]; Chiang et al. [6]). In particular, a number of studies have examined the interdependence of equity market volatility using the framework of autoregressive conditional heteroskedasticity (GARCH) time series models (inter alia: Saleem [3]; Hamao et al. [7]; Theodossiou and Lee [8]; Lin et al. [9]; Longin and Solnik [10]).
A strand of the aforementioned literature, has focused on how markets react to exogenous events and shocks including natural or anthropogenic catastrophes and accidents, political risk and violent events such as conflict and terrorism while the contagion potential of this reaction has also been the subject of empirical investigation (inter alia: Kaplanski and Levy [11]; Capelle-Blancard and Laguna, [12]; Asteriou and Siriopoulos [13]; Herbst et al. [14]; Blose et al. [15]; Kalra [16]; Bowen et al. [17]). Following mega-terrorist attacks of recent years, such as for instance 9/11 in New York, and the Madrid and London bomb attacks of 2004 and 2005 respectively, the number of studies that examine the impact terrorism exerts on the economy in general and on financial markets in particular, has steadily grown (inter alia: Brounrn and Derwall [18]; Ramiah et al. [19]; Graham and Ramiah [20]; Amelie and Darne [21]; Fernandez [22]; Nikkinen and Vahamaa [23]). As it has been pointed out in a number of previous papers (inter alia: Drakos, [24]; Kollias et al. [25,26]; Chesney et al. [27]), although the threat of a terrorist attack is omnipresent, particularly in countries such as Israel, Spain or the UK that are or have been the venues of systematic terrorist activity with the concomitant casualties and damages, terrorist events when they occur are unexpected. Depending among other things on their seriousness in terms of victims, damages or target(s) attacked, they have the potential to shake and rattle investors and markets. Just as in the case of natural or anthropogenic accidents, terrorist attacks are unanticipated. Hence, market agents cannot hedge against them. Such incidents can also have a high contagion potential as studies that have addressed this question and the channels of the cross-market transmission of terrorist induced shocks have shown (inter alia: Hon et al. [28]; Mun [29]; Drakos [30,31]). Factors that seem to affect the transmission potential of such exogenous shocks from the market of the country that has been targeted by the terrorists to others include the degree of bilateral integration between the stock markets and the degree of integration into the global economic and financial markets (see Drakos [30,31]). Moreover, Kollias et al. [32] indicate that terrorist attacks trigger a flight-to-safety effect (from stock to bond market within a country) primarily in France and Germany and to a smaller degree in Great Britain and Spain.
Within this particular thematic focus of this strand of literature, this paper addresses the cross-market transmission of the shock generated by a major European terrorist event. The study focuses on the 7 July 2005 London bomb attacks that, along with the 2004 Madrid bombings, are considered to be the European equivalent of 9/11 albeit on a much smaller scale in terms of the number of victims and destruction to property and infrastructure (Kollias et al. [26]). However, unlike previous studies those rely on daily data to assess the impact of terrorist events on financial markets as well as their contagion effect, this study uses high frequency data to investigate the issue at hand. By opening a window on high frequency data, investors may discover profit opportunities not easily detected in daily data. In total, each series of 10-minute interval frequency contains over 10,000 observations. As it has been argued and shown, intraday data help reveal a more accurate picture of how markets and market agents react and adapt to changes and exogenous shocks (inter alia: Connolly and Wang [33]; Hanousek [34]; Égert, and Kočenda [35]; Markelos et al. [36].). Consequently, the more detailed account and the information contained in high frequency data allow more reliable inferences and conclusions to be drawn vis-à-vis daily data.
Moreover, recently a series of papers propose successful methods on high-frequency predictions of trading volumes, market depth, bid-ask spreads and trading costs to optimize order placement and order execution. Among others, Groß-Klußmann and Hautsch [37] successfully apply a long memory autoregressive Poisson model to predict bid-ask spreads. Härdle, Hautsch and Mihoci [38] introduce a semiparametric dynamic factor approach to model high-dimensional order book curves. Hautsch, Schienle and Malec [39] propose a novel approach to model serially dependent positive-valued variables which realize a non-trivial proportion of zero outcomes, a quite common phenomenon on high frequency financial data.
The important role of automated news feeds on intraday dynamics is recognized by Groß-Klußmann and Hautsch [40]. Significant reactions in volatility and trading activity after the arrival of news items which are indicated to be relevant are identified. Moreover, Hautsch, Hess and Veredas [41] study the impact of the arrival of macroeconomic news on the informational and noise-driven components in high-frequency quote processes and their conditional variances. One of their major findings is that all volatility components reveal distinct dynamics and are positively influenced by news.
Therefore, this paper following this line of literature use a modified BEKK(1,1)-GARCH model on intraday data in order to incorporate any possible effect on stock market volatilities and covariance of the mega-terrorism event occurred in July 2005. This type of modeling suggested can be generalized to incorporate other insecurity shocks when studying two variables of interest. More specifically, it examines how two other major European stock markets—Paris and Frankfurt—were affected by the 7 July 2005 mega-terrorist attack in London. The choice of the markets was very much dictated by data availability constraints and the level of capitalization. In the section that follows we proceed with the presentation of the data and the methodology employed. In section three, the findings are presented and discussed, while section four concludes the paper.
2. Data and Methodology
The London terrorist incident, involved a series of coordinated suicide bomb attacks that targeted the city’s public transport system during the morning rush hour of 7 July 2005. The bomb blasts caused 52 fatalities and injured 700 people. They also caused extensive and widespread disruption of the city's transportation system and of the mobile telecommunications infrastructure. As the results reported by Kollias et al. [26] show, the London Stock Exchange (henceforth LSE) suffered significant negative abnormal returns on the day of the attack. Both the general as well as sectoral indices were negatively affected by the event. However, this impact was rather short lived since the market quickly recovered and rebounded. Market volatility was also significantly affected but again, this was of a transitory nature (Kollias et al. [26]). The use of 10-mimute interval data by this study will shed more light on how the market reacted and market agents adjusted to the event as it unfolded between 08:50 and 09:50 given that the bomb blasts took place in different moments in the morning of 7 July 2005. Furthermore, the paper will examine whether or not contagion between financial markets can be established in the case of this major terrorist incident that took place in a city that is one of the most important financial and trading centres of the world. Given LSE’s significance as one of the major financial markets globally with a market capitalisation well over $ 3 trillions 1, one would intuitively expect that the shock waves could have been transmitted to other major European markets. The possible contagion and shock transmission is examined through the use of multivariate GARCH models.
Apart from the London stock exchange, our data set consists of data for the German and French stock market returns over the period 21 January 2005to 28 October 20052. We have to mention at this point that all data are expressed in British summer time (BST) in order to take into account time differences between countries of the study and compare the results of our findings. Frankfurt and Paris are the second and third largest markets in Europe in terms of capitalization. Hence, one can intuitively expect that if shock waves were indeed transmitted from London to other European markets, Frankfurt and Paris are the markets with the highest probability of contagion given the degree of integration between these three large European Union economies and markets. The German stock returns are calculated from the DAX-30 index, the UK returns from the FTSE-100 index, and the French returns from the CAC-40 index. Apart from the information rich nature of such frequency data, a further advantage stemming from the use of intraday data over a short time period is that the possibility of structural breaks is much smaller compared to a longer time period needed if daily data was employed. Indeed, the multivariate GARCH model might give inaccurate forecasts if the underlying process which generates asset prices undergoes a structural break. Moreover, intraday data capture all the main features of the data generating process. In our case the bivariate unrestricted BEKK-GARCH (1,1) model, proposed by Engle and Kroner [42], is used to investigate any possible contagion effects between the London, the German and the French stock markets on the day of the terrorist attack in question. What will be examined is whether or not and to what extent this terrorist event affected the volatilities and the correlation of the stock markets in question using intraday data given that these effects may be hidden in a daily frequency (see for instance previous studies on daily data: Fernandez [22]; Ramiah et al. [19]). In order to avoid any severe convergence problems, the bivariate unrestricted version of the general BEKK(p,q)-GARCH model with p = q =1 is used:
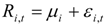 with
with 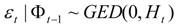 and
and
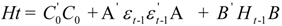 where Equation (1) gives the expression for the conditional mean; Ri,t, and ει, t are the return vector (i = 1 for the FTSE-100 index and 2 for the other two indices for each estimation), and the residual vector respectively; and μi is the mean of this process. In Equation (2) H is the conditional variance-covariance matrix that depends on its past values and on past values of ει, parameter. C0, is a 2 × 2 matrix, the elements of which are zero above the main diagonal; and A, B are matrices. More analytically:
where Equation (1) gives the expression for the conditional mean; Ri,t, and ει, t are the return vector (i = 1 for the FTSE-100 index and 2 for the other two indices for each estimation), and the residual vector respectively; and μi is the mean of this process. In Equation (2) H is the conditional variance-covariance matrix that depends on its past values and on past values of ει, parameter. C0, is a 2 × 2 matrix, the elements of which are zero above the main diagonal; and A, B are matrices. More analytically:
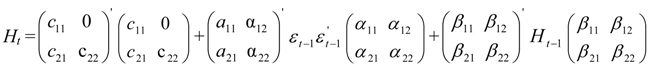
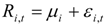
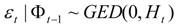 and
and
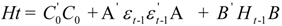
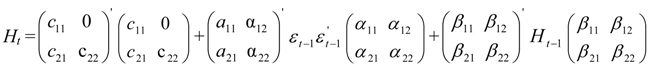
The main advantage of the BEKK-GARCH model is that it guarantees by construction that the covariance matrices in the system are positive (Engle and Kroner, [42]). Assuming multivariate General Error Distribution (GED), the maximum likelihood methodology is used to jointly estimate the parameters of the mean and the variance equations. More specifically, in an attempt to identify the possible effects the terrorist incident in question had on FTSE and y (where y =DAX or CAC) stock index returns co-movement, we employ the unrestricted BEKK-GARCH (1, 1) model including a dummy variable about terror activity in 7 July 2005 in the construction of variances and covariance matrices. This dummy variable takes the value of one for the 10-minute ticks between 7 July 2005 8:50 and 7 July 2005 10:50 (British summer time, BST) and zero anywhere else3. Therefore, the functional form of our model is the following:
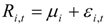 with
with 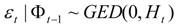 and
and
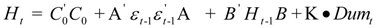 where the K is the coefficient matrix for terror index and the operator “•” is the element by element (Hadamard) product. In that case the model may be written in single equation format as follows:
where the K is the coefficient matrix for terror index and the operator “•” is the element by element (Hadamard) product. In that case the model may be written in single equation format as follows:
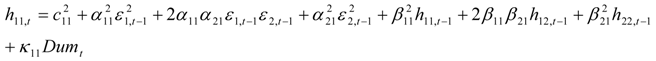
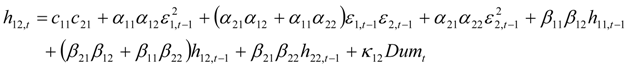
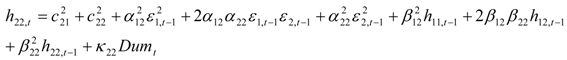
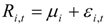
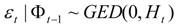 and
and
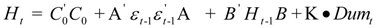
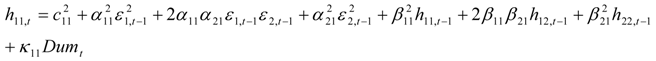
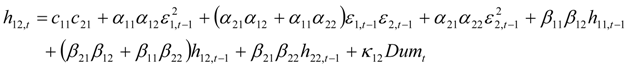
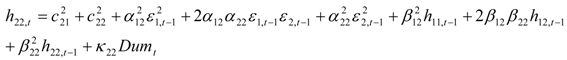
The error terms in each model represent the effect of news in each model on the different indices. In particular, the terms 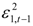 ,
, 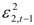 represent the deviations from the mean attributed to the unanticipated event in each market. The cross values of the error terms
represent the deviations from the mean attributed to the unanticipated event in each market. The cross values of the error terms 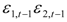 represent the news in the first and second index in time of period t – 1. By
represent the news in the first and second index in time of period t – 1. By 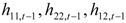 we describe the conditional variance for the first stock index (in our case FTSE-100) at time t – 1, conditional variance for the second stock index (in our case CAC-40 or DAX-30) at time t – 1, and the conditional covariance between the first and the second index in our model.
we describe the conditional variance for the first stock index (in our case FTSE-100) at time t – 1, conditional variance for the second stock index (in our case CAC-40 or DAX-30) at time t – 1, and the conditional covariance between the first and the second index in our model.
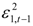 ,
, 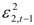 represent the deviations from the mean attributed to the unanticipated event in each market. The cross values of the error terms
represent the deviations from the mean attributed to the unanticipated event in each market. The cross values of the error terms 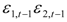 represent the news in the first and second index in time of period t – 1. By
represent the news in the first and second index in time of period t – 1. By 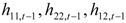 we describe the conditional variance for the first stock index (in our case FTSE-100) at time t – 1, conditional variance for the second stock index (in our case CAC-40 or DAX-30) at time t – 1, and the conditional covariance between the first and the second index in our model.
we describe the conditional variance for the first stock index (in our case FTSE-100) at time t – 1, conditional variance for the second stock index (in our case CAC-40 or DAX-30) at time t – 1, and the conditional covariance between the first and the second index in our model.3. Findings and Discussion
As mentioned above, daily data can often conceal a significant part of underlying dynamics of a time-series especially when it comes to the reaction and eventual adjustment to an unanticipated event such as the terrorist attack in question here. Table 1 provides information using daily data for ±1 days around the event day. As it can easily be seen, the markets in the event day exhibit negative returns (FTSE –1.37%, CAC –1.39% and DAX –1.86%). However, a more detailed scrutiny of the data presented in the last column of Table 1, reveals that the difference between the high and low values during the day is appreciably higher for each market compared to the relevant values of the ±1 days window. This reinforces the argument that high frequency data of the type used here contains a more accurate and credible account of how markets react and adjust to exogenous and unanticipated events; in this case the terrorist attacks of 7 July 2005 in London. Hence, vis-à-vis studies that employ daily observations to examine the impact terrorism exerts on financial markets, the intraday data used in the estimations that follow, have an advantage in that they allow for more reliable inferences to be drawn. Indeed, Figure 1, plotted with the use of high frequency 10-minute interval data, graphically reveals the magnitude of market agents’ reaction to the event in question as it unfolded between 08:50 and 09:50. All three stock markets exhibit a negative reaction to the news as the event started unfolding. It seems that, a considerable amount of selling orders exerted a significant downward pressure in all three cases. The markets begin to recover after 10:50, probably as a result of discounting the short-term economic, political and security repercussions of the incident4.

Table 1.
Stock Prices ± one day of the event—Daily data frequency.
| Date | Open | High | Low | Close | Daily Return | High-Low | |
|---|---|---|---|---|---|---|---|
| 6 July 2005 | 5190.10 | 5237.60 | 5190.10 | 5229.60 | 0.758% | 47.50 | |
| FTSE-100 Index | 7 July 2005 | 5229.60 | 5229.60 | 5022.10 | 5158.30 | –1.373% | 207.50 |
| 8 July 2005 | 5158.30 | 5232.20 | 5158.30 | 5232.20 | 1.422% | 73.90 | |
| 6 July 2005 | 4607.57 | 4636.96 | 4607.57 | 4615.49 | 0.257% | 29.39 | |
| DAX-30 Index | 7 July 2005 | 4595.23 | 4595.23 | 4444.94 | 4530.18 | –1.866% | 150.29 |
| 8 July 2005 | 4560.43 | 4597.97 | 4559.57 | 4597.97 | 1.485% | 38.40 | |
| 6 July 2005 | 4272.64 | 4292.07 | 4264.00 | 4279.95 | 0.638% | 28.07 | |
| CAC-40 Index | 7 July 2005 | 4269.56 | 4269.77 | 4089.27 | 4220.62 | –1.396% | 180.50 |
| 8 July 2005 | 4264.71 | 4300.31 | 4252.07 | 4300.31 | 1.871% | 48.24 |
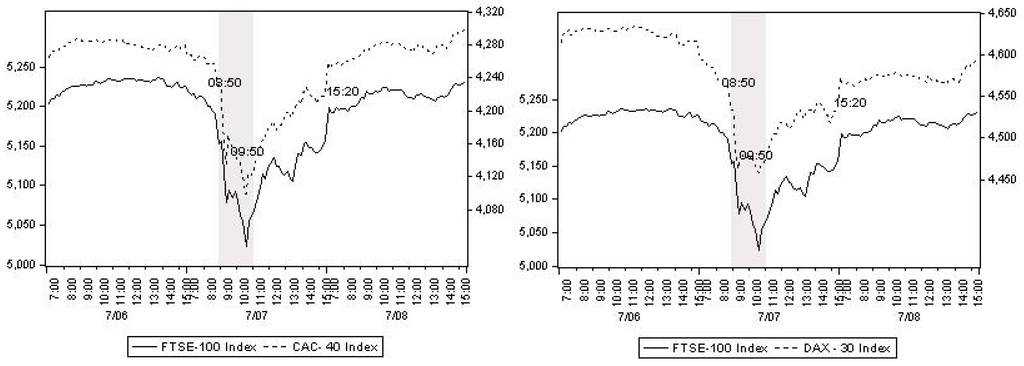
Figure 1.
Stock Prices the days around and during the event.
Figure 1.
Stock Prices the days around and during the event.
The stock market returns are used to conduct the empirical analysis that follows. Table 2 presents the descriptive statistics for the return series in all three stock markets. In terms of the mean, standard deviation and maximum returns, the three markets present fairly similar characteristics. Skewness and kurtosis measures indicate deviation from normality. The latter is confirmed by the Jarque-Bera test that provides evidence against normally distributed tick-by-tick returns. Therefore preliminary statistical analysis confirms well-known stylized facts of financial markets including significant asymmetry and kurtosis. Hence, the use of GARCH type models as a tool to take into account non-normal covariations between stock index returns seems to be appropriate.

Table 2.
Descriptive Statistics of Intraday data.
| CAC- 40 Index | DAX- 30 Index | FTSE -100 Index | |
|---|---|---|---|
| Mean | 1.16 × 10–5 | 1.35 × 10–5 | 8.09 × 10–6 |
| Maximum | 0.0128 | 0.0156 | 0.0101 |
| Minimum | –0.0168 | –0.0229 | –0.0138 |
| Std. Dev. | 0.0009 | 0.0011 | 0.0007 |
| Skewness | –0.9576 | –1.9041 | –0.7345 |
| Kurtosis | 40.8166 | 62.1455 | 40.6416 |
| Jarque-Bera | 612336.3 | 1500214 | 606051.9 |
| Probability | (0.00) *** | (0.00) *** | (0.00) *** |
| Observations | 10250 | 10250 | 10250 |
Notes: The sample contains every ten minutes index returns from 21 January 2005 to 28 October 2005. The total number of usable observations is 10250. The values in parenthesis are the actual probability values. *** indicates statistical significance at 1% level.
The estimated results for the unrestricted BEKK-GARCH (1,1) model are presented in Table 3 for both pairs of indices i.e., the FTSE-CAC (column RFTSE-RCAC) and FTSE-DAX (column RFTSE-RDAX) with the concomitant diagnostics. As far as the whole sample is concerned the majority of the estimated parameters are statistically significant, with the only exception being the coefficient c22 for the FTSE-CAC pair and the coefficient k12 for the FTSE-DAX pair.

Table 3.
BEKK-GARCH estimation results.
| RFTSE-RCAC | RFTSE-RDAX | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Whole Sample | Pre-Bomb period 21/01/2005-05/07/2005 | Post-Bomb period 07/07/2005-28/10/2005 | Whole Sample | Pre-Bomb period 21/01/2005-05/07/2005 | Post-Bomb period 07/07/2005-28/10/2005 | |||||||
| Coeff | Signif. | Coeff | Signif. | Coeff | Signif. | Coeff | Signif. | Coeff | Signif. | Coeff | Signif. | |
| μ1 | 2.06E-05 | (0.00) *** | 2.34E-05 | (0.00) *** | 1.20E-05 | (0.21) | 1.43E-05 | (0.01) ** | 2.20E-05 | (0.01) ** | 1.17E-05 | (0.19) |
| μ2 | 3.53E-05 | (0.00) *** | 3.70E-05 | (0.00) *** | 1.60E-05 | (0.23) | 2.29E-05 | (0.00) *** | 3.07E-05 | (0.00) *** | 1.89E-05 | (0.16) |
| c11 | 1.38E-04 | (0.00) *** | 1.21E-04 | (0.00) *** | −2.12E-04 | (0.00) *** | 1.69E-04 | (0.00) *** | 3.67E-04 | (0.00) *** | 1.71E-04 | (0.00) *** |
| c21 | -2.03E-04 | (0.00) *** | −1.97E-04 | (0.00) *** | 1.23E-04 | (0.00) *** | −1.71E-04 | (0.00) *** | −1.78E-04 | (0.00) *** | 2.10E-04 | (0.00) *** |
| c22 | -9.49E-08 | (0.99) | 3.40E-07 | (0.99) | −2.00E-09 | (0.99) | 9.05E-05 | (0.01) ** | −3.63E-07 | (0.99) | −2.86E-04 | (0.00) *** |
| α11 | 0.0708 | (0.00) *** | −0.0103 | (0.68) | 0.3132 | (0.00) *** | 0.0466 | (0.00) *** | −0.3445 | (0.00) *** | 0.1215 | (0.00) *** |
| α12 | -0.1859 | (0.00) *** | −0.0809 | (0.00) *** | 0.2333 | (0.00) *** | −0.3094 | (0.00) *** | −0.0891 | (0.00) *** | −0.3445 | (0.00) *** |
| α21 | 0.4181 | (0.00) *** | 0.5131 | (0.00) *** | −0.0476 | (0.09) * | 0.3560 | (0.00) *** | 0.5186 | (0.00) *** | 0.2712 | (0.00) *** |
| α22 | 0.6211 | (0.00) *** | 0.6166 | (0.00) *** | 0.3092 | (0.00) *** | 0.6613 | (0.00) *** | 0.6731 | (0.00) *** | 0.6776 | (0.00) *** |
| β11 | 0.9832 | (0.00) *** | 0.9825 | (0.00) *** | 0.6514 | (0.00) *** | 0.9622 | (0.00) *** | 0.0686 | (0.53) | 0.9693 | (0.00) *** |
| β12 | 0.2914 | (0.00) *** | 0.2375 | (0.00) *** | −0.1966 | (0.00) *** | 0.2865 | (0.00) *** | −0.1268 | (0.02) ** | 0.1226 | (0.00) *** |
| β21 | -0.1112 | (0.00) *** | −0.1316 | (0.00) *** | 0.2478 | (0.00) *** | −0.0851 | (0.00) *** | 0.5139 | (0.00) *** | −0.0756 | (0.00) *** |
| β22 | 0.6962 | (0.00) *** | 0.7085 | (0.00) *** | 0.9896 | (0.00) *** | 0.7365 | (0.00) *** | 0.9177 | (0.00) *** | 0.8010 | (0.00) *** |
| κ11 | 1.96E-03 | (0.00) *** | 1.34E-03 | (0.01) ** | ||||||||
| κ12 | 3.20E-03 | (0.00) *** | 1.20E-03 | (0.24) | ||||||||
| κ22 | 1.51E-03 | (0.00) *** | 1.79E-03 | (0.00) *** | ||||||||
| GED Parameter | 0.9268 | (0.00) *** | 0.9218 | (0.00) *** | 0.9117 | (0.00) *** | 0.9459 | (0.00) *** | 0.9122 | (0.00) *** | 0.9577 | (0.00) *** |
| Observations | 10250 | 6068 | 4182 | 10250 | 6068 | 4182 | ||||||
| Log Likelihood | 121740.71 | 72829.31 | 49053.41 | 120011.73 | 72276.21 | 48032.47 | ||||||
Notes: ***,**,* indicate statistical significance at 1%,5% and 10% level.
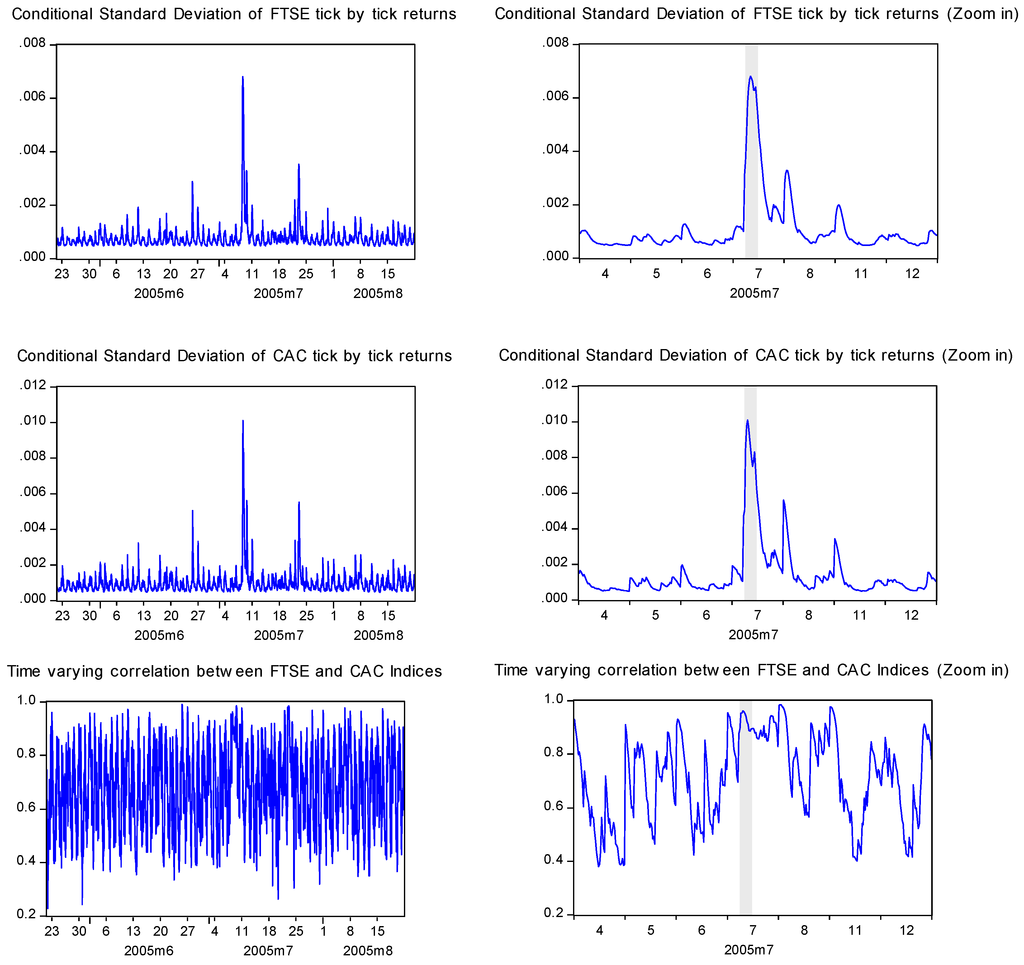
Figure 2.
Conditional Volatilities and Correlation for FTSE-CAC intraday stock returns.
Figure 2.
Conditional Volatilities and Correlation for FTSE-CAC intraday stock returns.
Note that the volatilities of the CAC and DAX indices are directly affected by the news generated within their own market ( 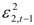 ) and they are also indirectly affected by news generated from the London market (
) and they are also indirectly affected by news generated from the London market ( 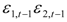 and
and 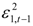 ). A reverse direction is also evident from the German and French markets to the London market but they are lower in magnitude as it can be deduced from the relevant coefficients in absolute terms (
). A reverse direction is also evident from the German and French markets to the London market but they are lower in magnitude as it can be deduced from the relevant coefficients in absolute terms ( 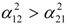 ). It is worth mentioning at that point that when we separate our sample into two sub-samples pre- and post- bomb period interesting findings appear5. More specifically,
). It is worth mentioning at that point that when we separate our sample into two sub-samples pre- and post- bomb period interesting findings appear5. More specifically, 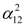 coefficient is higher in the post-bomb period for both DAX and CAC. Therefore, this event seems to affect the way that news is transmitted by London to the other two stock indices. Moreover, the statistical significant positive mean return over the first sub-period for both CAC and DAX indices, become insignificant over the second sub-period. The volatilities of all the indices’ returns are directly affected by their own past volatilities respectively in the whole sample estimation (the relevant coefficient is 0.96 for the British market and 0.48, 0.54 for the French and German market respectively). However, in the case of France, volatility persistence increased in the post-bomb period. Indirect effects of past volatilities are also present in each case. However, the indirect effects of the London market on the CAC and DAX volatilities respectively, are higher compared to the indirect effects of the latter on FTSE (
coefficient is higher in the post-bomb period for both DAX and CAC. Therefore, this event seems to affect the way that news is transmitted by London to the other two stock indices. Moreover, the statistical significant positive mean return over the first sub-period for both CAC and DAX indices, become insignificant over the second sub-period. The volatilities of all the indices’ returns are directly affected by their own past volatilities respectively in the whole sample estimation (the relevant coefficient is 0.96 for the British market and 0.48, 0.54 for the French and German market respectively). However, in the case of France, volatility persistence increased in the post-bomb period. Indirect effects of past volatilities are also present in each case. However, the indirect effects of the London market on the CAC and DAX volatilities respectively, are higher compared to the indirect effects of the latter on FTSE ( 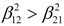 ) for the whole sample. Focusing on the covariance equation in the bivariate BEKK-GARCH models, unexpected shocks in the London market reduce the covariance between FTSE and CAC or DAX. However, unexpected shock in the French and German markets increases their covariance with the London market.
) for the whole sample. Focusing on the covariance equation in the bivariate BEKK-GARCH models, unexpected shocks in the London market reduce the covariance between FTSE and CAC or DAX. However, unexpected shock in the French and German markets increases their covariance with the London market.
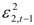 ) and they are also indirectly affected by news generated from the London market (
) and they are also indirectly affected by news generated from the London market ( 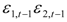 and
and 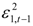 ). A reverse direction is also evident from the German and French markets to the London market but they are lower in magnitude as it can be deduced from the relevant coefficients in absolute terms (
). A reverse direction is also evident from the German and French markets to the London market but they are lower in magnitude as it can be deduced from the relevant coefficients in absolute terms ( 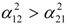 ). It is worth mentioning at that point that when we separate our sample into two sub-samples pre- and post- bomb period interesting findings appear5. More specifically,
). It is worth mentioning at that point that when we separate our sample into two sub-samples pre- and post- bomb period interesting findings appear5. More specifically, 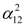 coefficient is higher in the post-bomb period for both DAX and CAC. Therefore, this event seems to affect the way that news is transmitted by London to the other two stock indices. Moreover, the statistical significant positive mean return over the first sub-period for both CAC and DAX indices, become insignificant over the second sub-period. The volatilities of all the indices’ returns are directly affected by their own past volatilities respectively in the whole sample estimation (the relevant coefficient is 0.96 for the British market and 0.48, 0.54 for the French and German market respectively). However, in the case of France, volatility persistence increased in the post-bomb period. Indirect effects of past volatilities are also present in each case. However, the indirect effects of the London market on the CAC and DAX volatilities respectively, are higher compared to the indirect effects of the latter on FTSE (
coefficient is higher in the post-bomb period for both DAX and CAC. Therefore, this event seems to affect the way that news is transmitted by London to the other two stock indices. Moreover, the statistical significant positive mean return over the first sub-period for both CAC and DAX indices, become insignificant over the second sub-period. The volatilities of all the indices’ returns are directly affected by their own past volatilities respectively in the whole sample estimation (the relevant coefficient is 0.96 for the British market and 0.48, 0.54 for the French and German market respectively). However, in the case of France, volatility persistence increased in the post-bomb period. Indirect effects of past volatilities are also present in each case. However, the indirect effects of the London market on the CAC and DAX volatilities respectively, are higher compared to the indirect effects of the latter on FTSE ( 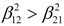 ) for the whole sample. Focusing on the covariance equation in the bivariate BEKK-GARCH models, unexpected shocks in the London market reduce the covariance between FTSE and CAC or DAX. However, unexpected shock in the French and German markets increases their covariance with the London market.
) for the whole sample. Focusing on the covariance equation in the bivariate BEKK-GARCH models, unexpected shocks in the London market reduce the covariance between FTSE and CAC or DAX. However, unexpected shock in the French and German markets increases their covariance with the London market. 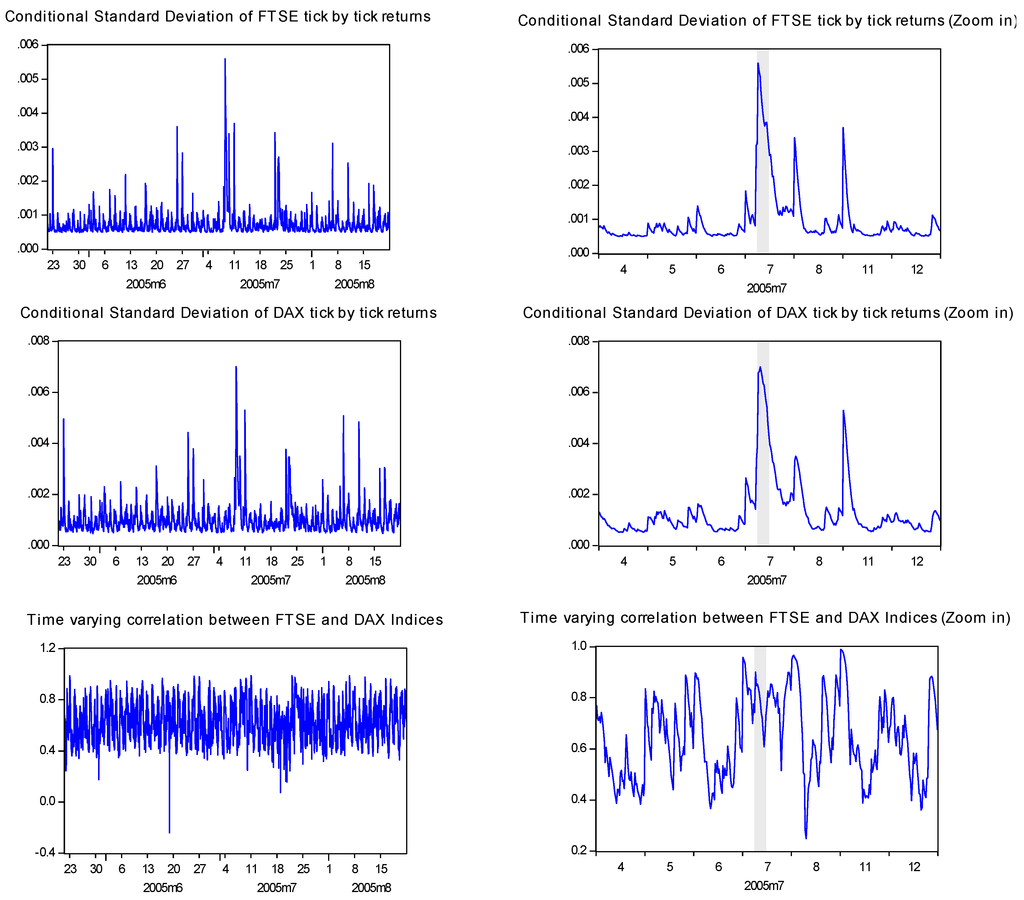
Figure 3.
Conditional Volatilities and Correlation for FTSE-DAX intraday stock returns.
Figure 3.
Conditional Volatilities and Correlation for FTSE-DAX intraday stock returns.
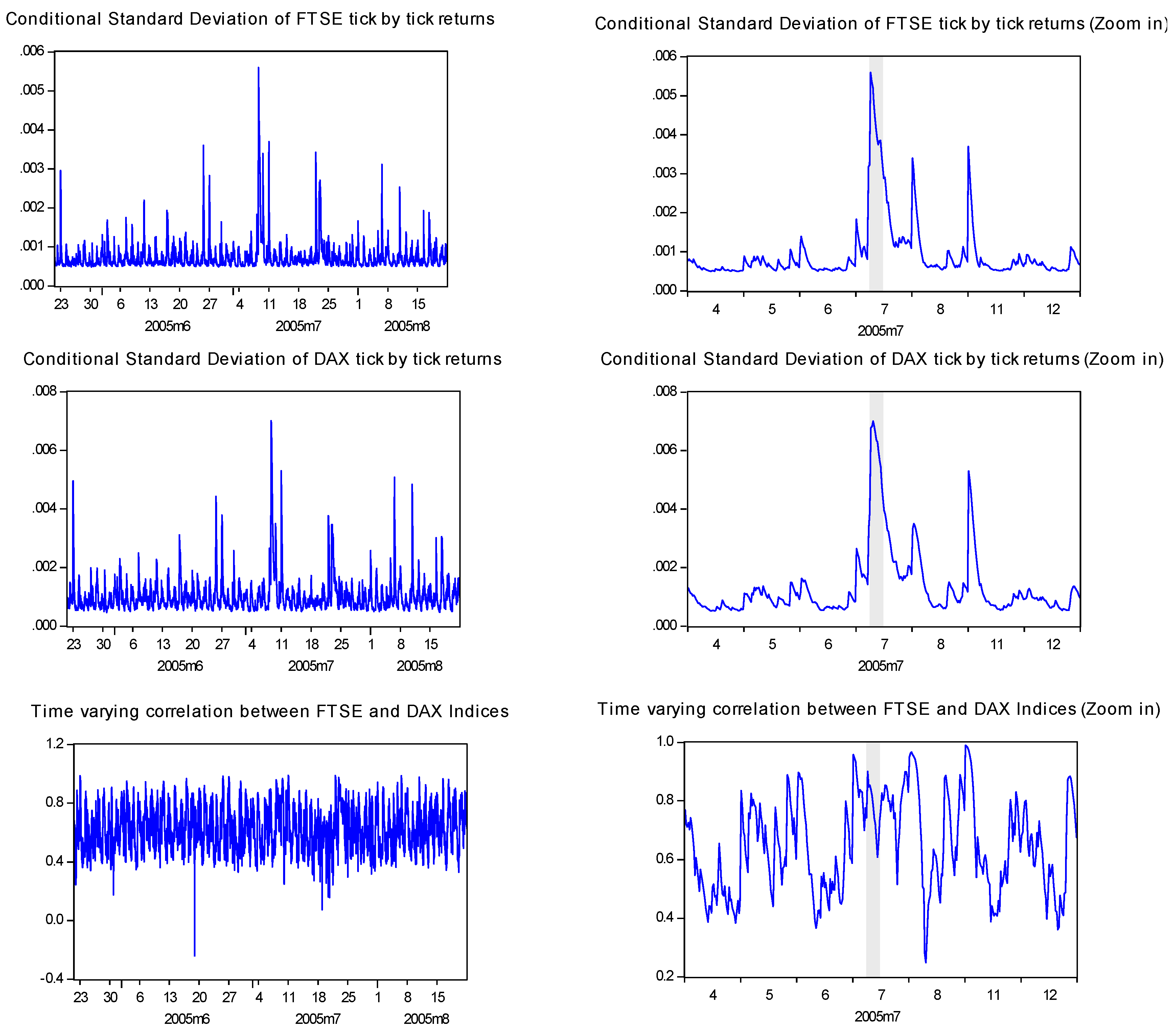
Overall, the results are uniformed in terms of the effect of the terrorism dummy variable on their respective volatilities. There is evidence of a positive and statistically significant effect (kii coefficients) on the volatilities of all three markets. As one would intuitively expect, the higher positive coefficient is present in the case of London. On the other hand, the direct effect of the terrorist attack on the correlation between the stock markets is not uniform. The correlation is directly, significantly and positively affected in the case of the FTSE - CAC pair (see coefficient k12). While for the FTSE–DAX pair, their correlation seems to not be affected in statistically significant degree. For both cases, indirect effects are present from the positive and statistically significant effect of the London market volatility on the covariance term (cross term β11β12). Finally, past correlation seems to affect in a similar way current correlation in every pair of the indices (β21β12 + β11β12). In Figure 2 and Figure 3, the significant positive effect on intraday stock market volatilities during the event day for the FTSE-CAC and the FTSE-DAX pairs of indices6 is clearly visible. Moreover, for the case of FTSE-CAC pair the correlation is significantly increased during the event minutes implying no diversification benefits across these two markets. This finding is in accordance with Chesnay and Jondeau [43] who argued that correlation between stocks returns really increase during turbulent periods. In contrast, the correlation is not affected in a statistically significant and positive manner for the FTSE-DAX pair of indices.
4. Conclusions
As many studies have shown (inter alia: Graham and Ramiah [20]; Fernandez [22]; Ramiah et al. [19]; Drakos [24]; Kollias et al. [26]) terrorist events exert a negative, albeit generally short-lived, impact on stock markets and equity returns. Shocks from terrorist events are also transmitted cross-nationally and affect other financial markets apart from the one of the country that was the venue of the attack (Hon et al. [28]; Mun [29]; Drakos [30,31]). The cross-market transmission of the shock caused by a major European terrorist event, namely the bomb attacks of 2005 in London, was the theme of this study using high frequency data. A general way of incorporating insecurity shocks on a standard multivariate GARCH model is proposed. Future research can use these types of modified models to test other insecurity shocks.
Results reported herein, indicate that the contagion effect, as it is defined by Forbes and Rigobon [44], is mainly present from the London to the Paris market. The correlation between the FTSE and CAC indices is increased significantly during the period the event unfolded in London. Moreover, there is also a significant positive effect of the London market volatility on the CAC and DAX indices’ volatilities. Investigation over sub-samples confirms our findings, indicating that news transmission from London, to Paris and Frankfurt is significantly changed after the terrorist attack. Volatility persistence increased significantly after the attack in case of CAC index. Changes in some parameters of interest are identified over the post-bomb period. Finally, over the time period of the event, stock market volatilities are high in all of our three cases, perhaps suggesting possible gains by intraday trading activity in derivative markets. Trading strategies based on volatility signals may lead to profitable trades.
Acknowledgments
The authors gratefully acknowledge insightful comments and constructive suggestions by three anonymous referees of this journal that helped to improve the paper. This paper was part of the research project “A New Agenda for European Security Economics”, funded by the 7th Framework Programme, to which the authors acknowledge financial support. The usual disclaimer applies.
Conflicts of Interest
The authors declare no conflict of interest.
References
- M. Pericoli, and M. Sbracia. “A primer on financial contagion.” J. Econ. Surv. 17 (2003): 571–608. [Google Scholar]
- W.N. Goetzmann, L. Li, and K.G. Rouwenhorst. “Long-term global market correlations.” J. Bus. 78 (2005): 1–38. [Google Scholar]
- K. Saleem. “International linkage of the Russian market and the Russian financial crisis: A multivariate GARCH analysis.” Res. Int. Bus. Financ. 23 (2009): 243–256. [Google Scholar] [CrossRef]
- I. Meric, and G. Meric. “Co-movements of European equity markets before and after the 1987 crash.” Multina. Financ. J. 2 (1997): 137–152. [Google Scholar]
- I. Asimakopoulos, J. Goddard, and C. Siriopoulos. “Interdependence between the US and major European equity markets: Evidence from spectral analysis.” Appl. Financ. Econ. 10 (2000): 41–47. [Google Scholar] [CrossRef]
- T.C. Chiang, B.N. Jeon, and H. Li. “Dynamic correlation analysis of financial contagion: Evidence from Asian markets.” J. Int. Money Financ. 26 (2007): 1206–1228. [Google Scholar] [CrossRef]
- Y. Hamao, R.W. Masulis, and V. Ng. “Correlations in price changes and volatility across international markets.” Rev. Financ. Stud. 3 (1990): 281–307. [Google Scholar] [CrossRef]
- P. Theodossiou, and U. Lee. “Mean and volatility spillovers across major national stock markets: Further empirical evidence.” J. Financ. Res. 16 (1993): 337–350. [Google Scholar]
- W. Lin, R. Engle, and T. Ito. “Do bulls and bears move across borders? International transmission of stock returns and volatility.” Rev. Financ. Stud. 7 (1994): 507–538. [Google Scholar] [CrossRef]
- F. Longin, and B. Solnik. “Is the correlation in international equity returns constant: 1960–1990? ” J. Int. Money Financ. 14 (1995): 3–26. [Google Scholar]
- G. Kaplanski, and H. Levy. “Sentiment and stock prices: The case of aviation disasters.” J. Financ. Econ. 95 (2010): 174–201. [Google Scholar] [CrossRef]
- G. Capelle-Blancard, and M. Laguna. “How does the stock market respond to chemical disasters? ” J. Environ. Econ. Ma. 59 (2009): 192–205. [Google Scholar] [CrossRef]
- D. Asteriou, and C. Siriopoulos. “The role of political instability in stock market development and economic growth: The case of Greece.” Econ. Notes 29 (2003): 355–374. [Google Scholar]
- A. Herbst, J. Marshall, and J. Wingender. “An analysis of the stock market’s response to the Exxon Valdez disaster.” Global Financ. J. 7 (1996): 101–114. [Google Scholar] [CrossRef]
- L. Blose, R. Bornkamp, M. Brier, K. Brown, and J. Frederick. “Catastrophic events, contagion and stock market efficiency: The case of the space shuttle Challenger.” Rev. Financ. Econ. 5 (1996): 117–129. [Google Scholar] [CrossRef]
- R. Kalra, G. Henderson, and G. Raines. “Contagion effects in the chemical industry following the Bhopal disaster.” J. Financ. Strategic Decis. 8 (1995): 1–11. [Google Scholar]
- R. Bowen, R. Castanias, and L. Daley. “Intra-industry effects of the accident at Three Mile Island.” J. Financ. Quant. Anal. 18 (1983): 87–112. [Google Scholar] [CrossRef]
- D. Brounrn, and J. Derwall. “The impact of terrorist attacks on international stock markets.” Eur. Financ. Ma. 16 (2010): 585–598. [Google Scholar] [CrossRef]
- V. Ramiah, M.A. Cam, M. Calabro, D. Maher, and S. Ghafouri. “Changes in equity returns and volatility across different Australian industries following the recent terrorist attacks.” Pac. Bas. Financ. J. 18 (2010): 64–76. [Google Scholar] [CrossRef]
- M. Graham, and V. Ramiah. “Global terrorism and adaptive expectations in financial markets: Evidence from Japanese equity market.” Res. Int. Bus. Fin. 26 (2012): 97–119. [Google Scholar] [CrossRef]
- C. Amelie, and O. Darne. “Large shocks and the September 11th terrorist attacks on international stock markets.” Econ. Model. 23 (2006): 683–698. [Google Scholar] [CrossRef]
- V. Fernandez. “The war on terror and its impact on the long-term volatility of financial markets.” Int. Rev. Financ. Anal. 17 (2008): 1–26. [Google Scholar] [CrossRef]
- J. Nikkinen, and S. Vahamaa. “Terrorism and stock market sentiment.” Financ. Rev. 45 (2010): 263–275. [Google Scholar] [CrossRef]
- K. Drakos. “Terrorism activity, investor sentiment, and stock returns.” Rev. Financ. Econ. 19 (2010): 128–135. [Google Scholar] [CrossRef]
- C. Kollias, E. Manou, S. Papadamou, and A. Stagiannis. “Stock markets and terrorist attacks: Comparative evidence from a large and a small capitalization market.” Eur. J. Pol. Econ. 27 (2011): 64–77. [Google Scholar] [CrossRef]
- C. Kollias, S. Papadamou, and A. Stagiannis. “Terrorism and capital markets: The effects of the Madrid and London bomb attacks.” Int. Rev. Econ. Financ. 20 (2011): 532–541. [Google Scholar] [CrossRef]
- M. Chesney, G. Reshetar, and M. Karaman. “The impact of terrorism on financial markets: An empirical study.” J. Bank. Financ. 35 (2011): 253–267. [Google Scholar] [CrossRef]
- M. Hon, J. Strauss, and S.-K. Yong. “Contagion in financial markets after September 11: Myth or reality? ” J. Financ. Res. 27 (2004): 95–114. [Google Scholar] [CrossRef]
- K.-C. Mun. “Contagion and impulse response of international stock markets around the 9–11 terrorist attacks.” Global Financ. J. 16 (2005): 48–68. [Google Scholar] [CrossRef]
- K. Drakos. “Behavioral channels in the cross-market diffusion of major terrorist shocks.” Risk Anal. 31 (2011): 143–159. [Google Scholar] [CrossRef]
- K. Drakos. “The determinants of terrorist shock’s cross-market transmission.” J. Risk Financ. 11 (2010): 147–163. [Google Scholar]
- C. Kollias, S. Papadamou, and V. Arvanitis. “Does terrorism affect the stock-bond covariance? evidence from european countries.” South. Econ. J. 79 (2013): 832–848. [Google Scholar] [CrossRef]
- R. Connolly, and A. Wang. “International equity market comovements: Economic fundamentals or contagion.” Pac. Bas. Financ. 11 (2003): 23–43. [Google Scholar] [CrossRef]
- J. Hanousek, E. Kočenda, and A. Kutan. “The reaction of asset prices to macroeconomic announcements in new EU markets: Evidence from intraday data.” J. Financ. Stab. 5 (2009): 199–219. [Google Scholar] [CrossRef]
- B. Égert, and E. Kočenda. “Interdependence between Eastern and Western European stock markets: Evidence from intraday data.” Econ. Syst. 31 (2007): 184–203. [Google Scholar] [CrossRef]
- R. Markellos, T. Mills, and C. Siriopoulos. “Intradaily behaviour of listed and unlisted security basket indices in the emerging Greek stock market.” Manage. Financ. 29 (2003): 29–54. [Google Scholar]
- A. Groß-Klußmann, and N. Hautsch. “Predicting bid-ask spreads using long memory autoregressive conditional poisson models, 2011.” Available online: http://ssrn.com/abstract=1884237 (accessed on 13 November 2013).
- W.K. Härdle, N. Hautsch, and A. Mihoci. “Modelling and forecasting liquidity supply using semiparametric factor dynamics.” J. Empir. Financ. 19 (2012): 610–625. [Google Scholar] [CrossRef]
- N. Hautsch, P. Malec, and M. Schienle. “Capturing the zero: A new class of zero-augmented distributions and multiplicative error processes, 2011.” Available online: http://ssrn.com/abstract=1711810 (accessed on 13 November 2013).
- A. Groß-Klußmann, and N. Hautsch. “When machines read the news: Using automated text analytics to quantify high frequency news-implied market reactions.” J. Empir. Financ. 18 (2011): 321–340. [Google Scholar] [CrossRef]
- N. Hautsch, D. Hess, and D. Veredas. “The impact of macroeconomic news on quote adjustments, noise, and informational volatility.” J. Bank. Financ. 35 (2011): 2733–2746. [Google Scholar] [CrossRef]
- R.F. Engle, and K. Kroner. “Multivariate simultaneous GARCH.” Economet. Theor. 11 (1995): 122–150. [Google Scholar] [CrossRef]
- F. Chesnay, and E. Jondeau. “Does correlation between stock returns really increase during turbulent periods? ” Econ. Notes 30 (2001): 53–80. [Google Scholar]
- K.J. Forbes, and R. Rigobon. “No contagion, only interdependence: Measuring stock market co-movements.” J. Financ. 57 (2002): 2223–2261. [Google Scholar] [CrossRef]
- 1LSE was the bigger in terms of market capitalization in 2005, in Europe followed by the German and French markets (see: www.world-exchanges.org/statistics).
- 2Data are collected by http://www.tickdata.com.
- 3In order to count for the effect induced by the events occurred in 08:50 and 09:50 respectively we have used a dummy taking the value of one from the first bomb explosion lasting one hour and for the second bomb also lasting also one hour.
- 4See for instance Kollias et al. [26] that compare this attack to the one in Madrid in 2004.
- 5We would like to thank one of the anonymous referees for his helpful comment to divide whole sample to sub-samples and investigate for possible differences among stock markets.
- 6The secd column of each graph zooms in on the event day window in order to present in a more clear manner the effect.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
