Next Article in Journal
Valorization of Pennisetum setaceum: From Invasive Plant to Fiber Reinforcement of Injected Composites
Next Article in Special Issue
MTDL-EPDCLD: A Multi-Task Deep-Learning-Based System for Enhanced Precision Detection and Diagnosis of Corn Leaf Diseases
Previous Article in Journal
Hydroxylated Cinnamates Enhance Tomato Resilience to Alternaria alternata, the Causal Agent of Early Blight Disease, and Stimulate Growth and Yield Traits
Previous Article in Special Issue
A Copy Paste and Semantic Segmentation-Based Approach for the Classification and Assessment of Significant Rice Diseases
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Plants
Volume 12
Issue 9
10.3390/plants12091776
plants-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Artificial Neural Network and Response Surface-Based Combined Approach to Optimize the Oil Content of Ocimum basilicum var. thyrsiflora (Thai Basil)

by
Akankshya Sahu
1,
Gayatree Nayak
1,
Sanat Kumar Bhuyan
2,*,
Abdul Akbar
3,
Ruchi Bhuyan
4,
Dattatreya Kar
4 and
Ananya Kuanar
1,*
1
Centre for Biotechnology, Siksha ‘O’ Anusandhan University, Kalinga Nagar, Ghatikia, Bhubaneswar 751003, Odisha, India
2
Institute of Dental Sciences, Siksha ‘O’ Anusandhan University, Bhubaneswar 751003, Odisha, India
3
Department of Biotechnology, Odisha University of Technology & Research, Bhubaneswar 751003, Odisha, India
4
Department of Medical Research, Health Science, IMS & SUM Hospital, Siksha ‘O’ Anusandhan University, Bhubaneswar 751003, Odisha, India
*
Authors to whom correspondence should be addressed.
Plants 2023, 12(9), 1776; https://doi.org/10.3390/plants12091776
Submission received: 17 December 2022 / Revised: 25 January 2023 / Accepted: 13 February 2023 / Published: 26 April 2023
(This article belongs to the Special Issue Deep Learning in Plant Sciences)
Browse Figures
Versions Notes

Abstract

:
Ocimum basilicum var. thyrsiflora is valuable for its medicinal properties. The barriers to the commercialization of essential oil are the lack of requisite high oil-containing genotypes and variations in the quantity and quality of essential oils in different geographic areas. Thai basil’s essential oil content is significantly influenced by soil and environmental factors. To optimize and predict the essential oil yield of Thai basil in various agroclimatic regions, the current study was conducted. The 93 datasets used to construct the model were collected from samples taken across 10 different agroclimatic regions of Odisha. Climate variables, soil parameters, and oil content were used to train the Artificial Neural Network (ANN) model. The outcome showed that a multilayer feed-forward neural network with an R squared value of 0.95 was the most suitable model. To understand how the variables interact and to determine the optimum value of each variable for the greatest response, the response surface curves were plotted. Garson’s algorithm was used to discover the influential predictors. Soil potassium content was found to have a very strong influence on responses, followed by maximum relative humidity and average rainfall, respectively. The study reveals that by adjusting the changeable parameters for high commercial significance, the ANN-based prediction model with the response surface methodology technique is a new and promising way to estimate the oil yield at a new site and maximize the essential oil yield at a particular region. To our knowledge, this is the first report on an ANN-based prediction model for Ocimum basilicum var. thyrsiflora.

1. Introduction

Ocimum basilicum var. thyrsiflora (Thai basil) is an important industrial medicinal plant belonging to the Ocimum species of the Lamiaceae family, which can be used in both raw and processed forms in traditional medicine and the pharmaceutical industry [1]. Ocimum species grow well in saline and alkaline soils with a moderately acidic pH, moderate to heavy rainfall, normal humidity, and high temperatures. This plant is mainly grown in tropical Asia, Africa, and Central and South America, although it is especially popular in China, Japan, Turkey, and Iran [2]. Ocimum species are well recognized for their essential oil, which is responsible for condiment flavour and plant aroma [3]. Thai basil oil has a significant commercial value because of the presence of phenylpropanoids such asestragole, methyl eugenol, (E)-α-bergamotene, and their derivatives, and terpenoids such as monoterpene alcohol linalool, limonene, and terpinolene. The most prevalent volatile components identified in the aroma profile of dried Thai basil included estragol, methyl eugenol, and (E)-α-bergamotene [4]. Over the past few decades, extensive research has shown that Ocimum basilicum extracts have antimicrobials, antioxidants [3], antiviral properties [5], anti-inflammatory properties [6], hypolipidemic effects [7], anti-platelet aggregation, and antithrombotic, antiulcerogenic, and anticarcinogenic [8] activities. It can decrease blood levels of LDL cholesterol while raising blood levels of HDL cholesterol, hence reducing cardiovascular diseases [9,10]. The export database reveals that India exported 1553 Rs per Kg of basil essential oil during 2016–2017 [11].
The major limitation in the commercial production of Thai basil is the lack of staging of high essential oil-containing genotypes and variation in the oil content in different agroclimatic regions. Because the production of essential oils is primarily driven by environmental conditions, it would be impossible to identify the genetically superior Thai basil with a high essential oil concentration using a simple chemotype. According to Rawat et al., there is a wide range of variations in the essential oil concentration of Ocimum species in various agroclimatic areas of Uttarakhand [12]. To ascertain the link between biochemical content and environmental variables, many statistical techniques are used. Multiple linear regression (MLR) analysis and correlation are two common statistical procedures that can only be used to find linear associations and are ineffective when applied to non-linear data [13]. Artificial neural networks (ANN) are increasingly routinely used to build and map non-linear relationships between inputs and outputs due to their improved prediction accuracy. ANN modelling is used to simulate how the human brain functions [14]. It was selected because it can quickly pick up lessons from events without first running statistical analyses on the parameters [15]. The input layer, hidden layers, and output layer of neurons are the three main divisions of an ANN [16]. The input layers’ neurons receive the input data, which is then adjusted before being sent to the hidden layer [17]. Each neuron in the layer below performs a linear combination of the data from the neurons in the input layer, adding weight values related to certain nodes to the result. The projected model is the outcome of the neurons in the hidden layer combining the linear data from the input layer with a transfer function (a specific non-linear function) [16]. The ANN model has been used to predict the bioactive content of the compounds podophyllotoxin from Podophyllum hexandrum [18]; hyperforin, hypericin, and pseudohypericin from Hypericum perforatum L. [13]; and bacoside A from Bacopa monnieri [19].
Therefore, it will be mandatory to analyze the soil parameters and climatic factors of different agroclimatic areas of Odisha for high essential oil content. An Artificial Network (ANN) model and a Response surface-based combined approach for essential oil content in Thai basil can be developed to predict the appropriate site and enhance the essential oil content at a particular site by managing the sensitive and variable factors.

2. Materials and Methods

2.1. Plant Materials and Sample Station

From June to October 2021, samples of Thai basil leaves were collected from 93 sites across 10 agroclimatic regions in several districts of Odisha, at varying altitudes ranging from 0.1 to 1204 m (Table 1). Three replicates of the leaf samples were taken from each site. The two duplicates were separated by 2 to 5 m. To get rid of the dust, the samples of freshly collected leaves were first washed with running tap water and then with distilled water. Following air drying at room temperature, samples of washed leaves were used to determine the essential oil contents. To analyze soil nutrients, triplicate soil samples were taken from each sampling site and brought to the lab. The documented monthly average data on environmental variables, such as rainfall, temperature, or humidity, were noted from each sampling site from June 2021 to October 2021.

2.2. Extraction of Essential Oil and Quantification

The air-dried leaves were crushed and powdered in a mortar and pestle before being hydrodistilled in a Clevenger-type apparatus made entirely out of glass. For later usage, the oil was dried with anhydrous sodium sulphate and stored in a sealed Eppendorf tube at 4 °C.

2.3. Quantitative Analysis of Soil

In triplicate, soil samples were taken from each sampling site within an agroclimatic region. A soil sample of approximately 250 g was taken and sieved through a 2-mm mesh. Nutrient analysis was performed using fine soil. Using the Systronics pH meter (Model MKVI), the pH of soil samples was identified in soil: water 1:2 ratio suspension after 30 min of equilibration with infrequent stirring.
Using Bray’s No 1 technique, the total phosphorus content of soil samples was determined. The solution was made by extracting 2 g of soil in 40 mL of Bray’s solution, which contains 0.03 NH4F and 0.025 N HCL. This mixture was then agitated vigorously for five minutes using a mechanical shaker and filtered through Whatman paper. A 25 mL flask was filled with a 0.5 mL aliquot. Ammonium molybdate solution (0.5 mL) and distilled water were added to bring the volume up to 25 mL. To make up the volume, diluted SnCl2 (0.5 mL was diluted in 66 mL) was added. The concentration of phosphorus was measured using a spectrophotometer (Model: Systronics 166) set at 660 nm. The concentration was measured using a standard graph created by varying the phosphorus content. The available phosphorus in the soil samples was determined by extracting the soil using Olsen’s reagent (0.5 M NaHCO3, pH 8.5). The phosphorous concentration was measured using a spectrophotometer (Model: Systronics 166) and the mechanism was ascorbic acid reduced to blue-colored sulphomolybdic acid in the sulphuric acid system at 882 nm [20]. Next, 5 g of the soil sample was placed in a 100 mL conical flask along with 25 mL of 1 N NH4OAc solution to determine the amount of potassium present in the soil. An automatic shaker was used to shake the mixture for 5 min, after which the filtrate’s potassium level was determined using a flame photometer (Model: Systronics 128). The Walkley and Black Wet Digestion Technique were used to calculate the organic carbon content in the soil sample by chemical analysis [21].
The alkaline KMnO4 method was used to calculate nitrogen content. Next, 20 g of the soil sample were placed in an 800 mL Kjeldahl flask together with 100 mL of a 0.32% KMnO4 solution, 2.5% NaOH solution, and distilled water. In a 250 mL conical flask containing 20 mL of 2% boric acid and a mixed indicator, the distillation process was continued, and the result was collected in a receiver tube. The available nitrogen was then calculated by titrating the distillate in a burette against 0.02 N H2SO4 to a pink colour endpoint [22].

2.4. Data Exploration

All computational work (model development, plot generation, etc.) was performed using R (R Core Team 2021, Vienna, Austria). The data set consists of 12 features and 93 instances. Out of the features, 11 are predictors. The predictors are phosphorous, nitrogen, potassium, the organic carbon content, pH of the soil, maximum and minimum relative humidity, average rainfall, maximum and minimum average temperature, and altitude. Thai basil oil content is the response. Standard deviations for all features were calculated using the mlbench [23] library (Appendix A).
The formula for standard deviation is provided below.
Standard   deviation = ( x − x − ) 2 n − 1
where x and x − are the value of each observation and mean of all observations, respectively.
Pearson’s correlation coefficient between features and data distribution in each feature were evaluated using the package psych [24]. Pearson’s correlation coefficient was calculated using equation 2. The correlation values were provided in the panel plot in the form of numeric values as well as a correlation ellipse (Figure 1).
The   Pearson ’ s   Correlation   coefficient   ( r ) = ∑ { ( x − x − ) ( y − y − ) } ∑ ( x − x − ) 2 ∑ ( y − y − ) 2
where x and y are the values of the two variables; x −   and   y − are the respective means.

2.5. Data Splitting

The dataset (total data) is divided into three sets: train, test, and validation with 70%, 20%, and 10% of data, respectively. The train set was used to develop the model by training. The model was evaluated using the test set. Finally, the model was validated using a validation set.

2.6. Artificial Neural Network Model Development

The Caret (classification and regression training) package [25] was used to develop the artificial neural network model. Data was scaled using minimum–maximum normalization. The train set was resampled with 15-fold cross-validation during training. A grid-tuning approach was used to ascertain the optimal number of layers and nodes within each layer. The logistic function was selected as the activation function. A learning rate of 0.02 was maintained. Error calculations were performed using the Sum of Squared Errors.
SSE = ∑ ( y − y ^ ) 2
where y and y ^ are the actual response and predicted response, respectively.

2.7. Model Evaluation and Selection

The final model was selected based on the values of root mean square error (RMSE), mean absolute error (MAE), and the coefficient of determination or R squared (R squared) values. The above evaluation metrics were calculated using the following formulae:
RMSE = ∑ ( y ^ − y ) 2 n
MAE = ∑ ( y − y ^ ) n
R   squared = ∑ ( y ^ − y − ) 2 ∑ ( y − y − ) 2

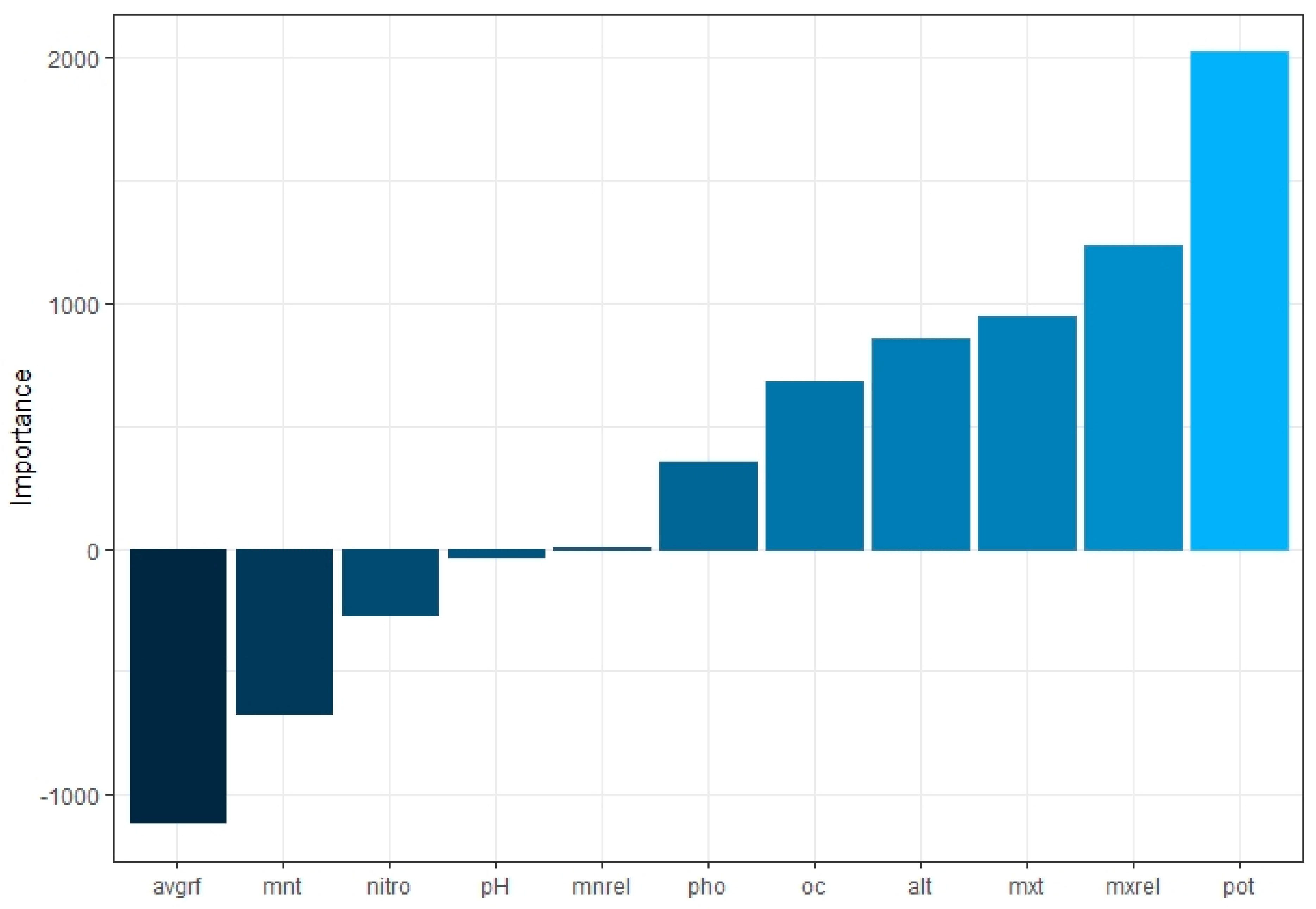
2.8. Variable Importance

The variable (different factors) importance of the response was evaluated using the Neural Net Tools [26] library. To determine the ranking importance of predictors, Olden’s method was used. To assess the significance of the predictors, the method analyzes the raw connection weights between input-hidden nodes and hidden-output nodes [27]. They have also compared several methods viz. input perturbation, partial derivatives, etc., and concluded that the connection weight approach—i.e., Olden’s method—is more reliable.

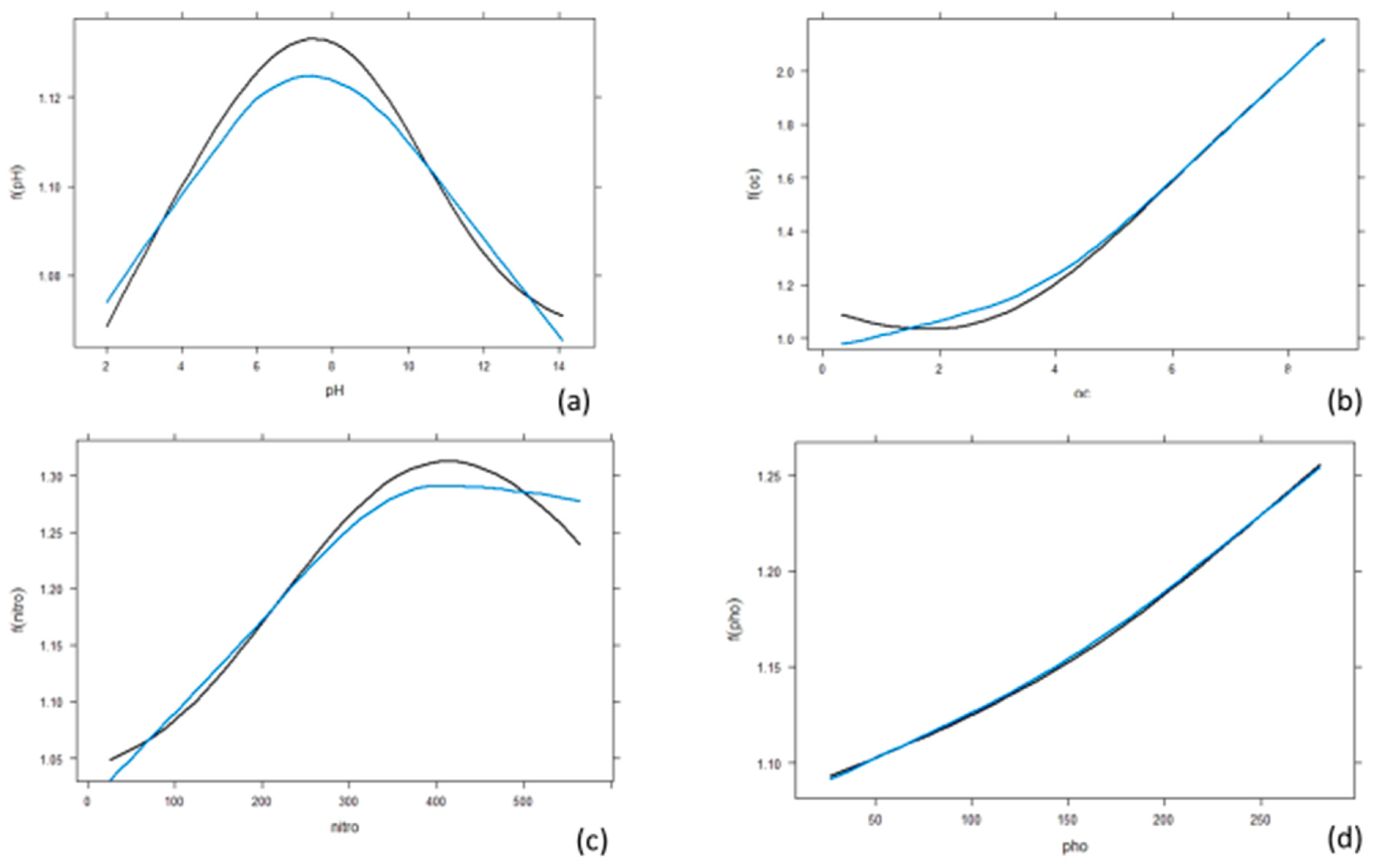
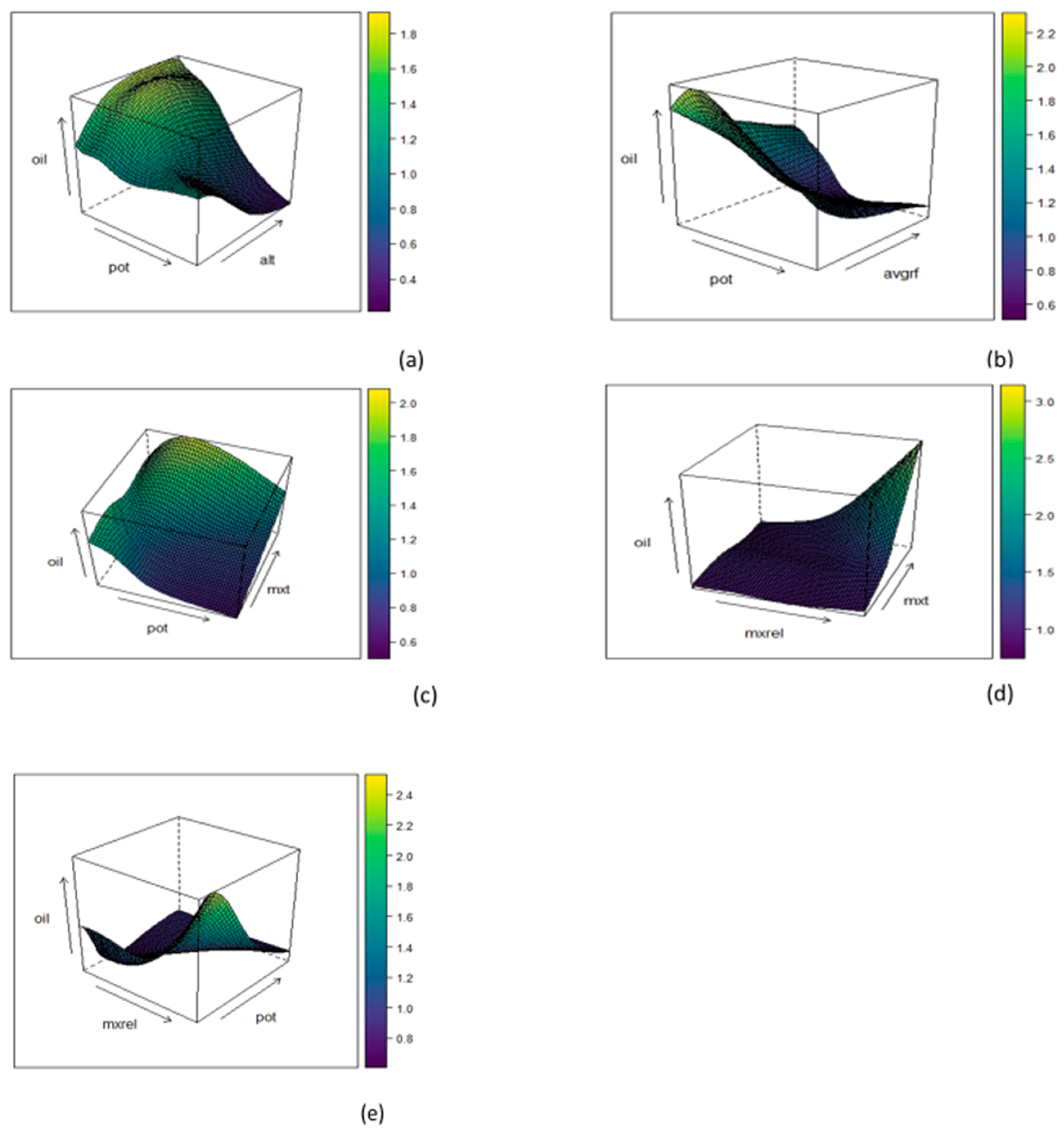
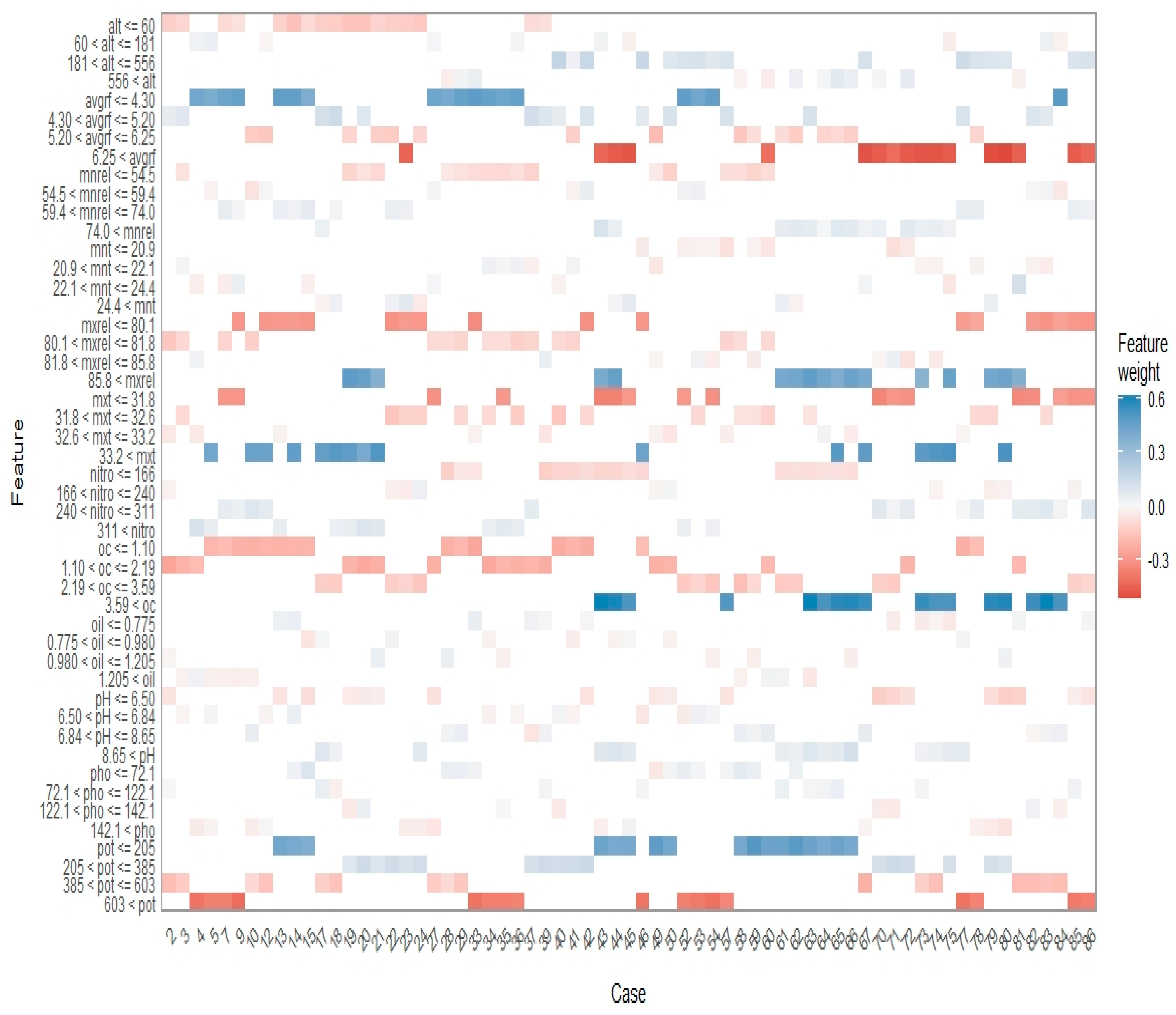
2.9. Partial Dependence Plots and Faceted Heatmap

Partial dependence plots (PDP) were generated to investigate the interaction of predictors with the response. These plots were generated using the PDP library. The use of linear plots is not suitable for explaining the complex relationship of different variables with the response. PDP plots are used to interpret the output of complex machine-learning models [28]. In this study, single-variable and multiple-variable PDPs are generated. Smoothing is applied using locally weighted regression (LOESS) in the case of single variable PDPs, which has popularity in the smoothing of scatterplots [29]. LOESS can perform well even if the response is a nonlinear function of the predictor [30]. The relationship of the response variable with two predictors is represented by a two-dimensional contour and three-dimensional PDPs.
Another type of plot called a faceted heatmap was used to identify the behavior of the response concerning precise value ranges of predictors. For this purpose, a lime [31] package was used.

2.10. Sensitivity Analysis

It is critical to identify the most important elements influencing essential oil content. Therefore, Garson’s algorithm was used to discover the influential predictors. The link strengths between the nodes are calculated to assess the relative importance of each predictor.

3. Results and Discussion

The pair plots (Figure 1) show four different data set representations through ellipse plots, scatter plots, correlation coefficients, and histograms. The trend lines represent the linear relationship among variables in scatter plots. The correlation ellipse characterizes the correlation strength. When the stretch is higher, the correlation coefficient is also higher. When the correlation coefficient value is between 0 to 0.1, 0.1 to 0.39, and 0.4 to 0.69, the correlation is negligible, weak, or moderate, respectively. Correlation is strong when the coefficient value is between 0.7 and 0.89, and very strong when the correlation coefficient value is between 0.9 and 1 [32]. From the plot, pH has a moderate correlation with variables viz. minimum relative humidity and minimum average temperature. Correlations of pH with remaining variables were found to be negligible to weak. Similarly, the correlation strengths among variables are represented in Figure 1. Only two variables, minimum relative humidity and minimum average temperature, have shown a strong correlation, i.e., 0.71. A correlation study among the predictors has significance in model evaluation. The machine learning algorithms are affected if any correlation exists among the predictors [33]. The data set shows multicollinearity among its variables. In such cases, artificial neural networks (ANN) are found to be suitable as the ANN models are least affected due to correlations among input variables [34,35].

3.1. Model Evaluation and Selection

The final model along with climatic data (Table 2), soil data (Table 3), different layers, nodes, and connection strengths are provided in Figure 2. Root mean square error (RMSE) and mean absolute error (MAE) were used as performance measures to select the best model. The data set has multicollinearity among variables, so the RMSE can be used as a performance measure [35]. The model that had the lowest RMSE and MAE was selected. The RMSE, mean absolute error (MAE), and the coefficient of determination (R-squared) values of the model for the train, test, and validation data sets are provided in Figure 3. The predictions and the actual responses for the train set are provided in Table 4. The RMSE, MAE, and R squared values for training were 0.00, 0.02, and 0.99, respectively (Figure 3).
After training, the model was evaluated using the test data set. The RMSE, MAE, and R squared values for test set data are 0.04, 0.13, and 0.95, respectively (Figure 3). Furthermore, the model was validated with a validation set. The model also performed well with RMSE, MAE, and R squared values of 0.09, 0.09, and 0.92, respectively. Table 5 and Table 6 show the predictions and actual responses for test and validation data, respectively. As far as we know, this is the first study to represent the extent of the essential oil content prediction of Thai basil. For predicting the essential oil content of Thai basil, the Artificial Neural Network (ANN) is recommended as one of the most promising methods. This networking system provides new possible approaches for the study of bioactive compounds in other plants as well as in other environmental conditions. As a predictive approach for maximizing the operating parameters during the extraction of various natural products, the ANN has been proposed by various researchers [36,37,38,39].
ANN does not require any inference of previous data structure; thus, it gathers an advantage over other statistical modeling techniques. It may detect complicated interactions and non-linear correlation, and expose the unknown linkage between previously input parameters [40]. The four statistical quality measures such as coefficient of determination (R squared), root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) are used to develop the ANN model. When the coefficient value is 0.9–1, the correlation is very strong, and 0.7–0.89 indicates a strong correlation. The correlation is negligible when the correlation coefficient value is between 0–0.1; likewise, 0–1–0.39 and 0.4–0.69 indicate that the correlation is weak and moderate, respectively [32]. In model evaluation, the correlation study among predictors has significance. If any correlation is present between the predictors, then the machine learning algorithms are affected [33]. The ANN model developed in this study determined the strong predictive potential for essential oil content for Thai basil because it was measured by correlation coefficient (R squared) and root mean square error (RMSE). Less variation between the projected value and experimental value is indicated by the model’s higher R squared value of 0.92 and lower RMSE value of 0.09. The ANN model is called stronger when the R squared value is closer to 1 and the RMSE value is lower. Hence, it is possible to conclude that the model developed for the prediction of the essential oil content of Thai basil is considerably accurate. Similar studies were published in which error values were lower with high predictive analysis of the ANN model [41,42,43].

3.2. Significant Predictor Identification

According to the model, soil potassium content was found to have a very strong influence on response, followed by maximum relative humidity and average rainfall, respectively (Table 7). Minimum relative humidity was found to have the least effect on oil content. The relative importance of all variables on output is provided in Figure 4. Garson’s algorithm was used to discern influential predictors and remove insignificant predictors. In an ANN, the coefficient in a generalized linear model is partially equivalent to the weights that connect neurons. There are different weights connecting one predictor to the outcome, and the weights’ combined influence shows how important each predictor is about the outcome variable. A large number of adjustable weights makes an ANN very flexible and nonlinear, but also creates difficulties in interpretation [44,45]. A single value ranging from 0 to 1 that illustrates the relative relevance of predictors is produced by combining and scaling all weights that are linked to a predictor. The Neural Networking Tools (Version 1.5.1) package in R can be used to determine the relative importance [17].

3.3. Effect of Individual Predictors on Essential Oil Content

Single variable PDPs are generated for all predictors and provided in Figure 5a–k. The multicollinearity among the features of the data set is shown in Figure 1. Most of the correlation among variables is weak to moderate. Minimum average temperature and minimum average relative humidity have shown a strong correlation (Figure 6). In such cases, ANN models provide promising results and are free from any biases due to multicollinearity [34]. Therefore, PDPs generated through artificial neural network models are suitable to study the change in response to predictors. The variation of oil content with soil potassium content was provided in Figure 5e. The essential oil content was found to be higher with low soil potassium content and average rainfall (Figure 5h). However, the oil content increased with an increase in organic carbon content (Figure 5b), nitrogen (Figure 5c), maximum average temperature (Figure 5i), maximum relative humidity (Figure 5f), etc. The oil content showed dramatic variation with variation in minimum average temperature (Figure 5j). Initially, the oil content was found to decrease with an increase in minimum average temperature. When the temperature is beyond 25 °C, the oil content gradually increased. Similarly, when the maximum relative humidity exceeded 85 (approx.), the oil yield also gradually increased (Figure 5f). Partial dependence plots (PDPs) were used to show how one or two variables affect the predictions of the model. In this study, a univariate partial dependence plot is displayed alongside each pairwise partial dependence plot in a matrix-style layout. An analyst can easily observe and identify the important pairs of variables that have a significant impact on the model using this partial dependence plot.

3.4. Mutual Effect of Two Predictors on Response

Partial dependence plots with two variables show the mutual contribution of the variables to the response. Such plots help identify the optimum range of predictor values for a maximum value of the response. Two-variable PDPs (Figure 7a–e and Figure 8a–e) are generated for the top five important variables (soil potassium content, altitude, maximum relative humidity, maximum average temperature, and average rainfall) to understand the mutual influence of these variables on response. For each pair of predictors, two different types of PDPs are generated: a 2D contour plot and 3D partial dependence plot. In each plot, the colour scale on the right-hand side shows the colour as a measure of essential oil content. From these values, it is evident that a lower value of soil potassium content, i.e., from 0 to 250 kg/ha (approx.), and an altitude range of 400 m to 800 m is favorable for higher oil content (Figure 7a and Figure 8a). Similarly, a low value of average rainfall, i.e., 4 mm was found to be favourable for essential oil content (Figure 7b and Figure 8b). The essential oil content is found to be higher when the maximum average temperature value is higher than 36 °C (Figure 7c and Figure 8c). From Figure 7d and Figure 8d, it is evident that a higher maximum relative humidity value (i.e., beyond 95) is found to be favourable for Thai basil oil.
In the case of all previous PDPs (single-variable and double-variable PDPs), the variation in oil content is represented as a gradual change in colour intensities. From these plots, it is notably challenging to conclude the precise value ranges of variables in which the response shows variation. In such situations, faceted heatmaps are found to be advantageous. A faceted heatmap for all predictors is provided in Figure 9. The colour scale shows the weight or influence of the predictor on response. The x-axis shows the instances. The y-axis shows the predictor value ranges. The dark blue colour represents positive feature weight, i.e., the variable range supports the response and the dark red color represents negative feature weight [46]. In the plot, the total altitude range is divided into four different groups: ≤60 kg/ha, between 60 kg/ha and 181 kg/ha, 181 to 556 kg/ha, and greater than 556 kg/ha. The first group, ≤60 kg/ha, has a mild negative feature weight; the third group, 181 to 556 kg/ha, has a mild positive feature weight. Average rainfall higher than 6.25 mm has a strong negative effect on basil oil content. The oil content is favoured when the potassium content is less than or equal to 205 kg/ha. Potassium content greater than 603 kg/ha is found to have a negative effect on the oil content. The oil content is found to be positively affected when the maximum relative humidity value is beyond 85.8. The feature weights for other variables are provided in Figure 9. Large multivariate data sets can be explored using heat maps. Color gradients or colour schemes are used to illustrate response variables. The right transformation along with row and column grouping might reveal interesting patterns in the data. In addition, they can be used to display the outcomes of statistical analysis, such as the variables that differ between treatment groups.
To the best of our knowledge, this research is the first to look into the impact of soil nutritional parameters and environmental factors on Thai basil oil content in 10 different agroclimatic regions of Odisha. According to this study, a combination of either two factors or more than two factors have greater impacts than a single factor on Thai basil oil content. It was found that adjusting parameters such as height, temperature, rainfall, humidity, and potassium content in the soil can maximize the oil content of Thai basil. The difference in oil content in different regions is influenced by various parameters that need to be further investigated. The prediction model developed in this study will be beneficial to obtain Thai basil oil content in a new site that is close to the experimental values.

4. Conclusions

To obtain the highest oil yield from Thai basil, it will be advantageous to use the artificial neural network (ANN) model developed to investigate the effect of various environmental factors and soil parameters on oil content. The outcome showed that by developing an ANN, we can forecast the oil concentration at a new site using a combination of environmental and soil data. By modifying the model’s input parameters (height, temperature, rainfall, humidity, and potassium), it is possible to increase the oil content of Thai basil. The ANN model is therefore highly helpful to predict and optimize the oil content of Thai basil at a particular site for commercial cultivation.

Author Contributions

Conceptualization, S.K.B.; Methodology, A.K. and A.A.; Software, A.A. and A.K.; Validation, A.S.; Formal Analysis, A.S.; Investigation, A.K. and A.S.; Resources, A.S.; Data Curation, A.S.; Writing—Original Draft Preparation, A.S.; Writing—Review and Editing, A.S.; Visualization, R.B., G.N. and D.K.; Supervision, A.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The study did not report any data.

Acknowledgments

The authors are grateful to Sanghamitra Nayak, Head, Centre of Biotechnology; Sudam Chandra Si, Dean, SPS; and Manoj Ranjan Nayak, President, Siksha ‘O’ Anusandhan University, Bhubaneswar, India for providing study facilities.

Conflicts of Interest

The authors declare that there are no conflict of interest regarding the financial and non-financial aspects of publication for this article.

Appendix A. Sample Code

  • library(readxl)
  • library(caret)
  • data<-as.data.frame(read_xlsx(“tb.xlsx”))
  • #calculate standard deviation
  • library(mlbench)
  • library(“openxlsx”)
  • # calculate standard deviation for all attributes
  • sd.table<-sapply(data[,1:12], sd)
  • sd.table<-as.data.frame(sd.table)
  • write.xlsx(sd.table,”Standarddeviation.xlsx”)
  •  
  • ######Correlations analysis
  • correlations <- cor(data[,1:10])
  • # display the correlation matrix
  • cor.table<-print(correlations)
  • cor.table
  • write.xlsx(cor.table,”Correlations.xlsx”)
  • #creating panel plot
  • library(psych)
  • pairs.panels(data[c(“pH”, “oc”, “nitro”, “pho”,”pot”,”mxrel”,”mnrel”,”avgrf”,”mxt”,”mnt”,”alt”)])
  •  
  • #############data splitting ###########
  • set.seed(212)
  • trainIndex<- createDataPartition(data$oil, p=0.8, list=FALSE)
  • train <- data[ trainIndex,] ####80% of total data including validation
  • test<- data[-trainIndex,]
  • validIndex<- createDataPartition(data$oil, p=0.9, list=FALSE)
  • train <- data[ validIndex,] ####70% of total data
  • valid<- data[-validIndex,] ######10% of total data
  •  
  • #######ANN model development######
  • trainControl <- trainControl(method=“cv”, number=15)
  • tunegrid<- expand.grid(layer1 = 16, layer2 =15, layer3=4)
  • metric <- “MAE”
  • set.seed(123)
  • fit.ann<-train(oil~., data = train, method=“neuralnet”, metric = metric, preProcess=c(“range”), tuneGrid = tunegrid, act.fct=“logistic”,trControl = trainControl,learningrate = 0.02, linear.output=T)
  • fit.ann
  • ####Plotting the final model#####
  • library(NeuralNetTools)
  • plotnet(fit.ann$finalModel)
  •  
  • ####Predicting for test set####
  • pr.ann <- predict(fit.ann, newdata=test)
  • pr.ann<-as.data.frame(pr.ann)
  • library(“openxlsx”)
  • output.table<-cbind(test$oil,pr.ann)
  • output.table
  • write.xlsx(output.table,’testVsPred.xlsx’)
  •  
  • #####Predicting for validation set
  • valid<-as.data.frame(read_xlsx(“valid.xlsx”))
  • val.ann <- predict(fit.ann, newdata=valid)
  • val.ann<-as.data.frame(val.ann)
  •  
  • ########Variable Importance
  • library(NeuralNetTools)
  • olden(fit.ann)
  • #####partial dependecnce plot
  • #####Single variable
  • library(pdp)
  • library(ggplot2)
  • partial(pred.var = “alt”) %>%
  • plotPartial(smooth = T, lwd = 2, ylab = expression(f(alt)))
  •  
  • partial(pred.var = “mnt”) %>%
  • plotPartial(smooth = T, lwd = 2, ylab = expression(f(mnt)))
  •  
  • partial(pred.var = “mxt”) %>%
  • plotPartial(smooth = T, lwd = 2, ylab = expression(f(mxt)))
  •  
  • partial(pred.var = “mxrel”) %>%
  • plotPartial(smooth = T, lwd = 2, ylab = expression(f(mxrelhum)))
  • partial(pred.var = “avgrf”) %>%
  • plotPartial(smooth = T, lwd = 2, ylab = expression(f(avgrainfall)))
  • partial(pred.var = “mnrel”) %>%
  • plotPartial(smooth = T, lwd = 2, ylab = expression(f(mnrel)))
  •  
  • partial(pred.var = “pot”) %>%
  • plotPartial(smooth = T, lwd = 2, ylab = expression(f(pot)))
  •  
  • partial(pred.var = “pho”) %>%
  • plotPartial(smooth = T, lwd = 2, ylab = expression(f(pho)))
  • partial(pred.var = “nitro”) %>%
  • plotPartial(smooth = T, lwd = 2, ylab = expression(f(nitro)))
  •  
  • partial(pred.var = “oc”) %>%
  • plotPartial(smooth = T, lwd = 2, ylab = expression(f(oc)))
  • partial(pred.var = “pH”) %>%
  • plotPartial(smooth = T, lwd = 2, ylab = expression(f(pH)))
  •  
  • ####without smoothing
  • fit.ann %>% # the %>% operator is read as “and then”
  • partial(pred.var = “alt”) %>%
  • plotPartial(smooth = F, lwd = 2, ylab = expression(f(alt)))
  •  
  • ######with two predictors#######
  • ######pot mxrel
  • par.mxrel.pot <- partial(fit.ann, pred.var = c(“mxrel”, “pot”))
  • plotPartial(par.mxrel.pot)
  •  
  • # Add contour lines and use a different color palette
  • rwb <- colorRampPalette(c(“red”, “white”, “blue”))
  • pdp2 <- plotPartial(par.mxrel.pot, contour = TRUE, col.regions = rwb)
  • pdp2
  •  
  • # 3-D surface
  • pdp3 <- plotPartial(par.mxrel.pot,rug=T,levelplot = FALSE,number=4, zlab = “oil”, drape = TRUE,colorkey = TRUE, screen = list(z =−40, x = −60))
  • pdp3
  •  
  • ###Maximum rel humidity and Max. avg. temperature
  • par.mxrel.mxt <- partial(fit.ann, pred.var = c(“mxrel”, “mxt”))
  • plotPartial(par.mxrel.mxt)
  •  
  • # Add contour lines and use a different color palette
  • rwb <- colorRampPalette(c(“red”, “white”, “blue”))
  • pdp.mxrel.mxt.2d <- plotPartial(par.mxrel.mxt, contour = TRUE, col.regions = rwb)
  • pdp.mxrel.mxt.2d
  •  
  • # 3-D surface
  • pdp.mxrel.mxt.3d <- plotPartial(par.mxrel.mxt,rug=T,levelplot = FALSE,number=4, zlab = “oil”, drape = TRUE,colorkey = TRUE, screen = list(z = −20, x = −60))
  • pdp.mxrel.mxt.3d
  •  
  • ###pot mxt
  • par.pot.mxt <- partial(fit.ann, pred.var = c(“pot”, “mxt”))
  • plotPartial(par.pot.mxt)
  •  
  • # Add contour lines and use a different color palette
  • rwb <- colorRampPalette(c(“red”, “white”, “blue”))
  • pdp.pot.mxt.2d <- plotPartial(par.pot.mxt, contour = TRUE, col.regions = rwb)
  • pdp.pot.mxt.2d
  •  
  • # 3-D surface
  • pdp.pot.mxt.3d <- plotPartial(par.pot.mxt,rug=T,levelplot = FALSE,number=4, zlab = “oil”, drape = TRUE,colorkey = TRUE, screen = list(z = −20, x = −40))
  • pdp.pot.mxt.3d
  •  
  • ######pot avgrf
  •  
  • par.pot.avgrf <- partial(fit.ann, pred.var = c(“pot”, “avgrf”))
  • plotPartial(par.pot.avgrf)
  •  
  • # Add contour lines and use a different color palette
  • rwb <- colorRampPalette(c(“red”, “white”, “blue”))
  • pdp.pot.avgrf.2d <- plotPartial(par.pot.avgrf, contour = TRUE, col.regions = rwb)
  • pdp.pot.avgrf.2d
  •  
  • # 3-D surface
  • pdp.pot.avgrf.3d <- plotPartial(par.pot.avgrf,rug=T,levelplot = FALSE,number=4, zlab = “oil”, drape = TRUE,colorkey = TRUE, screen = list(z = −40, x = −70))
  • pdp.pot.avgrf.3d
  •  
  • ######pot alt
  •  
  • par.pot.alt <- partial(fit.ann, pred.var = c(“pot”, “alt”))
  • plotPartial(par.pot.alt)
  •  
  • # Add contour lines and use a different color palette
  • rwb <- colorRampPalette(c(“red”, “white”, “blue”))
  • pdp.pot.alt.2d <- plotPartial(par.pot.alt, contour = TRUE, col.regions = rwb)
  • pdp.pot.alt.2d
  •  
  • # 3-D surface
  • pdp.pot.alt.3d <- plotPartial(par.pot.alt,rug=T,levelplot = FALSE,number=4, zlab = “oil”, drape = TRUE,colorkey = TRUE, screen = list(z = −40, x = −60))
  • pdp.pot.alt.3d
  • ##### Faceted heatmap#########
  • library(lime)
  • lime.fit<-lime(train,fit.ann)
  • exp.fit<-explain(train,lime.fit,n_features=10)
  • plot_explanations(exp.fit)
  • plot_features(exp.fit)

References

  1. Dhama, K.; Sharun, K.; Gugjoo, M.B.; Tiwari, R.; Alagawany, M.; Yatoo, M.I.; Thakur, P.; Iqbal, H.M.; Chaicumpa, W.; Michalak, I.; et al. A Comprehensive Review on Chemical Profile and Pharmacological Activities of Ocimum basilicum. Food Rev. Int. 2021, 24, 1–29. [Google Scholar] [CrossRef]
  2. Purushothaman, B.; Srinivasan, R.P.; Suganthi, P.; Ranganathan, B.; Gimbun, J.; Shanmugam, K. A Comprehensive Review on Ocimum basilicum. J. Nat. Remedies 2018, 18, 71–85. [Google Scholar] [CrossRef]
  3. Bora, K.S.; Arora, S.; Shri, R. Role of Ocimum basilicum L. in prevention of ischemia and reperfusion-induced cerebral damage, and motor dysfunctions in mice brain. J. Ethnopharmacol. 2011, 137, 1360–1365. [Google Scholar] [CrossRef] [PubMed]
  4. Łyczko, J.; Masztalerz, K.; Lipan, L.; Lech, K.; Carbonell-Barrachina, Á.A.; Szumny, A. Chemical determinants of dried Thai basil (O. basilicum var. thyrsiflora) aroma quality. Ind. Crops Prod. 2020, 155, 112769. [Google Scholar] [CrossRef]
  5. Chiang, L.-C.; Ng, L.-T.; Cheng, P.-W.; Chiang, W.; Lin, C.-C. Antiviral activities of extracts and selected pure constituents of Ocimum basilicum. Clin. Exp. Pharmacol. Physiol. 2005, 32, 811–816. [Google Scholar] [CrossRef]
  6. Selvakkumar, C.; Gayathri, B.; Vinaykumar, K.S.; Lakshmi, B.S.; Balakrishnan, A. Potential Anti-inflammatory Properties of Crude Alcoholic Extract of Ocimum basilicum L. in Human Peripheral Blood Mononuclear Cells. J. Health Sci. 2007, 53, 500–505. [Google Scholar] [CrossRef]
  7. Bravo, E.; Amrani, S.; Aziz, M.; Harnafi, H.; Napolitano, M. Ocimum basilicum ethanolic extract decreases cholesterol synthesis and lipid accumulation in human macrophages. Fitoterapia 2008, 79, 515–523. [Google Scholar] [CrossRef]
  8. Berić, T.; Nikolić, B.; Stanojević, J.; Vuković-Gačić, B.; Knežević-Vukčević, J. Protective effect of basil (Ocimum basilicum L.) against oxidative DNA damage and mutagenesis. Food Chem. Toxicol. 2008, 46, 724–732. [Google Scholar] [CrossRef]
  9. Tohti, I.; Tursun, M.; Umar, A.; Turdi, S.; Imin, H.; Moore, N. Aqueous extracts of Ocimum basilicum L. (sweet basil) decrease platelet aggregation induced by ADP and thrombin in vitro and rats arterio–venous shunt thrombosis in vivo. Thromb. Res. 2006, 118, 733–739. [Google Scholar] [CrossRef]
  10. Harnafi, H.; Caid, H.S.; Bouanani, N.E.H.; Aziz, M.; Amrani, S. Hypolipemic activity of polyphenol-rich extracts from Ocimum basilicum in Triton WR-1339-induced hyperlipidemic mice. Food Chem. 2008, 108, 205–212. [Google Scholar] [CrossRef]
  11. Available online: https://connect2india.com/global/Essential-Oil-Basil-export-from-india/1 (accessed on 25 May 2022).
  12. Rawat, R.; Tiwari, V.; Singh, R.; Bisht, I. Assessment of the Essential Oil Composition in Ocimum species of Uttarakhand. J. Essent. Oil Bear. Plants 2017, 20, 1331–1341. [Google Scholar] [CrossRef]
  13. Radusiene, J.; Stanius, Z.; Cirak, C.; Odabas, M. Quantitative effects of temperature and light intensity on the accumulation of bioactive compounds in St. John’s worth. In XXVIII International Horticultural Congress on Science and Horticulture for People (IHC2010): A New Look at Medicinal and Aromatic Plants Seminar; International Society for Horticultural Science: Angers, France, 2010; pp. 135–140. [Google Scholar]
  14. Saffariha, M.; Jahani, A.; Jahani, R. A comparison of artificial intelligence techniques for predicting hyperforin content in Hypericum perforatum L. in different ecological habitats. Plant Direct 2021, 5, e363. [Google Scholar] [CrossRef] [PubMed]
  15. Gopal, P.M.; Bhargavi, R. A novel approach for efficient crop yield prediction. Comput. Electron. Agric. 2019, 165, 104968. [Google Scholar] [CrossRef]
  16. Torkashvand Moradabadi, M. Sensitivity Analysis and Reexamination of the Techniques for Evaluating Adult Death Registration. Ph.D. Thesis, Tehran University, Tehran, Iran, 2017. [Google Scholar]
  17. Besalatpour, A.; Ayoubi, S.; Hajabbasi, M.; Mosaddeghi, M.; Schulin, R. Estimating wet soil aggregate stability from easily available properties in a highly mountainous watershed. Catena 2013, 111, 72–79. [Google Scholar] [CrossRef]
  18. Alam, M.A.; Naik, P.K. Impact of Soil Nutrients and Environmental Factors on Podophyllotoxin Content among 28 Podophyllum Hexandrum Populations of Northwestern Himalayan Region Using Linear and Nonlinear Approaches. Commun. Soil Sci. Plant Anal. 2009, 40, 2485–2504. [Google Scholar] [CrossRef]
  19. Padhiari, B.M.; Ray, A.; Champati, B.B.; Jena, S.; Sahoo, A.; Kuanar, A.; Halder, T.; Ghosh, B.; Naik, P.K.; Patnaik, J.; et al. Artificial neural network (ANN) model for prediction and optimization of bacoside A content in Bacopa monnieri: A statistical approach and experimental validation. Plant Biosyst.—Int. J. Deal. All Asp. Plant Biol. 2022, 156, 1346–1357. [Google Scholar] [CrossRef]
  20. Olsen, S.; Sommers, L. Phosphorus. In Methods of Soil Analysis, 2nd ed.; Page, L.A., Miller, R.H., Keeney, D.R., Eds.; American Society of Agronomy: Madison, WI, USA, 1982; pp. 403–430. [Google Scholar]
  21. Jackson, M.L. Soil Chemical Analysis; Prentice-Hall of India Pvt. Ltd.: New Delhi, India, 1973; pp. 38–204. [Google Scholar] [CrossRef]
  22. Subbaiah, B. A rapid procedure for estimation of available nitrogen in soil. Curr. Sci. 1956, 25, 259–260. [Google Scholar]
  23. Friedrich, L. mlbench: Machine Learning Benchmark Problems. R package version 2.1-3. Available online: https://rdrr.io/cran/mlbench/ (accessed on 1 January 2023).
  24. Revelle, W. psych: Procedures for Personality and Psychological Research; Northwestern University: Evanston, IL, USA, 2021. [Google Scholar]
  25. Kuhn, M. Caret: Classification and Regression Training. R Package Version 6.0-88. 2021. Available online: https://CRAN.R-project.org/package=caret (accessed on 1 January 2022).
  26. Beck, M.W. NeuralNetTools: Visualization and Analysis Tools for Neural Networks. J. Stat. Softw. 2018, 85, 1–20. [Google Scholar] [CrossRef] [PubMed]
  27. Olden, J.D.; Joy, M.K.; Death, R.G. An accurate comparison of methods for quantifying variable importance in artificial neural networks using simulated data. Ecol. Model. 2004, 178, 389–397. [Google Scholar] [CrossRef]
  28. Brandon, M.G. pdp: An R Package for Constructing Partial Dependence Plots. R J. 2017, 9, 421–436. [Google Scholar] [CrossRef]
  29. Muller, H.-G. Weighted Local Regression and Kernel Methods for Nonparametric Curve Fitting. J. Am. Stat. Assoc. 1987, 82, 231. [Google Scholar] [CrossRef]
  30. Cleveland, W.S.; Devlin, S.J. Locally Weighted Regression: An Approach to Regression Analysis by Local Fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
  31. Lin, P.T.; Michaël, B. lime: Local Interpretable Model-Agnostic Explanations. R Package Version 0.5.2. 2021. Available online: https://CRAN.R-project.org/package=lime (accessed on 1 January 2022).
  32. Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
  33. Nicodemus, K.K.; Malley, J.D. Predictor correlation impacts machine learning algorithms: Implications for genomic studies. Bioinformatics 2009, 25, 1884–1890. [Google Scholar] [CrossRef] [PubMed]
  34. De Veaux, R.D.; Ungar, L.H. Multicollinearity: A tale of two nonparametric regressions. In Selecting Models from Data: Artificial Intelligence and Statistics IV; Springer: New York, NY, USA, 1994; pp. 393–402. [Google Scholar] [CrossRef]
  35. Obite, C.P.; Olewuezi, N.P.; Ugwuanyim, G.U.; Bartholomew, D.C. Multicollinearity Effect in Regression Analysis: A Feed Forward Artificial Neural Network Approach. Asian J. Probab. Stat. 2020, 6, 22–33. [Google Scholar] [CrossRef]
  36. Khajeh, M.; Moghaddam, M.G.; Shakeri, M. Application of artificial neural network in predicting the extraction yield of essential oils of Diplotaenia cachrydifolia by supercritical fluid extraction. J. Supercrit. Fluids 2012, 69, 91–96. [Google Scholar] [CrossRef]
  37. Ghoreishi, S.; Heidari, E. Extraction of Epigallocatechin-3-gallate from green tea via supercritical fluid technology: Neural network modeling and response surface optimization. J. Supercrit. Fluids 2013, 74, 128–136. [Google Scholar] [CrossRef]
  38. Lashkarbolooki, M.; Shafipour, Z.S.; Hezave, A.Z. Trainable cascade-forward back-propagation network modeling of spearmint oil extraction in a packed bed using SC-CO2. J. Supercrit. Fluids 2013, 73, 108–115. [Google Scholar] [CrossRef]
  39. Pilkington, J.L.; Preston, C.; Gomes, R.L. Comparison of response surface methodology (RSM) and artificial neural networks (ANN) towards efficient extraction of artemisinin from Artemisia annua. Ind. Crops Prod. 2014, 58, 15–24. [Google Scholar] [CrossRef]
  40. Alvarez, R. Predicting average regional yield and production of wheat in the Argentine Pampas by an artificial neural network approach. Eur. J. Agron. 2009, 30, 70–77. [Google Scholar] [CrossRef]
  41. Sodeifian, G.; Sajadian, S.A.; Ardestani, N.S. Optimization of essential oil extraction from Launaea acanthodes Boiss: Utilization of supercritical carbon dioxide and cosolvent. J. Supercrit. Fluids 2016, 116, 46–56. [Google Scholar] [CrossRef]
  42. Akbar, A.; Kuanar, A.; Joshi, R.K.; Sandeep, I.S.; Mohanty, S.; Naik, P.K.; Mishra, A.; Nayak, S. Development of Prediction Model and Experimental Validation in Predicting the Curcumin Content of Turmeric (Curcuma longa L.). Front. Plant Sci. 2016, 7, 1507. [Google Scholar] [CrossRef] [PubMed]
  43. Akbar, A.; Kuanar, A.; Patnaik, J.; Mishra, A.; Nayak, S. Application of Artificial Neural Network modeling for optimization and prediction of essential oil yield in turmeric (Curcuma longa L.). Comput. Electron. Agric. 2018, 148, 160–178. [Google Scholar] [CrossRef]
  44. Garson, G.D. Interpreting neural network connection weights. Artif. Intell. Expert 1991, 6, 46–51. [Google Scholar] [CrossRef]
  45. Goh, A. Back-propagation neural networks for modeling complex systems. Artif. Intell. Eng. 1995, 9, 143–151. [Google Scholar] [CrossRef]
  46. Zhang, Z.; Beck, M.W.; Winkler, D.A.; Huang, B.; Sibanda, W.; Goyal, H.; on behalf of AME Big-Data Clinical Trial Collaborative Group. Opening the black box of neural networks: Methods for interpreting neural network models in clinical applications. Ann. Transl. Med. 2018, 6, 216. [Google Scholar] [CrossRef]
Plants 12 01776 g001 550
Figure 1. Panel plot to investigate the interaction of predictors with the response.
Figure 1. Panel plot to investigate the interaction of predictors with the response.
Plants 12 01776 g001
Plants 12 01776 g002 550
Figure 2. The selected resilient backpropagation ANN model with weight bracketing with three hidden layers, bias, and connection strengths.
Figure 2. The selected resilient backpropagation ANN model with weight bracketing with three hidden layers, bias, and connection strengths.
Plants 12 01776 g002
Plants 12 01776 g003 550
Figure 3. Mean absolute error (MAE), R squared, and Root mean squared error (RMSE) for train, test, and validation data.
Figure 3. Mean absolute error (MAE), R squared, and Root mean squared error (RMSE) for train, test, and validation data.
Plants 12 01776 g003
Plants 12 01776 g004 550
Figure 4. Relative importance of predictors.
Figure 4. Relative importance of predictors.
Plants 12 01776 g004
Plants 12 01776 g005a 550Plants 12 01776 g005b 550
Figure 5. (a) Partial dependence plot of response in terms of pH; (b) partial dependence plot of response in terms of organic carbon; (c) partial dependence plot of response in terms of nitrogen; (d) partial dependence plot of response in terms of phosphorous; (e) partial dependence plot of response in terms of potassium; (f) partial dependence plot of response in terms of maximum relative humidity; (g) partial dependence plot of response in terms of minimum relative humidity; (h) partial dependence plot of response in terms of average rainfall; (i) partial dependence plot of response in terms of maximum average temperature; (j) partial dependence plot of response in terms of minimum average temperature; (k) partial dependence plot of response in terms of altitude. Black color line is for response and blue color line is for different factor.
Figure 5. (a) Partial dependence plot of response in terms of pH; (b) partial dependence plot of response in terms of organic carbon; (c) partial dependence plot of response in terms of nitrogen; (d) partial dependence plot of response in terms of phosphorous; (e) partial dependence plot of response in terms of potassium; (f) partial dependence plot of response in terms of maximum relative humidity; (g) partial dependence plot of response in terms of minimum relative humidity; (h) partial dependence plot of response in terms of average rainfall; (i) partial dependence plot of response in terms of maximum average temperature; (j) partial dependence plot of response in terms of minimum average temperature; (k) partial dependence plot of response in terms of altitude. Black color line is for response and blue color line is for different factor.
Plants 12 01776 g005aPlants 12 01776 g005b
Plants 12 01776 g006 550
Figure 6. Sensitivity analysis of input parameters on oil yield (output).
Figure 6. Sensitivity analysis of input parameters on oil yield (output).
Plants 12 01776 g006
Plants 12 01776 g007 550
Figure 7. (a) Contour plot of soil potassium content, altitude, and essential oil content; (b) contour plot of soil potassium content, average rainfall, and essential oil content; (c) contour plot of soil potassium content, average temperature, and essential oil content; (d) contour plot of soil potassium content, average maximum relative humidity, and essential oil content; (e) contour plot of soil potassium content, pH, and essential oil content.
Figure 7. (a) Contour plot of soil potassium content, altitude, and essential oil content; (b) contour plot of soil potassium content, average rainfall, and essential oil content; (c) contour plot of soil potassium content, average temperature, and essential oil content; (d) contour plot of soil potassium content, average maximum relative humidity, and essential oil content; (e) contour plot of soil potassium content, pH, and essential oil content.
Plants 12 01776 g007
Plants 12 01776 g008 550
Figure 8. (a) 3D partial dependence plot for soil potassium content, altitude, and essential oil content; (b) 3D partial dependence plot for soil potassium content, average rainfall, and essential oil content; (c) 3D partial dependence plot for soil potassium content, average temperature, and essential oil content; (d) 3D partial dependence plot for soil potassium content, average maximum relative humidity, and essential oil content (e) 3D partial dependence plot for soil potassium content, pH, and essential oil content.
Figure 8. (a) 3D partial dependence plot for soil potassium content, altitude, and essential oil content; (b) 3D partial dependence plot for soil potassium content, average rainfall, and essential oil content; (c) 3D partial dependence plot for soil potassium content, average temperature, and essential oil content; (d) 3D partial dependence plot for soil potassium content, average maximum relative humidity, and essential oil content (e) 3D partial dependence plot for soil potassium content, pH, and essential oil content.
Plants 12 01776 g008
Plants 12 01776 g009 550
Figure 9. Faceted heatmap showing effect of various predictor value ranges on response.
Figure 9. Faceted heatmap showing effect of various predictor value ranges on response.
Plants 12 01776 g009
Table
Table 1. Geographic locations and habitat characteristics of Thai basil.
Table 1. Geographic locations and habitat characteristics of Thai basil.
SL. No.Agroclimatic ZonesDistrictsAccession No.LatitudeLongitudeAltitude
1.East and South East Coastal PlainJagatsingpurT120.2549° N86.1706° E46
T220.2553° N86.1735° E43
T320.2555° N86.1740° E41
KhurdaT420.1869° N86.1737° E75
T520.1863° N85.6223° E181
T620.1850° N85.6215° E195
PuriT720.1868° N85.6234° E0.1
T819.8135° N85.8312° E74
T919.8120° N85.8340° E85
NayagarhT1019.8142° N85.8318° E178
T1120.1231° N85.1038° E14
T1220.1251° N85.1045° E55
2.North Eastern Coastal PlainBhadrakT1321.0574° N86.4963° E23
T1421.0570° N86.4968° E23.6
T1521.0566° N86.4970° E24
BalasoreT1621.4934° N86.9135° E16
T1721.4940° N86.9140° E16.3
T1821.4944° N86.9145° E17
JajpurT1920.8341° N86.3326° E8
T2020.8348° N86.3330° E9
T2120.8352° N86.3338° E10
3.North Eastern GhatGanjamT2219.3874° N85.0515° E3
T2319.3870° N85.0520° E568
T2419.3866° N85.0525° E570
GajapatiT2519.1912° N84.1857° E180.5
T2619.1918° N84.1860° E180.7
T2719.1924° N84.1863° E181
KandhamalT2820.1342° N84.0167° E700
T2920.1348° N84.0170° E591
T3020.1354° N84.0173° E550
4.Mid Central Table LandAngulT3120.8444° N85.1511° E876
T3220.8450° N85.1520° E218.3
T3320.8456° N85.1526° E224
DhenkanalT3420.6505° N85.5981° E80
T3520.6510° N85.5988° E79.6
T3620.6515° N85.5995° E79
CuttackT3720.4625° N85.8830° E36
T3820.4630° N85.8840° E36
T3920.4635° N85.8850° E37
5.Western Central Table LandBoudhT4020.8418° N84.3200° E218
T4120.8420° N84.3202° E221
T4220.8422° N84.3204° E226
BargarhT4321.3470° N83.6320° E171
T4421.3472° N83.6322° E170
T4521.3474° N83.6324° E169
JharsugudaT4621.8554° N84.0062° E218
T4721.8562° N84.0065° E216
T4821.8560° N84.0065° E214
6.Eastern Ghat High LandNawarangpurT4919.2281° N82.5470° E557
T5019.2288° N82.5478° E553
T5119.2295° N82.5484° E548
RayagadaT5219.1712° N83.4163° E207
T5319.1718° N83.4169° E217
T5419.1724° N83.4174° E227
Koraput
(East)		T5518.8561° N82.7347° E218
T5618.8570° N82.7355° E218
T5718.8579° N82.7362° E219
7.North Central PlateauMayurbhanj (South)T5822.0087° N86.4187° E559
T5922.0090° N86.4193° E564
T6022.0093° N86.4197° E568
Keonjhar
(North)		T6121.6289° N85.5817° E596
T6221.6287° N85.5815° E593
T6321.6285° N85.5813° E590
Mayurbhanj
(North)		T6422.0087° N86.4187° E570
T6522.0091° N86.4196° E596
T6622.0095° N86.4205° E610
8.South Eastern GhatKeonjhar
(South)		T6721.6289° N85.5817° E193
T6821.6285° N85.5813° E193
T6921.6281° N85.5810° E193
Koraput
(South-East)		T7018.8561° N82.7347° E870
T7118.8566° N82.7354° E356
T7218.8572° N82.7359° E110
MalkangiriT7318.3436° N81.8825° E178
T7418.3441° N81.8821° E170
T7518.349° N81.8817° E162
9.North Western PlateauSundargarhT7622.1240° N84.0432° E233
T7722.1248° N84.0437° E231
T7822.1256° N84.0442° E229
DeogarhT7921.5383° N84.7289° E254
T8021.5388° N84.7293° E253
T8121.5392° N84.7297° E252
SambalpurT8221.4669° N83.9812° E135
T8321.4673° N83.9818° E252
T8421.4677° N83.9822° E312
10.Western Undulating ZoneKalahandiT8519.9137° N83.1649° E355
T8619.9141° N83.1653° E352
T8719.9146° N83.1657° E349
BolangirT8820.7011° N83.4846° E383
T8920.7017° N83.4848° E556
T9020.7023° N83.4850° E615
NuapadaT9120.8060° N82.5361° E1200
T9220.8068° N82.5368° E1202
T9320.8076° N82.5375° E1204
Table
Table 2. Climatic data for Thai basil from different agroclimatic regions of Odisha.
Table 2. Climatic data for Thai basil from different agroclimatic regions of Odisha.
SL. No.Agroclimatic ZonesDistrictsAccession No.pHMax. Rel.
Humidity		Min. Rel.
Humidity		Avg. RainfallMax. Avg. Temp.Min. Avg. Temp.Altitude
1.East and South East Coastal PlainJagatsingpurT16.581.754.34.832.921.946
T26.481.255.14.632.421.543
T36.381554.532.221.240
KhurdaT46.7482.156.83.232.822.875
T56.98159.75.433.921.6181
T66.9980.9859.95.94.121.1190
PuriT76.8480.262.93.430.623.40.1
T88.475.371.66.43424.174
T98.972.273.47.235.625.486
NayagarhT10781.359.45.633.521.7178
T115.1100.325.14.939.212.114
T125102.320.84.341.210.555
2.North Eastern Coastal PlainBhadrakT136.578.262.33.933.122.423
T146.978.662.53.533.222.823.6
T157.179.262.93.133.423.224
BalasoreT1613.783744.834.232.416
T1713.282.874.94.634.632.816.3
T1813.182.5754.434.933.216.9
JajpurT194.398.923.95.438.711.48
T204.798.223.15.938.111.79
T21897.922.86.437.712.110
3.North Eastern GhatGanjamT228.674.671.36.132273
T238.787.592.86.133.327.4568
T248.890.298.96.233.728.1569
GajapatiT256.0880.360.13.430.223.8180.5
T266.2180.159.83.530.423.9180.7
T276.4279.859.43.630.624181
KandhamalT287.380.553.84.332.822.1700
T299.297.484.35.232.324.4591
T3010.1106.297.86.131.726.2341
4.Mid Central Table LandAngulT317.6176.250.93.8231.218.1876
T326.7979.755.75.334.219.3218.3
T336.1281.260.17.537.620.2216.7
DhenkanalT346.7581.451.84.0831.821.480
T356.7981.951.44.1231.621.279.6
T367.1282.350.94.1631.42179.1
CuttackT376.8281.854.34.933.221.936
T386.8681.854.34.933.221.936
T396.918254.65.132.622.236.4
5.Western Central Table LandBoudhT406.680.758.45.132.522.3218
T416.4580.958.74.932.122.6221
T426.2381.159.24.530.922.9225
BargarhT4310.886.782.27.729.325.4171
T441187.1827.529.425.6170
T4511.387.881.97.329.525.9169
JharsugudaT466.880.155.35.134.619.5218
T476.4581534.53319216
T486.2481.851.53.932.618.5214
6.Eastern Ghat High LandNawarangpurT496.282.454.15.432.721.9557
T506.38354.35.532.521.6553
T516.483.454.75.932.221.3550
RayagadaT526.8382.554.9331.718.9207
T536.6581.553.64.632.819.1217
T546.4580.552.4533.319.6227
Koraput
(East)		T556.5181.353.14.733.119.2218
T566.5481.353.14.733.119.2218
T576.9881.653.85.233.819.6219
7.North Central PlateauMayurbhanj
(South)		T587.181.754.36.232.118.7559
T597.381.454.86.532.918.2564
T607.581.155.26.7333.317.8569
Keonjhar
(North)		T619.298855.532.824.8596
T629.197.684.65.432.524.6593
T63997.184.15.332.124.4590
Mayurbhanj
(North)		T648.987.8935.933.127.6570
T659.398855.532.824.8596
T669.698.3805.132.221.2605
8.South Eastern GhatKeonjhar
(South)		T677.689939.438.224.2193
T687.389939.438.224.2193
T697.990949.638.424.4194
Koraput
(South-East)		T705.885778.729.620.6870
T714.578.464.38.5925.823.7356
T72472.357.78.3421.426.7350
MalkangiriT7312.6868311.93622178
T7410.786.282.47.629.525.3170
T758.686.481.56.824.827.6162
9.North Western PlateauSundargarhT7611.366645.431.520.5233
T7710.965.864.35.231.220.3231
T7810.565.264.8530.920.1229
DeogarhT793.197.956.1113225254
T803.298.155.910.931.724.7253
T813.398.655.210.331.224.2252
SambalpurT827.979.459.14.531.320.9135
T833.498.155.910.931.824.7252
T842.999.351.216.232.527.3255
10.Western Undulating ZoneKalahandiT854.478648.762624355
T864.777.863.88.725.423.6352
T875.177.163.28.624.823.2350
BolangirT886.276748.0132.830.8383
T896.382.353.85.332.521.7556
T906.588.451.25.131.821.1565
NuapadaT912.192639.6930231200
T922.491.762.89.7129.8211202
T932.791.462.29.7529.1201201
Table
Table 3. Physicochemical properties of soil samples collected from different agroclimatic regions of Odisha.
Table 3. Physicochemical properties of soil samples collected from different agroclimatic regions of Odisha.
SL. No.Agroclimatic
Zones		DistrictsAccession No.Organic
Carbon (%)		NitrogenPhosphorousPotassium
1.East and South East Coastal PlainJagatsingpurT11.59236.279.4542.2
T21.61235.981.4538.7
T31.63235.581.8532.5
KhurdaT41.11503.7161.7918.4
T51.41166.5217.2493.2
T61.62160.7220.8490.5
PuriT70.99305.31265.1796.94
T81.7270.463.4408.3
T92255.362.5400.9
NayagarhT100.76250169.05491.9
T110.83250.4169.02491.2
T120.91250.8169491
2.North Eastern Coastal PlainBhadrakT130.87352.564.7201.6
T140.82352.164.2201.2
T150.78351.863.8200.8
BalasoreT163.2340.283.2602.3
T173.4179.5281.9209.4
T183.6178.9280.8208.7
JajpurT191.8375.4132.2302.5
T202381.5130.3294.6
T212.2385.7128.8290.2
3.North Eastern GhatGanjamT223.1183.7280.3208.3
T233.4340.683.8602.4
T243.6341.382.6601.1
GajapatiT251.36166.2217.5493.9
T261.2717626.5878.1
T271.11186.225.676.8
KandhamalT280.52141.237.2519
T290.58141.337.5519.7
T301.02141,537.9520.2
4.Mid Central Table LandAngulT310.94162.333.2771.6
T320.91162.733.7771.8
T330.89163.234.1772.1
DhenkanalT341.79562.5132.4921.6
T351.81562.1132.1921.3
T361.86558.5131.8920.8
CuttackT371.5251.296.3306
T383.61152.472.689.1
T393.89150.870.988.1
5.Western Central Table LandBoudhT400.32125127.91309.12
T410.35123128.1310.1
T420.37121128.7310.8
BargarhT435.2140.3142.330
T445.4140.7141.932
T455.6141.1141.433
JharsugudaT460.94112.575.5603.46
T470.91112.474.9602.9
T480.88112.374.4602.23
6.Eastern Ghat High LandNawarangpurT491.1417526.4877.95
T501.0111375.3603.8
T51111097.8602.4
RayagadaT523.27316.229.3924.8
T533.98164.582.493.4
T544.02163.884.794.6
Koraput
(East)		T554.61381.232.4961.3
T564.74380.632.1960.8
T574.82380.331.8960.4
7.North Central PlateauMayurbhanj
(South)		T582.2317550.7273.92
T594.01164.382.693.1
T606.32160.888.996.8
Keonjhar
(North)		T613.57152.772.889.3
T623.65152.572.489.1
T633.99152.37288.8
Mayurbhanj
(North)		T643.98164.582.493.4
T654.72383.232.7959.6
T665.88386.831.6960.6
8.South Eastern GhatKeonjhar
(South)		T678.4261145.2391.2
T688231152308.7
T697.6201165.9300.7
Koraput
(South-East)		T702.3242.3132.7296.3
T713.4340.483.5602.4
T724.6444.482.9603.9
MalkangiriT736.36216.4121.2386.4
T745.1140.1142.529.8
T755132.4162.630
9.North Western PlateauSundargarhT761.06285.3161.2603.4
T771.1285.1161.4603.1
T781.4284.8161.6603
DeogarhT798.1230.4152.3308.5
T808.3230.5152.7308.8
T818.5230.6153.1309.1
SambalpurT828.6262.5139.75594.8
T838.9263.7139.65592.6
T849.2264.1139.55590.4
10.Western Undulating ZoneKalahandiT852.4240.376.3813.7
T862.5240.476.2813.6
T872.6240.576.1813.5
BolangirT888.9290.489.1503.1
T898230.2152.7308.3
T907.2229.8153.8307.6
NuapadaT911.6270.363.2408.1
T921.18175.426.5177.81
T931.02174.325.6575.75
Table
Table 4. Predicted and actual Thai basil oil content for the train set.
Table 4. Predicted and actual Thai basil oil content for the train set.
SL. No.Agroclimatic ZonesDistrictsAccession no.Experimental Thai Basil Oil Yield (X1)Predicted Thai Basil Oil Yield (X2)Absolute = |X1 − X2|
1.East and South East Coastal PlainJagatsingpurT11.31.290.01
KhurdaT41.421.420
T51.211.210
T61.21.190.01
PuriT71.11.110.01
T81.651.670.02
2.North Eastern Coastal PlainBhadrakT130.760.760
T141.451.430.02
T150.810.790.02
JajpurT190.40.400
T200.90.880.02
T210.981.010.03
3.North Eastern GhatGanjamT220.970.980.01
GajapatiT250.810.770.04
T260.9410.06
T271.681.680
KandhamalT281.21.200
T291.071.060.01
T301.11.080.02
4.Mid Central Table LandAngulT310.780.790.01
T321.181.180
DhenkanalT340.980.960.02
CuttackT370.670.670
T38110
T390.650.650
5.Western Central Table LandBoudhT401.010.960.05
T410.780.800.02
BargarhT430.890.900.01
T440.980.980
JharsugudaT460.920.920
T470.760.750.01
6.Eastern Ghat High LandNawarangpurT490.730.730
T500.760.780.02
T511.271.240.03
RayagadaT520.90.900
T530.9510.05
T540.970.980.01
Koraput
(East)		T550.910.910
T560.930.950.02
T570.690.670.02
7.North Central PlateauMayurbhanj
(South)		T581.41.380.02
T591.21.250.05
T601.31.320.02
Keonjhar
(North)		T613.623.570.13
T623.53.520.02
Mayurbhanj
(North)		T640.930.980.05
T650.910.960.05
T661.11.070.03
8.South Eastern GhatKeonjhar
(South)		T673.943.940
T683.73.730.03
Koraput
(South-East)		T700.720.750.03
T711.020.970.05
T721.31.340.04
MalkangiriT730.640.610.03
T740.760.770.01
9.North Western PlateauSundargarhT760.680.690.01
T770.790.780.01
SambalpurT821.11.120.02
T831.251.270.02
T841.21.200
10.Western Undulating ZoneKalahandiT850.360.360
T860.120.130.01
BolangirT881.31.300
T891.51.450.05
T901.11.090.01
NuapadaT910.70.690.01
T920.90.890.01
Table
Table 5. Predicted and actual Thai basil oil content for test set.
Table 5. Predicted and actual Thai basil oil content for test set.
SL. No.Agroclimatic ZonesDistrictsAccession no.Experimental Thai Basil Oil Yield
(X1)		Predicted Thai Basil Oil Yield
(X2)		Absolute =
|X1 − X2|
1.East and South East Coastal PlainJagatsingpurT21.21.190.01
T31.21.270.07
NayagarhT101.31.270.030
T110.650.770.12
T121.391.410.02
2.North Eastern Coastal PlainBalasoreT160.810.840.03
T1711.290.29
T1811.280.28
3.North Eastern GhatGanjamT230.940.940
4.Mid Central Table LandDhenkanalT340.750.780.03
T350.690.730.04
5.Western Central TableLandBoudhT420.860.900.04
6.North Central PlateauKeonjhar
(North)		T613.723.160.56
7.South Eastern GhatKeonjhar
(South)		T674.14.460.36
MalkangiriT750.710.660.05
8.North Western PlateauSundargarhT780.950.960.01
DeogarhT7911.280.28
T800.750.780.03
T810.380.340.04
9.Western Undulating ZoneKalahandiT870.780.530.25
Table
Table 6. Predicted and actual Thai basil content for validation set.
Table 6. Predicted and actual Thai basil content for validation set.
SL. No.Agroclimatic ZonesDistrictsAccession No.Experimental Thai Basil Oil Yield (X1)Predicted Thai Basil Oil Yield (X2)Absolute =
|X1 − X2|
1.East and South East Coastal PlainPuriT90.130.140.01
2.North Eastern GhatGanjamT240.940.970.03
3.Mid Central Table LandAngulT330.780.600.18
4.Western Central Table LandBargarhT450.80.690.11
JharsugudaT480.770.550.22
5.Western Undulating ZoneNuapadaT930.130.130
Table
Table 7. Sensitivity values of different factors affecting oil production of Thai basil.
Table 7. Sensitivity values of different factors affecting oil production of Thai basil.
PredictorsSensitivity Value
pH2.32
Organic Carbon2.31
Nitrogen109.99
Phosphorous65.47
Potassium284.49
Maximum relative humidity6.62
Minimum relative humidity14.42
Average rainfall2.21
Maximum average temperature2.46
Minimum average temperature3.66
Altitude274.38
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Sahu, A.; Nayak, G.; Bhuyan, S.K.; Akbar, A.; Bhuyan, R.; Kar, D.; Kuanar, A. Artificial Neural Network and Response Surface-Based Combined Approach to Optimize the Oil Content of Ocimum basilicum var. thyrsiflora (Thai Basil). Plants 2023, 12, 1776. https://doi.org/10.3390/plants12091776

AMA Style

Sahu A, Nayak G, Bhuyan SK, Akbar A, Bhuyan R, Kar D, Kuanar A. Artificial Neural Network and Response Surface-Based Combined Approach to Optimize the Oil Content of Ocimum basilicum var. thyrsiflora (Thai Basil). Plants. 2023; 12(9):1776. https://doi.org/10.3390/plants12091776

Chicago/Turabian Style

Sahu, Akankshya, Gayatree Nayak, Sanat Kumar Bhuyan, Abdul Akbar, Ruchi Bhuyan, Dattatreya Kar, and Ananya Kuanar. 2023. "Artificial Neural Network and Response Surface-Based Combined Approach to Optimize the Oil Content of Ocimum basilicum var. thyrsiflora (Thai Basil)" Plants 12, no. 9: 1776. https://doi.org/10.3390/plants12091776

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop