Directional-Sensor Network Deployment Planning for Mobile-Target Search
Abstract
1. Introduction
2. Problem Definition and Background
2.1. Example Application: Wilderness Search and Rescue (WiSAR)
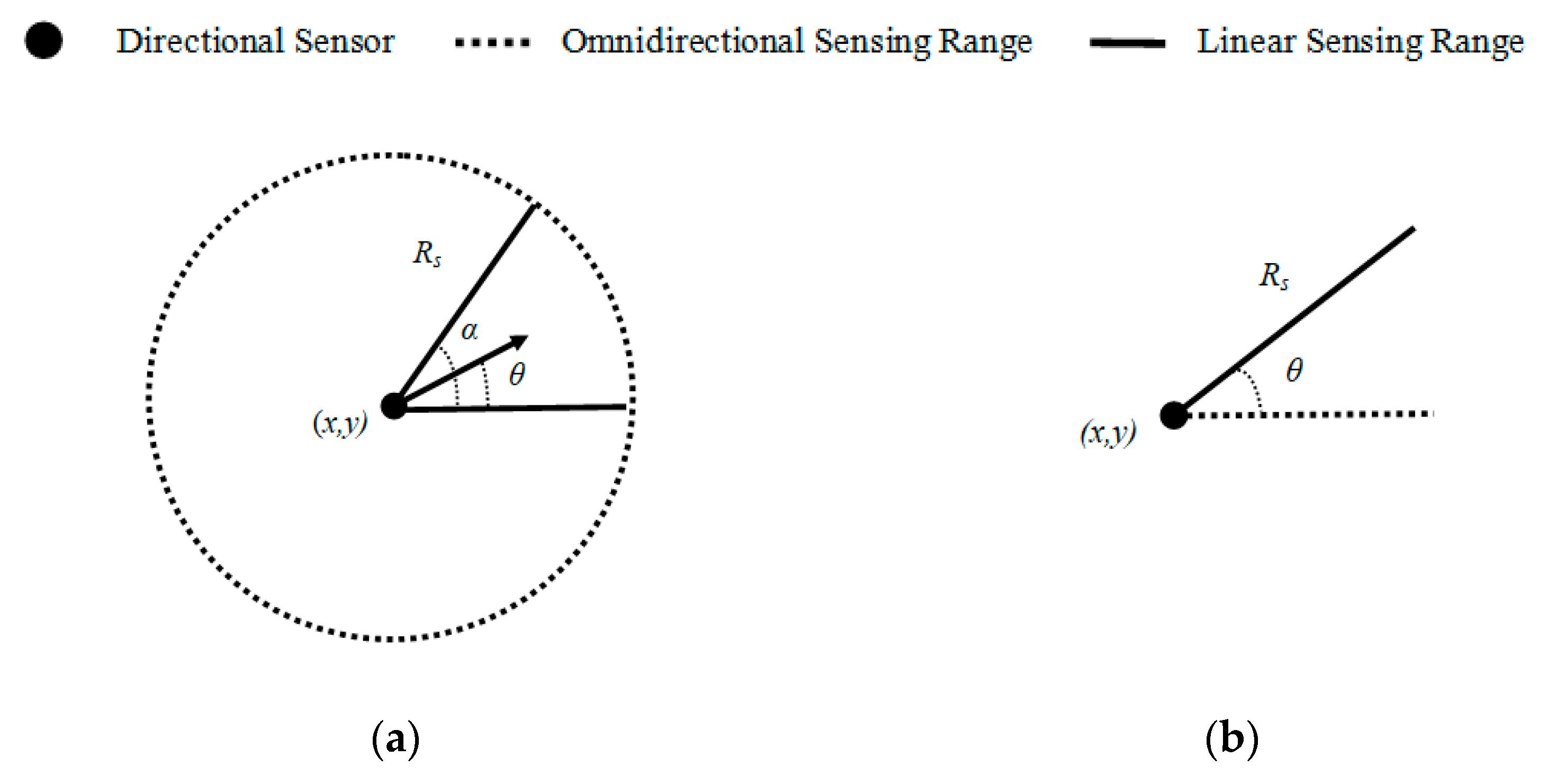
2.2. Line Approximation of a Directional-Sensor
2.3. Sensor Plan Performance Measure
2.4. Optimization Metric for Sensor Planning
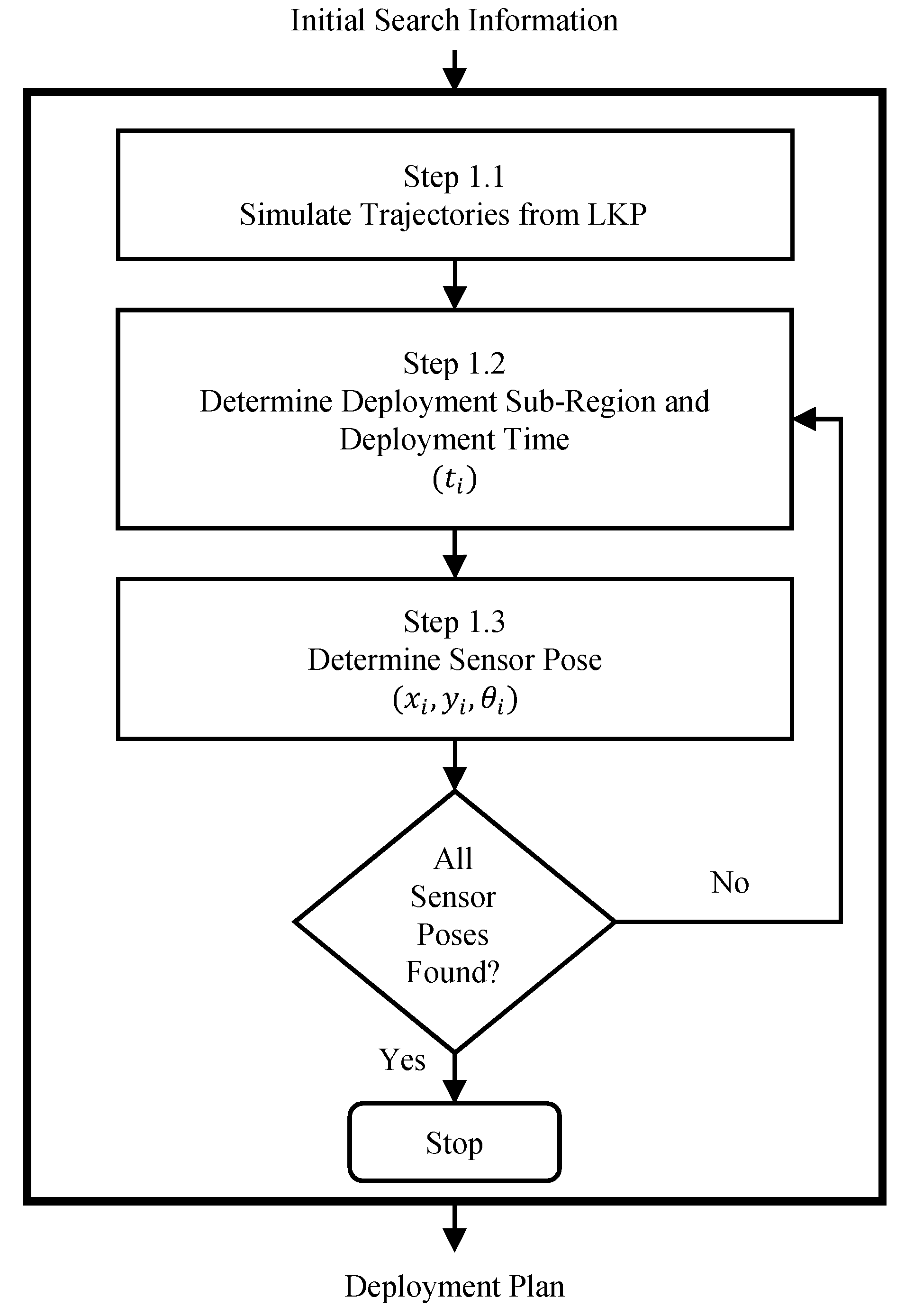
3. Proposed Deployment Methodology
3.1. Phase 1: Original Network Planning
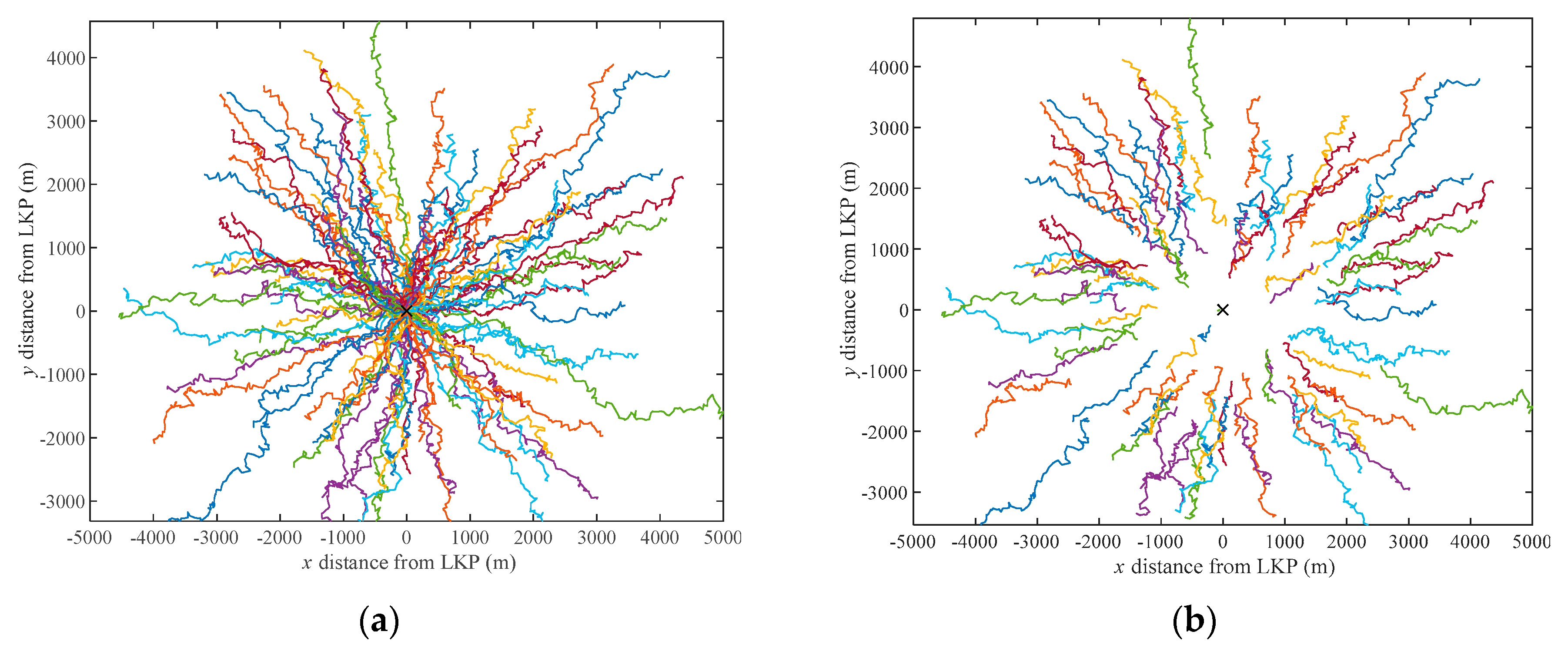
3.1.1. Step 1.1: Target Trajectory Generation
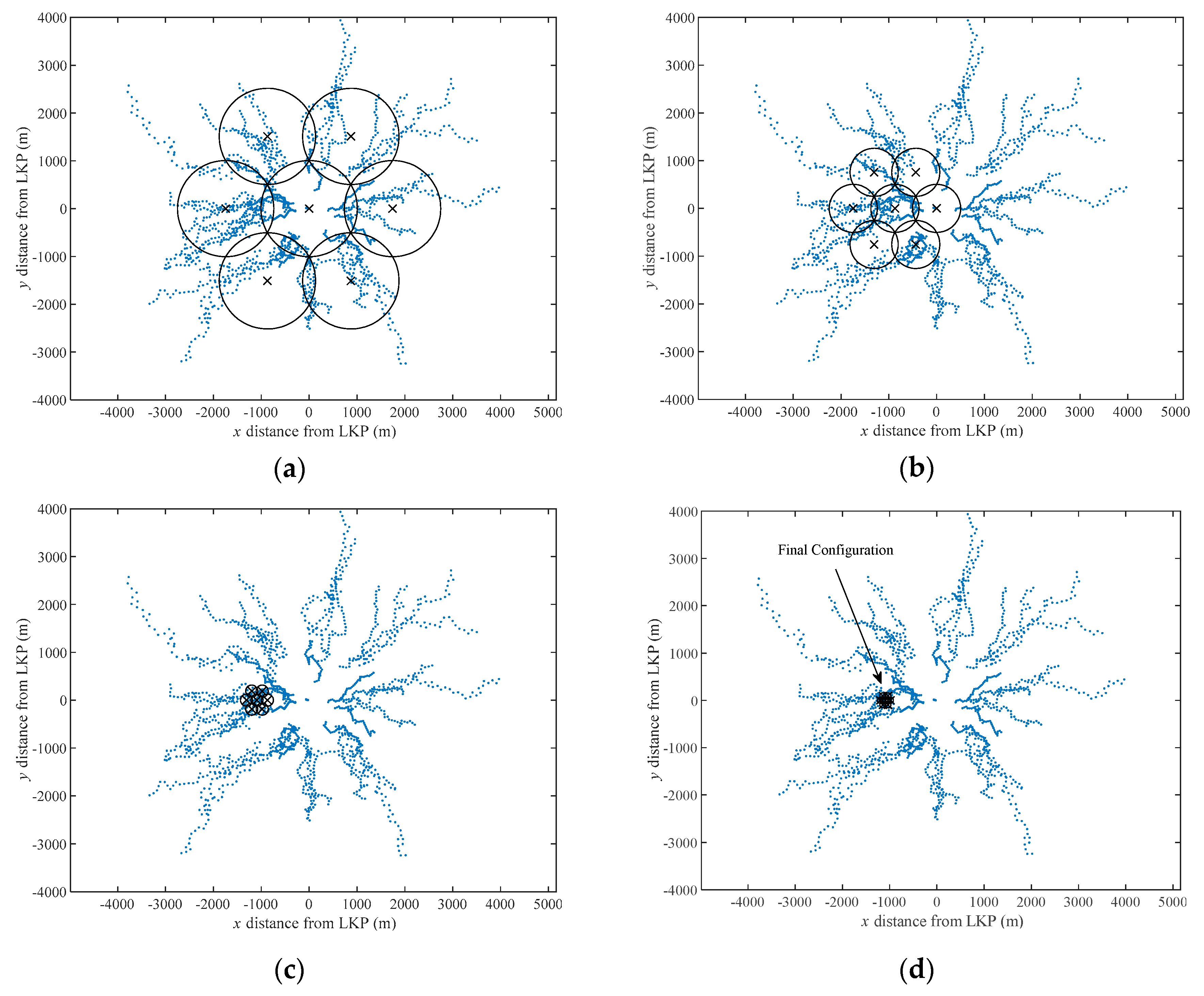
3.1.2. Step 1.2: Deployment Sub-Region and Time Determination
3.1.3. Step 1.3: Sensor Pose Determination
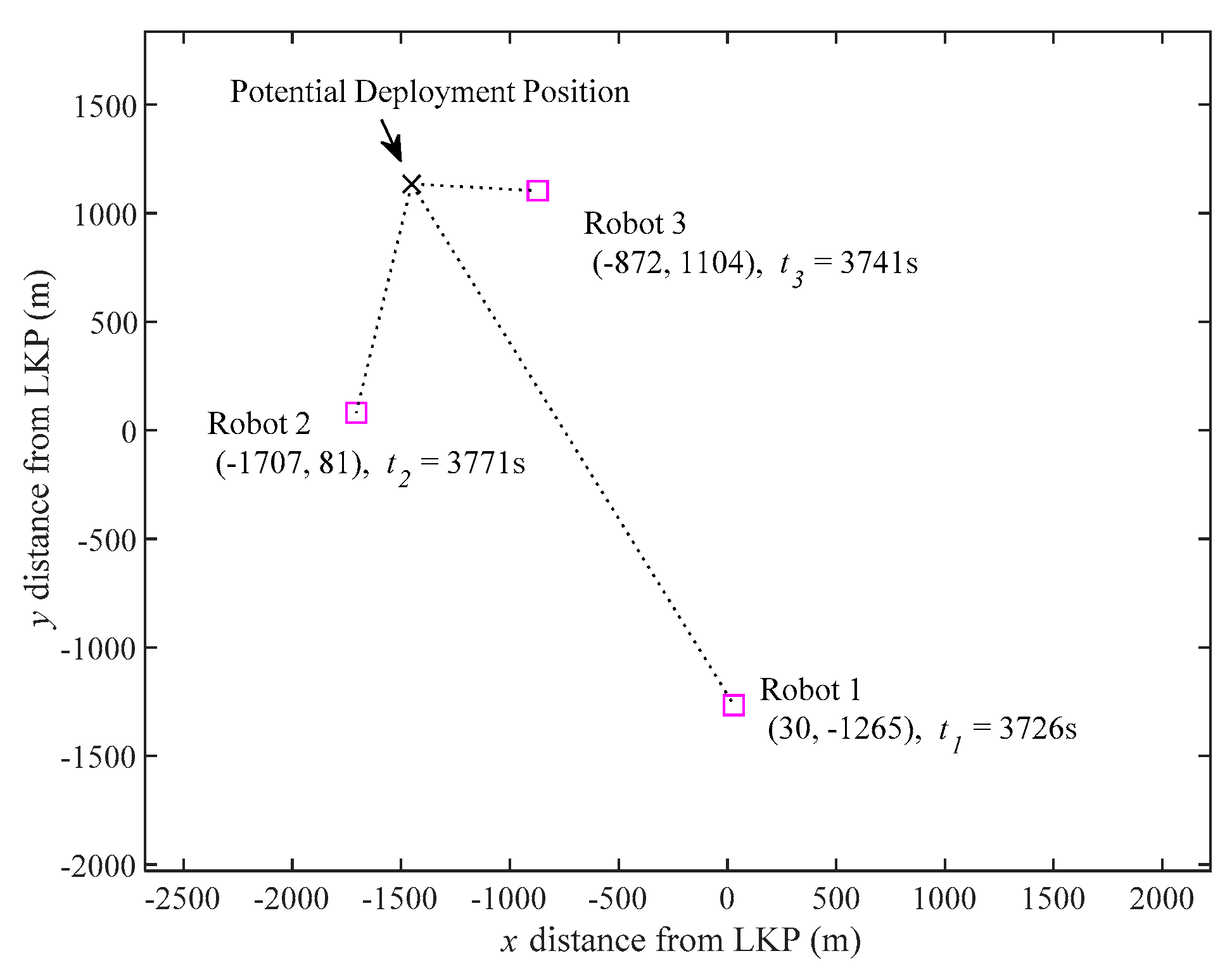
Deployment Example:
3.2. Phase 2: Network Deployment Execution
3.3. Phase 3: Network Re-Planning
4. Results
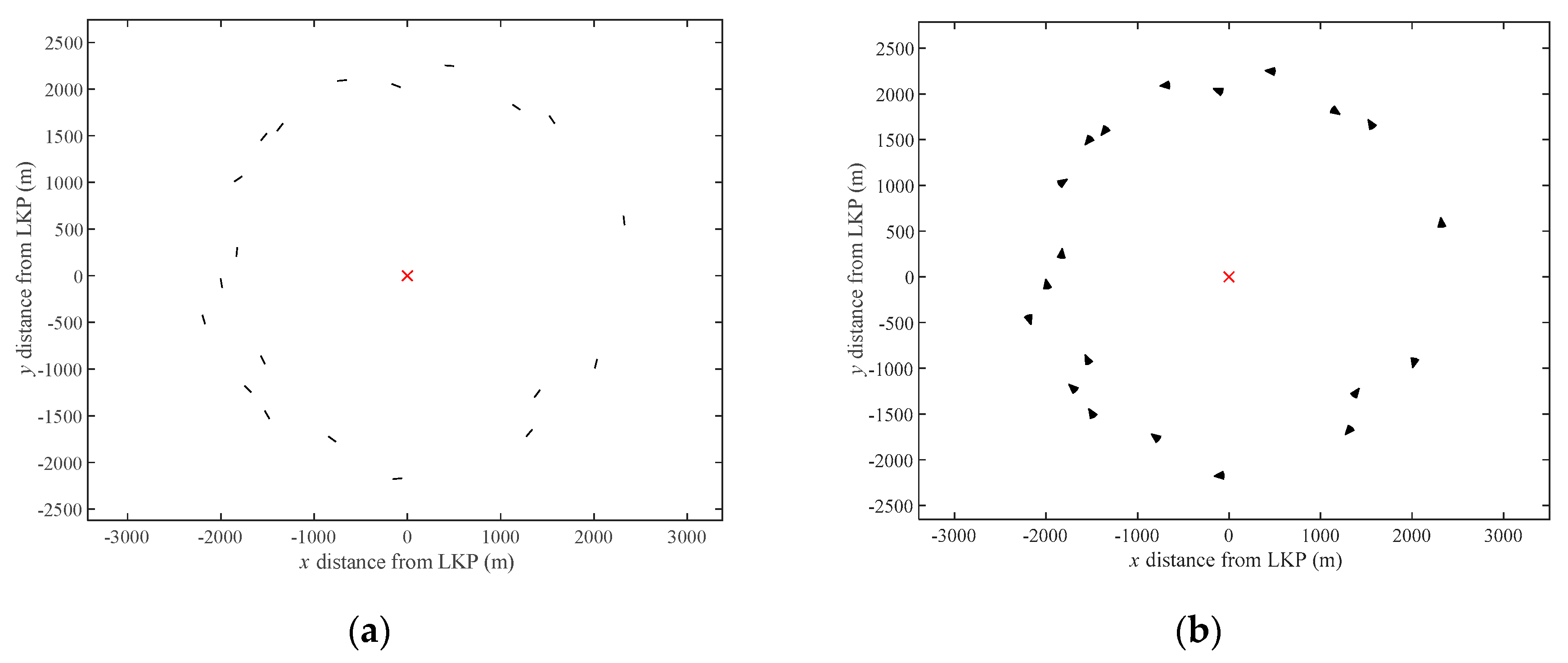
4.1. Illustrative Search Example
4.1.1. Phase 1: Off-Line Network Planning
4.1.2. Phase 2: Network Deployment Execution
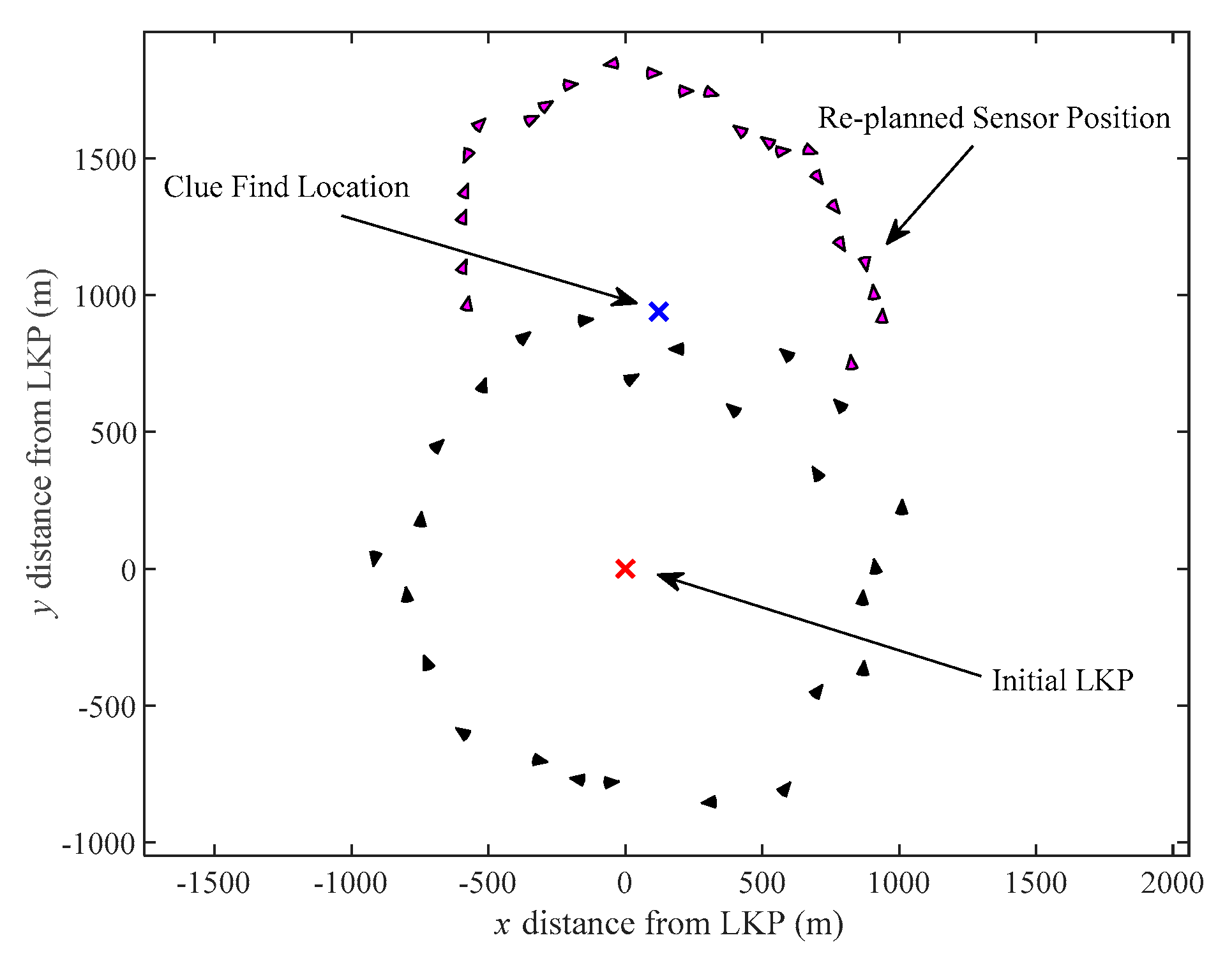
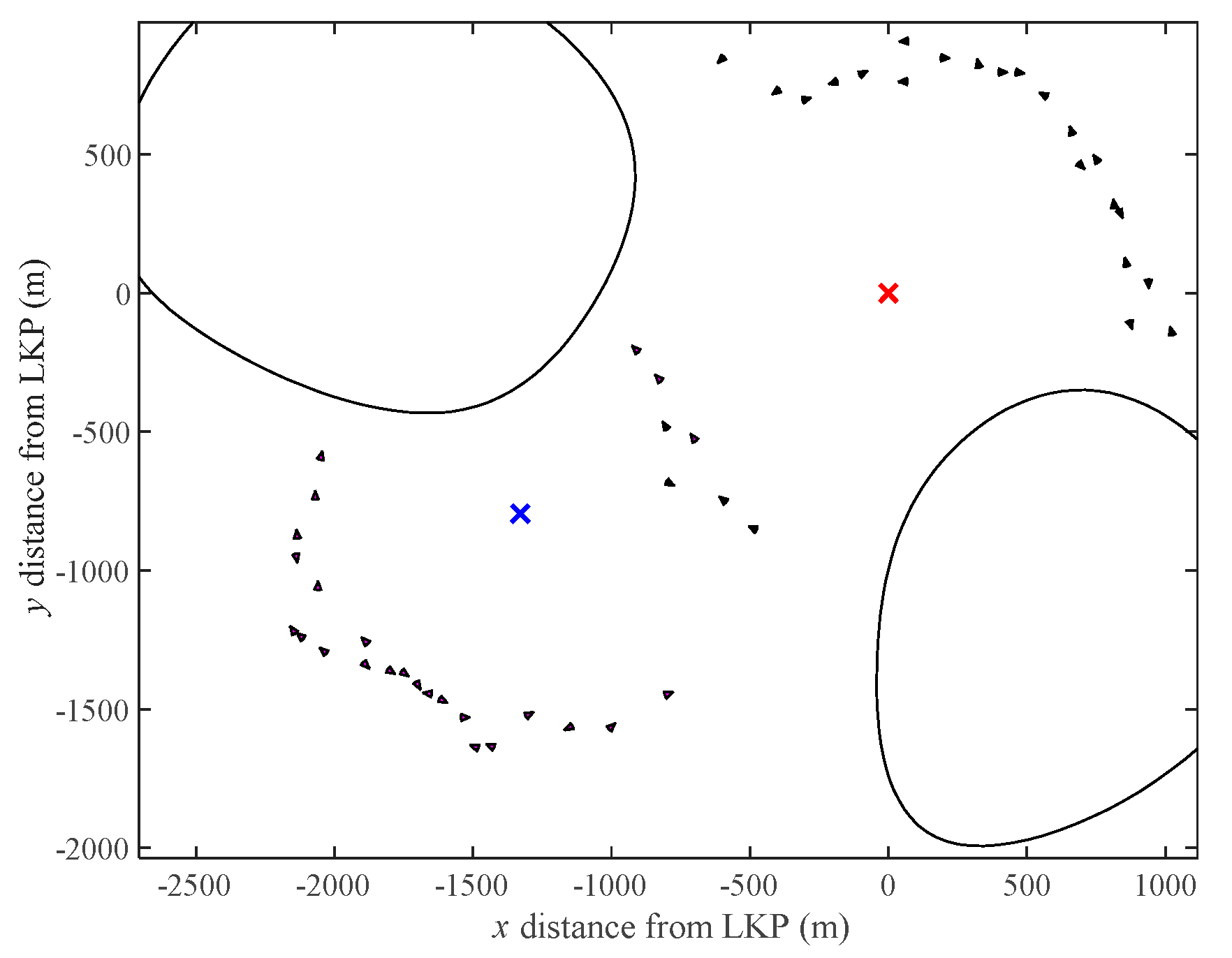
4.1.3. Phase 3: Network Re-Planning
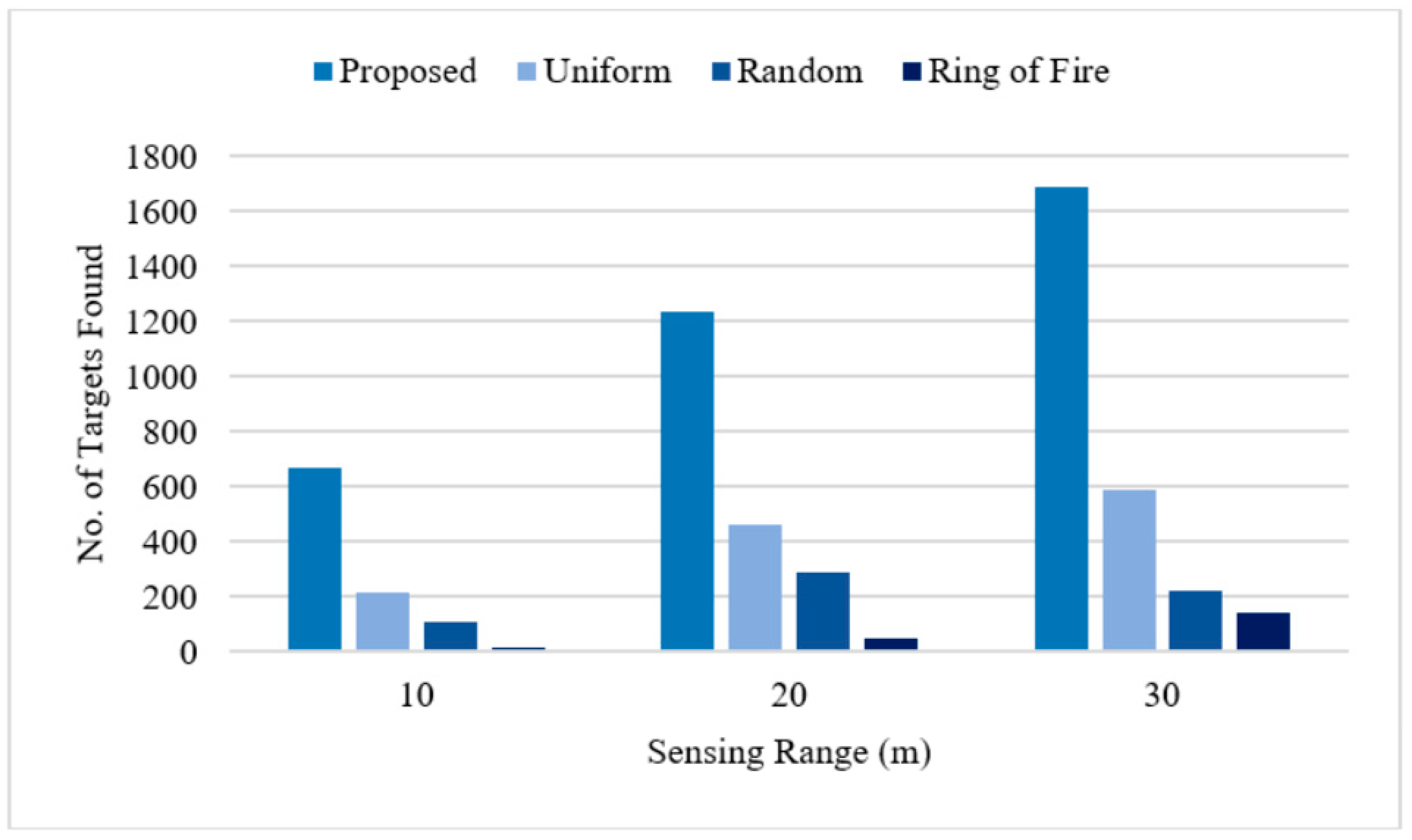
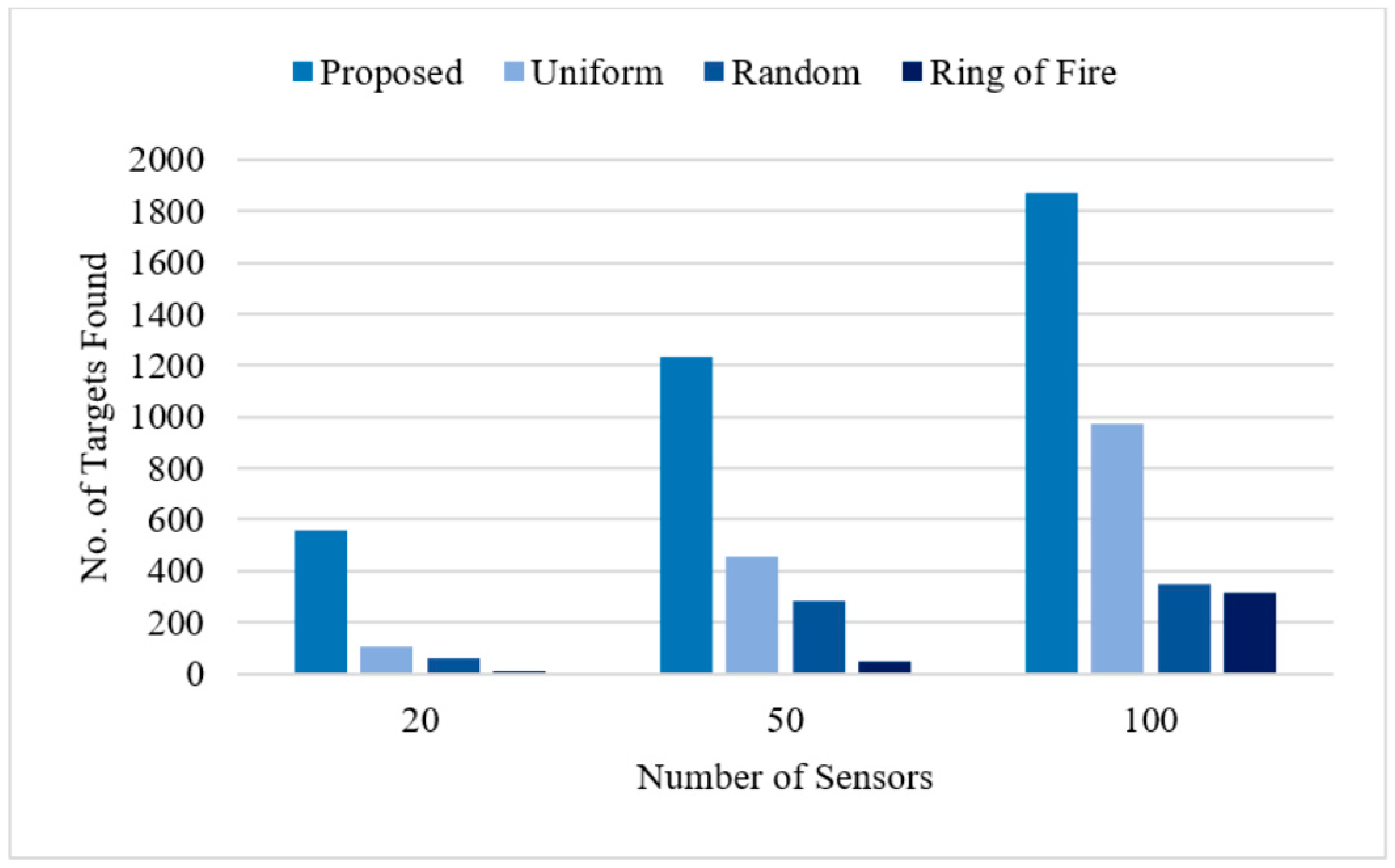
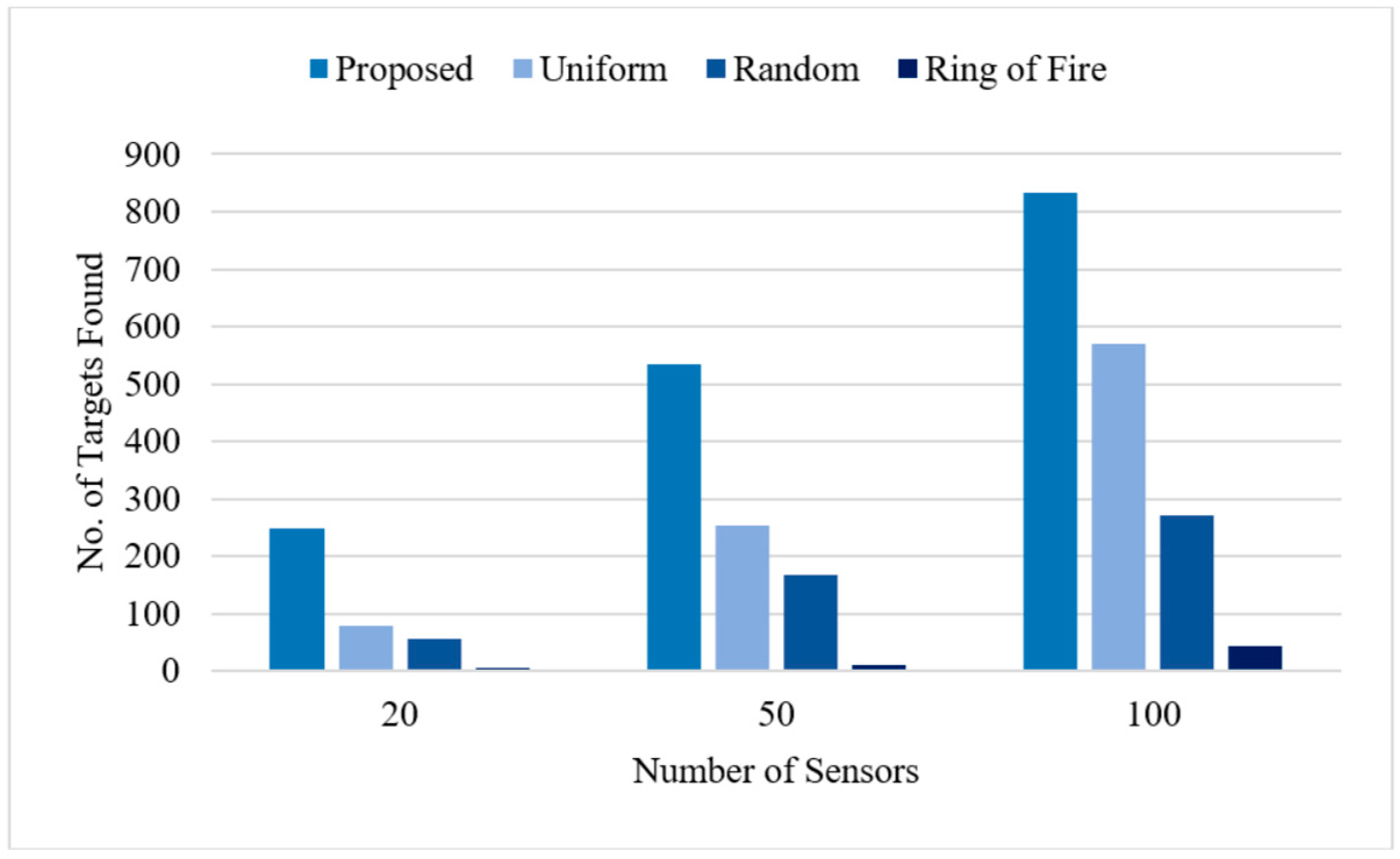
4.2. Comparative Study against Standard Topologies
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Algorithm 1: Overall Sensor Planning Algorithm |
|
Appendix B
| Algorithm 2: Simulating Target Trajectories |
|
Appendix C
| Algorithm 3: Determining the Deployment Sub-region and Time (Pattern Search Algorithm) |
|
Appendix D
| Algorithm 4: Sensor Orientation Optimization |
|
Appendix E
| Algorithm 5: Trajectory Re-simulation |
|
References
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless Sensor Networks: A Survey. Comput. Netw. 2002, 38, 30. [Google Scholar] [CrossRef]
- Serna, M.A.; Casado, R.; Bermúdez, A.; Pereira, N.; Tennina, S. Distributed Forest Fire Monitoring Using Wireless Sensor Networks. Int. J. Distrib. Sens. Networks 2015, 2015, 1–18. [Google Scholar] [CrossRef]
- Xu, Y.-H.; Sun, Q.-Y.; Xiao, Y.-T. An Environmentally Aware Scheme of Wireless Sensor Networks for Forest Fire Monitoring and Detection. Future Internet 2018, 10, 102. [Google Scholar] [CrossRef]
- Kadri, B.; Bouyeddou, B.; Moussaoui, D. Early Fire Detection System Using Wireless Sensor Networks. In Proceedings of the 2018 International Conference on Applied Smart Systems (ICASS), Medea, Algeria, 24–25 November 2018; pp. 1–4. [Google Scholar]
- Ramesh, M.V. Design, development, and deployment of a wireless sensor network for detection of landslides. Ad Hoc Netw. 2014, 13, 2–18. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Guo, B. Application of Collocated GPS and Seismic Sensors to Earthquake Monitoring and Early Warning. Sensors 2013, 13, 14261–14276. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Wang, P.; Vuran, M.C.; Al-Rodhaan, M.A.; Al-Dhelaan, A.M.; Akyildiz, I.F. BorderSense: Border patrol through advanced wireless sensor networks. Ad Hoc Netw. 2011, 9, 468–477. [Google Scholar] [CrossRef]
- Cashbaugh, J.; Kitts, C. Optimizing Sensor Locations in a Multisensor Single-Object Tracking System. Int. J. Distrib. Sens. Netw. 2015, 11, 741491. [Google Scholar] [CrossRef]
- Akter, M.; Rahman, O.; Islam, N.; Hassan, M.M.; AlSanad, A.; Sangaiah, A.K. Energy-Efficient Tracking and Localization of Objects in Wireless Sensor Networks. IEEE Access 2018, 6, 17165–17177. [Google Scholar] [CrossRef]
- Wen, Y.; Gao, R.; Zhao, H. Energy Efficient Moving Target Tracking in Wireless Sensor Networks. Sensors 2016, 16, 29. [Google Scholar] [CrossRef]
- Ochoa, S.F.; Santos, R.M. Human-centric wireless sensor networks to improve information availability during urban search and rescue activities. Inf. Fusion 2015, 22, 71–84. [Google Scholar] [CrossRef]
- Erdelj, M.; Król, M.; Natalizio, E. Wireless Sensor Networks and Multi-UAV systems for natural disaster management. Comput. Netw. 2017, 124, 72–86. [Google Scholar] [CrossRef]
- Francisco, J.; Fernando, G.-H.; Carlos, L.-A. A Coordinated Wilderness Search and Rescue Technique Inspired by Bacterial Foraging Behavior. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 318–324. [Google Scholar]
- Shin, J.C.L.; Kashino, Z.; Nejat, G.; Benhabib, B. A Sensor-Network-Supported Mobile-Agent-Search Strategy for Wilderness Rescue. Robotics 2019, 8, 61. [Google Scholar] [CrossRef]
- Guvensan, M.A.; Yavuz, A.G. On coverage issues in directional sensor networks: A survey. Ad Hoc Netw. 2011, 9, 1238–1255. [Google Scholar] [CrossRef]
- Plarre, K.; Kumar, P.R. Tracking Objects with Networked Scattered Directional Sensors. EURASIP J. Adv. Signal Process. 2007, 2008, 360912. [Google Scholar] [CrossRef]
- Guvensan, M.A.; Yavuz, A.G. A New Coverage Improvement Algorithm Based on Motility Capability of Directional Sensor Nodes. In Ad-hoc, Mobile, and Wireless Networks; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6811, pp. 206–219. [Google Scholar]
- Wu, C.-H.; Chung, Y.-C. A tiling-based approach for directional sensor network deployment. 2010 IEEE Sens. 2010, 1358–1363. [Google Scholar] [CrossRef]
- Liang, C.-K.; Tsai, C.-H.; He, M.-C. On area coverage problems in directional sensor networks. In Proceedings of the The International Conference on Information Networking 2011 (ICOIN2011), Barcelona, Spain, 26–28 January 2011; pp. 182–187. [Google Scholar]
- Sung, T.-W.; Lu, Y.-T.; Lin, F.-T.; Yang, C.-S. Direction Control Using Delaunay Triangulation for Coverage Improvement in Directional Sensor Networks. In Proceedings of the 2015 Third International Conference on Robot, Vision and Signal Processing (RVSP), Kaohsiung, Taiwan, 18–20 November 2015; pp. 290–293. [Google Scholar]
- Sung, T.-W.; Yang, C.-S. Distributed Voronoi-Based Self-Redeployment for Coverage Enhancement in a Mobile Directional Sensor Network. Int. J. Distrib. Sens. Netw. 2013, 9, 165498. [Google Scholar] [CrossRef]
- Han, X.; Cao, X.; Lloyd, E.L.; Shen, C.-C. Deploying Directional Sensor Networks with Guaranteed Connectivity and Coverage. In Proceedings of the 2008 5th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, San Francisco, CA, USA, 16–20 June 2008; pp. 153–160. [Google Scholar]
- Chen, U.-R.; Chiou, B.-S.; Chen, J.-M.; Lin, W. An Adjustable Target Coverage Method in Directional Sensor Networks. In Proceedings of the 2008 IEEE Asia-Pacific Services Computing Conference, Yilan, Taiwan, 9–12 December 2008; pp. 174–180. [Google Scholar]
- Akbarzadeh, V.; Gagné, C.; Parizeau, M.; Argany, M.; Mostafavi, M.A. Probabilistic Sensing Model for Sensor Placement Optimization Based on Line-of-Sight Coverage. IEEE Trans. Instrum. Meas. 2012, 62, 293–303. [Google Scholar] [CrossRef]
- Wang, J.; Niu, C.; Shen, R. Priority-based target coverage in directional sensor networks using a genetic algorithm. Comput. Math. Appl. 2009, 57, 1915–1922. [Google Scholar] [CrossRef]
- Singh, P.; Mini, S. A Heuristic to Deploy Directional Sensor Nodes in Wireless Sensor Networks. In Proceedings of the 2016 8th International Conference on Computational Intelligence and Communication Networks (CICN), Tehri, India, 23–25 December 2016; pp. 11–15. [Google Scholar]
- Osais, Y.E.; St-Hilaire, M.; Yu, F.R. Directional Sensor Placement with Optimal Sensing Range, Field of View and Orientation. Mob. Netw. Appl. 2009, 15, 216–225. [Google Scholar] [CrossRef]
- Varposhti, M.; Saleh, P.; Afzal, S.; Dehghan, M. Distributed area coverage in mobile directional sensor networks. In Proceedings of the 2016 8th International Symposium on Telecommunications (IST), Tehran, Iran, 26–27 September 2016; pp. 18–23. [Google Scholar] [CrossRef]
- Ma, H.; Liu, Y. On Coverage Problems of Directional Sensor Networks. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; pp. 721–731. [Google Scholar]
- Cortes, J.; Martinez, S.; Karatas, T.; Bullo, F. Coverage Control for Mobile Sensing Networks. IEEE Trans. Robot. Autom. 2004, 20, 243–255. [Google Scholar] [CrossRef]
- Ganguli, A.; Cortés, J.; Bullo, F. Distributed Coverage of Nonconvex Environments. In Networked Sensing Information and Control; Saligrama, V., Ed.; Springer: Boston, MA, USA, 2008; pp. 289–305. [Google Scholar]
- Kantaros, Y.; Zavlanos, M.M. Distributed communication-aware coverage control by mobile sensor networks. Automatica 2016, 63, 209–220. [Google Scholar] [CrossRef]
- Gusrialdi, A.; Hatanaka, T.; Fujita, M. Coverage control for mobile networks with limited-range anisotropic sensors. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 4263–4268. [Google Scholar]
- Stergiopoulos, Y.; Tzes, A. Cooperative positioning/orientation control of mobile heterogeneous anisotropic sensor networks for area coverage. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 1106–1111. [Google Scholar] [CrossRef]
- Lee, S.G.; Diaz-Mercado, Y.; Egerstedt, M. Multirobot Control Using Time-Varying Density Functions. IEEE Trans. Robot. 2015, 31, 489–493. [Google Scholar] [CrossRef]
- Miah, S.; Panah, A.Y.; Fallah, M.M.H.; Spinello, D. Generalized non-autonomous metric optimization for area coverage problems with mobile autonomous agents. Automatica 2017, 80, 295–299. [Google Scholar] [CrossRef]
- Kennedy, J.; Chapman, A.; Dower, P.M. Generalized Coverage Control for Time-Varying Density Functions. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 71–76. [Google Scholar]
- Lekien, F.; Leonard, N.E. Nonuniform coverage and cartograms. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 5518–5523. [Google Scholar]
- Amaldi, E.; Capone, A.; Cesana, M.; Filippini, I. Design of Wireless Sensor Networks for Mobile Target Detection. IEEE/ACM Trans. Netw. 2011, 20, 784–797. [Google Scholar] [CrossRef]
- Clouqueur, T.; Phipatanasuphorn, V.; Ramanathan, P.; Saluja, K.K. Sensor Deployment Strategy for Detection of Targets Traversing a Region. Mob. Netw. Appl. 2003, 8, 453–461. [Google Scholar] [CrossRef]
- Kashino, Z.; Vilela, J.; Kim, J.Y.; Nejat, G.; Benhabib, B. An adaptive static-sensor network deployment strategy for detecting mobile targets. In Proceedings of the 2016 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Lausanne, Switzerland, 23–27 October 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Rogge, J.A.; Aeyels, D. Multi-robot coverage to locate fixed and moving targets. In Proceedings of the 2009 IEEE International Conference on Control Applications, St. Petersburg, Russia, 8–10 July 2009; pp. 902–907. [Google Scholar]
- Grundel, D.A. Searching for a moving target: Optimal path planning. In Proceedings of the 2005 IEEE Networking, Sensing and Control, Tucson, AZ, USA, 19–22 March 2005; pp. 867–872. [Google Scholar]
- Macwan, A.; Vilela, J.; Nejat, G.; Benhabib, B. A Multirobot Path-Planning Strategy for Autonomous Wilderness Search and Rescue. IEEE Trans. Cybern. 2014, 45, 1784–1797. [Google Scholar] [CrossRef]
- Kashino, Z.; Nejat, G.; Benhabib, B. A Hybrid Strategy for Target Search Using Static and Mobile Sensors. IEEE Trans. Cybern. 2020, 50, 856–868. [Google Scholar] [CrossRef]
- Li, X.; Fletcher, G.; Nayak, A.; Stojmenovic, I. Randomized carrier-based sensor relocation in wireless sensor and robot networks. Ad Hoc Netw. 2013, 11, 1951–1962. [Google Scholar] [CrossRef]
- Kantaros, Y.; Schlotfeldt, B.; Atanasov, N.; Pappas, G.J. Asymptotically Optimal Planning for Non-Myopic Multi-Robot Information Gathering. In Proceedings of the Robotics: Science and Systems XV, Freiburg, Germany, 22–26 June 2019. [Google Scholar] [CrossRef]
- Atanasov, N.; Le Ny, J.; Daniilidis, K.; Pappas, G.J. Decentralized active information acquisition: Theory and application to multi-robot SLAM. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4775–4782. [Google Scholar]
- Kumar, V.; Rus, D.; Singh, S. Robot and Sensor Networks for First Responders. IEEE Pervasive Comput. 2004, 3, 24–33. [Google Scholar] [CrossRef]
- Kumar, A.A.; Sivalingam, K.M. Target tracking in a WSN with directional sensors using electronic beam steering. In Proceedings of the 2012 Fourth International Conference on Communication Systems and Networks (COMSNETS 2012), Bangalore, India, 3–7 January 2012; pp. 1–10. [Google Scholar]
- Mohajerzadeh, A.H.; Jahedinia, H.; Izadi-Ghodousi, Z.; Abbasinezhad-Mood, D.; Salehi, M. Efficient target tracking in directional sensor networks with selective target area’s coverage. Telecommun. Syst. 2017, 68, 47–65. [Google Scholar] [CrossRef]
- Tripathi, A.; Gupta, H.P.; Dutta, T.; Kumar, D.; Jit, S.; Shukla, K.K. A Target Tracking System Using Directional Nodes in Wireless Sensor Networks. IEEE Syst. J. 2019, 13, 1618–1627. [Google Scholar] [CrossRef]
- Wang, Z.; Liao, J.; Cao, Q.; Qi, H.; Wang, Z. Barrier Coverage in Hybrid Directional Sensor Networks. In Proceedings of the 2013 IEEE 10th International Conference on Mobile Ad-Hoc and Sensor Systems, Hangzhou, China, 14–16 October 2013; pp. 222–230. [Google Scholar]
- Zhao, L.; Bai, G.; Shen, H.; Tang, Z. Strong barrier coverage of directional sensor networks with mobile sensors. Int. J. Distrib. Sens. Netw. 2018, 14. [Google Scholar] [CrossRef]
- Benahmed, T.; Benahmed, K. Optimal barrier coverage for critical area surveillance using wireless sensor networks. Int. J. Commun. Syst. 2019, 32, e3955. [Google Scholar] [CrossRef]
- Liu, X.; Yang, B.; Chen, G. Full-view barrier coverage in mobile camera sensor networks. Wirel. Netw. 2018, 25, 4773–4784. [Google Scholar] [CrossRef]
- Kashino, Z.; Nejat, G.; Benhabib, B. A multi-robot sensor-delivery planning strategy for static-sensor networks. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6640–6647. [Google Scholar]
- Wang, Y.; Wu, C.-H. Robot-Assisted Sensor Network Deployment and Data Collection. In Proceedings of the 2007 International Symposium on Computational Intelligence in Robotics and Automation, Jacksonville, FI, USA, 20–23 June 2007; pp. 467–472. [Google Scholar]
- Shiu, L.C. The robot deployment scheme for wireless sensor networks in the concave region. In Proceedings of the 2009 International Conference on Networking, Sensing and Control, Okayama, Japan, 26–29 March 2009; pp. 581–586. [Google Scholar]
- Fletcher, G.; Li, X.; Nayak, A.; Stojmenovic, I. Back-Tracking Based Sensor Deployment by a Robot Team. In Proceedings of the 2010 7th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON), Boston, MA, USA, 21–25 June 2010; pp. 1–9. [Google Scholar]
- Wang, Y.-H.; Tsai, J.J.P.; Wu, Y.-H. Robot-based deployment mechanism for wireless sensor networks in unknown region. In Proceedings of the 2013 International Joint Conference on Awareness Science and Technology & Ubi-Media Computing (iCAST 2013 & UMEDIA 2013), Aizu-Wakamatsu, Japan, 2–4 November 2013; pp. 143–149. [Google Scholar]
- Mesa-Barrameda, E.; Santoro, N.; Shi, W.; Taleb, N. Sensor deployment by a robot in an unknown orthogonal region: Achieving full coverage. In Proceedings of the 2014 20th IEEE International Conference on Parallel and Distributed Systems (ICPADS), Hsinchu, Taiwan, 16–19 December 2014; pp. 951–960. [Google Scholar]
- Rajesh, M.; George, A.; Sudarshan, T.S.B. Energy efficient deployment of Wireless Sensor Network by multiple mobile robots. In Proceedings of the 2015 International Conference on Computing and Network Communications (CoCoNet), Trivandrum, India, 16–19 December 2015; pp. 72–78. [Google Scholar]
- Batalin, M.A.; Sukhatme, G.S. Coverage, Exploration and Deployment by a Mobile Robot and Communication Network. Telecommun. Syst. 2004, 26, 181–196. [Google Scholar] [CrossRef]
- Tuna, G.; Gungor, V.C.; Gulez, K. An autonomous wireless sensor network deployment system using mobile robots for human existence detection in case of disasters. Ad Hoc Netw. 2014, 13, 54–68. [Google Scholar] [CrossRef]
- Woiceshyn, K.; Kashino, Z.; Nejat, G.; Benhabib, B. Vehicle Routing for Resource Management in Time-Phased Deployment of Sensor Networks. IEEE Trans. Autom. Sci. Eng. 2018, 16, 716–728. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, X.; Qian, X. Carrier-based sensor deployment by a mobile robot for wireless sensor networks. In Proceedings of the 2012 12th International Conference on Control Automation Robotics & Vision (ICARCV), Guangzhou, China, 5–7 December 2012; pp. 1663–1668. [Google Scholar]
- Kashino, Z.; Kim, J.Y.; Nejat, G.; Benhabib, B. Spatiotemporal Adaptive Optimization of a Static-Sensor Network via a Non-Parametric Estimation of Target Location Likelihood. IEEE Sens. J. 2017, 17, 1479–1492. [Google Scholar] [CrossRef]
- Vilela, J.; Kashino, Z.; Ly, R.; Nejat, G.; Benhabib, B. A Dynamic Approach to Sensor Network Deployment for Mobile-Target Detection in Unstructured, Expanding Search Areas. IEEE Sens. J. 2016, 16, 4405–4417. [Google Scholar] [CrossRef]
- Yanmaz, E.; Guclu, H. Stationary and Mobile Target Detection Using Mobile Wireless Sensor Networks. In Proceedings of the 2010 INFOCOM IEEE Conference on Computer Communications Workshops, San Diego, CA, USA, 15–19 March 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Zou, Y.; Chakrabarty, K. Sensor deployment and target localization in distributed sensor networks. ACM Trans. Embed. Comput. Syst. 2004, 3, 61–91. [Google Scholar] [CrossRef]
- Koester, R.J. Lost Person Behavior: A Search and Rescue Guide on where to Look for Land, Air, and Water; dbS Productions: Charlottesville, VA, USA, 2008. [Google Scholar]
- Lin, L.; Goodrich, M.A. A Bayesian approach to modeling lost person behaviors based on terrain features in Wilderness Search and Rescue. Comput. Math. Organ. Theory 2010, 16, 300–323. [Google Scholar] [CrossRef]
- Hooke, R.; Jeeves, T.A. Direct Search Solution of Numerical and Statistical Problems. J. ACM 1961, 8, 212–229. [Google Scholar] [CrossRef]
- Garai, G.; Chaudhuri, B. A distributed hierarchical genetic algorithm for efficient optimization and pattern matching. Pattern Recognit. 2007, 40, 212–228. [Google Scholar] [CrossRef]
- Yun, Z.; Bai, X.; Xuan, D.; Lai, T.H.; Jia, W. Optimal Deployment Patterns for Full Coverage and k-Connectivity (k ≤ 6) Wireless Sensor Networks. IEEE/ACM Trans. Netw. 2010, 18, 934–947. [Google Scholar] [CrossRef]
- Gupta, H.P.; Tyagi, P.K.; Singh, M.P. Regular Node Deployment for k-Coverage in mm-Connected Wireless Networks. IEEE Sens. J. 2015, 15, 7126–7134. [Google Scholar] [CrossRef]
- Sakai, K.; Sun, M.-T.; Ku, W.-S.; Lai, T.-H.; Vasilakos, A.V. A Framework for the Optimal k-Coverage Deployment Patterns of Wireless Sensors. IEEE Sens. J. 2015, 15, 7273–7283. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder--Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Jou, E.D. Determine Whether Two Line Segments Intersect. In Modeling in Computer Graphics, Proceedings of the IFIP WG 5.10 Working Conference Tokyo, Japan, 8–12 April 1991; Kunii, T.L., Ed.; Springer: Tokyo, Japan, 1991; pp. 265–274. [Google Scholar]
- Künsch, H.R. Particle filters. Bernoulli 2013, 19, 1391–1403. [Google Scholar] [CrossRef]
- Biagioni, E.; Sasaki, G. Wireless sensor placement for reliable and efficient data collection. In Proceedings of the 36th Annual Hawaii International Conference on System Sciences, Big Island, HI, USA, 6–9 January 2003; p. 10. [Google Scholar]
- Zou, Y.; Chakrabarty, K. Sensor deployment and target localization based on virtual forces. In Proceedings of the IEEE INFOCOM Twenty-second Annual Joint Conference of the IEEE Computer and Communications Societies (IEEE Cat. No.03CH37428), San Francisco, CA, USA, 30 March–3 April 2003; Volume 2, pp. 1293–1303. [Google Scholar]
- Rout, M.; Roy, R. Dynamic deployment of randomly deployed mobile sensor nodes in the presence of obstacles. Ad Hoc Netw. 2016, 46, 12–22. [Google Scholar] [CrossRef]
- Han, S.P. A globally convergent method for nonlinear programming. J. Optim. Theory Appl. 1977, 22, 297–309. [Google Scholar] [CrossRef]
- Tan, G.; Jarvis, S.A.; Kermarrec, A.-M. Connectivity-Guaranteed and Obstacle-Adaptive Deployment Schemes for Mobile Sensor Networks. Available online: https://hal.inria.fr/inria-00432129/document (accessed on 6 October 2020).




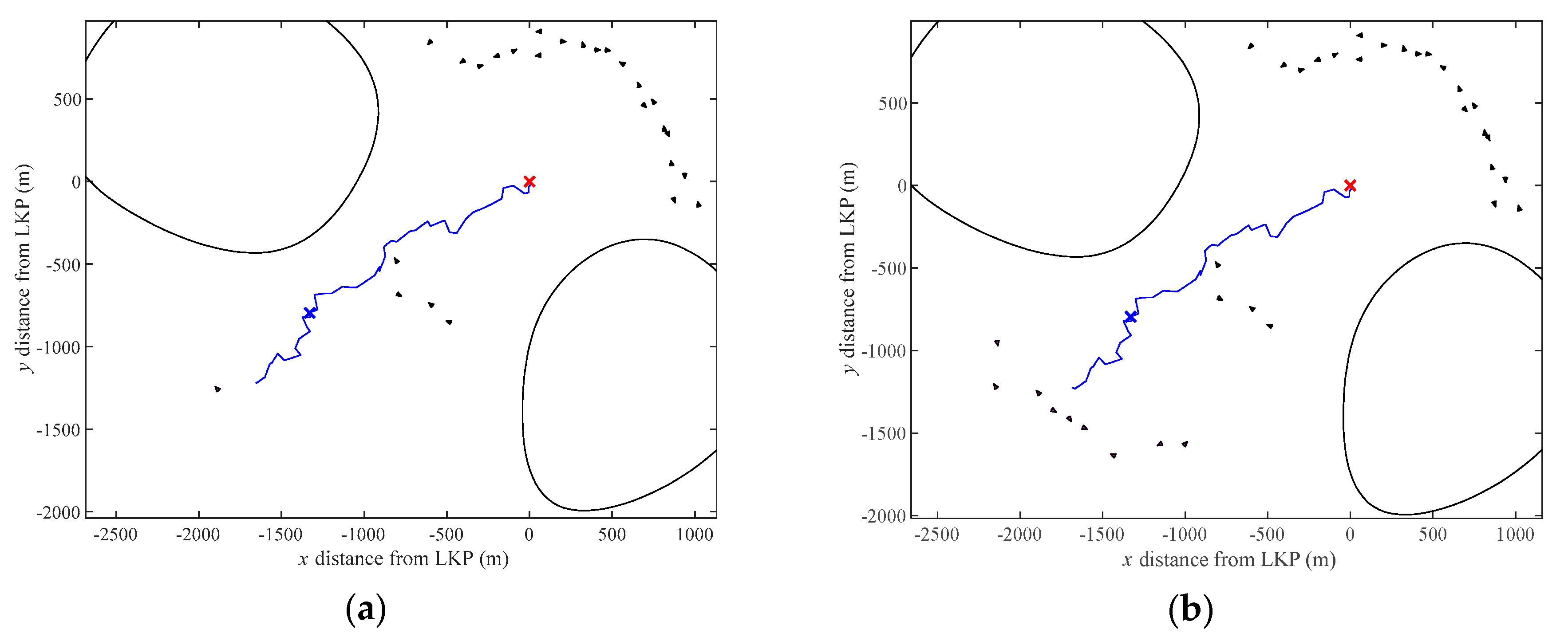
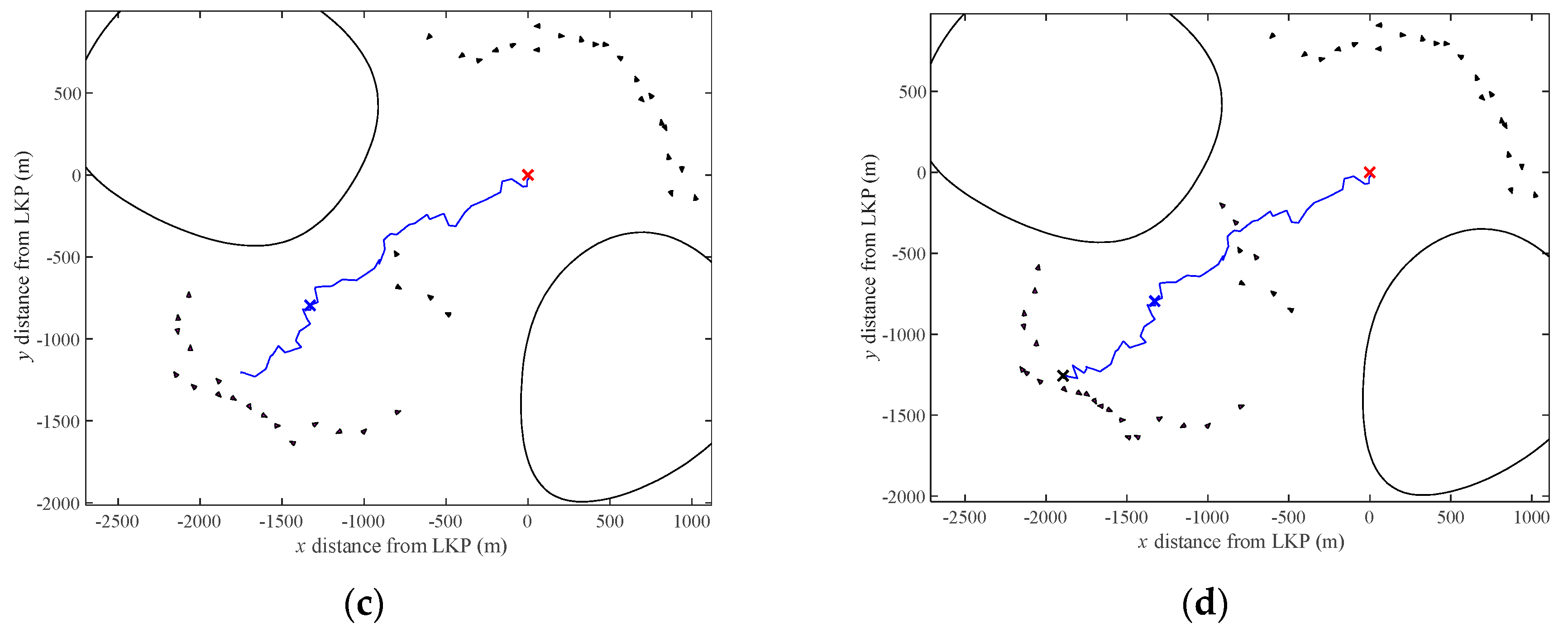


| Sensor # | Time of Deployment (s) | Deployment Position (m) | Sensor Orientation (rad) |
|---|---|---|---|
| 1 | 3683 | (896, 1418) | 1.55 |
| 2 | 3700 | (1794, −912) | 0.82 |
| 3 | 3701 | (355, 1994) | 1.16 |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 28 | 4287 | (−2011, −847) | 2.18 |
| 29 | 4293 | (−2189, 197) | 5.89 |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 48 | 4757 | (104, 2475) | 1.98 |
| 49 | 4807 | (−887, 2342) | 3.84 |
| 50 | 4902 | (−2524, 604) | 6.91 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wasim, S.; Kashino, Z.; Nejat, G.; Benhabib, B. Directional-Sensor Network Deployment Planning for Mobile-Target Search. Robotics 2020, 9, 82. https://doi.org/10.3390/robotics9040082
Wasim S, Kashino Z, Nejat G, Benhabib B. Directional-Sensor Network Deployment Planning for Mobile-Target Search. Robotics. 2020; 9(4):82. https://doi.org/10.3390/robotics9040082
Chicago/Turabian StyleWasim, Shiraz, Zendai Kashino, Goldie Nejat, and Beno Benhabib. 2020. "Directional-Sensor Network Deployment Planning for Mobile-Target Search" Robotics 9, no. 4: 82. https://doi.org/10.3390/robotics9040082
APA StyleWasim, S., Kashino, Z., Nejat, G., & Benhabib, B. (2020). Directional-Sensor Network Deployment Planning for Mobile-Target Search. Robotics, 9(4), 82. https://doi.org/10.3390/robotics9040082






