1. Introduction
As the variety of industrial tasks is increasing and robots are being more and more deployed in real-world settings, it becomes impossible to pre-program them for all the situations they may encounter. Imitation learning provides powerful methods to reduce the programming effort. By generalizing existing task knowledge for new situations, robots even have the potential to allow the realization of tasks with higher complexity than just by programming alone. Therefore, learning manipulation tasks from human demonstrations has many potential application domains ranging from service robotics to industrial applications.
The contribution of this paper is a concept for learning motor skills for tasks that have the following characteristics: First, the task can be represented by a sequence of object-relative point-to-point movements. Hence, the particular shape and execution speed of a movement are not relevant, but the goal of a movement is. Examples for goals are desired positions or orientations of an end-effector relative to an object in the scene, or the posture of the fingers of a hand. Second, the task involves a physical interaction with the environment. In phases where the robot interacts with an object, it may have to actively apply a force, for instance it may need to push an object. Therefore, movements are not restricted to the kinematic domain. Instead, a goal may also be comprised of a desired force or torque. We refer to tasks that have the aforementioned properties as sequential force interaction tasks.
In this paper, we present a novel motor skill learning framework for point-to-point movements, as well as for their composition. Furthermore, we propose a concept for reactive decision making, i.e., when to perform which of the movements skills during online execution. Motor skills may comprise force and/or kinematic control magnitudes. Force magnitudes control the interaction force between parts of the robot and the environment, for instance applying a force against a box with the robot’s end effector. Kinematic magnitudes control the position/velocity of robot parts, such as for instance the position of the end effector with respect to the above box. This hybrid force/kinematic representation allows learning tasks that are characterized by both kinematic and force interactions. These are of high relevance, for instance in the assembly domains where force control is essential to control the physical interaction.
Our particular focus is learning skills that generalize well to situations which were not demonstrated. Hence, the skill should be independent of absolute object positions, such that it can be generalized to object locations which have not been seen during teaching. Therefore, we demonstrate a task several times with varying object positions. From these demonstrations, the system learns the individual movements and decides for each movement if it should be performed relative to an object and if a force should be applied or not. After learning, we execute the resulting skill on a real robot with a different setup and, therefore, evaluate the generalization capabilities of the skill.
Throughout this paper, we will refer to the individual movements as movement primitives (MPs). The process of extracting attractor MPs representing the single point-to-point movements from the demonstrations will be referred to as task-decomposition. To represent the robot’s movements relative to objects in the scene, we use a hybrid position-force task-space controller (see
Section 1.2). A task-space is composed of a controlled entity (e.g., end-effector), control variables (e.g., position or force) and a coordinate frame which allows for controlling the robot relative to an object. We pre-define a set of task-spaces which are sufficient for performing a wide range of tasks. Applying our proposed task-decomposition method to the demonstrations then results in a set of MPs, whereas for each MP an appropriate task-space is selected and the most likely attractor goal is found. The basis of the approach is a probability distribution called Directional Normal Distribution. In this paper, we present the distribution and an Expectation-Maximization algorithm for inferring its parameters from data. The task-decomposition was introduced by Manschitz et al. [
1]. Compared to this paper, we provide a more in-depth discussion and evaluation of the method.
The task-decomposition results in a set of MPs controlling either the position or orientation of the end-effector or the joint angles of the robot’s hand. In a second step, we present a concept for learning to sequence these MPs. When executing a learned skill on a real robot, our system decides at run-time which of the MPs to activate. The system is based on the concept of a sequence graph which was introduced in Manschitz et al. [
2,
3]. In this paper, we extend the concept to allow for synchronizing the activations of the MPs controlling different entities of the robot (position, orientation, fingers).
In summary, this paper combines and extends two previously published approaches into one consistent sequential skill learning framework. We provide an extended in-depth discussion of the task-decomposition approach, and present additional experiments. Furthermore, we extend the sequence graph concept to allow for synchronizing the activations of the MPs resulting from the task-decomposition. The presented system is capable of learning sequential force interaction skills from only a few demonstrations. We conducted and evaluated experiments to show how the learned skills generalize to configurations of the scene that have never been seen during training.
1.1. Related Work
Decomposing tasks based on kinesthetic demonstrations has received a lot of attention in robotics research over recent years. Lioutikov et al. [
4] identify the underlying MPs of a task using an Expectation-Maximization (EM) algorithm. The authors assume the demonstrations are pre-segmented and their method prunes out false positive cut points between successive segments. Lemme et al. [
5] build a library of MPs from demonstrations. Their approach starts with a single simple MP. By modifying and recombining existing MPs, they are able to represent complex trajectories. Other approaches try to identify MPs using Bayesian Binning [
6], Transition State Clustering [
7], Conditional Random Fields [
8,
9], Gaussian Mixture Models [
10,
11,
12], Hidden Markov Models [
13,
14] or Temporal Alignment for Control [
15]. Changepoint methods can be used for decomposing a task in a two-step process. After segmenting demonstrations by detecting changepoints [
16,
17,
18,
19,
20,
21], the individual segments can be assigned to individual MPs. The advantage of such changepoint-based methods is that they can be used for online-analysis of movements. Additionally, the number of MPs is bound by the number of segments and therefore, does not have to be specified in advance.
Recently, also Inverse Reinforcement Learning (IRL) methods have been frequently used in the context of skill identification [
22,
23,
24]. Instead of directly extracting the MPs from the demonstrations, these methods try to infer reward functions for the (sub)tasks. This kind of approach has two interesting properties. First, instead of decomposing the motions itself, it attempts to capture the reason underlying the motions. Hence, if successful, the resulting models can generalize well to previously unknown situations. Second, the resulting reward functions can be directly used for Reinforcement Learning to improve the model over time afterward. Despite the advantages, one downside of IRL methods is that they are data-intensive, making them impractical for our purpose.
Introducing coordinate frames enables representing motions relative to objects in the scene. Therefore, they can help to improve the generalization capabilities of the system. Niekum et al. [
25] segment demonstrations using an auto-regressive Hidden Markov Model. After the segmentation, they extract the coordinate frames of the segments and split the states of the resulting model up to build a Finite State Machine representation of the task. Another approach that explicitly deals with coordinate frames is that of Rozo et al. [
26]. The authors use a task-parametrized Gaussian mixture model (TP-GMM) as trajectory representation. A TP-GMM is a hierarchical GMM with two layers. While on the upper layer each mixture represents a MP, the lower layer is used for representing the joint probability of the trajectory (and the velocity) in the different coordinate frames. In addition to learning a task-representation in different coordinate frames, they learn to vary the controller stiffness dynamically. As a result, their approach enables a robot to physically interact with a human co-worker. While human-robot collaboration (e.g., Maeda et al. [
27], Caccavale et al. [
28], Wu et al. [
29]) is an interesting research domain, our approach focuses on tasks where the robot is operating autonomously. A similar approach was proposed by Huang et al. [
30]. The authors introduce the Kernelized Movement Primitives (KMP) framework which they also extend to support multiple coordinate frames.
Not many approaches incorporate force information into the decomposition of the task (e.g., Gao et al. [
31]). Abu-Dakka et al. [
32] adapt the dynamic movement primitives (DMPs, Ijspeert et al. [
33]) framework so that the robot follows a desired force profile. Yet, they predefine if an MP is position or force-controlled. Steinmetz et al. [
34] learn a desired position and force profile with a DMP from a single demonstration. They present a control framework that is able to transition between phases of pure impedance control and force control based on the measured external force. The approach is not able to handle multiple demonstrations or sequences of MPs.
Ureche et al. [
35] extract the coordinate frames and control variables based on the variance of the data. If the variance of a variable is large within a time window for all demonstrations, they consider it to be significant for the task. The reason is that the variable changes its value and does that in a systematic way across all demonstrations. Kober et al. [
36] showed that under certain circumstances this assumption leads to an over-segmentation of the data. Therefore, they suggested incorporating the convergence behavior of the motion as well. Compared to our method, many approaches (e.g., Ureche et al. [
35], Kober et al. [
36], Pastor et al. [
37], Mühlig et al. [
38]) require demonstrations with identical sequential ordering of the employed MPs. Our approach is instead capable of decomposing a task if the demonstrated MP sequences vary across demonstrations. An example are demonstrations of a light bulb unscrewing task. Here, the number of unscrewing repetitions may vary over demonstrations depending on how firmly the light bulb is screwed in. Furthermore, our approach is able to simultaneously infer all possible MP sequences as well as the composition of the MPs. We will show that decomposing kinesthetic demonstrations of a force interaction task with our approach leads to meaningful and intuitive MPs.
Many approaches focus on task-decomposition. While these approaches are capable of identifying reoccurring motions and representing them as MPs, they do not aim to learn how to sequence them for performing a complex task. One approach that learns to sequence MPs is that of Kappler et al. [
39]. Here, the authors encode MPs as DMPs and link them with expected sensory data. Succeeding MPs are subsequently selected by comparing the current sensor values with the expected ones and choosing the best match. Other examples for sequence learning approaches are that of Ekvall and Kragic [
40], Nicolescu and Mataric [
41] or Pardowitz et al. [
42] and some of the aforementioned decomposition approaches (e.g., Niekum et al. [
25]). Medina and Billard [
43] represent demonstrations with a set of asymptotically stable linear parameter varying systems and additionally learn the termination conditions between individual movements.
Compared to the presented related work in the field of learning force interaction skills, we do not concentrate on single learning aspects. Instead, our approach supports the whole pipeline from acquiring the demonstrations to reproducing the task on a real robot in a setting which is different from the demonstrations.
1.2. Used Controller and MP Framework
In this paper, a MP corresponds to a single point-to-point movement and is represented by a dynamical system (DS) with a linear attractor behavior
where
and
are controller parameters. As we aim at learning skills where the execution speed is not important, the controller parameters are predefined. Each MP has a goal
in task space coordinates
that should be reached if it is activated. Throughout this paper, a single MP will always control either the position/force or orientation of the end-effector (in world coordinates or relative to an object in the scene) or the joint angles of the robot’s hand. For controlling the robot, we use a hybrid position-force controller based on task-level inverse dynamics. The controller as well as the used MP representation are for instance also used by Kober et al. [
36]. The (desired) joint torque
is given by
An overview of the variables used in (2) can be found in
Table 1.
is the task Jacobian and
its pseudo-inverse.
I is the identity matrix,
q and
are the joint angles and joint angle velocities, respectively. Vector
accounts for joint speed damping and joint limit avoidance and is projected into the null space of the movement.
,
and
denote the mass matrix, Coriolis forces and gravity, respectively. The MPs enter the equation via
and
. Vector
contains the concatenated desired forces of the individual MPs. Vector
is the output of a PID controller which tracks the desired task-space accelerations of all MPs. If a MP is composed of task-variables controlling force and position of a robot body (e.g., Cartesian
x and
y position of end-effector and force along
z component in a certain coordinate frame), the individual variables are split up and assigned to
or
according to what they control.
is a diagonal selection matrix which enables selecting either kinematic or force components of a task variable and
is a task-level damping term. Based on the activations of the individual MPs, the pseudo-inverse is scaled with a weighting matrix. In theory, the weighting matrix allows for continuously modulating the contributions of the individual MPs, but in this paper a single MP is either fully active or deactivated. The desired paths of a deactivated MP are ignored by the controller.
1.3. Learning Sequential Force Interaction Tasks
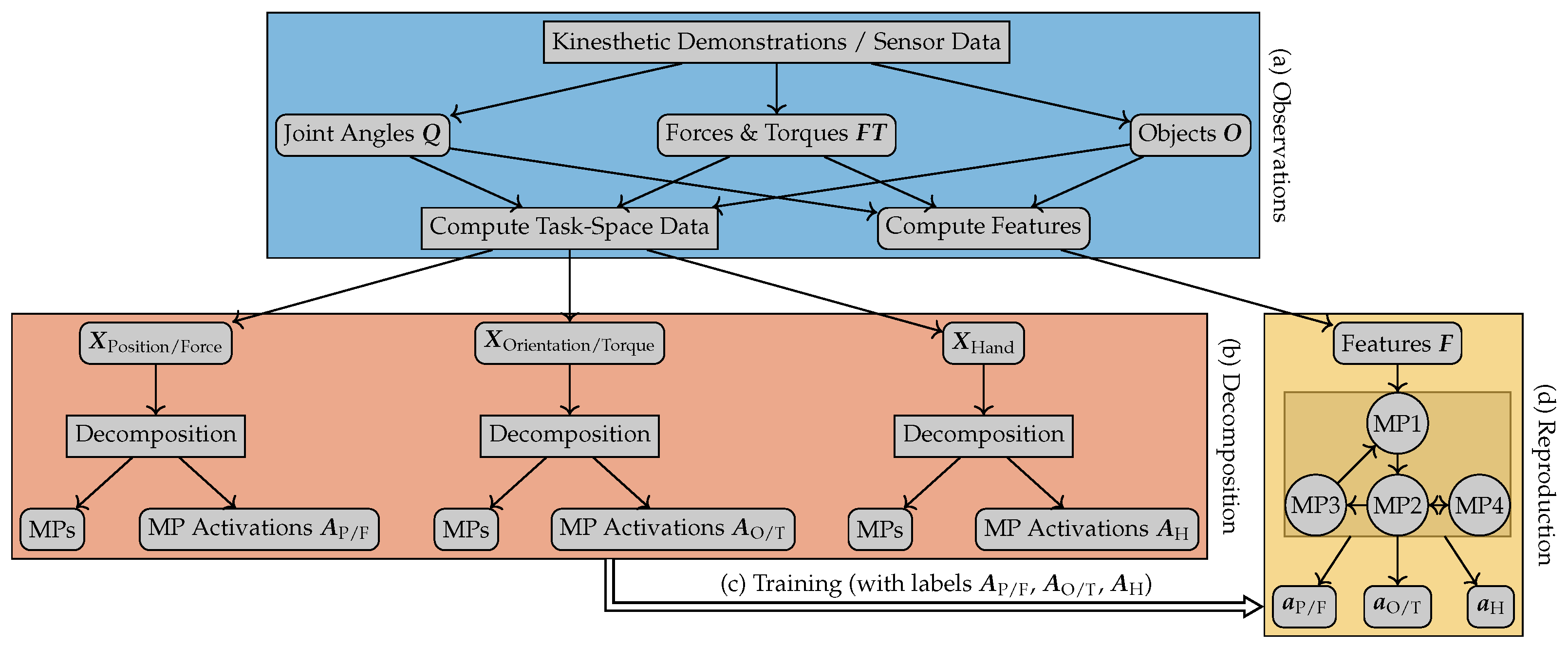
This section provides an overview of the presented method and the structure of the paper. Additionally, the notation that will be used throughout the paper is introduced. An overview of the approach is depicted in
Figure 1. The aim of the approach is to learn to perform a sequential task from kinesthetic demonstrations. To learn the task, two main steps are performed. First, a set of MPs is extracted from the demonstrations. Second, the method learns how to sequence the resulting MPs.
Our method operates on the data recorded during a set of kinesthetic demonstrations of the task. Each demonstration i of varying length with a robot that has joints results in a time-series of joint angles , forces and torques , as well as the 3D positions and 3D orientations of all objects in the scene . Here, contains the positions and orientations of the object for demonstration i. Each object and the world are associated with a coordinate frame. The forces and torques are measured at the wrist of the robot. The joint angles include the joints of the robot arm and the joints of the robot’s hand.
Subsequently, the demonstrations are projected onto a predefined set of task-spaces. For our tasks (as well as many industrial tasks), it is sufficient to control the position and orientation of the end-effector and the joint angles of the robot’s hand. These three entities (position, orientation, fingers) can be controlled largely independently. Therefore, we define the following task-spaces: We use task-spaces representing the position and force of the end-effector in the world frame and relative to every object in the scene. To represent the orientation and torque of the end-effector, also task-spaces are used for the world frame and all other coordinate frames. The fingers of the robot are controlled in joint-space. Therefore, one additional task-space is used to describe the finger joints. The projection results in the task-space data . Here, the matrix corresponds to the data of the ith demonstration represented in the kth task-space. Please note that the number of dimensions can vary for the individual task-spaces. Our method is not restricted to these task-spaces, but they are sufficient for performing a wide range of tasks, as the experimental evaluation will show.
The proposed method analyzes the generated task-space data and decomposes the task into a set of MPs. For each MP, the method estimates the target coordinates and selects a coordinate frame and the control variables. The MP framework we use allows the activation of multiple MPs at the same time. It is, therefore, possible to activate MPs controlling the three entities independently. This co-activation greatly simplifies our MPs. For instance, we can reach different positions with a constant orientation by changing only the MP controlling the position of the end-effector. As we can activate the MPs controlling the three entities independently, the decomposition is also performed independently. The task-space data is therefore split into three distinctive sets according to what the task-spaces control (see
Figure 1). Subsequently, the decomposition is performed on each set, resulting in a set of MPs and their activation probabilities over time for each controlled entity. The detailed explanation of our task-decomposition method can be found in the following
Section 2. The core of the method is the Directional Normal Distribution, which is introduced in
Section 3.
When reproducing a task on a real robot, the system has to decide when to activate which MP for each controlled entity (position, orientation, fingers). The decision which MPs to activate is made based on the current state of the robot and that of the environment, summarized in the feature set
. Here,
is the dimension of the feature set. To learn a mapping from features to MP activations, we record the features during the demonstrations
, as well. In general, the difference between the task-space vector and the feature vector is that the feature vector contains all the information that is necessary for deciding which movement to perform, while the task-space vector only represents the movements of the robot in relation to objects in the scene. Therefore, the feature vector may for instance also contain information about object sizes, color or texture if they are important for the task. However, in this paper, such an information is not needed and therefore, feature vector and task-space vector are equivalent. For more details on the sequencing method, the reader is referred to
Section 4.
After learning to sequence the MPs, the task is reproduced on a real robot. For the current point in time, we compute the features and feed them into the MP sequencing method which then decides which MPs to activate. From the MP activations, we let the MPs compute the desired task-space goal and subsequently use (2) to compute the control command that is sent to the robot. In
Section 5, we evaluate the proposed approach on three different tasks. Finally, we discuss the results and give a short outlook on future work in
Section 6.
2. Proposed Task-Decomposition Approach
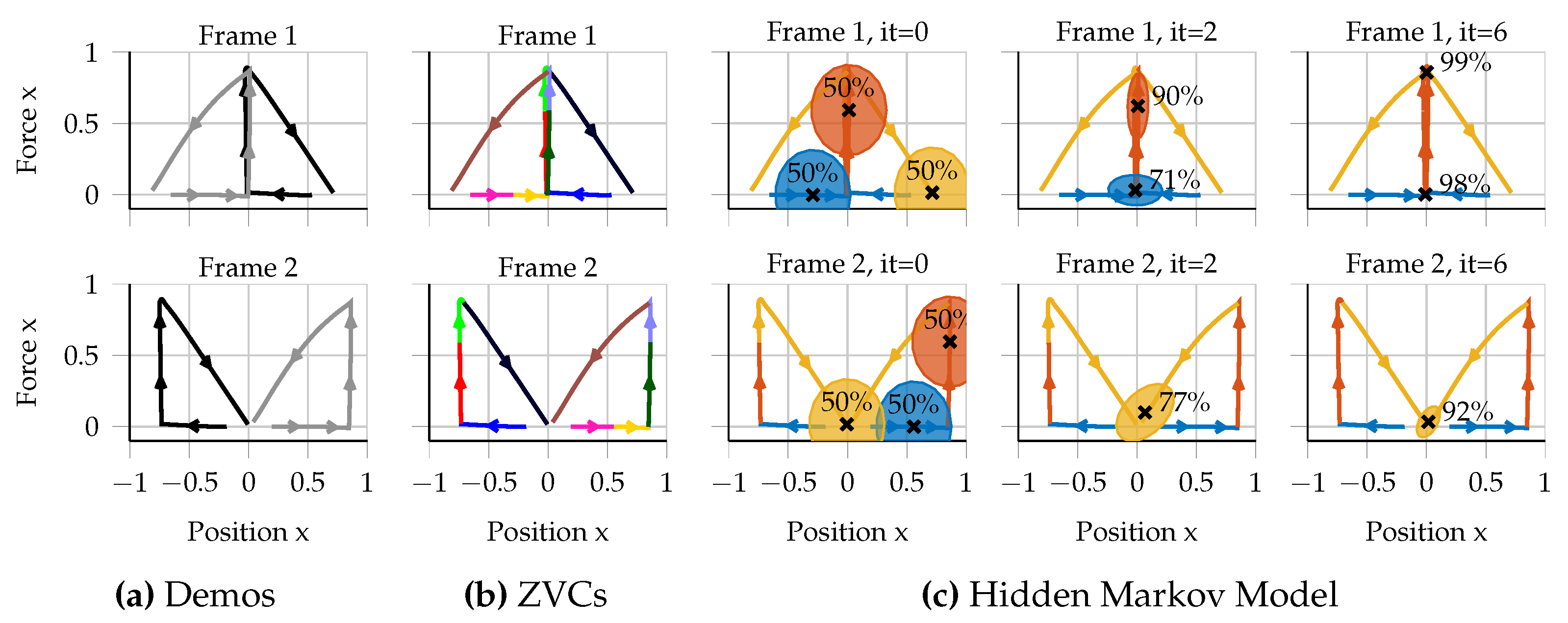
The task-decomposition approach consists of three steps. First, the demonstrations are split into smaller segments. Second, a model is trained which assigns the segments to individual MPs. Finally, the MPs are extracted from the parameters of the resulting model. The three steps will be explained in detail in the following subsections. The explanations are accompanied by a simple toy example that is using only position and force data. The reader can imagine the toy task as follows. The task is to first approach an object, subsequently push against the object and then move to a fixed final position.
Figure 2 depicts an overview of the toy example in the context of our task-decomposition method. As discussed earlier, the same method is used for the individual decompositions of the three controlled entities (position, orientation and fingers). However, handling orientations needs some adaptions that are explained in
Section 3.2).
2.1. Segmentation
As a first step, we split the demonstrations into smaller segments by finding the zero-velocity crossings (ZVCs) of the individual task-spaces. Hence, a segment is added if the robot gets into or looses contact with an object or if a controlled entity stopped and starts to move again. Flanagan et al. [
44] showed the relevance of ZVCs for dexterous manipulation from a biological point of view. Detecting ZVCs is therefore widely used as preprocessing step for task-decomposition approaches (e.g., Kober et al. [
36] or Lioutikov et al. [
4]). After the segmentation step, the task-space data is split into sequences of segments
Here,
is the number of points of the
lth segment of demonstration
i, projected onto the
kth task-space.
Figure 2b depicts the segmentation of our toy example. After the segmentation, we assume the data is over-segmented, e.g., because the teacher stopped temporarily for some reason not related to the task. Hence, we usually have more segments than MPs and therefore have to assign the individual segments to MPs according to a similarity measure.
2.2. Assignment of Segments to MPs
As we have assumed convergent attractor behavior of the MPs, we argue that segments converging to the same target (in at least one task-space) should be assigned to the same MP. The convergence property of the segments can be measured by a probability distribution which we call Directional Normal Distribution (DND). The distribution is needed as we assume our data is over-segmented. Therefore, we cannot simply cluster the end-points of the individual segments in order to check if multiple segments can be represented by the same point-to-point movement. Instead, multiple segments may point towards a common attractor goal, even though their end-points may be far away from each other. Such an example is also illustrated in
Figure 2. The DND ensures that we can analyze the convergence properties of the individual segments regardless of how close the end-points of the individual segments are.
This distribution is based on the normal distribution and has two parameters, a mean
and a Covariance matrix
. The difference to a Normal Distribution is the meaning of the
parameter. While
can also be interpreted as an uncertainty parameter, the mean is defined as an attractor target. Hence, for a given segment the distribution yields a probability that indicates how well the segment is converging towards the attractor target. During learning, a DND is used for each MP and hence
corresponds to the most likely target of the MP. The learning algorithm will be explained in detail in
Section 3. For this section, it is sufficient to know that given some segments, we can estimate the target of each MP in a probabilistic manner by using DNDs.
To find an assignment of segments to MPs, we use a Hidden Markov Model (HMM) to model the time-series sequence of segments. To incorporate the desired convergence property of the segments, we integrate the DND as state probability distribution in the HMM. As our data is represented in different task-spaces and we want to measure the convergence for each task-space and segment, we use a mixture of DNDs for each HMM state (and hence MP). One advantage of using an HMM is that we can perform model selection to choose the optimal number of MPs for the demonstrations. For this step, we use the Bayesian Information Criterion (BIC), a standard model selection criterion for probabilistic models.
2.3. Extraction of MP Parameters
The HMM training assigns each segment a probability of being generated by one of the MPs. In
Section 4, we show that this property can be used for learning to sequence the resulting MPs. In addition to the assigned probabilities, the parameters of the DND mixtures can be used to extract the MP parameters after the HMM training. For each MP, the largest mixture weight indicates in which of the task-spaces it is most likely represented (as it is converging best to its mean). The target of the MP is then defined s the mean of the mixture with the largest weight. Finally, if the assigned task-space of an MP is composed of forces and positions along the same axis, we explicitly decide whether force or position are chosen as the control variable. Here, we use a simple heuristic. Force is only chosen if the desired attractor force of the MP is higher than a threshold and the velocity mean of the segments assigned to this MP is below a threshold. Thus, if a force was measured along a certain axis and the robot was not moving in this direction, we assume the teacher wanted the robot to apply a force. The MP parameter extraction for the toy example is depicted in
Figure 2c.
3. Measuring Convergence with the Directional Normal Distribution
We introduce the DND as an instrument for measuring the convergence of the individual segments. The distribution has two parameters
. The mean
corresponds to an attractor target, while the covariance matrix
indicates the uncertainty about the location of
. To be used for our purpose, the distribution has to fulfill two properties. First, given a segment
the probability
should be large if the segment is converging to the target
, and small otherwise. Second, given a single or multiple segments, we need a method for estimating the most likely parameters of the distribution. In this section, we present the idea behind the distribution and its density function. In
Section 3.1, we then derive a method for estimating the parameters from data using a maximum likelihood approach.
For deriving the density function, we assume the following statement to hold. If a segment is converging to a given target, then on average, the velocity vector
corresponding to a data point
(in our context
d is the dimension of the task-space vector) from the segment should roughly point towards the target. Thus, the probability of a segment is computed as joint probability of the points from the segment
Here,
N is the number of points of the segment and
and
are the individual points from the segment. Taking into account the convergence property of an entire segment allows for inferring if a segment is converging to an attractor, even though the end-point of the segment may be far away from the attractor. Given a single data point
and its velocity vector
, the density function of a DND is defined as
Compared to a normal distribution, the DND also incorporates the direction of a data point, given by the velocity vector
. The scalar parameter
projects the point along its velocity vector. The idea is to choose the parameter so that the distance between the projection and the mean of the distribution becomes minimal. Hence, if a point
is moved along
for the duration
t, it reaches the minimum distance to
, under consideration of the uncertainty
. By rearranging (3), it can also be written as a normal distribution of
t
with normalization constant
. Due to the constraint
, we can assume that the posterior of
t is distributed to a truncated normal distribution
The equations for the variables
and
result from rearranging the exponential term in (3) such that it matches that of (5). In (5),
is the cumulative distribution function of a normal distribution with standard deviation one and mean zero. To avoid running into numerical issues, we set
to zero and
to one if the norm of the velocity is below a threshold. We would also like to point out that the projection parameter
t serves as a normalization constant for the velocity. For smaller velocities, the parameter will be larger, as only the direction of the velocity is considered. This property is beneficial for our purpose, as we are not interested in the velocity of a movement and do not have to preprocess the velocities. The joint probability of the data point and its projection is defined as
where we omitted the dependency of the joint probability on the parameters of the distribution. When learning the parameters of the distribution, we are not interested in the projection itself. Instead, we want to integrate it out, as it depends on the (unknown) parameters of the distribution. Given data
and
, the log-likelihood function is defined as
Here, we assumed that the values are independent of each other. We justify this assumption by the fact that given a fixed and , the ’s can be computed independently of each other. We would also like to point out that the individual points all come from a continuous trajectory with a continuously changing velocity vector . Therefore, the projections will automatically be close nearby for succeeding data points. To infer the parameters of our distribution, we want to maximize the log-likelihood function. The required integration over is intractable as the variables depend on the unknown parameters and . Therefore, we derive an Expectation-Maximization algorithm (EM) to get an iterative update scheme for the parameters.
3.1. Parameter Learning
In the context of the task-decomposition, the aim is to find the best attractor target for a given set of segments when learning the parameters of the distribution. As the probability is defined as the joint probability of the individual points from the segments, it does not matter if the parameters are learned for a single or multiple segments. Therefore, the notion of a segment is omitted in this section.
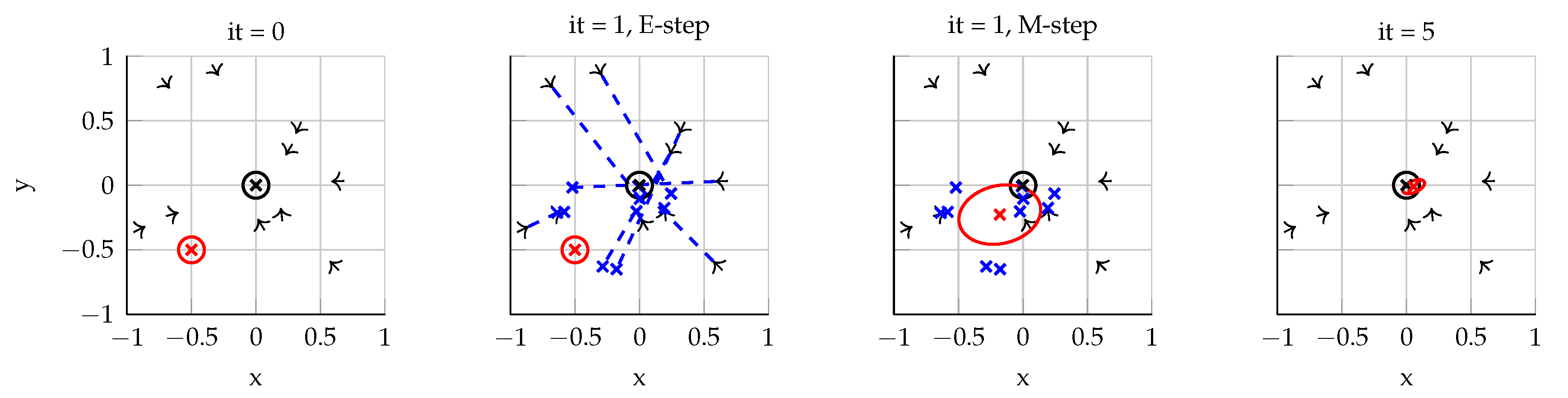
The principle of the EM algorithm is depicted in
Figure 3. In the Expectation step of the algorithm, we use the current parameter values
to estimate the posterior distribution of the latent variables
. Here,
is the concatenation of all projections. As the
’s are independent of each other, the estimation can be done for each data point separately as in (5). Intuitively, the E-step projects each data point as close as possible to the current mean of the distribution. In the Maximization step, we get new estimates for our parameters
by maximizing the expectation of the complete-data log-likelihood under the posterior of the latent variables with respect of the parameters
As the integral is evaluated for each data point separately, we omit the indices for the solution of the integral in the following. The integral evaluates to
The values of the constants can be found in
Appendix A. Please note that
are constants only for the integration, as they depend on the parameters
and
which we want to estimate. Upon evaluating this integral, the parameters can be obtained using (7). As the constants
to
depend on the parameters, we compute the derivatives of (8) with respect to
and
and set them to zero. Now we work again on the entire data set, so we will use the indices again.
Multiplying by
from the left and rearranging leads to the solution
Please note that the cumulative distribution function
is closely related to the error function erf by the relation
Therefore, the constants
and
could be further simplified. For instance,
equals one (proof skipped here) and so (9) can also be written as
For estimating the covariance matrix
, we compute the derivative with respect to its inverse
.
Rearranging then leads to the solution
In summary, the parameters of the distribution can be estimated iteratively by first computing the
c and
d constants for each data point according to
Appendix A (E-step). Second, a new estimate for the parameters of the distribution can be found by computing
and
according to (9) and (10) (M-step). The algorithm is summarized in Algorithm 1.
| Algorithm 1 EM-algorithm for DND | |
| Require: data , velocities , initial mean , initial cov | |
| 1 while not converged do | |
| 2 for all data points , do | ▹ Start E-step |
| 3 compute constants and (Appendix A) | |
| 4 end for | |
| 5 compute new mean (9) | ▹ Start M-step |
| 6 compute new covariance matrix (10) | |
| 7 end while | |
| 8 return mean , covariance matrix | |
3.2. Extension for Orientations
The Euclidean distance measure used in (3) is not suitable for 3D orientations. In this section, we show that by making some reasonable approximations, we can make our algorithm applicable also for orientations.
To be applicable, we have to define a projection
and a difference vector for orientations that can be written in the form
. We define the target orientation in the inertia frame with the rotation matrix
. The matrix
represents the start orientation rotated with the angle
t around the angular velocity axis. The rotation matrix is also given in the inertia frame. Hence, the projection parameter
t has a different meaning than for Euclidean task-spaces. Instead of projecting a position along its velocity vector, it rotates an orientation by an angle around the angular velocity axis. By writing the matrices as vectors
, we can define a difference vector with
Please note that the constants
,
and
are different from those derived before. The derivation can be found in
Appendix B. Now our difference vector can be written in the form
and we can estimate the target orientation with the same algorithm as in the previous section. Still, some details have to be taken care of. First, we approximated the sine and cosine terms with a first-order Taylor approximation around
. We therefore have to evaluate how good the approximation is. Second, the approximation introduced the parameter
and it is not clear how to choose it. Third, estimating the parameters of the distribution with our standard algorithm will result in a value for
which does not describe a proper orientation. Therefore, after applying our standard decomposition method, we reshape the target vector to a matrix and find the closest true rotation matrix to our matrix using [
45].
In the following, we introduce an intuitive way of choosing
. A natural way of measuring the difference between two orientations is the axis angle
of the relative transformation
The constants
are again different from those derived before, For the derivation, see
Appendix B.1. To project the current orientation as closely as possible to the target orientation, we compute the derivative of (12) with respect to
t and set it to zero
Hence, if we knew the target orientation without any uncertainty, we could compute a distance measure between the current orientation and the target in closed form. For the Taylor approximation, we can therefore make use of a trick. If we neglect the uncertainty , we can set the target orientation to the current estimate of the mean . Subsequently, we compute according to (13) and use it for the Taylor approximation . Therefore, we get a good approximation by developing the Taylor series about a value close to the true t. The approximation allows us to integrate orientations in our method in a straightforward way. Please note that we neglect the uncertainty about the target orientation only for the projection of the current orientation towards the current estimate of the target orientation. However, we still get an estimate of the uncertainty about the target rotation . We consider it future work to also integrate the uncertainty into the projection.
4. Movement Primitive Sequence Learning
The overall aim of our approach is learning a skill that has a reactive behavior. Instead of following a pre-computed path, the system is supposed to decide online when to stop a movement and which movement to start next. For a successful execution of a learned skill, the MPs have to be activated at the correct time points and in the correct order. The task-decomposition presented in the previous sections can be used for inferring when the teacher performed which point-to-point movement, but it is not a decision-making system which learns a reactive behavior. Hence, the task-decomposition method allows for inferring
when the teacher performed
which movement, but not
why. For answering this question, we use the sequence graph concept which was initially presented by Manschitz et al. [
2,
3]. In a sequence graph, a node corresponds to a MP. Each node is also associated with a local classifier. When executing a skill, one node in the graph is considered active and the associated classifier decides when to transition to a succeeding node, leading to the activation of another MP.
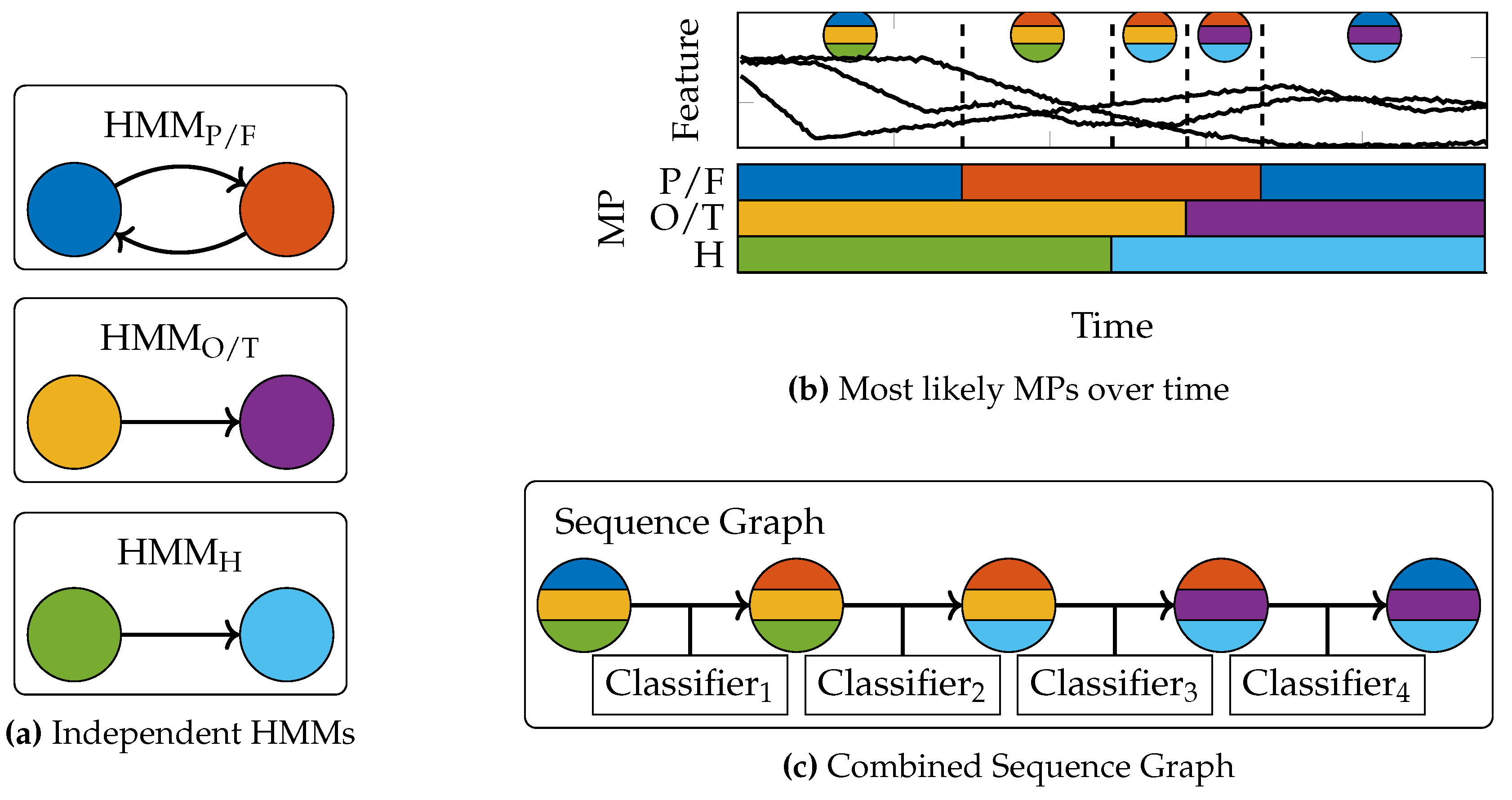
Applying our task-decomposition method to the demonstrations results in three independent sets of MPs, as the MPs controlling the position/force of the end-effector, its orientation and the joint angles of the fingers are learned independently of each other. For each set, we also get a HMM which reflects the potential sequential orderings of the MPs. While extracting the MPs of the three controlled entities independently of each other simplifies learning and leads to simple reusable MP, the MPs cannot be treated independently of each other when executing a skill on a real robot. For instance, the end-effector may only be allowed to move after an object has been grasped. Therefore, the decision when to execute which MP for one entity has to be conditioned on the state of the two other entities.
To account for the necessary synchronization of the MPs, we adapt the sequence graph concept for our purpose. Our system has to decide when to activate which of the MPs based on the current state of the robot and the state of the environment (e.g., current positions of objects in the scene). This decision has to be made based on the feature state , where is the dimension of the feature space. In theory, this feature state can be comprised of arbitrary values (e.g., camera input), but in this paper, it will be equivalent to the task-space data . Thus, it implicitly encodes the state of the robot in relation to all objects in the scene (including the forces) and contains the joint angles of the fingers as well as the measured forces.
To synchronize the activations of the MPs of the three different entities, we use a single sequence graph where the active node activates three MPs, one for each controlled entity. This process is depicted in
Figure 4. First, we use the HMMs resulting from the task-decomposition for labeling the demonstrations with the most likely MPs over time. From these labels, we generate the sequence graph representing the sequential structure of the MPs. Finally, we train the local classifiers for each node, where a classifier maps the feature state to three activation vectors
, one for each controlled entity. Therefore, when executing a learned skill on a robot, a transition leads to the activation of (up to) three new MPs. To train a classifier, each class is associated with the feature data that was recorded when the corresponding MP was considered active. For instance, the first classifier of the toy example in
Figure 4 has to decide when to transition to the second node in the graph. The feature data before the first dashed line in the feature plot is assigned to the preceding node, while the data between the first and second dashed line are assigned to the succeeding node. Based on these data, the classifier learns to discriminate both nodes. When executing the skill on the robot and the features reach a state which the classifier assigns to the succeeding node, the system will switch to this node and change the currently active MP. We use Logistic Regression for training, but in general any classifier can be used. Please note that there are also alternative more sophisticated ways to synchronize the sequences (e.g., generate three graphs and couple their transitions), but finding the best way to synchronize the controlled entities is beyond the scope of this paper.
5. Evaluation of the Approach
For evaluating our approach, we performed kinesthetic demonstrations on a gravity compensated seven degree of freedom (DoF) Barrett WAM robot with a four DOF hand. We performed three different tasks: box flipping, box stacking, and unscrewing a light bulb. For all tasks, we evaluate the decomposition and reproduction of the task. The purpose of the first task is to evaluate if our method is able to distinguish between position and force control. For the box stacking task, the focus is on finding the correct coordinate frames. The light bulb unscrewing task is a longer and more complex task which requires both, i.e., motions relative to multiple objects as well as force and position control. For the box stacking task, we also compare our decomposition method to a baseline method and two state-of-the-art methods.
All demonstrations for the experiments were performed by the same teacher which was one of the authors. The target of this paper is to evaluate whether our method can in principle be used for learning sequential skills from human demonstrations. We consider it future work to train the system on data from more users with different levels of experience. Please also note that it is hard to define evaluation metrics for learning from demonstration methods such as ours. Often, a system either can perform a task (resulting in success rate for this task) or fails completely. Therefore, we rather provide a qualitative comparison between our method and other state-of-the-art methods.
For simplicity, we predefined the MPs controlling the fingers of the robot for all tasks, despite that teaching grasps is possible with our approach. During the demonstrations, we activated these MPs manually by pressing a key on a keyboard. Please note that we predefined the MPs only for simplifying the teaching process. We still applied our task-decomposition to the resulting finger joint angles data. The kinesthetic demonstration data was recorded with 200Hz. As the force-torque measurements are quite noisy, we filtered the data using a Hann filter with a window size of 100. Due to the noisy force sensor and the different units (Newton vs. meters), the force data was additionally scaled by the factor 1/40, so that 4 N difference correspond to a position difference of 10 cm. For all experiments, force was chosen as the control variable for a dimension of a task-space if the target force was above the threshold of 2.5 N and the effector was not moving. An effector was considered to be not moving if the average velocity was below the threshold of
m/s (see
Section 2.3).
5.1. Box Flipping
For the box flipping task, the sequence of subtasks demonstrated by the teacher is shown in
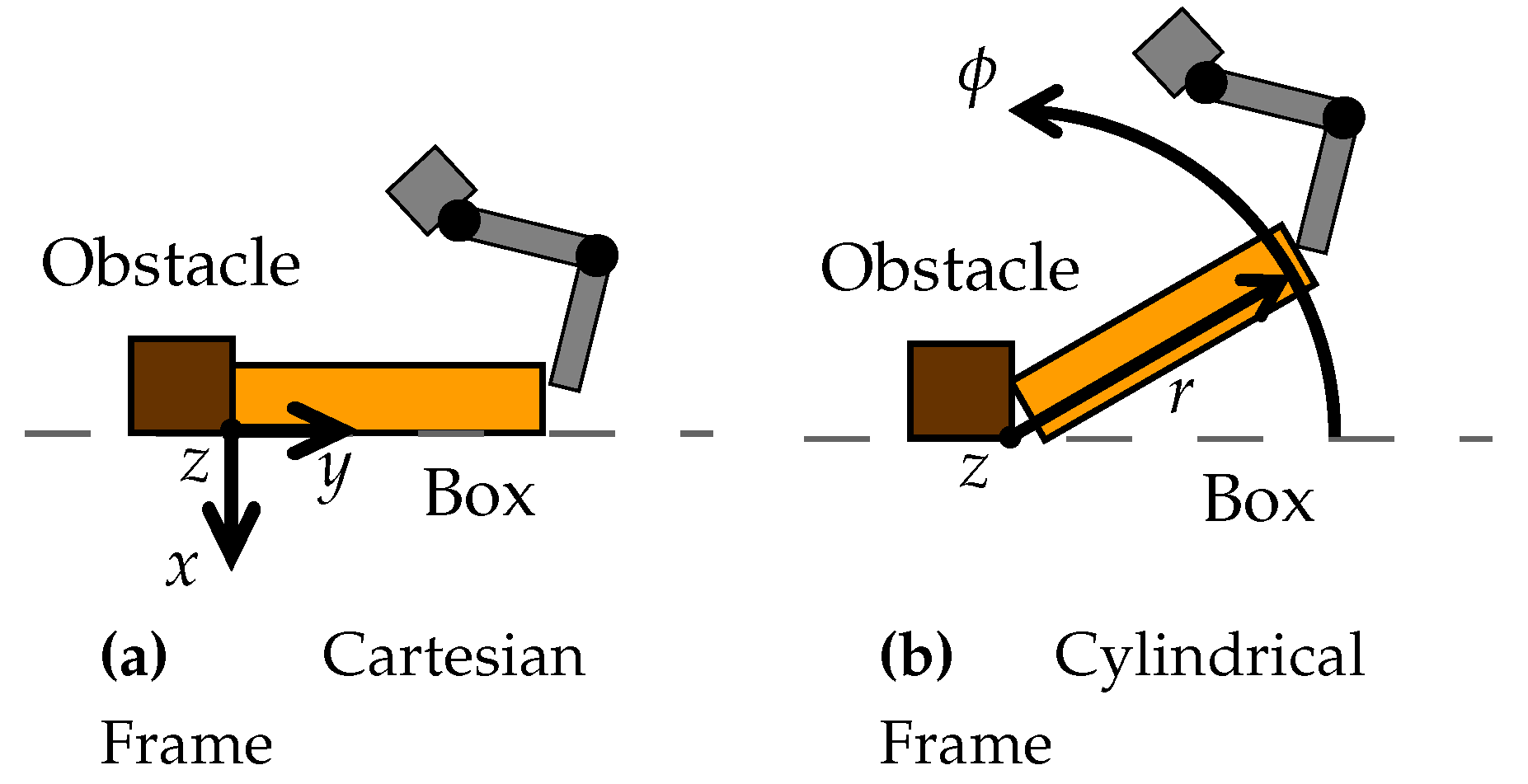
Figure 5. To flip the box, the teacher first pushed it against the obstacle. Then, he flipped it by pushing the box against the obstacle while rotating it. We demonstrated the task five times with slightly varying starting positions of the box. Two coordinate frames were defined for the task-decomposition, relative to the obstacle. A Cartesian frame and a cylindrical coordinate frame whose axis was aligned with the long side of the obstacle, as shown in
Figure 6. Kober et al. [
36] evaluated their approach on a similar box flipping task. They also used a cylindrical coordinate frame because it works very well for rotatory movements such as opening a door. Additionally, they stated that it is very robust with respect to inaccuracies in the rotation axis which is important when using force control. In contrast to their approach, we did not have to align the demonstrations in time to decompose the task. The orientation of the end-effector and the fingers were held constant throughout the demonstrations and are therefore neglected here.
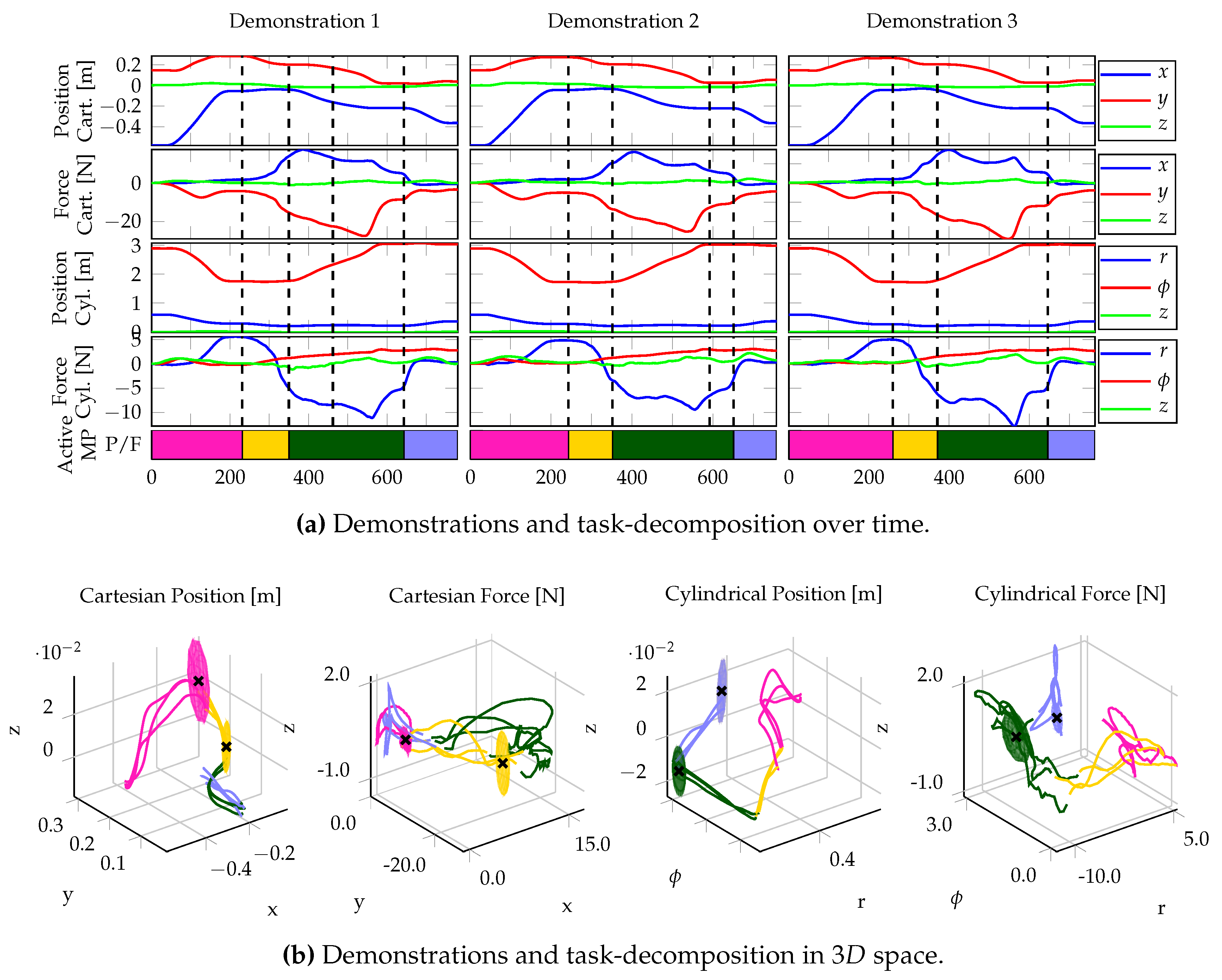
Our task-decomposition algorithm resulted in four MPs. Three of the five demonstrations and the corresponding results are depicted in
Figure 7. The results show that the decomposition is consistent over all demonstrations, even though the demonstrations are slightly over-segmented. The MPs closely resemble the behavior of the teacher (see
Table 2). Initially, the
●-MP approaches the box. Subsequently, the
●-MP pushes the object against the box. Then, the
●-MP flips the box and the
●-MP moves the end-effector to its final position. For the first two MPs, the algorithm chose the Cartesian frame, while for the latter two, it chose the Cylindrical frame. The frame choices can be better understood when looking at the demonstrations plotted spatially (see
Figure 7b). The box flipping resulted in a (green) curved line in Cartesian space and a straight line in the cylindrical space, which is why the algorithm choose the cylindrical frame for the
●-MP. For the remainder of the task, the teacher tried to move the end-effector in a straight line. Still, the algorithm chose the cylindrical frame for the final
●-MP. As shown in the plots, the final position slightly varied over the demonstrations and the teacher did not really move the end-effector in a straight line. The low confidence of 51.5% shows that the demonstrations seem to converge slightly better to a desired attractor target in the Cylindrical coordinate frame.
Only for the box flipping MP (●), the algorithm chose force control for one dimension of the coordinate frame. The reason is that while this MP was active, the radial distance to the origin of the coordinate frame was constant and hence the corresponding task coordinates did not change. As the target force of the MP along the radial axis of the coordinate frame exceeded the predefined threshold of 2.5 N and no velocity was measured, force control was chosen for this dimension of the task-space.
After decomposing the task and learning to sequence the MPs, the learned skill was successfully reproduced on the real robot. The found MPs were sufficient to perform the necessary movements and the transitions between MPs were triggered at the correct states. For the sequence learning, the following features were used: The end-effector position in the cylindrical frame and the Cartesian frame as well as the data from the force sensor at the wrist of the robot.
5.2. Box Stacking
The goal of the second task is to stack four boxes on top of each other. Position and orientation of the boxes are tracked with Augmented Reality (AR) markers using the ArUco library [
46]. We performed three demonstrations of the task. For each demonstration, the initial positions and orientations of the boxes were chosen randomly. The stacking sequence was the same for all demonstrations. First, the green box was put on the yellow box. Then, the red box was put on the green box and finally, the blue box was put on the red box.
Figure 8 shows a demonstration of the task. For a successful stacking of the boxes, it is important that all MPs use the correct coordinate frames. The task does not require any force control and therefore the force data is omitted here.
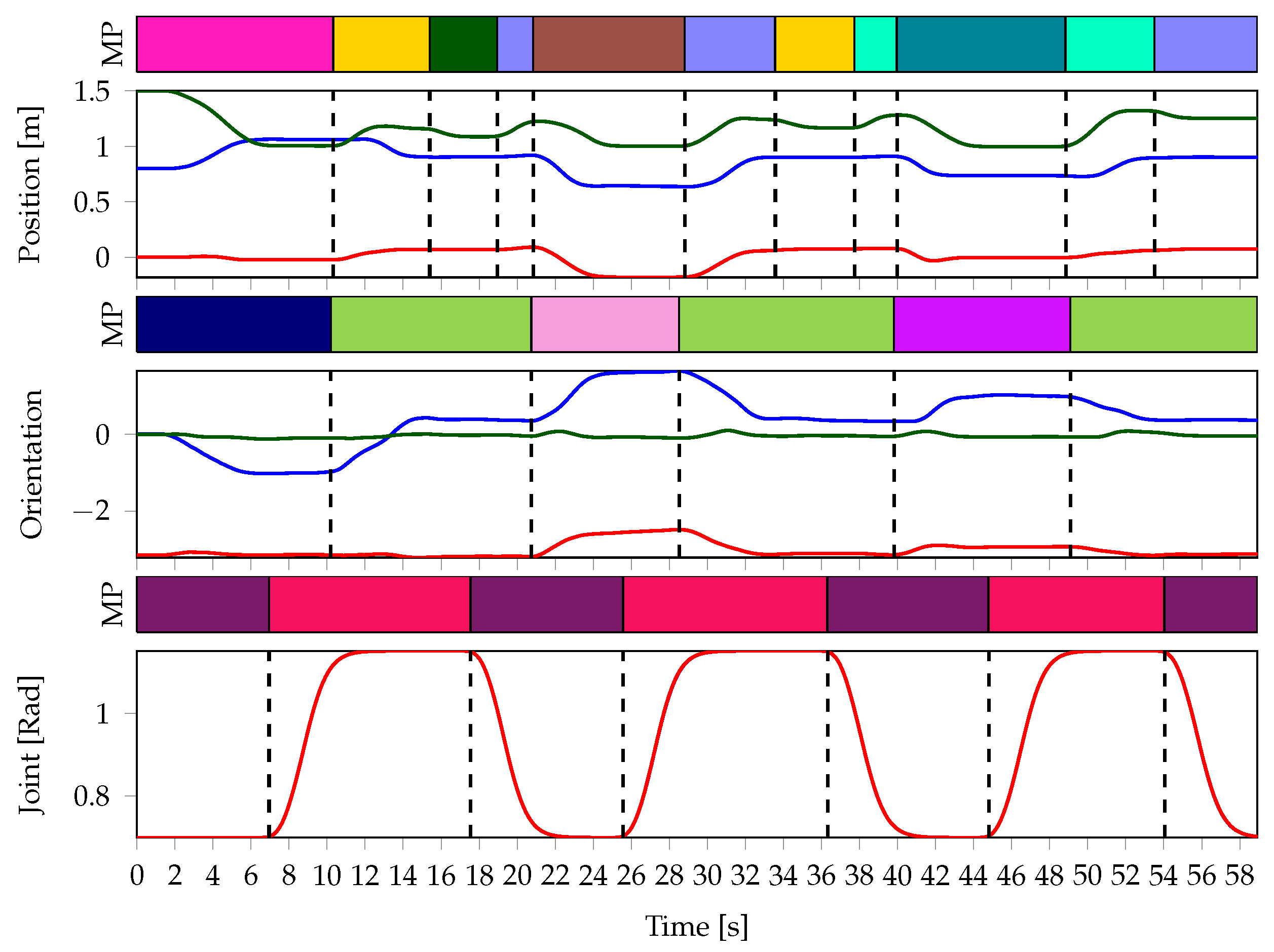
As an example,
Figure 9 depicts the data of one demonstration and the corresponding sequence of most likely MP activations. In total, our algorithm extracted seven position MPs, four orientation MPs and the two hand MPs corresponding to the ones we defined for grasping and opening the fingers. The MPs can be described as follows. In the beginning, the end-effector approaches the green box (
●) with opened fingers (
●). During this phase, the orientation is also controlled relative to the green box. After grasping the box (
●), the end-effector is moved to a position above of the yellow box (
●), with the orientation also aligned to the yellow box. Subsequently, it is lowered a few centimeters (
●) and the box is released. To avoid overturning the box stack, the end-effector is then moved up again (
●) before moving on to the next box. This scheme is continued until the task is complete. Three of the seven position MPs approach the different boxes that are supposed to be stacked on the yellow box. The remaining four MPs all represent positions above of the yellow box with different heights. The different heights result from the growing size of the box stack and are consistent with the data.
For the box stacking task, we also compared our method against three other approaches. As baseline, we clustered the end-points of the segments using a HMM with GMMs as state emissions. Thus, in contrast to our approach, this approach does not take into account the entire segment and its direction. The second approach is the TP-GMM, introduced by Calinon et al. [
47] and for instance used by Rozo et al. [
26]. The TP-GMM is a hierarchical Gaussian Mixture Model with two layers. On the higher layer, each mixture represent an MP. On the lower layer, the mixtures represent the trajectory in the different task-spaces. The main difference to our approach is the semantic of an MP. While in our approach an MP describes a goal-directed movement, the TP-GMM models a joint distribution of the position and velocities. By conditioning on the current position, the model can also be used to generate desired velocities, allowing the model to be used for the reproduction directly. The third approach is the BP-AR-HMM used by Niekum et al. [
25] for decomposing a task into a set of MPs. Their approach uses the Beta-Process Autoregressive HMM for segmenting the demonstrations in the world frame. After training, they cluster the end-points of all segments assigned to a single MP in each coordinate frame. The cluster with the minimum variance is chosen as coordinate frame for the MP. In contrast to our approach, the baseline and the TP-GMM, the authors first segment the demonstrations in the world frame and later assign coordinate frames to the resulting MPs.
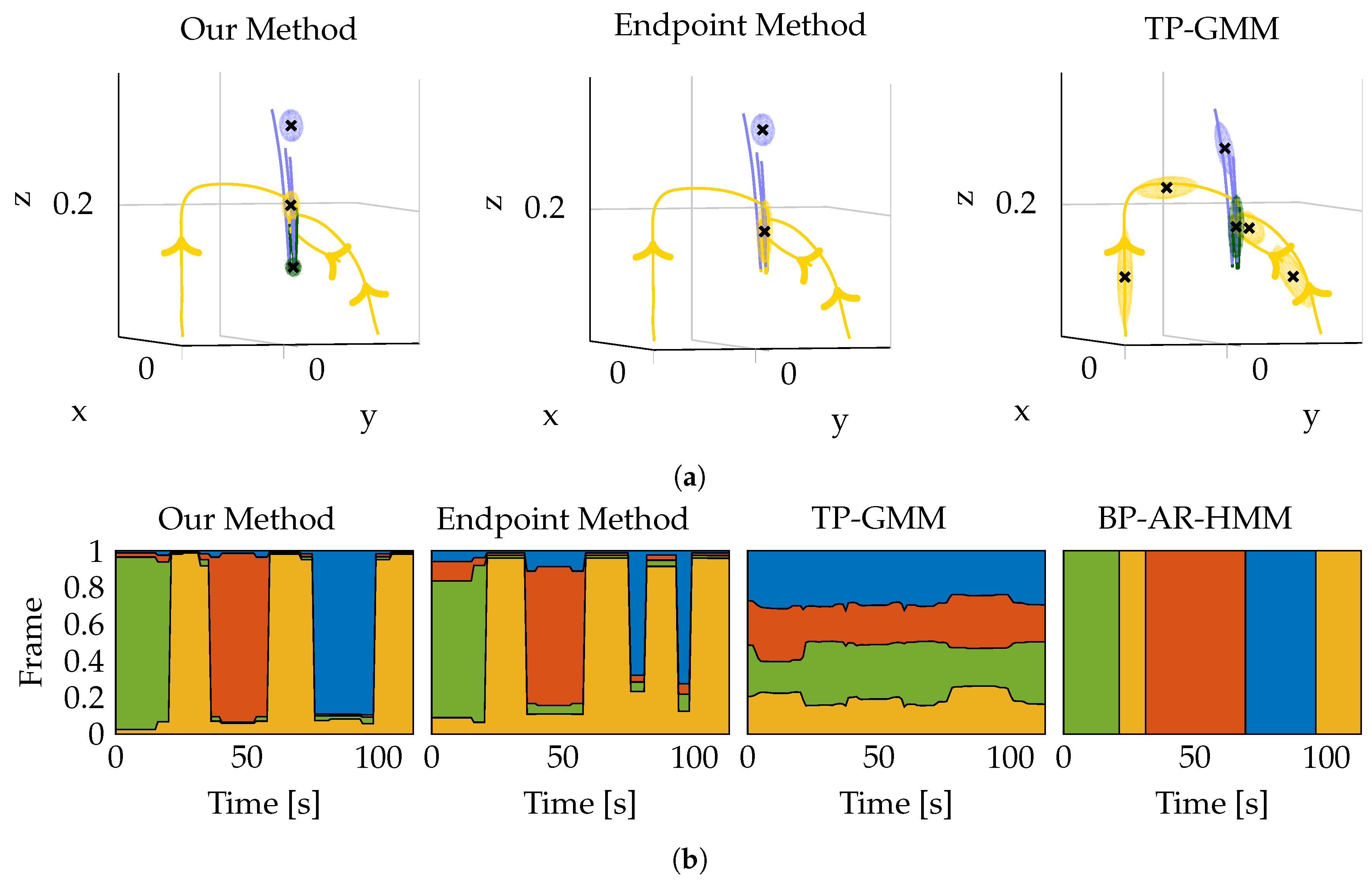
The decomposition resulted in a total of 13 MPs for our approach and the baseline approach, 9 MPs for the BP-AR-HMM and 65 MPs for the TP-GMM (for position, orientation and hand). The number of MPs for our approach, the baseline method and the TP-GMM has been determined using the Bayesian Information Criterion. For the BP-AR-HMM, we changed the hyperparameters of the method until we were satisfied with the results. A comparison of the resulting decompositions for all approaches is shown in
Figure 10. While our approach clearly discriminates the steps the teacher performed for stacking the boxes (e.g., align green box over yellow box before stacking), the baseline approach merges some of these steps to a single MP. Even though the resulting MPs are similar to the MPs of our approach, they cannot be used for reproducing the task properly. The green box will not be stacked on the yellow box, but will rather be released above the yellow box. In addition, it may not be aligned properly. The green box may land correctly on the yellow box, but success will be rather random. The results show that it is not sufficient to cluster the end-points of the segments, as it becomes harder to assign the proper coordinate frames to the different segments. By incorporating the convergence properties of the segments, our approach yields better results compared to the baseline approach. The TP-GMM results in significantly more MPs compared to our approach for two reasons. First, as it models the whole trajectory instead of only the attractor goals, more MPs are needed in general. Second, if for instance an object is approached from two different directions, the two trajectories will be very different (even in the coordinate frame of the object), but their target position will be the same. Therefore, our approach is able to model such movements with fewer MPs compared to the TP-GMM. While the TP-GMM has the advantage of being able to model arbitrarily non-linear trajectories, the coordinate frame assignments made by our model better resemble the natural structure of the demonstrated task (see
Figure 10b). We consider it future work to combine the advantages of both models. The BP-AR-HMM results in the fewest number of MPs. While the resulting coordinate frame assignments in
Figure 10b look promising at first, the phase where the red box is stacked on the yellow box is represented in the wrong coordinate frame. The reason is that the demonstrations are segmented in the world frame before assigning the coordinate frames to the individual MPs. As a result, segments which could be assigned to the same MP may be assigned to different MPs, as they are dissimilar in the world frame. Therefore, we believe that the coordinate frame assignment should be integrated into the segmentation process. We would also like to point out that none of the approaches chose the world frame for a task phase, which is a desired property for the box stacking task as all movements the teacher demonstrated were performed relative to one of the objects. Therefore, all approaches ignore the irrelevant world frame for the box stacking task.
As a proof of concept, we reproduced the task on the real robot on a setup that was not demonstrated to the robot (see
Figure 8). The reproduction showed that the robot can reproduce the task correctly. All MPs are represented in the correct coordinate frame and sequenced in the correct order. The boxes were successfully stacked on top of each other, even though they were not stacked as accurately as in the demonstrations. Most likely, the reason for the small displacement (approx. 0.5 cm to 1.0 cm) was due to the imprecision of the Kinect sensor used for tracking the objects.
5.3. Light Bulb Unscrewing
For the unscrewing task, the human teacher demonstrated the following sequence of subtasks. First, he approached the light bulb with the end-effector. Subsequently, the robot’s hand was closed. Next, the teacher rotated the wrist of the robot arm and unscrewed the bulb. During this movement, he also pulled the light bulb (by applying a force along the
z-axis), to test whether it is still in its holder. After turning the light bulb, the fingers were opened and the wrist was rotated back. This unscrewing cycle was repeated until the light bulb got loose. Next, the light bulb was pulled out of the holder and the end-effector was moved to a box where the hand was opened again. For the demonstrations, we put the light bulb holder and the box to three different positions and performed three kinesthetic demonstrations for each setup. The setups are depicted in
Figure 11. Two objects were tracked in the scene, the light bulb holder and the box.
Our method extracted nine MPs from the demonstrations, as shown in
Table 3. Four MPs control the position of the end-effector and one MP controls the position of the end-effector along the
x- and
y-axes, while applying a force along the
z-axis. Additionally, two MPs control the orientation of the end-effector and two MPs the finger configuration.
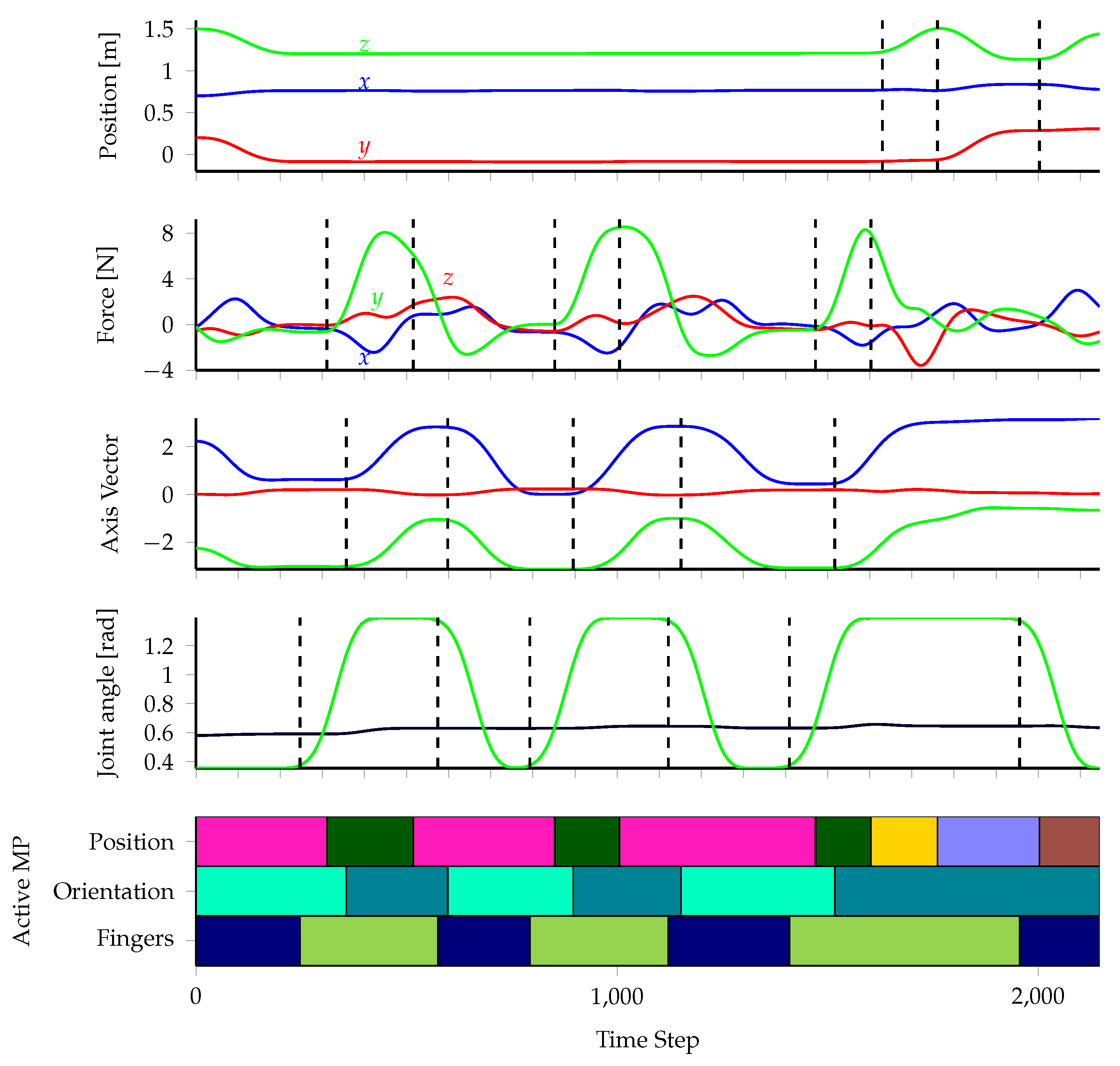
Figure 12 depicts the most likely MP for each point in time for one of the nine demonstrations. Except for small time gaps between changes of position, orientation and/or finger MPs, the MP sequences exactly reflect the subtask sequence the teacher performed and thus we can associate each MP with a meaningful description in
Table 3. Please note that the time gaps are not incorrect but instead reflect the behavior of the teacher. For instance, it is not possible to unscrew the bulb before closing the fingers. Therefore, the teacher usually waits for a short moment until he or she is sure the fingers are closed before starting to unscrew, causing the aforementioned time gaps in the data.
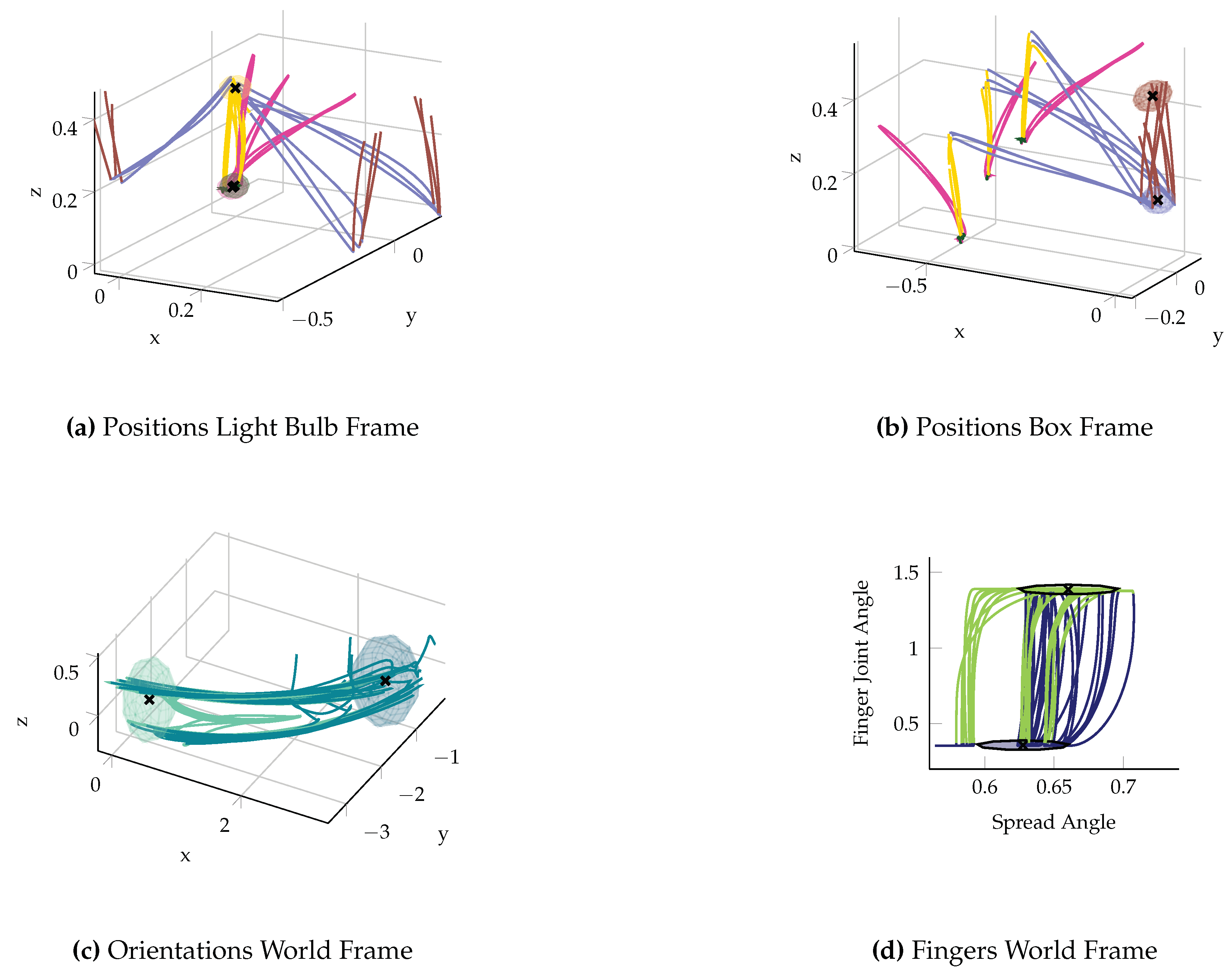
Even though the number of unscrewing repetitions varied over the demonstrations, all demonstrations were decomposed in a similar way. We illustrated this in
Figure 13, which shows all demonstrations spatially. As all subtasks performed by the teacher can be described relative to either the light bulb or the box, the world frame was not chosen for any MP controlling the position of the end-effector. During the demonstrations, the teacher was standing at a fixed position and aligned the orientations equally for all demonstrations. However, the objects and thus also their corresponding coordinate frames were rotated for the different setups. As a result, our algorithm chose the world frame for all orientation and finger configuration MPs.
For all position MPs, the resulting target forces are depicted in
Table 4. Only for the
●-MP the target force along the
z-axis is large enough so that the MP is force-controlled along this axis. The MP corresponds to the teacher pulling the light bulb while unscrewing. When reproducing the task, this force leads to an acceleration of the robot’s arm as soon as the light bulb gets loose, enabling the system to detect the loose bulb without any external sensors. The drawback is that we cannot detect whether the light bulb is still in the hand of the robot or if it slipped during reproduction.
For the reproduction of the task, we set the light bulb holder to five different positions and performed two trials for each position. In all ten trials, the robot was able to unscrew the light bulb and successfully put it in the container box.
5.4. Discussion of the Experiments
The experimental results show that our method segments the demonstrations properly and finds a meaningful decomposition for all tasks. The reproduction showed that our system can learn to perform the tasks successfully. Still, the method has some properties that need to be discussed and some limitations that need further research.
As already mentioned, we scaled the force data before training to compensate for the noisy sensor and the different units (Newton vs. meters). Additionally, the scale factor reflects an important issue occurring in kinesthetic demonstrations. While it is easy to guide a gravity compensated robot to a desired position, applying desired forces is difficult. For instance, in the light bulb task we tried to pull the bulb always with the same force. Still, the forces were roughly in a range of 5 to 15 N. Without scaling the force data, the method may incorrectly assign two pulling segments to different MPs, As they converge to very different force targets. We evaluated different scale factors and observed that the decomposition is the same for a broad range of values ( to yield the same results). Hence, there does not seem to be a need for fine-tuning the scale parameter for different tasks. Still, we state that from the force data of a kinesthetic demonstration, it is usually only clearly distinguishable whether the teacher wanted to push or pull in a certain direction or did not apply a force at all.
One limitation of the system is that the teacher has to know at least a little bit about the assumptions we make about the demonstrations. The teacher should be aware that he or she should pause between successive motions instead of co-articulating between them. The reason is that the decomposition relies on the segmentation, which uses ZVCs. Hence, no segments will be found if the end-effector does not stop between successive motions. Second, our MPs represent point-to-point motions in task-space. There is no need to move the end-effector in completely straight lines, but the teacher should at least roughly perform point-to-point motions. While this requirement seems to be very restrictive, a broad range of tasks can be performed using our framework. Still, we consider arbitrary trajectory shapes and co-articulation between successive motions interesting future research topics. An alternative to require the teacher to stop between successive motions would be to let the teacher tell the system about the transition points, such as proposed by Akgun et al. [
48].
6. Conclusions
We presented an approach for learning sequential force skills from kinesthetic demonstrations. To learn a skill, the approach decomposes the task into a set of MPs and learns to sequence them. The core of the decomposition method is the Directional Normal Distribution (DND). The probability distribution allows simultaneously determining the most likely sequence of MPs as well as their composition, i.e., their coordinate frames, control variables and target coordinates from the demonstrations. Determining the control variables allows distinguishing phases of force from position control, enabling a robot to explicitly apply forces only when needed. The resulting MP sequences resemble very closely the natural structure of the task. The evaluation showed that our method successfully learns to perform three different tasks from fewer than ten demonstrations. In future work, we plan to extend our MP framework and the decomposition method, such that we can learn more sophisticated tasks that for instance require to follow a desired force profile or arbitrarily shaped movements.