1. Introduction
Animals can adjust their motion to their environmental conditions. As typically observed in their locomotive behavior, they synchronize multiple periodic motions of the limbs and the body to each other, and make them adapt to the external force from the ground. This topic has long been discussed by biologists [
1,
2], including a well-known result showing that horses select a gait that is suitable for their speed [
3] in terms of energy consumption. On the other hand, in the field of robotics, adaptive motor coordination in animals still requires study.
An important keyword to discuss this topic is reflex. Reflex is an involuntary motor control, which is mainly used for relatively quick and simple motion tasks, while voluntary control is slower but suitable for complicated tasks. Research shows that this reflex control contributes to various quick adaptations. In particular, a classic study using decerebrated cats [
4] showed that the reflex control provides functions to adapt a muscle activity to changes in a load [
5] and stabilizes a gait pattern during walking [
6]. The reflex also contributes to human locomotions [
7], in terms of stability during standing [
8], walking [
9], and hopping [
10,
11,
12].
As an artificial scheme to generate rhythmic patterns, the idea of central pattern generators (CPGs) [
13] were proposed based on a model of neural circuits in the spinal cord. CPGs generate various locomotor patterns by designing a network connection between neuron modules.
Moreover, Owaki et al. [
14] proposed a simple decentralized control scheme that does not require any inter-neural communication. This controller allowed versatile gait transitions by exploiting a physical (non-neural) inter-limb interaction. This result suggests that physical interaction between the independent controllers through body dynamics is important for the generation of synchronized periodic motions.
When it comes to body physics, studies of a passive dynamic walker [
15,
16] demonstrated that the mechanical dynamics of the robot leg plays a large part in gait stability. A biped walker [
17] and passive quadrupeds [
18,
19] achieved gait transitions by only the body dynamics. Moreover, some results showed the functions of partial body dynamics for legged locomotion, including swing-leg retraction [
20], compliant legs [
21,
22], and torsos [
23]. Although the functions of partial body dynamics in animals were suggested in these studies, whole body dynamics is still entangled.
An alternative approach based on free vibration was taken in order to deal with whole body dynamics explicitly. Inspired by the experiment with horses [
3], a study [
24] suggested that there is a correspondence between the gaits of actual horses and the free vibration modes of a horse model. In this paradigm, some authors [
25,
26] proposed a methodology to control the whole body motion based on free vibration. Their robots had a simple elastic body and a vibration motor that achieves an energy-efficient hopping motion by exploiting the free vibration mode of the robot body.
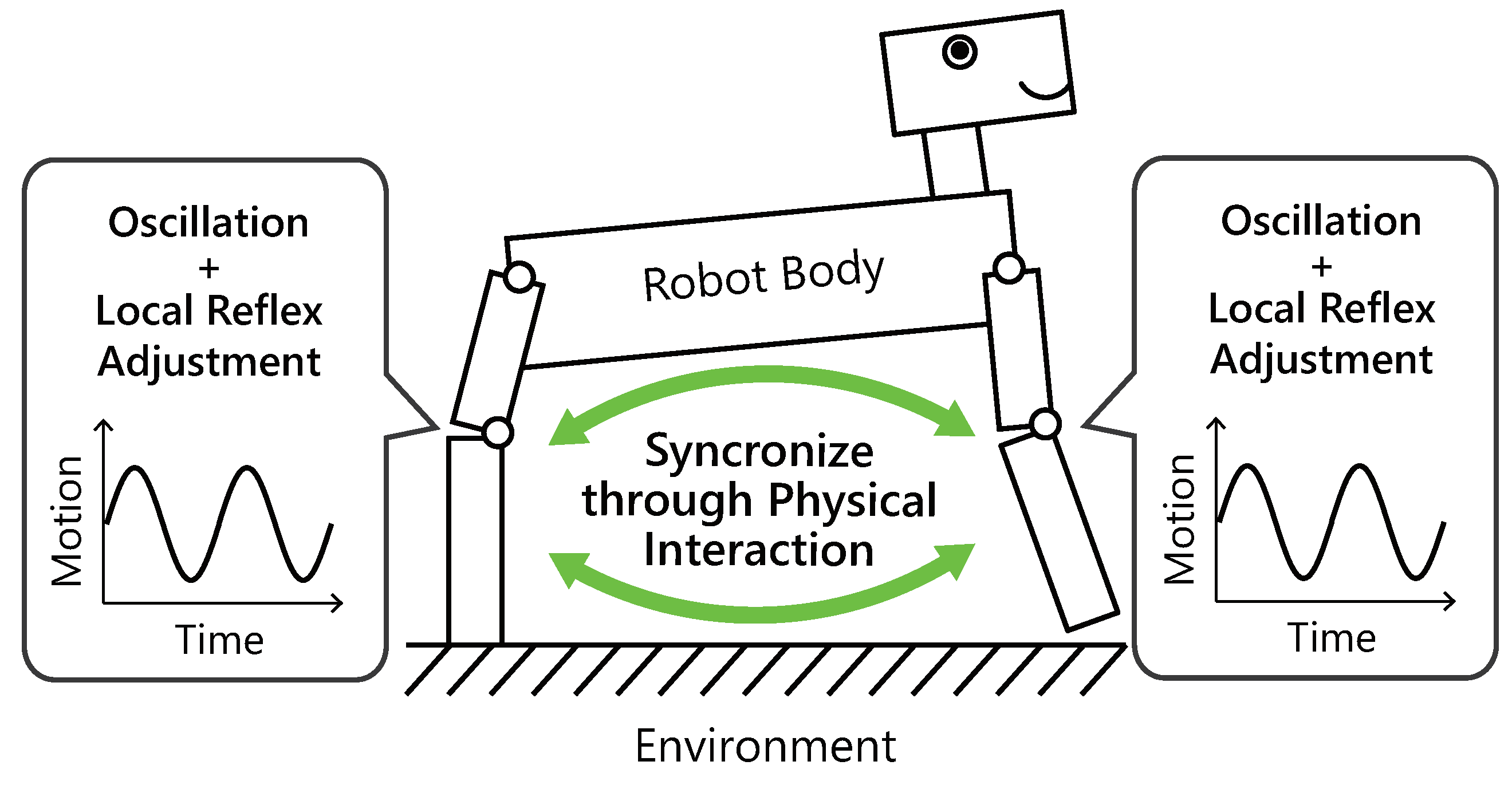
In this paper, we propose an extremely simple controller based on reflexes and investigate the controllers–body integration based on resonant oscillation. This paper shows that the simple controller can automatically generate versatile motion patterns, as animals do. In our approach, multiple controllers are decentralized in each part of the robot body as a control module. Each module is composed of an actuator part, which is modeled as a linear actuator with a spring–damper, and a controller part, which provides oscillation and a reflex function. If the controller module is subject to an external force from the robot body and environment, then the controller senses an internal force in the spring–damper, and it adjusts the natural length of the actuator part. This control strategy is based on the stretch reflex in animals that functions to maintain a current muscle length when the muscle senses internal force. To model this reflex function simply, the proposed controller maintains a current length of the linear actuator by delaying the oscillation speed according to the magnitude of the internal force in the actuator. This controller syncs the multiple controllers and the whole body dynamics with the resonant modes by only physical interaction. Moreover, by selecting a scalar parameter of the controllers, seamless transitions between the resonant modes are achieved. To evaluate this method, we conduct some simulations with linear and nonlinear systems, which interact with an external environment. The first simulation is with a linear spring–mass–damper system that has two reflex controllers, and the second is with a quadruped legged robot that is modeled in a sagittal plane [
27]. Finally, the simple controllers generate versatile gaits just by choosing a control parameter of “speeding up or down.”
2. Reflex Controller for Resonance Mode Excitation
This article describes an extremely simple controller to achieve the controllers–body integration based on resonant oscillation (
Figure 1). Let multiple controllers be decentralized in each part of the robot body as a control module.
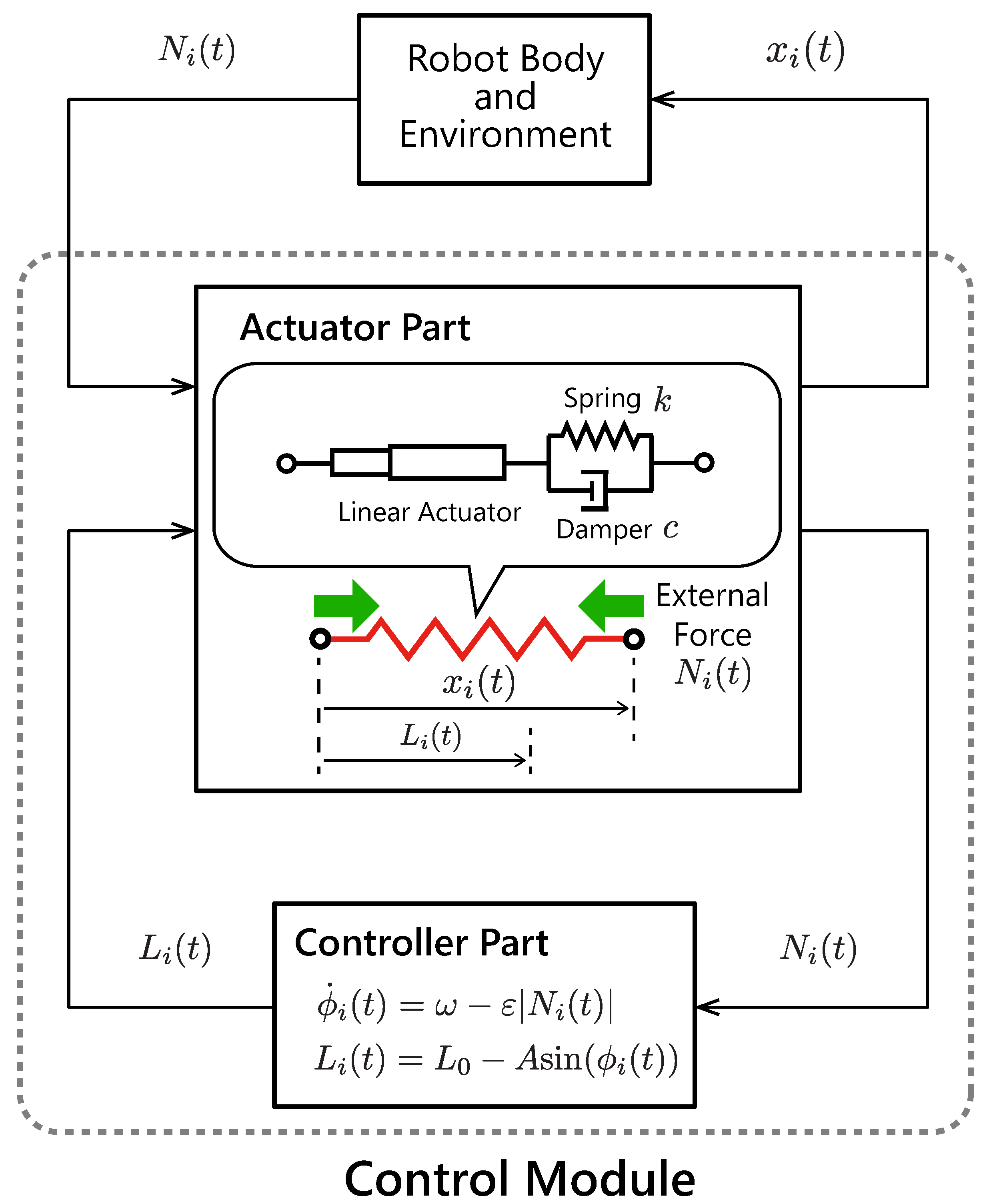
Figure 2 illustrates the structure of the proposed control module. Each module is composed of an actuator part, which is modeled as a linear actuator with a spring–damper, and a controller part, which provides oscillation and a reflex function. If the controller module is subjected to an external force from the robot body and environment, then the controller senses an internal force in the spring–damper and adjusts the natural length of the actuator part. This control strategy is based on the stretch reflex: a kind of involuntary control circuit in animals. When an animal muscle receives a force from the body or the external environment, the stretch reflex functions to maintain a current muscle length. To model this reflex function simply, the proposed controller maintains a current length of the linear actuator by delaying the oscillation speed according to the magnitude of the internal force in the actuator.
The proposed control strategy in the
i-th module is written as
where
is the phase of the
ith controller,
is the intrinsic angular velocity, and
is sensory gain.
is the internal force in the corresponding linear actuator.
Each linear actuator
i is modeled as a spring–damper, so the internal force
in the actuator and the actuator length
obey the following equation:
where
and
denote the viscoelastic constants. Each controller
i drives the natural length
of the actuator
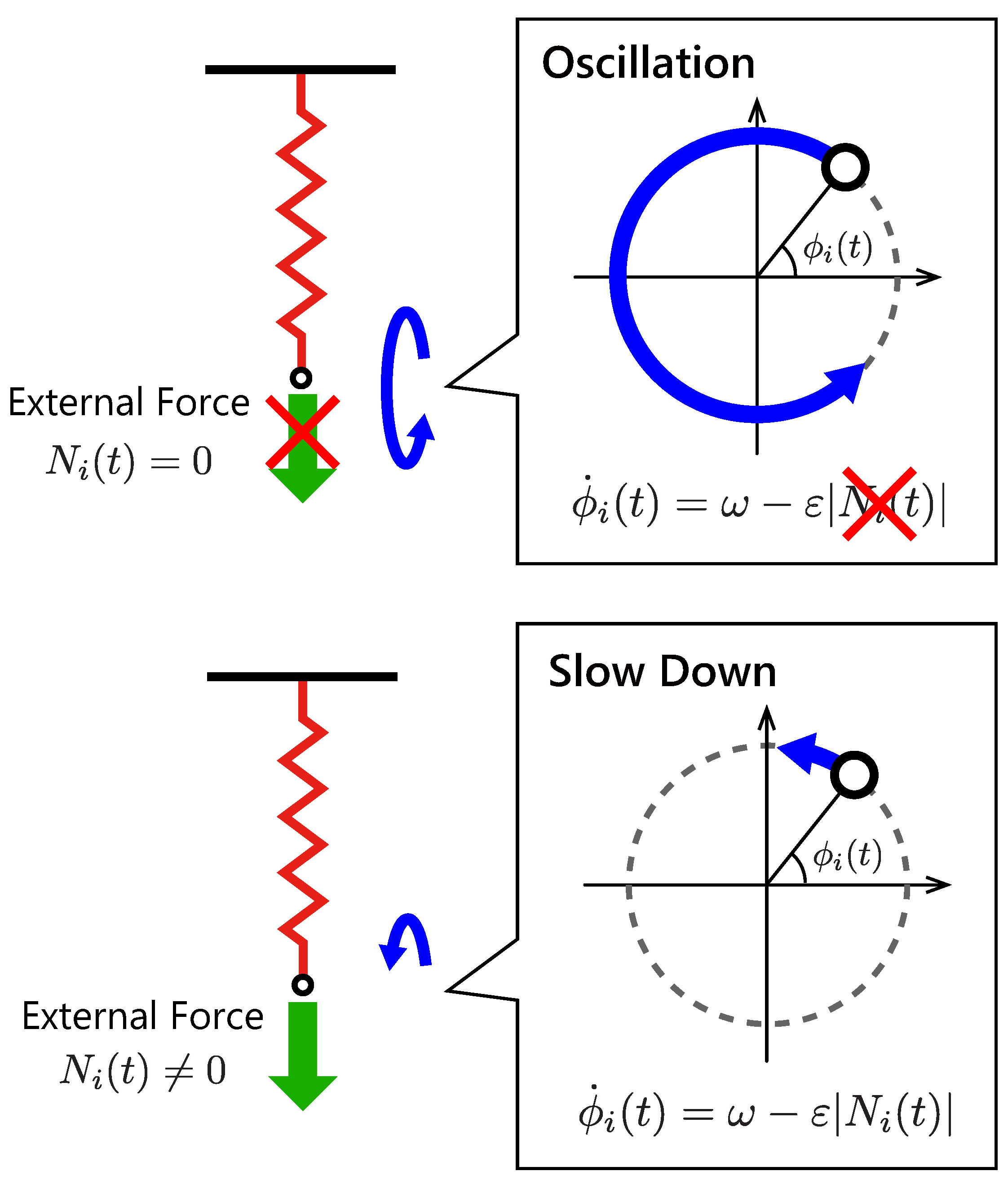
Figure 3 illustrates the feedback effect in the proposed controller. When the controller does not sense forces
, it oscillates the body in a constant frequency
by driving the linear actuator. If the controller senses a non-zero internal force
in the spring–damper, then the local feedback term
is activated, and it slows down the oscillation. To prevent the reverse rotation of the phase
, we determine the sensory gain so as to satisfy a condition
with an expected upper limit of the internal force
. In this paper, the expected upper limit of the internal force
was estimated through trial and error.
In other words, the proposed controller expressed by Equation (
1) delays the phases when there are unmatched forces to the actuator movement. As a result, the controllers converge on a steady state that decreases the unmatched forces in each actuator.
4. Gait Generation in Legged Robot Model
This section demonstrates some simulations with a simple legged robot model to evaluate the proposed controller.
The model of the robot is the simplified sagittal plane model for a quadruped robot [
27], which has two known resonant modes. We show that the simple robot model with two proposed control modules can generate versatile gaits that can be explained by resonant oscillation.
4.1. Model Formulation
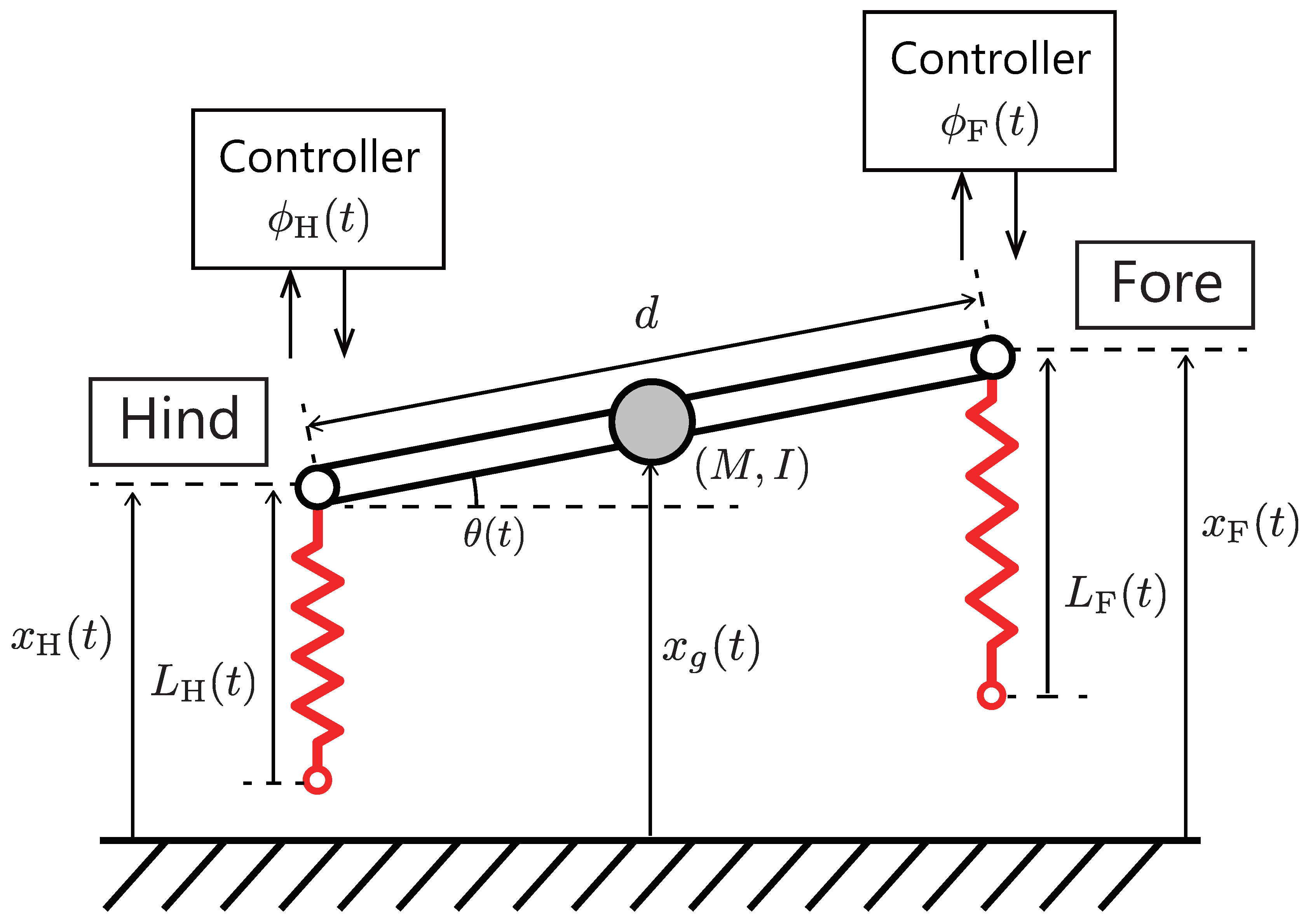
Figure 6 shows an overview of a simplified legged robot model moving on the vertical (sagittal) plane. We adopt a simple model that has two known resonant modes for a mode analysis as mentioned later. This model is based on the simplified sagittal plane model [
27], which can be considered as a quadruped robot model in two-dimensional space (side view). This model composed of fore and hind springy legs, and a rigid spine that joins these legs. Although the robot is quadruped, we assume that the motions of the left legs is mirrored to the right ones, and the legs are always perpendicular to the ground. The model is formulated as follows:
where
M and
I denotes the body mass and moment of inertia,
d is the body length, and
g is the gravity constant.
is the robot posture, and
is the position of the center of gravity.
and the hip heights
and
satisfy the following conditions:
The internal forces in the legs
and
are computed as follows:
where we assume that the viscoelastic parameters
k and
c are identical in each leg.
To describe the flight phase of legs, we defined a switching function
The natural length of fore and hind springy legs
are as follows:
The phases of the legs
are determined by two controllers as follows:
Here, we assume that the mass of the feet tip is sufficiently small. Thus, the internal forces and in each leg are zero when the corresponding leg leaves from the ground.
4.2. Resonance Frequency Analysis
In this section, we adopt a few assumptions for the resonant frequency analysis. We assume that the feet of the robot model are fixed on the ground, all of the natural lengths are equal (
), and the effect of the damper is sufficiently small. Assuming that the infinitesimal angle
, we have a linearized robot model around the origin
Let a new state variable
. Based on Equations (9) and (
19), the model in
Figure 4 is formulated as follows:
By using eigenvalue analysis of the state matrix of the model expressed by Equations (
20) and (
21), the resonant frequencies can be estimated as
where we assume that the rigid spine is a uniform rod (
). The frequency
corresponds to the pronk gait, the fore and hind legs are in an in-phase manner, and the
is the bound gait, the fore and hind legs are in an anti-phase manner.
4.3. Simulations of Resonance Mode Excitation
Finally, we show the simulations with the legged robot model.
The simulations are performed iteratively by changing the initial phase difference
and the intrinsic angular velocity
. We set the following parameters equal for all spring–dampers and actuators:
We set the initial states of each controller
and change
in
and
in
.
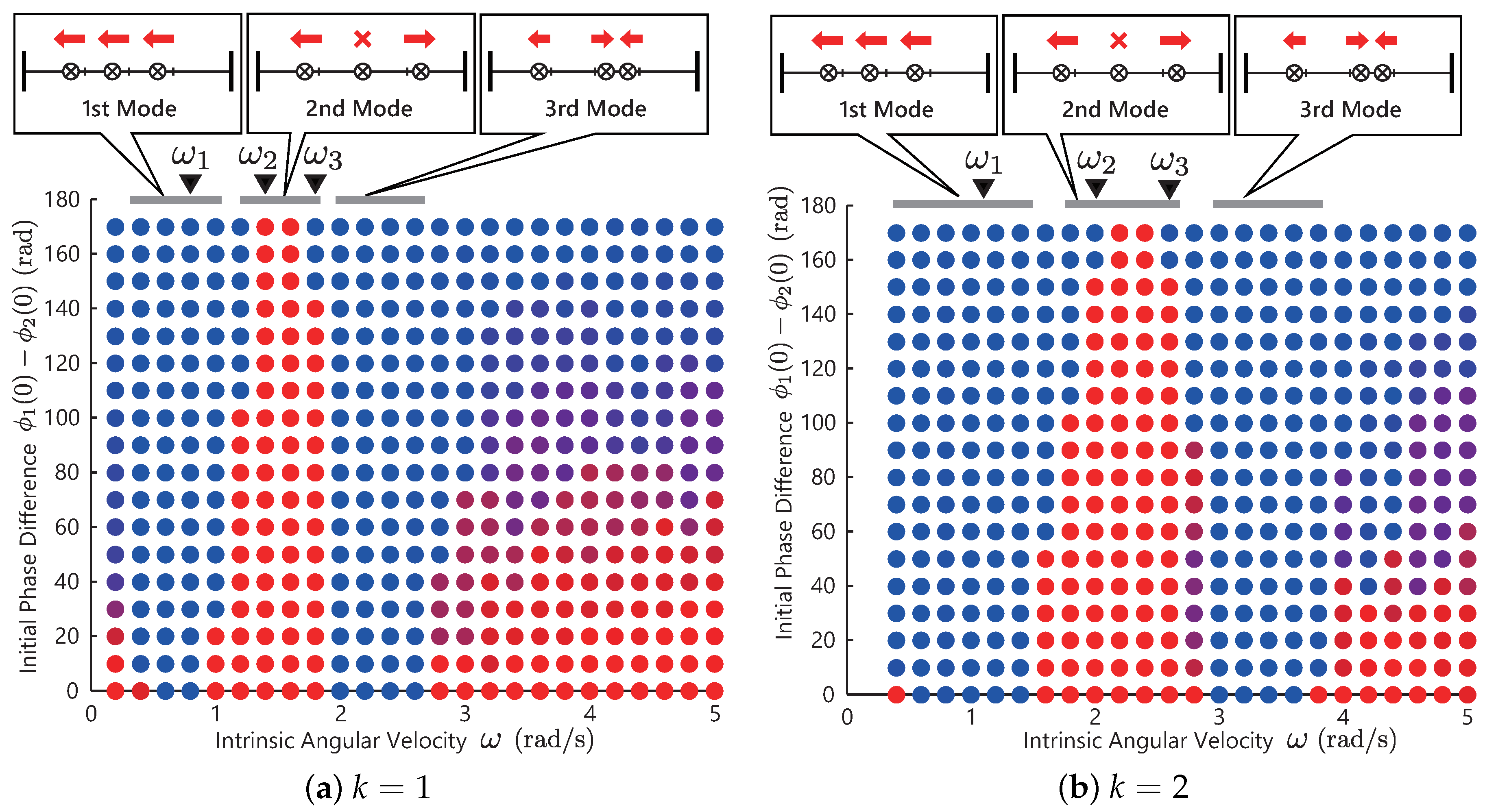
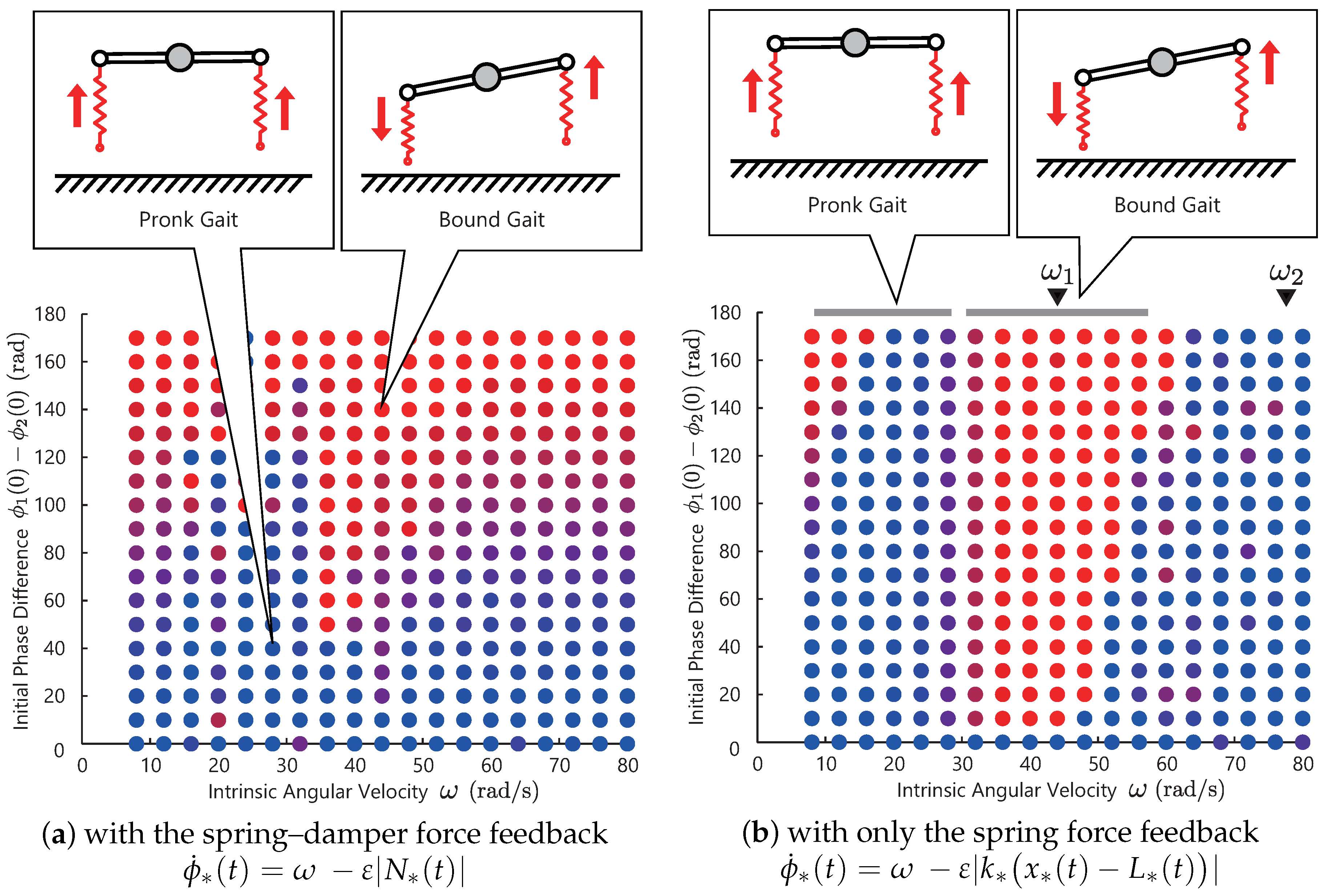
Figure 7a shows the simulation result. Similar to the previous simulations, the color of the bullet denotes the phase difference of the converged solutions of the two controllers. The blue bullet denotes the solutions that the two legs are in an in-phase manner, and the red bullet are the solutions in an anti-phase manner.
From this result, we observe that the resulting phase difference is sensitive to the choice of the initial values—not to the choice of the control parameter . This result means that there is no steady limit cycle or gaits. Now, let us consider selecting the motion pattern by choosing the control parameter and make it insensitive to the initial values (make the limit cycle steady). For this purpose, we propose a modification to the controller in the next subsection.
4.4. Modification to the Controller
Based on the result above, we apply an modification to the controllers. In this modification, we alter the sensory information (the spring–damper force in Equation (
18)) to the spring force as follows:
Although this modification was discovered by chance, some evidence in conventional research agrees with this result (see the discussion).
Figure 7b shows the result with the modified controller. The triangles at the top of graph indicates the resonant frequencies
and
that are analytically derived. Each solution converged to the resonant modes, as illustrated in the upper figure. As shown in these figures, the phase differences of converged solutions change as the intrinsic angular velocity
increases. From the upper figure, the in-phase gait is generated in
, and the anti-phase is generated in
. In other words, at around
, the following gait transition occurs:
4.5. Discussion of the Simulation
Based on
Figure 7a, when we use the spring–damper force feedback, we could not generate steady limit cycles. Based on
Figure 7b, the proposed controller achieved steady gait generation and transition automatically. However, at small frequencies
, the solutions depend on the initial values for the same reasons as
Figure 5. This model might explain the mechanism for the gait transition between the pronk and bound observed in gazelles.
By comparing these two results,
Figure 7a,b, in the legged model (a nonlinear system with the switching between the the swing and stance states), the spring force feedback is more effective than the spring–damper force feedback for steady gait generation. Although this modification was found heuristically, there is evidence in conventional research that agrees with our result. In biology, it is well known that the muscle spindle receptor, which contributes to the stretch reflex in animals, has two feedback pathways: one sends muscle displacement information, and the other one sends muscle velocity [
28]. Related to the function of the pathways, one study [
29] showed that the sensitivity of the muscle displacement was mainly activated during periodic motions in walking and running cats. In contrast, the receptor for the muscle velocity was deactivated during these periodic motions. Similar agreement was found in our recent study [
30]. In that study, we constructed a biological model of the stretch reflex circuit and confirmed that the sensory feedback of the muscle displacement generates resonant modes. These results suggest that the displacement feedback is effective in generating steady resonant modes.
Table 2 shows the resonant frequencies, which were analytically derived, and the excited frequencies in the simulations. There are large disagreements between the analytical and simulated frequencies: the simulated frequencies are almost half of the analytical ones. These disagreements are due to the modeling error based on the assumption that the feet of the robot model are fixed on the ground: the flight phase was not considered in the analysis. A similar phenomenon has also been reported in [
26].
5. Discussion
From the results above, an extremely simple controller based on reflex can automatically generate versatile motion patterns. This phenomenon can be explained by the controllers–body integration based on resonant oscillation.
The results in this paper provide a few suggestion for understanding animals’ motor function. First, the results suggest that the control from the upper central is not necessary required, and the physical interaction of the local reflex controllers are crucial to excite the periodic motions as resonant modes. Second, for generating the synchronized periodic motions, the muscle displacement information is more important than the muscle velocity information. The large amplitude motion at resonant modes helps to increase stride length. These results suggest that the simple and local reflex strategy in animals contribute a motion pattern generation by exploiting the physical interaction through the body dynamics.
Compared with a conventional controller [
14] that formulates as follows:
the proposal (
1) does not use any information of current phase
. Related to this approach, our conventional controller [
31], which uses the current phase
, also generates the various resonant modes. Although various experiments show that actual animals use the current phase information
during walking (reactions to ground reaction forces are changed according to the leg phase), this response is the behavior of whole systems, including neural circuits and inter-limb neural connection. The proposed method without the current phase information can explain the fundamental stabilization ability of the reflex strategy itself.
6. Conclusions
In this paper, we propose an extremely simple controller based on reflexes and investigate the controllers–body integration based on resonant oscillation. This paper shows that the simple controller can automatically generate versatile motion patterns, as animals do. This reflex controller syncs the multiple controllers and the whole body dynamics with the resonant modes by only physical interaction. In the simulations, the spring–mass–damper system shows an adaptability to changes in the vibration frequency and the body parameter. By selecting a frequency of the controller, seamless transitions between the resonant modes are achieved. In the legged robot model, we show a limitation of the proposed method due to the nonlinearity, and an alternative method to replace the sensory value with a spring force is proposed. Finally, the robot model with the simple controller generates the gazelles’ gaits just by choosing a control parameter of “speeding up or down.” This result suggest that the muscle displacement information is more important than the muscle velocity information for gait generation and resonant mode excitation.