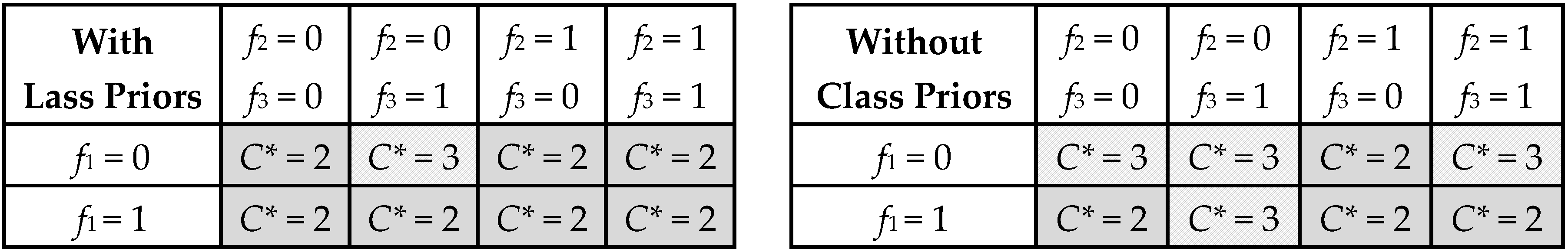Application of the Naive Bayes Classifier for Representation and Use of Heterogeneous and Incomplete Knowledge in Social Robotics
Abstract
:1. Introduction
1.1. Constraints in Learning during Interaction with Social Robots
1.2. Objectives of This Paper
- formalize empirical social behaviors into a dataset
- apply a learning technique to the dataset of correlations of features and actions
- make the robot actually learn socially appropriate actions through online adaptation
2. Methods
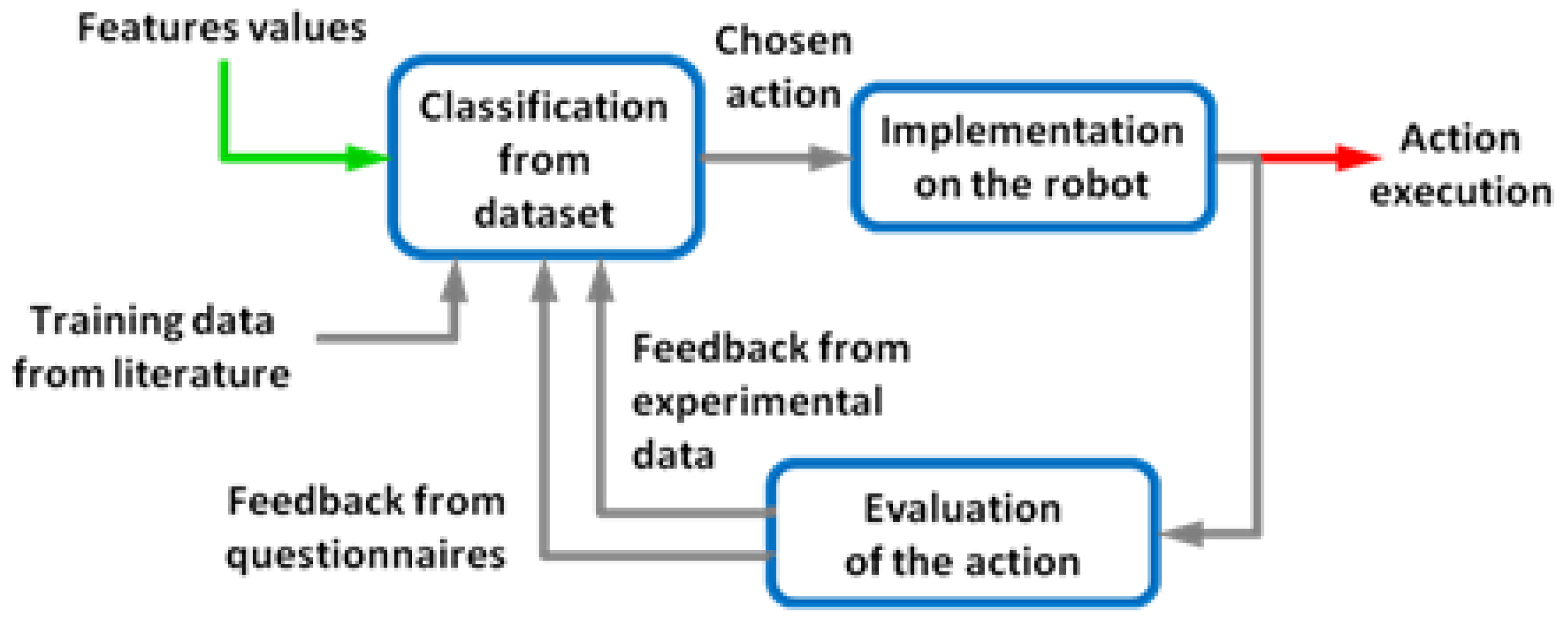
2.1. Generic Model
2.2. Classification of Training Data
2.2.1. Characteristics of Data
- Heterogeneous data types: some features (such as gender) are binary values; some other (such as age) are continuous but can be discretized; some others (such as nationality) are categorical and not ordinal. Classes also can be represented in percentages or as absolute values, and features may be associated with more than one class to different degrees. Baynesian networks have been used to synthesize the findings from these separate studies of sociology, biology and economics [20], and can be used for representing and predicting social behaviors [21]. However, they assume parent/child relations between variables, while in our problem we are assuming independence between class-condition feature probabilities.
- Incompleteness: studies are usually focused on a single or a couple of specific variables, whereas our model involves more variables. For example, a study with gender as a variable, may fix some variables (e.g., nationality of participants) while not specifying others (e.g., education level) which might be of interest. Missing data can make it difficult to use techniques for classification such as neural networks or to even just represent it in a space with principal component analysis. See [22] for a review of the problem from a statistical perspective.
- Set size: Small datasets limit the choice of training methods. Data from different sources can be integrated in order to expand the training dataset, but this will also cause the incompleteness problem stated above. In particular, when integrating human studies data with experimental data, we receive the data incrementally (rather than in batch). Online learning methods fit this kind of problem. Small experimental datasets have been used in modelling of complex processes successfully in [23], but the composition of the training datasets becomes critical, with designed sets performing better than random ones. Other learning models were compared for problems with small datasets in [24], where mixed results were found dependent on feature selection, and naive Bayes and its multinomial variation [25] were reported to outperform the others, including support vector machines, in many conditions.
2.2.2. Naive Bayes
2.3. Conversion of Heterogeneous Data into a Dataset
- (a)
- A percentage in which all (and only) the classes of our problem are considered (ideal).
- (b)
- A percentage in which one or more classes of our problem are not considered.
- (c)
- A percentage in which one of the classes (defined as “other”) may include the classes of our problem which are not specifically mentioned.
- (d)
- Absolute values of measurement without a known scale (e.g., “15 times”).
- (e)
- Absolute values of measurement, between a priori maximum and minimum values (e.g., “24 out of 30”). Likert scales and differential semantic scales fall into this category.
- Study 1: when feature 2 is 0, 55% of the population belongs to class CA and the rest to class CB, whereas when feature 2 is 1, the results change to 39% and 61%.
- Study 2: under different conditions (feature 1 = 1) and feature 3 fixed to 0, 50% of the population belongs to class CB, and the rest to classes CA and CC.
2.4. Customisation of Naive Bayes Formulas
2.4.1. Conditional Probability
2.4.2. Smoothing Technique
2.4.3. Incomplete Data
2.5. Adaptation through Rewards
2.6. Other Policies
2.6.1. Class Selection
- The set of features f* is not present in the dataset. In this case, naive Bayes is calculated.
- The set of features f* is already present in the dataset and the vector is associated with some weights. In this case, classification can be done either by:
- o
- using the current weights: generically speaking, in order for this option to be possible, data has to be consistent within all classes for f*, with missing data previously filled as explained in Section 2.3.
- o
- ignoring the current weights, and recalculating the probabilities through naive Bayes (leave-one-out cross-validation [33]).
- The simplest solution is to get the maximum value, as in the standard Equation (6) and Equation (7).
- Another possibility, which gives more emphasis to exploration, is to use a ε-greedy policy: with 0 < ε < 1, C* is the argmax with ε probability, and will be a random selection with 1 − ε probability.
- C* can be assigned any of the possible classes, with probability proportional to the list of weights. For example, in a weight vector <0.4, 0.2, 0.1, 0.3>, the first class would be selected with 0.4 probability.
2.6.2. Stopping Conditions
3. Results and Discussion
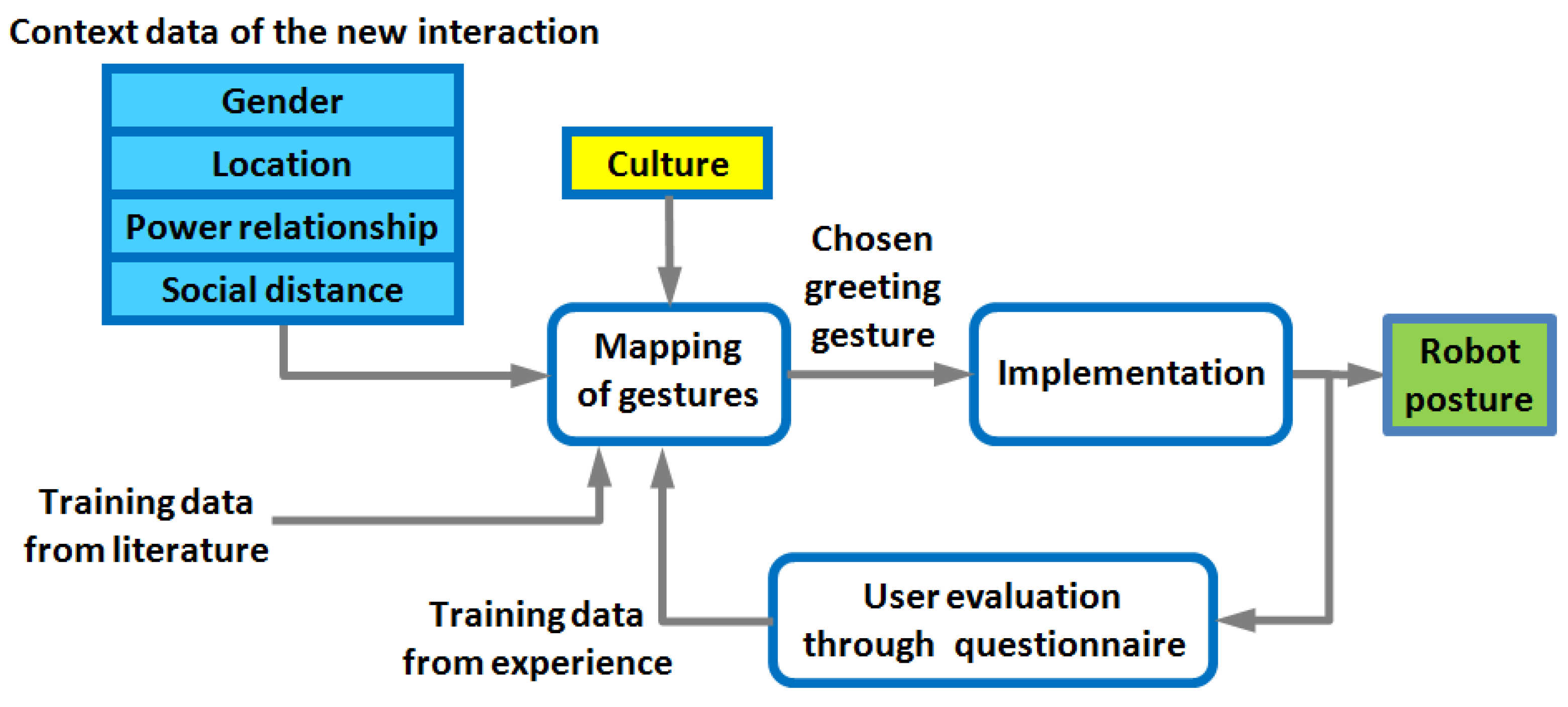
3.1. Application 1: Greeting Interaction
3.1.1. Purpose of the Study
3.1.2. Greeting Selection System
3.1.3. Rewards Calculation
- The dataset is built from training data: weights wj(f) corresponds to each vector added.
- Whenever a new feature vector f* is given as input, it is checked whether it is already contained in the dataset or not. In the former case, the weights are directly read from the dataset and the greeting corresponding to the highest weight is selected; in the latter case, classification is calculated through naive Bayes.
- In the naive Bayes classifier, the best greeting g* chooses the greeting gj that has the highest probability, calculated from its weights wi, using the add-ε smoothing technique and a multiplier δ, as in Equation (10).
- Once the greeting is chosen, the resulting probabilities are normalized. The stopping condition is then calculated as in Equations (13) and (14). If all conditions are satisfied, no updating will be performed, as the mapping has already been stabilized.
- Otherwise, the next step consists of getting the evaluation from the participant for the current selected greeting g*, whether appropriate or not according to the participant’s culture, to the current context f*. On a scale from 1 to 5, if it is greater than 3, the weight of that greeting for the present context is multiplied by a positive reward. If less than 3, is it multiplied by a negative reward; if it is exactly 3, nothing is done. All vectors f start with a counter s set to 0, and every time one vector is processed, its counter increases and makes the learning factor decrease, dampening the magnitude of the rewards.
- If the evaluation is less than or equal to 3, the participant is also asked to indicate which greeting type instead would have been appropriate in this context f*. The weight of that greeting g** is boosted.
- The participant is finally asked to indicate, for the chosen greeting type g*, which context f** would have sounded appropriate. If there is any, the weights corresponding to f** are updated with a boost for the current greeting; otherwise, if g* is judged inappropriate in any case, all the weights receive a negative reward. The vector f** is added to the dataset if new, or updated if already existing.
- All the new weights in the dataset are normalized (the sum of all probabilities of greeting types for a single context combination has to be 1). At this point, the algorithm is ready for a new input, and goes back to step 1. The next time that the input feature vector is the same as the one just added, the weights will be directly used (step 2 instead of 3).
| K | Number of samples in the dataset | i = 1 … I | Index of features |
| k = 1 … K | k-th sample <f, gj> in the dataset | f | Feature input vector |
| G | Set of greetings (classes) | fi | i-th feature of f |
| J = 5 | Number of possible greeting choices | f (k) | k-th feature vector in the dataset |
| j = 1 … J | Index of greetings | f * | Feature vector selected by the classifier |
| gj | j-th greeting in G | f ** | Feature vector suggested by the participant to match g* |
| g(k) | Greeting at the k-th element in the dataset | v | Value that can be taken by a feature fi |
| g* | Greeting chosen by the classifier | wj (f) | Weight of the gesture j for the feature vector f |
| g** | Greeting chosen by the participant in case g* receives a low score | m = 2 | Equivalent sample size of m-estimate formula |
| I = 4 | Number of input features | p = 1/J | Uniform prior estimation of the probability |
| s | Counter of visits of the current f* | r ={1, 0.5, 0, −0.5, −1} | Reward factor, depending on the evaluation of the user |
| l =exp(–s/4) | Learning factor. High (around 0.8) at the beginning and decreases following the e-x curve | S | Stopping conditions as in Equations (13) and (14), with W = 10 and q = 2/σTOT |
| δ(k) = {1, 0.2, 0} | Multiplier for incomplete data, as in Equation (11). Set empiricallylow in case of undefined fi, due to the high quantity of incomplete training data | ||
3.1.4. Experiment Results and Validation
3.2. Application 2: Attracting Attention
3.2.1. Purpose of the Study
3.2.2. Experiment Design
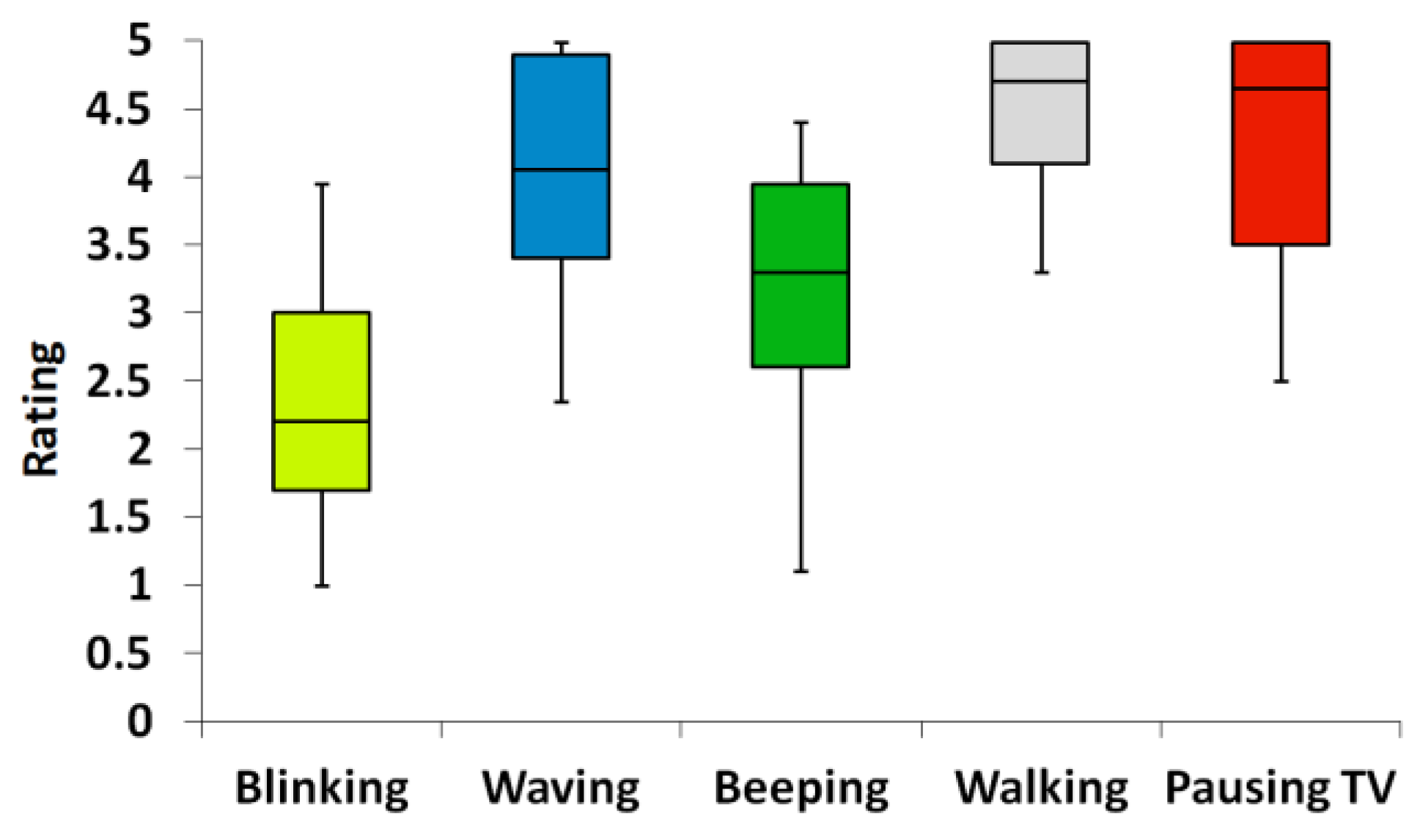
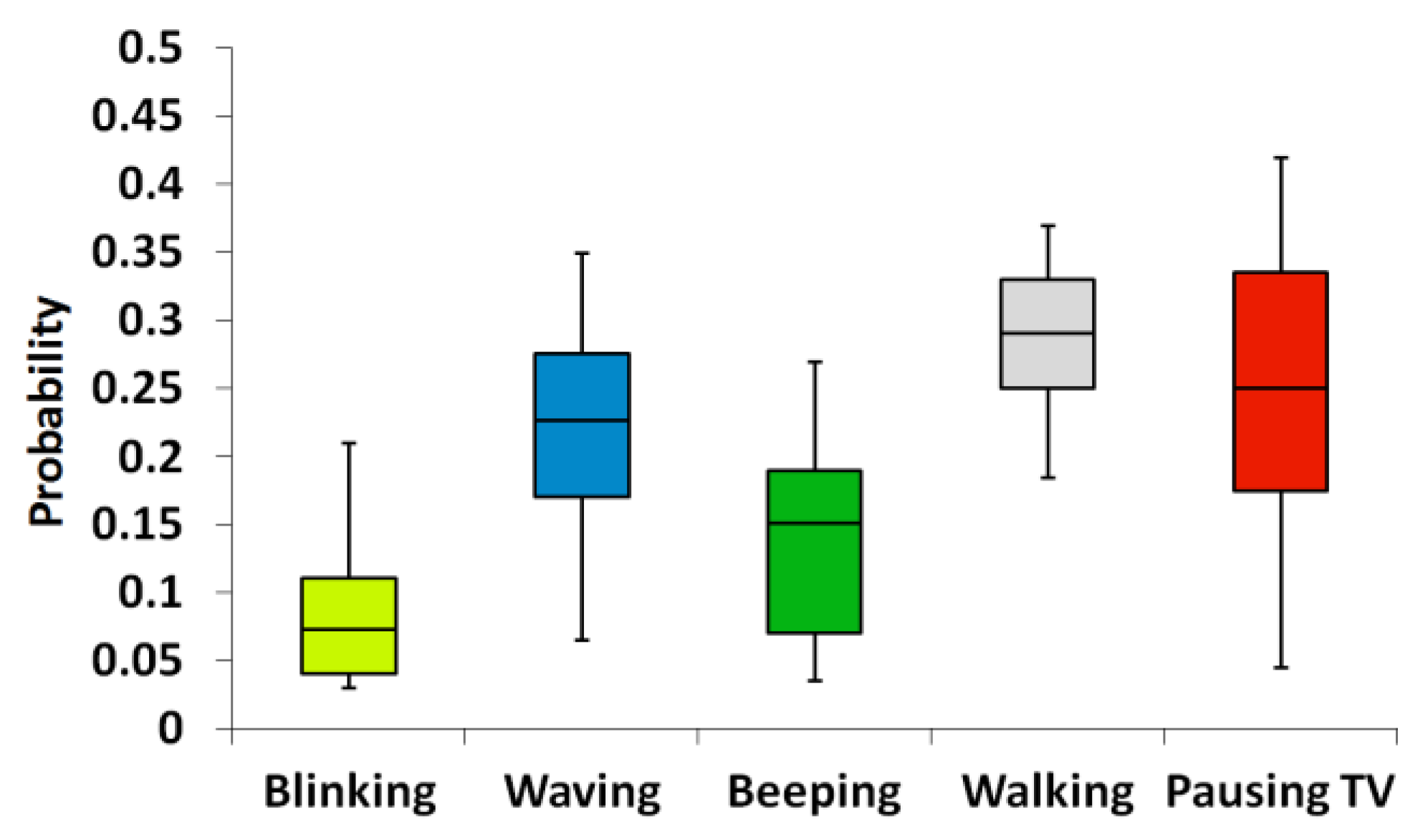
- Features and classes: the room conditions and possible behaviors listed in Table 8 refer to the first session. As all the features are binary, the mapping is composed of 16 possible combinations. The third experiment had a smaller number of features (three for a total of 12 combinations) and four behaviors.
- Measurement: in the first two experiments, feedback is provided by a questionnaire that is filled out every time the TV is paused. It is based on 5-point semantic differential scales, similar to the experiment in Section 3.1. In the third experiment, feedback comes from a cost/reward function calculated from other measurements such as reaction times, head direction, delay and a fixed cost of each of the robot’s behaviors. These factors are grouped as reward for action rA, which is positive or null; cost for the robot cR (depending on how expensive an action is); and cost for the human cH (measuring how much the human lost concentration).
- Class selection policy: in the third experiment we used leave-one-out cross-validation introduced in Section 2.6.1: classification is never taken directly from the current weights, but naive Bayes probabilities are recalculated every time, leaving the current features’ input out of the calculation.
3.2.3. Settings of the Algorithm
- The dataset of experience is initially empty. Whenever a new feature vector is given as input, it is checked whether it is already contained in the dataset or not. In the former case, the classification happens reading the weights directly from the dataset; in the latter case, they get assigned the values of probabilities calculated through our customized naive Bayes of Equation (10).
- Once the behavior b* is chosen and executed, we get the evaluation, on 5-point semantic differential scales, from the participant:
- whether b* was effective or not;
- if the evaluation was lesser or equal than 3 at point a, which behavior type b** instead would have been appropriate in this context f*;
- if the evaluation was lesser or equal than 3 at point a, in which context f** the behavior b* would have been effective.
- Weights are updated through the formula of Equation (12) w(T + 1) = w(T) + l · r · d where T is the current time step, l = exp(–s/4) is the learning factor (proportional to s, the counter of visit of each state), r is the reward factor {−1, −0.5, 0, 0.5, 1} depending on the rating, and d is 1−w(T) or w(T) depending on the rating being greater/lesser/equal to 3.
- New data obtained from these evaluations are then added to the dataset and normalized.
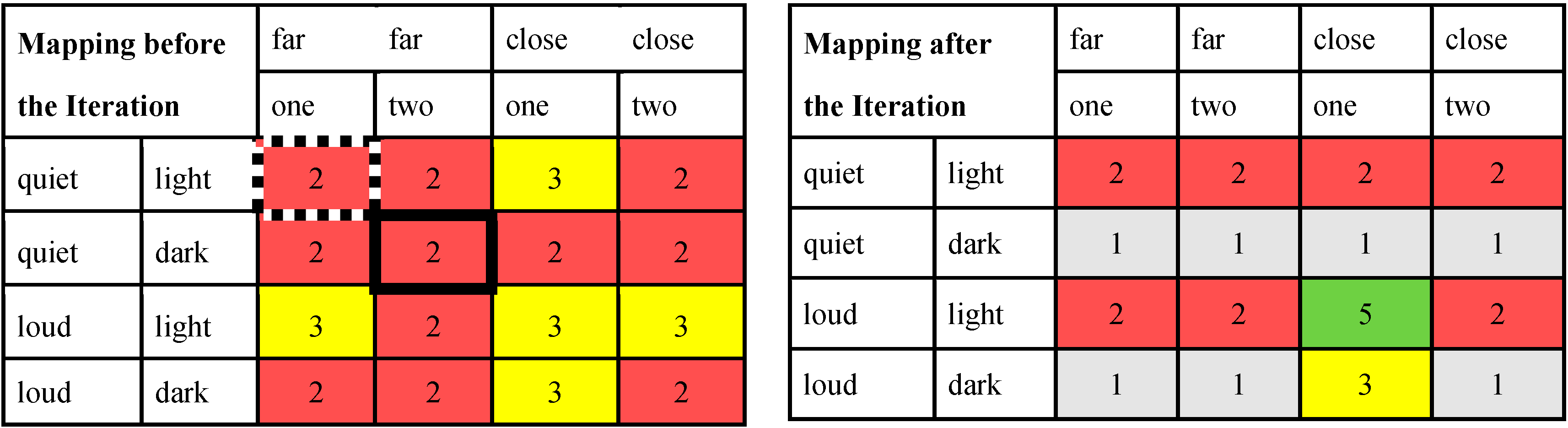
- Unlike in Section 3.1, in which the adaptation process was incremental for all participants, here we ran a separate whole set of interactions for each participant. This makes it possible to distinguish actual learning regardless of personal differences among participants. As for each one we fixed 12 iterations, there were no stopping conditions.
- There is no batch data for training. The mapping starts untrained, and this brings some complications. Initializing the first input vector with random values makes learning biased towards the classes that are (even slightly) more likely at the very beginning. Subsequent positive reward may cause a lack of exploration. This problem can be solved using a different policy of class selection, as explained in Section 2.6.1, such as ε-greedy, and/or removing the bias of the class priors, as introduced in Section 2.4.1. A stronger effect can even be obtained if the priors are replaced by another function that actuates a counter-bias.
3.2.4. Results
3.3. Discussion
3.3.1. About this Approach
3.3.2. Customization
- One feature turned into a discriminant in order to have two separate mappings
- Adaptation of one mapping made from literature to a new one VS adaptation without training dataset
- Rewards affecting more than one cell of the mapping through questionnaires
- Training data: from literature of human studies VS from corpora VS from experimental data
- Reward: from questionnaires VS from cost function
- Learning: incremental for all participants VS separate for each participant
- Class selection: using directly the weights VS leave-one-out cross-validation
- Class priors left out of the probability formula: alternative solutions are possible, such as a function that biases towards low probability classes using the inverse of the priors, or towards the classes that have been selected fewer times.
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Wolpert, D.H. The Lack of a Priori Distinctions between Learning Algorithms. Neural Comput. 1996, 8, 1341–1390. [Google Scholar] [CrossRef]
- Nguyen-Tuong, D.; Peters, J. Model learning for robot control: A survey. Cogn. Process. 2011, 12, 319–340. [Google Scholar] [CrossRef] [PubMed]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Bottou, L. Large-Scale Machine Learning with Stochastic Gradient Descent. In Proceedings of COMPSTAT’2010, Paris, France, 22–27 August 2010; Lechevallier, Y., Saporta, G., Eds.; Physica-Verlag HD: Paris, France; pp. 177–186.
- Yu, H.-F.; Hsieh, C.-J.; Chang, K.-W.; Lin, C.-J. Large Linear Classification When Data Cannot Fit in Memory. ACM Trans. Knowl. Discov. Data (TKDD) 2012, 5, 23:1–23:23. [Google Scholar] [CrossRef]
- Kober, J.; Bagnell, J.A.; Peters, J. Reinforcement learning in robotics: A survey. Int. J. Robot. Res. 2013, 32, 1238–1274. [Google Scholar] [CrossRef]
- Floreano, D.; Husbands, P.; Nolfi, S. Evolutionary Robotics. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1423–1451. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Goodrich, M.A.; Schultz, A.C. Human-Robot Interaction: A Survey. Found. Trends Hum.-Comput. Interact. 2007, 1, 203–275. [Google Scholar] [CrossRef]
- Franklin, D.W.; Milner, T.E.; Kawato, M. Single trial learning of external dynamics: What can the brain teach us about learning mechanisms? Int. Congress Series 2007, 1301, 67–70. [Google Scholar] [CrossRef]
- Spronck, P. Adaptive Game AI. Ph.D. Thesis, Maastricht University, Maastricht, The Netherlands, 2005. [Google Scholar]
- Klingspor, V.; Demiris, J.; Kaiser, M. Human-robot communication and machine learning. Appl. Artif. Intell. 1997, 11, 719–746. [Google Scholar]
- Fong, T.; Nourbakhsh, I.; Dautenhahn, K. A survey of socially interactive robots. Robot. Auton. Syst. 2003, 42, 143–166. [Google Scholar] [CrossRef]
- Dautenhahn, K. Socially intelligent robots: Dimensions of human–robot interaction. Philos. Trans. R Soc. Lond. B Biol. Sci. 2007, 362, 679–704. [Google Scholar] [CrossRef] [PubMed]
- Myagmarjav, B.; Sridharan, M. Knowledge Acquisition with Selective Active Learning for Human-Robot Interaction. In Proceedings of the Tenth Annual ACM/IEEE International Conference on Human-Robot Interaction Extended Abstracts; HRI’15 Extended Abstracts. ACM: New York, NY, USA, 2015; pp. 147–148. [Google Scholar]
- Lepora, N.F.; Evans, M.; Fox, C.W.; Diamond, M.E.; Gurney, K.; Prescott, T.J. Naive Bayes texture classification applied to whisker data from a moving robot. In Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010; pp. 1–8.
- Lepora, N.F.; Pearson, M.J.; Mitchinson, B.; Evans, M.; Fox, C.; Pipe, A.; Gurney, K.; Prescott, T.J. Naive Bayes novelty detection for a moving robot with whiskers. In Proceedings of the 2010 IEEE International Conference on Robotics and Biomimetics (ROBIO), Tianjin, China, 14–18 December 2010; pp. 131–136.
- Trovato, G.; Do, M.; Kuramochi, M.; Zecca, M.; Terlemez, Ö.; Asfour, T.; Takanishi, A. A Novel Culture-Dependent Gesture Selection System for a Humanoid Robot Performing Greeting Interaction. In Social Robotics; Beetz, M., Johnston, B., Williams, M.-A., Eds.; Springer International Publishing: Sydney, Australia, 2014; pp. 340–349. [Google Scholar]
- Trovato, G.; Galeazzi, J.; Torta, E.; Ham, J.R.C.; Cuijpers, R.H. Study on Adaptation of Robot Communication Strategies in Changing Situations. In Social Robotics; Tapus, A., André, E., Martin, J.-C., Ferland, F., Ammi, M., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 654–663. [Google Scholar]
- Levontin, P.; Kulmala, S.; Haapasaari, P.; Kuikka, S. Integration of biological, economic, and sociological knowledge by Bayesian belief networks: The interdisciplinary evaluation of potential management plans for Baltic salmon. ICES J. Mar. Sci. 2011, 68, 632–638. [Google Scholar] [CrossRef]
- Whitney, P.; White, A.; Walsh, S.; Dalton, A.; Brothers, A. Bayesian Networks for Social Modeling. In Social Computing, Behavioral-Cultural Modeling and Prediction; Salerno, J., Yang, S.J., Nau, D., Chai, S.-K., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 227–235. [Google Scholar]
- Ghahramani, Z.; Jordan, M.I. Learning from Incomplete Data. 1995. Available online: http://dspace.mit.edu/handle/1721.1/7202 (accessed on 20 January 2016).
- Lanouette, R.; Thibault, J.; Valade, J.L. Process modeling with neural networks using small experimental datasets. Comput. Chem. Eng. 1999, 23, 1167–1176. [Google Scholar] [CrossRef]
- Forman, G.; Cohen, I. Learning from Little: Comparison of Classifiers Given Little Training. In Knowledge Discovery in Databases: PKDD 2004; Boulicaut, J.-F., Esposito, F., Giannotti, F., Pedreschi, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 161–172. [Google Scholar]
- McCallum, A.; Nigam, K. A comparison of event models for naive Bayes text classification. In Proceedings of the AAAI-98 Workshop on Learning for Text Categorization, Madison, WI, USA, 26–30 July 1998; pp. 41–48.
- Mitchell, T.M. Machine Learning, 1st ed.; McGraw-Hill, Inc.: New York, NY, USA, 1997. [Google Scholar]
- Rish, I. An empirical study of the naive bayes classifier. In IJCAI 2001 Workshop on Empirical Methods in Artificial Intelligence; IBM: New York, NY, USA, 2001; Volume 3, pp. 41–46. [Google Scholar]
- Izbicki, M. Algebraic classifiers: A generic approach to fast cross-validation, online training, and parallel training. In Proceedings of the 30th International Conference on Machine Learning (ICML-13), Atlanta, GA, USA, 16–21 June 2013; pp. 648–656.
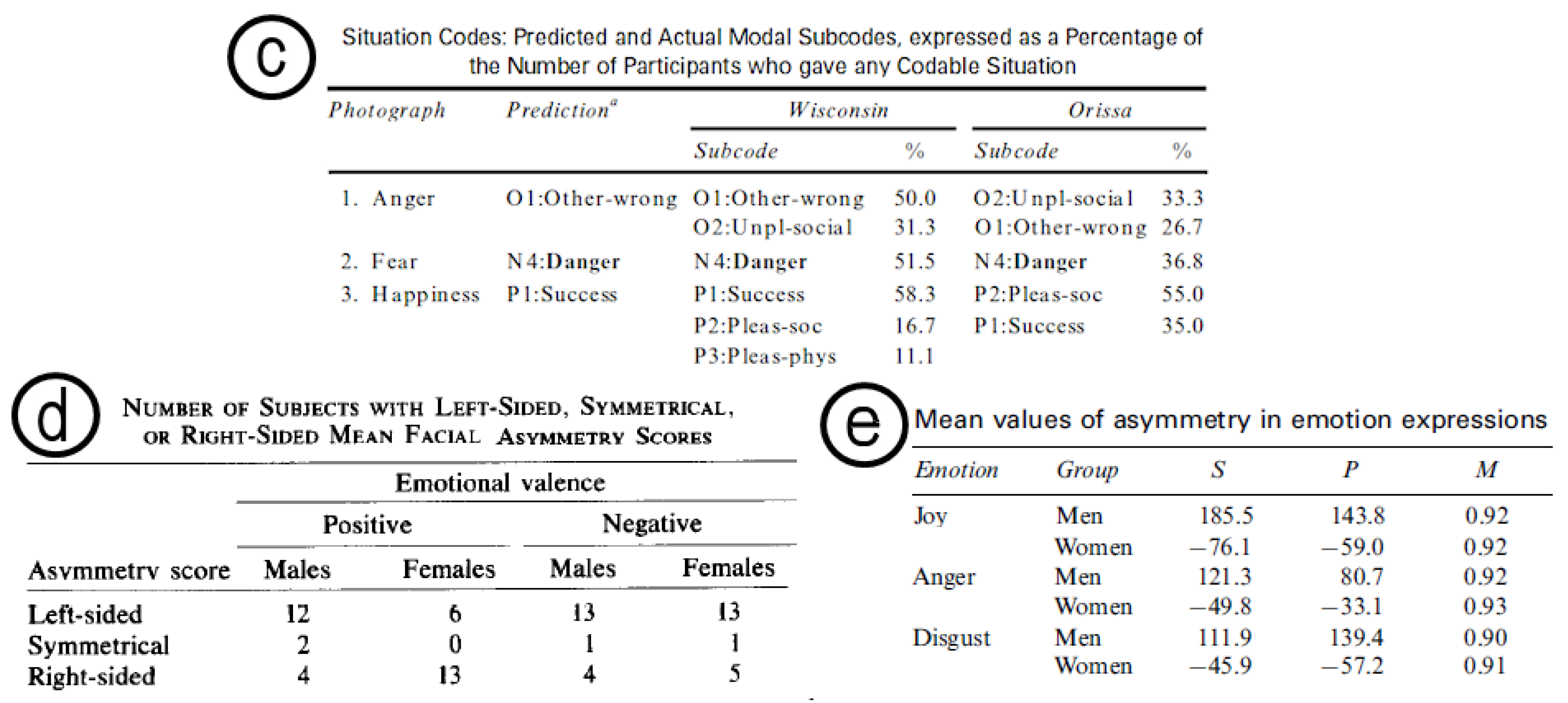
- Haidt, J.; Keltner, D. Culture and facial expression: Open-ended methods find more expressions and a gradient of recognition. Cogn. Emot. 1999, 13, 225–266. [Google Scholar] [CrossRef]
- Borod, J.C.; Koff, E.; White, B. Facial asymmetry in posed and spontaneous expressions of emotion. Brain Cogn. 1983, 2, 165–175. [Google Scholar] [CrossRef]
- Schmidt, K.L.; Liu, Y.; Cohn, J.F. The role of structural facial asymmetry in asymmetry of peak facial expressions. Laterality 2006, 11, 540–561. [Google Scholar] [CrossRef] [PubMed]
- Cestnik, B. Estimating Probabilities: A Crucial Task in Machine Learning. In Proceedings of the Ninth European Conference on Artificial Intelligence, Stockholm, Sweden, 6–10 August 1990; pp. 147–149.
- Devijver, P.A.; Kittler, J. Pattern Recognition: A Statistical Approach; Prentice Hall: Englewood Cliffs, NJ, USA, 1982. [Google Scholar]
- Rogers, E.M. Diffusion of Innovations, 5th ed.; Free Press: New York, NY, USA, 2003. [Google Scholar]
- Heenan, B.; Greenberg, S.; Aghel-Manesh, S.; Sharlin, E. Designing Social Greetings in Human Robot Interaction. In Proceedings of the 2014 Conference on Designing Interactive Systems, Vancouver, Canada, 21–25 June2014; pp. 855–864.
- Asfour, T.; Regenstein, K.; Azad, P.; Schroder, J.; Bierbaum, A.; Vahrenkamp, N.; Dillmann, R. ARMAR-III: An Integrated Humanoid Platform for Sensory-Motor Control. In Proceedings of the 2006 6th IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006; pp. 169–175.
- Feil-Seifer, D.; Mataric, M.J. Defining socially assistive robotics. In Proceedings of the 9th International Conference on Rehabilitation Robotics, ICORR 2005, Chicago, IL, USA, 28 June–1 July 2005; pp. 465–468.
- Torta, E.; Heumen, J.; van Cuijpers, R.H.; Juola, J.F. How Can a Robot Attract the Attention of Its Human Partner? A Comparative Study over Different Modalities for Attracting Attention. In Social Robotics; Ge, S.S., Khatib, O., Cabibihan, J.-J., Simmons, R., Williams, M.-A., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; pp. 288–297. [Google Scholar]
- Torta, E.; van Heumen, J.; Piunti, F.; Romeo, L.; Cuijpers, R. Evaluation of Unimodal and Multimodal Communication Cues for Attracting Attention in Human–Robot Interaction. Int. J. Soc. Robot. 2014, 7, 89–96. [Google Scholar] [CrossRef]
- Shamsuddin, S.; Ismail, L.I.; Yussof, H.; Ismarrubie Zahari, N.; Bahari, S.; Hashim, H.; Jaffar, A. Humanoid robot NAO: Review of control and motion exploration. In Proceedings of the 2011 IEEE International Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia, 25–27 November 2011; pp. 511–516.



| Feature 1 | Feature 2 | Feature 3 | Class Label | Weight |
|---|---|---|---|---|
| 0 | 0 | unknown | CA | 0.55 |
| 0 | 0 | unknown | CB | 0.45 |
| 0 | 1 | unknown | CA | 0.39 |
| 0 | 1 | unknown | CB | 0.61 |
| 1 | unknown | 0 | CA | 0.25 |
| 1 | unknown | 0 | CB | 0.5 |
| 1 | unknown | 0 | CC | 0.25 |
| Feature 1 | Feature 2 | Feature 3 | Class Label | Weight |
|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 0.2501 |
| 0 | 1 | 1 | 2 | 0.2497 |
| 0 | 1 | 1 | 3 | 0.2502 |
| 0 | 1 | 1 | 4 | 0.2500 |
| 1 | 1 | 0 | 2 | 0.5000 |
| Context (Features) | Feature Values | Greeting Types (Classes) |
|---|---|---|
| Gender of the human partner | 0. Male 1. Female | 1. Bow |
| Location | 0. Private 1. Public 2. Workspace | 2. Nod |
| Power relationship | 0. Inferior 1. Equal 2. Superior | 3. Raise hand |
| Social distance | 0. Close 1. Acquaintance 2. Unknown | 4. Handshake |
| Discriminant | Values | 5. Hug |
| Culture | 0. Japanese 1. German |
| Close | Close | Close | Acquain. | Acquain. | Acquain. | Unknown | Unknown | Unknown | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Inferior | Equal | Superior | Inferior | Equal | Superior | Inferior | Equal | Superior | ||
| Public | Male | 1 | 1 | 1 | 4 | 7 | 2 | 6 | 7 | 4 |
| Public | Female | 0 | 3 | 0 | 2 | 2 | 2 | 4 | 4 | 4 |
| Workplace | Male | 1 | 1 | 5 | 3 | 4 | 3 | 3 | 3 | 4 |
| Workplace | Female | 0 | 0 | 3 | 3 | 9 | 3 | 4 | 6 | 5 |
| 0.009 | 0.013 | 0.004 | 0.005 | 0.013 | 0.017 | 0.013 | 0.014 | 0.008 |
| 0.011 | 0.015 | 0.004 | 0.006 | 0.014 | 0.020 | 0.014 | 0.050 | 0.009 |
| 0.056 | 0.003 | 0.004 | 0.009 | 0.002 | 0.001 | 0.017 | 0.014 | 0.008 |
| 0.059 | 0.004 | 0.004 | 0.010 | 0.002 | 0.001 | 0.019 | 0.016 | 0.009 |
| 0.025 | 0.017 | 0.005 | 0.005 | 0.021 | 0.010 | 0.010 | 0.018 | 0.001 |
| 0.001 | 0.016 | 0.002 | 0.003 | 0.008 | 0.013 | 0.003 | 0.019 | 0.002 |
| 0.001 | 0.010 | 0.008 | 0.003 | 0.029 | 0.001 | 0.003 | 0.001 | 0.005 |
| 0.002 | 0.013 | 0.003 | 0.010 | 0.024 | 0.001 | 0.022 | 0.009 | 0.002 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 0.052 | 0.002 | 0.004 | 0.017 | 0.055 | 0.006 | 0.042 | 0.062 | 0.009 |
| 0.005 | 0.028 | 0.002 | 0.002 | 0.006 | 0.005 | 0.005 | 0.012 | 0.007 |
| 0.062 | 0.011 | 0.005 | 0.003 | 0.022 | 0.003 | 0.006 | 0.011 | 0.023 |
| 0.065 | 0.012 | 0.001 | 0.001 | 0.033 | 0.004 | 0.001 | 0.047 | 0.003 |
| Room Conditions (Features) | Feature Values | Behaviors (Classes) |
|---|---|---|
| Loudness | 0. Quiet 1. Loud | 1. Blinking 2. Waving 3. Beeping 4. Walking 5. Pausing TV |
| Ambient luminance | 0. Light 1. Dark | |
| Distance | 0. Far 1. Close | |
| Number of individuals | 0. Robot + participant 1. One additional person |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trovato, G.; Chrupała, G.; Takanishi, A. Application of the Naive Bayes Classifier for Representation and Use of Heterogeneous and Incomplete Knowledge in Social Robotics. Robotics 2016, 5, 6. https://doi.org/10.3390/robotics5010006
Trovato G, Chrupała G, Takanishi A. Application of the Naive Bayes Classifier for Representation and Use of Heterogeneous and Incomplete Knowledge in Social Robotics. Robotics. 2016; 5(1):6. https://doi.org/10.3390/robotics5010006
Chicago/Turabian StyleTrovato, Gabriele, Grzegorz Chrupała, and Atsuo Takanishi. 2016. "Application of the Naive Bayes Classifier for Representation and Use of Heterogeneous and Incomplete Knowledge in Social Robotics" Robotics 5, no. 1: 6. https://doi.org/10.3390/robotics5010006
APA StyleTrovato, G., Chrupała, G., & Takanishi, A. (2016). Application of the Naive Bayes Classifier for Representation and Use of Heterogeneous and Incomplete Knowledge in Social Robotics. Robotics, 5(1), 6. https://doi.org/10.3390/robotics5010006