Abstract
This paper addresses the challenge of coordinating task allocation and generating collision-free trajectories for a fleet of mobile robots in dynamic environments. Our approach introduces an integrated framework comprising a centralized task allocation system and a distributed trajectory planner. The centralized task allocation system, employing a heuristic approach, aims to minimize the maximum spatial cost among the slowest robots. Tasks and trajectories are continuously refined using a distributed version of CHOMP (Covariant Hamiltonian Optimization for Motion Planning), tailored for multiple-wheeled mobile robots where the spatial costs are derived from a high-level global path planner. By employing this combined methodology, we are able to achieve near-optimal solutions and collision-free trajectories with computational performance for up to 50 robots within seconds.
1. Introduction
Multi-Robot Systems (MRSs) are increasingly being deployed for a variety of applications, including warehouse automation [1], search and rescue [2], exploration tasks [3], mapping and surveying [4], and the agriculture industry [5,6], due to their efficiency and versatility. However, managing multiple mobile robots introduces significant challenges, particularly in motion planning. The two primary approaches to motion planning for MRSs are centralized and decentralized methods [7]. In centralized motion planning, the configuration spaces of individual robots are combined into a composite configuration space, which is then explored to find a path for the entire system [8]. In contrast, the decentralized approach involves computing individual paths for each robot and subsequently resolving any conflicts that arise between these paths [9,10]. Although the centralized approach yields a complete and optimal solution, it suffers from high computational complexity. The decentralized approach, while faster, often produces suboptimal solutions. Recent research has incorporated methodologies from the Operations Research community to address multi-robot task allocation and trajectory planning problems [11]. Integrating goal/task assignment with trajectory planning offers significant benefits over traditional methods [12,13]. However, most existing studies assume static environments, without dynamic obstacles after task assignment is accomplished, and rely on priority schemes to resolve conflicts among robots. In reality, environments are rarely static, necessitating path planners that can adapt to dynamic conditions, where achieving optimal paths is rarely feasible. Moreover, much of the previous work has focused on linear assignment problems between robots and tasks, assuming a one-to-one mapping relationship.
Due to these challenges, this paper presents a multi-robot navigational framework, termed extended-SPADES (Simultaneous Path Planning and Task Allocation in Dynamic EnvironmentS), which builds upon the foundational SPADES framework [14]. The original framework was designed to solve a linear task assignment problem where the number of robots M is equal to the number of tasks N. In this original framework, task assignment was determined using the Hungarian algorithm [15], which was subsequently refined by an individual path adaptor that adjusted the paths for each robot during motion based on priority. The extended-SPADES framework advances this work by addressing the more complex and practical problem of task allocation. In this scenario, the number of robots can be significantly less than the number of tasks (). Tasks are grouped, ordered, and then assigned to each robot in a optimal way. For such a task allocation problem, a more practical objective is to minimize the maximum time taken by the slowest robot, rather than simply minimizing the sum of spatial distances traveled by all robots. This objective ensures balanced load distribution across all robots, thereby preventing unexpected robot breakdowns. The task allocation plan is then converted into motion plans for individual robots, using the previously computed spatial costs. In dynamic environments, the trajectories of the robots are continuously refined to incorporate temporal and spatial constraints, using an enhanced extended-CHOMP algorithm that functions as a distributed path adaptor for all robots. This approach enables rapid adaptation of trajectories based on an optimal task allocation plan.
The contributions of this paper are threefold. Firstly, it introduces multi-robot task allocation into the previously developed SPADES framework, optimizing both task allocation and trajectory generation, which offers significant advantages over conventional approaches. This results in optimal solutions for one-to-many task allocation between robots and tasks, with very fast computation times. Secondly, by employing local-interaction-based trajectory planner as a distributed path adaptor, we generate faster collision-free paths under dynamic conditions. Thirdly, we evaluate this framework using real-world example scenarios and simulations, with a focus on load distribution optimization to minimize the maximum duration for the slowest robots, ensuring equitable workload distribution and preventing unexpected breakdowns for the complete robot fleet.
This paper is organized as follows. Section 2 reviews related work on methods used for task allocation in robotics with integrated planning. Section 3 describes the extended Simultaneous Planning and Assignment in Dynamic EnvironmentS framework. Section 3.3.1 and Section 3.3.2 discuss the two key components of the framework in detail. In Section 4, we present simulation and experimental studies and also evaluate it under various complex scenarios. Section 5 provides a detailed discussion of the results, and Section 6 concludes the paper with suggestions for future work.
2. Related Work
In Multi-Robot Systems (MRSs) [16], a group of robots work together to perform one or more tasks. The problem of assigning several robots to one or more tasks, while satisfying specific constraints, is known as the Multi-Robot Task Allocation (MRTA) problem [17,18,19]. This problem comes in various forms, depending on the assumptions, constraints, and objective functions involved. MRTA primarily deals with the allocation and scheduling of tasks to robots, aiming to optimize task distribution based on robot capabilities and task requirements. In contrast, the Multi-Robot Path Planning (MRPP) problem [20,21,22] focuses on planning paths for multiple robots, taking into account the robots’ kinematic and dynamic constraints, as well as environmental and temporal constraints. A related problem is the Multi-Agent Path Finding (MAPF) problem [23,24,25], which is an abstract, algorithmic approach to pathfinding. The challenge in MAPF is to compute optimal paths in a shared space, involving spatial–temporal coordination during conflicts. Unlike MRTA and MRPP, MAPF is applicable to all agents, not just robots, and therefore often lacks physical constraints. A complete survey of the multi-robot task and motion planning can be found in [26]. Recently, an integrated approach known as the Integrated Task Assignment and Path Finding (ITAPF) problem [27,28] has emerged in robotics and multi-agent systems. ITAPF combines the challenges of task assignment and pathfinding, aiming to minimize a global cost function that can include factors such as total task completion time (makespan), total distance traveled by all robots, or energy consumption. Similar to ITAPF, the Integrated Task Allocation and Path Planning (ITAPP) problem [29,30,31,32,33,34,35,36] addresses the challenge of solving task allocation and path planning simultaneously. These integrated approaches are particularly relevant in complex, dynamic environments where traditional methods might lead to suboptimal solutions. Some of the real-world applications for these problems include the container terminal between containers for automated trucks and automated guided vehicles. A simplistic view of an automated container terminal application is shown in Figure 1a. Another example is the warehouse automation between different types of robots and tasks to be performed is shown in Figure 1b developed in Gazebo simulation environment.
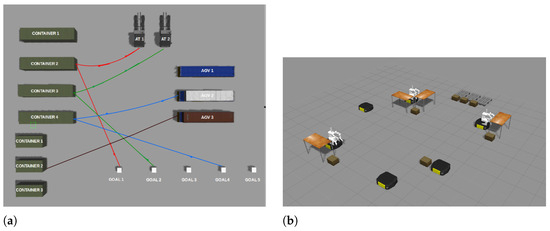
Figure 1.
(a) A Simplistic view of task allocation in container terminal between automated trucks (ATs) and autonomous guided vehicles (AGVs) to pick up different capacity of containers created using Gazebo simulation environment. (b) Two different type of robots—Ridgeback wheeled mobile robots and Yumi manipulator mounted on Ridgeback wheeled mobile robot with different tasks based on their ability created using Gazebo simulation environment.
Various approaches have been proposed to solve ITAPP. One common method is to formulate the problem as a Mixed-Integer Linear Programming (MILP) model [37], which can provide optimal solutions but is computationally expensive, especially for large-scale problems. Heuristic algorithms, such as genetic algorithms, ant colony optimization, or simulated annealing [38,39], are employed to find near-optimal solutions within a reasonable time frame, though they often do not consider the robots’ physical constraints. Hierarchical and decoupled methods [40,41] break down the problem into smaller sub-problems that are easier to solve, but these approaches are generally less optimal. More recently, reinforcement learning and other machine learning techniques [42,43] have been increasingly used to address ITAPP, particularly in dynamic or unpredictable environments. However, these methods have limitations, such as requiring large training datasets and significant computational resources [44,45]. In dynamic environments, models must adapt online as new data are collected, and implementing effective online learning strategies presents its own complexities [46,47].
The extended-SPADES framework is designed to solve the ITAPP problem. When the two NP-hard problems of task allocation and path planning are tackled separately, suboptimal solutions often result because the allocation may not consider the feasibility or efficiency of the resulting paths. By addressing both problems together, ITAPP can achieve more optimal solutions. Although ITAPP is computationally challenging, its objective is often to minimize a global cost function, which might include metrics like total travel distance, completion time (makespan), energy consumption, or a combination of these.
3. Extended-SPADES
3.1. Introduction
The SPADES framework [14] was originally designed to tackle the multi-robot path planning problem using an approach widely adopted in operations research. This method involves first calculating an optimal robot–task assignment, which is then used to guide path planning. In static environments, this approach is highly effective, producing optimal path plans for all robots. SPADES employs the Hungarian algorithm [15] for one-to-one robot–task assignments. The algorithm is well suited for solving linear assignment problems, offering computational complexity of for N vehicles, making it one of the most efficient methods for linear task assignment. The cost associated with each robot–task assignment is determined by the actual path lengths, which are calculated using a global path planner such as the E* algorithm [48]. This method consistently generates optimal solutions when the number of robots equals the number of tasks in a static environment.
However, in more complex and dynamic environments, especially those with a higher number of tasks relative to the number of robots, continuous replanning becomes necessary. To address these limitations, the extended-SPADES framework was developed. This enhanced version incorporates a comprehensive task planner integrated with a distributed trajectory planner. The framework tackles both the NP-hard problem of multi-robot task allocation [49] and the challenges of distributed trajectory planning [50,51], which have been studied and tested separately. In this work, these two problems are addressed within a single, cohesive framework, “extended-SPADES”, aiming to solve the Integrated Task Allocation and Path Planning (ITAPP) problem.
The MRTA problem can be expressed in various forms depending on specific assumptions, constraints, and objective functions. Each variant is NP-hard, requiring tailored approaches for resolution. This work focuses on a particular variant of the MRTA problem, which is highly applicable in real-world scenarios. Here, a number of robots are tasked with visiting a set of goals in any sequence, known as the Multi-Robot Routing (MRR) problem. The general objective is to minimize the makespan of all robots. However, this can lead to scenarios where some robots bear a disproportionate load, completing their tasks much later than others. To address this imbalance, a new objective is introduced: minimizing the maximum makespan of the slowest robot, known as the “min–max objective”. This objective aims to evenly distribute the workload among all robots, reducing the risk of robot breakdown due to unbalanced task distribution. In our framework, we address the MRR problem with the min–max objective, as illustrated in Figure 2. A Potts neuron-based deterministic annealing method, as well as a heuristic search method, have been proposed [49] to minimize the maximum makespan. These methods have shown promise for small to medium-sized problems in terms of both computation time and solution quality.
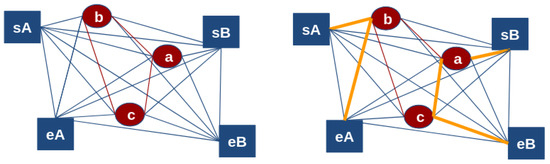
Figure 2.
Illustration of multi-robot routing problem (MRR) with min–max objective. and represent initial positions of robots A and B, while and denote their corresponding end positions, respectively. Red lines represent utility costs between tasks (T) named a, b, and c, while blue lines indicate costs between robots (R) and tasks. Solution involves allocating tasks in sequential order to each robot such that maximum cost incurred by any one robot is minimized. In this case, and is optimal task allocation shown in orange lines.
The trajectory planner tested within the framework is a modified version of the Covariant Hamiltonian Optimization and Motion Planning (CHOMP) algorithm [52], which is adapted for both mobile robots [50] and non-holonomic vehicles [51]. Despite optimal task allocation, individual robots may lose optimal paths while executing collision-free trajectories due to the movements of other robots attempting to do the same. Therefore, in this extended framework, a distributed multi−CHOMP algorithm is introduced. This algorithm generates collision-free trajectories while preserving the initial optimal task allocation, thereby avoiding the need for further replanning.
3.2. Assumptions and Terminology
In a complex but well-defined environment, assuming no map uncertainties, we consider M robots and N tasks, where . The utility cost between M robots and N tasks is divided into two components: (a) the transfer costs between any two consecutive tasks i and j, expressed in the utility or transfer cost matrix , and (b) , the cost to perform task i, expressed in the task vector T. The transfer cost matrix is calculated using a global map with localization data for each of the robots M and tasks N. The cost could be based on the length of global paths between tasks or the time required to move between them. In this paper, path length (the path length between tasks i and j) is considered, calculated using a global path planner such as or Dijkstra algorithm. This utility cost is particularly relevant for robots engaged in applications like warehouse operations [27]. The task vector can be assigned values based on the nature of the tasks. Since all robots are assumed to have identical capabilities, enabling them to perform any available task, we assume that all tasks require similar amounts of time, so is considered to be 1 units. Using M, N, , and , a task allocation matrix V is calculated by the task planner. This task allocation matrix V, along with the set of for each task order sequence, is then provided to each robot for execution. The robots then use the multi−CHOMP algorithm to resolve any conflicts that may arise during trajectory execution.
The problem formulation allows for asymmetric utility costs, meaning that these costs do not necessarily adhere to the triangle inequality. The transit costs between tasks are influenced by the order in which tasks are performed. Robots may start from different locations (multiple depots) and are not required to return to their starting position after completing their assigned tasks (open tours). It is important to note that this problem does not focus on scheduling tasks for each robot—determining the specific times at which tasks should be performed—but rather emphasizes the sequential ordering of tasks and their assignment to each robot based on the utility costs between tasks. While temporal constraints, such as waiting and arrival times, can be incorporated into the utility costs, the problem formulation does not address the detailed time schedule for the robots.
In a real-world robotics scenario, we consider an environment similar to an automated warehouse. We assume perfect communication, ignoring bandwidth limitations and map uncertainties, so all robots have access to complete information at all times. The acceleration and deceleration of the robots are inherently managed by the trajectory planner. The number of robots and tasks used in the experiments is based on a typical warehouse data [28].
3.3. Overview of the Method
In this section, we provide an overview of the new framework, as shown in Figure 3, followed by an in-depth explanation. This framework consists of a centralized task planner and individual local path adaptors for each robot. The task planner computes the task allocation for all the robots based on the global path planner and the utility costs between the robots and tasks. It produces an optimal task allocation and the corresponding global paths for all the robots to execute. However, the given task allocation and its corresponding paths can overlap, potentially causing path conflicts between the robots, which can lose the optimal task allocation solutions. To address this issue, the paths are converted into collision-free trajectories by the multi−CHOMP algorithm, avoiding the need to recompute the task allocation. The local path adaptor, multi−CHOMP, takes the input global paths for all the robots and resolves conflicts by modifying the time factor of the trajectories of each robot, ensuring that they do not overlap at any given time. By resolving the path conflicts locally, the overall optimal solution provided by the task planner is preserved, eliminating the need for complete replanning of the system. The algorithm is explained in Algorithm 1. The details of the task planner are explained in Figure 2 and the details of the path adaptor are explained in Figure 4. The details of the task planner have been heavily explored in earlier research work, so this work will focus on the path adaptor and its impact on the complete framework.
| Algorithm 1: Extended-SPADES Framework |
 |
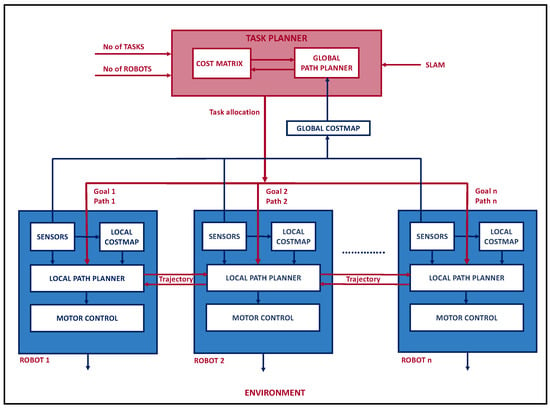
Figure 3.
Extended-SPADES planning framework explaining the schematic flow of tasks and paths for each robot.
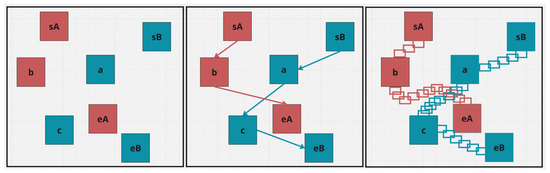
Figure 4.
In this example, there are two robots A (red color) and B (blue color) with starting points at and and end points at and respectively. The task planner produces the optimal task allocation and its corresponding paths are and . There is a path conflict between the paths and . The path conflicts are resolved by the centralized multi−CHOMP, which produces conflict-free trajectories.
3.3.1. Task Planner
As illustrated in Figure 3, the task planner computes the optimal task allocation for all the robots. It requires the global map with Simultaneous Localization and Mapping (SLAM) data to obtain the localization poses of the M robots and N tasks. A simple 2D costmap is constructed using a 2D occupancy grid map along with map inflation, which is used as the input of the framework. It is assumed that the locations of the robots (or start points) and the tasks (intermediate via points) are all available as poses in the global coordinate system of the map. Any sampling-based planner that is complete or probabilistically complete can be used to calculate global paths. With the help of a A* global path planner, path lengths for all combinations of robot–task, task–task, and task–robot are calculated, producing individual global paths between any two consecutive points (robot–task, task–task, task–robot) as shown in the following video: https://youtu.be/clFyK9Sv7JI?si=7nH9Qa6ma1cYVJtp accessed on 25 January 2025. The task costs T are assumed to be one. These values are then used to create the utility cost matrix . Thus, the task planner will have real-time paths and their timing constraints in continuous space. The global path planner module can also be used for complete replanning if there are significant conflicts that the local trajectory planner cannot handle in a worst-case scenario. For the extended-SPADES framework, both and [48] are used as the path planners, depending on the environment. While is simple, efficient, and preferred in a static environment, supports dynamic replanning and path cost interpolation, resulting in lightweight repairing of plans and smooth paths during execution. Hence, it can be used in a dynamic environment to calculate global paths.
The optimal task allocation is computed using the deterministic annealing method for small- to medium-sized problems [53] and the heuristic search method for large-sized problems [12]. A detailed overview of these methods, the algorithms, and the results are discussed in detail in [49,54]. The following two outputs are obtained from the task allocation method: the optimal task allocation in the form of the solution matrix V (optimal task order sequence for each robot) and the corresponding global paths for each robot based on this solution. If we consider a scenario involving two robots, denoted as A and B, each tasked with completing three specific tasks labeled a, b, and c—as in the example in Figure 2—the ideal task allocation is as follows: robot A follows the sequence (robot A starts at position , performs task b, and subsequently moves to end position ), while robot B follows (second robot task allocation is robot B begins at position , executes task a followed by task c, and then proceeds to end position ). So, the corresponding global paths for each robot are then computed as follows: The global path for robot A is given by the sum of the path segments and , expressed as . For robot B, the global path is the sum of , , and expressed as .
The task planner generates an optimally assigned robot–task list and a set of global paths for each robot using the global planner. However, these paths may not be collision-free, as they can conflict with each other or with dynamic obstacles. Therefore, the extended-SPADES framework incorporates a local path adaptor that ensures collision-free trajectories by considering the trajectories of all robots. In this context, we present the extended version of CHOMP, referred to as multi−CHOMP, which serves as the local path adaptation framework for individual robots. Each robot is assigned an optimized task allocation along with planned trajectories connecting these tasks, enhancing navigation efficiency and task execution while adhering to operational constraints.
3.3.2. Path Adaptor
The path adaptation method utilized in this framework is CHOMP, or Covariant Hamiltonian Optimization for Motion Planning, introduced by [52]. CHOMP is a trajectory optimization technique designed for high-dimensional motion planning, producing near-optimal solutions that comply with dynamic constraints. The algorithm iteratively refines an initial trajectory by optimizing an objective functional (Appendix A) that balances smoothness and obstacle avoidance. CHOMP operates under two key assumptions. First, it leverages exact gradient information, as opposed to relying on gradient estimation via sampling, enabling efficient computation of functional gradients in complex tasks by utilizing the robot’s workspace for the obstacle functional’s cost field c. Second, its formulation ensures covariance to reparametrization, allowing consistent behavior regardless of the trajectory parametrization. This property enables rapid convergence and effective path replanning in deadlock situations.
Furthermore, CHOMP has been adapted to handle non-holonomic constraints, such as those encountered in mobile robots and trucks, as demonstrated in [50,51]. In our adaptation, we introduce an interference objective to resolve conflicts between the trajectories of multiple robots. While CHOMP is tailored for individual robots, the interference objective accounts for the trajectories of all robots, ensuring the generation of conflict-free paths. In this section, a brief overview of the two objective functions—smoothness and obstacle avoidance—is given. In Section 3.3.3, the interference objective is explained in detail.
Given a trajectory mapping time to robot configurations, CHOMP optimizes the functional :
where penalizes trajectories based on dynamic criteria such as velocities and accelerations to promote smooth paths, penalizes proximity to obstacles to encourage obstacle-free trajectories, and addresses conflicts between the trajectories of multiple robots. A uniform discretization samples the trajectory function over equal time steps of length :
Each robot configuration represents a point in the discretized trajectory and contains by itself an x- and y-coordinate, . As already done before, the vector arrow is eschewed for the sake of simplicity. Furthermore, it is assumed that the starting and ending points are fixed, given as and , respectively. Now, the overall functional gradient is a combination of three components: the gradient of the obstacle objective and the gradient of the smoothness objective, scaled by a parameter .
The smoothness gradient indicates that the smoothness of a trajectory is related to minimizing abrupt changes in acceleration. A trajectory is smoother if its second derivative (acceleration) is minimized. It is given by the following:
The obstacle gradient is defined as the following:
where J is the kinematic Jacobian relating joint velocities to end-effector velocities, represents the velocity of a body point along the trajectory, is the normalized velocity vector, B typically represents a set or space related to the body points of the robot or the workspace, and is the curvature vector, which provides information about how sharply the trajectory is bending. The latter is defined as follows:
The matrix is a projection matrix that ensures updates to the trajectory gradient are orthogonal to the direction of motion. This means the updates from the workspace gradient will not directly influence the speed profile of the trajectory, focusing instead on improving obstacle avoidance while maintaining trajectory smoothness.
3.3.3. Interference Objective Functional
The design of an interference objective functional aims to maintain a safe distance between intersecting robots. Initially, we focus on a scenario involving two robots and subsequently generalize the approach to accommodate n robots. The problem is framed in the context of two independent trajectories, each defined by four total starting and ending points. Importantly, the multi−CHOMP framework remains unified, without dividing it into separate optimizers. Instead, each additional robot and its corresponding trajectory are appended to the existing trajectory representation. With the chosen parametrization, every robot’s configuration point q also represents a specific timestamp of the robot’s motion. Points that are closer together correspond to slower velocities, while those that are further apart imply faster movements. A significant advantage of this parametrization is that only one point from each trajectory needs to be compared, leading to a substantial reduction in computational effort.
The interference objective functional can be formulated in two distinct ways. The first approach employs normalized vectors of the distances between trajectory points. Consider a configuration point from the first trajectory and the corresponding point from the second trajectory. The distance between these two points is expressed as , and the unit vector associated with this distance is computed for each point as . The corresponding point of the second robot has the same unit vector but with a negative sign. These vectors indicate the direction in which the objective should push the points apart if they are too close to each other. Consequently, a cost function is necessary to regulate how much the points are penalized. Thus, the interference objective can be constructed as follows:
To derive the functional gradient of this objective, we express it as follows:
The principle of Equation (8) is straightforward. The unit vector provides the geometric direction in which the trajectory should be optimized. If the two robots are too close, they need to be pushed apart to maintain a safe distance, facilitated by the cost function based on their distance. Although Equation (8) may appear simple, it yields effective results, with the primary advantage of faster convergence compared to the subsequent approach. The second approach utilizes the obstacle objective to prevent collisions between robots. This method is particularly suitable since robots can be perceived as obstacles that must mutually avoid each other. The functional gradient in this scenario is given by the following:
In this formulation, the cost function remains dependent on the distance between two corresponding robot points. Here, denotes the normalized velocity, and is the curvature vector. The normalized workspace velocity is multiplied by the difference of two terms. The first term, , acts as a projection matrix, ensuring that workspace gradients are applied orthogonally to the trajectory’s direction of motion. As explained in [52], this projection guarantees that the workspace gradient does not directly influence the trajectory’s speed profile. The second term accounts for the weighted curvature, which is subtracted to correct for excessive curvature. While this approach may exhibit slower convergence and increased sensitivity when near obstacles, it offers the significant advantage of greater robustness in specific trajectory configurations. In summary, the development of the interference objective functional presents two viable approaches for maintaining safe distances between robots. The first approach emphasizes computational efficiency, while the second approach provides enhanced robustness in complex environments.
4. Experiments and Results
4.1. Implementation
4.1.1. multi−CHOMP
A simple graphical user interface developed by [55] to study CHOMP was extended to multi-robots with the interference objective (https://github.com/jenniferdavid/multi-CHOMP accessed on 15 January 2025) by [56]. It was implemented using C++11 with the Eigen library and the GTK (GIMP ToolKit) library to demonstrate the interference objective in a simple way. For example, in Figure 5, the interference of two intersecting trajectories is explained where the closer points mean the velocity is slower and the further apart points imply faster velocity. Figure 6 explains two different scenarios featuring trajectory interference. In the first one, the starting point of robot is the end point of robot and vice versa. Hence, the robots start to move towards each other at the same time and as they get closer, especially at the mid-point of the trajectory, they tend to move further away to avoid collision. In the second scenario, the two robot starting points are next to each other but both robots have the same end point. So, the robots move together at the same speed and adapt the trajectory such that the distance between them is large and when they reach the end point, the robot A is prioritized over robot B.
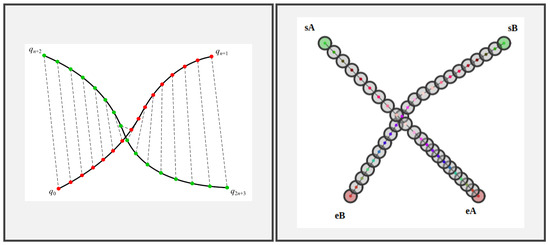
Figure 5.
An illustration of two intersecting trajectories. In the left figure, the positions of each robot at the same time are connected with a dashed line using the CHOMP interference objective where and are the end and start points of robot B and and are the start and end points of robot A. In the right figure, , and represent the start (shown in green) and end positions (shown in red) of robot A and B, respectively in the CHOMP GUI.
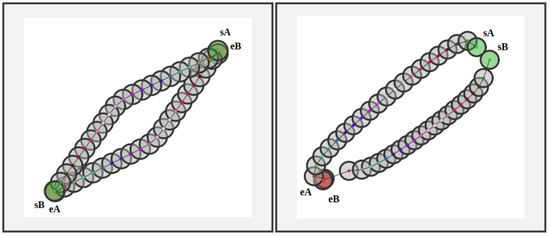
Figure 6.
Two scenarios to illustrate interference objective with time parametrization. , and represent start and end positions of robot A and B, respectively. The start positions are shown in green and the end points are shown in red color.
4.1.2. Extended-SPADES
The multi−CHOMP algorithm was implemented into the SPADES framework in ROS Melodic running on Ubuntu 20.04 with an octa-core Intel i7 processor and 15.6 GB memory. The complete framework was tested on the 2.5D simulation environment Stage with a number of ROS stacks for mapping and navigation (https://github.com/jenniferdavid/taskallocation accessed on 15 January 2025), as shown in Figure 7. Stage is a light-weight simulator that can be used to easily show important performance metrics like the scalability, computational time complexity, and computational resources of a framework. Simulation worlds were created by designing a virtual world with the required entities. The simple non-holonomic constraints were also incorporated into the differential drive robots of the simulation. A small part of the experiment was also performed in a 3D simulation environment like Gazebo (https://github.com/jenniferdavid/Gazebo_Harbour_Models accessed on 15 January 2025). However, the experiments were limited to smaller environments and fewer robots due to the complexity of the 3D robots, as well as the considerations of the physics engine and dynamics in Gazebo as shown in Figure 1b. The extended SPADES framework was built on the ROS navigational stack that makes use of amcl localization package for individual robots to publish the base ground truth pose for each of them. The corresponding map of the world was created using the gmapping package. Additional simulation worlds and maps were also taken from the ROS repositories.
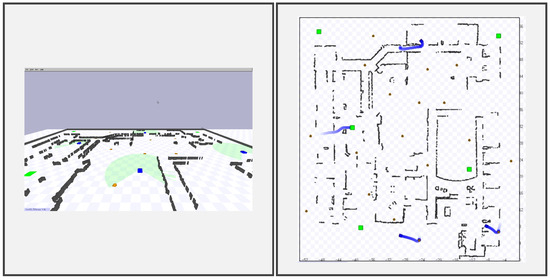
Figure 7.
2D perspective view (left) and top view (right) of the Stage simulator world of a Willow–Garage map. There are 7 robots (blue), 18 tasks (orange), and 7 drop-offs (green). The robots’ sonar can be seen via the light green color in the left picture. The path trails of each of the robots can be seen in the fading blue color.
To begin with, the initial positions of the robots, tasks, and goals are used to calculate the initial cost matrix in the given occupancy grip map. In our case, the cost matrix is the path length between the tasks, goals, and robots calculated using the global path planner A* algorithm, as shown in the video in Section 3.3.1. The computation time varies with the size of the problem. For example, with five robots and 18 tasks, it takes up to 52 s. This cost matrix is then used by the task planner to calculate the optimal task allocation at that given instant. However, this is for the first set of task allocation tasks; the subsequent task allocation can exploit this knowledge, which can give faster solutions. After the cost matrix is computed, the optimal task allocation for five robots and 18 tasks is calculated in 0.02 s using the heuristic method. It should be noted that this is the complete and unique optimal task allocation solution for this problem set under the static conditions. Our task allocation method uses either the heuristic method or the deterministic annealing method. The tasks are then allocated to each of the robots in an ordered way. The task planner also publishes the corresponding paths to each of the robots. The robots then start executing the tasks by moving using the move base ROS package as shown in Figure 8. In the next step, as the robots move, each of the local motion planner multi−CHOMP interact with each other to avoid path conflicts (https://youtu.be/gXSRuJjHJDM accessed on 15 January 2025. multi−CHOMP reparametrizes the time factor in the conflicting trajectories without losing their initial optimal paths. This can be seen in Figure 9 where the two set of robots avoid each other efficiently.
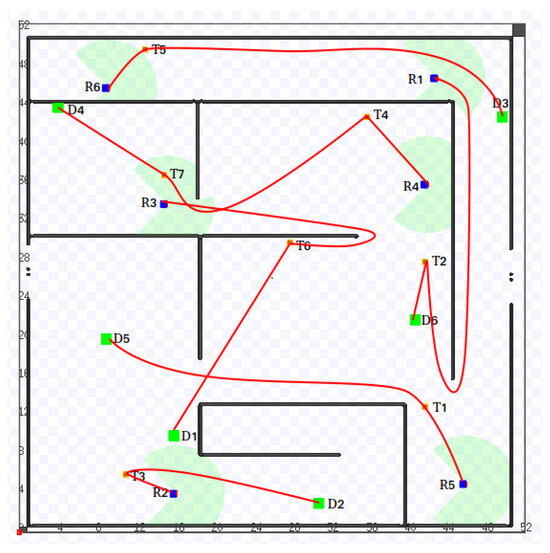
Figure 8.
Extended-SPADES running on a Stage simulator world of a maze map with 6 robots (blue), 7 tasks (orange), and 6 dropoffs (green) that shows the task allocation and the paths taken by each robot in red color. The solution cost here is 55.97, the optimal solution which is the sum of all the path costs.
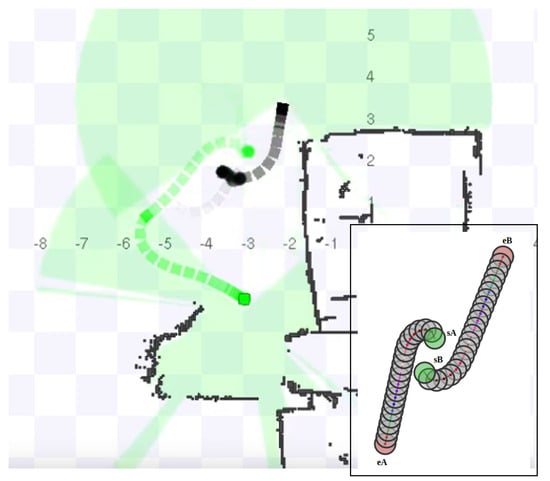
Figure 9.
Illustration of local path conflict resolution carried out using multi−CHOMP shown in Stage simulation environment; picture inside is corresponding visualization in GUI.
4.2. Experiments
The experimental setup was conducted on the 2D simulation environment Stage with ROS Melodic. The occupancy grid maps have a number of complex scenarios. Figure 14 and the robot model consists of simple differential drive robots with sonar for navigation and mapping. The tests were conducted for different maps generated with different scenarios. A series of experiments were conducted to evaluate the performance metrics of the interference objective in both the multi−CHOMP and extended-SPADES frameworks. The evaluation focused on key metrics including scalability, computational time, complexity, task completion time, path conflicts, optimality, completeness, and adaptability. These experiments were performed on several complex 2.5D environments from ROS repositories such as WillowGarage, Maze, Harbour, and Playpen. Additionally, three commonly studied challenging scenarios, depicted in Figure 14, were also considered. The first scenario is the corridor bottleneck problem, where two robots positioned at opposite ends of a narrow corridor, with space for only one robot at a time, must traverse without collision. The multi-robot planner must ensure that only one robot occupies the corridor at any given moment. The second scenario is the narrow passage problem, where two robots must swap positions in a constrained passage with insufficient space for direct swapping. The optimal solution requires the robots to move into a more open corridor to execute the swap efficiently. The third scenario is the intersection problem, where all robots must traverse across a circular intersection, ensuring they reach the opposite side without collisions, while maintaining an optimal path.
5. Results and Discussion
In the extended-SPADES framework, the task planner employs either a heuristic-based approach or a deterministic annealing method to allocate tasks to robots based on the path length. The result of this allocation process is an optimized or near-optimized mapping of tasks to robots, determined by scalability and path lengths computed using A* algorithms. These allocations are then distributed to all robots, which collaboratively execute a centralized multi−CHOMP algorithm to generate discretized, conflict-free trajectories for each robot. This centralized approach ensures that the task allocation optimality from the prior step is maintained. For this, several experiments were carried out to evaluate the performance metrics of the multi−CHOMP algorithm and the integrated extended-SPADES framework. Figure 8 explains the simulation setup and the solution computed by extended-SPADES is shown. In this example, the task planner computes the solution cost of 55.97, which is the optimal solution based on the initial conditions. When the robots starts moving, multi−CHOMP preserves the optimal path by resolving path conflicts.
5.1. multi−CHOMP
multi−CHOMP was compared to the standard gradient descent method in terms of computational resources (time), scalability, convergence rate, smoothness, and execution time. Scalability—As seen in Figure 10, multi−CHOMP consistently incurs higher computational costs compared to gradient descent, and as the problem size increases (>10), this difference becomes more pronounced and multi−CHOMP eventually slows down when compared to the standard method after 10 robots. To address this, an alternative approach—“Hybrid multi−CHOMP” was tested wherein the initially planned paths were divided into “n” segments. CHOMP is executed individually for each robot’s planned path, while multi−CHOMP is applied selectively to resolve conflicts only in conflicting path segments. This reduces resource consumption and computational complexity. This hybrid approach preserves the overall optimality of the solution while improving scalability, performance, and efficiency in dynamic and large-scale environments. It scales well for robots >50 than the gradient descent method, as seen in the figure. The system also accounts for uncertainties, such as unknown environmental conditions, sensor failures, and the presence of other dynamic objects beyond the robots themselves, which can disrupt the planned trajectories. An additional advantage of this approach is that the initial path planned and discretized for multi−CHOMP significantly reduces the likelihood of the algorithm becoming trapped in local minima, a common issue with other path planning methods. This robustness makes multi−CHOMP as well as hybrid multi−CHOMP particularly effective in dynamic environments. It is worth noting that while multi−CHOMP is not entirely immune to local minima, the issue can be effectively mitigated by providing a well-planned initial path as input. Additionally, the use of perturbation techniques helps address local minima problems, ensuring smoother performance in multi−CHOMP.
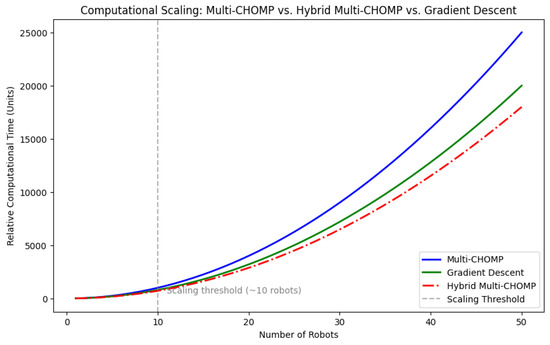
Figure 10.
Computational scaling of multi−CHOMP vs. gradient descent vs. hybrid multi−CHOMP. A scaling threshold (10 robots) is highlighted, beyond which the gap between the three methods becomes more pronounced.
Computational Time—When it comes to computational time, as shown in Figure 11, the multi−CHOMP algorithm does not grow linearly compared to the gradient descent method and performs poorly. Table 1 gives the complexity analysis of these three methods.
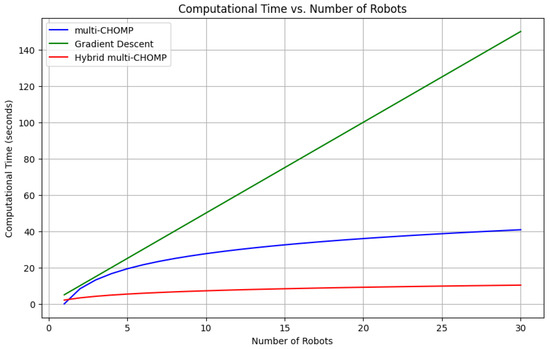
Figure 11.
Computational time comparison between the three methods.

Table 1.
Complexity comparison based on optimized implementations.
Convergence rate—As shown in Figure 12, the multi−CHOMP algorithm converges faster than the standard method. However, hybrid multi−CHOMP performs better than the other two methods easily. This is because of well-planned path as input, which reduces the chances of getting stuck in local minima. Execution time—When it comes to the execution time from Figure 13, it is clearly seen that the multi−CHOMP takes much longer to execute than the other two methods because of its computational complexity, which increases after 10 robots.
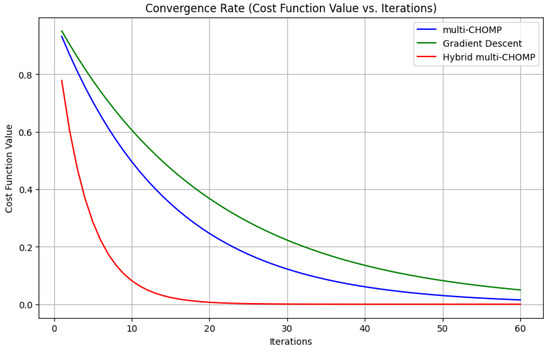
Figure 12.
Convergence rate of multi−CHOMP and its hybrid method vs. gradient descent in terms of iterations.
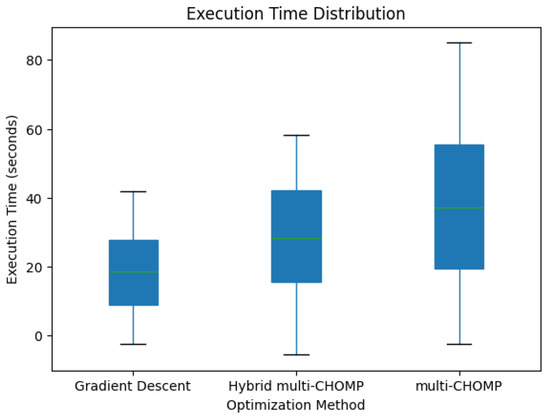
Figure 13.
Execution time for each method.
5.2. Extended-SPADES
In the context of a complete planner framework like extended-SPADES, key considerations include optimality, computational efficiency, scalability, replanning capabilities, and collision avoidance. The task planner is designed to consistently generate optimal or near-optimal solutions. multi−CHOMP ensures these solutions retain their quality by employing a centralized approach. In cluttered environments, conflicting path segments are resolved using multi−CHOMP without compromising solution quality. The total computational time for extended-SPADES includes the task planner’s computation, cost-path matrix calculations, path execution, and conflict resolution using multi−CHOMP. The primary bottlenecks are the task planner and multi−CHOMP, with scalability challenges becoming evident for scenarios involving more than 50 robots, as shown in Figure 11. For smaller to mid-sized problems, the framework delivers optimal, conflict-free solutions. multi−CHOMP enhances replanning capabilities and addresses collision avoidance in a detailed and centralized as well as local way, contributing to the overall efficiency and optimality of the framework. Its scalability and real-time applicability make it suitable for various robotics applications for up to 50 robots. However, the main challenges for this framework include computational complexity and the need for careful parameter tuning. Additionally, as the number of robots increases, real-time performance and computational demands become bottlenecks. This can be seen in Table 2. Extended-SPADES is compared with the GAP algorithm [11], which also focuses on both near-optimal solutions and computational complexity. In Table 2, it can be observed that extended-SPADES has the best makespan solution out of the three methods. Though the computational time is little longer than GAP, it ensures the solution optimality is preserved. The success rate of finding a solution is always above the threshold of 0.7 compared to the other two methods.

Table 2.
Performance comparison of extended-SPADES, SPADES, and GAP in terms of optimal solution cost or makespan (mkspn), computational time (time), and path execution success rate.
Limitations—In order to understand the limitation of our method, three challenging scenarios are introduced as shown in Figure 14. As seen from the results in Table 3, it can be clearly seen that both SPADES and extended-SPADES did not perform well under the first two corridor scenarios. The algorithm is not able to find a solution and lacks completeness. The framework manages to maintain path smoothness and the obstacle avoidance success rate but fails to find a path. The main reason was due to path oscillations and local minima in trajectory planning. Though adaptive learning models and more efficient heuristic-based optimizations can improve performance, it is not guaranteed that our method will work in such complex scenarios.

Figure 14.
Three complex scenarios for multi-robot path planning problem—the corridor bottleneck, narrow passage, and intersection problems, which can explain the completeness of the algorithm.

Table 3.
Comparison of the three methods for the given 3 complex scenarios in terms of completeness, path smoothness and obstacle avoidance success rate.
6. Conclusions
In this paper, we enhanced the SPADES framework to address more practical robotic applications that require near-optimal solutions as well as computational efficiency. The original SPADES framework uses the classical Hungarian algorithm to generate optimal task assignment solutions, assuming an equal number of tasks and robots. Each robot then executes its trajectory using an individual CHOMP-based motion planner while interacting with other robots. However, this approach has limitations, such as the assumption of equal numbers of robots and tasks, and a decline in solution quality when robots operate in cluttered or dynamic environments. In the extended-SPADES framework, we reformulated the task assignment problem into a task allocation problem, allowing for scenarios where the number of robots is significantly fewer than the number of tasks. Using heuristic methods or deterministic annealing, we compute optimal or near-optimal solutions depending on the problem’s scale. The quality of these solutions are maintained through a centralized motion planner, multi−CHOMP, which incorporates a specialized interference objective to resolve conflicts among robots’ paths in conflicting trajectories. This planner was also implemented as a hybrid type that addresses the computational load in a much easier way. When the number of robots was more than 50 robots, the computational time also increased. The method also suffers from issues relating to local minima and fails to find a path when used in complex corridor problems. This integrated approach achieves near-optimal task allocation solutions and ensures collision-free trajectories, with computational efficiency for scenarios involving up to 50 robots in a dynamic environment. For small to mid-size problems, the framework looks promising for dynamic environments. Future work will involve using adaptive learning methods to address the issue of path oscillations and local minima.
Author Contributions
Conceptualization J.D.; methodology, J.D. and R.V.; software, J.D.; investigation, J.D. and R.V.; writing—original draft preparation, J.D.; writing—review and editing, J.D. and R.V.; supervision, R.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Source codes are available at https://github.com/jenniferdavid/taskallocation accessed on 15 January 2025.
Acknowledgments
The authors would like to thank Pascal Bosshard for his implementation of the multi−CHOMP method, which inspired this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Objective Functionals in Detail
The smoothness objective aims to determine an optimal path by penalizing the acceleration along a trajectory . The objective can be expressed in a series of finite differences using waypoint parametrization as follows:
These equations are presented in [52] where denote the forward kinematics, mapping a robot configuration and a particular body point to a point in the workspace. This equation can be expressed using a finite differencing matrix K and boundary condition vector e:
where , , and , A is a symmetric matrix (the Hessian matrix), b is a vector, and c is a constant term. Now, for the optimization steps, the gradient of the smoothness objective is given by the following:
If the matrix A and vector b can be defined for the specific problem at hand, the functional gradient of can be computed efficiently.
Next, to obtain collision free trajectories, the robot is penalized when near obstacles. Therefore, the obstacle objective and its gradient presented in [52] are used.
where the general cost function is , which represents the cost of any point in the workspace. It is defined as follows:
where is the distance from the point x to the nearest obstacle and is a small constant used to smooth the transition near obstacles. Using the same discretized waypoint parametrization as for , the gradient of the obstacle objective becomes
where
is the normalized velocity vector. Since we defined the configuration space and workspace to be the same, the Jacobian J simplifies to the identity matrix: and the curvature can be expressed as follows:
where is the first derivative of the trajectory and is the acceleration.
References
- Daniel, C.; Frans, O.; Hendrik, B.; Karl, T. Decentralised online planning for multi-robot warehouse commissioning. In Proceedings of the 16th Conference on Autonomous Agents489 and MultiAgent Systems, International Foundation for Autonomous Agents and Multiagent490 Systems, Sao Paulo, Brazil, 8–12 May 2017; pp. 492–500. [Google Scholar]
- Baxter, J.L.; Burke, E.K.; Garibaldi, J.M.; Norman, M. Multi-robot search and rescue: A potential field based approach. In Autonomous Robots and Agents; Springer: Berlin/Heidelberg, Germany, 2007; pp. 9–16. [Google Scholar]
- Burgard, W.; Moors, M.; Stachniss, C.; Schneider, F.E. Coordinated multi-robot exploration. IEEE Trans. Robot. 2005, 21, 376–386. [Google Scholar] [CrossRef]
- Fox, D.; Ko, J.; Konolige, K.; Limketkai, B.; Schulz, D.; Stewart, B. Distributed multirobot exploration and mapping. Proc. IEEE 2006, 94, 1325–1339. [Google Scholar] [CrossRef]
- Ye, L.; Wu, F.; Zou, X.; Li, J. Path planning for mobile robots in unstructured orchard environments: An improved kinematically constrained bi-directional RRT approach. Comput. Electron. Agric. 2023, 215, 108453. [Google Scholar] [CrossRef]
- Chen, M.; Chen, Z.; Luo, L.; Tang, Y.; Cheng, J.; Wei, H.; Wang, J. Dynamic visual servo control methods for continuous operation of a fruit harvesting robot working throughout an orchard. Comput. Electron. Agric. 2024, 219, 108774. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- LaValle, S.M.; Hutchinson, S.A. Optimal motion planning for multiple robots having independent goals. IEEE Trans. Robot. Autom. 1998, 14, 912–925. [Google Scholar] [CrossRef]
- Van Den Berg, J.P.; Overmars, M.H. Prioritized motion planning for multiple robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 430–435. [Google Scholar]
- Van Den Berg, J.; Guy, S.J.; Lin, M.; Manocha, D. Reciprocal n-Body Collision Avoidance. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 3–19. [Google Scholar]
- Turpin, M.; Mohta, K.; Michael, N.; Kumar, V. Goal assignment and trajectory planning for large teams of interchangeable robots. Auton. Robot. 2014, 37, 401–415. [Google Scholar] [CrossRef]
- Matthew, T.; Nathan, M.; Vijay, K. An approximation algorithm for time optimal multi-robot routing. In Algorithmic Foundations of Robotics XI; Springer: Berlin/Heidelberg, Germany, 2015; pp. 627–640. [Google Scholar]
- Liu, L.; Shell, D.A. An anytime assignment algorithm: From local task swapping to global optimality. Auton. Robot. 2013, 35, 271–286. [Google Scholar] [CrossRef]
- David, J.; Philippsen, R. Task Assignment and Trajectory Planning in Dynamic environments for Multiple Vehicles. In Robotics Science and System, Workshop on Task and Motion Planning; IOS Press: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Cao, Y.U.; Kahng, A.B.; Fukunaga, A.S. Cooperative mobile robotics: Antecedents and directions. Auton. Robot. 1997, 4, 7–27. [Google Scholar] [CrossRef]
- Gerkey, B.P.; Matarić, M.J. A formal analysis and taxonomy of task allocation in multi-robot systems. Int. J. Robot. Res. 2004, 23, 939–954. [Google Scholar] [CrossRef]
- Ayorkor, K.G.; Anthony, S.; Bernardine, D.M. A comprehensive taxonomy for multi-robot task allocation. Int. J. Robot. Res. 2013, 32, 1495–1512. [Google Scholar]
- Sameh, S.; Tucker, B. Efficient multi-robot coordination through auction-based task allocation and behavior-based execution. J. Artif. Intell. Res. 2009, 35, 725–755. [Google Scholar]
- LaValle, S.M. Rapidly-exploring random trees: Progress and prospects. In Algorithmic and Computational Robotics: New Directions: The Fourth Workshop on the Algorithmic Foundations of Robotics; CRC: Boca Raton, FL, USA, 2000; pp. 293–308. [Google Scholar]
- Choset, H. Coverage for robotics—A survey of recent results. Ann. Math. Artif. Intell. 2001, 31, 113–126. [Google Scholar] [CrossRef]
- Yang, L.; Gu, D.; Chen, L.; Hu, H. Multi-robot task allocation for robot soccer. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 1202–1207. [Google Scholar]
- Stern, R.; Sturtevant, N.; Felner, A.; Koenig, S.; Ma, H.; Walker, T.; Li, J.; Atzmon, D.; Cohen, L.; Kumar, T.K.; et al. Multi-agent pathfinding: Definitions, variants, and benchmarks. arXiv 2019, arXiv:1906.08291. [Google Scholar] [CrossRef]
- Silver, D. Cooperative pathfinding. In Proceedings of the First Artificial Intelligence and Interactive Digital Entertainment Conference, Marina Del Rey, CA, USA, 1–2 June 2005. [Google Scholar]
- Sharon, G.; Stern, R.; Felner, A.; Sturtevant, N.R. Conflict-based search for optimal multi-agent pathfinding. Artif. Intell. 2015, 219, 40–66. [Google Scholar] [CrossRef]
- Antonyshyn, L.; Silveira, J.; Givigi, S.; Marshall, J. Multiple Mobile Robot Task and Motion Planning: A Survey. ACM Comput. Surv. 2023, 55, 213. [Google Scholar] [CrossRef]
- Moon, S.; Oh, E.; Shim, D.H. An integral framework of task assignment and path planning for multiple unmanned aerial vehicles in dynamic environments. J. Intell. Robot. Syst. 2013, 70, 303–313. [Google Scholar] [CrossRef]
- Masehian, E.; Nejad, A.H. A hierarchical decoupled approach for multi robot motion planning on trees. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 3604–3609. [Google Scholar]
- Chen, Z.; Alonso-Mora, J.; Bai, X.; Harabor, D.D.; Stuckey, P.J. Integrated task assignment and path planning for capacitated multi-agent pickup and delivery. IEEE Robot. Autom. Lett. 2021, 6, 5816–5823. [Google Scholar] [CrossRef]
- Brown, K.; Peltzer, O.; Sehr, M.A.; Schwager, M.; Kochenderfer, M.J. Optimal sequential task assignment and path finding for multi-agent robotic assembly planning. In Proceedings of the 2020 IEEE546 International Conference on Robotics and Automation (ICRA), Virtual, 31 May–31 August 2020; pp. 441–447. [Google Scholar]
- Xu, X.; Yin, Q.; Fu, Y.; Yu, M. Solving multi-goal task assignment and path finding problem with a Single Constraint Tree. In Proceedings of the 43rd Chinese Control Conference (CCC), Kunming, China, 28–31 July 2024; pp. 5704–5709. [Google Scholar]
- Qiu, Z.; Long, J.; Yu, Y.; Chen, S. Integrated task assignment and path planning for multi-type robots in an intelligent warehouse system. Transp. Res. Part Logist. Transp. Rev. 2025, 194, 103883. [Google Scholar] [CrossRef]
- Liu, S.; Feng, B.; Bi, Y.; Yu, D. An Integrated Approach to Precedence-Constrained Multi-Agent Task Assignment and Path Finding for Mobile Robots in Smart Manufacturing. Appl. Sci. 2024, 14, 3094. [Google Scholar] [CrossRef]
- Xia, G.; Sun, X.; Xia, X. Multiple task assignment and path planning of a multiple unmanned surface vehicles system based on improved self-organizing mapping and improved genetic algorithm. J. Mar. Sci. Eng. 2021, 9, 556. [Google Scholar] [CrossRef]
- Fang, C.; Mao, J.; Li, D.; Wang, N.; Wang, N. A coordinated scheduling approach for task assignment and multi-agent path planning. J. King Saud-Univ.-Comput. Inf. Sci. 2024, 36, 101930. [Google Scholar] [CrossRef]
- Murphey, R.A. Integrated Assignment and Path Planning. Doctoral Thesis, University of Florida, Gainesville, FL, USA, 2005. [Google Scholar]
- Umay, I.; Fidan, B.; Melek, W. An integrated task and motion planning technique for multi-robot-systems. In Proceedings of the 2019 IEEE International Symposium on Robotic and Sensors Environments (ROSE), Ottawa, ON, Canada, 17–18 June 2019; pp. 1–7. [Google Scholar]
- Guo, H.; Miao, Z.; Ji, J.C.; Pan, Q. An effective collaboration evolutionary algorithm for multi-robot task allocation and scheduling in a smart farm. Knowl.-Based Syst. 2024, 289, 111474. [Google Scholar] [CrossRef]
- Edison, E.; Shima, T. Integrated task assignment and path optimization for cooperating uninhabited aerial vehicles using genetic algorithms. Comput. Oper. Res. 2011, 38, 340–356. [Google Scholar] [CrossRef]
- Tuna, G.; Gungor, V.C.; Gulez, K. An autonomous wireless sensor network deployment system using mobile robots for human existence detection in case of disasters. Ad. Hoc. Netw. 2014, 13, 54–68. [Google Scholar] [CrossRef]
- Nigam, N. Dynamic replanning for multi-UAV persistent surveillance. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013; p. 4887. [Google Scholar]
- Emam, Y.; Mayya, S.; Notomista, G.; Bohannon, A.; Egerstedt, M. Adaptive task allocation for heterogeneous multi-robot teams with evolving and unknown robot capabilities. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 7719–7725. [Google Scholar]
- Luo, X.; Liu, C. Simultaneous Task Allocation and Planning for Multi-Robots under Hierarchical Temporal Logic Specifications. arXiv 2024, arXiv:2401.04003. [Google Scholar]
- Xu, X.; de Soto, B.G. Deep reinforcement learning-based task assignment and path planning for multi-agent construction robots. In Proceedings of the 2nd Future of Construction Workshop at the International Conference on Robotics and Automation (ICRA 2023), London, UK, 29 May–2 June 2023. [Google Scholar]
- Vu, C.-T.; Liu, Y.-C. Deep Reinforcement Learning for Multi-Robot Local Path Planning in Dynamic Environments. In Proceedings of the 13th International Workshop on Robot Motion and Control590 (RoMoCo), Poznan, Poland, 2–4 July 2024; pp. 267–272. [Google Scholar]
- Zheng, Y.; Li, B.; An, D.; Li, N. A multi-agent path planning algorithm based on hierarchical reinforcement learning and artificial potential field. In Proceedings of the 11th International Conference on Natural Computation (ICNC), Zhangjiajie, China, 15–17 August 2015; pp. 363–369. [Google Scholar]
- Bae, H.; Kim, G.; Kim, J.; Qian, D.; Lee, S. Multi-robot path planning method using reinforcement learning. Appl. Sci. 2019, 9, 3057. [Google Scholar] [CrossRef]
- Philippsen, R.; Siegwart, R. Smooth and efficient obstacle avoidance for a tour guide robot. IEEE Int. Conf. Robot. Autom. 2003, 1, 446–451. [Google Scholar]
- David, J.; Rognvaldsson, T.; Soderberg, B.; Ohlsson, M. Deterministic Annealing based on Potts-spin model for Multi Robot Routing Problem. Springer J. Intell. Robot. Syst. 2021, 15, 321–334. [Google Scholar]
- David, J.; Valencia, R.; Philippsen, R.; Iagnemma, K. Local Path Optimizer for an Autonomous Truck in a Harbor Scenario. In Springer Field and Service Robotics: Results of the 11th International Conference; Springer: Geneva, Switzerland, 2018; pp. 499–512. [Google Scholar]
- David, J.; Valencia, R.; Philippsen, R.; Bosshard, P.; Iagnemma, K. Gradient based path optimization method for autonomous driving. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 4501–4508. [Google Scholar]
- Zucker, M.; Ratliff, N.; Dragan, A.D.; Pivtoraiko, M.; Klingensmith, M.; Dellin, C.M.; Bagnell, J.A.; Srinivasa, S.S. CHOMP: Covariant Hamiltonian optimization for motion planning. Int. J. Robot. Res. 2013, 32, 1164–1193. [Google Scholar] [CrossRef]
- Hakkinen, J.; Lagerholm, M.; Peterson, C.; Soderberg, B. Local routing algorithms based on Potts neural networks. IEEE Trans. Neural Netw. 2000, 11, 970–977. [Google Scholar] [CrossRef] [PubMed][Green Version]
- David, J.; Rögnvaldsson, T. Multi-Robot Routing Problem with Min–Max Objective. Robotics 2021, 10, 122. [Google Scholar] [CrossRef]
- Philippsen, R. Robotics Motion Planning Library. 2016. Available online: https://github.com/poftwaresatent/trychomp (accessed on 15 January 2025).
- Pascal, B.; Roland, P. Investigation of Trajectory Optimization for Multiple Car-Like Vehicles. Semester Thesis, Halmstad University, Halmstad, Sweden, 2015. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).