1. Introduction
Uncertainty is an inherent part of robotics that must be dealt with explicitly through the robust design of sensors, mechanics, and algorithms. Unlike many other engineering research areas that also have to deal with uncertainties, robotics problems usually also consist of a heterogeneous set of interconnected sub-problems and have strict real-time requirements, making it even harder to deal with uncertainty in an appropriate manner [
1].
A common approach to model uncertainties in robotics is to employ probability mass functions and/or probability density functions, hereinafter jointly referred to as probability distributions, over model variables. One can then represent many classical robotics problems as a joint distribution,
, over observable variables,
x, and latent variables,
z. Given the knowledge that the observable variables,
x, can be assigned specific values
, solving the problem then boils down to solving the posterior inference problem given by the conditional distribution
Unfortunately, the marginalization by the integral in the denominator of Equation (
2) is, in general, intractable to compute in most realistic problems, and thereby the reason why one often has to resort to approximate inference [
2].
The classical solution to this problem has been to simplify the model of a problem,
p, sufficiently to obtain an approximate problem definition,
, for which one can derive or use analytical solutions such as the Kalman filter [
3], henceforth referred to as the “model simplification method”. Typically, it is only possible to derive analytical solutions for a very limited set of probability distributions. Thereby, it may be necessary to apply crude approximations to obtain a solution, making it a rather inflexible method. However, such solutions tend to be computationally efficient, which is why they were commonly used in the early days of probabilistic robotics where computational resources were limited. One good example of this is Kalman filter-based simultaneous localization and mapping (SLAM). It is well known that in many cases the true posterior,
p, is multi-modal, e.g., due to ambiguities and changes in the environment [
4]. However, Kalman filter-based SLAM implicitly assumes a uni-modal Gaussian posterior,
q, which in some cases can lead to poor solutions.
Another possibility is to use Monte Carlo methods such as particle filters. These methods have the benefit that they usually do not enforce any restrictions on the model,
p, making these methods highly flexible. Furthermore, with these methods, it is often possible to obtain any degree of accuracy at the cost of losing computational efficiency. The computational complexity usually makes these methods unsuitable for solving complex robotics problems in real-time. An example of the use of Monte Carlo methods in robotics is the particle filter-based SLAM algorithm called FastSLAM [
5], which only utilizes a particle filter to estimate the posterior of the robots pose and settles for Kalman filters for estimating the pose of landmarks.
The third set of methods, that have gained increasing interest in the last decade due to the advancement in stochastic optimization and increase in computational resources, is the optimization-based method called variational inference. In variational inference, optimization is used to approximate the distribution, , that we are interested in finding, by another simpler distribution , called the variational distribution. Like analytical solutions, variational inference assumes an approximation model, q, and thereby introduces a bias into the solution. The set of possible models that can be employed in modern variational inference is wide, making the method very flexible for modelling robotics problems. This optimization-based approach also makes the distinction between the model of the real problem, p, and the model used to find an approximate solution, q, very explicit and gives a measure of the applicability of the approximate model, q. Furthermore, the use of an approximate model, q, usually allows this set of methods to be more computationally efficient than Monte Carlo methods. As such, variational inference can be viewed as a compromise between the computational efficiency of the model simplification method and the flexibility of Monte Carlo methods. This makes variational inference especially interesting for robotics applications.
Initial efforts on applying variational inference for robot applications have shown promising results in various problems. In [
6] variational inference is used to solve several tasks related to navigation in spatial environments for a single robot. In [
7] variational inference is used to learn low-level dynamics as well as meta-dynamics of a system, which is subsequently used to plan actions at multiple temporal resolutions. In a similar fashion, it is also demonstrated in [
8] how variational inference can be used to learn both low-level and high-level action policies from demonstrations. In [
9], variational inference with a mixture model as the variational distribution is used to find approximate solutions to robot configurations satisfying multiple objectives. Variational inference has also been used in some distributed settings. In [
10], they perform centralised training with decentralised execution for cooperative deep multi-agent reinforcement learning, where a variational distribution is used in the approximation of a shared global mutual information objective common for all the agents. In [
11], variational inference is used to learn a latent variable model that infers the role and index assignments for a set of demonstration trajectories, before these demonstrations are passed to another algorithm that than learns the optimal policy for each agent in a coordinated multi-Agent problem. Common for [
10,
11] is that variational inference is used to learn global parameters in a centralized fashion. In [
12], a more decentralized approach is taken. Here, variational inference is used locally on each robot in a swarm to estimates a Bayesian Hilbert Map. These locally estimated maps are subsequently merged through a method called Conflation. A method applicable due to an assumption about normal distributed random variables. While others have successfully used variational inference for robotics applications even in distributed settings, the use of a combination of stochastic variational inference and message-passing for decentralized distributed robotic problems has been an untouched topic to date.
In the present effort, we unite these two major solution approaches in variational inference to outline a flexible framework for solving probabilistic robotics problems in a distributed way. The main contribution of this paper is:
In
Section 2, we formally present the basics of variational inference, message-passing, and stochastic variational inference. In
Section 3, we introduce the problem of and derive the algorithm for multi-robot navigation with cooperative avoidance under uncertainty. In
Section 4, we present the results of simulations and a real-world experiment. Finally, in
Section 5 and
Section 6, we conclude upon the obtained results and discuss the potential use cases of the proposed approach.
2. Variational Inference
Variational inference uses optimization to approximate one distribution
by another, simpler distribution
called the variational distribution. Notice that, in general,
does not need to be a conditional distribution,
, as in Equation (
2). However, for the sake of the topic in this paper, we will focus on the conditional distribution case. Thus, we will concentrate on solving a variational inference problem on the form
where
D is a so-called divergence measure, measuring the similarity between
p and
q, and
Q is the family of variational distributions from which we want to find our approximation. The notation
denotes that we are dealing with a divergence measure and that the order of arguments,
x and
y, matters. The family of variational distributions,
Q, is usually selected as a compromise between how good an approximation one wants and computational efficiency. The divergence measure,
D, can have a rather large impact on the approximation. However, experiments have shown that for the family of
-divergences, subsuming the commonly used Kullback–Leibler divergence, all choices will give similar results as long as the approximating family,
Q, is a good fit to the true distribution [
13].
Section 2.1 and
Section 2.2 present two solution approaches commonly used in variational inference, namely message-passing algorithms and stochastic variational inference. Message-passing algorithms exploit the dependency structure of a given variational inference problem to decompose the overall problem into a series of simpler variational inference sub-problems, that can be solved in a distributed fashion [
13]. Message-passing algorithms do not give specific directions on how to solve these sub-problems, and thus classically required tedious analytical derivations, that effectively limited the usability of the method. On the other hand, modern stochastic variational inference methods directly solve such variational inference problems utilizing stochastic optimization that inherently permits the incorporation of modern machine learning models, such as artificial neural networks, into the problem definition [
14,
15]. As such, the fusion of these two approaches can potentially result in a transparent and flexible framework in which complex problems can be solved distributively, making it a perfect fit for a broad interdisciplinary research area such as robotics, inherently accommodating recent trends in research fields such as deep learning, cloud robotics and multi-robot systems.
2.1. Message-Passing
The overall idea behind message-passing algorithms is to take a possible complicated problem as defined by Equation (
3) and break it down into a series of more tractable problems that depend on the solution of the other problems [
13,
16]. This way of solving a variational inference problem is known as message-passing because the solution of each sub-problem can be interpreted as a message sent to the other sub-problems. This is achieved by assuming that the model of our problem,
, naturally factorizes into a product of probability distributions
where superscript
is used to denote the index of the
a’th factor. Notice that the factorization need not be unique and that each probability distribution,
, can depend on any number of the variables of
. The choice is up to us. Similarly, we can choose a variational distribution,
, that factorizes into a similar form
Now by defining the product of all other than the
a’th factor of
and
, respectively as
and by further assuming that
is in fact a good approximation, it is possible to rewrite our full problem in Equation (
3) into a series of approximate sub-problems on the form
Assuming a sensible choice of factor families,
, from which
can be chosen, the problem in Equation (
8) can be more tractable than the original problem, and by iterating over these coupled sub-problems as shown in Algorithm 1, we can obtain an approximate solution to our original problem.
| Algorithm 1: The generic message-passing algorithm. |
- 1:
Initialize for all - 2:
repeat - 3:
Pick a factor - 4:
Solve Equation ( 8) to find - 5:
until converges for all
|
The approach is not guaranteed to converge for general problems. Furthermore, Equation (
8) might still be a hard problem to solve, thus previously in practice, the approach has been limited to problems for which Equation (
8) can be solved analytically such as fully discrete or Gaussian problems [
13]. However, besides breaking the original problem into a series of more tractable sub-problems, this solution approach also gives a principle way of solving the original problem in a distributed fashion, which can be a huge benefit in robotics applications. Furthermore, depending on the dependency structure of the problem, a sub-problem might only depend on the solution of some of the other sub-problems, which can significantly reduce the amount of communication needed due to sparsely connected networks.
2.2. Stochastic Variational Inference
Stochastic Variational Inference (SVI) reformulates the minimization problem of a variational inference problem, e.g., Equation (
3) or Equation (
8), into a dual maximization problem with an objective,
L, that is suited for stochastic optimization. To use stochastic optimization, we need to assume that the variational distribution,
q, is parameterized by some parameters,
. We will denote the parameterized variational distribution by
. The steps and assumptions taken to obtain this dual problem and the objective function,
L, of the resulting maximization problem of course depends on whether we have chosen the Kullback–Leibler divergence [
17,
18,
19],
-divergences [
20], or another divergence measure [
21]. However, the resulting maximization problem ends up being on the form
This dual objective function,
L, does not depend on the posterior,
, but only the variational distribution,
and the unconditional distribution
making the problem much easier to work with. Furthermore, by, for example, utilizing the reparameterization trick or the REINFORCE-gradient, it is possible to obtain an unbiased estimate of the gradient,
, of the dual objective
L. Stochastic gradient ascent can then be used to iteratively optimize the objective through the updated equation
where superscript
l is used to denote the
l’th iteration. If the sequence of learning rates,
, follows the Robbins–Monro conditions,
then stochastic gradient ascent converges to a maximum of the objective function
L, and Equation (
9) is dual to the original minimization problem, thus providing a solution to the original problem.
An unbiased gradient estimator with low variance is pivotal for this method, and variance reduction methods are often necessary. However, a discussion of this subject is outside the scope of this paper and can often be achieved automatically by probabilistic programming libraries/languages such as Pyro [
14]. Besides providing the basic algorithms for stochastic variational inference, such modern probabilistic programming languages also provide ways of defining a wide variety of probability distributions and extensions to stochastic variational inference that permits incorporating and learning of parameterized functions, such as neural networks, into the unconditional distribution
, thereby making the approach very versatile. The benefit of solving variational inference problems with stochastic optimization is that noisy estimates of the gradient are often relatively cheap to compute due to, e.g., subsampling of data. Furthermore, the use of noisy gradient estimates can cause algorithms to escape shallow local optima of complex objective functions [
19].
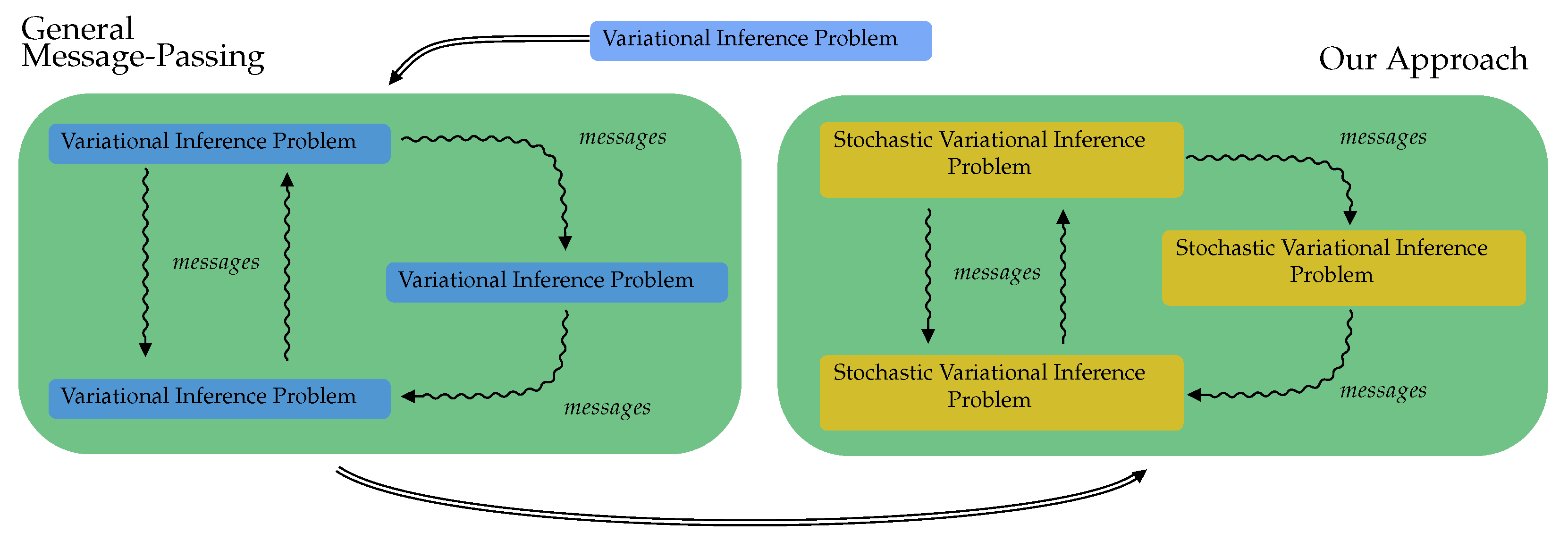
To summarize, if we want to distribute a complex inference problem, one potential solution is to first find variational inference sub-problems via the message-passing method, and then use stochastic variational inference to solve these sub-problems. This procedure is illustrated in
Figure 1, and the next section explains the usage of our method for a distributed multi-robot system.
3. Navigation with Cooperative Avoidance under Uncertainty
Multi-robot collision avoidance is the problem of multiple robots navigating a shared environment to fulfil their respective objective without colliding. It is a problem that arises in many situations such as warehouse management and transportation, collaborative material transfer and construction [
22], entertainment [
23], search and rescue missions [
24], and connected autonomous vehicles [
25]. Due to its importance in these and other applications, multi-robot collision avoidance has been extensively studied in the literature. In non-cooperative collision avoidance, each robot assumes that other robots do not actively take actions to avoid collisions, i.e., a worst case scenario. A common approach to non-cooperative collision avoidance is velocity obstacles [
26,
27,
28]. Velocity obstacles geometrically characterize the set of velocities for the robot that result in a collision at some future time, assuming that the other robots maintains the observed velocity. By only allowing robots to take actions that keep them outside of this set, they avoid collisions. However, non-cooperative approaches are conservative by nature as they neglect the fact that other robots, in most cases, will also try to avoid collisions. Cooperative collision avoidance alleviates this conservatism by assuming that the responsibility of avoiding collisions is shared between the robots. Such approaches include the extensions to velocity obstacles referred to as reciprocal collision avoidance [
29,
30,
31,
32], but also includes approaches relying on centralized computations of actions, and decentralized approaches in which robots communicate their intentions to each other. For both non- and cooperative collision avoidance, action decision is commonly based on a deterministic optimization/model predictive control formulations [
28,
33,
34,
35]. However, optimal control [
36], Lyapunov theory [
37,
38], and even machine learning approaches [
39] have also been used.
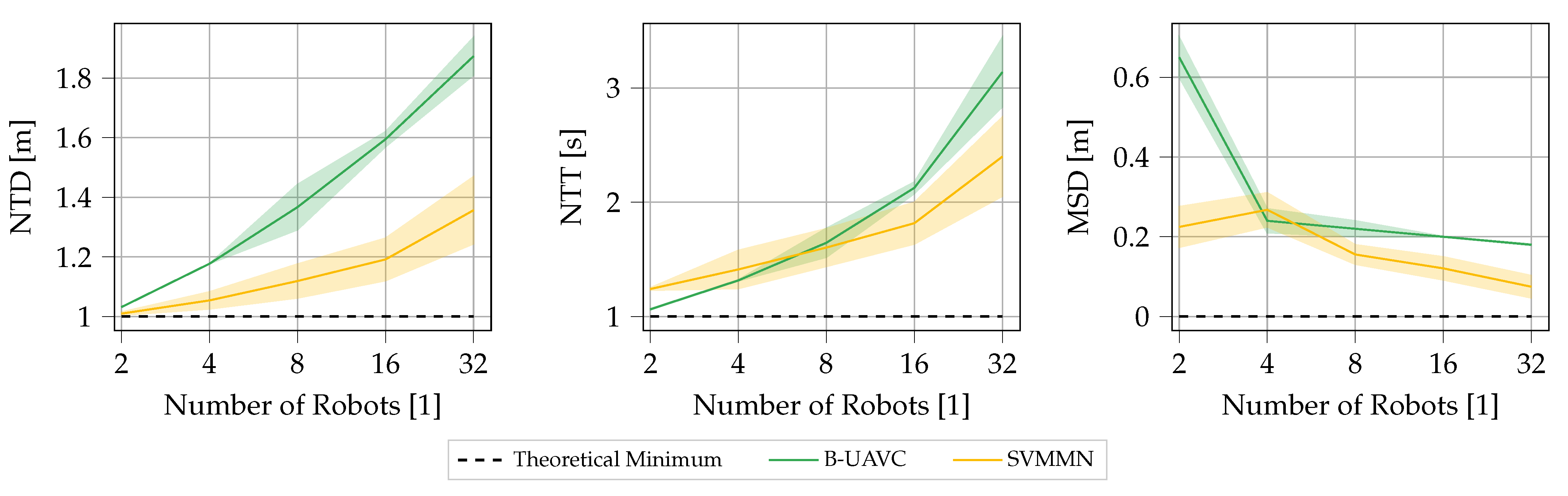
Despite many claims of guaranteed safety in the literature, uncertainty is often totally neglected, treated in an inapt way, or only to a limited extent. An inapt but common approach to handle uncertainties is to derive deterministic algorithms assuming no uncertainties, and afterwards artificially increase the size of robots used in the algorithm by an arbitrary number, as in [
28,
30]. For example, in [
30], uncertainties are handled by artificially increasing the radii of robots with 33%. Despite being stated otherwise in the paper, it is clear from the accompanying video material (
https://youtu.be/s9lvMvFcuCE?t=144 Accessed on 1 February 2022) that this is not sufficient to avoid contact between robots during a real-world experiment. When uncertainty is treated in an appropriate way, it is usually only examined for a single source of uncertainty, e.g., position estimation error as in [
27,
35,
38], presumably due to the difficulties of other methods mentioned in
Section 1, such as deriving analytical solutions or computing solutions in real-time, which is only further complicated by the need for distributed solutions.
Within this section, we illustrate how the approach outlined in
Section 2 can be utilized to solve the multi-robot collision avoidance problem in a cooperative and distributed way that appropriately treats multiple sources of uncertainty.
Section 3.1 introduces the problem dealt with in this paper, in
Section 3.2 the algorithm is derived and explained, and finally, in
Section 4, the result of simulations and a real-world experiment is presented, validating the approach.
3.1. Problem Definition and Modelling
Consider
N uni-cycle robots placed in the same environment. Each of them have to navigate to a goal location,
, by controlling their translational and rotational velocities while communicating with the other robots to avoid collision. We will consider the two-dimensional case where the robots can obtain a mean and covariance estimate of their own current pose at time
t,
, e.g., from a standard localization algorithm such as Adaptive Monte Carlo Localization (AMCL) from the Nav2 ROS2 package [
40]. Therefore, we model the current pose of the
n’th robot as the following normal distribution
We do not consider the dynamics of the robots but settle for a standard discrete kinematic motion model of a uni-cycle robot given by
where
,
and
are the translational and rotational velocities of the
n’th robot at time
normalized to the range
, respectively,
A is a linear scaling of the velocity to be in the range
corresponding to the minimum and maximum velocities of the
n’th robot, and
is the temporal difference between
and
. As Equation (
13), among other things, does not consider the dynamics of the motion, an estimate based on this will yield an error. To model this error, we employ an uniform distribution and define
where
M is a constant vector that captures the magnitude of the model error. As Equation (
13) is obtained through the use of the forward Euler method,
M could potentially be obtained as an upper bound by analysing the local truncation error. However, this would probably be too conservative. Instead, we consider
M as a tuning parameter. The robots do not naturally have any preference for selecting specific translational and rotational velocities, thus, we also model the prior over the normalized velocities as a uniform distribution. That is
So far, we have modelled everything we need to describe the uncertainty in the motion of each of the robots. Now, we turn to the problem of modelling optimality and constraints. The only criteria of optimality that we will consider are that the robots grow closer to their respective goal locations,
. To do so, we define the following simple reward function
where
To include the optimality into the probabilistic model, we use a trick commonly utilized in probabilistic Reinforcement Learning and Control [
41]. We start by defining a set of binary optimality variables,
, for which
denotes that time step
is optimal for the
n’th robot, and conversely
denotes that time step
is not optimal. We now define the distribution of this optimality variable at time
,
, conditioned on the pose of the robot at time
,
, as
where
is a tuning constant. Notice that, as
, it follows that
. The intuition behind Equation (
17) is that the state with the highest reward has the highest probability and states with lower reward have exponentially lower probability.
As stated, the robots should avoid colliding with each other. Therefore, we would like to impose a constraint on the minimum distance,
, that the
n’th and
m’tn robots should keep. To do so we define
where
. Similarly, as we modeled optimality we can now also define binary constraint variables,
, for which
denotes that the minimum distance constraint between the
n’th and
m’tn robot is violated at time
, and model the constraint by the distribution given by
where
is a tuning constant. Again, when the distance between two robots becomes larger, it has an exponentially lower probability of violating the distance constraint. With the above variable definitions, we can now formulate a solution to the navigation problem at time
t as the following conditional probability distribution
where
To capitalize, Equation (
20) states that we are interested in finding the distribution over the next action,
, that each robot should take conditioned on that it should be optimal, specified by the “observations”
, and should not result in violation of the constraints, specified by the “observations”
. Furthermore, it states that we can obtain this distribution as the marginal to the conditional distribution on the right-hand side of the equal sign. If we can evaluate this problem efficiently in real-time, it will act as probabilistic model predictive control, taking the next
k time-steps into account. However, as discussed in the introduction, solving such a problem is, in general, intractable. Therefore, the next section will derive an approximate solution based on message-passing and Stochastic Variational Inference.
3.2. Algorithm Derivation
Instead of solving Equation (
20), in this section we will show how to find an approximate solution based on variational inference. The derived algorithm is shown in Algorithm 2. At each time step,
t, we want to approximate Equation (
20) by solving the following problem
while making sure that it is easy to obtain the marginals for the variables of interest,
, from this approximation. To utilize the idea of message-passing, we need to find a natural factorization of the model of the problem. By applying the definition of conditional probability together with the chain rule, and by considering the dependency structure of the model, the conditional probability distribution on the right-hand side of Equation (
20) can be rewritten as
From Equation (
22), it is seen that the model naturally factorizes into a fraction related to the constraints and
N factors related to the pose, actions, and optimality variables of each of the
N robots. Thus, it is natural to choose a variational distribution that factorizes as
Now considering Equation (
8) we can distribute the computations by letting the
n’th robot solve a problem on the form
and broadcast the result,
, to the rest of the vehicles. This could be repeated until convergence, or simply until a solution for the next time step,
, has to be found. However, Equation (
24) still includes the unknown term
. To overcome this hurdle, we utilize stochastic variational inference, for which we can work with the unconditional distribution given by Equation (
25) instead.
where
| Algorithm 2: Navigation with Cooperative Avoidance under Uncertainty. |
- 1:
On each of the n robots - 2:
repeat - 3:
- 4:
Get from localization algorithm - 5:
Initialize - 6:
repeat - 7:
if messages available for then - 8:
Store , and - 9:
end if - 10:
Solve Equation ( 29) to find - 11:
Broadcast , and - 12:
until converges or time is up. - 13:
until Suitable stop criteria; e.g., goal reached.
|
All terms in Equation (
25) except for the variational distribution,
, were defined in
Section 3.1. To choose an appropriate variational distribution,
, consider Equation (
26) describing the motion of the robot. The only distribution in Equation (
26) that can actually be directly controlled is
, as
is the current best estimate of the
n’th robots’ current location provided by a localization algorithm, and
is derived from the kinematics of the robots. Therefore, an appropriate choice of variational distribution is
leaving only the distribution
left to be chosen.
has a direct connection to
in Equation (
15), and thus it is natural to choose a distribution that shares some of the same properties such as the support. Therefore, we have chosen
which has the exact same support as and even subsumes
. To summarize, at each time-step,
t, each robot,
n, has to iteratively solve a sub-problem through stochastic variational inference represented by
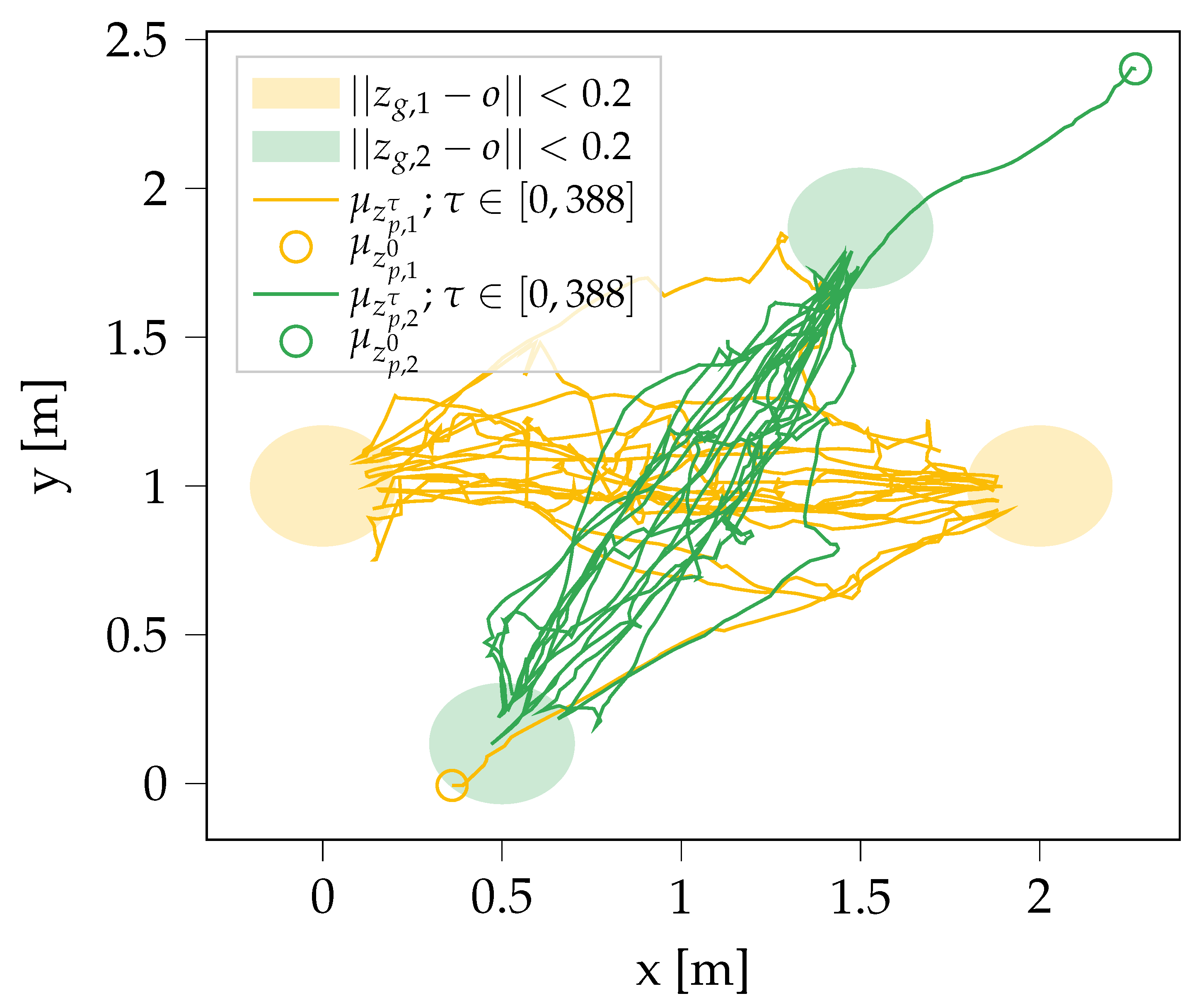
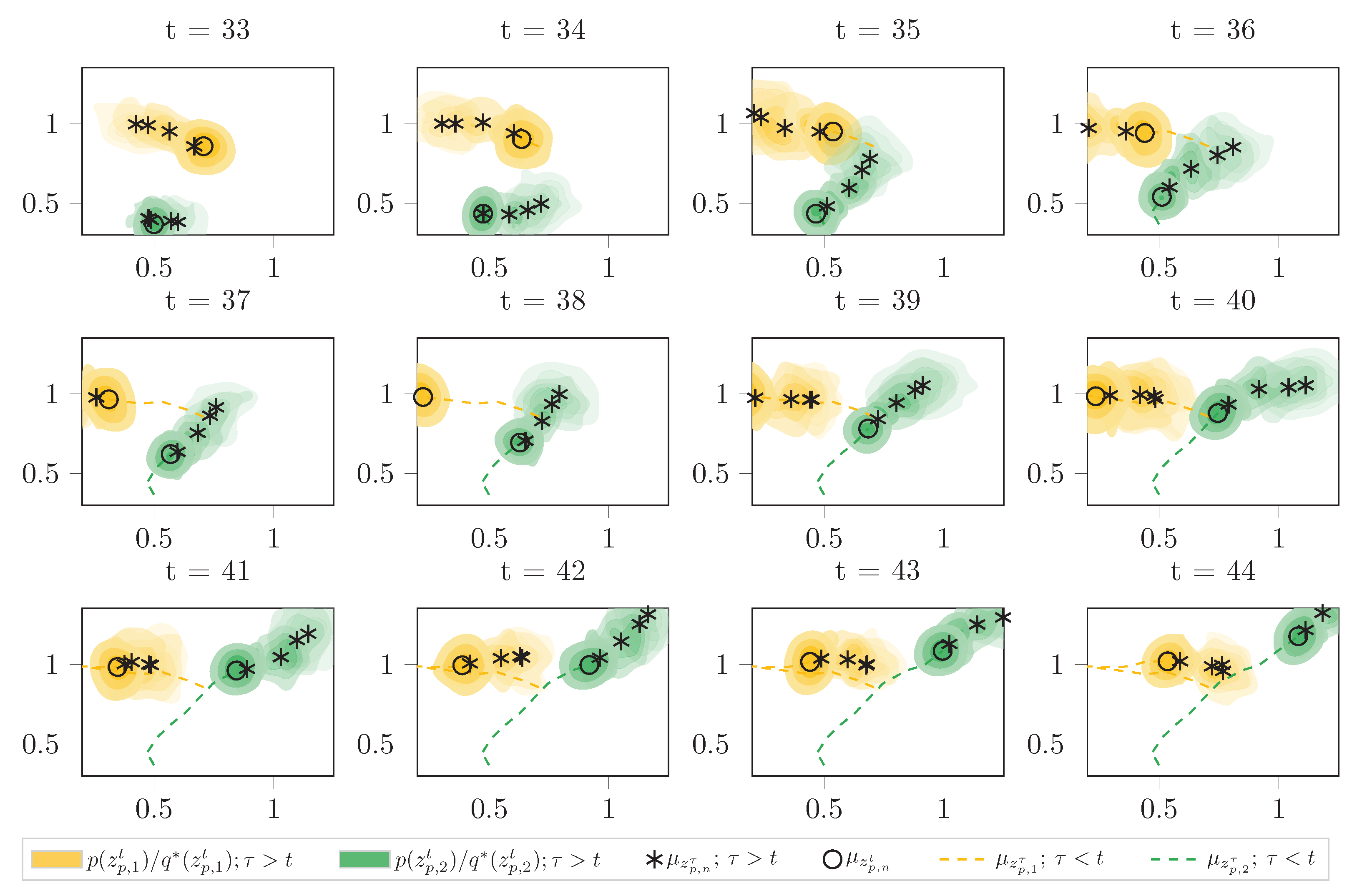
where
, and broadcast the result
to the other vehicles as illustrated in
Figure 2. In practice, to ease the computational burden, some of the terms can be removed from Equation (
29), as only the evaluation of the constraints involving the
n’th robot is non-constant. Overall we have divided the original approximation problem in Equation (
21) into a series of less computationally demanding sub-problems that can be solved distributively by each of the robots. The next section presents a simulation study and a real world experiment utilizing this algorithm to make multiple robots safely navigate the same environment, and we will refer to it as “Stochastic Variational Message-passing for Multi-robot Navigation” (SVMMN).