Abstract
We propose a promising model of discrete spacetime based on nonassociative geometry and complex networks. Our approach treats space as a simplicial 3-complex (or complex network), built from “atoms” of spacetime and entangled states forming n-dimensional simplices (). At large scales, a highly connected network is a coarse, discrete representation of a smooth spacetime. We show that, for high temperatures, the network describes disconnected discrete space. At the Planck temperature, the system experiences phase transition, and for low temperatures, the space becomes a triangulated discrete space. We show that the cosmological constant depends on the Universe’s topology. The “foamy” structure, analogous to Wheeler’s “spacetime foam”, significantly contributes to the effective cosmological constant, which is determined by the Euler characteristic of the Universe.
1. Introduction
In classical general relativity, the cosmological constant, , added in the Einstein equations, governs the Universe’s accelerated expansion. However, the equivalence principle of general relativity requires that every form of energy gravitates similarly. Therefore, accordingly to this principle, the enormous energy of the quantum vacuum fluctuations must produce a large gravitational effect. Moreover, the virtual particles contributing to the vacuum energy density, , should alternate the value of the cosmological constant [1,2]. Although we do not know how to compute precisely, the quantum field theory (QFT) allows one to estimate its value. Unfortunately, the estimates disagree with observational data by a factor of . It is the worst prediction of the theoretical physics, also known as the cosmological constant problem (for a review, see the references [3,4,5,6,7,8,9,10,11,12,13]). There is no generally accepted explanation for this discrepancy, although many papers have been written on it.
In the middle of the last century, Pauli assumed that the vacuum energies of bosons and fermions might compensate for each other [14]. This assumption is based on the fact that the vacuum energy of fermions and bosons have opposite signs: the energy of bosons has a positive sign, whereas that of fermions has a negative one. Later, Zeldovich developed this approach to link the vacuum energy to the cosmological constant. Instead of eliminating the divergences through a boson–fermion cancellation, he suggested a covariant Pauli–Villars regularization yielding the finite residual vacuum energy and negative pressure corresponding to a cosmological constant [1,2].
Recently, the approach based on the Pauli–Zeldovich cancellation of the vacuum energy divergences has been revived to attack the cosmological constant problem by combining both ideas [15,16,17]. The Pauli suggestion was used for canceling all the ultraviolet divergences in the vacuum energy. Zeldovich’s approach was used to prove that the remaining finite part of the vacuum energy yields an effective cosmological constant. Several simple toy models, having particles with equal masses and spin 0 and , illustrated the method, wherein interactions can be quite non-trivial. However, the problem is still far from its resolution.
The standard formulation of the cosmological constant problem is problematic since the spacetime and the vacuum energy density are highly inhomogeneous and wildly fluctuate at the Planck scales. The importance of quantum fluctuations in spacetime topology at small scales has been emphasized by many authors (see, for instance, refs. [18,19,20,21,22,23,24]). Assuming that vacuum fluctuations at the Planck-length scale might generate a cosmological constant requires quantum gravity [3,5,6,8,9,10,11,12]. The search for a quantum theory of gravity faces the challenge of comprehending and describing the quantum nature of space and time [25,26,27]. One can distinguish two general strategies to achieve these goals [28,29]. The first strategy consists of quantizing a classical structure that later is recovered as a limit of the quantum theory. The second strategy assumes that the classical structures are emergent from the other theory, the more fundamental theory from the beginning. In the second approach, a formulation of the quantum theory may require omitting the use of continuum concepts a priori. This means that, at the Planck scale, the standard concept of spacetime must be replaced by some discrete structure (see, for instance, refs. [29,30,31,32,33,34,35,36,37,38,39]).
In [40,41,42,43,44,45,46], we proposed a new unified algebraic approach, based on nonassociative geometry, for describing both continuum and discrete spacetimes. In our model of spacetime, time is quantized, and a random/stochastic process governs the evolution of spacetime geometry. As a result, we obtained a partially ordered set of events with spacetime geometry encoded in the nonassociative structure of spacetime [46]. Among advanced models that propose discreteness, three are related to our work: causal sets [47,48,49], causal dynamical triangulations [32,50,51,52,53,54,55,56] and complex quantum network manifolds (CQNMs) [39,57,58]. The CS and CDT models are based on the hypothesis that spacetime is discrete and causality is a fundamental principle. The CQNM approach treats spacetime as a simplicial complex, with the quantum network states being characterized by quantum occupation numbers assigned to the nodes, links and faces of 2-simplices.
This paper addresses the cosmological constant derivation within the discrete spacetime model proposed in [46] by employing the Pauli–Zeldovich cancellation of vacuum bosonic and fermionic degrees of freedom. We treat 3-dimensional space as a simplicial 3-complex (complex network). Vertices (0-simplices) of the network are the atoms of spacetime, and it is assumed that they are fermions with a spin of 1/2. Edges, or 1-simplices, are entangled particle states and have a spin of 1. The 2-simplex is built from 3 vertices. Thus, the 2-simplex is formed as an entangled state with a total spin of 3/2. The 3-simplex is the entangled state of 4 atoms with a total spin of 2. At large scales, a highly connected complex network is a coarse, discrete representation of a smooth spacetime.
The properties of spacetime are described by methods of statistical physics based on the information Shannon–Gibbs entropy [59,60,61]. For high temperatures, the space is presented by a simpilicial 0-complex (or a disconnected discrete space). When decreasing the temperature of the network, the process of triangulation begins with the formation of low-dimensional complices and clusters. At the Planck temperature, , the system experiences a phase transition; for low temperatures, , the network becomes a simplicial 3-complex (or a triangulated discrete space).
We show that the “foamy” structure, analogous to Wheeler’s “spacetime foam” [18], significantly contributes to the effective cosmological constant, . The latter is defined by the Universe’s Euler characteristic, ; , where denotes the Planck length and V is the volume of the Universe. It is our main result.
The paper is organized as follows. Section 2 discusses the statistical properties of complex undirected networks with a fixed number of vertices and a varying number of links, described by the grand canonical ensemble. As a particular application, we considered in detail simple (fermionic) graphs with only one edge allowed between any pair of vertices. In Section 3, we briefly introduce a discrete spacetime model based on nonassociative geometry. In Section 4, we introduce and explore in detail a spacetime model based on the fermionic network. In Section 5, we derive the cosmological constant and show that the Euler characteristic of the Universe defines it. In the conclusion, we summarize our results and discuss possible generalizations of our approach.
Throughout the paper, we use the natural units, setting .
2. Statistical Description of Complex Networks
Unlike the conventional approach to statistical mechanics, where the Gibbs distribution is derived by assuming a system in weak interaction with the environment, the statistical description of complex networks is based on the informational Shannon–Gibbs entropy, subject to certain constraints [59,60,61]. For a graph , belonging to an ensemble of graphs , let us denote by the probability of obtaining this graph. Then, the Shannon–Gibbs entropy reads
Assume that the following constraints are imposed: and , where is the graph Hamiltonian, and E is the expectation value of the energy of the system. Next, employing the principle of maximum entropy,
where and are the Lagrange multipliers, we obtain the Gibbs distribution:
where the partition function is given by
Using these results, we obtain
The relation shows that the Lagrange multiplier is the inverse “temperature” of the network.
For an undirected network with a fixed number of vertices and a varying number of links, the probability of obtaining a graph G can be written as [59,62,63,64]
where is the partition function, is an inverse network temperature, is the chemical potential and is the number of links in the graph G. An adjacency matrix, , takes a value of 1 or 0 in the entry for each existing or non-existing link between pairs of nodes (). The network connectivity is characterized by the connection probability , i.e., the probability that a pair of nodes is connected. This probability is equivalent to the expected number of edges between vertices i and j, namely .
To obtain the grand potential, , which we will refer to as the Landau free energy, we use the relation . Next, one can recover the Helmholtz free energy F, internal energy E and entropy S using the following relations:
At last, with Landau free energy, one can find the expected number of links: .
Let us assign the “energy” to each edge . Then, the graph Hamiltonian can be written as , and the partition function is given by [63]
Using the partition function, one can obtain the connection probability of the existing link between nodes i and j as the derivative of the partition function [65,66,67,68]:
Fermionic Graphs
Consider a set of undirected graphs with only one edge allowed between any pair of vertices (so-called fermionic graphs). The computation of the partition function yields
where the product is over the ordered pairs . Employing Equation (10), we obtain the Fermi–Dirac distribution [59]:
Using the relation , we obtain
The computation of the expected number of links, , yields
3. Building Discrete Spacetime
Our approach is based on nonassociative geometry, a statistical description of complex networks, and the following assumptions [42,46,69]:
- Vertices or nodes of the network are “atoms” of spacetime.
- The distance between two neighboring atoms cannot be less than the fundamental length, .
- Spacetime geometry is encoded in the nonassociative structure of the network.
- The interaction between atoms of spacetime, being nonlocal, defines the spacetime geometry.
- Time is quantized and the evolution of spacetime geometry is governed by a random/stochastic process.
- The spacetime dimension is a dynamical variable.
We treated a discrete space as a simplicial 3-complex (see Figure 1). Vertices (0-simplices) of the network are the atoms of spacetime, and it was assumed that they are fermions with a spin of 1/2. Edges, or 1-simplices, are entangled particle states with a spin of 1. The 2-simplex is built from 3 entangled atoms; its total spin is . The 3-simplex has 4 atoms. It is considered as the entangled state with a spin of 2.
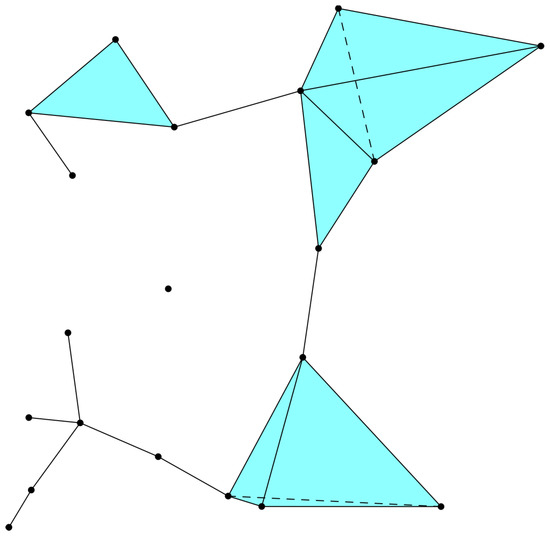
Figure 1.
A network presented as a simplicial 3-complex.
The curvature of 2-simplices is associated with their faces and described by an elementary holonomy. It contrasts the Regge model, where curvature resides at vertices [70,71,72]. The elementary holonomy of a 2-simplex can be written as , where is its area, is the curvature and an upper/lower sign corresponds to positive/negative curvature, respectively. The null curvature corresponds to the limit .
As an example, consider the homogeneous network with positive curvature. This network can be mapped onto the two-dimensional sphere with radius R, which we treat as a discrete toy model of the two-dimensional Universe (see Figure 2: Left). The network is wholly disconnected, and the space is represented by the simplicial 0-complex (Middle), which is a partially triangulated space, described by a simplicial 2-complex. Together with isolated 0-simplices and 1-simplices, one can observe the formation of two-dimensional clusters connected by simplicial 1-complexes (Right). The network becomes completely connected, corresponding to the triangulated space.

Figure 2.
Homogeneous discrete space with positive curvature. Left: a simplicial 0-complex (a non-triangulated, completely disconnected space). Middle: a simplicial 2-complex (a partially triangulated space). Right: a homogeneous simplicial 2-complex (a triangulated space).
4. Spacetime as a Complex Network
A simplicial complex admits only one link between two given nodes. Therefore, only fermionic graphs can be used for its description as a complex network. In what follows, we consider the modified version of the Hamiltonian proposed in [69],
Here, denotes the elementary holonomy of a 2-simplex associated with the triplet of sites forming a left triangle concerning the edge , and . The first term in (15) describes the contribution of the quantum bosonic vacuum fluctuation and curvature, and the second one represents the quantum fermionic vacuum fluctuations. The summation over 1-simplices and 2-simplices is denoted as and , respectively.
Within the mean field approximation, the Hamiltonian (15) is replaced by the effective Hamiltonian
where the effective energy is given by
The equilibrium state of the system is described by the generalized Fermi–Dirac distribution for the connection probability (12),
Employing Equation (17), one can rewrite (18) in the equivalent form
We assume that the network is highly connected for low temperatures, and that it has a low connectance for high temperatures:
This implies that the space is represented by a simplicial 0-complex for high temperatures (or a completely disconnected discrete space), and it becomes a simplicial 3-complex (or a triangulated space) for low temperatures.
In the limit of low/high temperatures, the energy of the system is given by
where is the total number of edges (1-simplices) of the network, denotes the number of the 2-simplices, and
Here, is the average area of 2-simplices. The dimensionless parameter defines the average curvature of the network. In particular, describes the network with the null average spatial curvature. By employing Equation (21), in the limit of a low temperature, we obtain the vacuum energy density as
where V is the volume of the Universe.
4.1. Toy Homogeneous Model
In what follows, we consider the case of a homogeneous network, assuming that . With this assumption, the Hamiltonian (15) can be recast as follows:
We assume that each 2-simplex is represented by an equilateral triangle with edges of length so that . Using this relation, we obtain
Within the mean-field approximation, the Hamiltonian (24) is replaced by the effective Hamiltonian
where is the total number of 1-simplices, is the total number of 2-simplices of the the network, and is the effective energy. The equilibrium state of the system is described by the Fermi–Dirac distribution,
Substituting , one can rewrite (27) as
In the limit of low/high temperatures, the energy of the system is given by
Equations (20) and (28) impose the following constraints on the chemical potential:
Thus, for , we obtain a triangulated space and, for , the space becomes disconnected.
For illustrative purposes, we chose the dependence of the chemical potential on the temperature to be . The typical behavior of the connection probability is shown in Figure 3. The graph is depicted for the choice of parameters: , and , where is the Planck temperature. One can see that the system experiences a phase transition at the critical temperature forming the fermionic condensate with the maximally entangled states. This transition is quick, and the Universe becomes a wholly triangulated space at the temperature ∼, where ∼ is the temperature of the grand unification epoch beginning.
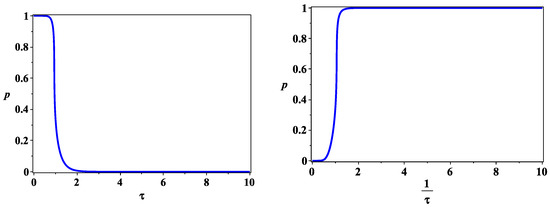
Figure 3.
Connection probability as a function of dimensionless temperature, (left) and inverse dimensionless temperature (right).
4.2. Spacetime Evolution
In our approach, space and time are quantized in the Planck units, and a random/ stochastic process governs spacetime evolution. The cosmological scale factor, , is defined by a random walk with a reflecting barrier at and a step , where is the Planck length. After n steps, the average cosmological scale factor grows as [46]
where is the scale factor related to the initial 3-simplex defining the minimal size of the Universe.
Numerical simulations show that creating the primordial Universe corresponds to the temperature ∼ (see Figure 3). Therefore, considering as the initial time of the Universe’s evolution is reasonable. After ∼ steps in Planck units of time, which correspond to pre-inflationary time, ∼ (time of the beginning of inflation) and temperature , the cosmological scale factor would be ∼. A comparison with the pre-inflationary Universe’s scale factor, ∼, estimated within the CDM-model as , yields a good agreement with our prediction.
We assume that space consists of many fluctuating simplicial regions that grow as “mini-universes” (clusters) and form a multiverse. The mini-universes may merge and create pre-inflationary universes (bubbles). This multiverse state can be metastable and lead to the nucleation of bubbles and their further merging due to the first-order phase transition (inflation). Suppose that the duration of the phase transition is short enough. In this case, the nucleation of bubbles of the new phase and their merging may have an exponential character typical for the inflation era of the Universe.
5. The Cosmological Constant Problem
Writing the Einstein equations as
one can observe that space with a non-zero cosmological constant produces the same gravitational field as matter with mass density and pressure . Thus, one can speak about the energy density of the vacuum and its pressure.
According to the equivalence principle of general relativity, the energy of the quantum vacuum fluctuations must produce a gravitational field, and the semiclassical Einstein equations describe their contribution:
where is the expectation value of the quantum vacuum energy–momentum tensor.
Lorentz invariance requires that takes the form
where is the expectation value of the energy density of the matter fields in the vacuum state. Employing (33), one can recast Equation (31) as
where is the effective (observable) cosmological constant.
The QFT estimates the vacuum density energy as , where is the Planck energy. The current Hubble expansion rate yields an upper bound for [73],
where is the Hubble constant describing the acceleration of the Universe. Thus, one has a huge disagreement between the observed value of the cosmological constant and the theoretical prediction of its value resulting from the QFT.
The general form of the vacuum energy density, including the contribution of different fermionic and bosonic fields, can be written as [74,75,76]
where M is the mass of corresponding field, and is the ultraviolet energy cut-off. In particular, if the vacuum is completely homogeneous and static, all the parameters vanish, corresponding to a zero cosmological constant. In the presence of the interface between two different vacua, the energy density can depend not only on the mass M but also on the mass of the quantum field in the neighboring vacuum [76].
The standard computation of the cosmological constant assumes that the spacetime is homogeneous and isotropic, and that the theory is Lorentz-invariant. These assumptions are reasonable at a cosmological scale but questionable at a small (Planck) scale [73,77,78]. In addition, the QFT cannot be applied on Planckian scales since spacetime is discrete. Instead of QFT, we use the statistical description of the spacetime, treating the latter as a complex network.
Borrowing the approach of the QFT, we define the effective cosmological constant as
where is the energy density of the vacuum state defined by the contribution of all bosonic and fermionic fields of the simplicial complex, . If one takes into account the contributions from all simplices, we obtain
where is the vacuum energy of the i-simplex. Replacing the vacuum energy of simplices by its upper bound, , and assuming , in the limit of , we obtain
where is the number of i-simplices in the network. Employing Eqaution (37), we find
where is the Euler characteristic of the simplicial complex [79]. Thus, a non-vanishing cosmological constant implies a non-trivial topology of spacetime.
To estimate the Euler characteristic, we use Equation (40), writing
where . Unfortunately, the real size of the Universe is unknown. For a lower estimate, we take V as the volume of the observable Universe, . This yields ∼. Taking , we obtain ∼. This huge number means that the topology of spacetime is highly non-trivial due to vacuum fluctuations, which lead to forming a foamy structure, a version of Wheeler’s “spacetime foam” [18].
Remark 1.
If is a simplicial decomposition of the three-dimensional manifold, then [79]. Thus, a non-trivial topology of the Universe is mandatory for a non-vanishing cosmological constant.
6. Discussion and Conclusions
We have shown how complex networks with hidden geometry lead to the emergence of discrete spacetime from entanglement. This phenomenon can be treated as a first-order phase transition from the free fermionic gas to the fermionic condensate formed by maximally entangled states of spacetime’s atoms. This transition and the formation of our Universe occurred before the grand unification epoch.
In our approach, spacetime is treated as an evolving complex network, and a random/stochastic process governs its evolution. The first feature of our model of discrete spacetime is the obvious absence of an initial singularity. The other important feature is a natural emergence of a causal structure and an arrow of time. The irreversibility of evolution occurs due to information loss and the existence of the fundamental Planck length. In the pre-inflation epoch, the cosmological scale factor grows as , which agrees with changing the cosmological scale factor for a radiation-dominated era. The post-inflationary Universe results from the nucleation and merging of baby mini-universes, occurring during a strong first-order phase transition [80,81,82]. The existence of the fundamental length as a minimal admissible length scale in the Universe implies that the emergence of space in the expanding cosmological models is a continuous process. The models with eternal inflation support this point of view [80,83].
Among recent attempts to describe a discrete spacetime, the closest to our approach is the CQNM. The main difference between the CQNM and our model is the method of building the discrete space. Whereas the CQNM treats the discrete space as a simplicial decomposition of the n-dimensional manifold (), in our approach, a three-dimensional simplicial complex presents the discrete space. As a consequence, our model allows for a non-trivial topology compared to the CQNM admitting only trivial topology. Another critical difference is the description of the curvature. In our approach, the curvature is associated with the faces of 2-simplices and presented by the elementary holonomy. The elementary holonomy converts into the manifold’s curvature in the continuous limit. In the CQNM, the curvature is defined on each network node by the degree of the node and the number of triangles passing through the node. The connection with the manifold’s curvature in the continuous limit is an open issue.
We point out that the standard formulation of the cosmological constant problem is problematic since the spacetime and the vacuum energy density are highly inhomogeneous and wildly fluctuate at the Planck scales. We have shown that the non-trivial topology of the Universe is mandatory for a non-vanishing cosmological constant. The “foamy” structure, analogous to Wheeler’s “spacetime foam” [18], significantly contributes to the effective cosmological constant defined by spacetime’s topology. Explicitly, , where is the Euler characteristic of the simplicial complex , and V is its volume. Taking V as the volume of the observable Universe, we find ∼. This enormous number implies that the topology of spacetime is highly non-trivial due to vacuum fluctuations. The fluctuations create the foamy structure that may be formed by micro-universes connected by the Einstein–Rosen bridges with wormhole topology. One can consider the obtained dependence of the cosmological constant on the Euler characteristic as a self-tuning solution to the cosmological constant problem, free from the fine-tuning issue associated with the cosmological constant. Among open issues requiring further study, one can list the contribution of the curvature and vacuum fluctuations of quantum fields to the cosmological constant during the grand unification epoch. Another critical question is: has the observable magnitude of the cosmological constant been gained before or after the inflation epoch? In conclusion, our approach paves the avenue to solving the cosmological constant problem. This work is in progress.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
I would like to thank P. H. Mata Villafuerte for valuable discussions. The present work was supported by the CONACyT (Mexico).
Conflicts of Interest
The author declares no conflict of interest.
References
- Zel’dovich, Y.B. The cosmological constant and the theory of elementary particles. Sov. Phys. Uspekhi 1968, 11, 381. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. The Cosmological Constant and Elementary Particles. JETP Lett. 1967, 6, 316. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problems (Talk given at Dark Matter 2000, February, 2000). arXiv 2000. [Google Scholar] [CrossRef]
- Carroll, S.M.; Press, W.H.; Turner, E.L. The Cosmological Constant. Annu. Rev. Astron. Astrophys. 1992, 30, 499–542. [Google Scholar] [CrossRef]
- Dolgov, A.D. The Problem of Vacuum Energy and Cosmology (A lecture presented at the 4th Colloque Cosmologie, Paris, June, 1997). arXiv 1997. [Google Scholar] [CrossRef]
- Carroll, S.M. The Cosmological Constant. Living Rev. Relativ. 2001, 4, 1. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant–the weight of the vacuum. Phys. Rep. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Rugh, S.; Zinkernagel, H. The quantum vacuum and the cosmological constant problem. Stud. Hist. Philos. Sci. Part Stud. Hist. Philos. Mod. Phys. 2002, 33, 663–705. [Google Scholar] [CrossRef]
- O’Raifeartaigh, C.; O’Keeffe, M.; Nahm, W.; Mitton, S. One hundred years of the cosmological constant: From “superfluous stunt” to dark energy. Eur. Phys. J. H 2018, 43, 73–117. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinsky, A. The Case for a Positive Cosmological Λ-term. Int. J. Mod. Phys. D 2000, 09, 373–443. [Google Scholar] [CrossRef]
- Pauli, W. Pauli Lectures on Physics, Volume VI: Selected Topics in Field Quantization; Pauli Lectures on Physics Delivered in 1950–1951 at the Swiss Federal Institute of Technology; Dover Publications: North Hempstead, NY, USA, 2000. [Google Scholar]
- Kamenshchik, A.Y.; Starobinsky, A.A.; Tronconi, A.; Vardanyan, T.; Venturi, G. Pauli–Zeldovich cancellation of the vacuum energy divergences, auxiliary fields and supersymmetry. Eur. Phys. J. C 2018, 78, 200. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Tronconi, A.; Vacca, G.P.; Venturi, G. Vacuum energy and spectral function sum rules. Phys. Rev. D 2007, 75, 083514. [Google Scholar] [CrossRef]
- Berkov, A.; Narozhny, N.; Okun, L. I Ya Pomeranchuk and Physics at the Turn of the Century; World Scientific: Singapore, 2004. [Google Scholar] [CrossRef]
- DeWitt, C.M.; Wheeler, J.A. Superspace and the Nature of Quantum Geometrodynamics. In Battelle Rencontres: 1967 Lectures in Mathematics and Physics; Benjamin: Tokyo, Japan, 1968. [Google Scholar]
- Hawking, S. Spacetime foam. Nucl. Phys. B 1978, 144, 349–362. [Google Scholar] [CrossRef]
- Hawking, S.W. The Cosmological Constant [and Discussion]. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1983, 310, 303–310. [Google Scholar] [CrossRef]
- Strominger, A. Vacuum Topology and Incoherence in Quantum Gravity. Phys. Rev. Lett. 1984, 52, 1733–1736. [Google Scholar] [CrossRef]
- Carlip, S. Spacetime Foam and the Cosmological Constant. Phys. Rev. Lett. 1997, 79, 4071–4074. [Google Scholar] [CrossRef]
- Carlip, S. Spacetime foam: A review. Rep. Prog. Phys. 2023, 86, 066001. [Google Scholar] [CrossRef]
- Loll, R.; Silva, A. Measuring the homogeneity of the quantum universe. Phys. Rev. D 2023, 107, 086013. [Google Scholar] [CrossRef]
- Ashtekar, A.; Stachel, J. (Eds.) Conceptual Problems of Quantum Gravity; Einstein Studies 2; Birkhüser: Boston, MA, USA, 1991. [Google Scholar]
- Gross, D. (Ed.) The Quantum Structure of Space and Time: Proceedings of the 23rd Solvay Conference on Physics Brussels, Brussels, Belgium, 1–3 December 2005; World Scientific: Singapore, 2007. [Google Scholar]
- Murugan, J.; Weltman, A.; Ellis, G.F.R. (Eds.) Foundations of Space and Time: Reflections on Quantum Gravity; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Oriti, D. (Ed.) Approaches to Quantum Gravity: Toward a New Understanding of Space, Time and Matter; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Butterfield, J.; Isham, C. Spacetime and the Philosophical Challenge of Quantum Gravity. In Physics Meets Philosophy at the Planck Scale; Callender, C., Huggett, N., Eds.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Majid, S.; Polkinghorne, J.; Penrose, R.; Taylor, A.; Connes, A.; Heller, M. On Space and Time; Canto Classics, Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Ambjørn, J. Discrete Quantum Gravity. In Approaches to Quantum Gravity: Toward a New Understanding of Space, Time and Matter; Oriti, D., Ed.; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Loll, R. Discrete Approaches to Quantum Gravity in Four Dimensions. Living Rev. Relativ. 1998, 1, 13. [Google Scholar] [CrossRef] [PubMed]
- ’t Hooft, G. Quantum mechanics, statistics, standard model and gravity. Gen. Relativ. Gravit. 2022, 54, 56. [Google Scholar] [CrossRef]
- Van Raamsdonk, M. Building up spacetime with quantum entanglement. Gen. Relativ. Gravit. 2010, 42, 2323–2329. [Google Scholar] [CrossRef]
- Swingle, B. Spacetime from Entanglement. Annu. Rev. Condens. Matter Phys. 2018, 9, 345–358. [Google Scholar] [CrossRef]
- Padmanabhan, T. Atoms of Spacetime and the Nature of Gravity. J. Phys. Conf. Ser. 2016, 701, 012018. [Google Scholar] [CrossRef]
- Dowker, F. The birth of spacetime atoms as the passage of time. Ann. N. Y. Acad. Sci. 2014, 1326, 18–25. [Google Scholar] [CrossRef]
- Padmanabhan, T. Distribution Function of the Atoms of Spacetime and the Nature of Gravity. Entropy 2015, 17, 7420–7452. [Google Scholar] [CrossRef]
- Bianconi, G.; Rahmede, C. Complex Quantum Network Manifolds in Dimension d > 2 are Scale-Free. Sci. Rep. 2015, 5, 13979. [Google Scholar] [CrossRef] [PubMed]
- Sabinin, L.V. Smooth Quasigroups and Loops; Kluwer Academic Publishers: Dordrecht, The Netherland, 1999. [Google Scholar]
- Nesterov, A.I.; Sabinin, L.V. Non-associative geometry and discrete structure of spacetime. Comment. Math. Univ. Carolin. 2000, 41, 347–358. [Google Scholar]
- Nesterov, A.I.; Sabinin, L.V. Nonassociative geometry: Towards discrete structure of spacetime. Phys. Rev. D 2000, 62, 081501. [Google Scholar] [CrossRef]
- Sabinin, L. Nonassociative Geometry and Discrete Space-Time. Int. J. Theor. Phys. 2001, 40, 351–358. [Google Scholar] [CrossRef]
- Nesterov, A.I.; Sabinin, L.V. Nonassociative Geometry: Friedmann-Robertson-Walker Spacetime. IJGMMP 2006, 3, 1481–1491. [Google Scholar] [CrossRef]
- Nesterov, A. Gravity within the Framework of Nonassociative Geometry. In Non-Associative Algebra and Its Applications; Sabinin, L., Sbitneva, L., Shestakov, I., Eds.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2006; pp. 299–311. [Google Scholar]
- Nesterov, A.I.; Mata, H. How Nonassociative Geometry Describes a Discrete Spacetime. Front. Phys. 2019, 7, 32. [Google Scholar] [CrossRef]
- Dowker, F. Causal Sets and Discrete Spacetime. AIP Conf. Proc. 2006, 861, 79–88. [Google Scholar] [CrossRef]
- Bombelli, L.; Lee, J.; Meyer, D.; Sorkin, R.D. Space-time as a causal set. Phys. Rev. Lett. 1987, 59, 521–524. [Google Scholar] [CrossRef]
- Dowker, F.; Zalel, S. Evolution of universes in causal set cosmology. Comptes Rendus Phys. 2017, 18, 246–253. [Google Scholar] [CrossRef]
- Ambjørn, J.; Carfora, M.; Marzuoli, A. The Geometry of Dynamical Triangulations; Springer: Heidelberg/Berlin, Germany, 1997. [Google Scholar]
- Ambjørn, J.; Loll, R. Non-perturbative Lorentzian quantum gravity, causality and topology change. Nucl. Phys. B 1998, 536, 407–434. [Google Scholar] [CrossRef]
- Loll, R. The emergence of spacetime or quantum gravity on your desktop. Class. Quantum Gravity 2008, 25, 114006. [Google Scholar] [CrossRef]
- Ambjørn, J.; Jurkiewicz, J.; Loll, R. Reconstructing the Universe. Phys. Rev. D 2005, 72, 064014. [Google Scholar] [CrossRef]
- Ambjørn, J.; Jordan, S.; Jurkiewicz, J.; Loll, R. Quantum spacetime, from a practitioner’s point of view. AIP Conf. Proc. 2013, 1514, 60–66. [Google Scholar] [CrossRef]
- Glaser, L.; Loll, R. CDT and cosmology. Comptes Rendus Phys. 2017, 18, 265–274. [Google Scholar] [CrossRef]
- Ambjørn, J.; Görlich, A.; Jurkiewicz, J.; Loll, R. Nonperturbative quantum gravity. Phys. Rep. 2012, 519, 127–210. [Google Scholar] [CrossRef]
- Bianconi, G.; Rahmede, C.; Wu, Z. Complex quantum network geometries: Evolution and phase transitions. Phys. Rev. E 2015, 92, 022815. [Google Scholar] [CrossRef]
- Wu, Z.; Menichetti, G.; Rahmede, C.; Bianconi, G. Emergent Complex Network Geometry. Sci. Rep. 2015, 5, 10073. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Newman, M.E.J. Statistical mechanics of networks. Phys. Rev. E 2004, 70, 066117. [Google Scholar] [CrossRef]
- Squartini, T.; Garlaschelli, D. Maximum-Entropy Networks: Pattern Detection, Network Reconstruction and Graph Combinatorics; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- van der Hoorn, P.; Lippner, G.; Krioukov, D. Sparse Maximum-Entropy Random Graphs with a Given Power-Law Degree Distribution. J. Stat. Phys. 2018, 173, 806–844. [Google Scholar] [CrossRef]
- Garlaschelli, D.; Loffredo, M.I. Maximum likelihood: Extracting unbiased information from complex networks. Phys. Rev. E 2008, 78, 015101. [Google Scholar] [CrossRef] [PubMed]
- Garlaschelli, D.; Ahnert, S.E.; Fink, T.M.A.; Caldarelli, G. Low-Temperature Behaviour of Social and Economic Networks. Entropy 2013, 15, 3148–3169. [Google Scholar] [CrossRef]
- Cimini, G.; Squartini, T.; Saracco, F.; Garlaschelli, D.; Gabrielli, A.; Caldarelli, G. The statistical physics of real-world networks. Nat. Rev. Phys. 2019, 1, 58–71. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J.; Strogatz, S.H.; Watts, D.J. Random graphs with arbitrary degree distributions and their applications. Phys. Rev. E 2001, 64, 026118. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Nesterov, A.I.; Mata Villafuerte, P.H. Complex networks in the framework of nonassociative geometry. Phys. Rev. E 2020, 101, 032302. [Google Scholar] [CrossRef]
- Regge, T. General relativity without coordinates. Il Nuovo Cimento (1955–1965) 1961, 19, 558–571. [Google Scholar] [CrossRef]
- Williams, R.M.; Tuckey, P.A. Regge calculus: A brief review and bibliography. Class. Quantum Gravity 1992, 9, 1409–1422. [Google Scholar] [CrossRef]
- Regge, T.; Williams, R.M. Discrete structures in gravity. J. Math. Phys. 2000, 41, 3964–3984. [Google Scholar] [CrossRef]
- Wang, Q. Reformulation of the Cosmological Constant Problem. Phys. Rev. Lett. 2020, 125, 051301. [Google Scholar] [CrossRef] [PubMed]
- Ossola, G.; Sirlin, A. Considerations concerning the contributionsof fundamental particles to the vacuum energy density. Eur. Phys. J.-Part. Fields 2003, 31, 165–175. [Google Scholar] [CrossRef]
- Akhmedov, E.K. Vacuum energy and relativistic invariance. arXiv 2002. [Google Scholar] [CrossRef]
- Volovik, G.E. On Contributions of Fundamental Particles to the Vacuum Energy. In I Ya Pomeranchuk and Physics at the Turn of the Century; World Scientific: Singapore, 2004; pp. 234–244. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, Z.; Unruh, W.G. How the huge energy of quantum vacuum gravitates to drive the slow accelerating expansion of the Universe. Phys. Rev. D 2017, 95, 103504. [Google Scholar] [CrossRef]
- Carlip, S. Hiding the Cosmological Constant. Phys. Rev. Lett. 2019, 123, 131302. [Google Scholar] [CrossRef] [PubMed]
- Klaus, S. On combinatorial Gauss-Bonnet Theorem for general Euclidean simplicial complexes. Front. Math. China 2016, 11, 1345. [Google Scholar] [CrossRef]
- Guth, A.H. Inflation and eternal inflation. Phys. Rep. 2000, 333–334, 555–574. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Kolb, E.W. First-order inflation. Phys. Scr. 1991, T36, 199–217. [Google Scholar] [CrossRef]
- Linde, A. A brief history of the multiverse. Rep. Prog. Phys. 2017, 80, 022001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).