The Evolution of a Higher-Dimensional FRW Universe with Variable G and Λ and Particle Creation
Abstract
1. Introduction
2. The Metric and Fields Equations
2.1. Thermodynamics Formulations
2.2. The EFEs
3. System of DEs in Redshift Space
4. Cosmological Models
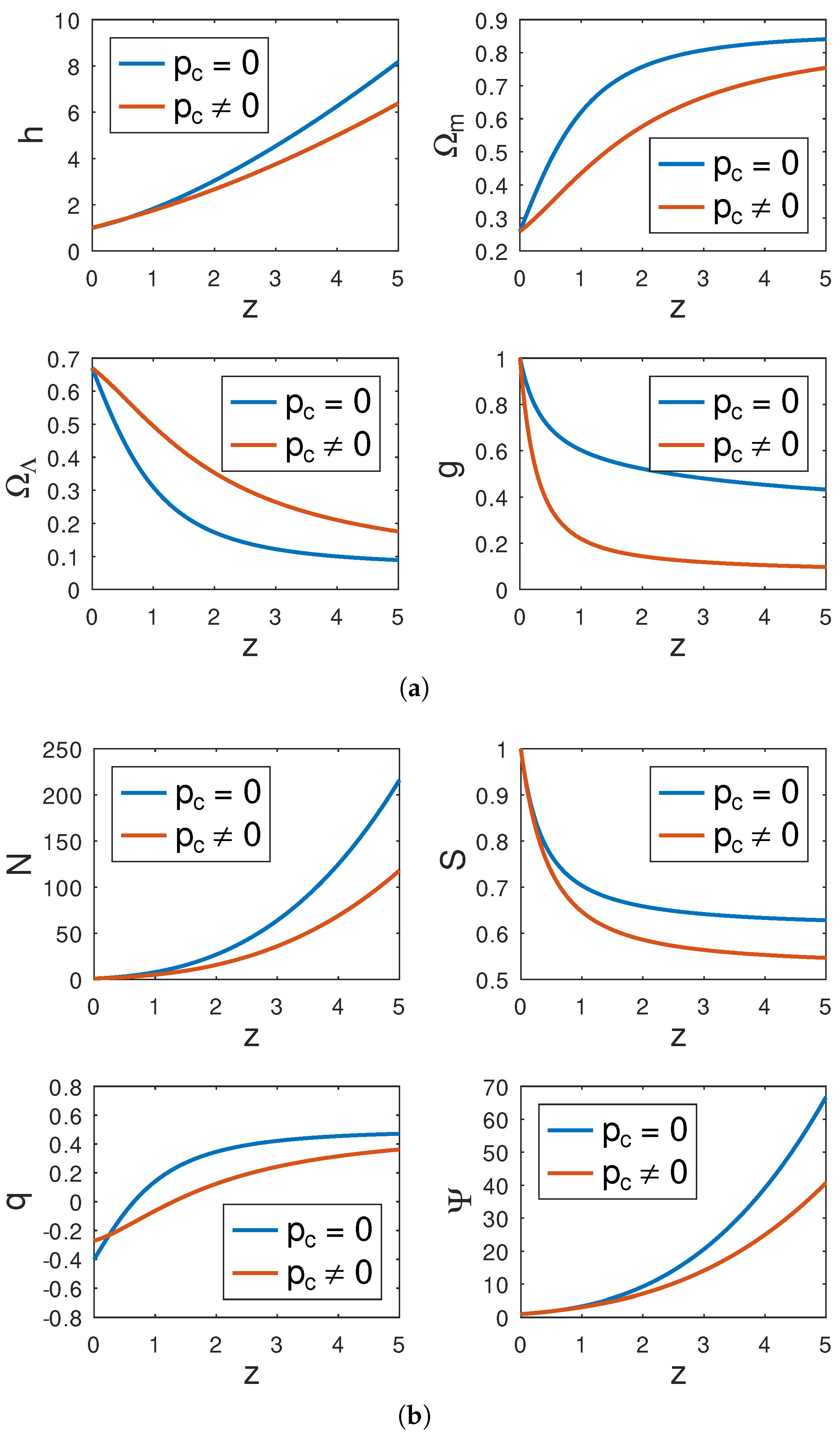
4.1. Model I
- Dust
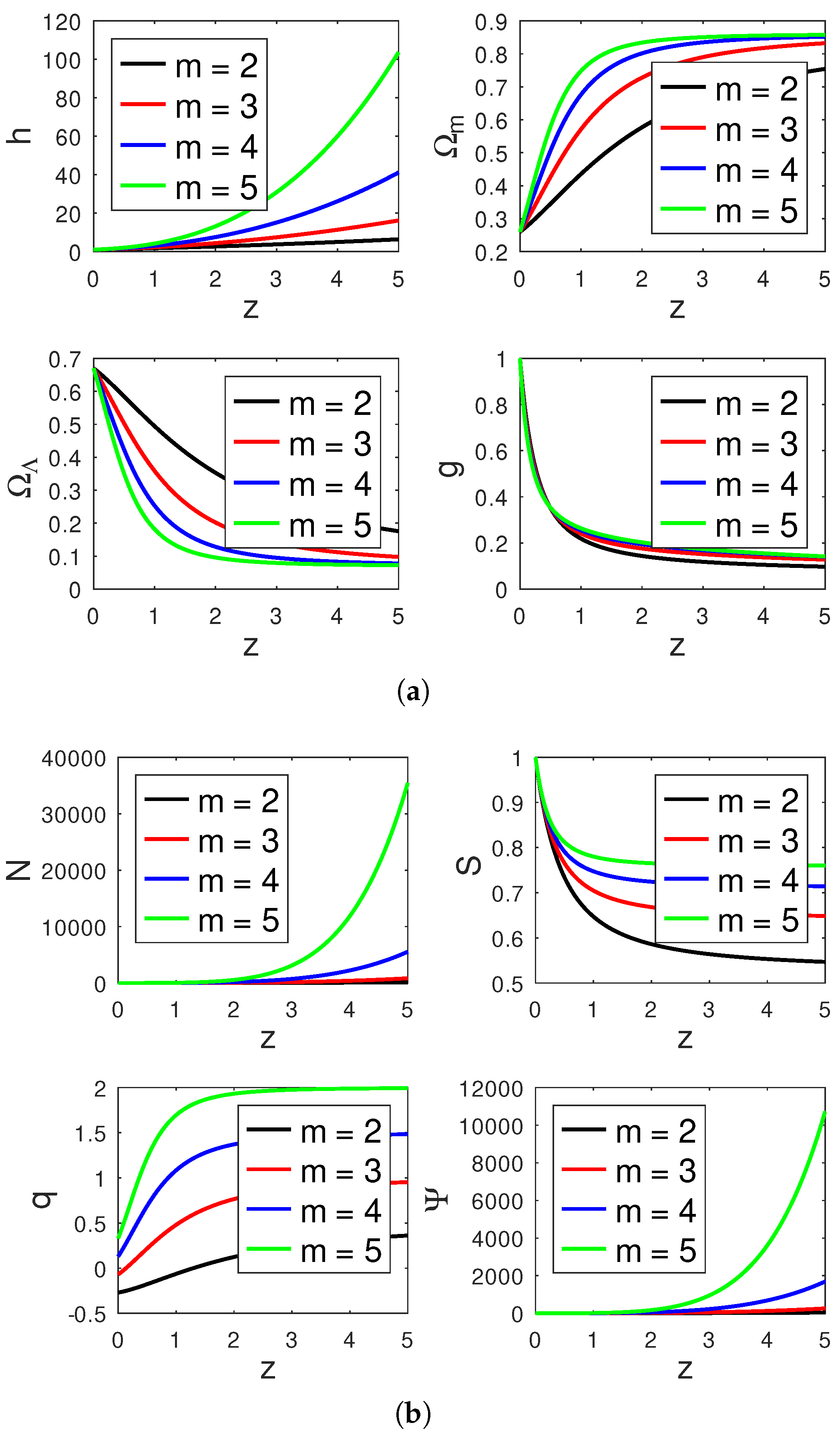
- Radiation
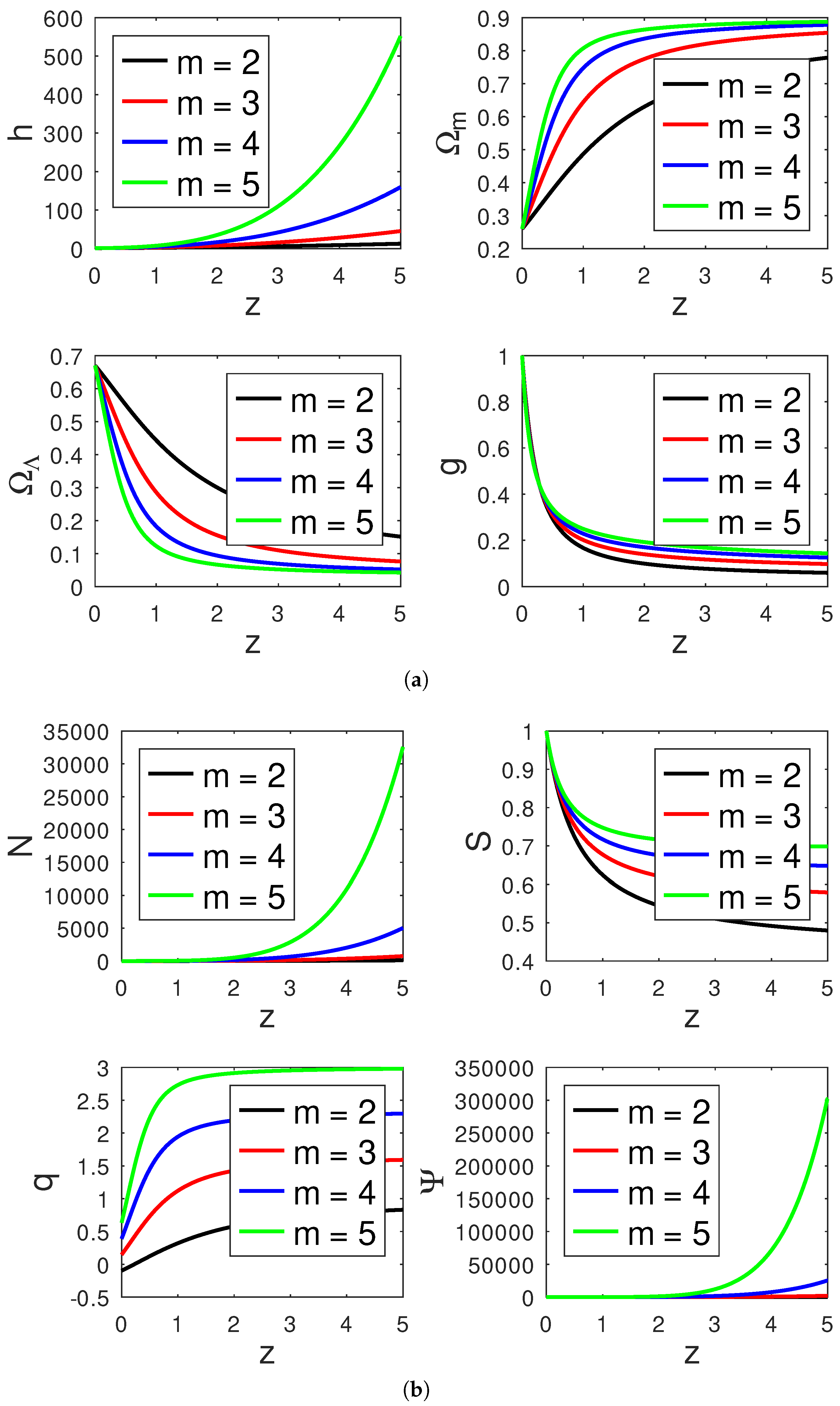
- Dark Energy

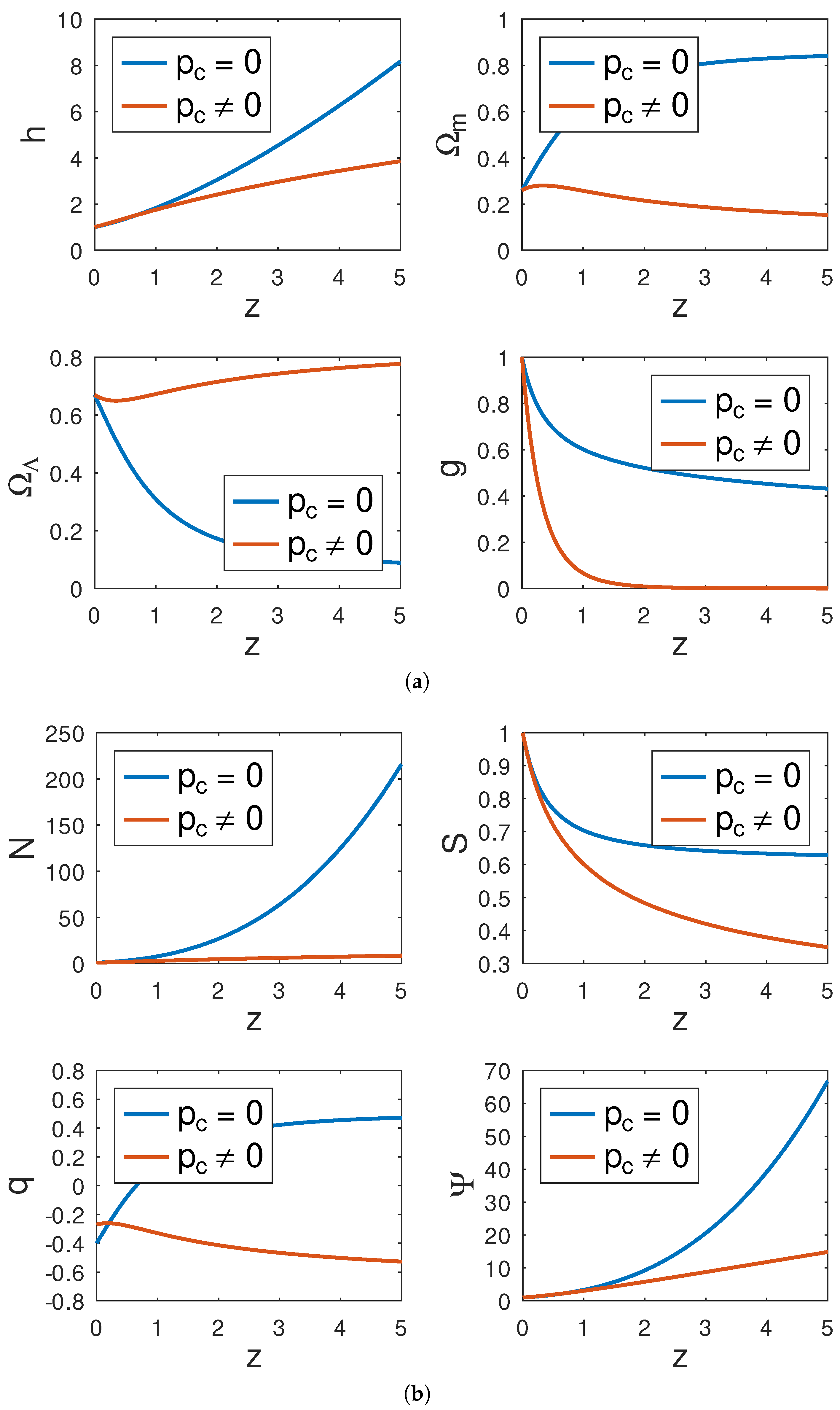
4.2. Model II
- Dust
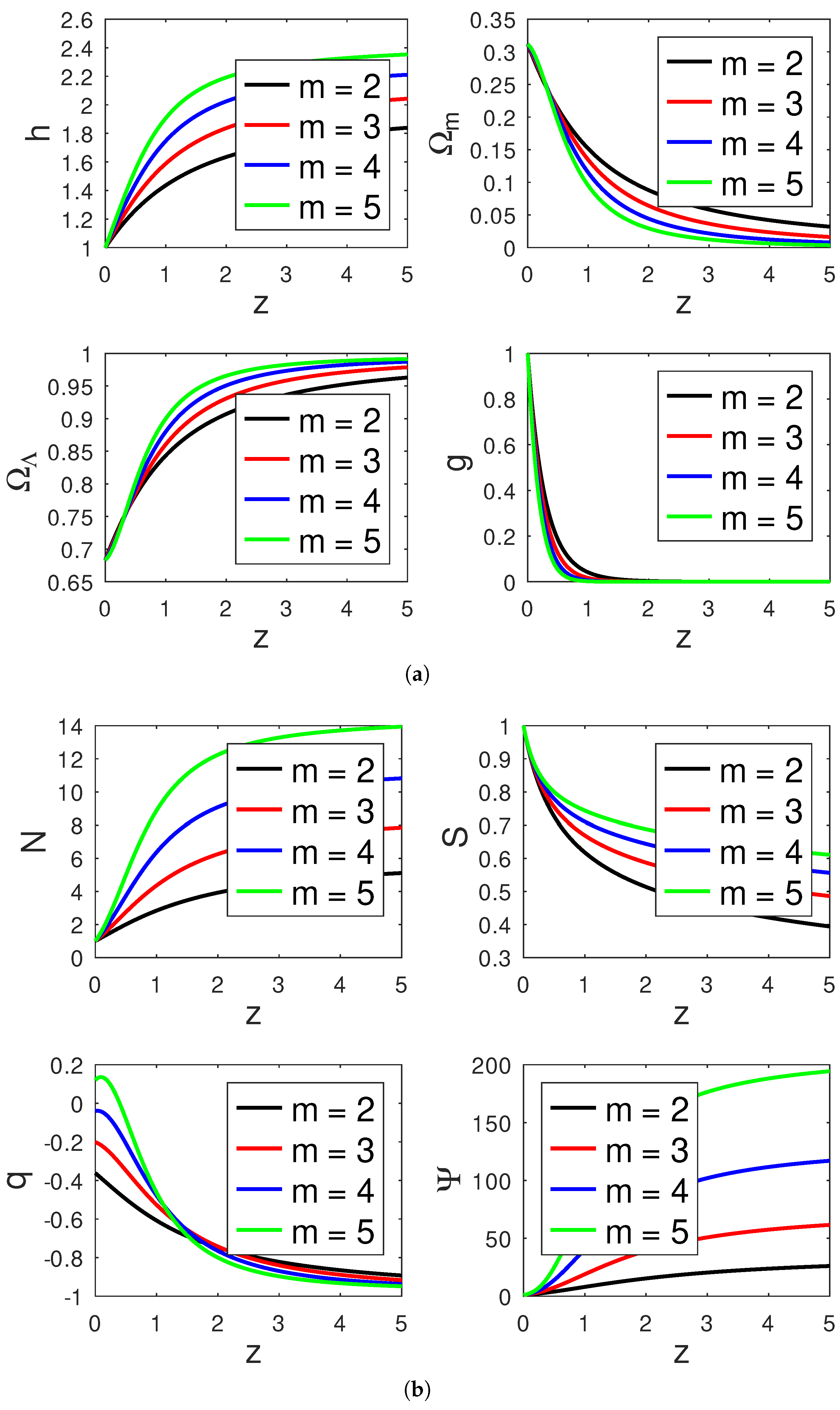
- Radiation
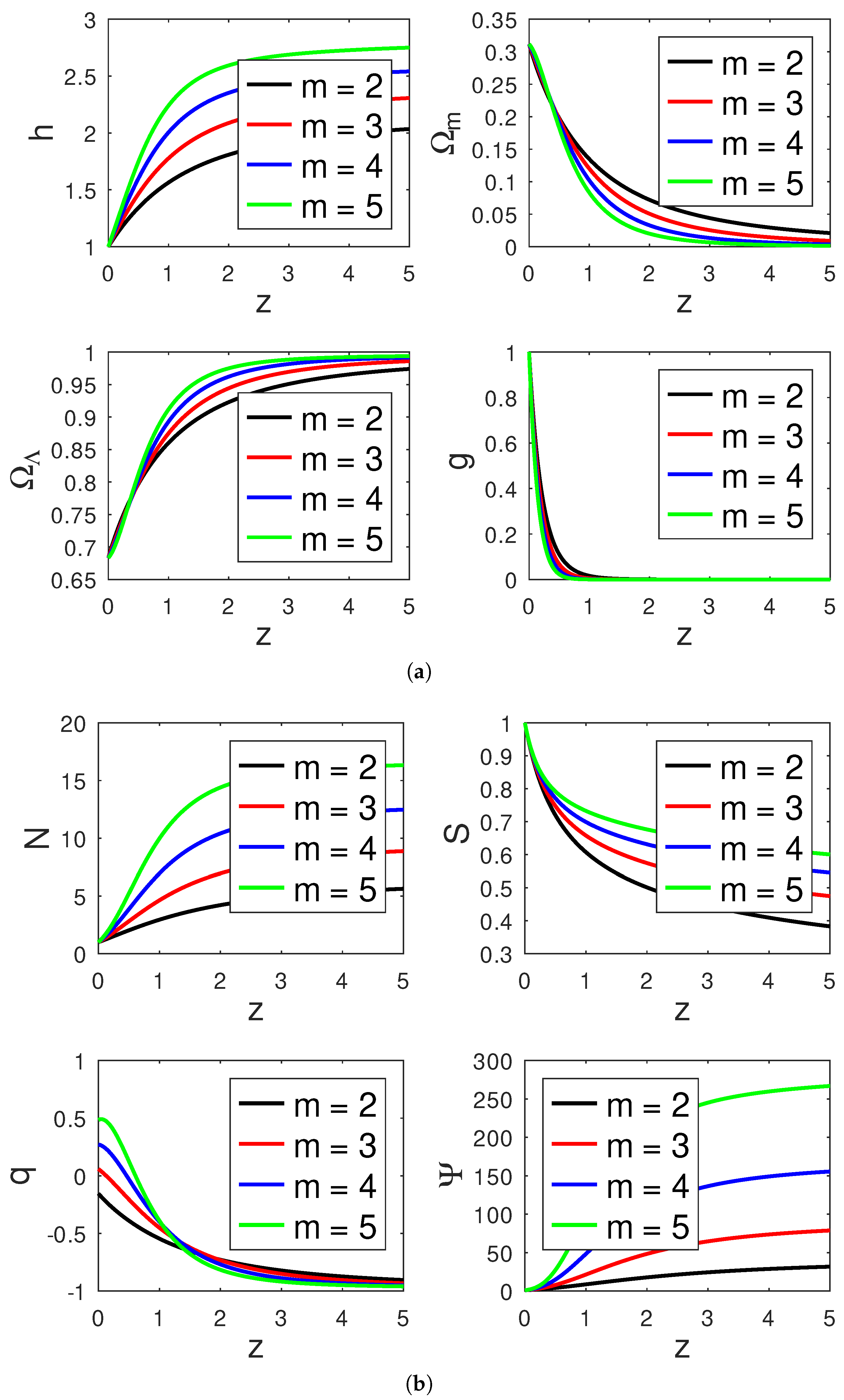
- Dark Energy

5. Conclusions
- The values of h, , , , , and g are in agreement with their expected values today.
- In Model I, the behaviour of q changes depending w and m. For a matter-dominated universe, when , if m is equal to 2 and 3, q takes a negative values less than , and the universe accelerates; if m is equal to 4 and 5, q takes positive values between and , and the universe decelerates; for a radiation-dominated universe, when , if , q changes sign from positive in the past to a negative value in the present time at , and if m = 3,4, and 5, q remains positive and gradually decreases to its current approximated values , respectively; finally, for a dark energy type of fluid, when , if , q is constant and takes the values , respectively.
- In Model II, it is observed that q behaves differently depending on the number of space m and w. For instance, for a matter-dominated universe, when , if m = 2, 3 and 4, q takes negative values between and , the universe expands with negative acceleration, and if , q changes sign from in the past to a value at . For a radiation-dominated universe, when , if , q is negative and asymptotically evolves to rich for large values of z, if , q flips signs from negative in the past to the positive values 0.055, 0.26 and 0.49 at current value of z. Finally, for an energy-dominated universe, when , for , respectively, and the universe expands with a constant rate of acceleration.
- It is noted that, as the universe expands, the particle reduces the amplitude of the physical parameters.
Funding
Data Availability Statement
Conflicts of Interest
References
- Kaluza, T. Zum Unitätsproblem der Physik; Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften: Berlin, Germany, 1921; pp. 966–972. [Google Scholar]
- Klein, O. Quantentheorie und fünfdimensionale Relativitätstheorie. Z. Phys. 1926, 37, 895–906. [Google Scholar] [CrossRef]
- Chodos, A.; Detweiler, S. Where has the fifth dimension gone? Phys. Rev. D 1980, 21, 2167. [Google Scholar] [CrossRef]
- Perlmutter, S.; Gabi1, S.; Goldhaber, G.; Goobar, A.; Groom, D.E.; Hook, I.M.; Kim, A.G.; Kim, M.Y.; Lee1, J.C.; Pain, R.; et al. Measurements of the Cosmological Parameters Ω and Λ from the First Seven Supernovae at z≥0.35. Astrophys. J. 1997, 483, 565. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Valle, M.D.; Deustua, S.; Ellis, R.S.; Fabbro, S.; Fruchter, A.; Goldhaber, G.; Groom, D.E.; Hook, I.M.; et al. Discovery of a supernova explosion at half the age of the Universe. Nature 1998, 391, 51–54. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Dirac, P.A. The cosmological constants. Nature 1937, 139, 323. [Google Scholar] [CrossRef]
- Dirac, P.A.M. A new basis for cosmology. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1938, 165, 199–208. [Google Scholar] [CrossRef]
- Prigogine, I.; Geheniau, J.; Gunzing, E.; Nardone, P. Thermodynamics of cosmological matter creation. Proc. Natl. Acad. Sci. USA 1988, 85, 7428. [Google Scholar] [CrossRef]
- Prigogine, I.; Geheniau, J.; Gunzing, E.; Nardone, P. Thermodynamics and cosmology. Gen. Relativ. Gravity 1989, 21, 767. [Google Scholar] [CrossRef]
- Harko, T.; Mak, M.K. Particle creation in cosmological models with varying gravitational and cosmological “constants”. Gen. Relativ. Gravit. 1999, 31, 849–862. [Google Scholar] [CrossRef]
- Mak, M.K.; Harko, T. Cosmological particle production in five-dimensional Kaluza-Klein theory. Class. Quantum Gravity 1999, 16, 4085. [Google Scholar] [CrossRef]
- Singh, C.P.; Beesham, A. Particle creation in higher dimensional spacetime with variable G and Lambda. Int. J. Theor. Phys. 2012, 51, 3951. [Google Scholar] [CrossRef]
- Dixit, A.; Garg, P.; Pradhan, A. Particle creation in FLRW higher dimensional universe with gravitational and cosmological constants. Can. J. Phys. 2021, 99, 670–680. [Google Scholar] [CrossRef]
- Sevinc, Ö.; Aydiner, E. Particle Creation in Friedmann-Robertson-Walker Universe. Gravit. Cosmol. 2019, 25, 397–406. [Google Scholar] [CrossRef]
- Singh, G.P.; Beesham, A.; Deshpande, R.V. Particle production in higher derivative theory. Pramana 2000, 54, 729–736. [Google Scholar] [CrossRef]
- Calvao, M.O.; Lima, J.A.S.; Waga, I. On the thermodynamics of matter creation in cosmology. Phys. Lett. A 1992, 162, 223. [Google Scholar] [CrossRef]
- Alcaniz, J.S.; Lima, J.A.S. Closed and open FRW cosmologies with matter creation: Kine-matic tests. Astron. Astrophys. 1999, 349, 729. [Google Scholar]
- Lima, J.A.S.; Silva, F.E.; Santos, R.C. Accelerating Cold Dark Matter Cosmology (ΩΛ≡0). Class. Quant. Grav. 2008, 25, 1. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Calvao, M.O.; Waga, I. Cosmology, Thermodynamics and Matter Creation, Frontier Physics, Essay in Honor of Jayme Tiomno; World Scientific: Singapore, 1990. [Google Scholar]
- Steigman, G.; Santos, R.C.; Lima, J.A.S. An accelerating cosmology without dark energy. Astropart. Phys. 2009, 6, 33. [Google Scholar] [CrossRef]
- Singh, S.S.; Chanu, S.K. Particle Production in Higher-Dimensional Universe with Time-Dependent Λ and G. Braz. J. Phys. 2021, 51, 1364–1370. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Rubin, S.G. Black Holes, Cosmology and Extra Dimensions; World Scientific: Singapore, 2013. [Google Scholar]
- Marciano, W.J. Time variation of the fundamental “constants” and Kaluza-Klein theories. Phys. Rev. Lett. 1984, 52, 489. [Google Scholar] [CrossRef]
- Demaret, J.; Hanquin, J.L. Anisotropic Kaluza-Klein cosmologies. Phys. Rev. D 1985, 31, 258. [Google Scholar] [CrossRef]
- Wesson, P.S. Five-Dimensional Physics: Classical and Quantum Consequences of Kaluza-Klein Cosmology; World Scientific: Singapore, 2006. [Google Scholar]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C. Ballardini, M., et al. Planck 2018 results-VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alfedeel, A.H.A. The Evolution of a Higher-Dimensional FRW Universe with Variable G and Λ and Particle Creation. Universe 2023, 9, 255. https://doi.org/10.3390/universe9060255
Alfedeel AHA. The Evolution of a Higher-Dimensional FRW Universe with Variable G and Λ and Particle Creation. Universe. 2023; 9(6):255. https://doi.org/10.3390/universe9060255
Chicago/Turabian StyleAlfedeel, Alnadhief H. A. 2023. "The Evolution of a Higher-Dimensional FRW Universe with Variable G and Λ and Particle Creation" Universe 9, no. 6: 255. https://doi.org/10.3390/universe9060255
APA StyleAlfedeel, A. H. A. (2023). The Evolution of a Higher-Dimensional FRW Universe with Variable G and Λ and Particle Creation. Universe, 9(6), 255. https://doi.org/10.3390/universe9060255






