Estimate of SMBH Spin for Narrow-Line Seyfert 1 Galaxies
Abstract
1. Introduction
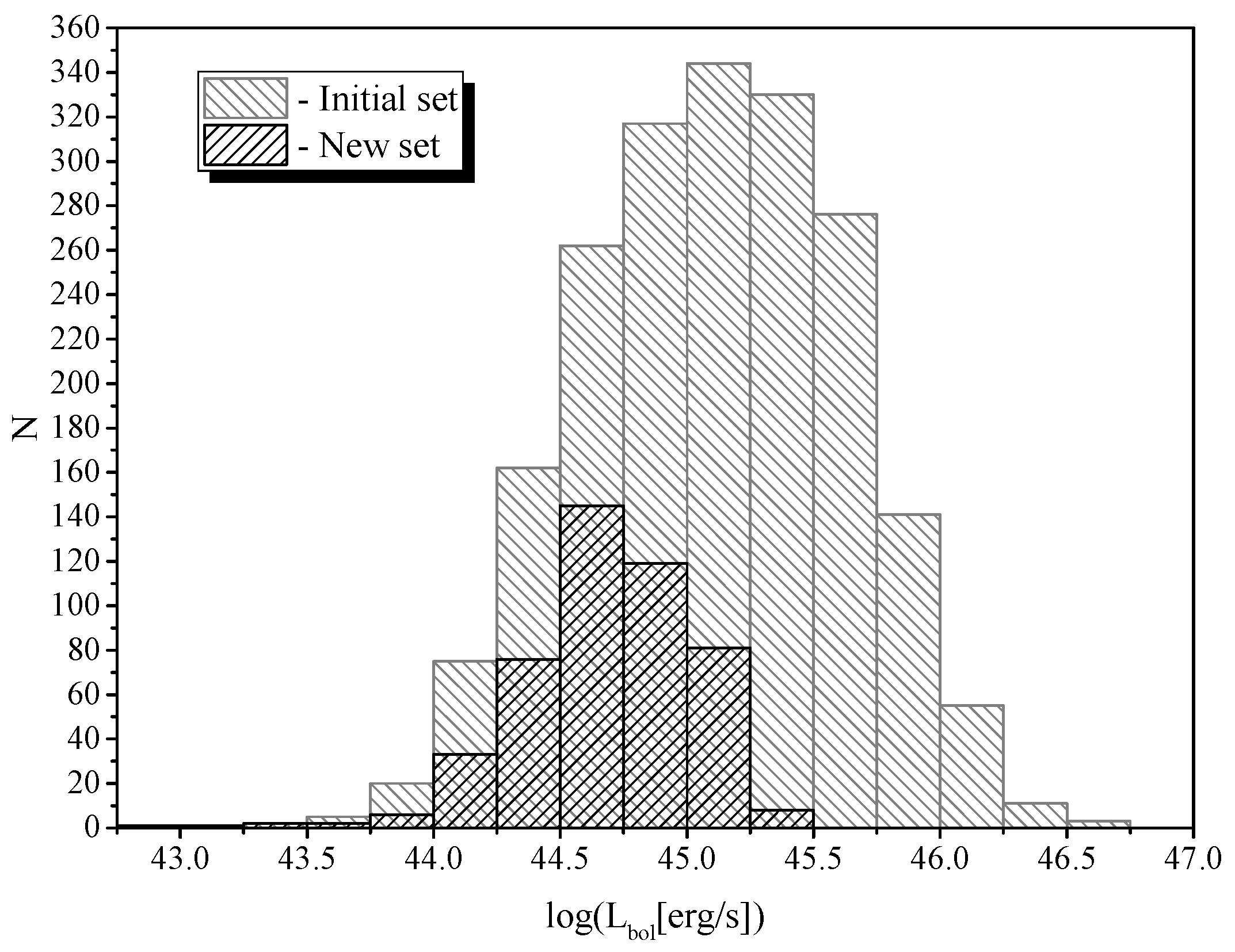
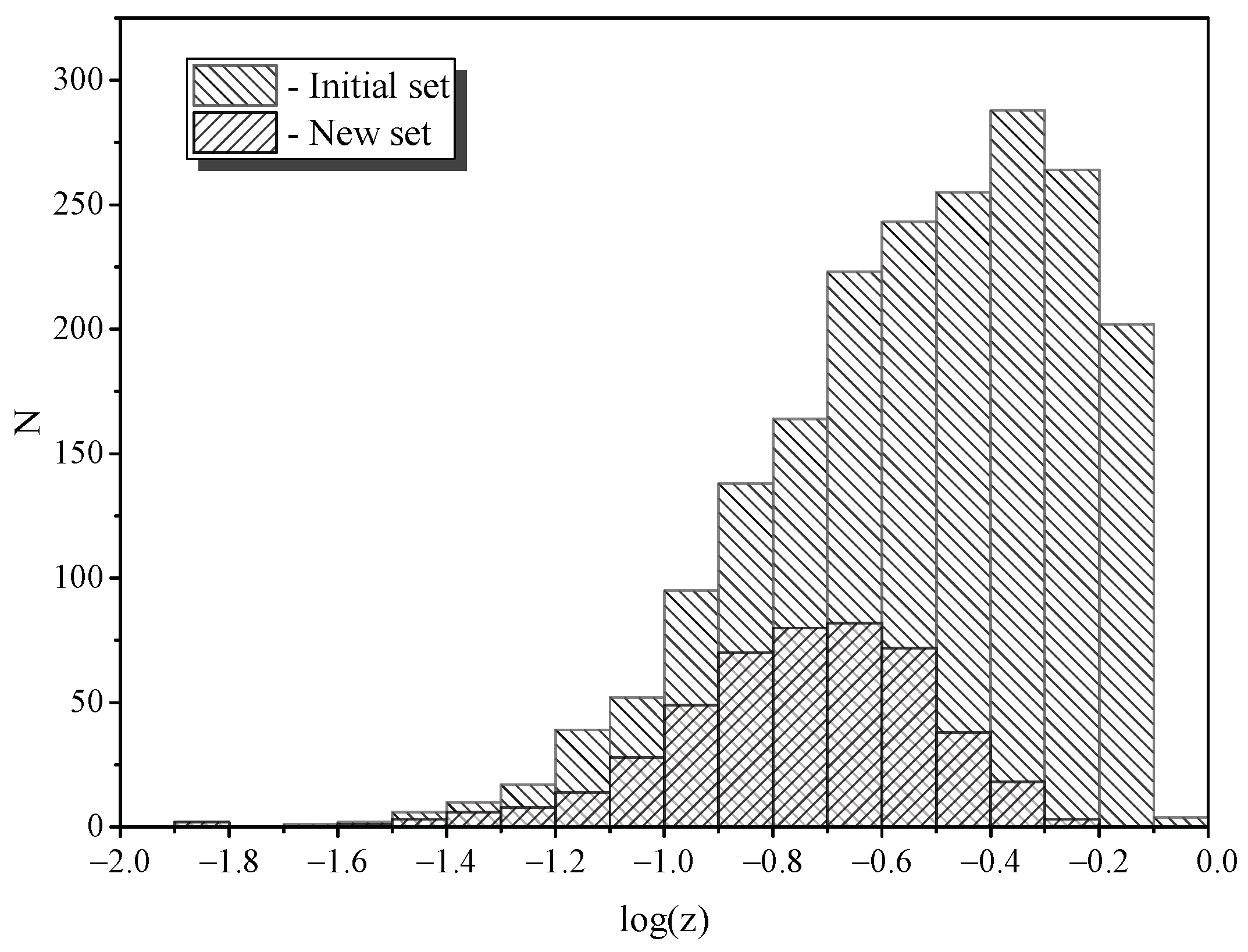
2. Examination of Initial Data
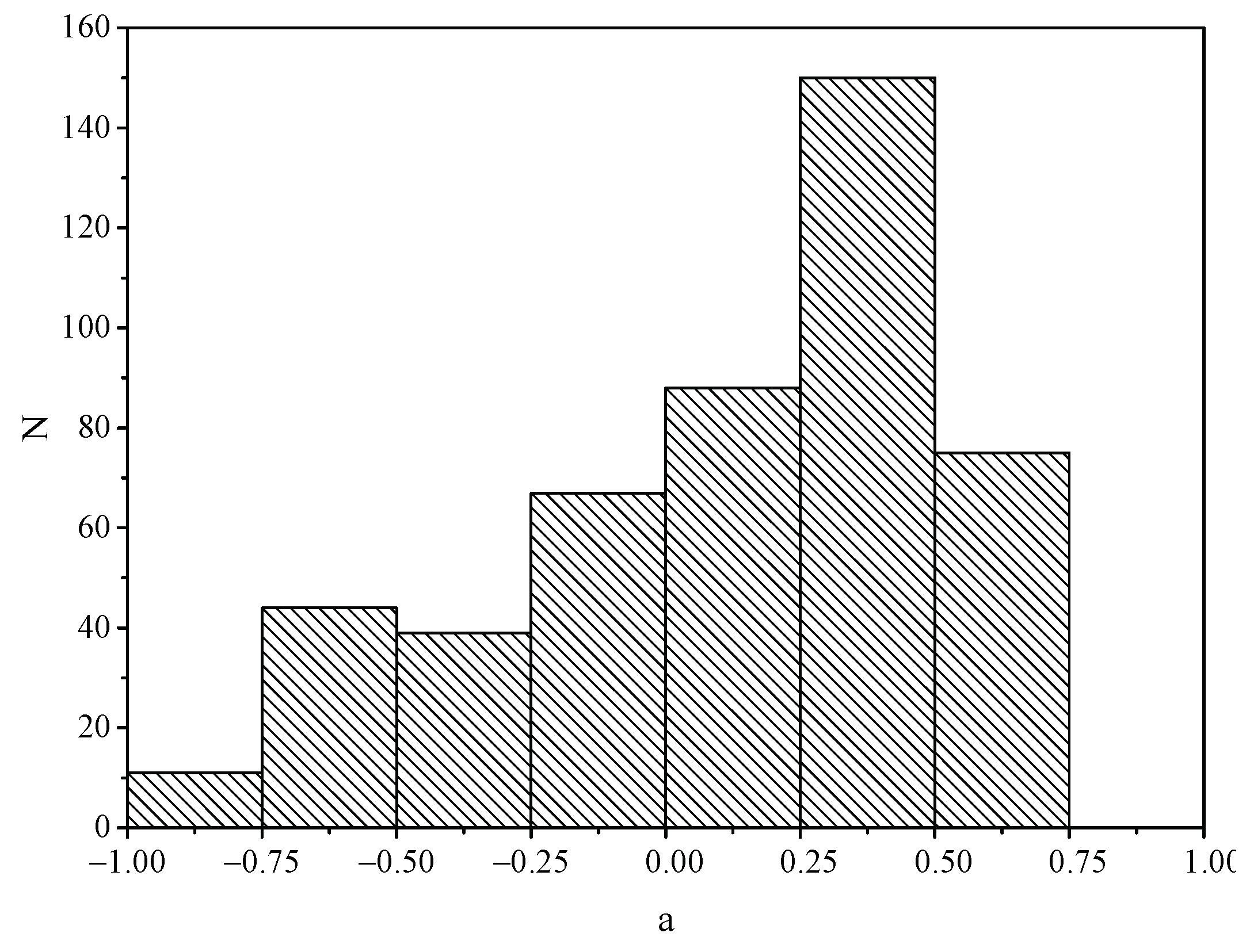
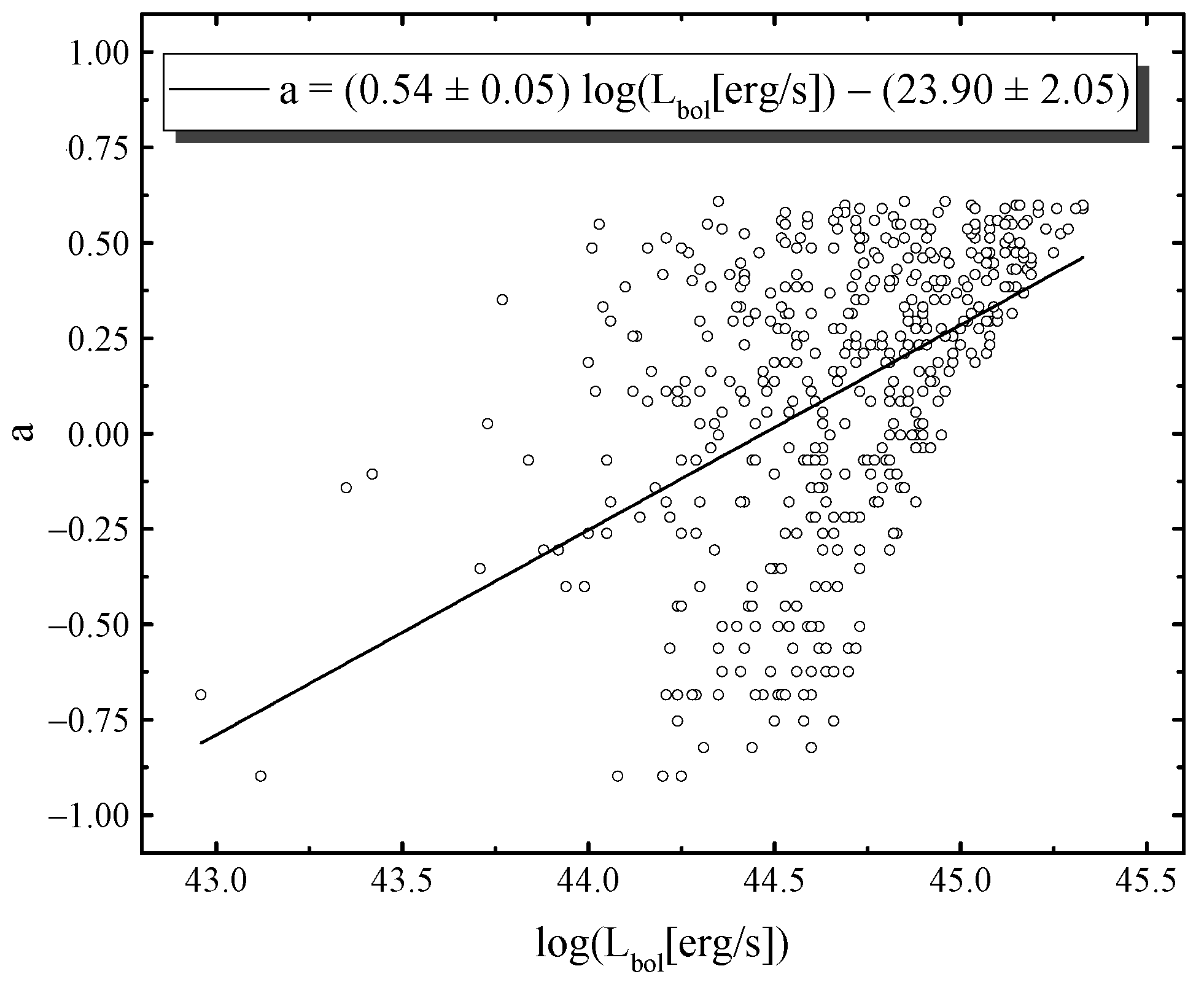
3. Estimation of Spin Values
4. Analysis of Objects Using Estimated Spin Values
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Object | z | a | |||
|---|---|---|---|---|---|
| SDSS J000154.27+000732.4 | 0.139595 | 44.32 | 0.126 | 7.11 | 0.254 |
| SDSS J001010.03+005126.6 | 0.387000 | 45.18 | 0.293 | 7.60 | 0.430 |
| SDSS J001137.24+144201.4 | 0.131834 | 44.74 | 0.165 | 7.41 | 0.512 |
| SDSS J001630.43-093853.5 | 0.239935 | 45.09 | 0.269 | 7.55 | 0.416 |
| SDSS J002053.31+003812.7 | 0.144371 | 44.33 | 0.135 | 7.09 | 0.162 |
| SDSS J002213.00-004832.5 | 0.213941 | 44.54 | 0.195 | 7.14 | −0.038 |
| SDSS J002527.35+160226.8 | 0.110662 | 44.26 | 0.131 | 7.03 | 0.084 |
| SDSS J002752.39+002615.7 | 0.205309 | 44.89 | 0.245 | 7.39 | 0.232 |
| SDSS J002830.95-002402.4 | 0.167345 | 44.56 | 0.147 | 7.28 | 0.416 |
| SDSS J002947.82-002258.5 | 0.228873 | 44.81 | 0.228 | 7.34 | 0.210 |
| SDSS J003238.20-010035.2 | 0.091861 | 44.38 | 0.147 | 7.10 | 0.136 |
| SDSS J003542.67+004735.1 | 0.148886 | 44.42 | 0.183 | 7.05 | −0.180 |
| SDSS J003644.72+160830.7 | 0.465128 | 45.13 | 0.259 | 7.61 | 0.512 |
| SDSS J003646.45+145936.9 | 0.089210 | 44.05 | 0.125 | 6.84 | −0.262 |
| SDSS J003711.00+002127.8 | 0.235101 | 44.96 | 0.235 | 7.48 | 0.400 |
| SDSS J003803.51+145057.3 | 0.138844 | 44.60 | 0.282 | 7.04 | −0.686 |
| SDSS J003846.90+150708.1 | 0.438353 | 45.19 | 0.295 | 7.61 | 0.446 |
| SDSS J004241.90+150926.1 | 0.101278 | 44.36 | 0.151 | 7.07 | 0.056 |
| SDSS J004742.58-004249.7 | 0.147298 | 44.63 | 0.229 | 7.16 | −0.142 |
| SDSS J004809.94+151454.5 | 0.114583 | 44.24 | 0.127 | 7.03 | 0.110 |
| SDSS J010009.31+010115.1 | 0.312451 | 44.94 | 0.193 | 7.54 | 0.580 |
| SDSS J010044.84+144535.9 | 0.291464 | 44.90 | 0.295 | 7.32 | −0.038 |
| SDSS J010407.00+011412.9 | 0.311880 | 45.26 | 0.275 | 7.71 | 0.590 |
| SDSS J010546.50+000704.9 | 0.263738 | 44.76 | 0.188 | 7.38 | 0.384 |
| SDSS J010950.84+152730.8 | 0.179014 | 44.60 | 0.277 | 7.05 | −0.686 |
| SDSS J011009.01-100843.5 | 0.058116 | 44.00 | 0.118 | 6.82 | −0.262 |
| SDSS J012801.99+135551.0 | 0.409060 | 44.82 | 0.242 | 7.33 | 0.136 |
| SDSS J013521.68-004402.1 | 0.098500 | 44.55 | 0.184 | 7.17 | 0.084 |
| SDSS J013556.98+003056.9 | 0.137892 | 44.42 | 0.215 | 6.98 | −0.564 |
| SDSS J014019.06-092110.4 | 0.135279 | 44.73 | 0.285 | 7.17 | −0.354 |
| SDSS J014105.88-100948.1 | 0.126420 | 44.64 | 0.262 | 7.11 | −0.402 |
| SDSS J014153.62+125726.9 | 0.198901 | 44.73 | 0.162 | 7.41 | 0.512 |
| SDSS J014248.31-100840.1 | 0.090390 | 44.51 | 0.154 | 7.21 | 0.274 |
| SDSS J014248.86+142125.9 | 0.133879 | 44.64 | 0.286 | 7.07 | −0.624 |
| SDSS J014559.44+003524.7 | 0.165335 | 44.45 | 0.140 | 7.19 | 0.314 |
| SDSS J014951.65+002536.4 | 0.252437 | 44.92 | 0.197 | 7.52 | 0.536 |
| SDSS J015046.68+132359.9 | 0.094126 | 44.06 | 0.122 | 6.87 | −0.180 |
| SDSS J015219.33+141206.5 | 0.248238 | 45.12 | 0.264 | 7.59 | 0.474 |
| SDSS J015313.07-091418.7 | 0.298273 | 44.88 | 0.287 | 7.31 | −0.038 |
| SDSS J020132.56+002353.2 | 0.078002 | 44.10 | 0.089 | 7.04 | 0.384 |
| SDSS J020844.09+140332.9 | 0.361032 | 45.25 | 0.307 | 7.65 | 0.474 |
| SDSS J021529.30-001448.0 | 0.180980 | 44.66 | 0.153 | 7.37 | 0.486 |
| SDSS J022008.96-090410.0 | 0.231675 | 44.97 | 0.229 | 7.50 | 0.446 |
| SDSS J022226.12-085701.3 | 0.166732 | 44.74 | 0.252 | 7.23 | −0.070 |
| SDSS J022347.48-083655.7 | 0.260775 | 45.02 | 0.275 | 7.47 | 0.294 |
| SDSS J022821.38-082106.2 | 0.171374 | 44.56 | 0.263 | 7.03 | −0.624 |
| SDSS J023038.88-000114.5 | 0.133688 | 44.60 | 0.211 | 7.16 | −0.070 |
| SDSS J023315.91-081633.4 | 0.265553 | 44.88 | 0.285 | 7.31 | −0.004 |
| SDSS J023414.57+005708.0 | 0.269222 | 44.81 | 0.307 | 7.21 | −0.306 |
| SDSS J024225.87-004142.6 | 0.382742 | 44.59 | 0.186 | 7.21 | 0.136 |
| SDSS J024546.10-085842.2 | 0.148299 | 44.87 | 0.210 | 7.44 | 0.400 |
| SDSS J024621.02+001919.0 | 0.182892 | 44.66 | 0.198 | 7.25 | 0.162 |
| SDSS J024727.54-001041.5 | 0.339179 | 45.04 | 0.232 | 7.57 | 0.512 |
| SDSS J024934.59-082742.6 | 0.520684 | 45.23 | 0.284 | 7.67 | 0.536 |
| SDSS J025416.89-084544.0 | 0.302060 | 45.01 | 0.249 | 7.50 | 0.400 |
| SDSS J030639.57+000343.1 | 0.107344 | 44.87 | 0.229 | 7.40 | 0.294 |
| SDSS J031532.27+005503.5 | 0.487399 | 45.13 | 0.265 | 7.60 | 0.486 |
| SDSS J031722.16-065343.0 | 0.156204 | 44.34 | 0.148 | 7.06 | 0.026 |
| SDSS J032801.70+002100.1 | 0.322078 | 44.93 | 0.214 | 7.49 | 0.460 |
| SDSS J033502.22-005637.9 | 0.193281 | 44.69 | 0.242 | 7.20 | −0.106 |
| SDSS J034131.94-000933.0 | 0.223370 | 44.66 | 0.252 | 7.15 | −0.262 |
| SDSS J035827.45-050535.1 | 0.199733 | 44.53 | 0.145 | 7.26 | 0.384 |
| SDSS J073606.62+375038.8 | 0.262155 | 44.81 | 0.276 | 7.26 | −0.106 |
| Object | z | a | |||
|---|---|---|---|---|---|
| SDSS J073642.77+320915.4 | 0.184817 | 44.91 | 0.224 | 7.45 | 0.384 |
| SDSS J074035.86+402234.6 | 0.177275 | 44.51 | 0.234 | 7.03 | −0.506 |
| SDSS J074255.78+234252.4 | 0.336502 | 44.92 | 0.266 | 7.39 | 0.162 |
| SDSS J074548.27+284838.0 | 0.158396 | 44.89 | 0.283 | 7.33 | 0.026 |
| SDSS J074615.57+302400.4 | 0.206192 | 44.50 | 0.169 | 7.16 | 0.136 |
| SDSS J074906.25+354133.7 | 0.225995 | 44.63 | 0.220 | 7.18 | −0.070 |
| SDSS J074940.91+375508.2 | 0.116532 | 44.41 | 0.180 | 7.04 | −0.180 |
| SDSS J075141.57+353914.8 | 0.306203 | 45.08 | 0.295 | 7.50 | 0.294 |
| SDSS J075209.09+414235.5 | 0.258357 | 45.10 | 0.295 | 7.52 | 0.314 |
| SDSS J075347.92+240429.7 | 0.320213 | 45.03 | 0.272 | 7.49 | 0.314 |
| SDSS J075433.59+401209.2 | 0.519061 | 44.80 | 0.266 | 7.26 | −0.070 |
| SDSS J075525.29+391109.8 | 0.033513 | 44.22 | 0.172 | 6.87 | −0.564 |
| SDSS J075606.59+292501.9 | 0.160578 | 44.30 | 0.159 | 6.99 | −0.180 |
| SDSS J075613.68+391513.4 | 0.298794 | 45.05 | 0.275 | 7.50 | 0.332 |
| SDSS J075616.70+252410.9 | 0.284962 | 45.03 | 0.209 | 7.60 | 0.598 |
| SDSS J075659.43+240846.0 | 0.376471 | 44.95 | 0.308 | 7.35 | −0.004 |
| SDSS J075838.13+414512.4 | 0.093531 | 44.44 | 0.177 | 7.08 | −0.070 |
| SDSS J075922.36+332709.0 | 0.137888 | 44.32 | 0.097 | 7.22 | 0.548 |
| SDSS J080135.10+270214.1 | 0.191474 | 44.66 | 0.292 | 7.08 | −0.624 |
| SDSS J080203.03+435940.1 | 0.074398 | 44.01 | 0.073 | 7.04 | 0.486 |
| SDSS J080252.91+314226.1 | 0.483675 | 45.14 | 0.265 | 7.61 | 0.500 |
| SDSS J080416.30+292721.6 | 0.443993 | 44.94 | 0.288 | 7.37 | 0.084 |
| SDSS J080439.54+315809.4 | 0.374000 | 45.13 | 0.246 | 7.63 | 0.558 |
| SDSS J080515.99+334548.6 | 0.247069 | 44.60 | 0.229 | 7.13 | −0.220 |
| SDSS J080538.22+244214.8 | 0.098837 | 44.24 | 0.186 | 6.86 | −0.686 |
| SDSS J080710.87+245105.9 | 0.328634 | 45.08 | 0.251 | 7.57 | 0.474 |
| SDSS J080742.46+375332.1 | 0.229941 | 45.01 | 0.272 | 7.47 | 0.294 |
| SDSS J080807.15+251545.6 | 0.233955 | 44.70 | 0.200 | 7.29 | 0.232 |
| SDSS J081231.43+441620.8 | 0.296883 | 45.33 | 0.299 | 7.74 | 0.590 |
| SDSS J081252.45+402348.8 | 0.188447 | 44.82 | 0.170 | 7.48 | 0.568 |
| SDSS J081321.36+393109.0 | 0.204989 | 44.77 | 0.276 | 7.22 | −0.180 |
| SDSS J081345.89+381049.7 | 0.079960 | 44.21 | 0.090 | 7.15 | 0.512 |
| SDSS J081422.67+293419.0 | 0.224970 | 44.71 | 0.189 | 7.32 | 0.314 |
| SDSS J081427.49+031031.3 | 0.436499 | 45.15 | 0.297 | 7.57 | 0.384 |
| SDSS J081427.69+433705.1 | 0.224183 | 45.12 | 0.257 | 7.60 | 0.500 |
| SDSS J081503.09+293649.5 | 0.264458 | 44.96 | 0.191 | 7.57 | 0.608 |
| SDSS J081516.87+460430.8 | 0.041184 | 44.29 | 0.196 | 6.89 | −0.686 |
| SDSS J081823.29+304637.9 | 0.170442 | 44.73 | 0.306 | 7.13 | −0.506 |
| SDSS J081835.73+285022.4 | 0.077240 | 44.34 | 0.178 | 6.98 | −0.306 |
| SDSS J081836.56+364334.9 | 0.106051 | 44.41 | 0.119 | 7.22 | 0.446 |
| SDSS J082050.48+472047.5 | 0.129067 | 44.38 | 0.119 | 7.19 | 0.416 |
| SDSS J082405.19+445246.0 | 0.219632 | 45.14 | 0.280 | 7.58 | 0.430 |
| SDSS J082432.99+514123.3 | 0.111106 | 44.06 | 0.090 | 7.00 | 0.294 |
| SDSS J082447.43+302554.2 | 0.365092 | 45.18 | 0.259 | 7.66 | 0.558 |
| SDSS J082921.18+375227.5 | 0.275902 | 44.88 | 0.198 | 7.47 | 0.486 |
| SDSS J083013.45+520541.7 | 0.302577 | 45.03 | 0.227 | 7.56 | 0.524 |
| SDSS J083052.73+481959.4 | 0.223419 | 44.69 | 0.225 | 7.23 | 0.026 |
| SDSS J083105.42+484231.6 | 0.169707 | 44.77 | 0.177 | 7.41 | 0.474 |
| SDSS J083202.15+461425.7 | 0.045906 | 44.12 | 0.110 | 6.97 | 0.110 |
| SDSS J083225.22+304608.3 | 0.089738 | 44.16 | 0.118 | 6.98 | 0.084 |
| SDSS J083237.43+365613.9 | 0.265764 | 45.21 | 0.262 | 7.68 | 0.580 |
| SDSS J083352.82+394333.9 | 0.244864 | 44.99 | 0.251 | 7.48 | 0.368 |
| SDSS J083454.08+542644.5 | 0.101118 | 44.30 | 0.107 | 7.16 | 0.430 |
| SDSS J083651.68+465333.9 | 0.248637 | 44.83 | 0.305 | 7.24 | −0.262 |
| SDSS J083810.01+350642.0 | 0.263217 | 44.84 | 0.228 | 7.37 | 0.254 |
| SDSS J084000.14+443737.9 | 0.125391 | 44.70 | 0.187 | 7.32 | 0.314 |
| SDSS J084314.95+384250.4 | 0.121095 | 44.46 | 0.124 | 7.26 | 0.474 |
| SDSS J084818.23+045643.2 | 0.437673 | 45.05 | 0.247 | 7.55 | 0.460 |
| SDSS J084855.35+422247.3 | 0.202080 | 44.71 | 0.178 | 7.35 | 0.384 |
| SDSS J085026.98+324651.8 | 0.219877 | 44.60 | 0.294 | 7.02 | −0.824 |
| SDSS J085039.70+333843.5 | 0.174862 | 44.45 | 0.169 | 7.11 | 0.026 |
| SDSS J085256.69+391734.4 | 0.250059 | 44.90 | 0.271 | 7.36 | 0.110 |
| SDSS J085315.22+340432.6 | 0.189949 | 44.64 | 0.237 | 7.16 | −0.180 |
| Object | z | a | |||
|---|---|---|---|---|---|
| SDSS J085457.23+544820.5 | 0.255907 | 45.09 | 0.268 | 7.55 | 0.416 |
| SDSS J085613.17+363144.8 | 0.171102 | 44.58 | 0.207 | 7.15 | −0.070 |
| SDSS J085655.29+442653.3 | 0.179081 | 44.66 | 0.144 | 7.39 | 0.558 |
| SDSS J085738.56+452513.9 | 0.242305 | 44.74 | 0.176 | 7.39 | 0.446 |
| SDSS J085858.79+533917.8 | 0.242489 | 44.94 | 0.232 | 7.46 | 0.384 |
| SDSS J090005.80+005835.5 | 0.250564 | 44.76 | 0.233 | 7.28 | 0.084 |
| SDSS J090015.28+510800.1 | 0.126035 | 44.72 | 0.202 | 7.30 | 0.232 |
| SDSS J090102.33+424957.4 | 0.213868 | 44.71 | 0.262 | 7.18 | −0.220 |
| SDSS J090117.82+043656.1 | 0.319724 | 45.17 | 0.306 | 7.57 | 0.368 |
| SDSS J090210.16+444625.5 | 0.266220 | 45.01 | 0.247 | 7.51 | 0.400 |
| SDSS J090354.72+350959.8 | 0.241401 | 44.79 | 0.262 | 7.26 | −0.038 |
| SDSS J090523.95+413107.3 | 0.494868 | 44.90 | 0.207 | 7.47 | 0.460 |
| SDSS J090611.61+510928.8 | 0.097854 | 44.26 | 0.126 | 7.05 | 0.136 |
| SDSS J090720.90+053833.2 | 0.383351 | 45.00 | 0.278 | 7.45 | 0.232 |
| SDSS J090734.53+491911.7 | 0.141860 | 44.52 | 0.122 | 7.32 | 0.558 |
| SDSS J090741.40+500814.1 | 0.208675 | 44.95 | 0.255 | 7.43 | 0.274 |
| SDSS J090927.69+393229.9 | 0.152103 | 44.21 | 0.177 | 6.85 | −0.686 |
| SDSS J091034.21+533725.9 | 0.187304 | 44.61 | 0.182 | 7.24 | 0.210 |
| SDSS J091113.39+400111.1 | 0.200499 | 44.84 | 0.291 | 7.27 | −0.142 |
| SDSS J091245.77+450046.5 | 0.318832 | 44.91 | 0.199 | 7.50 | 0.512 |
| SDSS J091313.72+365817.2 | 0.107321 | 44.54 | 0.185 | 7.16 | 0.056 |
| SDSS J091400.03+462937.3 | 0.136733 | 44.24 | 0.189 | 6.85 | −0.754 |
| SDSS J091508.55+530310.2 | 0.248602 | 45.12 | 0.234 | 7.64 | 0.590 |
| SDSS J091512.23+013412.1 | 0.455930 | 44.72 | 0.199 | 7.31 | 0.254 |
| SDSS J091513.89+571233.2 | 0.195095 | 44.35 | 0.198 | 6.94 | −0.564 |
| SDSS J091953.24+595128.8 | 0.215659 | 44.77 | 0.189 | 7.38 | 0.400 |
| SDSS J092019.52+463608.9 | 0.155863 | 44.51 | 0.253 | 7.00 | −0.686 |
| SDSS J092050.41+422408.0 | 0.174452 | 44.55 | 0.254 | 7.04 | −0.564 |
| SDSS J092057.50+510700.3 | 0.200458 | 44.80 | 0.177 | 7.44 | 0.512 |
| SDSS J092351.17+032231.6 | 0.179751 | 44.85 | 0.292 | 7.27 | −0.142 |
| SDSS J092506.70+390708.0 | 0.247477 | 44.97 | 0.283 | 7.41 | 0.162 |
| SDSS J092704.38+563351.4 | 0.219553 | 44.69 | 0.141 | 7.43 | 0.598 |
| SDSS J092810.50+411129.1 | 0.152623 | 44.69 | 0.145 | 7.42 | 0.580 |
| SDSS J093147.74+433119.2 | 0.132046 | 44.39 | 0.132 | 7.16 | 0.294 |
| SDSS J093312.47+611936.3 | 0.122705 | 44.04 | 0.086 | 6.99 | 0.332 |
| SDSS J093607.86+051034.4 | 0.207456 | 44.82 | 0.259 | 7.30 | 0.026 |
| SDSS J093919.90+072755.0 | 0.409697 | 45.14 | 0.308 | 7.54 | 0.314 |
| SDSS J094109.86+081404.5 | 0.125429 | 44.22 | 0.148 | 6.94 | −0.220 |
| SDSS J094456.07+054642.9 | 0.212865 | 44.90 | 0.290 | 7.33 | −0.004 |
| SDSS J094529.36+093610.4 | 0.013277 | 43.12 | 0.055 | 6.27 | −0.898 |
| SDSS J094616.90+025459.4 | 0.117764 | 44.60 | 0.192 | 7.21 | 0.110 |
| SDSS J094621.26+471131.3 | 0.230494 | 45.13 | 0.289 | 7.56 | 0.384 |
| SDSS J094842.67+502931.4 | 0.056464 | 44.47 | 0.162 | 7.15 | 0.136 |
| SDSS J094903.55+474653.9 | 0.214958 | 44.75 | 0.252 | 7.24 | −0.070 |
| SDSS J095017.60+070317.9 | 0.108707 | 44.30 | 0.175 | 6.95 | −0.402 |
| SDSS J095221.96+632438.9 | 0.119716 | 44.33 | 0.115 | 7.16 | 0.384 |
| SDSS J095310.69+032725.5 | 0.184362 | 44.53 | 0.125 | 7.32 | 0.548 |
| SDSS J095553.14+633742.7 | 0.356415 | 45.03 | 0.238 | 7.54 | 0.474 |
| SDSS J095730.15+413301.6 | 0.318701 | 45.02 | 0.255 | 7.50 | 0.384 |
| SDSS J095931.67+504449.0 | 0.143226 | 45.08 | 0.300 | 7.49 | 0.254 |
| SDSS J100201.77+620816.3 | 0.133791 | 44.56 | 0.226 | 7.10 | −0.262 |
| SDSS J100706.25+084228.4 | 0.373343 | 45.19 | 0.300 | 7.60 | 0.416 |
| SDSS J100723.15+014546.8 | 0.355111 | 44.73 | 0.266 | 7.19 | −0.220 |
| SDSS J100954.65+481514.6 | 0.178805 | 44.65 | 0.169 | 7.31 | 0.368 |
| SDSS J101341.90-000925.7 | 0.277105 | 44.98 | 0.267 | 7.44 | 0.254 |
| SDSS J101437.45+440639.1 | 0.200135 | 45.16 | 0.270 | 7.62 | 0.500 |
| SDSS J101549.33+424243.0 | 0.498800 | 45.33 | 0.296 | 7.75 | 0.598 |
| SDSS J101645.11+421025.5 | 0.055322 | 44.58 | 0.280 | 7.02 | −0.754 |
| SDSS J101852.45+495800.4 | 0.154811 | 44.63 | 0.208 | 7.20 | 0.026 |
| SDSS J101936.27+002029.7 | 0.147878 | 44.61 | 0.250 | 7.10 | −0.402 |
| SDSS J102000.45+623944.6 | 0.136020 | 44.44 | 0.211 | 7.01 | −0.452 |
| SDSS J102049.68+060446.9 | 0.110954 | 44.41 | 0.154 | 7.11 | 0.110 |
| SDSS J102148.89+030732.2 | 0.061838 | 44.25 | 0.143 | 6.98 | −0.070 |
| Object | z | a | |||
|---|---|---|---|---|---|
| SDSS J102307.02+454500.1 | 0.256396 | 44.73 | 0.166 | 7.40 | 0.486 |
| SDSS J102402.59+062943.9 | 0.044014 | 43.94 | 0.117 | 6.76 | −0.402 |
| SDSS J102448.57+003538.0 | 0.095475 | 44.33 | 0.154 | 7.03 | −0.038 |
| SDSS J102531.28+514034.8 | 0.044884 | 44.47 | 0.242 | 6.98 | −0.686 |
| SDSS J102712.37+050320.9 | 0.338470 | 44.98 | 0.280 | 7.42 | 0.186 |
| SDSS J102748.92+651337.4 | 0.444910 | 44.98 | 0.279 | 7.42 | 0.210 |
| SDSS J102754.27+063107.4 | 0.159051 | 44.50 | 0.217 | 7.05 | −0.354 |
| SDSS J102905.51+052555.3 | 0.122770 | 44.41 | 0.132 | 7.18 | 0.332 |
| SDSS J102955.38+471346.6 | 0.175436 | 44.78 | 0.218 | 7.33 | 0.232 |
| SDSS J103103.52+462616.8 | 0.093244 | 44.48 | 0.171 | 7.14 | 0.056 |
| SDSS J104153.59+031500.6 | 0.093442 | 44.27 | 0.099 | 7.16 | 0.474 |
| SDSS J104241.08+520012.8 | 0.136249 | 44.63 | 0.242 | 7.14 | −0.262 |
| SDSS J104331.50-010732.8 | 0.361906 | 45.15 | 0.274 | 7.60 | 0.474 |
| SDSS J104413.32-000324.7 | 0.279814 | 45.13 | 0.291 | 7.56 | 0.384 |
| SDSS J104840.49+541302.3 | 0.104141 | 44.28 | 0.194 | 6.88 | −0.686 |
| SDSS J105237.41+503042.1 | 0.245730 | 45.08 | 0.259 | 7.56 | 0.446 |
| SDSS J110501.99-004454.7 | 0.332404 | 45.08 | 0.238 | 7.59 | 0.536 |
| SDSS J110522.54+510727.1 | 0.307074 | 45.05 | 0.288 | 7.48 | 0.274 |
| SDSS J110608.03+582609.1 | 0.118018 | 44.45 | 0.217 | 7.00 | −0.506 |
| SDSS J110711.32+080538.4 | 0.281045 | 45.08 | 0.233 | 7.60 | 0.558 |
| SDSS J110735.68+060758.6 | 0.380035 | 45.19 | 0.290 | 7.62 | 0.460 |
| SDSS J111012.07+011327.8 | 0.094936 | 45.10 | 0.302 | 7.51 | 0.294 |
| SDSS J111233.81+034007.0 | 0.321768 | 44.86 | 0.223 | 7.40 | 0.314 |
| SDSS J111407.35-000031.1 | 0.072649 | 44.14 | 0.136 | 6.90 | −0.220 |
| SDSS J111528.48-003454.7 | 0.232516 | 44.69 | 0.199 | 7.28 | 0.210 |
| SDSS J111928.85+042655.5 | 0.153477 | 44.56 | 0.167 | 7.23 | 0.254 |
| SDSS J111949.75+020256.5 | 0.207822 | 44.60 | 0.221 | 7.15 | −0.142 |
| SDSS J112016.16+491428.8 | 0.149581 | 44.40 | 0.208 | 6.97 | −0.506 |
| SDSS J112108.58+535121.0 | 0.102907 | 45.27 | 0.298 | 7.69 | 0.524 |
| SDSS J112114.22+032546.7 | 0.152033 | 45.07 | 0.267 | 7.53 | 0.400 |
| SDSS J112209.40+011719.3 | 0.058292 | 44.08 | 0.164 | 6.76 | −0.898 |
| SDSS J112328.12+052823.2 | 0.101336 | 44.42 | 0.145 | 7.15 | 0.232 |
| SDSS J112606.43+002349.9 | 0.169536 | 44.85 | 0.169 | 7.51 | 0.608 |
| SDSS J112747.17+632542.7 | 0.341665 | 44.54 | 0.209 | 7.11 | −0.180 |
| SDSS J112805.72-005850.9 | 0.284739 | 45.04 | 0.226 | 7.58 | 0.536 |
| SDSS J112836.17+024550.6 | 0.238576 | 44.65 | 0.168 | 7.31 | 0.368 |
| SDSS J113001.88+494434.7 | 0.244338 | 45.29 | 0.301 | 7.70 | 0.536 |
| SDSS J113003.11+655629.1 | 0.132687 | 44.62 | 0.276 | 7.07 | −0.564 |
| SDSS J113102.27-010122.0 | 0.242137 | 44.52 | 0.256 | 7.00 | −0.686 |
| SDSS J113110.64+043856.0 | 0.144594 | 44.66 | 0.184 | 7.29 | 0.274 |
| SDSS J113111.94+100231.3 | 0.074401 | 44.05 | 0.112 | 6.89 | −0.070 |
| SDSS J113151.04+100915.5 | 0.119481 | 44.31 | 0.213 | 6.87 | −0.824 |
| SDSS J113223.43+641958.4 | 0.209867 | 45.17 | 0.261 | 7.64 | 0.548 |
| SDSS J113229.54+092042.0 | 0.305157 | 45.04 | 0.214 | 7.60 | 0.590 |
| SDSS J113320.91+043255.1 | 0.248058 | 45.15 | 0.241 | 7.66 | 0.598 |
| SDSS J113842.84-031403.3 | 0.212339 | 44.92 | 0.210 | 7.49 | 0.474 |
| SDSS J113900.50+591347.2 | 0.115052 | 44.68 | 0.187 | 7.30 | 0.274 |
| SDSS J114203.66+054850.4 | 0.274033 | 44.86 | 0.198 | 7.45 | 0.460 |
| SDSS J114208.48+531526.0 | 0.067965 | 44.20 | 0.097 | 7.10 | 0.416 |
| SDSS J114341.97-014434.4 | 0.105223 | 44.93 | 0.275 | 7.38 | 0.136 |
| SDSS J114514.00+494523.4 | 0.192336 | 44.56 | 0.261 | 7.03 | −0.624 |
| SDSS J114632.86+030506.9 | 0.191294 | 44.45 | 0.179 | 7.09 | −0.070 |
| SDSS J114928.27-000442.5 | 0.175967 | 44.67 | 0.149 | 7.39 | 0.536 |
| SDSS J114958.08+575107.7 | 0.100556 | 44.44 | 0.244 | 6.94 | −0.824 |
| SDSS J115050.20+004505.7 | 0.139474 | 44.52 | 0.128 | 7.30 | 0.512 |
| SDSS J115215.83+042456.2 | 0.132674 | 44.30 | 0.136 | 7.06 | 0.110 |
| SDSS J115655.88+084850.2 | 0.496092 | 45.26 | 0.275 | 7.71 | 0.590 |
| SDSS J115713.04+535312.8 | 0.272882 | 44.84 | 0.254 | 7.32 | 0.084 |
| SDSS J115715.19+093456.7 | 0.271835 | 44.79 | 0.160 | 7.48 | 0.590 |
| SDSS J115723.17+045201.0 | 0.176083 | 44.43 | 0.211 | 7.00 | −0.452 |
| SDSS J115741.75+041250.6 | 0.094812 | 44.29 | 0.148 | 7.01 | −0.070 |
| SDSS J115755.47+001704.0 | 0.260770 | 44.93 | 0.227 | 7.46 | 0.400 |
| SDSS J115852.57+563152.5 | 0.234345 | 44.60 | 0.270 | 7.06 | −0.624 |
| Object | z | a | |||
|---|---|---|---|---|---|
| SDSS J115905.80+024802.6 | 0.168560 | 44.65 | 0.216 | 7.21 | −0.004 |
| SDSS J120014.08-004638.7 | 0.179389 | 44.93 | 0.236 | 7.45 | 0.350 |
| SDSS J120322.36+621505.7 | 0.270417 | 44.82 | 0.303 | 7.23 | −0.262 |
| SDSS J120517.71+520109.1 | 0.189541 | 44.72 | 0.210 | 7.29 | 0.186 |
| SDSS J120628.97+503001.5 | 0.171971 | 44.58 | 0.272 | 7.03 | −0.686 |
| SDSS J121117.80-000212.4 | 0.181317 | 44.72 | 0.177 | 7.36 | 0.416 |
| SDSS J121157.48+055801.1 | 0.067820 | 44.18 | 0.136 | 6.94 | −0.142 |
| SDSS J121255.27+512221.1 | 0.282823 | 44.85 | 0.241 | 7.36 | 0.210 |
| SDSS J121333.20-013220.7 | 0.197743 | 44.63 | 0.204 | 7.21 | 0.056 |
| SDSS J121343.76-010002.5 | 0.328065 | 44.90 | 0.239 | 7.41 | 0.294 |
| SDSS J121407.35+655228.6 | 0.235552 | 45.10 | 0.238 | 7.61 | 0.558 |
| SDSS J121513.83+023334.4 | 0.224435 | 44.72 | 0.157 | 7.41 | 0.536 |
| SDSS J121544.73+592639.1 | 0.095815 | 44.21 | 0.122 | 7.01 | 0.110 |
| SDSS J121948.93+054531.7 | 0.113866 | 44.48 | 0.166 | 7.15 | 0.110 |
| SDSS J122342.82+581446.2 | 0.014527 | 42.96 | 0.042 | 6.22 | −0.686 |
| SDSS J122450.55+100545.4 | 0.167900 | 44.91 | 0.244 | 7.41 | 0.274 |
| SDSS J122506.20-030100.4 | 0.239966 | 44.70 | 0.297 | 7.12 | −0.564 |
| SDSS J122624.42+014020.7 | 0.219884 | 44.83 | 0.176 | 7.47 | 0.548 |
| SDSS J122801.33+623948.1 | 0.271290 | 44.99 | 0.251 | 7.48 | 0.368 |
| SDSS J122908.95+561109.1 | 0.265475 | 44.78 | 0.180 | 7.41 | 0.460 |
| SDSS J122950.61+024652.7 | 0.336083 | 45.15 | 0.284 | 7.59 | 0.430 |
| SDSS J123003.50+611904.7 | 0.148374 | 44.73 | 0.276 | 7.18 | −0.306 |
| SDSS J123012.17+544719.8 | 0.276800 | 44.82 | 0.201 | 7.41 | 0.400 |
| SDSS J123132.52+574624.8 | 0.259910 | 44.85 | 0.218 | 7.40 | 0.332 |
| SDSS J123339.58+052034.7 | 0.215649 | 44.64 | 0.226 | 7.18 | −0.106 |
| SDSS J123340.07+680022.4 | 0.343372 | 44.96 | 0.244 | 7.46 | 0.350 |
| SDSS J123450.50+040845.4 | 0.121252 | 44.63 | 0.244 | 7.13 | −0.262 |
| SDSS J123831.33+643456.5 | 0.101584 | 44.73 | 0.221 | 7.28 | 0.110 |
| SDSS J124110.10+104143.7 | 0.156232 | 44.24 | 0.168 | 6.91 | −0.452 |
| SDSS J124129.34+681533.9 | 0.150972 | 44.24 | 0.128 | 7.02 | 0.084 |
| SDSS J124328.04+565237.9 | 0.106616 | 44.29 | 0.165 | 6.96 | −0.262 |
| SDSS J124504.57+650122.7 | 0.206591 | 44.66 | 0.295 | 7.08 | −0.624 |
| SDSS J124504.93+504446.2 | 0.129684 | 44.59 | 0.209 | 7.16 | −0.070 |
| SDSS J124519.73-005230.5 | 0.221020 | 44.61 | 0.234 | 7.13 | −0.220 |
| SDSS J125051.04+060910.0 | 0.182047 | 45.14 | 0.308 | 7.54 | 0.314 |
| SDSS J125156.50+015249.6 | 0.329416 | 45.31 | 0.292 | 7.73 | 0.590 |
| SDSS J125224.22+645901.4 | 0.220729 | 44.66 | 0.245 | 7.16 | −0.220 |
| SDSS J125227.32+032353.6 | 0.132687 | 44.81 | 0.233 | 7.33 | 0.186 |
| SDSS J125248.49+015236.3 | 0.287988 | 44.84 | 0.178 | 7.48 | 0.548 |
| SDSS J125357.41+640534.8 | 0.267455 | 44.71 | 0.258 | 7.19 | −0.220 |
| SDSS J125635.87+500852.3 | 0.245337 | 44.67 | 0.203 | 7.25 | 0.136 |
| SDSS J130030.67+485042.5 | 0.251725 | 44.90 | 0.190 | 7.51 | 0.548 |
| SDSS J130052.10+564105.9 | 0.071838 | 44.41 | 0.126 | 7.20 | 0.384 |
| SDSS J130421.89+014915.9 | 0.153597 | 44.53 | 0.217 | 7.08 | −0.262 |
| SDSS J130547.00+504034.0 | 0.055124 | 43.92 | 0.109 | 6.77 | −0.306 |
| SDSS J130717.75+033447.5 | 0.161346 | 44.30 | 0.143 | 7.03 | 0.026 |
| SDSS J131136.37+580801.5 | 0.071088 | 44.16 | 0.087 | 7.11 | 0.486 |
| SDSS J131234.32+655240.1 | 0.217351 | 44.45 | 0.236 | 6.97 | −0.686 |
| SDSS J131305.81+012755.9 | 0.029361 | 43.71 | 0.088 | 6.65 | −0.354 |
| SDSS J132026.49+051113.5 | 0.098391 | 44.51 | 0.238 | 7.02 | −0.506 |
| SDSS J132231.12-001124.6 | 0.172930 | 44.67 | 0.147 | 7.39 | 0.536 |
| SDSS J132428.34+590423.8 | 0.239623 | 44.81 | 0.247 | 7.31 | 0.084 |
| SDSS J132447.09+530257.6 | 0.292005 | 44.90 | 0.234 | 7.42 | 0.314 |
| SDSS J132640.04+650427.4 | 0.400867 | 45.07 | 0.290 | 7.50 | 0.294 |
| SDSS J132704.54-003627.5 | 0.301717 | 44.90 | 0.268 | 7.36 | 0.110 |
| SDSS J132705.88-012415.5 | 0.167808 | 44.81 | 0.272 | 7.26 | −0.070 |
| SDSS J132731.98+654848.3 | 0.219769 | 44.72 | 0.187 | 7.34 | 0.350 |
| SDSS J133059.07+602128.4 | 0.291747 | 45.04 | 0.223 | 7.58 | 0.548 |
| SDSS J133138.03+013151.7 | 0.080473 | 44.42 | 0.159 | 7.11 | 0.084 |
| SDSS J133248.59+442452.7 | 0.077438 | 44.13 | 0.101 | 7.02 | 0.254 |
| SDSS J133315.25+560859.8 | 0.343105 | 45.21 | 0.263 | 7.68 | 0.580 |
| SDSS J133328.96+613513.3 | 0.151516 | 44.67 | 0.141 | 7.41 | 0.580 |
| SDSS J133627.97+442917.7 | 0.137809 | 44.56 | 0.243 | 7.06 | −0.452 |
| Object | z | a | |||
|---|---|---|---|---|---|
| SDSS J133729.04+563907.6 | 0.143501 | 44.61 | 0.213 | 7.17 | −0.070 |
| SDSS J134313.40+654110.4 | 0.240726 | 44.90 | 0.231 | 7.43 | 0.332 |
| SDSS J134351.06+000434.7 | 0.073693 | 44.36 | 0.104 | 7.23 | 0.536 |
| SDSS J134452.91+000520.2 | 0.087099 | 44.42 | 0.124 | 7.22 | 0.416 |
| SDSS J134524.69-025939.8 | 0.085402 | 44.59 | 0.156 | 7.29 | 0.384 |
| SDSS J134730.70+603742.8 | 0.143551 | 44.56 | 0.146 | 7.28 | 0.416 |
| SDSS J135343.63-011801.3 | 0.145193 | 44.53 | 0.168 | 7.19 | 0.186 |
| SDSS J135350.63+571725.8 | 0.234458 | 44.81 | 0.274 | 7.26 | −0.106 |
| SDSS J135622.94+574150.9 | 0.309698 | 44.96 | 0.292 | 7.38 | 0.110 |
| SDSS J135643.69+664128.4 | 0.172599 | 44.59 | 0.257 | 7.07 | −0.506 |
| SDSS J135756.53+655902.9 | 0.197031 | 44.83 | 0.284 | 7.27 | −0.106 |
| SDSS J135842.27+024925.1 | 0.148016 | 44.56 | 0.170 | 7.22 | 0.232 |
| SDSS J135848.54+430435.6 | 0.252436 | 44.81 | 0.242 | 7.32 | 0.110 |
| SDSS J135944.07+045649.5 | 0.085623 | 44.25 | 0.169 | 6.91 | −0.452 |
| SDSS J140046.05+531920.2 | 0.388442 | 45.17 | 0.285 | 7.61 | 0.460 |
| SDSS J140219.69+521059.4 | 0.279175 | 44.88 | 0.271 | 7.34 | 0.056 |
| SDSS J140322.10+022232.9 | 0.250159 | 44.66 | 0.308 | 7.06 | −0.754 |
| SDSS J140527.68+505546.5 | 0.106561 | 44.53 | 0.153 | 7.24 | 0.314 |
| SDSS J140926.77+473127.3 | 0.143403 | 44.41 | 0.220 | 6.96 | −0.624 |
| SDSS J141108.51+424428.9 | 0.173315 | 44.58 | 0.170 | 7.24 | 0.254 |
| SDSS J141419.84+533815.3 | 0.164455 | 44.98 | 0.269 | 7.44 | 0.254 |
| SDSS J141424.90+465348.5 | 0.149731 | 44.79 | 0.220 | 7.34 | 0.232 |
| SDSS J141820.32-005953.8 | 0.253638 | 44.94 | 0.269 | 7.40 | 0.186 |
| SDSS J141838.27+620718.5 | 0.138792 | 44.59 | 0.134 | 7.35 | 0.548 |
| SDSS J142103.52+515819.4 | 0.263543 | 44.59 | 0.130 | 7.37 | 0.568 |
| SDSS J142214.89+431357.4 | 0.323267 | 45.09 | 0.263 | 7.56 | 0.446 |
| SDSS J142509.12+011911.4 | 0.199814 | 44.50 | 0.192 | 7.11 | −0.106 |
| SDSS J142542.55+652716.9 | 0.241476 | 44.77 | 0.259 | 7.25 | −0.070 |
| SDSS J142830.16+555931.3 | 0.351431 | 45.14 | 0.252 | 7.63 | 0.548 |
| SDSS J143030.21-001115.0 | 0.103284 | 44.12 | 0.100 | 7.01 | 0.254 |
| SDSS J143223.67+400533.8 | 0.140651 | 44.47 | 0.158 | 7.16 | 0.162 |
| SDSS J143249.68+451338.2 | 0.306872 | 45.07 | 0.308 | 7.47 | 0.210 |
| SDSS J143407.20+452732.2 | 0.254952 | 44.67 | 0.269 | 7.13 | −0.402 |
| SDSS J143601.55+044807.7 | 0.194125 | 44.90 | 0.272 | 7.36 | 0.110 |
| SDSS J143704.11+000705.1 | 0.140363 | 44.80 | 0.229 | 7.33 | 0.186 |
| SDSS J143715.12+545243.8 | 0.252154 | 45.00 | 0.270 | 7.46 | 0.274 |
| SDSS J143952.91+392358.9 | 0.111999 | 44.36 | 0.198 | 6.95 | −0.506 |
| SDSS J144013.89-015708.3 | 0.463581 | 44.83 | 0.197 | 7.43 | 0.430 |
| SDSS J144205.04+545904.7 | 0.104628 | 44.17 | 0.112 | 7.01 | 0.162 |
| SDSS J144237.72+542851.4 | 0.155188 | 44.67 | 0.259 | 7.15 | −0.306 |
| SDSS J144249.70+611137.8 | 0.047858 | 43.42 | 0.056 | 6.56 | −0.106 |
| SDSS J144328.40+542933.1 | 0.226942 | 44.79 | 0.216 | 7.35 | 0.254 |
| SDSS J144507.31+593649.8 | 0.128030 | 43.88 | 0.104 | 6.75 | −0.306 |
| SDSS J144705.46+003653.2 | 0.095493 | 43.84 | 0.088 | 6.78 | −0.070 |
| SDSS J144920.25+553429.4 | 0.468295 | 45.17 | 0.278 | 7.62 | 0.474 |
| SDSS J144945.69+422243.2 | 0.262760 | 45.08 | 0.245 | 7.58 | 0.512 |
| SDSS J145123.01-000625.8 | 0.138613 | 44.53 | 0.131 | 7.30 | 0.500 |
| SDSS J145201.55+025335.1 | 0.433702 | 45.12 | 0.286 | 7.55 | 0.384 |
| SDSS J145235.27+495142.1 | 0.144921 | 44.53 | 0.120 | 7.34 | 0.580 |
| SDSS J145624.00+421800.2 | 0.189834 | 44.88 | 0.187 | 7.50 | 0.548 |
| SDSS J145643.88+503756.4 | 0.131486 | 44.56 | 0.244 | 7.06 | −0.452 |
| SDSS J145801.49+544056.1 | 0.144858 | 44.40 | 0.129 | 7.18 | 0.332 |
| SDSS J145921.17+521749.6 | 0.167019 | 44.72 | 0.153 | 7.43 | 0.558 |
| SDSS J150034.45+465234.1 | 0.298022 | 45.04 | 0.253 | 7.53 | 0.416 |
| SDSS J150238.69+501524.0 | 0.172268 | 44.61 | 0.195 | 7.21 | 0.084 |
| SDSS J150346.94+420323.1 | 0.168316 | 44.74 | 0.212 | 7.30 | 0.210 |
| SDSS J150816.95+520541.7 | 0.193395 | 44.76 | 0.258 | 7.24 | −0.106 |
| SDSS J150832.91+583422.4 | 0.502172 | 45.07 | 0.249 | 7.56 | 0.474 |
| SDSS J151020.05+554722.0 | 0.149693 | 44.53 | 0.259 | 7.01 | −0.686 |
| SDSS J151024.93+005844.0 | 0.072262 | 44.41 | 0.153 | 7.11 | 0.110 |
| SDSS J151101.89+520350.0 | 0.211340 | 45.07 | 0.257 | 7.55 | 0.446 |
| SDSS J151131.33+502219.0 | 0.219845 | 45.02 | 0.222 | 7.56 | 0.536 |
| SDSS J151616.18+463515.3 | 0.208271 | 44.54 | 0.242 | 7.05 | −0.506 |
| Object | z | a | |||
|---|---|---|---|---|---|
| SDSS J151617.16+472805.0 | 0.197851 | 44.62 | 0.227 | 7.15 | −0.142 |
| SDSS J151956.57+001614.6 | 0.114398 | 44.69 | 0.257 | 7.17 | −0.220 |
| SDSS J152209.56+451124.0 | 0.065732 | 44.02 | 0.098 | 6.92 | 0.110 |
| SDSS J152224.45-010838.4 | 0.321221 | 45.21 | 0.257 | 7.69 | 0.598 |
| SDSS J152342.49+033147.9 | 0.221423 | 44.53 | 0.235 | 7.05 | −0.452 |
| SDSS J152447.13+520759.1 | 0.160840 | 44.49 | 0.214 | 7.05 | −0.354 |
| SDSS J152526.40+400914.3 | 0.355817 | 45.13 | 0.256 | 7.61 | 0.512 |
| SDSS J152621.69+432349.5 | 0.155615 | 44.92 | 0.270 | 7.38 | 0.136 |
| SDSS J152628.19-003809.4 | 0.123334 | 44.77 | 0.162 | 7.45 | 0.558 |
| SDSS J152840.26+383525.9 | 0.152598 | 44.30 | 0.120 | 7.11 | 0.294 |
| SDSS J152843.94+000740.6 | 0.094440 | 44.25 | 0.157 | 6.94 | −0.262 |
| SDSS J152912.14+031815.4 | 0.169956 | 44.35 | 0.095 | 7.26 | 0.608 |
| SDSS J153006.30+010626.0 | 0.239339 | 44.56 | 0.174 | 7.21 | 0.186 |
| SDSS J153252.95+384330.5 | 0.134003 | 44.63 | 0.246 | 7.13 | −0.306 |
| SDSS J153458.50+024214.0 | 0.389458 | 45.10 | 0.294 | 7.52 | 0.314 |
| SDSS J153607.72+364806.8 | 0.277578 | 45.12 | 0.266 | 7.59 | 0.474 |
| SDSS J153651.27+541442.6 | 0.366706 | 45.08 | 0.306 | 7.48 | 0.232 |
| SDSS J153705.95+005522.8 | 0.136419 | 45.09 | 0.289 | 7.52 | 0.332 |
| SDSS J153937.82+374340.4 | 0.165048 | 44.54 | 0.155 | 7.24 | 0.314 |
| SDSS J154113.94+492034.5 | 0.308087 | 44.87 | 0.222 | 7.41 | 0.350 |
| SDSS J154623.61+475122.3 | 0.103287 | 44.21 | 0.145 | 6.94 | −0.180 |
| SDSS J154656.62+005719.6 | 0.211019 | 44.92 | 0.301 | 7.33 | −0.038 |
| SDSS J154814.75+450027.7 | 0.037268 | 43.35 | 0.053 | 6.52 | −0.142 |
| SDSS J155427.26+404441.3 | 0.116805 | 44.43 | 0.139 | 7.18 | 0.294 |
| SDSS J155451.13+461917.3 | 0.116881 | 44.44 | 0.213 | 7.00 | −0.452 |
| SDSS J155637.99+540308.3 | 0.203331 | 44.86 | 0.240 | 7.37 | 0.232 |
| SDSS J155755.23+331625.8 | 0.277693 | 45.03 | 0.294 | 7.45 | 0.210 |
| SDSS J155851.33+280719.6 | 0.282557 | 45.02 | 0.262 | 7.49 | 0.350 |
| SDSS J155904.06+382422.2 | 0.137065 | 44.25 | 0.096 | 7.16 | 0.486 |
| SDSS J160344.44+264651.3 | 0.085673 | 44.60 | 0.166 | 7.27 | 0.314 |
| SDSS J160404.51+493820.5 | 0.148582 | 44.00 | 0.092 | 6.93 | 0.186 |
| SDSS J160426.88+525130.3 | 0.107031 | 44.35 | 0.212 | 6.91 | −0.686 |
| SDSS J160558.12+440319.5 | 0.044438 | 44.03 | 0.070 | 7.07 | 0.548 |
| SDSS J160806.68+424057.8 | 0.084737 | 44.44 | 0.207 | 7.01 | −0.402 |
| SDSS J161527.68+403153.6 | 0.083355 | 44.20 | 0.190 | 6.81 | −0.898 |
| SDSS J161713.51+515618.8 | 0.198799 | 44.52 | 0.149 | 7.24 | 0.332 |
| SDSS J161951.31+405847.3 | 0.037858 | 43.77 | 0.062 | 6.87 | 0.350 |
| SDSS J162755.24+470453.0 | 0.271820 | 44.88 | 0.234 | 7.40 | 0.294 |
| SDSS J163128.59+404535.9 | 0.181227 | 44.76 | 0.211 | 7.32 | 0.232 |
| SDSS J163152.22+345328.6 | 0.072234 | 44.28 | 0.107 | 7.14 | 0.400 |
| SDSS J163214.84+333412.8 | 0.174118 | 44.85 | 0.186 | 7.47 | 0.512 |
| SDSS J163247.87+383239.6 | 0.139247 | 44.62 | 0.270 | 7.08 | −0.506 |
| SDSS J163417.81+474453.1 | 0.177306 | 44.86 | 0.258 | 7.34 | 0.110 |
| SDSS J163625.42+421346.9 | 0.141250 | 44.70 | 0.308 | 7.10 | −0.624 |
| SDSS J163737.38+341205.5 | 0.235658 | 44.56 | 0.150 | 7.27 | 0.384 |
| SDSS J163927.71+354343.3 | 0.317929 | 44.88 | 0.212 | 7.44 | 0.416 |
| SDSS J164100.10+345452.6 | 0.164078 | 44.82 | 0.183 | 7.45 | 0.500 |
| SDSS J164207.32+344834.2 | 0.207533 | 44.60 | 0.144 | 7.33 | 0.486 |
| SDSS J164225.29+391742.2 | 0.184353 | 44.57 | 0.135 | 7.33 | 0.512 |
| SDSS J164416.85+423158.4 | 0.160893 | 44.63 | 0.218 | 7.18 | −0.038 |
| SDSS J164626.09+392932.1 | 0.100365 | 44.50 | 0.255 | 6.98 | −0.754 |
| SDSS J164907.63+642422.2 | 0.183524 | 44.60 | 0.259 | 7.08 | −0.506 |
| SDSS J165437.25+301653.9 | 0.185698 | 44.66 | 0.250 | 7.15 | −0.262 |
| SDSS J165636.98+371439.5 | 0.062757 | 43.73 | 0.074 | 6.75 | 0.026 |
| SDSS J165658.36+630051.1 | 0.168969 | 44.55 | 0.253 | 7.04 | −0.564 |
| SDSS J165757.51+382327.7 | 0.181496 | 44.74 | 0.191 | 7.35 | 0.350 |
| SDSS J165914.68+313423.4 | 0.264525 | 44.89 | 0.260 | 7.37 | 0.162 |
| SDSS J170002.15+383258.1 | 0.166573 | 44.53 | 0.159 | 7.22 | 0.274 |
| SDSS J170546.91+631059.1 | 0.119182 | 44.49 | 0.141 | 7.23 | 0.368 |
| SDSS J171033.21+584456.8 | 0.280701 | 45.04 | 0.300 | 7.45 | 0.186 |
| SDSS J171526.52+291923.5 | 0.208273 | 44.91 | 0.253 | 7.40 | 0.232 |
| SDSS J171540.93+560654.8 | 0.297139 | 45.12 | 0.246 | 7.62 | 0.548 |
| SDSS J171943.77+581112.3 | 0.350752 | 44.86 | 0.264 | 7.33 | 0.084 |
| Object | z | a | |||
|---|---|---|---|---|---|
| SDSS J204404.53-011214.6 | 0.172451 | 44.52 | 0.223 | 7.06 | −0.354 |
| SDSS J204731.68+002056.3 | 0.181679 | 44.42 | 0.126 | 7.21 | 0.400 |
| SDSS J205418.80+004915.9 | 0.227509 | 45.16 | 0.243 | 7.66 | 0.598 |
| SDSS J210533.44+002829.3 | 0.054312 | 43.99 | 0.124 | 6.79 | −0.402 |
| SDSS J210629.86+110109.0 | 0.304460 | 45.05 | 0.287 | 7.48 | 0.274 |
| SDSS J211436.68-004938.4 | 0.145364 | 44.49 | 0.148 | 7.21 | 0.294 |
| SDSS J212210.99+104200.1 | 0.299016 | 44.95 | 0.232 | 7.48 | 0.400 |
| SDSS J212327.26+001439.9 | 0.182258 | 44.78 | 0.277 | 7.23 | −0.180 |
| SDSS J213059.76+004438.0 | 0.130070 | 44.66 | 0.292 | 7.08 | −0.624 |
| SDSS J213245.28+121256.8 | 0.125566 | 44.73 | 0.149 | 7.45 | 0.590 |
| SDSS J214054.55+002538.1 | 0.083841 | 44.88 | 0.308 | 7.28 | −0.180 |
| SDSS J214249.64-085434.4 | 0.135292 | 44.50 | 0.162 | 7.18 | 0.186 |
| SDSS J214733.86+004021.0 | 0.124192 | 44.64 | 0.277 | 7.09 | −0.564 |
| SDSS J215147.60-080922.4 | 0.120572 | 44.68 | 0.204 | 7.26 | 0.162 |
| SDSS J220042.72-073056.4 | 0.110624 | 44.49 | 0.243 | 6.99 | −0.624 |
| SDSS J220735.12-082457.7 | 0.213227 | 44.79 | 0.277 | 7.24 | −0.142 |
| SDSS J221953.18-083258.7 | 0.305785 | 44.87 | 0.282 | 7.31 | −0.004 |
| SDSS J222115.58-004030.4 | 0.171926 | 44.56 | 0.137 | 7.31 | 0.486 |
| SDSS J222255.55+005033.7 | 0.112503 | 44.25 | 0.199 | 6.84 | −0.898 |
| SDSS J224605.44-091925.1 | 0.118466 | 44.35 | 0.154 | 7.05 | −0.004 |
| SDSS J225452.22+004631.3 | 0.090735 | 44.72 | 0.308 | 7.12 | −0.564 |
| SDSS J230108.39-084848.8 | 0.171870 | 44.81 | 0.199 | 7.40 | 0.384 |
| SDSS J230323.47-100235.3 | 0.180613 | 44.90 | 0.285 | 7.34 | 0.026 |
| SDSS J230723.24+001708.1 | 0.112685 | 44.36 | 0.209 | 6.93 | −0.624 |
| SDSS J231309.71+002633.7 | 0.285273 | 44.96 | 0.261 | 7.43 | 0.254 |
| SDSS J233811.52+002045.7 | 0.278855 | 44.81 | 0.198 | 7.40 | 0.400 |
| SDSS J234114.22-102828.8 | 0.277839 | 44.96 | 0.219 | 7.51 | 0.474 |
| SDSS J234150.81-004329.0 | 0.250595 | 44.81 | 0.260 | 7.29 | −0.004 |
| SDSS J234208.30-094747.5 | 0.191234 | 44.61 | 0.210 | 7.18 | −0.038 |
| SDSS J234229.45-004731.4 | 0.315655 | 44.84 | 0.269 | 7.30 | −0.004 |
| SDSS J234601.30-101549.0 | 0.191210 | 44.42 | 0.113 | 7.26 | 0.524 |
| SDSS J234725.29-010643.7 | 0.182002 | 44.88 | 0.236 | 7.40 | 0.274 |
| SDSS J235340.46-093709.0 | 0.311753 | 44.86 | 0.227 | 7.39 | 0.294 |
References
- Netzer, H. Revisiting the Unified Model of Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 2015, 53, 365–408. [Google Scholar] [CrossRef]
- Robson, I. Active Galactic Nuclei; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Antonucci, R. Unified models for active galactic nuclei and quasars. Annu. Rev. Astron. Astrophys. 1993, 31, 473–521. [Google Scholar] [CrossRef]
- Osterbrock, D.E.; Pogge, R.W. The spectra of narrow-line Seyfert 1 galaxies. Astrophys. J. 1985, 297, 166–176. [Google Scholar] [CrossRef]
- Goodrich, R.W. Spectropolarimetry of “Narrow-Line” Seyfert 1 Galaxies. Astrophys. J. 1989, 342, 224. [Google Scholar] [CrossRef]
- Leighly, K.M. A Comprehensive Spectral and Variability Study of Narrow-Line Seyfert 1 Galaxies Observed by ASCA. II. Spectral Analysis and Correlations. Astrophys. J. Suppl. 1999, 125, 317–348. [Google Scholar] [CrossRef]
- Mathur, S. Narrow-line Seyfert 1 galaxies and the evolution of galaxies and active galaxies. Mon. Not. R. Astron. Soc. 2000, 314, L17–L20. [Google Scholar] [CrossRef]
- Boller, T.; Brandt, W.N.; Fink, H. Soft X-ray properties of narrow-line Seyfert 1 galaxies. Astron. Astrophys. 1996, 305, 53. [Google Scholar] [CrossRef]
- Moran, E.C.; Halpern, J.P.; Helfand, D.J. Classification of IRAS-selected X-ray Galaxies in the ROSAT All-Sky Survey. Astrophys. J. Suppl. 1996, 106, 341. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation. Astrophys. J. 1972, 178, 347–370. [Google Scholar] [CrossRef]
- Novikov, I.D.; Thorne, K.S. Astrophysics of black holes. In Black Holes (Les Astres Occlus); Dewitt, C., Dewitt, B.S., Eds.; Gordon and Breach: New York, NY, USA, 1973; pp. 343–450. [Google Scholar]
- Krolik, J.H. Making black holes visible: Accretion, radiation, and jets. In Proceedings of the 2007 STScI Spring Symposium on Black Holes, Baltimore, MD, USA, 23–26 April 2007; pp. 309–321. [Google Scholar]
- Krolik, J.H.; Hawley, J.F.; Hirose, S. The Relationship between Accretion Disks and Jets. In Revista Mexicana de Astronomia y Astrofisica; Revista Mexicana de Astronomia y Astrofisica Conference Series; Instituto de Astronomía Distrito Federal: Ciudad de México, Mexico, 2007; Volume 27, pp. 1–7. [Google Scholar]
- Zhou, H.; Wang, T.; Yuan, W.; Lu, H.; Dong, X.; Wang, J.; Lu, Y. VizieR Online Data Catalog: Narrow line Seyfert 1 galaxies from SDSS-DR3 (Zhou+, 2006). VizieR Online Data Cat. 2017. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, T.; Yuan, W.; Lu, H.; Dong, X.; Wang, J.; Lu, Y. A Comprehensive Study of 2000 Narrow Line Seyfert 1 Galaxies from the Sloan Digital Sky Survey. I. The Sample. Astrophys. J. Suppl. 2006, 166, 128–153. [Google Scholar] [CrossRef]
- Davis, S.W.; Laor, A. The Radiative Efficiency of Accretion Flows in Individual Active Galactic Nuclei. Astrophys. J. 2011, 728, 98. [Google Scholar] [CrossRef]
- Raimundo, S.I.; Fabian, A.C.; Vasudevan, R.V.; Gandhi, P.; Wu, J. Can we measure the accretion efficiency of active galactic nuclei? Mon. Not. R. Astron. Soc. 2012, 419, 2529–2544. [Google Scholar] [CrossRef]
- Du, P.; Hu, C.; Lu, K.X.; Wang, F.; Qiu, J.; Li, Y.R.; Bai, J.M.; Kaspi, S.; Netzer, H.; Wang, J.M.; et al. Supermassive Black Holes with High Accretion Rates in Active Galactic Nuclei. I. First Results from a New Reverberation Mapping Campaign. Astrophys. J. 2014, 782, 45. [Google Scholar] [CrossRef]
- Trakhtenbrot, B. The Most Massive Active Black Holes at z ∼ 1.5–3.5 have High Spins and Radiative Efficiencies. Astrophys. J. Lett. 2014, 789, L9. [Google Scholar] [CrossRef]
- Lawther, D.; Vestergaard, M.; Raimundo, S.; Grupe, D. A catalogue of optical to X-ray spectral energy distributions of z ≈ 2 quasars observed with Swift—I. First results. Mon. Not. R. Astron. Soc. 2017, 467, 4674–4710. [Google Scholar] [CrossRef]
- Piotrovich, M.Y.; Buliga, S.D.; Natsvlishvili, T.M. Determination of supermassive black hole spins in local active galactic nuclei. Astron. Nachr. 2022, 343, e10020. [Google Scholar] [CrossRef]
- Afanasiev, V.L.; Gnedin, Y.N.; Piotrovich, M.Y.; Natsvlishvili, T.M.; Buliga, S.D. Determination of Supermassive Black Hole Spins Based on the Standard Shakura-Sunyaev Accretion Disk Model and Polarimetric Observations. Astron. Lett. 2018, 44, 362–369. [Google Scholar] [CrossRef]
- Marin, F. Are there reliable methods to estimate the nuclear orientation of Seyfert galaxies? Mon. Not. R. Astron. Soc. 2016, 460, 3679–3705. [Google Scholar] [CrossRef]
- Richards, G.T.; Lacy, M.; Storrie-Lombardi, L.J.; Hall, P.B.; Gallagher, S.C.; Hines, D.C.; Fan, X.; Papovich, C.; Vanden Berk, D.E.; Trammell, G.B.; et al. Spectral Energy Distributions and Multiwavelength Selection of Type 1 Quasars. Astrophys. J. Suppl. 2006, 166, 470–497. [Google Scholar] [CrossRef]
- Hopkins, P.F.; Richards, G.T.; Hernquist, L. An Observational Determination of the Bolometric Quasar Luminosity Function. Astrophys. J. 2007, 654, 731–753. [Google Scholar] [CrossRef]
- Cheng, H.; Yuan, W.; Liu, H.Y.; Breeveld, A.A.; Jin, C.; Liu, B. Modelling accretion disc emission with generalized temperature profile and its effect on AGN spectral energy distribution. Mon. Not. R. Astron. Soc. 2019, 487, 3884–3903. [Google Scholar] [CrossRef]
- Netzer, H. Bolometric correction factors for active galactic nuclei. Mon. Not. R. Astron. Soc. 2019, 488, 5185–5191. [Google Scholar] [CrossRef]
- Duras, F.; Bongiorno, A.; Ricci, F.; Piconcelli, E.; Shankar, F.; Lusso, E.; Bianchi, S.; Fiore, F.; Maiolino, R.; Marconi, A.; et al. Universal bolometric corrections for active galactic nuclei over seven luminosity decades. Astron. Astrophys. 2020, 636, A73. [Google Scholar] [CrossRef]
- Vestergaard, M.; Peterson, B.M. Determining Central Black Hole Masses in Distant Active Galaxies and Quasars. II. Improved Optical and UV Scaling Relationships. Astrophys. J. 2006, 641, 689–709. [Google Scholar] [CrossRef]
- Thorne, K.S. Disk-Accretion onto a Black Hole. II. Evolution of the Hole. Astrophys. J. 1974, 191, 507–520. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Netzer, H.; Trakhtenbrot, B. Bolometric luminosity black hole growth time and slim accretion discs in active galactic nuclei. Mon. Not. R. Astron. Soc. 2014, 438, 672–679. [Google Scholar] [CrossRef]
- Liu, Z.; Yuan, W.; Lu, Y.; Zhou, X. Relativistic Fe Kα line revealed in the composite X-ray spectrum of narrow-line Seyfert 1 galaxies—Do their black holes have averagely low or intermediate spins? Mon. Not. R. Astron. Soc. 2015, 447, 517–529. [Google Scholar] [CrossRef]
- Chen, Y.; Gu, Q.; Fan, J.; Yu, X.; Ding, N.; Xiong, D.; Guo, X. Curvature of the Spectral Energy Distribution, Compton Dominance, and Synchrotron Peak Frequency in Jetted Active Galactic Nuclei. Astrophys. J. 2023, 944, 157. [Google Scholar] [CrossRef]
- Yuan, W.; Zhou, H.Y.; Komossa, S.; Dong, X.B.; Wang, T.G.; Lu, H.L.; Bai, J.M. A Population of Radio-Loud Narrow-Line Seyfert 1 Galaxies with Blazar-Like Properties? Astrophys. J. 2008, 685, 801–827. [Google Scholar] [CrossRef]
- Berton, M.; Congiu, E.; Järvelä, E.; Antonucci, R.; Kharb, P.; Lister, M.L.; Tarchi, A.; Caccianiga, A.; Chen, S.; Foschini, L.; et al. Radio-emitting narrow-line Seyfert 1 galaxies in the JVLA perspective. Astron. Astrophys. 2018, 614, A87. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piotrovich, M.; Buliga, S.; Natsvlishvili, T. Estimate of SMBH Spin for Narrow-Line Seyfert 1 Galaxies. Universe 2023, 9, 175. https://doi.org/10.3390/universe9040175
Piotrovich M, Buliga S, Natsvlishvili T. Estimate of SMBH Spin for Narrow-Line Seyfert 1 Galaxies. Universe. 2023; 9(4):175. https://doi.org/10.3390/universe9040175
Chicago/Turabian StylePiotrovich, Mikhail, Stanislava Buliga, and Tinatin Natsvlishvili. 2023. "Estimate of SMBH Spin for Narrow-Line Seyfert 1 Galaxies" Universe 9, no. 4: 175. https://doi.org/10.3390/universe9040175
APA StylePiotrovich, M., Buliga, S., & Natsvlishvili, T. (2023). Estimate of SMBH Spin for Narrow-Line Seyfert 1 Galaxies. Universe, 9(4), 175. https://doi.org/10.3390/universe9040175






