New Localization Method of Abelian Gauge Fields on Bloch Branes
Abstract
:1. Introduction
2. Review of Bloch Brane Model
2.1. Case I: Degenerate I Bloch Brane
2.2. Case II: Degenerate II Bloch Brane
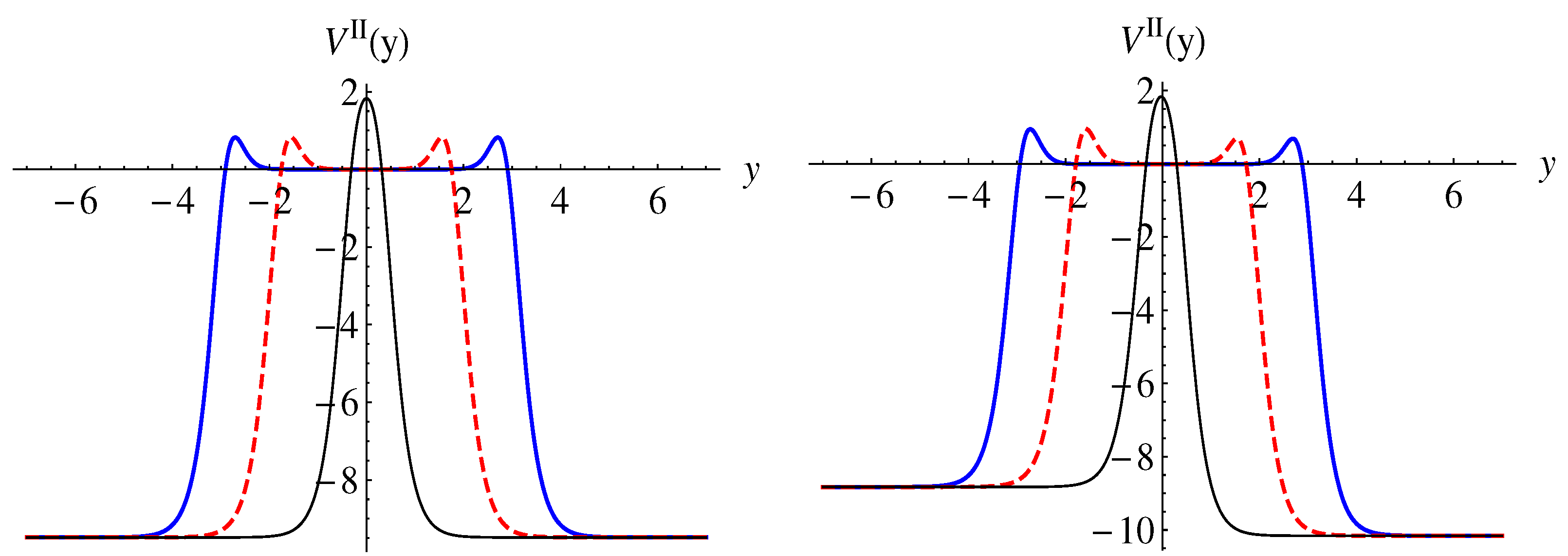
3. Localization of Abelian Gauge Field
3.1. Equation of Motion and Decoupling Actions
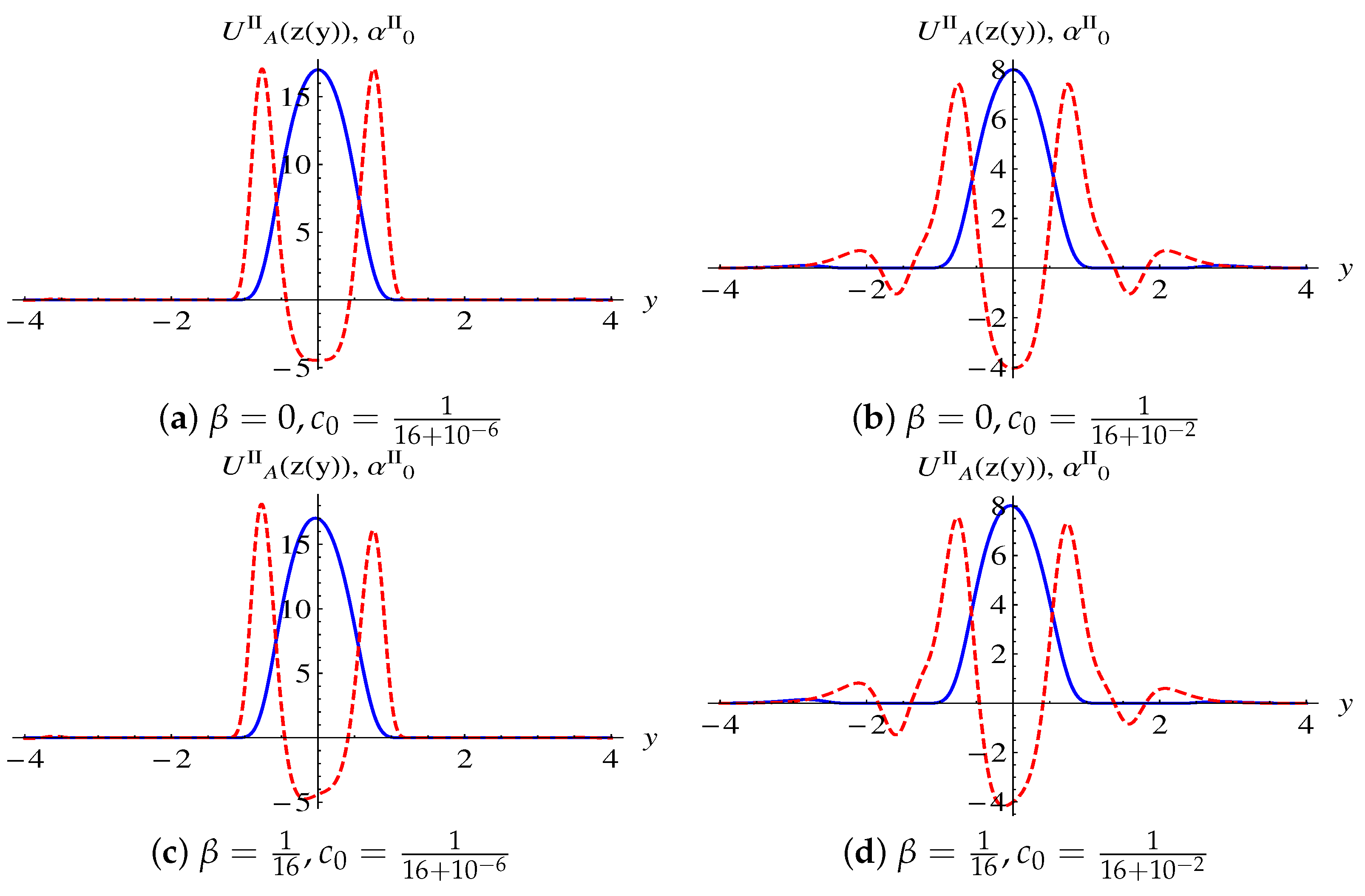
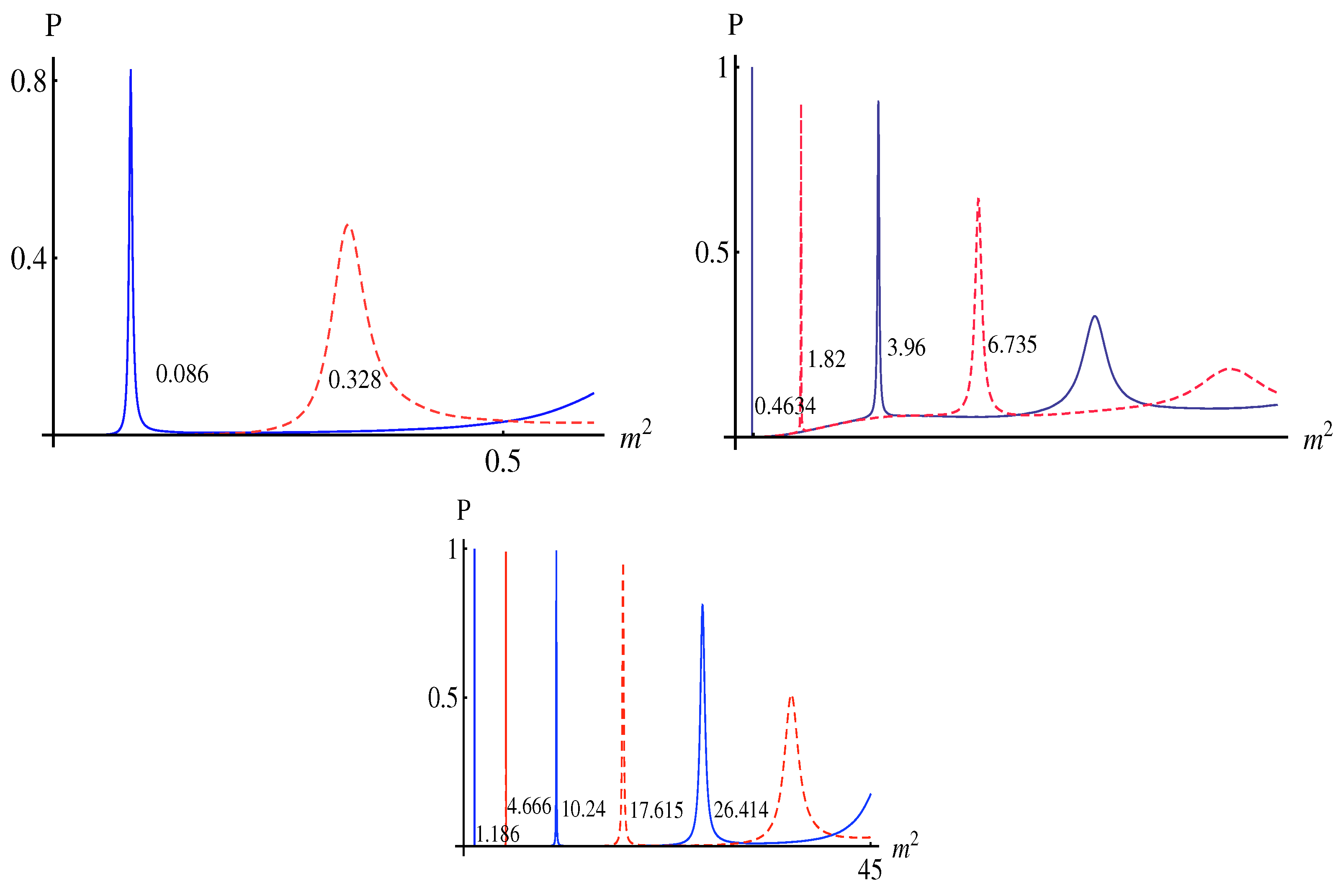
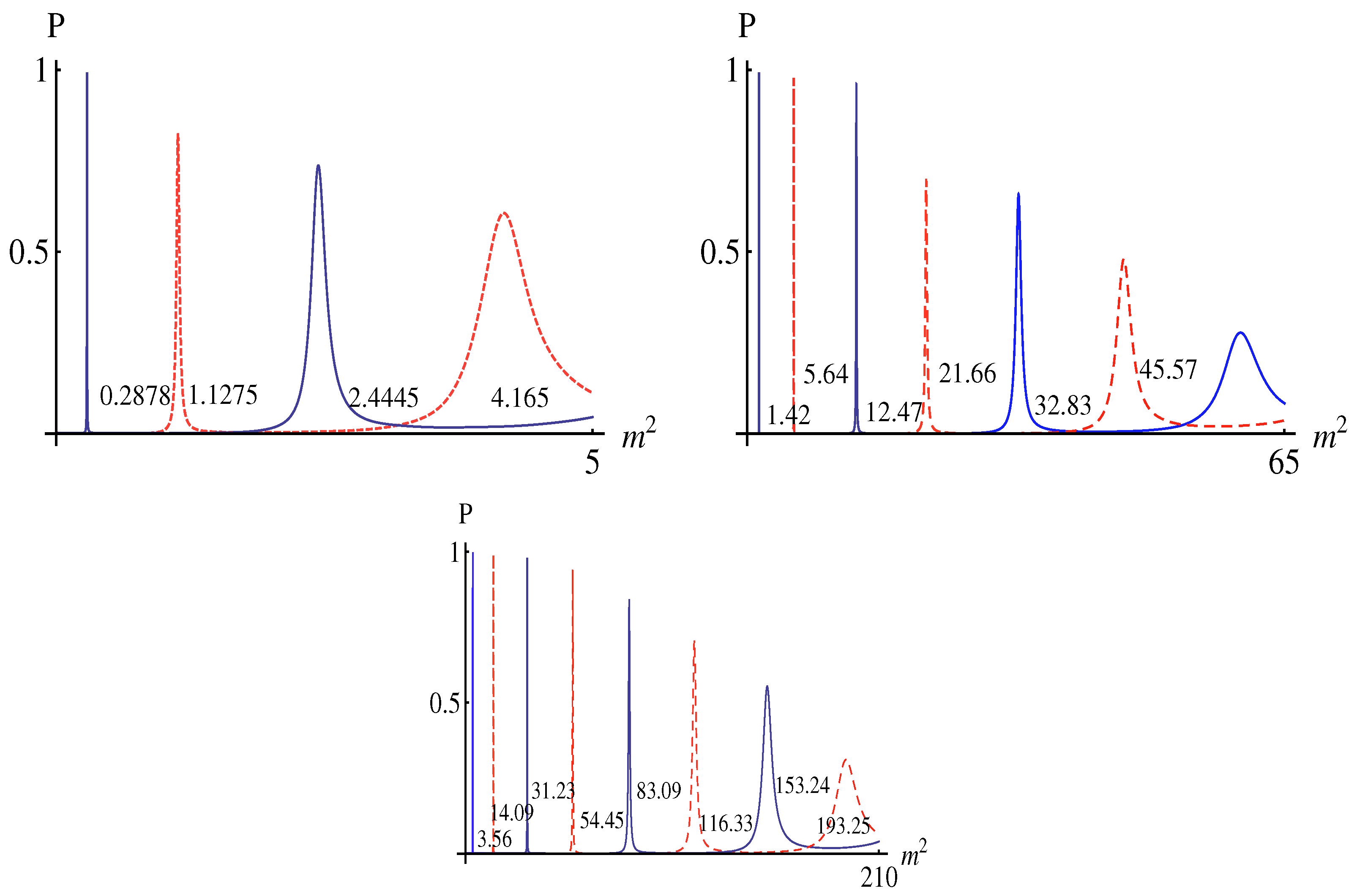
3.2. Localization of Vector Degree
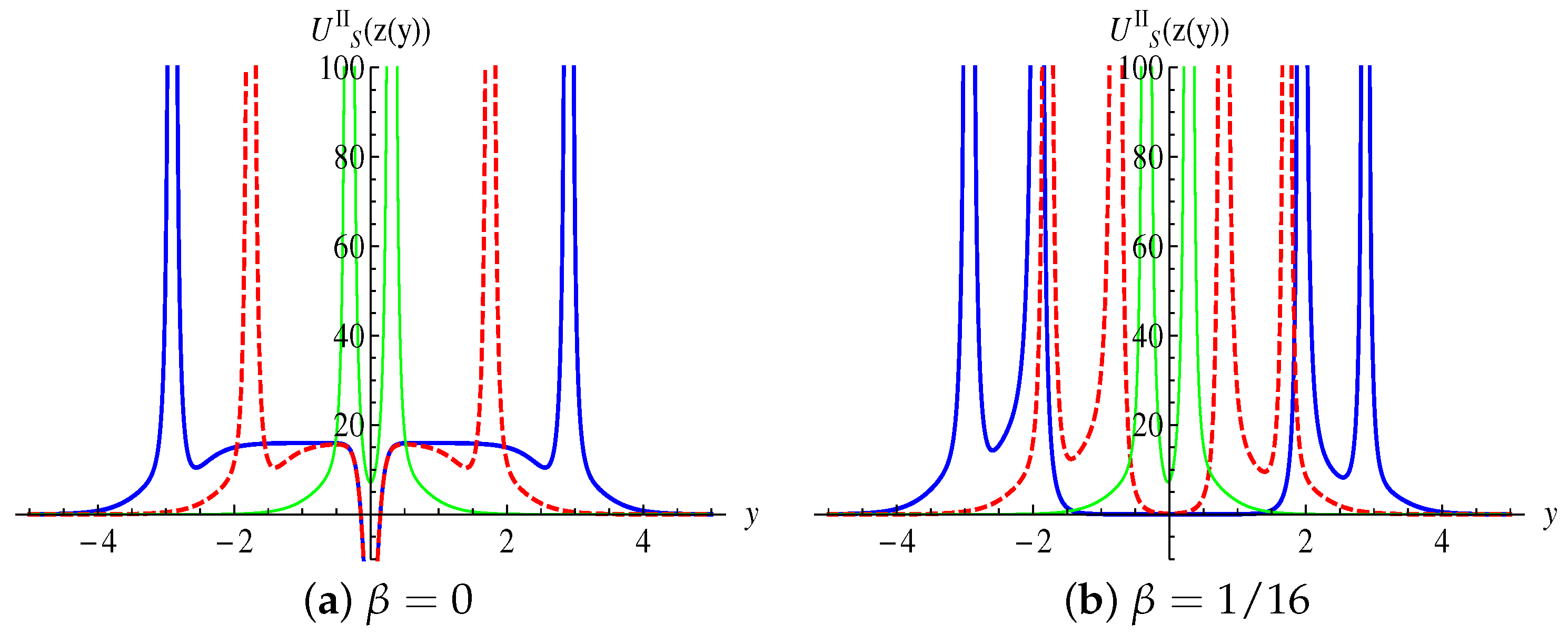
3.3. Localization of Scalar Degree Sector
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Randall, L.; Sundrum, R. A large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 1999, 83, 3370. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. An alternative to compactification. Phys. Rev. Lett. 1999, 83, 4690. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G. The hierarchy problem and new dimensions at a millimeter. Phys. Lett. 1998, 29, 263–272. [Google Scholar] [CrossRef]
- Antoniadis, I.; Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G. New dimensions at a millimeter to a fermi and superstrings at a Tev. Phys. Lett. 1998, 436, 257–263. [Google Scholar] [CrossRef]
- Gremm, M. Thick domain walls and singular spaces. Phys. Rev. D Part. Fields 2000, 62, 044017. [Google Scholar] [CrossRef]
- Gass, R.; Mukherjee, M. Domain wall space-times and particle motion. Phys. Rev. 1999, 60, 065011. [Google Scholar]
- Gremm, M. Four-dimensional gravity on a thick domain wall. Phys. Lett. B 2000, 478, 434–438. [Google Scholar] [CrossRef]
- Afonso, V.I.; Bazeia, D.; Losano, L. First-order formalism for bent brane. Phys. Lett. B 2006, 634, 526–530. [Google Scholar] [CrossRef]
- Bazeia, D.; Gomes, A.R. Bloch brane. J. High Energy Phys. 2004, 2004, 012. [Google Scholar] [CrossRef]
- de Souza Dutra, A.; de Faria, A.C.A., Jr.; Hott, M. Degenerate and critical bloch branes. Phys. Rev. D Part. Fields 2008, 78, 043526. [Google Scholar] [CrossRef]
- de Souza Dutra, A.; Amaro de Faria, A.C., Jr.; Hott, M. Degenerate and critical domain walls and accelerating universes driven by bulk particles. arXiv 2009, arXiv:0903.5533. [Google Scholar]
- Bajc, B.; Gabadadze, G. Localization of matter and cosmological constant on a brane in anti de sitter space. Phys. Lett. B 2000, 474, 282–291. [Google Scholar] [CrossRef]
- Oda, I. Localization of matters on a string-like defect. Phys. Lett. B 2000, 496, 113–121. [Google Scholar] [CrossRef]
- Melfo, A.; Pantoja, N.; Tempo, J.D. Fermion localization on thick branes. Phys. Rev. D Part. Fields 2006, 73, 04403. [Google Scholar] [CrossRef]
- Liang, J.; Duan, Y.-S. Localization and mass spectrum of spin-1/2 fermionic field on a thick brane with poincare symmetry. Europhys. Lett. 2009, 87, 40005. [Google Scholar] [CrossRef]
- Chumbes, A.E.R.; da Silva, J.M.H.; Hott, M.B. A model to localize gauge and tensor fields on thick branes. Phys. Rev. D 2012, 85, 085003. [Google Scholar] [CrossRef]
- Barbosa-Cendejas, N.; Herrera-Aguilar, A. Localization of 4-d gravity on pure geometrical thick branes. Phys. Rev. DPart. Fields 2006, 73, 084022. [Google Scholar] [CrossRef]
- Alencar, G.; Landim, R.; Tahim, M.; Filho, R.C. Gauge field localization on the brane through geometrical coupling. Phys. Lett. B 2014, 739, 125–127. [Google Scholar] [CrossRef]
- Zhao, Z.-H.; Xie, Q.-Y.; Zhong, Y. New localization method of u(1) gauge vector field on flat branes in (asymptotic) ads5 spacetime. Class. Quantum Gravity 2015, 32, 035020. [Google Scholar] [CrossRef]
- Stueckelberg, E.C.G. Interaction energy in electrodynamics and in the field theory of nuclear forces. Helv. Phys. Acta 1938, 11, 225–244. [Google Scholar]
- Vaquera-Araujo, C.A.; Corradini, O. Localization of abelian gauge fields on thick branes. Eur. Phys. J. C Part. Fields 2015, 75, 48. [Google Scholar] [CrossRef]
- Belchior, F.M.; Moreira, A.R.P.; Maluf, R.V.; Almeida, C.A.S. Localization of abelian gauge fields with stueckelberg-like geometrical coupling on f(t, b)-thick brane. Eur. Phys. J. C Part. Fields 2023, 83, 388. [Google Scholar] [CrossRef]
- Correa, R.A.C.; de Souza Dutra, A.; Hott, M.B. Fermion localization on degenerate and critical branes. Class. Quantum Grav. 2011, 28, 155012. [Google Scholar] [CrossRef]
- Cruz, W.T.; Lima, A.R.P.; Almeida, C.A.S. Gauge field localization on the bloch brane. Phys. Rev. D Part. Fields 2013, 87, 045018. [Google Scholar] [CrossRef]
- Xie, Q.-Y.; Zhao, Z.-H.; Yang, J.; Yang, K. Fermion localization and degenerate resonances on brane array. Class. Quantum Gravity 2019, 37, 025012. [Google Scholar] [CrossRef]
- Zhao, Z.-H.; Liu, Y.-X.; Zhong, Y. U(1) gauge field localization on a bloch brane with chumbes-holf da silva-hott mechanism. Phys. Rev. D Part. Fields 2014, 90, 045031. [Google Scholar] [CrossRef]
- Bazeia, D.; Ferreira, D.A.; Marques, M.A. Internal structure of cuscuton Bloch brane. Eur. Phys. J. C 2021, 81, 619. [Google Scholar] [CrossRef]
- Xie, Q.-Y.; Yang, J.; Zhao, L. Resonance mass spectra of gravity and fermion on bloch branes. Phys. Rev. D Part. Fields 2013, 88, 105014. [Google Scholar] [CrossRef]
- Guerrero, R.; Melfo, A.; Pantoja, N.; Rodriguez, R.O. Close to the edge: Hierarchy in a double braneworld. Phys. Rev. D Part. Fields 2006, 74, 084025. [Google Scholar] [CrossRef]
- Batell, B.; Gherghetta, T. Yang-mills localization in warped space. Phys. Rev. D Part. Fields 2007, 75, 025022. [Google Scholar] [CrossRef]
- Almeida, C.A.S.; Casana, R.; Ferreira, M.M.; Gomes, A.R. Fermion localization and resonances on two-field thick branes. Phys. Rev. D Part. Fields 2009, 79, 125022. [Google Scholar] [CrossRef]
- Liu, Y.-X.; Zhao, Z.-H.; Wei, S.-W.; Duan, Y.-S. Bulk matters on symmetric and asymmetric de sitter thick branes. J. Cosmol. Astropart. Phys. 2009, 2009, 003. [Google Scholar] [CrossRef]
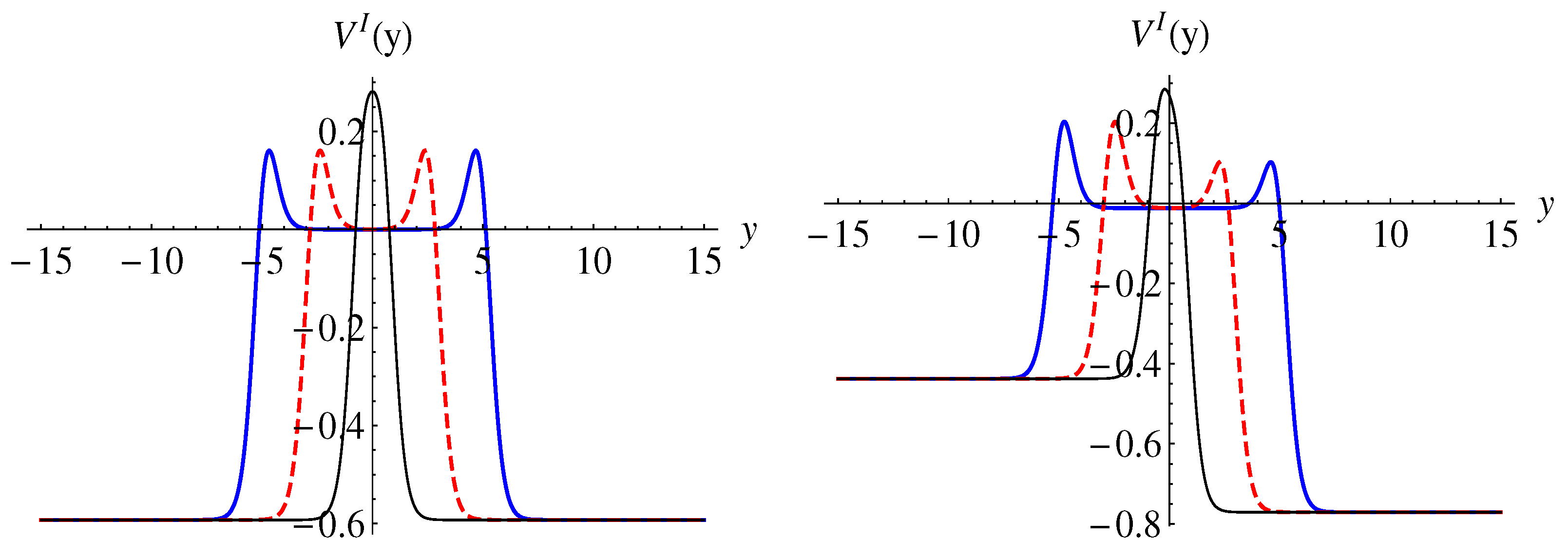
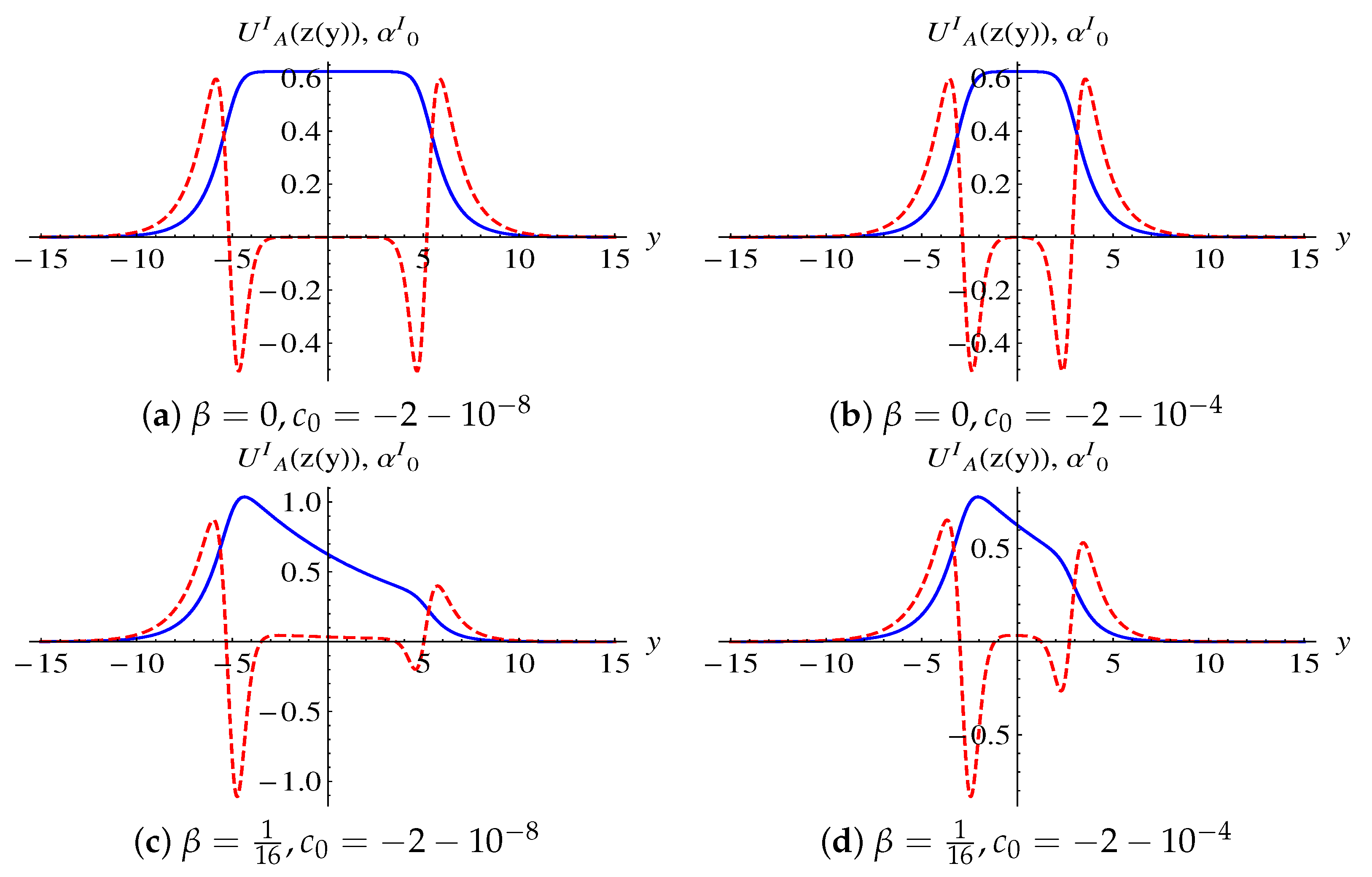

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, Y.; Du, Y.-Z. New Localization Method of Abelian Gauge Fields on Bloch Branes. Universe 2023, 9, 450. https://doi.org/10.3390/universe9100450
Zhong Y, Du Y-Z. New Localization Method of Abelian Gauge Fields on Bloch Branes. Universe. 2023; 9(10):450. https://doi.org/10.3390/universe9100450
Chicago/Turabian StyleZhong, Yi, and Yun-Zhi Du. 2023. "New Localization Method of Abelian Gauge Fields on Bloch Branes" Universe 9, no. 10: 450. https://doi.org/10.3390/universe9100450
APA StyleZhong, Y., & Du, Y.-Z. (2023). New Localization Method of Abelian Gauge Fields on Bloch Branes. Universe, 9(10), 450. https://doi.org/10.3390/universe9100450




