Abstract
Determining the types of light curves has been a challenge due to the massive amount of light curves generated by large sky survey programs. In the literature, the light curves classification methods are overly dependent on the imaging quality of the light curves, so the classification results are often poor. In this paper, a new method is proposed to classify the Kepler light curves from Quarter 1, and consists of two parts: feature extraction and classification neural network construction. In the first part, features are extracted from the light curves using three different methods, and then the features are fused (transform domain features, light curve flux statistics features, and Kepler photometry features). In the second part, a classification neural network RLNet, based on Residual Network (ResNet) and Long Short Term Memory (LSTM), is proposed. The experiment involved the classification of approximately 150,000 Kepler light curves into 11 categories. The results show that this new method outperforms seven other methods in all metrics, with an accuracy of 0.987, a minimum recall of 0.968, and a minimum precision of 0.970 under all categories.
1. Introduction
The Kepler telescope provided the first long-baseline, high-precision photometry for large numbers of stars, in which K1 collected ultra-high-precision photometric data from about 200,000 stars over about 4 years [1]. For the light curves generated by such a wide range of photometric measurements, manual classification becomes unsuitable and so there has been a boost for the automatic classification techniques.
These automatic techniques can generally be separated into two classes: one is the traditional pattern recognition method, which firstly extracts key features and, secondly, uses classifiers to distinguish different types of light curves; the other is the machine learning method, which uses NN in most conditions. For traditional pattern recognition methods, complex calculations are required to reduce the dimensionality of the light curves, such as the Fourier transform [2,3,4], Kepler photometry features [5], amplitude and coherence time scale features [6], or using the Markov Chain Monte Carlo Technique [7]. Machine learning methods are currently popular in astronomy, which includes supervised learning [8,9,10,11,12] and unsupervised learning [13,14].
It is known that many light curves from these surveys are noisy and contain temporal gaps, for various reasons related to observational constraints and survey design. Also, the difference in cadence choices among different surveys can potentially make the feature extraction and classification process heterogeneous and survey-dependent [15]. Accurate classification of light curves can be challenging when relying solely on traditional pattern recognition or machine learning methods. In this paper, both of these complementary methods are used. The light curves are initially summarized with important features, which are then fed into a neural network. This approach uses the latest neural networks to increase the accuracy of the light curves’ classification while also reducing the computational complexity during feature extraction. By combining these techniques, the paper aims to achieve more robust and efficient classification results.
The organization of this paper is as follows: Section 2 describes the dataset and the feature extraction methods; Section 3 introduces the classification model RLNet; and Section 4 presents the experimental results and discussion. Finally, Section 5 gives the conclusions and describes the future work.
2. Data
Each light curve contains a table of flux measurements and time, stored in a corresponding fits file. Two different fluxes have been released: the simple aperture photometry (SAP) flux and the pre-search data conditioning (PDC) SAP flux. The PDC SAP flux eliminates instrumental variation and noise from the data. Therefore, the PDC SAP flux is suitable to be used to construct light curves [3].
Each light curve in the dataset comprises 1639 time points, including 15 temporal gaps. As these gaps are all within one cycle, directly deleting them does not have a significant impact on the light curve. The processed light curve, as illustrated in Figure 1b, maintains its integrity. This preprocessing ensures that the light curves are ready for effective use in the neural networks.
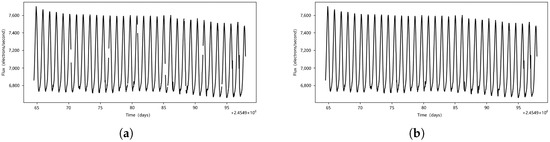
Figure 1.
(a) Raw light curve with temporal gaps. (b) The light curve after removing the temporal gaps.
2.1. Data Set
When using neural networks for classification, a training set containing all classification categories is required. This work uses the same dataset as Bass and Borne [5].
Table 1’s second column displays the various categories of light curves present in the dataset, while Figure 2 illustrates the selected light curves from each category. The categories and numbers of light curves are shown in the third column of Table 1, and the ratio between MISC and RVTAU is 24,251:1, which is a serious imbalance problem. In order to obtain the best classification effect, this paper uses SMOTE to improve the imbalance problem of the light curves. SMOTE does not address the imbalance problem solely by duplicating a few samples from the minority class. Instead, it enhances the performance of the decision boundary, enabling it to more effectively capture the characteristics of the minority classes, and the balanced results are shown in the fourth column of Table 1.

Table 1.
Number of light curves with given classification, the number of light curves simulated (via SMOTE) of each category in the training set, and the number of categories finally classified.
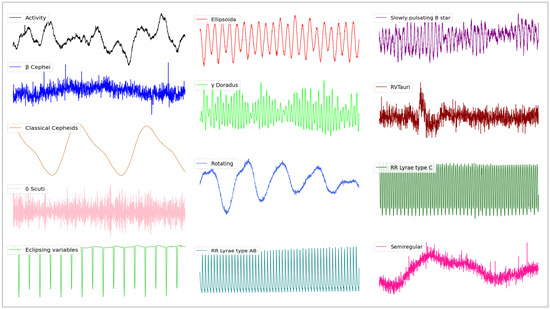
Figure 2.
Examples of light curves in the Activity, Cephei, Classical Cepheids, Scuti, Eclipsing variables, Ellipsoida, Doradus, Rotating, RR Lyrae type AB, RR Lyrae type C, RVTauri, Slowly pulsating B star, and Semiregular classes selected in the training set, respectively.
Figure 3 presents similar light curves among ACT and MISC, BCEP and ECL, and DSCUT and GDOR. To address the confusion between these categories, this work merged them into broader groups. Subsequently, the merged categories were categorized separately. The fifth column of Table 1 displays the categories and corresponding numbers after the light curves were merged.
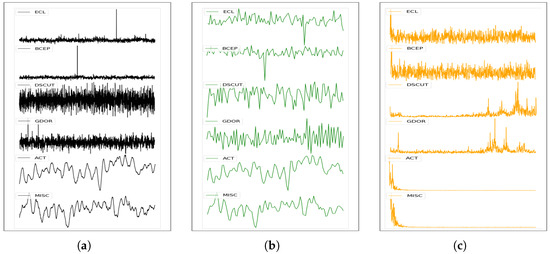
Figure 3.
(a) Similar light curves in different types. (b) Fourier transform spectral images of similar light curves. (c) Wavelet transform low-frequency spectral images of similar light curves.
2.2. Feature Extraction
In the literature, the classification of light curves usually relies on the periodic features from the light curves [8,15], which has two main challenges. Firstly, temporal gaps and noise in the light curves can impact the accurate determination of periods. Secondly, for certain variable stars with long periods, it may not be possible to obtain complete light curves within a single observation period, leading to difficulties in classification due to the absence of a clear period.
2.2.1. Frequency Domain Attributes
To make up for the limitations of time domain classification, the light curves are mathematically transformed to extract information in the transform domain that is not readily observable in the time domain. The Fourier transform is often used for conversion between the time domain and frequency domain because of its ease of use [3,5,16]. However, the Fourier transform is limited to smooth signals, and for non-smooth signals, it can only provide frequency components present in the signal fragments. As a result, the periods of light curves cannot be determined reliably from the frequency spectrum. In the Kepler program, the observation period for long-period variable stars is 30 min. While most variable stars can be fully observed within this period, the absence of periodicity can have an impact on the classification process.
The wavelet transform is a new approach in light curve analysis; Alves et al. [17] used wavelet transform decomposition to extract features and obtained excellent results. The wavelet transform builds upon and enhances the localization concept of short-time Fourier transform, overcoming its limitation of fixed window size across frequencies. Moreover, the technique is model-independent and can be applied to any time series data [18,19], making it an excellent tool for signal time-frequency analysis and processing.
Different basis functions of the wavelet transform have different effects, and the choice of basis function is crucial; in this paper, the Dowbetsis wavelet is used. This wavelet has scale invariant and translation invariant properties, and is good at striking a balance between the time and frequency domains, making it ideal for extracting light curves’ features.
Figure 4 displays the spectral images generated using the Fourier transform and wavelet transform on the same light curve. The wavelet transform decomposes the light curve into high-frequency information (b) and low-frequency information (c). The high-frequency informations captures finer details and noise in the light curve. On the other hand, the low-frequency information exhibits more pronounced periodicity, encompassing contour details of the light curve. High frequencies and low frequencies obtained through the wavelet transform undergo dimensionality reduction, frequency normalization, and outlier smoothing.
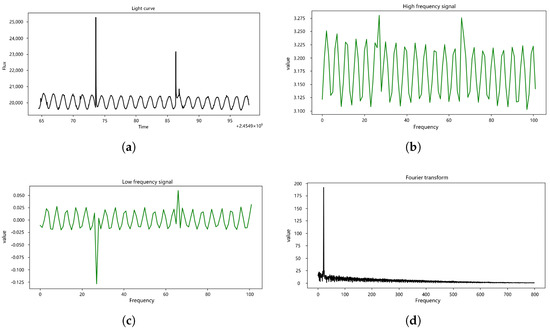
Figure 4.
(a) The light curve after removing the temporal gaps. (b) Low-frequency image generated by the wavelet transform. (c) High-frequency images generated by wavelet transform. (d) Spectral image generated by Fourier transform.
In contrast, in (d) of Figure 4, the spectrum generated by the Fourier transform is normalized and taken in half. For (a), the light curve containing noise, the Fourier transform tends to focus more on outliers, potentially leading to ineffective feature extraction. Additionally, the transformed dimension remains unchanged, and the frequency domain information lacks the time domain information, which is less conducive to model learning.
2.2.2. Other Attributes
The higher classification accuracy can be obtained by using features that contain more information about the light curves [16,20]. In addition to the frequency features, the standard deviation of the flux and median of the flux are calculated. It is noteworthy that these statistical features exhibited variations across different types of variable stars. For instance, pulsars typically exhibited prominent peaks, while RR-type variables are smoother. And, the Kepler photometry features, effective surface temperature, stellar radius, etc., are also used. These supplementary features provided valuable contextual information, aiding in the differentiation of various types of variable stars. Table 2 lists the features that are filtered out to help with the classification. The importance of features are calculated using the random forest algorithm, as shown in Figure 5.

Table 2.
Statistical and Kepler photometry features of the light curves, except for the frequency features.
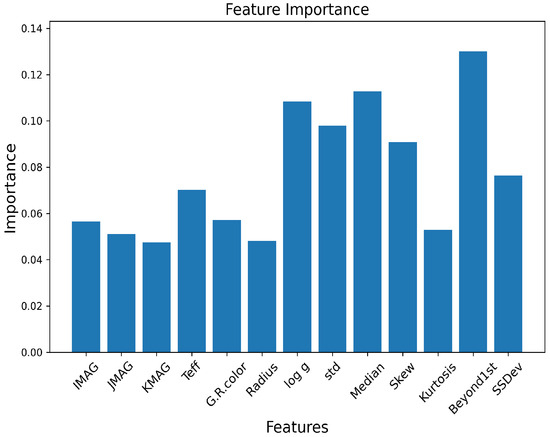
Figure 5.
The importance of different features and the height of the bar correspond to the average importance degree evaluated during the multi-classification period.
2.3. Dimension of Features
Reducing the number of features used in classifying light curves with a neural network can accelerate the training process. The wavelet transform can reduce the dimensionality of the light curves during frequency feature extraction, and the reduced dimension can only be of the original dimension (n is an integer). To determine the best number of features, this work is tested in four different dimensions.
Table 3 shows the accuracy obtained with two methods at different dimensions. It can be seen that when the number of feature is 115, it is most suitable to be used for light curves’ classification. At this point, the number of wavelet transform features is 104, level = 4, the number of Kepler photometry features is 7, and the number of light curves’ statistical features is 4. The wavelet transform consistently demonstrates higher accuracy compared to the Fourier transform when using an equal number of features. Moreover, the accuracy remains relatively stable, even with varying numbers of features. However, when the number of features is reduced to 65, there is a significant decrease in accuracy. This reduction can be attributed to the insufficient number of features to adequately represent the complex characteristics of the light curves.

Table 3.
Classification accuracy in different dimensions using the wavelet transform and Fourier transform, respectively.
In contrast, the Fourier transform exhibits a trend where higher numbers of features result in higher accuracy. This observation suggests that the features extracted by the Fourier transform might not fully capture the intricacies of the light curves, potentially affecting the subsequent classification task.
3. Models
Two well-known artificial neural network architectures are the Convolutional Neural Network (CNN) and the Recurrent Neural Network (RNN). The CNN is a feedforward neural network with convolution computation and depth structure [21], consisting of an input layer, an output layer, and multiple hidden layers, and are often used to solve classification problems in astronomy [9,22]. ResNet [23] is a specialized deep convolutional neural network architecture designed to overcome challenges like gradient disappearance, gradient explosion, and performance degradation encountered during training deep neural networks.
The RNN is specifically designed for modeling and processing sequential data and shows considerable potential in time series data [3,24]. A variant of the RNN, known as Long Short Term Memory (LSTM), has emerged, offering notable advantages over traditional RNNs [25]. LSTM successfully addresses the issues of gradient disappearance and gradient explosion by incorporating a gate function within its cell structure. This gate function effectively controls the flow of information, enabling the capture of long-term dependencies in sequential data [26].
3.1. RLNet
RLNet, as shown in Figure 6, incorporates two of the same branches, each comprising the CNN structure and the RNN structure. The CNN structure within each branch excels at extracting spatial features from input data, enabling the detection of local patterns and relationships. Meanwhile, the RNN structure within each branch is adept at capturing temporal dependencies and learning long-term patterns in continuous data [15,27].
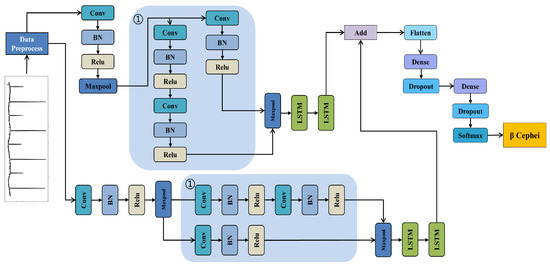
Figure 6.
The specific structure diagram of the RLNet classification network. The network is used to distinguish the variable stars into 11 categories. Note (The blue area 1 is the improved residual structure).
By combining the strengths of the CNN and RNN, RLNet effectively captures both spatial and temporal information, facilitating a comprehensive understanding of features. The use of two of the same branches enhances the network’s capacity to learn and model complex patterns, and abstract features through parallel processing and information aggregation.
The CNN consists of two modules: the first module extracts shallow features from the input data, while the second module focuses on extracting deep features. In the first module, the input features undergo convolutional layer processing, and the output is passed to the BN (batch normalization) layer. The BN layer normalizes each pixel point in the input feature map to enhance the network’s generalization ability and suppress overfitting. The parameters then pass through the ReLU activation function, allowing neurons to undergo a linear transformation and produce a nonlinear output, thus enhancing the neural network’s expressive power. Finally, a MaxPooling layer is applied, which retains the maximum value from each section of the input, leading to feature generalization and reduction, thereby facilitating quicker training of the CNN.
The structure of the second module is shown in the blue area in Figure 6, and consists of three convolutional layers, BN layers, and ReLU activation functions, which is a modified residual structure. The constant mapping in the residual structure is replaced by one convolutional layer, BN layer, and ReLU activation function, and the kernel size is 3 × 3 with 64 kernels. This structure facilitates the construction of a rich network structure, expedites network convergence, and addresses the problems of gradient expansion and gradient disappearance.
After the CNN module, a MaxPooling layer is used to reduce the dimensionality of the features, which are then passed to two LSTM modules with 16 and 32 LSTM units. The LSTM modules are employed to establish associations between different observations on varying time scales, enabling the effective utilization of past and present information to extract deep temporal features from the data [22].
Then, the features from the two branches are fused and passed through multiple dense layers. These dense layers allow for non-linear transformations that facilitate the extraction of correlations between different features, by connecting neurons to all activations of the previous layers. Finally, the softmax layer is used for classification and recognition. The softmax function calculates the predicted probability of each category based on the fused features obtained from the dense layer. This, in turn, determines the class of each light curve.
Figure 7 shows the changes of loss and accuracy of RLNet during the first 100 epochs. As the number of training epochs increases, the model’s loss gradually decreases, and the accuracy value steadily increases, indicating that RLNet is not suffering from overfitting or underfitting issues. The observed convergence trend in just 20 epochs demonstrates RLNet’s fast convergence rate, implying that the model is effectively learning from the data and refining its predictions.
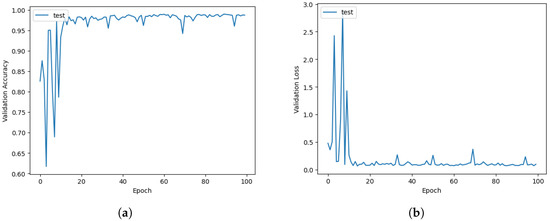
Figure 7.
The curve of RLNet validation set accuracy (a) and loss (b) with training epochs.
3.2. Training Strategy
In this work, the model’s design and the choice of parameters are tailored to the unique characteristics of the light curves task, guided by the underlying physics of the classification. However, it is worth noting that the hyperparameters undergo continuous optimization throughout the training process. Neural networks with a large number of parameters indeed possess powerful learning capabilities. However, an issue that arises is overfitting, where a model becomes overly complex and starts memorizing noise and specific details from the training data. As a result, the model’s performance on the test set may not be as good as on the training data [28]. To address overfitting, two techniques are employed in RLNet:
- BN layers are added after each convolutional layer. These BN layers normalize the activations of the previous layers, helping to stabilize and accelerate the training process.
- Dropout layers are added after each dense layer. Dropout randomly removes units (along with their connections) from the neural network during training, preventing the units from becoming overly dependent on each other and reducing co-adaptation [29].
In addition, the Adaptive Moment Estimation (Adam) optimizer is chosen for RLNet. Adam is a popular training algorithm used in many machine learning frameworks [30]. It computes first-order moment estimates and second-order moment estimates of the gradients, allowing for independent adaptive learning rates for different parameters. This adaptive optimization strategy contributes to more efficient and effective model training.
4. Results
In assessing the performance of a model, various evaluation metrics are utilized to measure the results. These metrics are not employed during the training process but prove valuable when evaluating how effectively the model performed on a specific task [3]. In this paper, accuracy, precision, and recall are used as the basis for evaluating the network performance, and their calculation formulas correspond to Equations (1), (2) and (3), respectively.
TP (true positive) is the number of positive samples whose model predicts positives. TN (true negative) is the number of negative samples whose model predicts negatives. FP (false positive) is the number of positive samples whose model predicts negatives. FN (false negative) is the number of negative samples whose model predicts positives. Accuracy is the ratio of the number of correct predictions to the total number of predictions. Precision is the ratio of the number of positive samples correctly predicted to the total number of positive samples predicted. Recall is the number of correctly predicted samples as a percentage of the total number of positive samples [31].
4.1. Evaluation Metrics
4.1.1. Confusion Matrix
The confusion matrix is the most basic, intuitive, and simple method to measure the accuracy of a classification model. The metric where the input true predicted class labels are plotted against each other is called the confusion matrix, with the predicted class in each column and the true class in each row [32].
In the case of unbalanced categories, the normalized confusion matrix provides a more intuitive explanation of which categories are misclassified. In the best case, the confusion matrix is expected to be purely diagonal, with non-zero elements on the diagonal, otherwise zero, elements [10]. The normalized confusion matrix is shown in Figure 8.
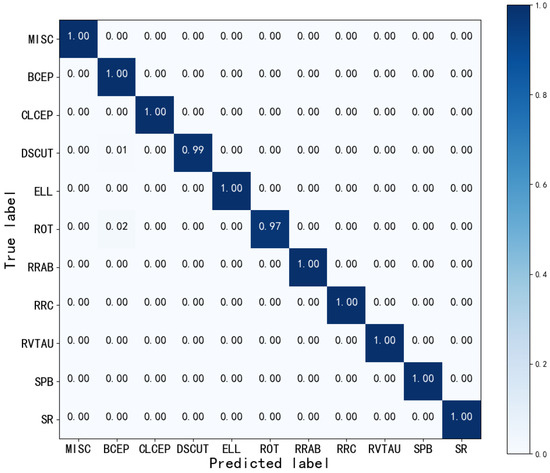
Figure 8.
The normalized confusion matrix using RLNet. The closer the diagonal value is to 1, the better the classification performance. The values in the plot are rounded to two decimal places.
4.1.2. ROC Curve
A receiver operating characteristics (ROC) graph is a technique for visualizing, organizing, and selecting based on a model’s performance [33]. The ROC curve reflects the ratio of negative samples incorrectly assigned to the positive sample to the total number of all negative samples (FPR) by the model, and the ratio of correctly identified positive examples to the total positive samples (TPR) by the model [22], and the ideal classifier maximizes TPR while minimizing FPR.
Therefore, a more favorable classification result is indicated when the curve is closer to the upper-left corner [20]. The area under the ROC curve (AUC) serves as a performance metric for machine learning algorithms [34]. The AUC is closely associated with the classification effect, and an AUC greater than 0.9 is generally regarded as indicative of a highly effective classifier [35]. Equations (4) and (5) form the ROC curve, which is shown in Figure 9.
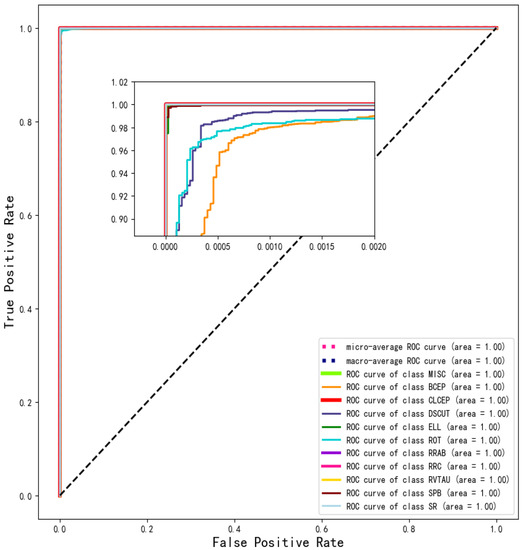
Figure 9.
ROC curve of each type. Each curve represents a category, and the values in brackets represent the area under the ROC curve (AUC). Macro-average curves and micro-average curves representing all categories were also drawn. The dotted line represents the “random opportunity” curve.
4.1.3. PR Curve
In the case of data imbalance, the PR curve (precision recall) serves as a complementary metric to the ROC curve, displaying a more variable shape. The PR curve is constructed with recall on the horizontal axis and precision on the vertical axis. The performance of the model’s classification can be assessed by measuring the area (AP) between the PR curve and the axes, as described in Equation (6). The larger the AP, the better the classification performance. The PR curve for the classification result is displayed in Figure 10.
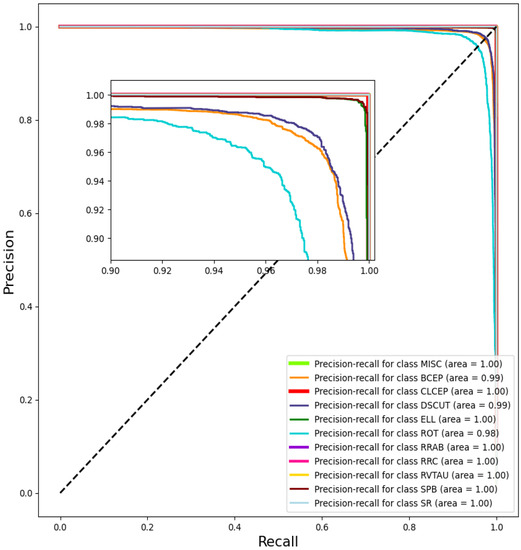
Figure 10.
PR curve of each type. Each curve represents a category, and the values in brackets represent the area under the P-R curve (AP).
In Figure 8, the confusion matrix reveals that there is minimal confusion between categories, with each category’s probability of correct prediction being higher than 0.970. The ROC curves for each category in Figure 9 cluster in the upper left corner, which is indicative of excellent performance. Achieving a predicted value of is generally considered acceptable, and RLNet surpasses this threshold with a predicted value of 0.990 in each category. PR curves are sensitive to data imbalance, and changes in the proportion of positive and negative samples can lead to significant fluctuations in the PR curves. The PR curves in Figure 10 remain smooth and display an AP above 0.980 for each category.
Based on these results, it is evident that this work performs exceptionally well in the classification task on Kepler light curves from Quarter 1. It demonstrates robust feature extraction capabilities and can effectively classify even with a small number of light curves.
4.2. Representing Light Curves in a High-Dimensional Feature Space
To better understand the structure of light curves in high-dimensional feature spaces, this work investigates 2D t-SNE visualisations (t-distribution random adjacent embedding) [22]. While t-SNE is an unsupervised technique, light curves are meaningfully organized according to their labelled class, and light curves with similar characteristics tend to be located close together in space [16].
The 2D t-SNE is shown in Figure 11, where each point is a light curve. The visualisation results show a very high differentiability between the categories, with clear boundaries between the light curves of the different categories. The 2D t-SNE image of the light curve shows the reasonableness of the classification according to the 11 categories in Table 1.
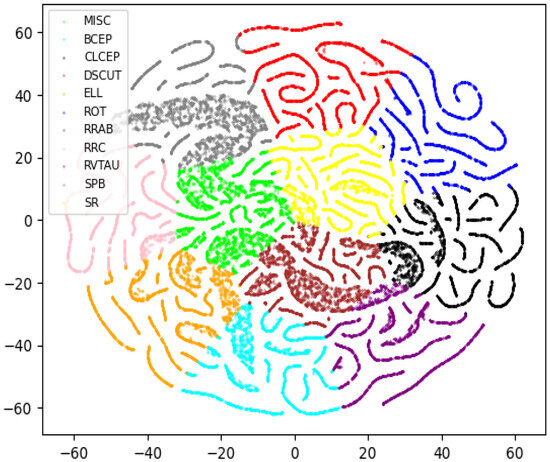
Figure 11.
2D t-SNE projection of 10% of Kepler training set, where each point is a light curve, and each light curve is colored by its category label.
4.3. Clustering Results
In this paper, the reduction in the number of light curve categories to only 11 is indeed a limitation. As a result, the study takes the initiative to compensate for this limitation by conducting classification and clustering analyses between the merged categories. The clustering results are in Figure 12 and the normalization confusion matrix results are in Figure 13.
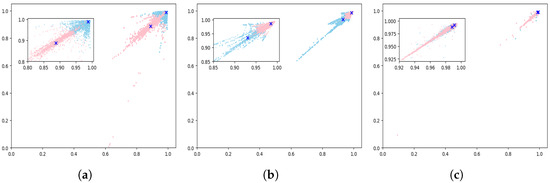
Figure 12.
Clustering results between the merging categories, with different colors representing different categories and the blue crosses × are the clustering centers. (a) ECL and BCEP. (b) DSCUT and GDOR. (c) ACT and MISC.
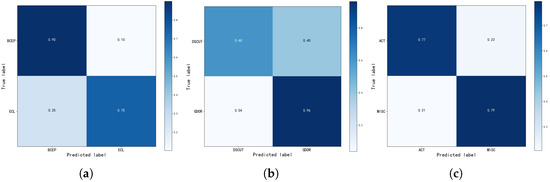
Figure 13.
Normalization confusion matrix using RLNet in the merging categories. (a) ECL and BCEP. (b) DSCUT and GDOR. (c) ACT and MISC. The closer the diagonal value is to 1, the better the classification performance. The values in the plot are rounded to two decimal places.
Among the merged light curves, the clustering centers between ECL and BCEP are the farthest apart, resulting in the largest clustering range and significant differences between the two categories. The confusion matrix of the classification results is shown in Figure 13a, where BCEP can be recognized well. However, some light curves of the ECL overlap with BCEP, leading to inaccurate recognition of ECL.
For DSCUT and GDOR, the clustering results and classification results are similar to those of ECL and BCEP. The clustering centers between DSCUT and GDOR are closer, and the clustering range is smaller, aggravating the confusion between the two categories. Consistent with Figure 13b, the classification of DSCUT is worse than that of ECL.
Regarding ACT and MISC, their cluster centers are the closest, and they have the smallest cluster ranges, indicating poor separability between these two categories. The large overlap in the clustering range between the two categories is consistent with the similar level of confusion between them in Figure 13c.
4.4. Comparison Experiment
4.4.1. Comparison with Typical Methods
This paper compares RLNet with several typical classification methods, including the random forest, Alexnet [36], and the light curves classification model [2,9,10,37,38]. Table 4 shows the accuracy achieved by the seven classifiers, with RLNet achieving the best accuracy.

Table 4.
The accuracy results measured using seven typical light curve classification networks under the same test set.
In machine learning, accuracy is often used as a measure of classifier performance. However, when dealing with unbalanced datasets, precision and recall can provide more insightful information about the model’s performance [39]. Therefore, precision and recall are used together as measures to measures classifier performance [40]. Using seven different classifiers, the precision and recall for 11 categories are shown in Table 5 and Table 6.

Table 5.
Using seven typical light curves to classify the precision of network measurements under different categories. The bold entries in the table highlight the best results in each column.

Table 6.
Using seven typical light curves to classify the recall of network measurements under different categories. The bold entries in the table highlight the best results in each column.
Table 5 and Table 6 illustrate that the precision and recall results for different categories are unsatisfactory under the comparison models. Other models, especially when dealing with a small number of DSCUT and SR, exhibit poor results. In particular, the model of Morales et al. [9] achieves a high accuracy of 0.934. However, for DSCUT, the precision only reaches 0.791, indicating that the high accuracy is attributed to misclassifying the minority class into the majority class.
RLNet outperforms other networks in terms of recall and precision. For BCEP and ROT, both precision and recall results are poor, but RLNet still manages to achieve precision and recall scores over 0.970 and 0.968, respectively.
In summary, in other classification models, precision and recall are low for categories with a small number of light curves. However, RLNet remains unaffected by these factors, indicating its strong feature extraction ability and its capability to extract effective classification information from the features.
4.4.2. Comparison with Ensemble Classifier
There has been no more work on the classification of Kepler long period light curves from Quarter 1, except for the ensemble classifier [5]. Therefore, a brief comparison with this work is made here. Bass and Borne [5] used a series of calculations such as the Fourier transform, the symbolic aggregation approximation, and Kepler photometry to parameterize the light curves. Then, an ensemble classifier was used to determine the class of the light curves.
In this work, the wavelet transform is utilized to convert the light curves from the time domain to the frequency domain, providing both periodic and non-periodic information through simpler calculations than the Fourier transform. The frequency domain features, statistical features of the light curves, and Kepler photometry features are combined to enhance the robustness of the extracted features. By employing the multi-branch neural network RLNet, an accuracy of 0.920 is achieved, which is an improvement of 0.155.
For quantitative comparison, this work provides the confusion matrix and ROC curves. The confusion matrix of the Bass and Borne [5], the accuracy is quite low for light curves with a small number of samples, such as RRAB, RRC, RVTAU, and SR. Particularly for SR, the accuracy is approximately 50%, indicating that the ensemble classifier struggles to differentiate these light curves effectively.
The confusion matrix for RLNet is shown in Figure 14, and the classification results exhibit significant improvements compared to the ensemble classifier, particularly for SR, with an increase in accuracy of approximately 40%. However, the results for ACT and DSCUT are slightly lower compared to the ensemble classifiers. It is essential to consider that the confusion matrix is based on automated classification results from Blomme et al. [41], and Section 2.1 suggests potential errors in the dataset. Therefore, the confusion between ACT and MISC does not necessarily imply poor performance of RLNet. Figure 15 presents the ROC curve results, showing a high TPR and low FPR across all categories, with AUC values exceeding 0.990. These results indicate that RLNet achieves excellent performance in light curve classification.
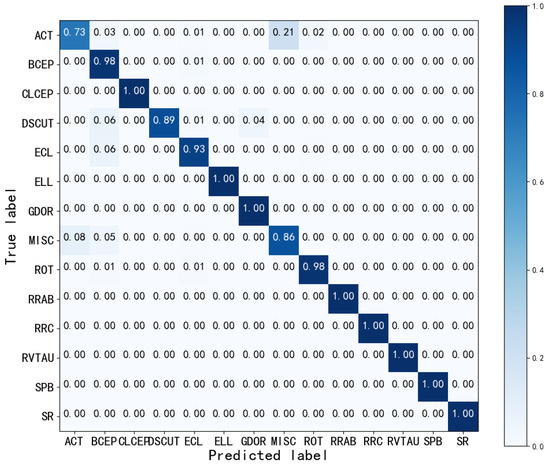
Figure 14.
Normalization confusion matrix using RLNet in the same category as the ensemble classifier. The closer the diagonal value is to 1, the better the classification performance. The values in the plot are rounded to two decimal places.
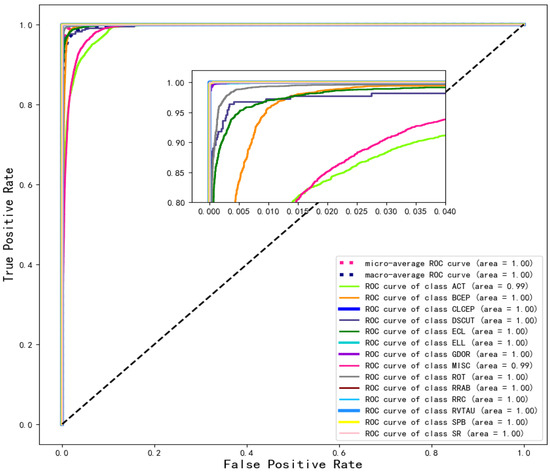
Figure 15.
ROC curve when the light curve is classified into 14 categories. Each curve represents a category, and the values in brackets represent the area under the ROC curve (AUC). Macro-average curves and micro-average curves representing all categories were also drawn. The dotted line represents the “random opportunity” curve.
5. Conclusions
This paper provides a detailed description of the process for extracting classification features and constructing the classification model. The data preprocessing involves the removal of temporal gaps in the light curves to enable frequency domain transformation. The wavelet transform is applied to the light curves to obtain frequency domain features containing periods, and the feature dimensions are reduced to 1/16 of the initial dimensions, resulting in reduced training costs.
To enhance the confidence of the classification features, the statistical features of the light curves, frequency domain features, and Kepler photometry features are fused and used as inputs for RLNet. RLNet is a multi-branch classification network based on the CNN and LSTM. The Kepler light curves from Quarter 1 are classified into 11 categories: Miscellaneous/No-variable, Cephei, Classical Cepheids, Scuti, Ellipsoida, Rotating, RR Lyrae type AB, RR Lyrae type C, RVTauri, Slowly pulsating B star, and Semiregular. Comparisons are made with seven typical classification models, on RLNet, obtaining an accuracy of 0.987, a minimum recall of 0.968, and a minimum precision of 0.970, under all categories. A comparison is also made with the experiments of the ensemble classifier and the accuracy is improved by 0.155. To ensure the diversity of light curve categories, clustering and classification are performed between the three groups of categories that are merged.
The Kepler program has produced high-quality light curves, making it possible to rely on one-dimensional information for successful classification. However, relying solely on one-dimensional information has significant limitations. The next task is to classify the light curves using image-based classification methods, which have achieved good results on TESS data.
Unsupervised learning is a task that goes even further. The search for unique stars has always been an exciting topic in astronomical research. At present, the categories of the light curves and looking for unknown stars are severely limited by supervised learning. Unsupervised learning can handle unclassified and unlabeled datasets, which is useful for finding new stars and locating unusual, variable stars. Therefore, unsupervised learning will be the next focus of research.
Author Contributions
Methodology, J.Y.; data curation, J.Y.; writing—original draft preparation, J.Y.; writing—review and editing, J.Y., H.W., B.Q., A.-L.L. and F.R.; supervision, H.W., B.Q., A.-L.L. and F.R.; project administration, B.Q.; funding acquisition, B.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Tianjin, 22JCYBJC00410, the Joint Research Fund in Astronomy, National Natural Science Foundation of China, U1931134.
Data Availability Statement
We are grateful for KEPLER that provide us with light curves. KEPLER Q1 Website: at https://archive.stsci.edu/missions-and-data/kepler/kepler-bulk-downloads/, accessed on 6 April 2022.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kirk, B.; Conroy, K.; Prša, A.; Abdul-Masih, M.; Kochoska, A.; MatijeviČ, G.; Hambleton, K.; Barclay, T.; Bloemen, S.; Boyajian, T.; et al. Kepler eclipsing binary stars. VII. The catalog of eclipsing binaries found in the entire Kepler data set. Astron. J. 2016, 151, 68. [Google Scholar] [CrossRef]
- Mahabal, A.; Sheth, K.; Gieseke, F.; Pai, A.; Djorgovski, S.; Drake, A.; Graham, M.; Collaboration, C. Deep-learnt classification of light curves. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; IEEE: New York, NY, USA, 2017; p. 2757. [Google Scholar]
- Hinners, T.A.; Tat, K.; Thorp, R. Machine learning techniques for stellar light curve classification. Astron. J. 2018, 156, 7. [Google Scholar] [CrossRef]
- Masci, F.J.; Hoffman, D.I.; Grillmair, C.J.; Cutri, R.M. Automated classification of periodic variable stars detected by the wide-field infrared survey explorer. Astron. J. 2014, 148, 21. [Google Scholar] [CrossRef]
- Bass, G.; Borne, K. Supervised ensemble classification of Kepler variable stars. Mon. Not. R. Astron. Soc. 2016, 459, 3721–3737. [Google Scholar] [CrossRef]
- Zinn, J.; Kochanek, C.; Kozłowski, S.; Udalski, A.; Szymański, M.; Soszyński, I.; Wyrzykowski, Ł.; Ulaczyk, K.; Poleski, R.; Pietrukowicz, P.; et al. Variable classification in the LSST era: Exploring a model for quasi-periodic light curves. Mon. Not. R. Astron. Soc. 2017, 468, 2189–2205. [Google Scholar] [CrossRef]
- Sánchez-Sáez, P.; Reyes, I.; Valenzuela, C.; Förster, F.; Eyheramendy, S.; Elorrieta, F.; Bauer, F.; Cabrera-Vives, G.; Estévez, P.; Catelan, M.; et al. Alert classification for the ALeRCE broker system: The light curve classifier. Astron. J. 2021, 161, 141. [Google Scholar] [CrossRef]
- Adassuriya, J.; Jayasinghe, J.; Jayaratne, K. Identifying Variable Stars from Kepler Data Using Machine Learning. Eur. J. Appl. Phys. 2021, 3, 32–35. [Google Scholar] [CrossRef]
- Morales, A.; Rojas, J.; Huijse, P.; Ramos, R.C. A Comparison of Convolutional Neural Networks for RR Lyrae Light Curve Classification. In Proceedings of the 2021 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Temuco, Chile, 2–4 November 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Szklenár, T.; Bódi, A.; Tarczay-Nehéz, D.; Vida, K.; Marton, G.; Mező, G.; Forró, A.; Szabó, R. Image-based Classification of Variable Stars: First Results from Optical Gravitational Lensing Experiment Data. Astrophys. J. Lett. 2020, 897, L12. [Google Scholar] [CrossRef]
- Burhanudin, U.; Maund, J.; Killestein, T.; Ackley, K.; Dyer, M.; Lyman, J.; Ulaczyk, K.; Cutter, R.; Mong, Y.; Steeghs, D.; et al. Light-curve classification with recurrent neural networks for GOTO: Dealing with imbalanced data. Mon. Not. R. Astron. Soc. 2021, 505, 4345–4361. [Google Scholar] [CrossRef]
- Demianenko, M.; Samorodova, E.; Sysak, M.; Shiriaev, A.; Malanchev, K.; Derkach, D.; Hushchyn, M. Supernova Light Curves Approximation based on Neural Network Models. J. Phys. Conf. Ser. 2023, 2438, 012128. [Google Scholar] [CrossRef]
- Modak, S.; Chattopadhyay, T.; Chattopadhyay, A.K. Unsupervised classification of eclipsing binary light curves through k-medoids clustering. J. Appl. Stat. 2020, 47, 376–392. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, D.; Kirk, J.; Lam, K.; McCormac, J.; Osborn, H.; Spake, J.; Walker, S.; Brown, D.; Kristiansen, M.; Pollacco, D.; et al. K2 variable catalogue—II. Machine learning classification of variable stars and eclipsing binaries in K2 fields 0–4. Mon. Not. R. Astron. Soc. 2015, 456, 2260–2272. [Google Scholar] [CrossRef]
- Bassi, S.; Sharma, K.; Gomekar, A. Classification of variable stars light curves using long short term memory network. Front. Astron. Space Sci. 2021, 8, 718139. [Google Scholar] [CrossRef]
- Barbara, N.H.; Bedding, T.R.; Fulcher, B.D.; Murphy, S.J.; Van Reeth, T. Classifying Kepler light curves for 12 000 A and F stars using supervised feature-based machine learning. Mon. Not. R. Astron. Soc. 2022, 514, 2793–2804. [Google Scholar] [CrossRef]
- Alves, C.S.; Peiris, H.V.; Lochner, M.; McEwen, J.D.; Allam, T.; Biswas, R.; Collaboration, L.D.E.S. Considerations for optimizing the photometric classification of supernovae from the rubin observatory. Astrophys. J. Suppl. Ser. 2022, 258, 23. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Rhif, M.; Ben Abbes, A.; Farah, I.R.; Martínez, B.; Sang, Y. Wavelet transform application for/in non-stationary time-series analysis: A review. Appl. Sci. 2019, 9, 1345. [Google Scholar] [CrossRef]
- McWhirter, P.R.; Steele, I.A.; Al-Jumeily, D.; Hussain, A.; Vellasco, M.M. The classification of periodic light curves from non-survey optimized observational data through automated extraction of phase-based visual features. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: New York, NY, USA, 2017; pp. 3058–3065. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Pasquet, J.; Pasquet, J.; Chaumont, M.; Fouchez, D. Pelican: Deep architecture for the light curve analysis. Astron. Astrophys. 2019, 627, A21. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Charnock, T.; Moss, A. Deep recurrent neural networks for supernovae classification. Astrophys. J. Lett. 2017, 837, L28. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Zou, Q. Time series prediction and anomaly detection of light curve using lstm neural network. J. Phys. Conf. Ser. 2018, 1061, 012012. [Google Scholar] [CrossRef]
- Ying, X. An overview of overfitting and its solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Bock, S.; Weiß, M. A proof of local convergence for the Adam optimizer. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; IEEE: New York, NY, USA, 2019; pp. 1–8. [Google Scholar]
- Shi, J.H.; Qiu, B.; Luo, A.L.; He, Z.D.; Kong, X.; Jiang, X. A photometry pipeline for SDSS images based on convolutional neural networks. Mon. Not. R. Astron. Soc. 2022, 516, 264–278. [Google Scholar] [CrossRef]
- Heydarian, M.; Doyle, T.E.; Samavi, R. MLCM: Multi-label confusion matrix. IEEE Access 2022, 10, 19083–19095. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Kirzhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Muthukrishna, D.; Narayan, G.; Mandel, K.S.; Biswas, R.; Hložek, R. RAPID: Early classification of explosive transients using deep learning. Publ. Astron. Soc. Pac. 2019, 131, 118002. [Google Scholar] [CrossRef]
- Linares, R.; Furfaro, R.; Reddy, V. Space objects classification via light-curve measurements using deep convolutional neural networks. J. Astronaut. Sci. 2020, 67, 1063–1091. [Google Scholar] [CrossRef]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 233–240. [Google Scholar]
- Juba, B.; Le, H.S. Precision-recall versus accuracy and the role of large data sets. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4039–4048. [Google Scholar]
- Blomme, J.; Sarro, L.; O’Donovan, F.; Debosscher, J.; Brown, T.; Lopez, M.; Dubath, P.; Rimoldini, L.; Charbonneau, D.; Dunham, E.; et al. Improved methodology for the automated classification of periodic variable stars. Mon. Not. R. Astron. Soc. 2011, 418, 96–106. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).