Local Quantum Uncertainty and Quantum Interferometric Power in an Anisotropic Two-Qubit System
Abstract
1. Introduction
2. Local Quantum Uncertainty and Quantum Interferometric Power
3. Model and Its Solution
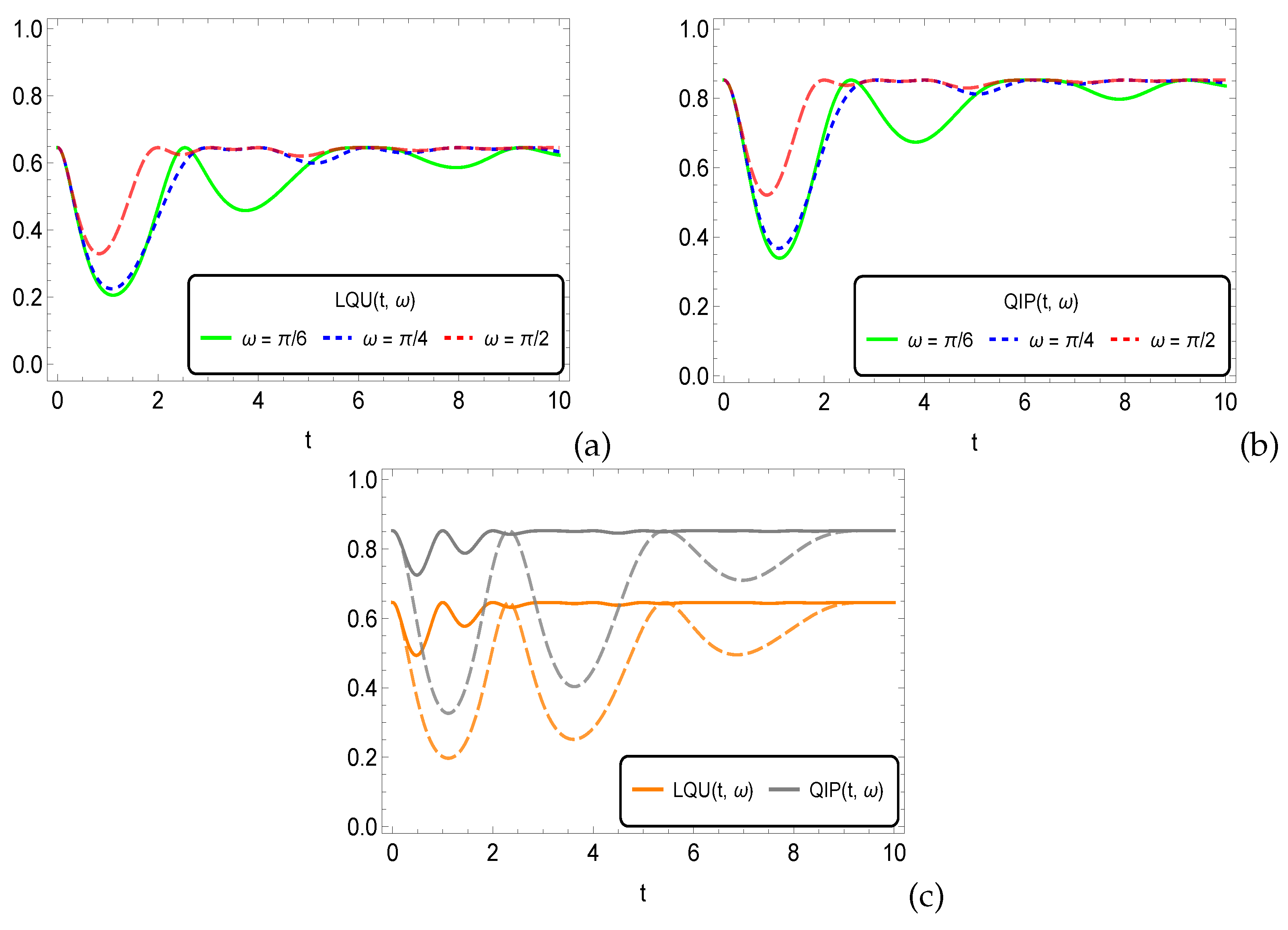
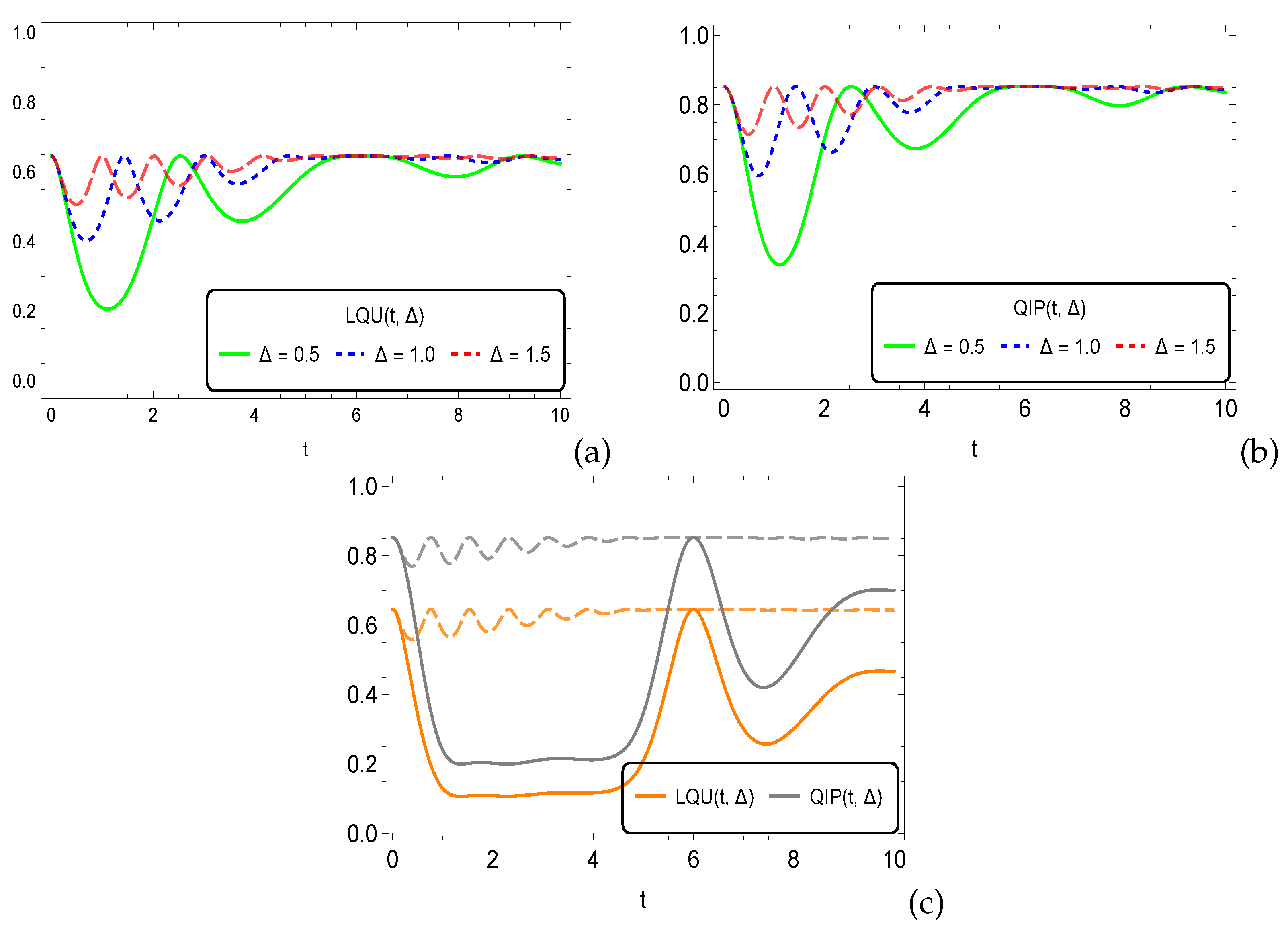
4. Main Results: Key Discussions
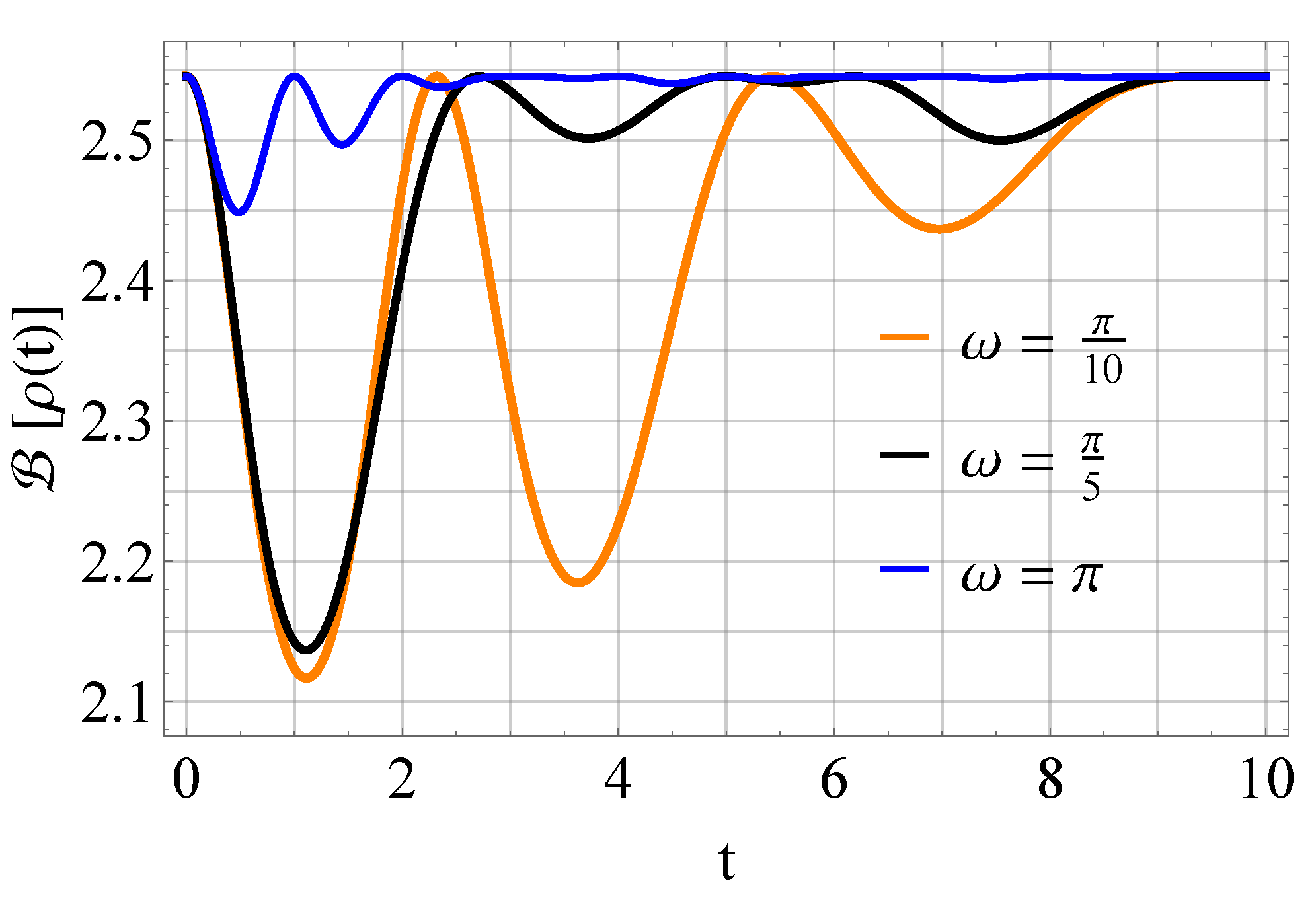
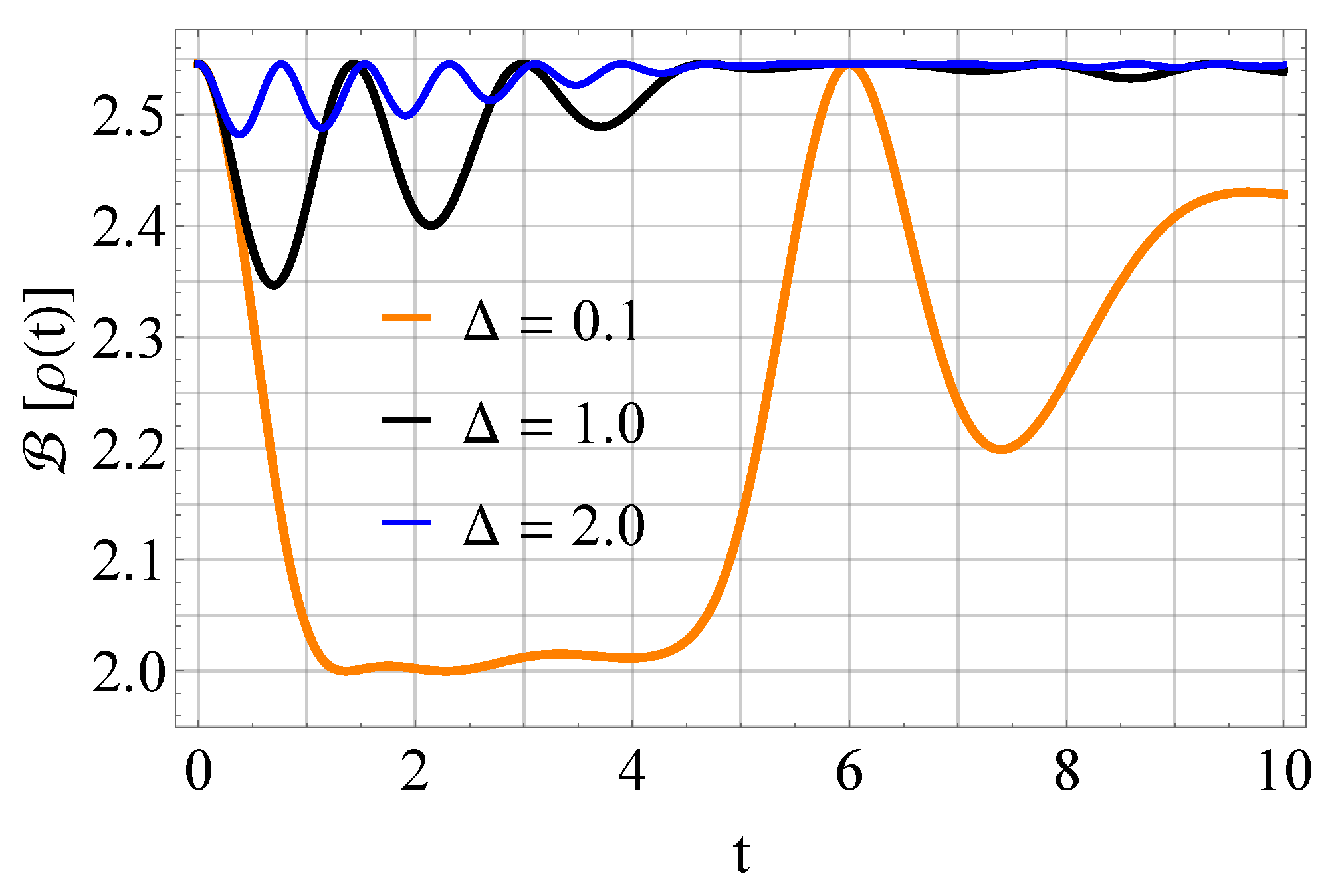
5. Analysis of Quantum Correlations with the Bell-Nonlocality Violation Parameter
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LQU | Local quantum uncertainty |
| MIN | measurement-induced non-locality |
| QFI | quantum Fisher information |
| QIP | Quantum interferometric power |
References
- Adesso, G.; Bromley, T.R.; Cianciaruso, M. Measures and applications of quantum correlations. J. Phys. A Math. Theor. 2016, 49, 473001. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]
- Czerwinski, A. Entanglement characterization by single-photon counting with random noise. Quantum Inf. Comput. 2022, 22, 1–16. [Google Scholar] [CrossRef]
- Marletto, C.; Vedral, V. Gravitationally induced entanglement between two massive particles is sufficient evidence of quantum effects in gravity. Phys. Rev. Lett. 2017, 119, 240402. [Google Scholar] [CrossRef] [PubMed]
- Martín-Martínez, E.; Brown, E.G.; Donnelly, W.; Kempf, A. Sustainable entanglement production from a quantum field. Phys. Rev. A 2013, 88, 052310. [Google Scholar] [CrossRef]
- Roch, N.; Schwartz, M.E.; Motzoi, F.; Macklin, C.; Vijay, R.; Eddins, A.W.; Korotkov, A.N.; Whaley, K.B.; Sarovar, M.; Siddiqi, I. Observation of measurement-induced entanglement and quantum trajectories of remote superconducting qubits. Phys. Rev. Lett. 2014, 112, 170501. [Google Scholar] [CrossRef]
- Bloch, I. Quantum coherence and entanglement with ultracold atoms in optical lattices. Nature 2008, 453, 1016. [Google Scholar] [CrossRef]
- Cheng, W.W.; Gong, L.Y.; Shan, C.J.; Sheng, Y.B.; Zhao, S.M. Geometric discord characterize localization transition in the one-dimensional systems. Eur. Phys. J. D 2013, 67, 121. [Google Scholar] [CrossRef]
- Qiang, W.C.; Zhang, H.P.; Zhang, L. Geometric global quantum discord of two-qubit X states. Int. J. Theor. Phys. 2016, 55, 1833. [Google Scholar] [CrossRef]
- Mohamed, A.B.A.; Khedr, A.N.; Haddadi, S.; Rahman, A.U.; Tammam, M.; Pourkarimi, M.R. Intrinsic decoherence effects on nonclassical correlations in a symmetric spin–orbit model. Results Phys. 2022, 39, 105693. [Google Scholar] [CrossRef]
- Luo, S. Using measurement-induced disturbance to characterize correlations as classical or quantum. Phys. Rev. A 2008, 77, 022301. [Google Scholar] [CrossRef]
- Mohamed, A.B.A.; Khalil, E.M. Atomic non-locality dynamics of two moving atoms in a hybrid nonlinear system: Concurrence, uncertainty-induced non-locality and Bell inequality. Opt. Quant. Electron. 2021, 53, 612. [Google Scholar] [CrossRef]
- Girolami, D.; Tufarelli, T.; Adesso, G. Characterizing nonclassical correlations via local quantum uncertainty. Phys. Rev. Lett. 2013, 110, 240402. [Google Scholar] [CrossRef]
- Gibilisco, P.; Girolami, D.; Hansen, F. A unified approach to local quantum uncertainty and interferometric power by metric adjusted skew information. Entropy 2021, 23, 263. [Google Scholar] [CrossRef]
- Sbiri, A.; Mansour, M.; Oulouda, Y. Local quantum uncertainty versus negativity through Gisin states. Int. J. Quantum Inf. 2021, 19, 2150023. [Google Scholar] [CrossRef]
- Khalid, U.; Jeong, Y.; Shin, H. Measurement-based quantum correlation in mixed-state quantum metrology. Quantum Inf. Process. 2018, 17, 343. [Google Scholar] [CrossRef]
- Wu, S.X.; Zhang, Y.; Yu, C.S. Local quantum uncertainty guarantees the measurement precision for two coupled two-level systems in non-Markovian environment. Ann. Phys. 2018, 390, 71. [Google Scholar] [CrossRef]
- Lu, X.M.; Yu, S.; Oh, C.H. Robust quantum metrological schemes based on protection of quantum Fisher information. Nat. Commun. 2015, 6, 7282. [Google Scholar] [CrossRef]
- Dhar, H.S.; Bera, M.N.; Adesso, G. Characterizing non-Markovianity via quantum interferometric power. Phys. Rev. A 2015, 91, 032115. [Google Scholar] [CrossRef]
- Girolami, D.; Souza, A.M.; Giovannetti, V.; Tufarelli, T.; Filgueiras, J.G.; Sarthour, R.S.; Adesso, G. Quantum discord determines the interferometric power of quantum states. Phys. Rev. Lett. 2014, 112, 210401. [Google Scholar] [CrossRef]
- Laghmach, R.; El Hadfi, H.; Kaydi, W.; Daoud, M. Dynamic of quantum Fisher information and quantum interferometric power in multipartite coherent states. Eur. Phys. J. D 2019, 73, 194. [Google Scholar] [CrossRef]
- Guo, Y.N.; Yang, C.; Tian, Q.L.; Wang, G.Y.; Zeng, K. Local quantum uncertainty and interferometric power for a two-qubit system under decoherence channels with memory. Quantum Inf. Process. 2019, 18, 375. [Google Scholar] [CrossRef]
- Gessner, M.; Smerzi, A. Statistical speed of quantum states: Generalized quantum Fisher information and Schatten speed. Phys. Rev. A 2018, 97, 022109. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, H.; Lu, X.M.; Wang, X. Quantum Fisher information matrix and multiparameter estimation. J. Phys. A Math. Theor. 2019, 53, 023001. [Google Scholar] [CrossRef]
- Petz, D.; Ghinea, C. Introduction to quantum Fisher information. In Quantum Probability and Related Topics; World Scientific Publishing: Singapore, 2011; pp. 261–281. [Google Scholar]
- Frahm, H.; Yu, N.C.; Fowler, M. The integrable XXZ Heisenberg model with arbitrary spin: Construction of the Hamiltonian, the ground-state configuration and conformal properties. Nucl. Phys. B 1990, 336, 396. [Google Scholar] [CrossRef]
- Santos, L.F. Integrability of a disordered Heisenberg spin-1/2 chain. J. Phys. A Math. Gen. 2004, 37, 4723. [Google Scholar] [CrossRef]
- Essler, F.H.; Piroli, L. Integrability of one-dimensional Lindbladians from operator-space fragmentation. Phys. Rev. E 2020, 102, 062210. [Google Scholar] [CrossRef]
- Heisenberg, W. Zur theorie des ferromagnetismus. Z. Physik 1928, 49, 619. [Google Scholar] [CrossRef]
- Serban, D.; Staudacher, M. Planar = 4 gauge theory and the Inozemtsev long range spin chain. JHEP06 2004, 2004, 001. [Google Scholar] [CrossRef][Green Version]
- Hernandez, R.; Lopez, E. The SU(3) spin chain sigma model and string theory. JHEP04 2004, 2004, 052. [Google Scholar] [CrossRef]
- Lovesey, S.W.; Balcar, E. A theory of the time-dependent properties of Heisenberg spin chains at infinite temperature. J. Phys. Condens. Matter. 1994, 6, 1253. [Google Scholar] [CrossRef]
- Arian Zad, H.; Ananikian, N. Phase transitions and thermal entanglement of the distorted Ising–Heisenberg spin chain: Topology of multiple-spin exchange interactions in spin ladders. J. Phys. Condens. Matter. 2017, 29, 455402. [Google Scholar] [CrossRef]
- Haddadi, S.; Pourkarimi, M.R.; Akhound, A.; Ghominejad, M. Thermal quantum correlations in a two-dimensional spin star model. Mod. Phys. Lett. A 2019, 34, 1950175. [Google Scholar] [CrossRef]
- Hu, M.L.; Gao, Y.Y.; Fan, H. Steered quantum coherence as a signature of quantum phase transitions in spin chains. Phys. Rev. A 2020, 101, 032305. [Google Scholar] [CrossRef]
- Khedif, Y.; Daoud, M. Thermal quantum correlations in the two-qubit Heisenberg XYZ spin chain with Dzyaloshinskii–Moriya interaction. Mod. Phys. Lett. A 2021, 36, 2150074. [Google Scholar] [CrossRef]
- Khedif, Y.; Haddadi, S.; Pourkarimi, M.R.; Daoud, M. Thermal correlations and entropic uncertainty in a two-spin system under DM and KSEA interactions. Mod. Phys. Lett. A 2021, 36, 2150209. [Google Scholar] [CrossRef]
- Ait Chlih, A.; Habiballah, N.; Nassik, M. Dynamics of quantum correlations under intrinsic decoherence in a Heisenberg spin chain model with Dzyaloshinskii–Moriya interaction. Quantum Inf. Process. 2021, 20, 92. [Google Scholar] [CrossRef]
- Oumennana, M.; Rahman, A.U.; Mansour, M. Quantum coherence versus non-classical correlations in XXZ spin-chain under Dzyaloshinsky–Moriya (DM) and KSEA interactions. Appl. Phys. B 2022, 128, 162. [Google Scholar] [CrossRef]
- Benabdallah, F.; Anouz, K.E.; Daoud, M. Toward the relationship between local quantum Fisher information and local quantum uncertainty in the presence of intrinsic decoherence. Eur. Phys. J. Plus 2022, 137, 548. [Google Scholar] [CrossRef]
- Benabdallah, F.; Anouz, K.E.; Strecka, J.; Daoud, M. Thermal non-classical correlation via skew information, quantum Fisher information, and quantum teleportation of a spin-1/2 Heisenberg trimer system. Eur. Phys. J. Plus 2022, 137, 1096. [Google Scholar] [CrossRef]
- Haseli, S. Local quantum Fisher information and local quantum uncertainty in two-qubit Heisenberg XYZ chain with Dzyaloshinskii–Moriya interactions. Laser Phys. 2020, 30, 105203. [Google Scholar] [CrossRef]
- Khedif, Y.; Haddadi, S.; Daoud, M.; Dolatkhah, H.; Pourkarimi, M.R. Non-classical correlations in a Heisenberg spin model with Heitler–London approach. Quantum Inf. Process. 2022, 21, 235. [Google Scholar] [CrossRef]
- Malvezzi, A.L.; Karpat, G.; Çakmak, B.; Fanchini, F.F.; Debarba, T.; Vianna, R.O. Quantum correlations and coherence in spin-1 Heisenberg chains. Phys. Rev. B 2016, 93, 184428. [Google Scholar] [CrossRef]
- Shi, W.N.; Ming, F.; Wang, D.; Ye, L. Entropic uncertainty relations in the spin-1 Heisenberg model. Quantum Inf. Process. 2019, 18, 70. [Google Scholar] [CrossRef]
- Werlang, T.; Trippe, C.; Ribeiro, G.A.P.; Rigolin, G. Quantum correlations in spin chains at finite temperatures and quantum phase transitions. Phys. Rev. Lett. 2010, 105, 095702. [Google Scholar] [CrossRef]
- Zheng, Y.; Mao, Z.; Zhou, B. Thermal quantum correlations of a spin-1/2 Ising–Heisenberg diamond chain with Dzyaloshinskii–Moriya interaction. Chinese Phys. B 2018, 27, 090306. [Google Scholar] [CrossRef]
- Yurischev, M.A. On the quantum correlations in two-qubit XYZ spin chains with Dzyaloshinsky–Moriya and Kaplan–Shekhtman– Entin-Wohlman–Aharony interactions. Quantum Inf. Process. 2020, 19, 336. [Google Scholar] [CrossRef]
- Benabdallah, F.; Rahman, A.U.; Haddadi, S.; Daoud, M. Long-time protection of thermal correlations in a hybrid-spin system under random telegraph noise. Phys. Rev. E 2022, 106, 034122. [Google Scholar] [CrossRef]
- Alenezi, M.; Zidan, N.; Alhashash, A.; Rahman, A.U. Quantum Fisher Information Dynamics in the Presence of Intrinsic Decoherence. Int. J. Theor. Phys. 2022, 61, 153. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Caves, C.M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 1994, 72, 3439. [Google Scholar] [CrossRef]
- Elghaayda, S.; Dahbi, Z.; Mansour, M. Local quantum uncertainty and local quantum Fisher information in two-coupled double quantum dots. Opt. Quant. Electron. 2022, 54, 419. [Google Scholar] [CrossRef]
- Luo, S. Wigner–Yanase skew information versus quantum Fisher information. Proc. Am. Math. Soc. 2003, 132, 885. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M. Violating Bell inequality by mixed spin-1/2 states: Necessary and sufficient condition. Phys. Lett. A 1995, 200, 340. [Google Scholar] [CrossRef]
- Hu, M.L. Relations between entanglement, bell-inequality violation and teleportation fidelity for the two-qubit X states. Quant. Inf. Process. 2013, 12, 229. [Google Scholar] [CrossRef]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 1969, 23, 880. [Google Scholar] [CrossRef]
- Haseli, S.; Haddadi, S.; Pourkarimi, M.R. Entropic uncertainty lower bound for a two-qubit system coupled to a spin chain with Dzyaloshinskii–Moriya interaction. Opt. Quant. Electron. 2020, 52, 465. [Google Scholar] [CrossRef]
- Hashem, M.; Mohamed, A.B.A.; Haddadi, S.; Khedif, Y.; Pourkarimi, M.R.; Daoud, M. Bell nonlocality, entanglement, and entropic uncertainty in a Heisenberg model under intrinsic decoherence: DM and KSEA interplay effects. Appl. Phys. B 2022, 128, 87. [Google Scholar] [CrossRef]
- Benabdallah, F.; Haddadi, S.; Arian Zad, H.; Pourkarimi, M.R.; Daoud, M.; Ananikian, N. Pairwise quantum criteria and teleportation in a spin square complex. Sci. Rep. 2022, 12, 6406. [Google Scholar] [CrossRef]
- Haddadi, S.; Pourkarimi, M.R.; Khedif, Y.; Daoud, M. Tripartite measurement uncertainty in a Heisenberg XXZ model. Eur. Phys. J. Plus 2022, 137, 66. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zidan, N.; Rahman, A.U.; Haddadi, S.; Czerwinski, A.; Haseli, S. Local Quantum Uncertainty and Quantum Interferometric Power in an Anisotropic Two-Qubit System. Universe 2023, 9, 5. https://doi.org/10.3390/universe9010005
Zidan N, Rahman AU, Haddadi S, Czerwinski A, Haseli S. Local Quantum Uncertainty and Quantum Interferometric Power in an Anisotropic Two-Qubit System. Universe. 2023; 9(1):5. https://doi.org/10.3390/universe9010005
Chicago/Turabian StyleZidan, Nour, Atta Ur Rahman, Saeed Haddadi, Artur Czerwinski, and Soroush Haseli. 2023. "Local Quantum Uncertainty and Quantum Interferometric Power in an Anisotropic Two-Qubit System" Universe 9, no. 1: 5. https://doi.org/10.3390/universe9010005
APA StyleZidan, N., Rahman, A. U., Haddadi, S., Czerwinski, A., & Haseli, S. (2023). Local Quantum Uncertainty and Quantum Interferometric Power in an Anisotropic Two-Qubit System. Universe, 9(1), 5. https://doi.org/10.3390/universe9010005







