Abstract
In this manuscript, we review the motion of a two-body celestial system (planet–sun) for a Yukawa-type correction on Newton’s gravitational potential using Hamilton’s formulation. We reexamine the stability using the corresponding linearization Jacobian matrix, and verify that the conditions of Bertrand’s theorem are met for radii m, meaning that bound closed orbits are expected. Applied to the solar system, we present the equation of motion of the planet, then solve it both analytically and numerically. Making use of the analytical expression of the orbit, we estimate the Yukawa strength and find it to be larger than the nominal value () adopted in previous studies, in that it is of order () for the terrestrial planets (Mercury, Venus, earth, Mars, and Pluto) and even larger () for the giant planets (Jupiter, Saturn, Uranus, and Neptune). Taking the inputs () observed by NASA, we analyse the orbits analytically and numerically for both the estimated and nominal values of and determine the corresponding trajectories. For each obtained orbit, we recalculate the characterizing parameters () and compare their values according to the potential (Newton with/without Yukawa correction) and method (analytical and/or numerical) used. When compared to the observational data, we conclude that the path correction due to Yukawa correction is on the order of up to 80 million km (20 million km) as the maximum deviation occurring for Neptune (Pluto) for a nominal (estimated) value of .
1. Introduction
The past several years have witnessed a resurgence of interest in experimental testing of gravity, particularly in the possibility of deviations from the predictions of Newtonian gravity, which is considered an excellent approximation of General Relativity (GR) on large distance scales [1]. Many theoretical models suggest the existence of a new and relatively weak intermediate-range force coexisting with gravity such that the net resulting interaction behaves as a new correction to the potentials defining the gravitational field. It is known [2] that there are only two types of central potentials, namely, the Newton and Harmonic potentials, where any finite motion of an object leads to a closed path subject to this central potential (Bertrand’s theorem). There are ‘exceptions’ to this statement, in the sense that there might be closed-bound trajectories for a central potential different from the Newtonian and Harmonic, which have been studied in [3,4]. In this contribution, we revisit the effect of Yukawa correction to the gravitational force over large distances.
Theories of massive gravity [5,6] that add a mass term to the graviton (the carrier of gravity) have raised wide interest, and the Yukawa potential is the popular parametrization of such theories. Actually, many works describing deviations from Newton’s inverse square law have addressed Yukawa-type correction. Assuming that gravity is exerted by exchanges of gravitons, it is clear that a test for the graviton mass () is to ask whether the Newton potential () shows any evidence of dying at large distances because of Yukawa exponential cutoff (). Beginning in the 1970s [7], bounds on the mass of the graviton ( eV) have been used to place a bound on its Compton wavelength, considered as a distance scale for Yukawa correction ( MPc). The authors of [8] provided a bound on the Yukawa range () in the order of ( AU), corresponding to () eV.
Theories such as Scalar-Tensor-Vector Gravity Theory [9] predict a Yukawa-like fifth force. The authors of [10] showed that screened modified gravity can suppress the fifth force in dense regions, allowing theories to evade the solar system and laboratory tests of the weak equivalence principle. In [11], an extended theory of gravity with a modified potential including post-Newtonian terms called ‘vacuum bootstrapped Newtonian gravity’ for which expansion is different from that of Yukawa correction, was subjected to solar system tests through a procedure which was applied to Yukawa corrections at the Galactic center [12]. No significant deviations from GR were found.
In [13], a Keplerian-type parametrization was shown as a solution of the equations of motion for a Yukawa-type potential between two bodies. In fact, the two-body solution for alternative theories yielded a strong constraint for the solar system [14,15], whereas several analyses of Yukawa potential for a two-body system in different contexts were carried out as well [16,17]. The orbit of a single particle moving under Yukawa potential was studied in [18], and precessing ellipse-type orbits were observed. In [19], it was noted that modified gravity with a Yukawa-like long-range potential was (un)successful on astrophysical scales (in the solar system), whereas an analysis of the Yukawa potential in gravity was provided in [20]. The work of [21] showed that a Yukawa fifth force is expected to be sub-dominant in satellite dynamics and space geodesy experiments as long as they are performed at altitudes greater than a few hundred kilometres. The Yukawa strength was estimated in [22] to be (–) for distances of order cm, whereas the use of laser data from LAGEOS satellites yielded a constraint on of the order of .
In this article, we build on work from [23], in which the dynamics and stability of the two-body problem with a Newtonian potential corrected by a Yukawa term were explored. In particular, we have reproduced their analytical results and applied them to the study of all the planets of our solar system. Analytically, by solving the planet equation of motion one finds an elliptical trajectory, which can be obtained numerically using the Runge–Kutta method. Starting from the observed values of the perihelion distance and velocity and of the trajectory eccentricity e stated in NASA public results [24]1, it is possible to determine the ellipsis equation and estimate for the Yukawa corrected potential, i.e., the Yukawa strength . This estimated value, or another nominal value taken from other studies, can then be used to either draw the analytical trajectory and recalculate the characterizing parameters (the shortest (longest) distance to the Sun , the semi major (minor) axis , and the eccentricity e), or to solve the equations of motion with the Yukawa-corrected potential numerically in order to check the closedness of the resulting trajectory, the characteristics of which are to be reevaluated again. Later, we compared these results to those calculated for the Keplerian motion of planets subject to the pure Newtonian potential, and showed the compatibility of the results with the observational NASA data.
More specifically, for the two-body system (planet–sun), the Newtonian potential is provided by
where is the gravitational Newton constant and () is the planet (sun) mass. With a Yukawa correction, the gravitational potential becomes
where is the Yukawa correction to the Newtonian potential and () represents the strength (range) of the Yukawa correction. Previous studies [23,25] have provided the nominal values ( m). However, our estimations result in a larger order of magnitude for the Yukawa strength: for the terrestrial planets (Mercury, Venus, Earth, Mars, and Pluto) and for the giant planets (Jupiter, Saturn, Uranus, and Neptune), which are in line with [13].
We found that for the estimated , the maximum deviation from observed data (which increases the further the planet is (20 million km for Pluto)), is less than that of the nominal value of (80 million km for Neptune), which is plausible considering that the estimation of is performed by identifying the factor containing it in the observational data.
For each of the nominal and estimated values of , we analysed the planet trajectories both analytically and numerically. Analytics-wise, we started from the NASA observational data () and reconstructed the closed ellipse trajectory, for which we then re-evaluated the characteristics () and compared it with both the pure Newton case and the observational data. Numerics-wise, determines the potential under which the planet moves; thus, one can solve the equations of motion numerically using the Runge–Kutta method, taking as initial conditions the observed data of () to check whether closed trajectories are obtained in excellent agreement with the elliptical shapes, for which the evaluated characteristics can then be compared to the pure Newtonian case, the analytical method results, and the observed data.
The rest of this manuscript is organized as follows. In Section 2, we revise the system dynamics using Hamilton’s method. In Section 3, we state the types of stability and determine the one corresponding to the system under study. In Section 4, and following [23], we discuss Bertrand’s theorem and obtain the analytical solution to the equation of motion. Finally, in Section 5 we obtain the obtained approximative analytical results for the study of the solar system planets in order to estimate the Yukawa strength and re-determine the trajectory characteristics for both the estimated and nominal values of , as well as to solve the equations numerically. The results of comparing the analytical/numerical outputs with the observed data according to the used potential are presented in form of plots for all the planets, whereas the corresponding tables are provided in the appendices. We end the paper with our conclusions in Section 6.
2. Hamiltonian Formulation
We start with the Hamiltonian , where T is the kinetic energy of both masses and V is the gravitational potential energy:
where are the positions (velocities) of the two masses with corresponding momenta , . Changing to the center of mass frame (c.o.m), with
we have
Here, we have defined as the reduced mass of the system and . We switch to polar coordinates in the c.o.m to obtain
From the canonical equations [26] and because the Hamiltonian is cyclic in (i.e., it does not depend explicitly on ), we have
where ℓ is the angular momentum of the two-body system; therefore, Hamilton’s equations for r become
Again, because is constant during the motion of the masses [26] and because , we have a lower bound for the total energy of the system:
The right hand side of Equation (15) is defined to be the “reduced potential”, which is common in the Kepler problem moving from two degrees of freedom to only one (with the Yukawa correction):
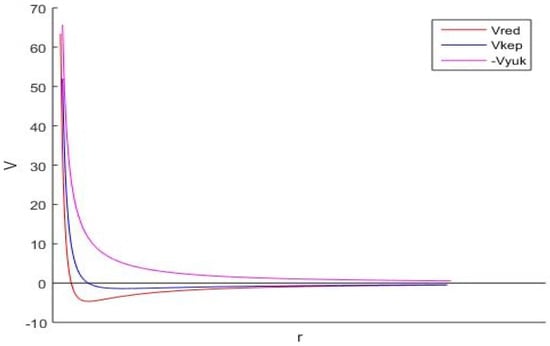
One can draw the function for a fixed ℓ given the allowed regions of motion (see Figure 1); note that and .
3. The Linearization Matrix
Following [27], in order to determine the stability of the equilibrium points of the system, we must form a matrix differential equation using the system equations of motion (Hamilton’s Equations (13) and (14) for ). The linear system has the following form:
Considering that m for orbits of sizes comparable to the solar system’s dimensions [28], we can assume that is small enough to use Taylor expansion on the exponential and ignore the terms of , leading to
Thus,
with the Yukawa effect within this approximation being limited to replacing K with , which tells us that the potential shape remains Newtonian (); thus, according to Bertrand’s theorem, every bound trajectory is closed for small . This fact can be seen directly from Equation (16); compared to the Keplerian potential, with a small shift in addition to the replacement (), which does not interfere in the equations of motion, it provides
Consequently, the Jacobian matrix takes the form
where terms of the order are ignored and where the equilibrium point satisfies . We can determine r at equilibrium using (Equation (14)) to reach the leading order:
We can now test for stability by choosing values of () and finding the eigenvalues of the Jacobian matrix (20) after substituting the equilibrium solution found above (Equation (21)). Recall that the eigenvalues are found by solving the following equation:
with referring to the identity matrix. Thus, we have
The characteristic equation (the eigenvalue equation) becomes
Following [29], the stability is determined by the sign of the eigenvalues. Because , we have the following cases:
- , a stable node
- , a stable spiral
- , an unstable node
- , an unstable spiral
- , a neutrally stable center (which is our case)
Actually, the stability refers to how the solution behaves near the equilibrium point, in that unstable solutions grow to infinity, whereas stable solutions tend to zero. Furthermore, the imaginary cases are the ones resulting in bound orbital solutions (specifically, the center case), whereas the stable and unstable imaginary cases have bound solutions tending towards or away from zero.
4. Stability and Bertrand’s Theorem
First, we rewrite the eigenvalue equation in the form
leading to
Note that we can study the case for a purely Newtonian Potential by letting . Similarly, by ignoring the terms derived from the Newtonian potential, we can single out the pure Yukawa contribution. In these two extreme cases, the characteristic equations becomes
resulting in
Thus, the equilibrium points for the purely Newtonian, the purely Yukawa, and the Newton plus Yukawa potentials remain center solutions. This implies that the motion remains restricted to ellipses about the equilibrium point; thus, orbits near the equilibrium point are possible (further away from the equilibrium point, we would have unbounded solutions, as Figure 1 shows). This proves that for small we have stable closed orbits.
For the Keplerian orbit equation, this can be written as
where denotes the Binet transformation providing the following differential equation for small :
the solution of which is provided by
with e the eccentricity of the orbit. The purely Newtonian and purely Yukawa cases follow respectively from (34):
Finally, in order to satisfy Bertrand’s theorem, the following condition should be satisfied:
where the reduced potential is provided by (16). With the approximations of (Equation 18)) and ignoring terms of order , this condition becomes
which is true, because , in general and in the special cases of the purely Newtonian () and purely Yukawa potentials. This shows that the Yukawa plus Newtonian potential satisfies Bertrand’s theorem for small .
5. Application to the Solar System
We now present our results, consisting of first determining the parameters of the models () by comparing the previous approximative analytical solutions with the NASA data. Then, we solve the equations of motion numerically using Matlab and the fourth-order Runge–Kutta method with no approximation, allowing for comparison with the analytical solutions and the observed NASA data. We applied this for all the planets of the solar system. For each sun–planet pair, we used the following values: kg, m. Table 1 lists the initial conditions used in the analytical and numerical calculations (the period is used only in the numerical solution to determine the corresponding ‘step’):

Table 1.
Initial conditions used in the calculations, where denotes the planet mass, the orbit period, the perihelion, and the perihelion velocity.
5.1. Analytical Method
The analytical ellipsis equation is of the form
where, for a y-axis perpendicular to the polar axis in the orbit plane,
Thus, analytically we can start with (), observed by NASA in [24], to compute2
and estimate the strength of from
When the analytical equation is determined, we can then plot the trajectory and recompute the characteristics () using Equations (41) and (42). We call this procedure the “analytical--estimated” approach.
In addition, we can use the nominal value of in Equation (40), where are taken from the observed data, to re-evaluate () from
We call this procedure the “analytical--nominal” approach, which can be considered as a method with three inputs instead of the three inputs () used in the other approach.
5.2. Numerical Method
Here, we use the fourth-order Runge–Kutta method to solve the Newton’s law equation of motion in the c.o.m frame numerically with initial conditions taken from NASA. Thus, we solve the following equations:
under the initial conditions provided by the NASA data ():
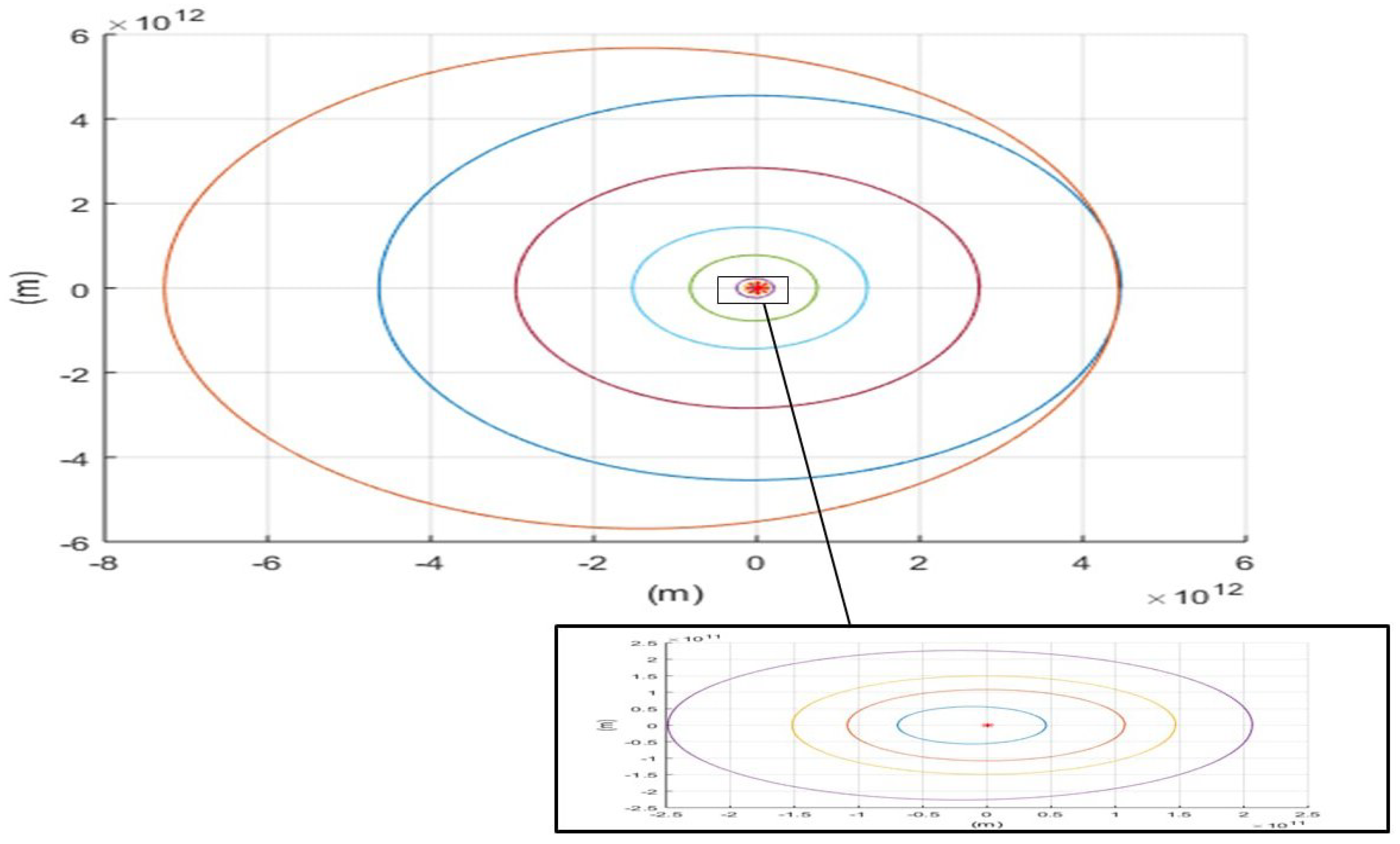
After the trajectory is solved numerically, we check that it is closed, as Figure 2 shows for both the purely Newton and purely Yukawa corrections (as the differences are not visible on the figure scale containing all the planets). For each obtained orbit, we recalculate the corresponding characteristics ().
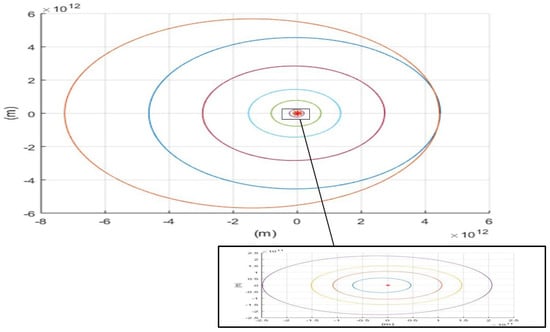
Figure 2.
Closed - bound planet trajectories with and without Yukawa correction with nominal strength .
5.3. Results
In the Tables of Appendix A (from Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11, Table A12, Table A13, Table A14, Table A15, Table A16, Table A17 and Table A18), we report the calculated characteristics of the resulting trajectories for all the planets in the solar system corresponding to the pure Newton and Newton corrected with Yukawa potentials in both the analytical and the numerical approaches. The odd (even) numbered tables correspond to the nominal (estimated) Yukawa strength . The number of moons of each planet is determined according to [30]. Below, we explain the meanings of the symbols used in the tables:
- : numerical calculations using the Newtonian potential
- : analytical calculations using the Newtonian potential
- %: percentage ratio of the numerical to the analytical results for the Newton potential
- : numerical calculations using the modified potential
- : analytical calculations using the modified potential
- %: percentage ratio of the numerical to the analytical results for the modified potential
- %: percentage ratio of the numerical results to the observed results using the Newtonian potential
- %: percentage ratio of the analytical results to the observed results using the Newtonian potential
- %: percentage ratio of the numerical results to the observed results using the modified potential
- %: percentage ratio of the analytical results to the observed results using the modified potential.
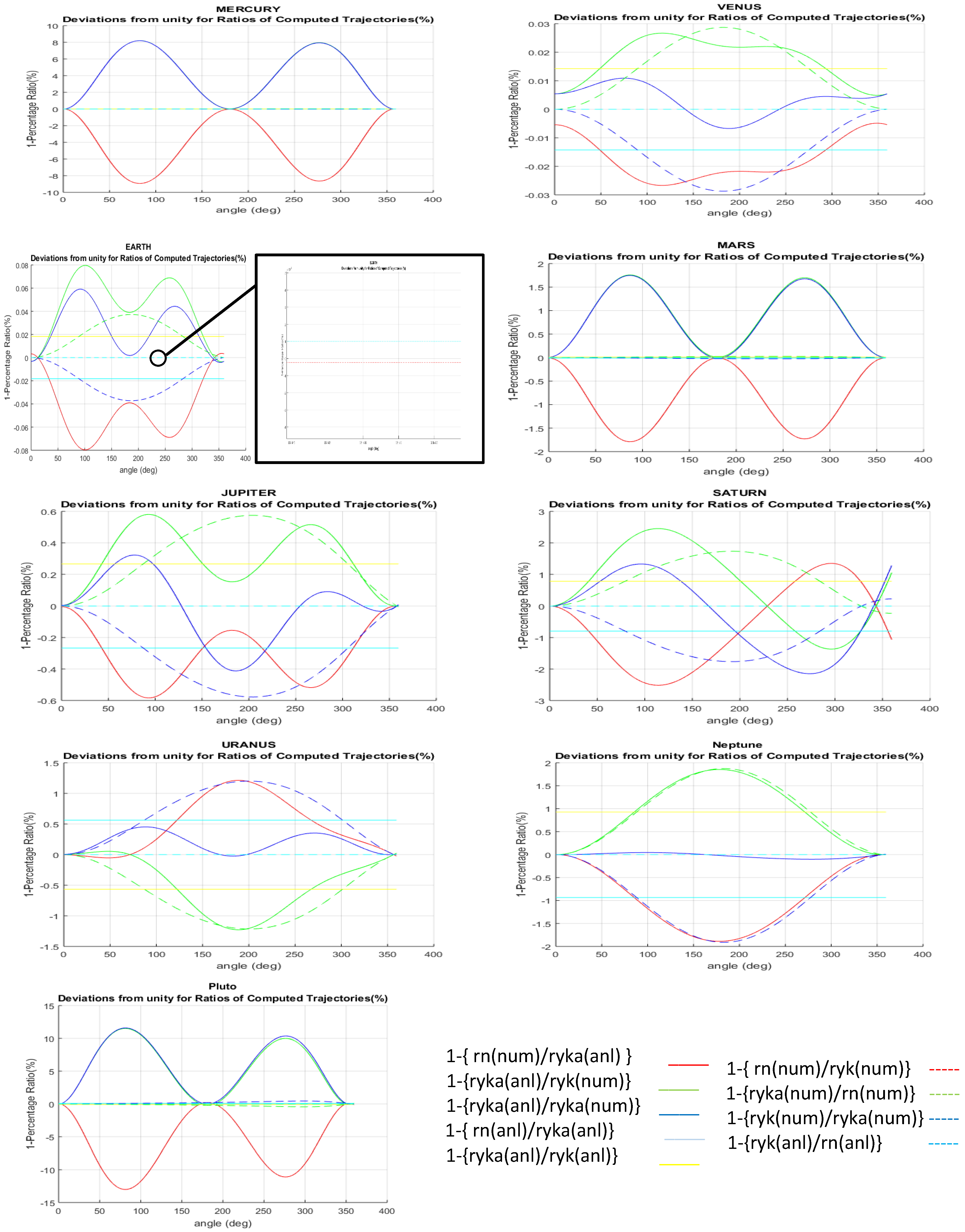
In order to summarize the findings of the Tables, in Figure 3 we present plots showing the deviation from unity of the ratio between two quantities of the following for each planet and at every polar angle, allowing for comparison of the effects of the considered potential (Newton vs. Newton + Yuakawa) and/or the used method (numerical vs. analytical) and/or the Yukawa strength determination (nominal vs. estimated):
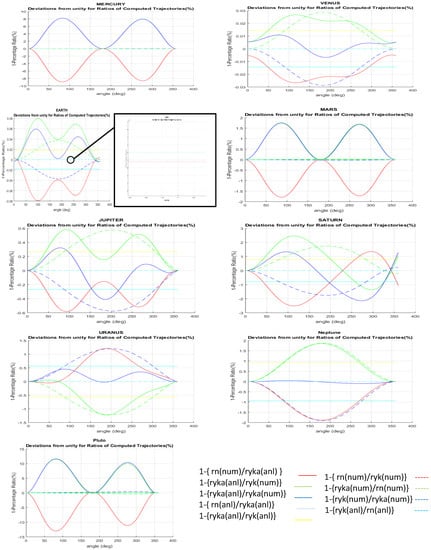
Figure 3.
Deviation from unity of ratios of the computed trajectories at each polar angle according to the considered potential (Newton vs. Newton + Yukawa) and/or the used method (numerical vs. analytical) and/or the Yukawa strength determination (nominal vs. estimated). The zoomed region shows, for the generic case of one planet (Earth), that the dashed red and sky blue curves are very near each other; the same applies to the green and blue curves in the case of Mercury.
- , representing the trajectory equation of the numerical approach with Newton potential
- , representing the trajectory equation of the analytical approach with Newton potential
- , representing the trajectory equation of the numerical approach with Newton+Yukawa potential and nominal
- , representing the trajectory equation of the analytical approach with Newton+Yukawa potential and nominal
- , representing the trajectory equation of the numerical approach with Newton+Yukawa potential and estimated
- , representing the trajectory equation of the analytical approach with Newton+Yukawa potential and estimated .
It can be seen that several ratios (e.g., the dashed red and sky blue) do coincide near zero deviation from one, meaning that there is no tangible effect when adding the Yukawa correction in either the analytic or numeric method as long as one takes the nominal value of . Furthermore, local extremums for the deviations from unity at polar angles that are multiples of can be noted as a generic feature in many plots. We can interpret the large values of the deviations for the nearest (Mercury) and farthest (Pluto) planets in that for the former, the perturbative effect of solar wind, which is important approaching the sun, was not taken into consideration; for the latter, the accumulated gravitational screening effects of the other planets and their moons, which were not considered in the study, become important, especially for a small sized-planetoid such as Pluto.
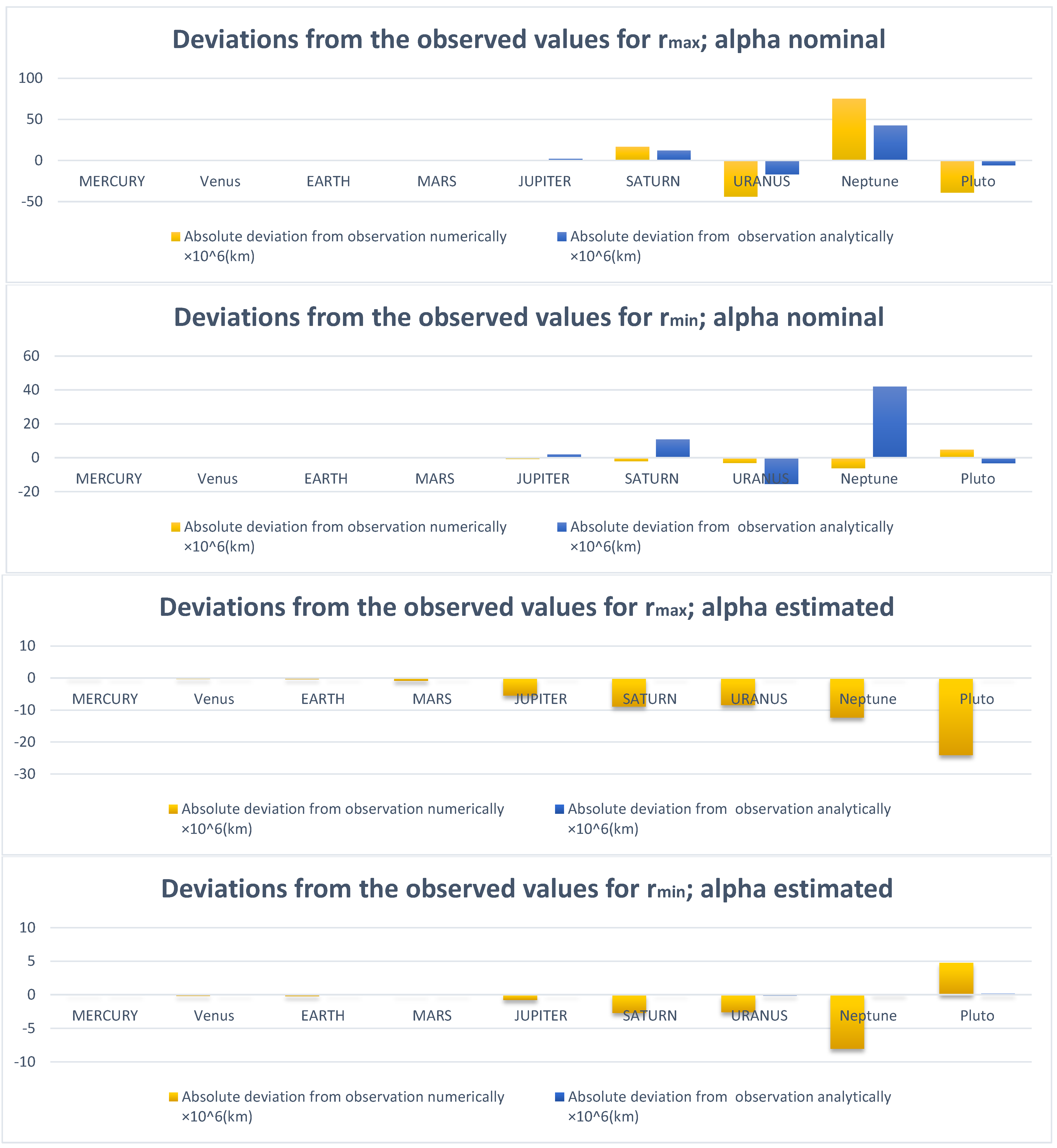
In order to show the effects of the separating distance effect, we should compute the absolute deviations from observed data for each planet. In Appendix B, Table A19 and Table A20 (Table A21 and Table A22) report the deviation from observation for each planet, , respectively, in the case of nominal (estimated) . We summarize these findings in Figure 4.
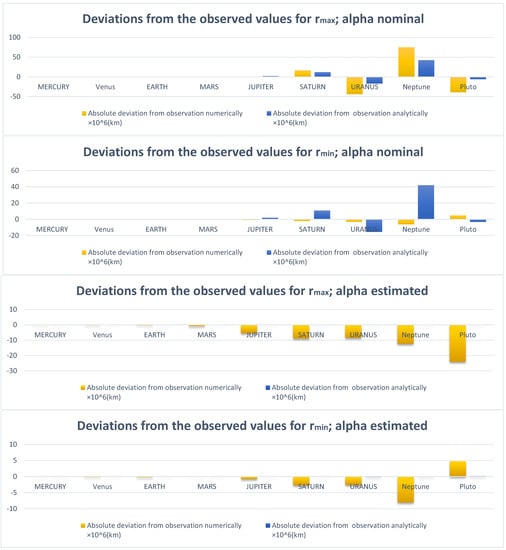
Figure 4.
Absolute deviations from observed data for each planet according to the used method (numerical vs. analytical) and/or the Yukawa strength determination (nominal vs. estimated).
It can be seen that the agreement between the numerical and analytical solutions is excellent in both estimated and nominal cases. Though the deviations due to Yukawa correction are not large, it should be noted that:
- 1.
- For estimated :
- -deviation: the numerical deviation is larger by about times the analytical deviation. In general, it increases the further out the planet is, and reaches a maximum of order ( million km) (less than the observed value) for Pluto.
- -deviation: again, the numerical deviation is larger by about (–)-order of magnitude than the analytical deviation, and is largest for Neptune ( million km); however, it reverses sign and becomes ( million km) more than the observation for Pluto.
- 2.
- For nominal :
- -deviation: the numerical deviation is larger than the analytical deviation, though they are of the same order, reaching a maximum of () million km for Neptune using the numerical (analytical) method. For Pluto and Uranus, we obtain () million km using the numerical method (less than observed).
- -deviation: the analytical deviation is larger, and sometimes reverses sign compared to the numerical deviation. For example, for Neptune the analytical approach provides a deviation of (+40 million km) from observation, whereas the numerical approach provides a deviation of million km (less than the observed value).
Actually, the disagreements with observations are due to several reasons; the first is physical in nature, in that it results from neglecting the perturbation due to third bodies, or more generally, the effect of natural satellites such as moons or asteroids. In addition, we did not take into account the physical effects of either the radiation or the solar wind. Moreover, the results were obtained as a two-body problem; hence, the movement of more distant planets might have been be affected by planets closer to the sun, which can be present in the higher orders of expansion even if they are not in the dominant term. The second factor lies on the computational side, and concerns the numerical method used, the value of the step size, and the high sensitivity of the problem to the initial conditions. It should be mentioned that, for the analytical solution, we restricted our study to the leading order, neglecting higher orders in the expansion of exponentials, whereas for the numerical solution the entire exponential was considered.
6. Summary and Conclusions
In this work, we followed [23] and used Hamilton’s formulation in order to obtain the differential equation of motion and the path equation for gravitational two-body systems. The developments were carried out in the case of the pure Newtonian potential, the Newtonian corrected with Yukawa potential, and the pure Yukawa potential. As in [23], we reviewed the stability problem, constructed the linearization matrix, and tested the stability of the system for Yukawa correction, finding that it is of a central solution type, which implies stable solutions near the fixed point. We repeated the=is analysis for a purely Yukawa force and found similar results, and confirmed that the modified potential obeys Bertrand’s theorem.
Then, we determined the parameter set corresponding to the planets of the solar system, starting from the observed () and estimating . For estimated and nominal values of , we determined the characteristics of the trajectories both numerically and analytically and compared the methods with the observed data. We explained the extent to which these results are consistent with the observational data, presenting the absolute deviation from observation in the form of histograms. The results included an upper deviation of order 80 million km for Neptune using nominal and 20 million km for Pluto using estimated .
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Acknowledgments
N. Chamoun acknowledges support from the ICTP-Associate program, from the Humboldt Foundation, and from the CAS-PIFI scholarship.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Tables of Calculated/Observed Parameters of the Planets

Table A1.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Mercury, whose number of moons is 0.
Table A1.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Mercury, whose number of moons is 0.
| Mercury | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 46 | 69.832 | 57.916 | 56.67679158 | 0.205744228 | |
| 47 | 72.043 | 59.756 | 58.47840586 | 0.205646344 | |
| % | 97 | 96.930 | 96.921 | 96.91918025 | 99.95242442 |
| 46 | 69.831 | 57.916 | 56.67678243 | 0.205738221 | |
| 47 | 72.043 | 59.756 | 58.47840528 | 0.205646344 | |
% | 97 | 96.930 | 96.921 | 96.91916556 | 99.95534277 |
| Observation | 46 | 69.818 | 57.909 | _____ | 0.20563069 |
% | 100 | 99.980 | 99.988 | _____ | 99.94481595 |
% | 97 | 96.911 | 96.909 | _____ | 99.9923879 |
% | 100 | 99.981 | 99.988 | _____ | 99.94773407 |
% | 97 | 96.911 | 96.909 | _____ | 99.9923879 |
| nominal | |||||

Table A2.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Mercury, whose number of moons is 0.
Table A2.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Mercury, whose number of moons is 0.
| Mercury | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 46 | 69.623 | 57.826 | 56.65144795 | 0.2022 | |
| 46 | 69.819 | 57.912 | 56.67470066 | 0.2056 | |
| % | 100 | 99.719 | 99.851 | 99.95897162 | 98.3743 |
| 46 | 69.613 | 57.820 | 56.64729064 | 0.2022 | |
| 46 | 69.815 | 57.908 | 56.6714469 | 0.2056 | |
% | 100 | 99.711 | 99.847 | 99.9573749 | 98.3408 |
| Observation | 46 | 69.818 | 57.909 | _____ | 0.2056 |
% | 100 | 99.721 | 99.856 | _____ | 98.3817 |
% | 100 | 100.001 | 100.005 | _____ | 100.0075 |
% | 100 | 99.706 | 99.847 | _____ | 98.3482 |
% | 100 | 99.995 | 99.999 | _____ | 100.0075 |
| estimated | |||||

Table A3.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Venus, whose number of moons is 0.
Table A3.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Venus, whose number of moons is 0.
| Venus | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 107.30 | 108.689 | 107.99 | 107.9982364 | 0.0044 | |
| 107.48 | 108.961 | 108.22 | 108.2222348 | 0.0072 | |
| % | 99.83 | 99.750 | 99.79 | 99.79301998 | 60.8187 |
| 107.30 | 108.689 | 107.99 | 107.9982353 | 0.0044 | |
| 107.48 | 108.961 | 108.22 | 108.2222337 | 0.0072 | |
% | 99.83 | 99.750 | 99.79 | 99.79301998 | 60.8189 |
| Observation | 107.48 | 108.941 | 108.21 | _____ | 0.0068 |
% | 99.83 | 99.769 | 99.80 | _____ | 64.7150 |
% | 100.00 | 100.018 | 100.01 | _____ | 106.4063 |
% | 99.83 | 99.769 | 99.80 | _____ | 64.7152 |
% | 100.00 | 100.018 | 100.01 | _____ | 106.4063 |
| nominal | |||||

Table A4.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Venus, whose number of moons is 0.
Table A4.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Venus, whose number of moons is 0.
| Venus | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 107.30 | 108.689 | 107.99 | 107.9982364 | 0.0044 | |
| 107.48 | 108.961 | 108.22 | 108.2222348 | 0.0072 | |
| % | 99.83 | 99.750 | 99.79 | 99.79301998 | 60.8187 |
| 107.30 | 108.658 | 107.98 | 107.9821956 | 0.0045 | |
| 107.47 | 108.945 | 108.20 | 108.2068155 | 0.0072 | |
% | 99.84 | 99.736 | 99.78 | 99.79241613 | 63.0300 |
| Observation | 107.48 | 108.941 | 108.21 | _____ | 0.0068 |
% | 99.83 | 99.769 | 99.80 | _____ | 64.7150 |
% | 100.00 | 100.018 | 100.01 | _____ | 106.4063 |
% | 99.83 | 99.740 | 99.78 | _____ | 67.0680 |
% | 99.99 | 100.004 | 99.99 | _____ | 106.4063 |
| estimated | |||||

Table A5.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Earth, whose number of moons is 0.
Table A5.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Earth, whose number of moons is 0.
| Earth | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 146.884 | 151.7 | 149.336 | 149.319847 | 0.0156 | |
| 147.126 | 152.1 | 149.625 | 149.6034965 | 0.0168 | |
| % | 99.835 | 99.7 | 99.806 | 99.81039915 | 92.5721 |
| 146.884 | 151.7 | 149.336 | 149.3198455 | 0.0156 | |
| 147.126 | 152.1 | 149.625 | 149.603495 | 0.0168 | |
% | 99.835 | 99.7 | 99.806 | 99.81039915 | 92.5720 |
| Observation | 147.095 | 152.1 | 149.598 | _____ | 0.0167 |
% | 99.8572 | 99.7 | 99.825 | _____ | 93.5903 |
% | 99.978 | 99.9 | 99.981 | _____ | 98.9120 |
% | 99.857 | 99.7 | 99.825 | _____ | 93.5902 |
% | 99.978 | 99.9 | 99.981 | _____ | 98.9120 |
| nominal | |||||

Table A6.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Earth, whose number of moons is 0.
Table A6.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Earth, whose number of moons is 0.
| Earth | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 146.884 | 151.7 | 149.336 | 149.319847 | 0.0156 | |
| 147.126 | 152.1 | 149.625 | 149.6034965 | 0.0168 | |
| % | 99.835 | 99.7 | 99.806 | 99.81039915 | 92.5721 |
| 146.883 | 151.7 | 149.307 | 149.2910008 | 0.0154 | |
| 147.099 | 152.0 | 149.597 | 149.5762082 | 0.01688 | |
% | 99.853 | 99.7 | 99.805 | 99.80932302 | 91.4700 |
| Observation | 147.095 | 152.1 | 149.598 | _____ | 0.0167 |
% | 99.8572 | 99.7 | 99.825 | _____ | 93.5903 |
% | 99.978 | 99.9 | 99.981 | _____ | 98.9120 |
% | 99.856 | 99.7 | 99.805 | _____ | 92.4761 |
% | 100.003 | 99.9 | 99.999 | _____ | 101.0999 |
| estimated | |||||

Table A7.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Mars, whose number of moons is 0.
Table A7.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Mars, whose number of moons is 0.
| Mars | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 206.57 | 248.480 | 227.52 | 226.6509159 | 0.0898 | |
| 206.64 | 249.277 | 227.96 | 226.9631182 | 0.0935 | |
| % | 99.96 | 99.680 | 99.80 | 99.8624436 | 96.0965 |
| 206.57 | 248.480 | 227.52 | 226.6509134 | 0.0898 | |
| 206.64 | 249.277 | 227.96 | 226.9631159 | 0.0935 | |
% | 99.96 | 99.680 | 99.80 | 99.86244351 | 96.0965 |
| Observation | 206.65 | 249.261 | 227.94 | _____ | 0.0935 |
% | 99.96 | 99.687 | 99.81 | _____ | 96.1252 |
% | 99.99 | 100.006 | 100.01 | _____ | 100.0298 |
% | 99.96 | 99.687 | 99.81 | _____ | 96.1252 |
% | 99.99 | 100.006 | 100.01 | _____ | 100.0298 |
| nominal | |||||

Table A8.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Mars, whose number of moons is 0.
Table A8.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Mars, whose number of moons is 0.
| Mars | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 206.57 | 248.480 | 227.52 | 226.6509159 | 0.0898 | |
| 206.64 | 249.277 | 227.96 | 226.9631182 | 0.0935 | |
| % | 99.96 | 99.680 | 99.80 | 99.8624436 | 96.0965 |
| 206.57 | 248.425 | 227.49 | 226.6249874 | 0.0897 | |
| 206.62 | 249.252 | 227.93 | 226.9402451 | 0.0935 | |
% | 99.97 | 99.668 | 99.80 | 99.86108339 | 95.9861 |
| Observation | 206.65 | 249.261 | 227.94 | _____ | 0.0935 |
% | 99.96 | 99.687 | 99.81 | _____ | 96.1252 |
% | 99.99 | 100.006 | 100.01 | _____ | 100.0298 |
% | 99.96 | 99.664 | 99.80 | _____ | 96.0147 |
% | 99.98 | 99.996 | 99.99 | _____ | 100.0298 |
| estimated | |||||

Table A9.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Jupiter, whose number of moons is 0.
Table A9.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Jupiter, whose number of moons is 0.
| Jupiter | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 739.902 | 815.533 | 777.717 | 776.9190412 | 0.0469 | |
| 742.542 | 818.568 | 780.555 | 779.626266 | 0.04873 | |
| % | 99.644 | 99.629 | 99.636 | 99.65275352 | 96.3711 |
| 739.902 | 815.533 | 777.717 | 776.9190329 | 0.0469 | |
| 742.542 | 818.568 | 780.555 | 779.6262582 | 0.0487 | |
% | 99.644 | 99.629 | 99.636 | 99.65275345 | 96.3711 |
| Observation | 740.595 | 816.363 | 778.479 | _____ | 0.0487 |
% | 99.906 | 99.898 | 99.902 | _____ | 96.4399 |
% | 100.262 | 100.270 | 100.266 | _____ | 100.0714 |
% | 99.906 | 99.898 | 99.902 | _____ | 96.4399 |
% | 100.262 | 100.270 | 100.266 | _____ | 100.0714 |
| nominal | |||||

Table A10.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Jupiter, whose number of moons is 0.
Table A10.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Jupiter, whose number of moons is 0.
| Jupiter | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 739.902 | 815.533 | 777.717 | 776.9190412 | 0.0469 | |
| 742.542 | 818.568 | 780.555 | 779.626266 | 0.04873 | |
| % | 99.644 | 99.629 | 99.636 | 99.65275352 | 96.3711 |
| 739.837 | 810.932 | 775.385 | 774.6852056 | 0.0441 | |
| 740.567 | 816.390 | 778.478 | 777.5526264 | 0.0487 | |
% | 99.901 | 99.331 | 99.602 | 99.63122486 | 90.6263 |
| Observation | 740.595 | 816.363 | 778.479 | _____ | 0.0487 |
% | 99.906 | 99.898 | 99.902 | _____ | 96.4399 |
% | 100.262 | 100.270 | 100.266 | _____ | 100.0714 |
% | 99.897 | 99.334 | 99.602 | _____ | 90.6911 |
% | 99.996 | 100.003 | 99.999 | _____ | 100.0714 |
| estimated | |||||

Table A11.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Saturn, whose number of moons is 0.
Table A11.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Saturn, whose number of moons is 0.
| Saturn | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 1355.461 | 1523.344 | 1439.403 | 1437.455093 | 0.055 | |
| 1368.378 | 1518.496 | 1443.437 | 1441.481829 | 0.052 | |
| % | 99.056 | 100.319 | 99.720 | 99.72065302 | 106.042 |
| 1355.461 | 1523.344 | 1439.403 | 1437.455078 | 0.055 | |
| 1368.378 | 1518.496 | 1443.437 | 1441.481815 | 0.052 | |
% | 99.056 | 100.319 | 99.720 | 99.72065294 | 106.042 |
| Observation | 1357.554 | 1506.527 | 1432.041 | _____ | 0.052 |
% | 99.845 | 101.116 | 100.514 | _____ | 106.081 |
% | 100.797 | 100.794 | 100.795 | _____ | 100.036 |
% | 99.845 | 101.116 | 100.514 | _____ | 106.081 |
% | 100.797 | 100.794 | 100.795 | _____ | 100.036 |
| nominal | |||||

Table A12.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Saturn, whose number of moons is 0.
Table A12.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Saturn, whose number of moons is 0.
| Saturn | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 1355.461 | 1523.344 | 1439.403 | 1437.455093 | 0.055 | |
| 1368.378 | 1518.496 | 1443.437 | 1441.481829 | 0.052 | |
| % | 99.056 | 100.319 | 99.720 | 99.72065302 | 106.042 |
| 1354.869 | 1497.652 | 1426.261 | 1424.954776 | 0.046 | |
| 1357.574 | 1506.507 | 1432.040 | 1430.100672 | 0.052 | |
% | 99.800 | 99.412 | 99.596 | 99.64017246 | 89.244 |
| Observation | 1357.554 | 1506.527 | 1432.041 | _____ | 0.052 |
% | 99.845 | 101.116 | 100.514 | _____ | 106.081 |
% | 100.797 | 100.794 | 100.795 | _____ | 100.036 |
% | 99.802 | 99.410 | 99.596 | _____ | 89.277 |
% | 100.001 | 99.998 | 99.999 | _____ | 100.036 |
| estimated | |||||

Table A13.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Uranus, whose number of moons is 0.
Table A13.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Uranus, whose number of moons is 0.
| Uranus | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 2729.595 | 2957.44 | 2843.519 | 2841.649275 | 0.0381 | |
| 2717.213 | 2984.63 | 2850.921 | 2847.766462 | 0.0469 | |
| % | 100.455 | 99.08 | 99.740 | 99.78519352 | 81.2504 |
| 2729.595 | 2957.44 | 2843.519 | 2841.649245 | 0.0381 | |
| 2717.213 | 2984.63 | 2850.921 | 2847.766434 | 0.0469 | |
% | 100.455 | 99.08 | 99.740 | 99.78519344 | 81.2504 |
| Observation | 2732.696 | 3001.39 | 2867.043 | _____ | 0.0469 |
% | 99.886 | 98.53 | 99.179 | _____ | 81.3684 |
% | 99.433 | 99.44 | 99.437 | _____ | 100.1452 |
% | 99.886 | 98.53 | 99.179 | _____ | 81.3684 |
% | 99.433 | 99.44 | 99.437 | _____ | 100.1452 |
| nominal | |||||

Table A14.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Uranus, whose number of moons is 0.
Table A14.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Uranus, whose number of moons is 0.
| Uranus | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 2729.595 | 2957.44 | 2843.519 | 2841.649275 | 0.0381 | |
| 2717.213 | 2984.63 | 2850.921 | 2847.766462 | 0.0469 | |
| % | 100.455 | 99.08 | 99.740 | 99.78519352 | 81.2504 |
| 2730.116 | 2992.91 | 2861.516 | 2858.935401 | 0.0441 | |
| 2732.578 | 3001.50 | 2867.042 | 2863.869614 | 0.0469 | |
% | 99.909 | 99.71 | 99.807 | 99.82770818 | 94.0932 |
| Observation | 2732.696 | 3001.39 | 2867.043 | _____ | 0.0469 |
% | 99.886 | 98.53 | 99.179 | _____ | 81.3684 |
% | 99.433 | 99.44 | 99.437 | _____ | 100.1452 |
% | 99.905 | 99.71 | 99.807 | _____ | 94.2299 |
% | 99.995 | 100.00 | 99.999 | _____ | 100.1452 |
| estimated | |||||

Table A15.
The values of the calculated and observational astronomical parameters, for nominal , of the planet, Neptune whose number of moons is 0.
Table A15.
The values of the calculated and observational astronomical parameters, for nominal , of the planet, Neptune whose number of moons is 0.
| Neptune | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 4464.81 | 4634.099 | 4549.454 | 4548.810665 | 0.0177 | |
| 4512.97 | 4601.381 | 4557.176 | 4556.953752 | 0.0097 | |
| % | 98.93 | 100.711 | 99.830 | 99.82130416 | 180.8744 |
| 4464.81 | 4634.098 | 4549.454 | 4548.810617 | 0.0177 | |
| 4512.97 | 4601.381 | 4557.176 | 4556.953706 | 0.0097 | |
% | 98.93 | 100.711 | 99.830 | 99.82130411 | 180.8743 |
| Observation | 4471.05 | 4558.857 | 4514.953 | _____ | 0.0097 |
% | 99.86 | 101.650 | 100.764 | _____ | 182.6474 |
% | 100.93 | 100.932 | 100.935 | _____ | 100.9802 |
% | 99.86 | 101.650 | 100.764 | _____ | 182.6473 |
% | 100.93 | 100.932 | 100.935 | _____ | 100.9802 |
| nominal | |||||

Table A16.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Neptune, whose number of moons is 0.
Table A16.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Neptune, whose number of moons is 0.
| Neptune | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 4464.81 | 4634.099 | 4549.454 | 4548.810665 | 0.0177 | |
| 4512.97 | 4601.381 | 4557.176 | 4556.953752 | 0.0097 | |
| % | 98.93 | 100.711 | 99.830 | 99.82130416 | 180.8744 |
| 4463.01 | 4546.479 | 4504.745 | 4504.517794 | 0.0096 | |
| 4471.15 | 4558.747 | 4514.952 | 4514.73215 | 0.0097 | |
% | 99.81 | 99.730 | 99.773 | 99.77375499 | 98.6587 |
| Observation | 4471.05 | 4558.857 | 4514.953 | _____ | 0.0097 |
% | 99.86 | 101.650 | 100.764 | _____ | 182.6474 |
% | 100.93 | 100.932 | 100.935 | _____ | 100.9802 |
% | 99.82 | 99.728 | 99.773 | _____ | 99.6259 |
% | 100.00 | 99.997 | 99.999 | _____ | 100.9802 |
| estimated | |||||

Table A17.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Pluto, whose number of moons is 0.
Table A17.
The values of the calculated and observational astronomical parameters, for nominal , of the planet Pluto, whose number of moons is 0.
| Pluto | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 4439.709 | 7265.423 | 5852.566 | 5684.326067 | 0.2397 | |
| 4431.722 | 7298.614 | 5865.168 | 5687.267307 | 0.2444 | |
| % | 100.180 | 99.545 | 99.785 | 99.94828377 | 98.0832 |
| 4439.709 | 7265.423 | 5852.566 | 5684.325992 | 0.2397 | |
| 4431.722 | 7298.614 | 5865.168 | 5687.26725 | 0.2444 | |
% | 100.180 | 99.545 | 99.785 | 99.94828346 | 98.0832 |
| Observation | 4434.987 | 7304.326 | 5869.656 | _____ | 0.2444 |
% | 100.106 | 99.467 | 99.708 | _____ | 98.0882 |
% | 99.926 | 99.921 | 99.923 | _____ | 100.0051 |
% | 100.106 | 99.467 | 99.708 | _____ | 98.0882 |
% | 99.926 | 99.921 | 99.923 | _____ | 100.0051 |
| nominal | |||||

Table A18.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Pluto, whose number of moons is 0.
Table A18.
The values of the calculated and observational astronomical parameters, for estimated , of the planet Pluto, whose number of moons is 0.
| Pluto | ( km) | ( km) | a ( km) | b ( km) | Eccentricity |
|---|---|---|---|---|---|
| 4439.709 | 7265.423 | 5852.566 | 5684.326067 | 0.2397 | |
| 4431.722 | 7298.614 | 5865.168 | 5687.267307 | 0.2444 | |
| % | 100.180 | 99.545 | 99.785 | 99.94828377 | 98.0832 |
| 4439.740 | 7280.242 | 5859.991 | 5690.112819 | 0.2407 | |
| 4435.112 | 7304.196 | 5869.654 | 5691.616958 | 0.2444 | |
% | 100.104 | 99.672 | 99.835 | 99.97357273 | 98.4812 |
| Observation | 4434.987 | 7304.326 | 5869.656 | _____ | 0.2444 |
% | 100.106 | 99.467 | 99.708 | _____ | 98.0882 |
% | 99.926 | 99.921 | 99.923 | _____ | 100.0051 |
% | 100.107 | 99.670 | 99.835 | _____ | 98.4862 |
% | 100.002 | 99.998 | 99.999 | _____ | 100.0051 |
| estimated | |||||
Appendix B. Tables of Absolute Deviations from Observation of the Planets

Table A19.
Absolute deviation of from observation with nominal , evaluated in ( km).
Table A19.
Absolute deviation of from observation with nominal , evaluated in ( km).
| Observed | |||||
|---|---|---|---|---|---|
| Mercury | 99.721 | 100.001 | 69.818 | −0.194 | 0.001 |
| Venus | 99.769 | 100.018 | 108.941 | −0.251 | 0.020 |
| Earth | 99.794 | 99.984 | 152.100 | −0.312 | −0.024 |
| Mars | 99.687 | 100.006 | 249.261 | −0.780 | 0.016 |
| Jupiter | 99.898 | 100.270 | 816.363 | −0.829 | 2.205 |
| Saturn | 101.116 | 100.794 | 1506.527 | 16.817 | 11.969 |
| Uranus | 98.535 | 99.441 | 3001.390 | −43.947 | −16.759 |
| Neptune | 101.650 | 100.932 | 4558.857 | 75.241 | 42.524 |
| Pluto | 99.467 | 99.921 | 7304.326 | −38.902 | −5.711 |

Table A20.
Absolute deviation of from observation with nominal , evaluated in ( km).
Table A20.
Absolute deviation of from observation with nominal , evaluated in ( km).
| Observed | |||||
|---|---|---|---|---|---|
| Mercury | 100.062 | 100.012 | 46.000 | 0.028 | 0.005 |
| Venus | 99.839 | 100.008 | 107.480 | −0.172 | 0.009 |
| Earth | 99.857 | 99.978 | 147.095 | −0.210 | −0.031 |
| Mars | 99.962 | 99.999 | 206.650 | −0.077 | −0.001 |
| Jupiter | 99.906 | 100.262 | 740.595 | −0.692 | 1.947 |
| Saturn | 99.845 | 100.797 | 1357.554 | −2.092 | 10.824 |
| Uranus | 99.886 | 99.433 | 2732.696 | −3.100 | −15.482 |
| Neptune | 99.860 | 100.937 | 4471.050 | −6.239 | 41.922 |
| Pluto | 100.106 | 99.926 | 4434.987 | 4.722 | −3.264 |

Table A21.
Absolute deviation of from observation with estimated , evaluated in ( km).
Table A21.
Absolute deviation of from observation with estimated , evaluated in ( km).
| Observed | |||||
|---|---|---|---|---|---|
| Mercury | 99.706 | 99.995 | 69.818 | −0.204 | −0.002 |
| Venus | 99.740 | 100.004 | 108.941 | −0.282 | 0.004 |
| Earth | 99.757 | 99.997 | 152.100 | −0.369 | −0.003 |
| Mars | 99.664 | 99.996 | 249.261 | −0.835 | −0.008 |
| Jupiter | 99.334 | 100.003 | 816.363 | −5.430 | 0.027 |
| Saturn | 99.410 | 99.998 | 1506.527 | −8.874 | −0.019 |
| Uranus | 99.717 | 100.003 | 3001.390 | −8.472 | 0.117 |
| Neptune | 99.728 | 99.997 | 4558.857 | −12.377 | −0.109 |
| Pluto | 99.670 | 99.998 | 7304.326 | −24.083 | −0.12907 |

Table A22.
Absolute deviation of from observation with estimated , evaluated in ( km).
Table A22.
Absolute deviation of from observation with estimated , evaluated in ( km).
| Observed | |||||
|---|---|---|---|---|---|
| Mercury | 100.062 | 100.006 | 46.000 | 0.028 | 0.002 |
| Venus | 99.838 | 99.994 | 107.480 | −0.173 | −0.005 |
| Earth | 99.856 | 100.003 | 147.095 | −0.211 | 0.004 |
| Mars | 99.962 | 99.989 | 206.650 | −0.077 | −0.022 |
| Jupiter | 99.897 | 99.996 | 740.595 | −0.757 | −0.027 |
| Saturn | 99.802 | 100.001 | 1357.554 | −2.684 | 0.020 |
| Uranus | 99.905 | 99.995 | 2732.696 | −2.579 | −0.117 |
| Neptune | 99.820 | 100.002 | 4471.050 | −8.037 | 0.107 |
| Pluto | 100.107 | 100.002 | 4434.987 | 4.753 | 0.125 |
Notes
| 1 | Although the standard deviations of the planetary trajectories are not quoted in the NASA public website, one can consider that the corresponding error is equal to the last digit of the quoted significant numbers. In our computations, we used the whole digits allowed by machine precision; however, the results in the tables in the appendices show only significant digits equal to those from the observed data. |
| 2 |
References
- Fischbach, E.; Talmadge, C.L. The Search for Non-Newtonian Gravity; Springer: Berlin, Germany, 1998. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics (Mechanics); Pergamon Press: Oxford, UK, 1969; Volume 1, Chapter 3, Section 14; p. 32. [Google Scholar]
- Rodriguez, I.; Brun, J.L. Closed orbits in central forces distinct from Coulomb or harmonic oscillator type. Eur. J. Phys. 1998, 19, 41–49. [Google Scholar] [CrossRef]
- Brun, J.L.; Pacheco, A.F. On closed but non-geometrically similar orbits. Celest. Mech. Dyn. Astr. 2006, 96, 311–316. [Google Scholar] [CrossRef]
- Hinterbichler, K. Theoretical Aspects of Massive Gravity. Rev. Mod. Phys. 2012, 84, 671. [Google Scholar] [CrossRef]
- De Rham, C. Massive Gravity. Living Rev. Relativ. 2014, 17, 7. [Google Scholar] [CrossRef] [PubMed]
- Goldhabert, A.S.; Nieto, M.M. Mass of the graviton. Phys. Rev. D 1974, 9, 1119. [Google Scholar] [CrossRef]
- Dong, Y.; Shao, L.; Hu, Z.; Miaoc, X.; Wang, Z. Prospects for Constraining the Yukawa Gravity with Pulsars around Sagittarius A*. J. Cosmol. Astropart. Phys. 2022, 2022, 051. [Google Scholar] [CrossRef]
- Moffat, J.W. Scalar-tensor-vector gravity theory. J. Cosmol. Astropart. Phys. 2006, 3, 4. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, T.; Zhao, W. Gravitational radiation from compact binary systems in screened modified gravity. Phys. Rev. D 2017, 95, 104027. [Google Scholar] [CrossRef]
- D’Addio, A.; Casadio, R.; Giusti, A.; Laurentis, M.D. Orbits in bootstrapped Newtonian gravity. Phys. Rev. D 2021, 105, 104010. [Google Scholar] [CrossRef]
- Monica, R.D.; de Martino, I.; Laurentis, M.D. Orbital precession of the S2 star in Scalar–Tensor–Vector Gravity. Mon. Not. R. Astron. Soc. 2022, 510, 4757–4766. [Google Scholar]
- Benisty, D. Testing modified gravity via Yukawa potential in two body problem: Analytical solution and observational constraints. Phys. Rev. D 2022, 106, 043001. [Google Scholar] [CrossRef]
- Banik, I.; Zhao, H. Testing gravity with wide binary stars like α Centauri. Mon. Not. R. Astron. Soc. 2018, 480, 2660, [Erratum: Mon. Not. R. Astron. Soc. 2019, 482, 3453. Erratum: Mon. Not. R. Astron. Soc. 2019, 484, 1589]. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, F.; Lu, Y. Prospects for constraining the spin of the massive black hole at the galactic center via the relativistic motion of a surrounding star. Astrophys. J. 2016, 827, 114. [Google Scholar] [CrossRef]
- Pricopi, D. Stability of the celestial body orbits under the influence of Yukawa potential. Astrophys. Space Sci. 2016, 361, 277. [Google Scholar] [CrossRef]
- Edwards, J.P.; Gerber, U.; Schubert, C.; Trejo, M.A.; Weber, A. The Yukawa potential: Ground state energy and critical screening. Prog. Theor. Exp. Phys. 2017, 2017, 083A01. [Google Scholar] [CrossRef]
- Mukherjee, R.; Sounda, S. Single particle closed orbits in Yukawa potential. Indian J. Phys. 2018, 92, 197. [Google Scholar] [CrossRef]
- Iorio, L. Putting Yukawa-Like Modified Gravity (MOG) on the Test in the Solar System. Sch. Res. Exch. 2008, 2008, 238385. [Google Scholar] [CrossRef]
- Laurentis, M.D.; Martino, I.D.; Lazkoz, R. Analysis of the Yukawa gravitational potential in f(R) gravity II: Relativistic periastron advance. Phys. Rev. D 2018, 97, 104068. [Google Scholar] [CrossRef]
- Bergé, J.; Brax, P.; Pernot-Borràs, M.; Uzan, J.-P. Interpretation of geodesy experiments in non-Newtonian theories of gravity. Class. Quant. Grav. 2018, 35, 234001. [Google Scholar] [CrossRef]
- Iorio, L. Constraints on a Yukawa gravitational potential from laser data of LAGEOS satellites. Phys. Lett. A 2002, 298, 315–318. [Google Scholar] [CrossRef]
- Cavan, E.; Haranas, I.; Gkigkitzis, I.; Cobbett, K. Dynamics and stability of the two body problem with Yukawa correction. Astrophys. Space Sci. 2020, 365, 2. [Google Scholar] [CrossRef]
- Available online: https://nssdc.gsfc.nasa.gov/planetary/factsheet/index.html (accessed on 5 January 2023).
- Rujula, A. Remnants of the Fifth Force; CERN-TH 4466/86; Viki-Fest: Erice, Italiy, 1986. [Google Scholar]
- Goldstein, H. Classical Mechanics, 2nd ed.; Addison-Wesley Publishing Company: Reading, MA, USA, 1980. [Google Scholar]
- Meiss, J.D. Differential Dynamical Systems; Revised Edition; SIAM-Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2017. [Google Scholar]
- Fackler, O.; Van, J.T.T. EDITIONS FRONTIERES, B. P.33, 91192 Gif-sur-Yvette Cedex-France. In Proceedings of the 5th Force Neutrino Physics: Proceedings of VIIIth Moriond Workshop, Les Arcs, France, 23–30 January 1988. [Google Scholar]
- Ross, S.L. Differential Equations; John Willey & Sons: New York, NY, USA, 1984; p. 661. [Google Scholar]
- Wakker, K. Fundamentals of Astrodynamics; TU Delft Library: Delft, The Netherland, 2015; ISBN 9789461864192. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).