Abstract
In the first part of the paper, we try to identify the presence of gravity, at a microscopic level, by introducing conical defects and maintaining an approach that assumes topological equivalence among the underlying manifolds that form the tissue of the D-brane itself. In the second part, we will present an alternative to the conical defects, considering the theory of teleparallel gravity, in which the presence of the torsion and the construction of the brane always occurs within the context of our new interpretation of emergent spaces.
1. Introduction and Preliminaries
It is possible that at the most fundamental level, spacetime, or at least space, is not continuous but discrete. This implies that the low-energy symmetries relying on continuous spacetime models may break down when spacetime is probed at high enough energies. Some models also attempt to preserve at least some remnant of the low-energy theory at high energies. Ideas of discrete spacetime go at least back to H. Snyder’s work on Lorentz invariant discrete spacetime [1]. Since that work, a number of interesting theories have developed that deal in discrete spacetime. These include: nonassociative geometry [2], causal set theory [3], causal dynamical triangulations [4], and loop quantum gravity [5]. A nice phenomenological review of the consequences of discrete spacetime can be found in [6]. Since many of these theories claim to represent, at least to some approximation, a quantum theory of gravity, it is therefore worthwhile to seriously study discrete theories, as quantum gravitation is one of the most important unsolved issue in theoretical physics. Although the discretization of spacetime should be small, it is not necessarily untestable [7], and therefore, experimental observation could in the future rule out some discrete theories in favor of others or steer the field in a completely new direction altogether. In the field of nonassociative geometry, it was shown that at the Planck scales, the spacetime is described as a “diodular discrete structure”, which at macroscopic scales resembles a differentiable manifold [8]. In causal set theory, it naturally arises that finite volume regions in the continuum contain only a finite number of elements of the causal set, giving spacetime a fundamentally discrete “atomic” structure. This fundamental discreteness in causal set theory does not violate local Lorentz invariance in the continuum approximation [9]. In causal dynamical triangulations, it has been shown how the discrete structure allows for a more sensible gravitational path integral [10]. In the arena of loop quantum gravity, the discrete nature of spacetime is not a priori assumed but instead is a prediction of the theory. This discreteness has provided a quantum gravitational explanation for the entropy associated with black holes [11,12]. Further, the loop quantum gravity paradigm seems to indicate that the issue of the singularity within a black hole [13], or at the Big Bang [14], may be resolved by this theory.
Partially negative dimensional product manifold (PNDP-manifold for short) was introduced in [15], and the authors used PNDP-theory for a new approach to D-Branes. Specifically, the work is about a new geometric/topological approach, in which everything arises from fundamental spatial dimensions, and tries to propose a new possible link between different energy scales in the context of gravity. The authors identify topological defects (as non-orientability) with gravitational interactions, and through a mechanism triggered by these hypotheses, they obtain an effect known in mathematics as a “parallelism defect”, to which we associate the appearance of an effective curvature on low-energy scales (macroscopic level).
Always keeping valid all the background present in [15] is the PNDP approach, which determines a discrete gravity in which the latter is understood as a “defect” already present in the D-brane tissue. In our approach, we start with the defects that are responsible for determining gravity at the microscopic level. We will no longer consider orientability, but we will replace this with the presence or absence of conical defects. Recall that the term “flat” is understood in the sense of Riemann–Christoffel. Additionally, since the Riemann tensor is a measure of intrinsic curvature, most of the statements here apply only to intrinsic curvature, which is important for gravitation.
An easy way to visualize a flat space with an angular defect is to take a flat sheet and to cut a wedge out of it. Then, one identifies the sides of the wedge. This is illustrated in Figure 1.
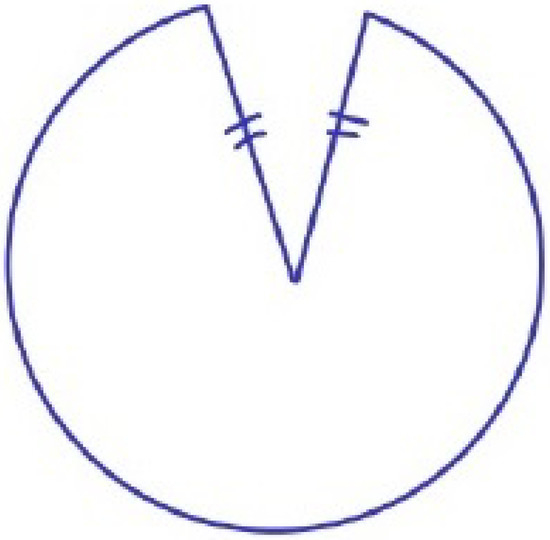
Figure 1.
A flat sheet with a wedge cut out of it and the wedge’s sides identified. Here it is drawn circular, but this does not matter.
The 2D line-element on such a sheet is given by , where the angular defect vanishes when . It can be easily checked that the Riemann–Christoffel tensor of this space vanishes. The submanifold of the spacetime outside of a cosmic string has a metric similar to this.
The geodesics on this sheet are still straight lines whether or not the wedge is there. However, with the identification of the edges of the wedge, two lines that are initially parallel and are parallelly transported on the manifold will eventually cross if they straddle the wedge (see Figure 2). This violates Euclid’s parallellism axiom, which is known to be violated in curved spaces, so this mimics curvature even though the manifold is flat. The greater the angular defect () is, the greater the effective curvature will be.
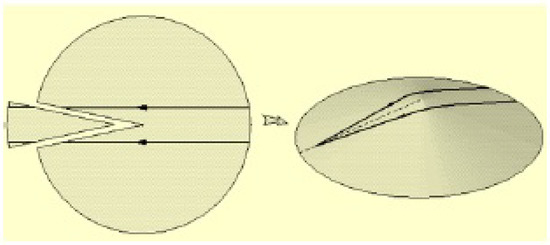
Figure 2.
Initially parallel lines will cross if they straddle the wedge.
If we consider the cone missing its vertex , the holonomy is nonzero around any parallel , and this happens since the curve does not bound a region in M. The organization of this paper is as follows. In Section 2, we explore the PNDP with conical defects. In Section 3, we investigate teleparallel gravity theory in the PNDP approach. Finally, conclusions are presented in Section 4.
2. PNDP with Conical Defects
Before introducing the conical defect in PNDP manifolds, we present the definition of a PNDP manifold, and for more details concerning the structure of the D-branes within the PNDP theory, we refer the reader to [15] (in particular, Section 1).
A warped product manifold (where () is the base manifold and () is the fiber manifold), with , is Einsteinian if only if:
where and are constants, d is the dimension of F, , and are, respectively, the Hessian, the Laplacian and the gradient of f for g, with a smooth positive function.
Contracting first Equation (1), we obtain:
where n and are the dimension and the scalar curvature of B, respectively, and from third equation, considering and , we have:
Now, from Equations (2) and (3) we obtain:
We call the PNDP manifold a warped product manifold that satisfies (1), where the base-manifold is a Riemannian (or pseudo-Riemannian) product-manifold with , where is an Einstein manifold (i.e., where is the same for (1) and is the metric for ), with , , so . The warping function is (where each is a function on its individual manifold, i.e., and ) and can also be a constant function. The fiber manifold is a derived Riemann-flat manifold with negative “virtual” integer dimensions m, where the derived smooth manifold is considered a smooth Riemannian flat manifold by adding a vector bundle of obstructions. In particular, we consider, for F, only with orthogonal Cartesian coordinates such that by adding a vector bundle of obstructions, , with the dimension , where . In fact, in this circumstance, if we consider a Kuranishi neighborhood , with manifold , obstruction bundle , and section (see [16]), then the dimension of the derived smooth manifold F is . Moreover, in the case (i.e., positive “virtual” dimension), we consider (the “virtual” dimension of M, , which coincides with ). In the special case where with also an Einstein manifold with the same Einstein-, then we consider only the case .
Now, let us consider the PNDP deprived of the point , where are the coordinates of the point. Then, (note that is similar to consider ), and the missing point is the “fragility” place of the PNDP manifold. If the attached string strongly interacts (also here, as seen in [17], the authors’ approach considers the emergent parts of the PNDP manifolds as topologically equivalent to open or closed strings), that is, it vibrates, then from the “puncture” (missing point) the underlying manifold “splits”, creating a missing sector with an arbitrary small angle, i.e., a wedge is cut out of it. However, being a topological approach, it seems entirely sensible to us to require that nature wants to maintain the topological equivalence between the underlying manifolds that make up the D-brane, i.e., (at least) a homeomorphism that preserves the topological properties between them, dealing with differentiable manifolds, we will consider diffeomorphism. Therefore, the sides of the wedge will glue together, creating a conical defect without a vertex (this is illustrated in Figure 3), and it is well-known that there is a homeomorphism between and the cone without its vertex; for example, as subsets of , there is a diffeomorphism in the most intuitive way: ). With this imposition, the differentiable structure of is carried to the cone, and as we said at the end of the previous section, this allows us to consider that some , which have the conical defect, have a non-zero holonomy.

Figure 3.
The vibrating string from the “puncture” (missing point) splits the underlying manifold , creating a missing sector with an arbitrary small angle ; a wedge is cut of it. To preserve the topological properties, the sides of the wedge glue together to create a conical defect without a vertex.
If instead the attached string does not interact, i.e., it does not vibrate, then the “puncture” does not break, and the underlying manifold will not have a conical defect.
The conical defect obtained will in any case emerge as a point-like manifold due to its interacting dimensions that compose it, and therefore, only the string () will remain attached to the point-like manifold.
At this point, returning to the scenario described in [15], in which the PNDP manifolds glue together to form the flat D-brane, instead of having Möbius strips or cylinders, now we have PNDP manifolds with arbitrarily small conical defect μ (described above) and others without. A vector placed on the point manifold will undergo the holonomy detected on the underlying surface (as in [15], the point-like manifold is equivalent to the underlying surface; it corresponds only to the way it emerges, so there will be a closed curve on the underlying surface if it has a conical defect, such that the vector detects a nonzero holonomy, while if the underlying one has no conical defect, then the holonomy will be zero). Again, as in [15], not knowing a priori the effective connection that will be mimicked at the macroscopic level, we cannot parallelly transport a vector. For this reason, we want to consider a closed loop on the D-brane as a plane curve (the D-brane has a flat connection and will only mimic the curvature on a macroscopic level) and define our parallel mode of transport. The vector to be transported on the D-brane at each point (point-like manifold) will have a direction influenced by the holonomy present on the underlying surface. As the vector slips to the next point, it adds the holonomy detected in the previous point with that detected on the current one (because the vector will start the loop on the underlying surface of the new point with the direction acquired at the end of the loop on the underlying surface of the previous point), and so on until the cycle on the D-brane is complete. Thus, the more conical defects there are, the greater the holonomy at the end of the loop on the D-brane.
3. Conus Geometry
3.1. Conus with Torsion
The conus coordinate can be expressed in the form
where b describes the strength of the “dislocation defect”, and the metrics are
where and . The missing angle to create a conus is (see Figure 1)
In this case, the only nonzero torsion components are
3.2. Conus with Curvature
The another possibility of a conus with a defect is
The metrics in this case are
The nonzero curvature tensor components are
We can see that when the parameter , both the torsion and the curvature are zero.
Remark 1.
We consider the theory presented in this work as a “fundamental” theory and we say that at the fundamental (microscopic) level the “fabric” appears as an “irregular forest” of cones, each PNDP emerges as point-like, but in reality it is a conical defect, and by gluing the PNDPs together, we will have a fabric that punctually “hides” conical defects that are not necessarily identical to each other (each PNDP will glue to the other, and each of them is a conical defect).
In this section, we have a hypothetical parameterization and explain how to obtain the curvature or torsion of each conical defect. Each conical defect presents holonomy, and we describe it (in the previous section) as a hypothetical vector that completes a closed loop on the brane passing through the underlying conical defects of the brane, which will provide us with an effective curvature at the macroscopic level. Therefore, we might think that the “hidden” conical defects, which make up this irregular “forest of cones”, are actually (in our interpretation) quantum foam, which exists as an underlying manifold of the brane tissue, upon which we are allowed to measure/precisely describe its geometry because it is possible to define a parameterization.
We used the term “irregular forest of cones”, because (as described in Section 2) the conical defects are not the same; they depend on the “crack” that the string creates by vibrating on the PNDP. The wider the crack, the greater the conical defect. Thus, for a single cone, we know the curvature point by point, or the torsion, because we associate it with a map that parameterizes it, but it is the transition to an adjacent cone that will occur with discontinuous, i.e., discrete, curvature (or torsion), because if we think like a manifold (in which each point of the collector corresponds to a cone), it will be composed of cones all different from each other. In fact, we could pass from a cone (point) almost devoid of curvature to an adjacent one with the highest curvature value. The manifold will emerge flat, but at a microscopic level, it is composed of underlying cones, some flatter, others steeper. The holonomy of the conical defect derives directly from its curvature, i.e., the curvature at one point of the defect is interpreted as the infinitesimal holonomy over a closed loop, the infinitesimal parallelogram on the conical defect. Due to the random nature of the bonding between PNDPs, it is reasonable to think that there will be areas of the brane in which this discrete “jump” of the curvature (or torsion) between point and point will be more consistent than others where it will be more pronounced.
4. Teleparallel Gravity Theory in PNDP Approach
In this section, we want to consider a different scenario from both [15] and Section 2.
In particular, this approach will not be aimed at string theory, and furthermore, the PNPD manifolds that we consider the “fundamental components at the microscopic level” will be a type of PNDP manifold, which in this context we call Type-, where are closed intervals with Planck length (therefore, the entire underlying manifold has four dimensions) and with . Therefore, its dimension is zero, and thus, it emerges as a point-like manifold.
As in both [15] and Section 2, we continue to consider that the brane has a Levi–Civita flat connection and is composed of flat PNDP manifolds glued together. Since it is a geometrical/topological approach, we want nature to act with a certain rigidity, supposing that the gluing that takes place determines the formation of smooth structures.
The gluing that occurs between the emerging point-like manifolds is the topological gluing (theory of surgery) and takes place between the underlying manifolds with boundary. An important result of Morse theory states that:
Let with be smooth manifolds with a boundary, let be unions of connected components of the boundaries of and , respectively, and let be a diffeomorphism. Then, there exists a smooth structure on the space that arises by gluing to along . This structure is unique up to a diffeomorphism that leaves all points from the original boundaries of , including , fixed.
This result indicates that a diffeomorphism between the connected components of the boundaries is sufficient to obtain a smooth structure on the resulting manifolds. In this approach, as in Section 2, it is believed that there is a search for a certain regularity on the part of nature capable of preserving the topological characteristics. Therefore, being differentiable manifolds, diffeomorphisms are considered rather than homeomorphisms.
Let us assume there are multiple brane-universes. Suppose that these branes-universes can collide with each other and create an effective torsion on their connection.
NOTE 1: The PNDP theory is developed on the basis of the Einstein warped product manifold, and everything is executed in a "canonical" way with the Levi–Civita connection. In this case, we consider that the collisions suffered between the branes, which is an n-dimensional Euclidean spaceform, will affect the connection—not the connection of the PNDP manifolds that compose it, but the connection of the D-branes themselves. In particular, it is as if the collision "rotates" the affected PNDP manifolds, making the tangent spaces twist about a geodesic when they are parallelly transported because the tangent space of the underlying manifold of the point-like manifolds (PNDP Type-α), which is affected and makes up the D-brane, could be no longer, consequently, aligned with that of the others.
Therefore, having chosen a point P on the D-brane, and having chosen two tangent vectors u and v, we can experience the torsion, performing an infinitesimal parallel transport of u and v in the direction of v and u, respectively, at the end of which they do not close.
Therefore, we obtain a connection without curvature but with torsion (see Figure 4).
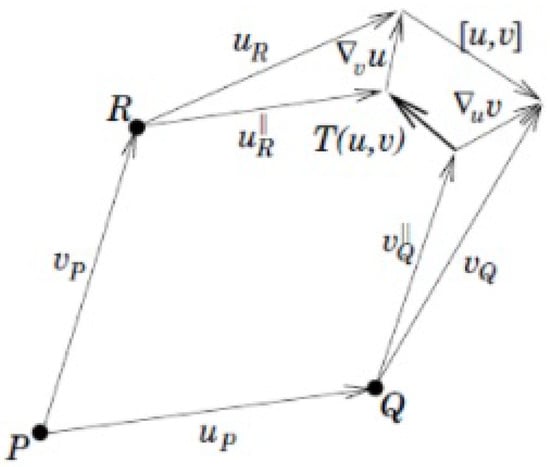
Figure 4.
The effect of torsion is shown.
We can summarize what has been said with the following points:
(1) The PNDPs have a Levi–Civita connection and therefore have no torsion.
(2) Here, we assume a kind of PNDP manifold called Type-.
(3) The Type- is a 4D flat manifold (it is microscopic Euclidean spatial form) that emerges as point-like manifold. They can glue together (topological gluing) and form the brane preserving the flat Levi–Civita connection of the Type- (as also hypothesized in [15]). The brane will be a D-dimensional Euclidean space form.
(4) When two or more branes collide with each other, they alter their connection.
(5) Since the branes are formed with the gluing of the PNDP manifolds of Type- that emerge as point-like manifolds (point-like PNDP manifolds), in each point (i.e., the glued point-like manifold) of the brane, the tangent space is the tangent space of the point-like PNDP manifold.
(6) We consider the 4-dimensional brane, therefore, as mentioned in the previous point (5); we can consider that punctually, the tangent space to the 4-brane is the tangent space to the point-like PNDP-manifold that emerges as that point. Therefore, it is clear that when the 4-brane is impacted by another one or more branes, this collision will create a shock wave that will involve their PNDP manifolds Type- (which make up the 4-branes) by rotating them and then rotating their tangent space; consequently, the tangent spaces of the branes will show torsion (Figure 5).
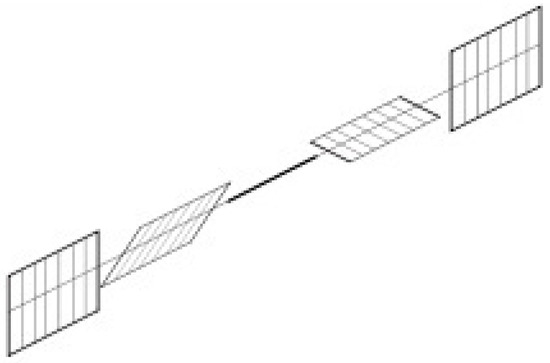
Figure 5.
Torsion along a geodesic.
NOTE 2: A Euclidean space is an affine space; therefore, it is parallelizable, but it is torsion-free. We consider the 4-brane as a 4-dimensional Euclidean space. If it is composed of PNDP manifolds, so that each of its points corresponds to a point-like manifold (with its own tangent space), where the underlying PNDP manifold at each point-like manifold is a microscopical portion of 4-dimensional Euclidean space, we can see these last as the parallelization of the 4-brane at every point-like because the vectors of the tangent space of the PNDP manifold can be trivially considered the base of the tangent space of 4-brane at every . Rotating the PNDP-manifold as in our speculative case (as described in point (6)), it happens that by parallel transporting, at the microscopic level on the 4-brane, two vectors of that base in P, one in the direction of the other, we experience a torsion. Therefore, using PNDP-manifolds in this speculative way, the Euclidean space can mimic a flat, not-torsion-free effective connection, as well.
At this point, we can consider that the 4-brane mimics a 4-manifold with a flat connection that is not torsion-free. For example, a 4-manifold that admits a flat connection that is not torsion-free can be ; in fact, R, both admit lie group structures, so their product admits a lie group structure and hence admits a flat connection, the one that makes left invariant vector fields parallel. Since we have an extra spatial dimension, we can think that the 4-brane mimics , where is a closed linear microscopic interval.
Being microscopic, the extra spatial dimension is not perceived. We could think that it is superfluous to life; in fact, the 3D-spatial dimensions are the minimum sufficient to support life, and the fourth spatial dimension exists only for construction reasons, that is, to obtain point-like PNDP-manifolds. Due to this, it has no reason to grow in size.
The universe, therefore, as it is perceived by everyday experience, could be considered a 3-sphere (equipped with a flat connection with torsion) plus time.
Another example is that if we consider minus the origin O, we obtain the same thing, that is, a flat connection with torsion.
Since the 4th dimensions is microscopic, we could also consider the scenario in which the 4-brane mimics plus time.
A theory that predicts the absence of curvature, attributing gravity to torsion only, is the teleparallel gravity theory. As mentioned in [18], the teleparallel gravity theory considers a non-degenerate matrix composed of components of four vector fields , , which form an orthonormal basis in the tangent space at each point. The inverse matrix is denoted by , and the metric components can be calculated as:
Very importantly, if we are given a metric, the tetrad fields are only defined up to an arbitrary local Lorentz rotation , since this is the natural freedom of choosing an orthonormal basis.
In the classical formulation of teleparallel gravity, one uses the Weitzenböck connection given by , or equivalently , which is obviously curvature-free, , and has the following torsion: .
We can denote the determinant of by , and under the Weitzenböck assumption (i.e., ), the action is , where is the torsion scalar.
Remark 2.
As described at the end of Section 3, for curvature, similarly, we can use the parameterization shown to think that at the fundamental (microscopic) level, there is an underlying quantum foam of the branal tissue, which is an irregular forest of cones and has a discrete torsion other than zero, which determines a further new interpretation at the teleparallel gravity.
5. Conclusions
In this the paper, we tried to identify the presence of gravity at a microscopic level by introducing conical defects and maintaining an approach that assumes topological equivalence among the underlying manifolds that form the tissue of the D-brane itself. Furthermore, we presented an alternative to the conical defects, considering the theory of teleparallel gravity, in which the presence of the torsion and the construction of the brane always occurs within the context of our new interpretation of emergent spaces. Indeed, it is our intention to understand the study of gravity, considering approaches that respect the topological equivalence between the structures involved. Working with differentiable manifolds, this equivalence is certainly respected with the presence of a diffeomorphism. We, therefore, show how conical and torsion defects can arise in this context in order to define a discrete, alternative, theory of gravity. The onset of a torsion in a scenario that foresees the clash between branes arises with the intention of being able to consider teleparallel gravity theory from a new point of view. In recent years, the main motivation to study teleparallel gravity and its extension (the so-called gravity, where T is the torsion scalar in teleparallelism) is to explain the late-time cosmic acceleration, namely, the issue of dark energy and modified gravity theories (for recent reviews, see, e.g., Refs. [19,20,21,22,23,24,25,26,27,28,29,30,31]). There have been proposed a number of methods for the modification of teleparallel gravity and cosmological investigations in them. In the light of fundamental physics’ point of view, it is significant to find some clue as to the theoretical conditions (or requirements) of the form of , in other words, the effective theory of modified teleparallel gravity.
In conclusion, we also show two possible scenarios for quantum foam as an underlying presence of the brane tissue.
Author Contributions
Formal analysis, A.P.; Inverstigation, A.P., R.P., S.J. and C.Ö.; Writing, A.P. and S.J.; Methodology, R.P.; Figures, C.Ö. All authors have read and agreed to the published version of the manuscript.
Funding
The work was partially funded by Slovak Grant Agency for Science VEGA under the grant number VEGA 2/0076/23.
Data Availability Statement
Not applicable.
Acknowledgments
The authors appreciate the referees’ comments, which improved the content and presentation of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Snyder, H. Quantized Space-Time. Phys. Rev. 1947, 71, 38. [Google Scholar] [CrossRef]
- Nesterov, A.I.; Mata, H. How Nonassociative Geometry Describes a Discrete Spacetime. Front. Phys. 2019, 7, 32. [Google Scholar] [CrossRef]
- Dowker, F. Causal sets as discrete spacetime. Contemp. Phys. 2006, 47, 1–9. [Google Scholar] [CrossRef]
- Ambjorn, J.; Jurkiewicz, J.; Loll, R. Causal Dynamical Triangulations and the Quest for Quantum Gravity. In Foundations of Space and Time: Reflections on Quantum Gravity; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Ashtekar, A. An Introduction to Loop Quantum Gravity Through Cosmology. In Il Nuovo Cimento B; Società Italiana di Fisica: Bologna, Italy, 2007; pp. 135–155. [Google Scholar] [CrossRef]
- Hossenfelder, S. Experimental Tests of Quantum Gravity and Exotic Quantum Field Theory Effects. Adv. High Energy Phys. 2014, 2014, 192712. [Google Scholar]
- Belenchia, A.; Benincasa, D.M.T.; Liberati, S.; Marin, F.; Marino, F.; Ortolan, A. Testing Quantum Gravity Induced Nonlocality via Optomechanical Quantum Oscillators. Phys. Rev. Lett. 2016, 116, 161303. [Google Scholar] [CrossRef]
- Nesterov, A.I.; Sabinin, L.V. Nonassociative geometry: Towards discrete structure of spacetime. Phys. Rev. 2000, 62, 081501. [Google Scholar] [CrossRef]
- Surya, S. The causal set approach to quantum gravity. Liv. Rev. Relat. 2019, 22, 5. [Google Scholar] [CrossRef]
- Loll, R.; Ambjorn, J.; Jurkiewicz, J. The Universe from Scratch. Contemp. Phys. 2006, 47, 103. [Google Scholar]
- Rovelli, C. Black Hole Entropy from Loop Quantum Gravity. Phys. Rev. Lett. 1996, 77, 3291. [Google Scholar] [CrossRef]
- Kloster, S.; Brannlund, J.; DeBenedictis, A. DeBenedictis, Phase-space and Black Hole Entropy of Higher Genus Horizons in Loop Quantum Gravity. Class. Quant. Grav. 2008, 25, 065008. [Google Scholar] [CrossRef]
- DeBenedictis, A. On the black hole singularity issue in loop quantum gravity. Can. J. Phys. 2009, 87, 255. [Google Scholar] [CrossRef]
- Singh, P. Understanding big bang in loop quantum cosmology: Recent advances. J. Phys. Conf. Ser. 2008, 140, 012005. [Google Scholar] [CrossRef]
- Pincak, R.; Pigazzini, A.; Jafari, S.; Özel, C. DeBenedictis-A topological approach for emerging D-branes and its implications for gravity. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150227. [Google Scholar] [CrossRef]
- Joyce, D. A new definition of Kuranishi space. arXiv 2014, arXiv:1409.6908. [Google Scholar]
- Pincak, R.; Pigazzini, A.; Jafari, S.; Özel, C. The “emerging” reality from “hidden” spaces. Universe 2021, 7, 75. [Google Scholar] [CrossRef]
- Golovnev, A. Introduction to teleparallel gravities. arXiv 2018, arXiv:1801.06929v1. [Google Scholar]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Padmanabhan, T. Dark energy and gravity. Gen. Rel. Grav. 2008, 40, 529–564. [Google Scholar] [CrossRef]
- Durrer, R.; Maartens, R. Dark Energy and Dark Gravity. Gen. Rel. Grav. 2008, 40, 301–328. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified Gravity and Cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. ECONF 2006, C0602061, 06. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories of Gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Rel. 2010, 13, 3. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Capozziello, S.; de Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; de Laurentis, M.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rep. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D. Inflationary cosmology in modified gravity theories. Symmetry 2015, 7, 220–240. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-Time Evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).