Selected Results in Heavy-Quark Fragmentation
Abstract
1. Introduction
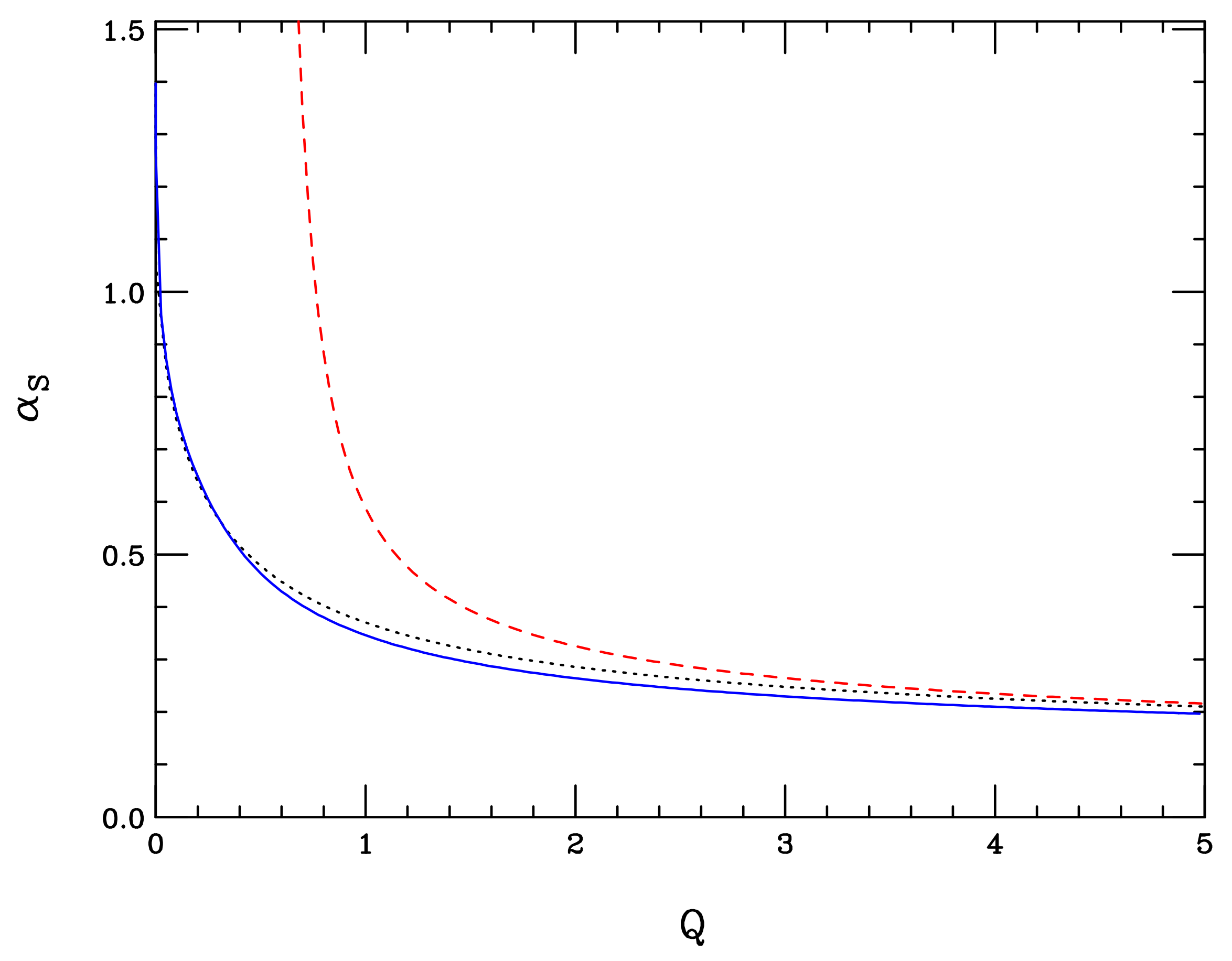
2. Perturbative Calculations for Heavy-Quark Fragmentation
3. Non-Perturbative Corrections to Heavy-Quark Fragmentation
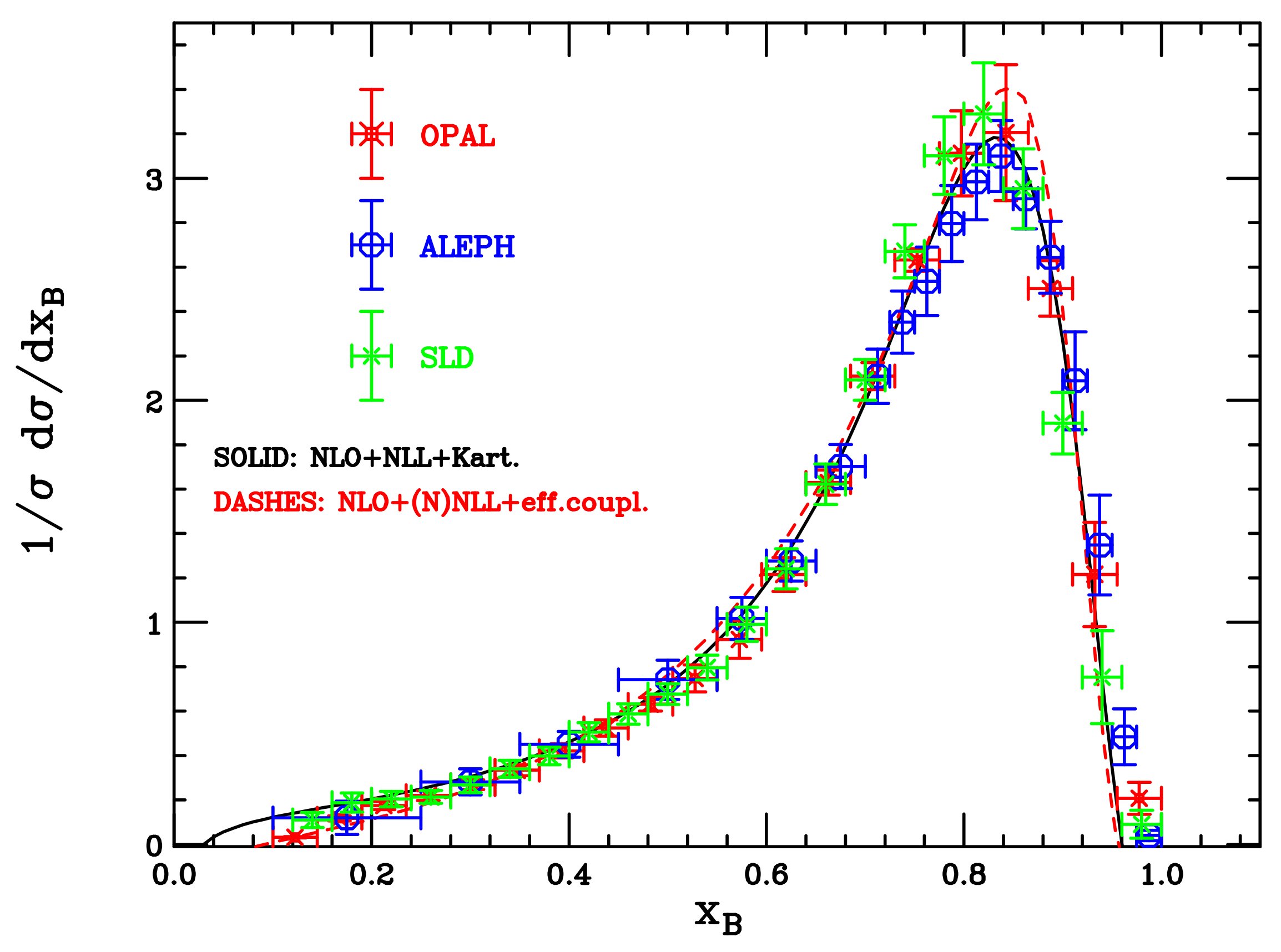
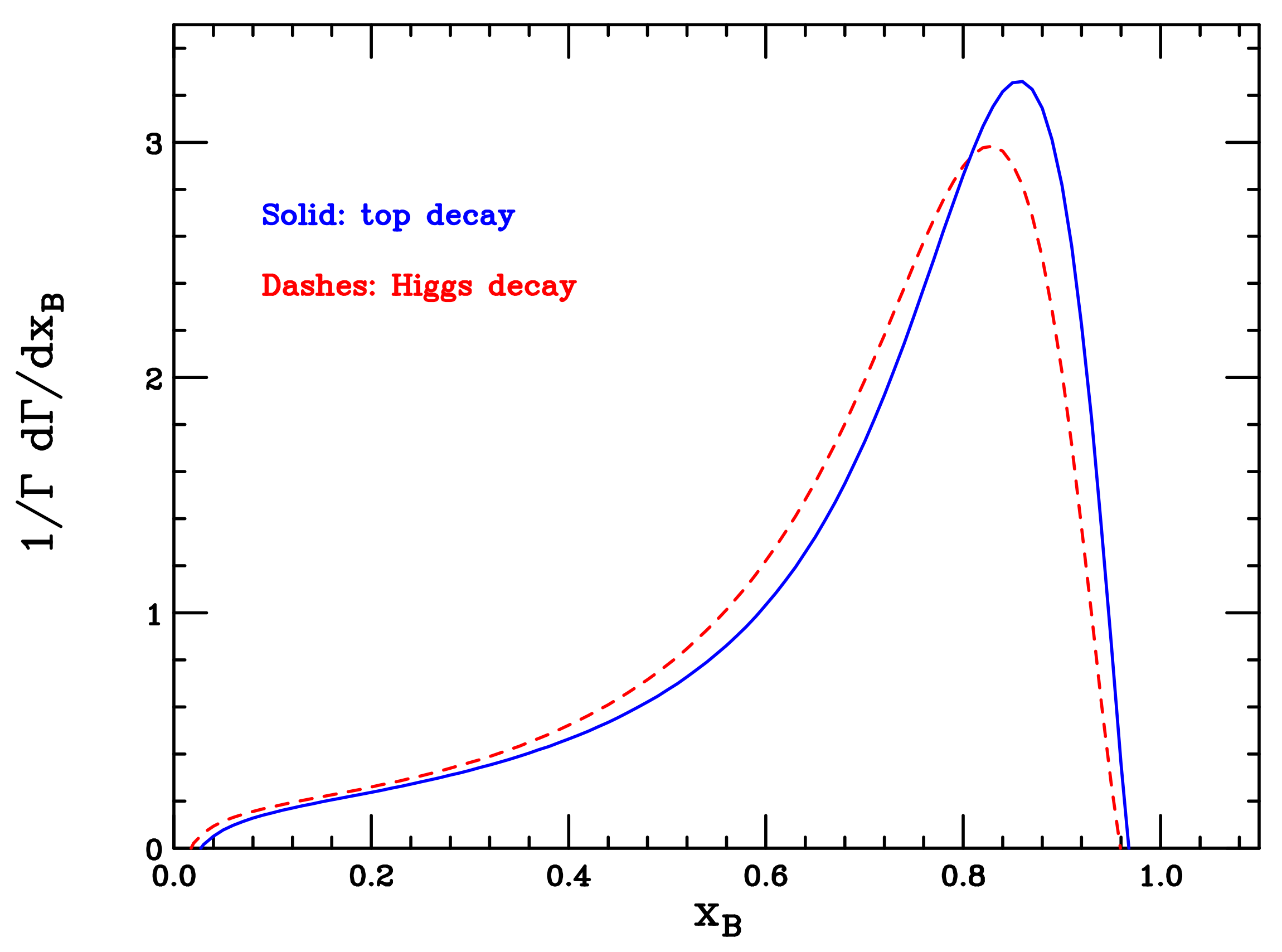
4. Results—B Production
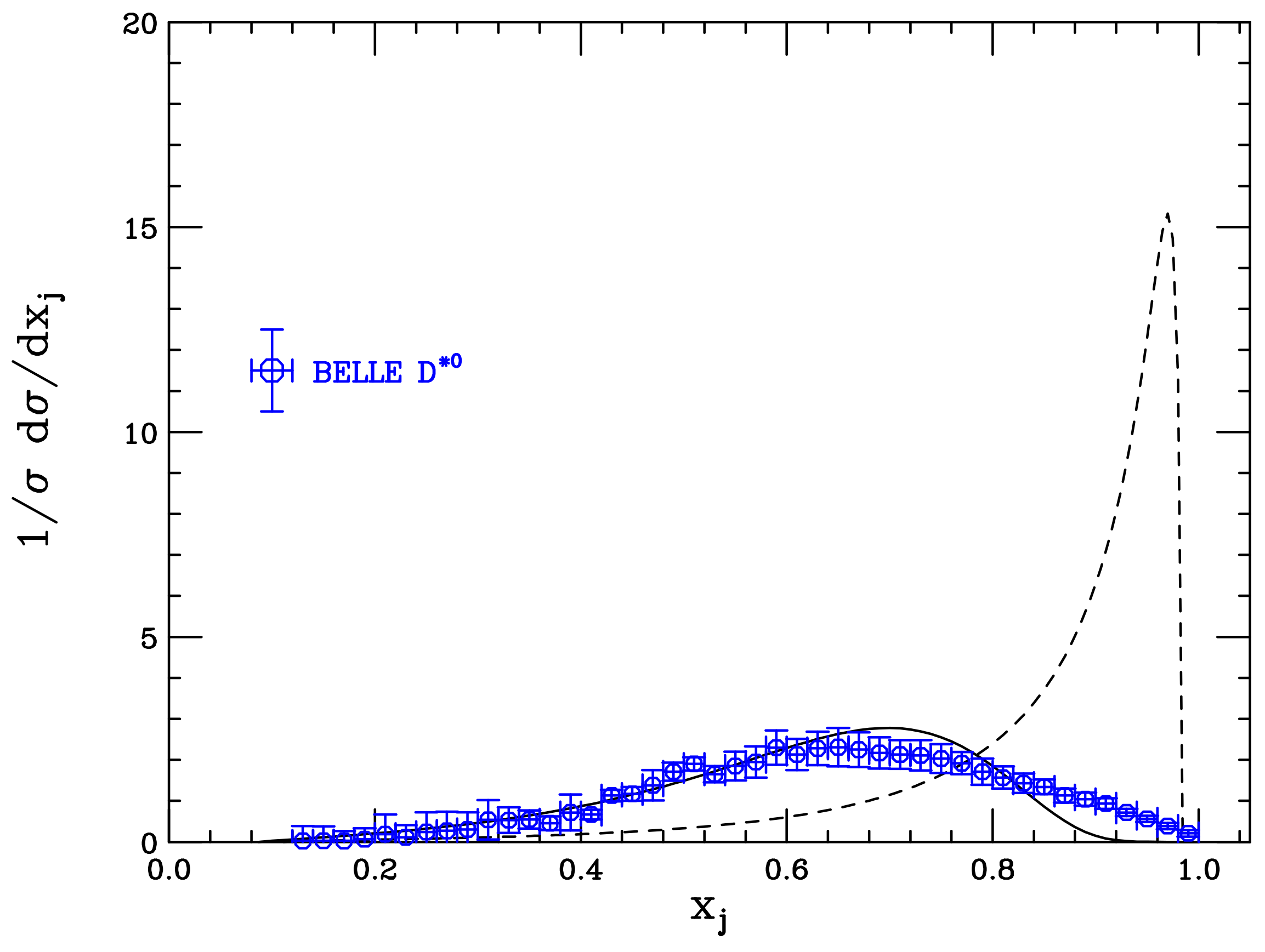
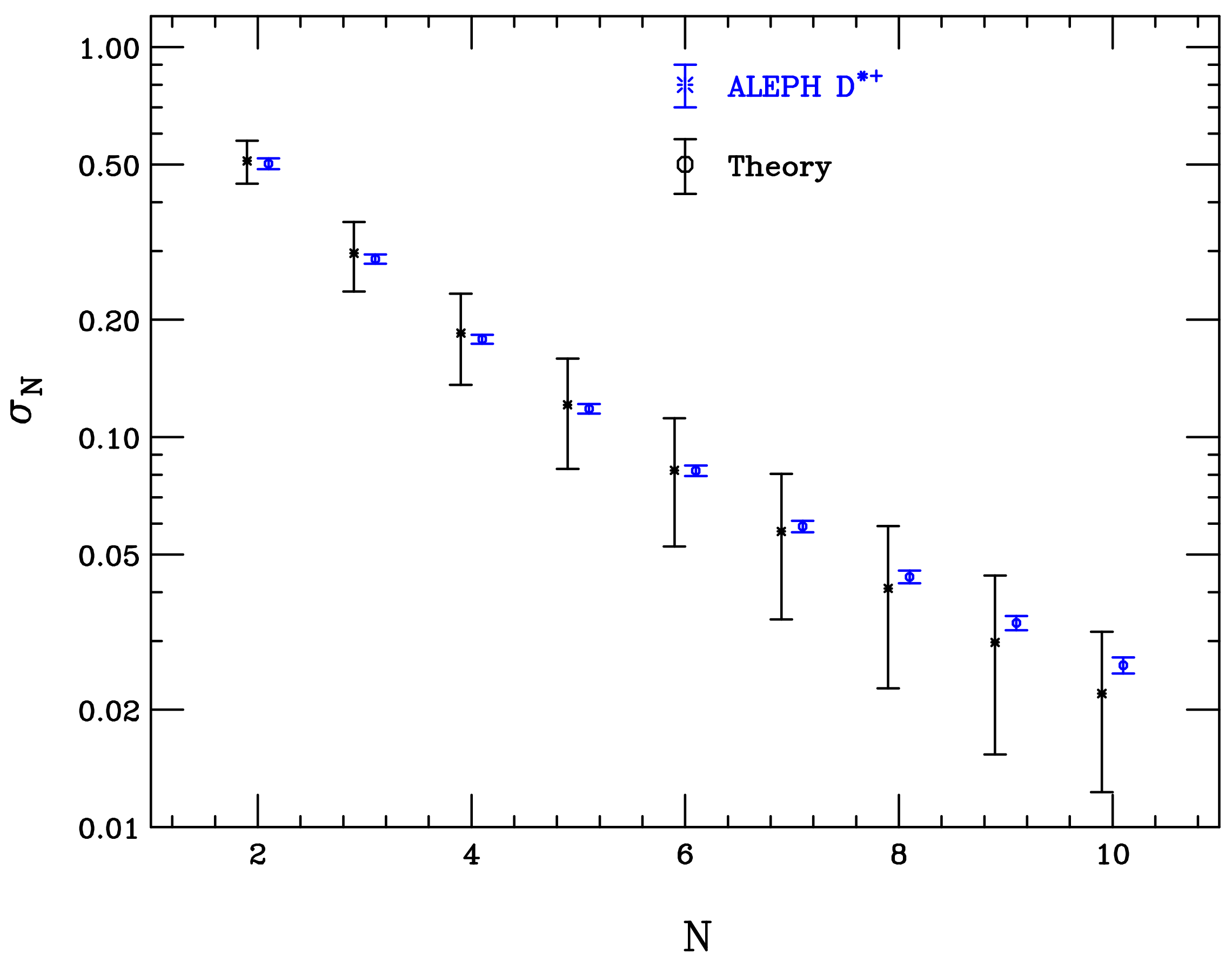
5. Results—D Production
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
| 1 | |
| 2 | After performing a calculation in dimensions, the scheme is defined in such a way that the term is subtracted off. |
| 3 | The Mellin transform of a function , with , is defined as . |
References
- Mele, B.; Nason, P. The fragmentation function for heavy quarks in QCD. Nucl. Phys. B 1991, 361, 626–644, Erratum in Nucl. Phys. B 2017, 921, 841–842. [Google Scholar] [CrossRef]
- Kartvelishvili, V.G.; Likhoded, A.K.; Petrov, V.A. On the fragmentation functions of heavy quarks into hadrons. Phys. Lett. B 1978, 78, 615–617. [Google Scholar] [CrossRef]
- Peterson, C.; Schlatter, D.; Schmitt, I.; Zerwas, P.M. Scaling violations in inclusive e+e− annihilation spectra. Phys. Rev. D 1983, 27, 105–111. [Google Scholar] [CrossRef]
- Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. QCD and resonance physics. Theoretical foundations. Nucl. Phys. B 1979, 147, 385–447. [Google Scholar] [CrossRef]
- Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. QCD and resonance physics: Applications. Nucl. Phys. B 1979, 147, 448–518. [Google Scholar] [CrossRef]
- Cacciari, M.; Catani, S. Soft gluon resummation for the fragmentation of light and heavy quarks at large x. Nucl. Phys. B 2001, 617, 253–290. [Google Scholar] [CrossRef]
- Cacciari, M.; Oleari, C.; Nason, P. A Study of heavy flavored meson fragmentation functions in e+e− annihilation. J. High Energy Phys. 2006, 2006, 006. [Google Scholar] [CrossRef]
- Corcella, G.; Mitov, A.D. Bottom quark fragmentation in top quark decay. Nucl. Phys. B 2002, 623, 247–270. [Google Scholar] [CrossRef]
- Cacciari, M.; Corcella, G.; Mitov, A.D. Soft gluon resummation for bottom fragmentation in top quark decay. J. High Energy Phys. 2002, 2002, 015. [Google Scholar] [CrossRef]
- Corcella, G. Fragmentation in processes. Nucl. Phys. B 2005, 705, 363–383, Erratum in Nucl. Phys. B 2005, 713, 609–610. [Google Scholar] [CrossRef]
- Corcella, G.; Mitov, A.D. Soft gluon resummation for heavy quark production in charged current Deep Inelastic Scattering. Nucl. Phys. B 2004, 676, 346–364. [Google Scholar] [CrossRef]
- Altarelli, G.; Parisi, G. Asymptotic freedom in parton language. Nucl. Phys. B 1977, 126, 298–318. [Google Scholar] [CrossRef]
- Dokshitzer, Y.L. Calculation of the structure functions for Deep Inelastic Scattering and e+e− annihilation by perturbation theory in Quantum Chromodynamics. Sov. Phys. JETP 1977, 46, 641–653, Zh. Eksp. Teor. Fiz. 1977, 73, 1216–1240. [Google Scholar]
- Gribov, V.N.; Lipatov, L.N. Deep Inelastic ep Scattering in perturbation theory. Sov. J. Nucl. Phys. 1972, 15, 438–450, Yad. Fiz. 1972, 15, 781–807. [Google Scholar]
- Melnikov, K.; Mitov, A. Perturbative heavy quark fragmentation function through . Phys. Rev. 2004, 70, 034027. [Google Scholar]
- Mitov, A. Perturbative heavy quark fragmentation function through : Gluon initiated contribution. Phys. Rev. D 2005, 71, 054021. [Google Scholar] [CrossRef]
- Mitov, A.; Moch, S.; Vogt, A. Next-to-next-to-leading order evolution of non-singlet fragmentation functions. Phys. Lett. B 2006, 638, 61–67. [Google Scholar] [CrossRef]
- Sterman, G.F. Summation of large corrections to short distance hadronic cross-sections. Nucl. Phys. B 1987, 281, 310–364. [Google Scholar] [CrossRef]
- Catani, S.; Trentadue, L. Resummation of the QCD perturbative series for hard processes. Nucl. Phys. B 1989, 327, 323–352. [Google Scholar] [CrossRef]
- Dokshitzer, Y.L.; Webber, B.R. Calculation of power corrections to hadronic event shapes. Phys. Lett. B 1995, 352, 451–455. [Google Scholar] [CrossRef]
- Shirkov, D.V.; Solovtsov, I.L. Analytic model for the QCD running coupling with universal αs(0) value. Phys. Rev. Lett. 1997, 79, 1209–1212. [Google Scholar] [CrossRef]
- Aglietti, U.; Corcella, G.; Ferrera, G. Modelling non-perturbative corrections to bottom-quark fragmentation. Nucl. Phys. B 2007, 775, 162–201. [Google Scholar] [CrossRef]
- Corcella, G.; Ferrera, G. Charm-quark fragmentation with an effective coupling constant. J. High Energy Phys. 2007, 2007, 029. [Google Scholar] [CrossRef]
- Braaten, E.; Fleming, S.; Yuan, T.C. Production of heavy quarkonium in high-energy colliders. Ann. Rev. Nucl. Part. Sci. 1996, 46, 197–235. [Google Scholar] [CrossRef]
- Braaten, E.; Fleming, S.; Leibovich, A.K. NRQCD analysis of bottomonium production at the Tevatron. Phys. Rev. D 2001, 63, 094006. [Google Scholar] [CrossRef]
- Baumgart, M.; Leibovich, A.K.; Mehen, T.; Rothstein, I.Z. Probing quarkonium production mechanisms with jet substructure. J. High Energy Phys. 2014, 2014, 003. [Google Scholar] [CrossRef]
- Catani, S.; Mangano, M.; Nason, P.; Trentadue, L. The Resummation of soft gluons in hadronic collisions. Nucl. Phys. B 1996, 478, 273–310. [Google Scholar] [CrossRef]
- Moch, S.; Vermaseren, J.A.M.; Vogt, A. Higher-order corrections in threshold resummation. Nucl. Phys. B 2005, 726, 317–335. [Google Scholar] [CrossRef]
- Fickinger, M.; Fleming, S.; Kim, C.; Mereghetti, E. Effective field theory approach to heavy quark fragmentation. J. High Energy Phys. 2016, 2016, 095. [Google Scholar] [CrossRef]
- Corcella, G.; Czakon, M.; Generet, T.; Mitov, A.; Poncelet, R. NNLO B-fragmentation fits and their application to tt¯ production and decay at the LHC. 2022; in preparation. [Google Scholar]
- Czakon, M.; Generet, T.; Mitov, A.; Poncelet, R. B-hadron production in NNLO QCD: Application to LHC tt¯ events with leptonic decays. J. High Energy Phys. 2021, 2021, 216. [Google Scholar] [CrossRef]
- Heister, A. et al. [ALEPH Collaboration] Study of the fragmentation of b quarks into B mesons at the Z peak. Phys. Lett. B 2001, 512, 30–48. [Google Scholar] [CrossRef]
- OPAL Collaboration Inclusive analysis of the b quark fragmentation function in Z decays at LEP. Eur. Phys. J. C 2003, 29, 463–478. [CrossRef]
- Abdallah, J. et al. [The Delphi Collaboration] A study of the b-quark fragmentation function with the DELPHI detector at LEP I and an averaged distribution obtained at the Z pole. Eur. Phys. J. C 2011, 71, 1557. [Google Scholar] [CrossRef]
- Abe, K.; Abe, K.; Abe, T.; Adam, I.; Akimoto, H.; Aston, D.; Baird, K.G.; Baltay, C.; Band, H.R.; Barklow, T.L.; et al. Precise measurement of the b quark fragmentation function in Z0 boson decays. Phys. Rev. Lett. 2000, 84, 4300–4304. [Google Scholar] [CrossRef]
- Corcella, G.; Drollinger, V. Bottom-quark fragmentation: Comparing results from tuned event generators and resummed calculations. Nucl. Phys. B 2005, 730, 82–102. [Google Scholar] [CrossRef][Green Version]
- Corcella, G.; Mescia, F. A phenomenological study of bottom quark fragmentation in top quark decay. Eur. Phys. J. C 2010, 65, 171–180, Erratum in Eur. Phys. J. C 2010, 68, 687–690. [Google Scholar] [CrossRef]
- Neubert, M. Factorization analysis for the fragmentation functions of hadrons containing a heavy quark. arXiv 2007, arXiv:0706.2136. [Google Scholar]
- Amati, D.; Bassetto, A.; Ciafaloni, M.; Marchesini, G.; Veneziano, G. A treatment of hard processes sensitive to the infrared structure of QCD. Nucl. Phys. B 1980, 173, 429–455. [Google Scholar] [CrossRef]
- Cacciari, M.; Nason, P. Is there a significant excess in bottom hadroproduction at the Tevatron? Phys. Rev. Lett. 2002, 89, 122003. [Google Scholar] [CrossRef]
- Barker, G.; Ben-Haim, E.; Feindt, M.; Kerzel, U.; Roudeau, P.; Ramler, L.; Savoy-Navarro, A. A Study of the b Quark Fragmentation Function with the DELPHI Detector at LEP I. ICHEP 2002 Note; DELPHI 2002-069 CONF 603. Available online: https://cds.cern.ch/record/994376 (accessed on 22 July 2002).
- Artuso, M. et al. [CLEO Collaboration] Charm meson spectra in e+e− annihilation at 10.5 GeV c.m.e. Phys. Rev. D 2004, 70, 112001. [Google Scholar] [CrossRef]
- Seuster, S. et al. [BELLE Collaboration] Charm hadrons from fragmentation and B decays in annihilation at = 10.6 GeV. Phys. Rev. D 2006, 73, 032002. [Google Scholar] [CrossRef]
- Barate, R. et al. [ALEPH Collaboration] Study of charm production in Z decays. Eur. Phys. J C 2000, 16, 597–611. [Google Scholar] [CrossRef]
- Corcella, G.; Knowles, I.G.; Marchesini, G.; Moretti, S.; Odagiri, K.; Richardson, P.; Seymour, M.H.; Webber, B.R. HERWIG 6: An event generator for hadron emission reactions with interfering gluons (including supersymmetric processes). J. High Energy Phys. 2001, 2001, 010. [Google Scholar] [CrossRef]



| data | ||||
| 0.7801 | 0.6436 | 0.5479 | 0.4755 | |
| 0.9169 | 0.8392 | 0.7731 | 0.7163 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corcella, G. Selected Results in Heavy-Quark Fragmentation. Universe 2022, 8, 490. https://doi.org/10.3390/universe8090490
Corcella G. Selected Results in Heavy-Quark Fragmentation. Universe. 2022; 8(9):490. https://doi.org/10.3390/universe8090490
Chicago/Turabian StyleCorcella, Gennaro. 2022. "Selected Results in Heavy-Quark Fragmentation" Universe 8, no. 9: 490. https://doi.org/10.3390/universe8090490
APA StyleCorcella, G. (2022). Selected Results in Heavy-Quark Fragmentation. Universe, 8(9), 490. https://doi.org/10.3390/universe8090490







