Abstract
In the broader methodical framework of the quantization of gravity, the crypto-Hermitian (or non-Hermitian) version of Dirac’s interaction picture is considered. The formalism is briefly outlined and shown to be well suited for an innovative treatment of certain cosmological models. In particular, it is demonstrated that the Wheeler-DeWitt equation could be a promising candidate for the description of the evolution of the quantized Universe near its initial Big Bang singularity.
1. Introduction
The concept of the wave function of the Universe (introduced, 55 years ago, as a solution of the Einstein–Schrödinger alias Wheeler-DeWitt (WDW) equation [1,2]) is contradictory. On the positive side, this concept played a key role during the development of the canonical quantization of gravity [3]. These efforts climaxed in the recent comparatively satisfactory and constructive formulation of the so-called loop quantum gravity (LQG, [4,5,6]). At the same time, Mostafazadeh pointed out, in his review of the recent progress in quantum theory [7], that the solutions themselves remain “void of a physical meaning”, without “finding an appropriate inner product on the space of solutions of the WDW equation” (see p. 1291 in review [7]). In loc. cit., Mostafazadeh also emphasized that “the lack of a satisfactory solution to this problem has been one of the major obstacles in transforming canonical quantum gravity and quantum cosmology into genuine physical theories”. Precisely, this obstacle is to be addressed and discussed in what follows.
In the cited review, we can further read that “in … quantum cosmology … the relevant field equations … are second order differential equations in a time variable … [which] have the … general form
where t denotes a dimensionless time variable, is a function taking values in some separable Hilbert space , and is a positive-definite operator that may depend on t”. Treating the latter variable as “a fictitious evolution parameter in quantum cosmology” (see p. 1292 in [7]), the same author later adds that “the cases in which D is t-dependent (that arises in quantum cosmological models) require a more careful examination”. In this sense, we are prepared to discuss some of the open questions and subtleties of the theory.
In loc. cit., Mostafazadeh redirected interested readers to his earlier study [8]. In a series of our subsequent unpublished comments on this topic [9] (which were later finalized and summarized in papers [10,11]), we showed that an appropriate means of “dealing with these cases” is, simultaneously, less complicated and more complicated than it seems—less complicated in the sense that some of the technical obstacles have later been found surmountable, and more complicated because it appeared necessary to amend the overall quantum-theoretical framework and to replace the non-Hermitian Schrödinger picture (NSP) interpretation of the evolution of (as presented, basically, in [7] or [8]) by the more involved formalism called the interaction picture (IP) (or Dirac’s representation; see a comprehensive review of its non-Hermitian form (NIP) in [12]).
In what follows, we intend to outline the implementation of the NIP approach in the WDW case. The key purpose of our paper is to provide an explicit explanation of the connection between several challenging and open physical questions (a typical one concerns the quantum Big Bang problem, as formulated in Section 2) and the most recent progress in the hidden unitary version of quantum mechanics (the basic features of this theoretical innovation are reviewed). Our main message (viz, the detailed description of the theory and of its application to the WDW equation) will finally be outlined in Section 3 (devoted to a specific schematic toy model of the quantum geometry of the Universe), in Section 4 (on the fully fledged NIP formalism), and in Section 5 (in which the mechanism of transition to the Big Bang singularity will be given its ultimate model-independent construction recipe form). Our results will be discussed in Section 6 and summarized in Section 7.
2. Challenge: Quantum Big Bang Problem
At present, it is widely believed that up to the “youngest age” of the Universe (i.e., for times with s), the evolution (i.e., slow expansion) of the Universe is more or less safely controlled by the classical theoretical cosmology. In contrast, in the interval of times (where denotes the hypothetical time of the Big Bang), we still lack a fully consistent and rigorous quantum theory behind the early history of the Universe [3].
2.1. Could the Degeneracy Survive Quantization? Yes, It Could
In our present study, we felt strongly motivated by the deep relevance of the understanding of the evolution of the Universe near its Big Bang origin, i.e., in a genuine quantum dynamical regime. In this regime, the theoretically most ambitious LQG formalism still seems to lead to at least some contradictory results. In one of the LQG predictions [13], for example, the Big Bang singularity (compatible with the classical Einstein theory of gravity) has been found to be smeared out by the quantization. In the series of papers [14,15,16,17,18,19] or in Section 8 in [5]), for example, it is claimed that the Big Bang singularity of classical theory must necessarily be replaced by a regularized “Big Bounce” mechanism. In contrast, more recently, Wang with Stankiewicz [20] came forward with the opposite conclusion, claiming that, within the scale-invariant LQG framework, “the quantized Big Bang is not replaced by a Big Bounce”.
At first sight, the latter claim appears suspicious. In Rovelli’s words, the quantization-related “absence of singularities” is in fact “what one would expect from a quantum theory of gravity” (see p. 297 in [5]). An elementary support of such an intuitive expectation can be provided by the following schematic observable
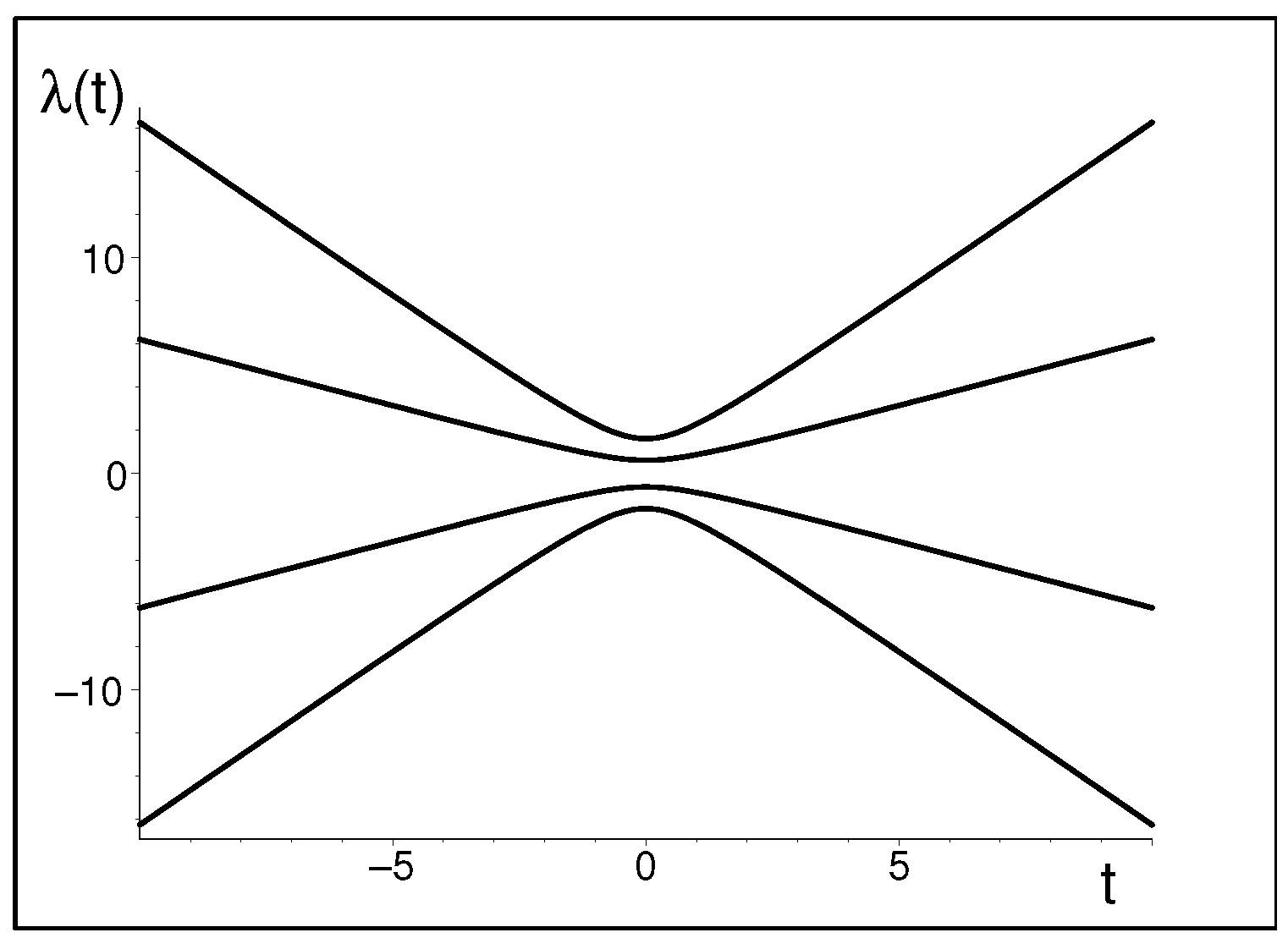
and by the inspection of its spectrum (see Figure 1). As long as the matrix is Hermitian, its spectrum must be real. Moreover, in the generic case (i.e., unless we impose a symmetry upon the matrix), the spectrum must remain non-degenerate. This is the reason that the levels avoid the crossing (which would simulate the regularized Big Bounce). In our example, the proof of the phenomenon is elementary: up to a small vicinity of the “Big Bang time” , the matrix as well as its spectrum are dominated by their asymptotic components, which are strictly linear in t. One might even suspect that the eigenvalues could cross due to an accidental symmetry emerging at , but such a symmetry is manifestly broken by the t-independent component of the model.
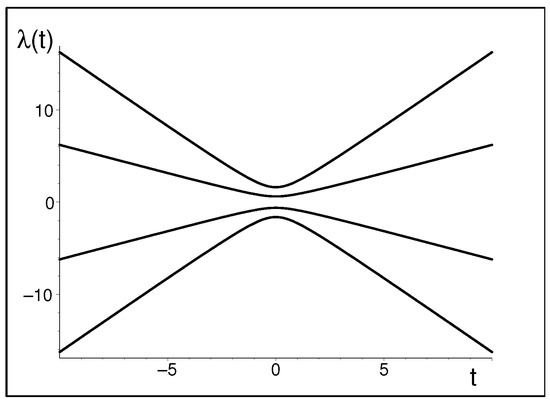
Figure 1.
Eigenvalues of matrix (2) (avoided-crossing phenomenon).
We intend to show that, against all expectations, the latter argument is not foolproof. Admitting that it need not necessarily lead to the wrong conclusions, we will only show that Wang’s and Stankiewicz’s alternative scenario [20] may equally well be supported by an equally elementary toy model. The essence of such a claim is that the Hermiticity property (cf. relation satisfied by our toy model matrix (2), with the superscript marking the matrix transposition plus complex conjugation) depends on a mathematically motivated a priori specification of the inner product in our physical Hilbert space of states [21].
A deeper abstract foundation of our “constructive scepticism” concerning the genericity of the Big Bounce may be found in the literature on quantum mechanics using non-Hermitian operators [7,22,23,24]. In this sense, the common requirement of the self-adjointness of the operators of observables can be weakened and replaced by the condition of their Hermitizability alias quasi-Hermiticity [22]. In many non-Hermitian models, indeed, the Hermiticity may be restored by the mere ad hoc amendment of the inner product [25].
In our present paper, we will narrow the scope of the discussion to the Big Bang and to the WDW equations. Simultaneously, we will broaden the theoretical framework, emphasizing that, in the genuine Big Bang spatial-degeneracy context, it is necessary to replace the most common NSP mathematics with its perceivably more complicated NIP amendment. In a preparatory step, let us now return to the toy model (2) and let us Wick-rotate the time and shift the origin, . The resulting new matrix
is simply a hidden Hermitian (i.e., via an amendment of the inner product, Hermitizable) candidate for a toy model observable representing, in the context of quantum cosmology, say, a potentially measurable discrete spatial grid [26,27,28,29,30].
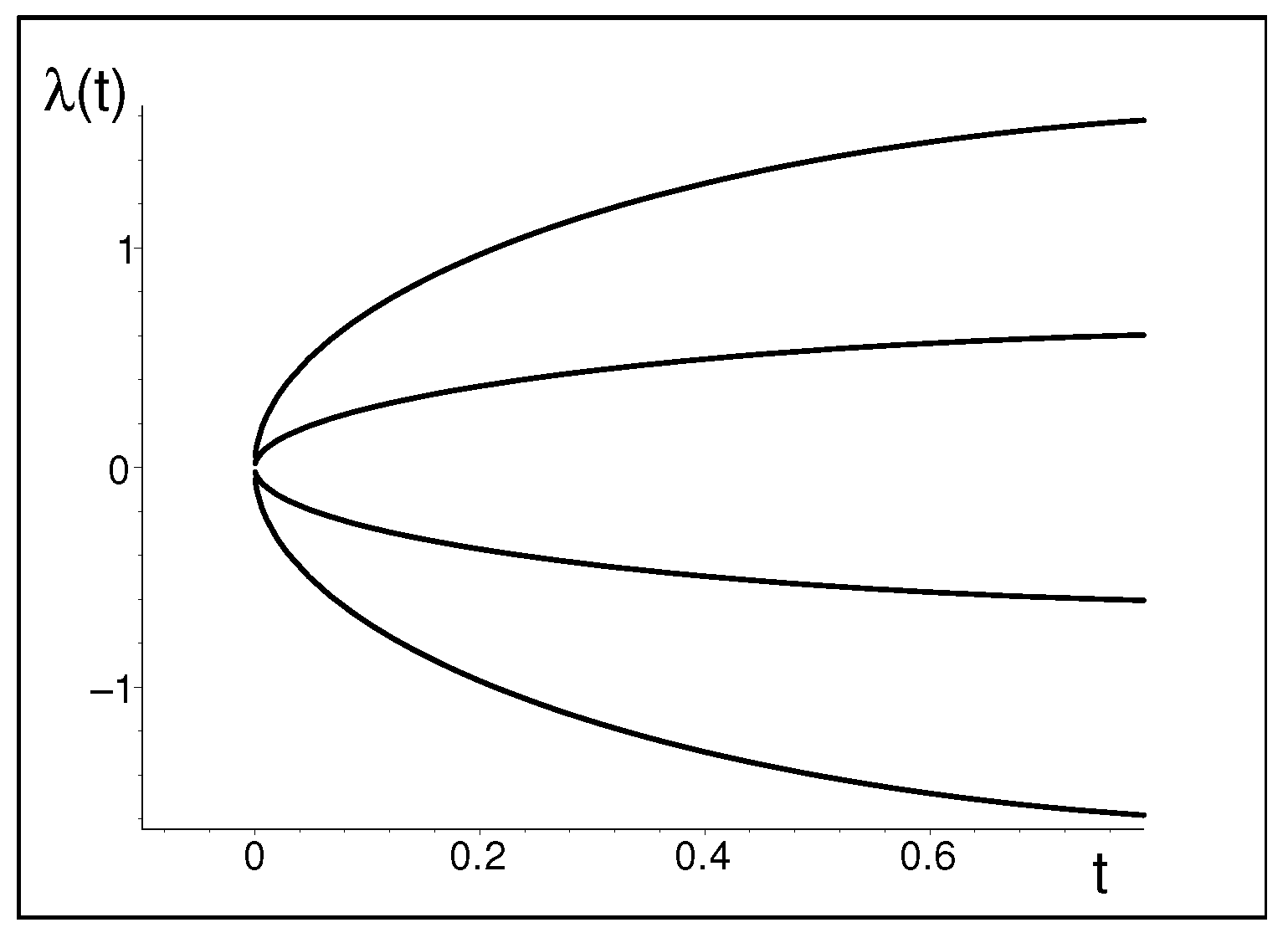
In essence, the latter example indicates that the Big-Bang-type singularities need not necessarily be smeared out by the quantization. Indeed, at the not too large values of the positive time parameter , the spectrum of our manifestly non-Hermitian model (3) may be shown to be real and non-degenerate. This is illustrated in Figure 2. At , the spectrum becomes degenerate and the matrix itself ceases to be diagonalizable.
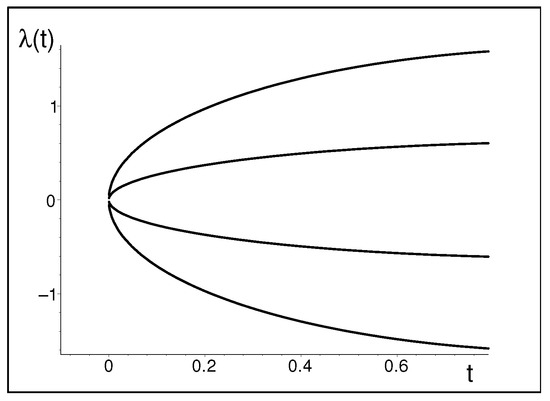
Figure 2.
The reality of the spectrum of non-Hermitian matrix (3) at not too large .
The latter simulation of the Big Bang singularity is called the exceptional point (EP) in mathematics [31,32]. In the complementary context of physics, the spatial-grid interpretation of the time-dependent eigenvalues as sampled in Figure 2 enables us to speak about the “inflation period” of the history of the related hypothetical and highly schematic (i.e., four-point) quantized Universe immediately after its birth. Naturally, the corresponding internally consistent quantum theory must be reformulated accordingly [22].
2.2. Stationary Theory (Non-Hermitian Schrödinger Picture, NSP)
In the pedagogically oriented and compact review of the history of quantum mechanics [33], the authors emphasized that there exists no universal version of quantum theory and that “no formulation produces a royal road to quantum mechanics”. This explains the incessant emergence of new versions of the theory, including its recent “non-selfadjoint-operator” formulations [23].
Incidentally, the “non-selfadjoint-operator” characteristics of these theories could be misleading. As we have already indicated, the mathematical concept of non-selfadjointness (or, in the shorthand terminology used by physicists, of non-Hermiticity) is ambiguous, covering, in various branches of physics, both the generators of the unitary evolution [22] and of the non-unitary evolution [34]. It is necessary to emphasize that only the former (i.e., unitarity-compatible) meaning of the word "non-Hermiticity" will be considered and taken into account in what follows.
The disambiguation in fact deserves an early mention because the difference is often less clear in applications. Moreover, the formulation of the hphysical background of the problems happens to suffer from ambiguities. The details will be discussed later (see, first of all, the introduction to the problem, as given in Appendix A). Now, let us only repeat that the questions that we intend to discuss have their origin in the field of quantum gravity [3]. In this broad context, our attention will be paid, first of all, to the possible role played by the WDW equation and to the questions of physics near the Big Bang (BB) singularity.
2.3. Stationary Wheeler-DeWitt Equation
In the stationary case, the WDW problem becomes formally equivalent to the Klein–Gordon (KG) problem known in the relativistic quantum mechanics [8]. In their simplest versions, both of these problems may be characterized, in suitable units, by the linear differential equation. Thus, in the KG case (where the suitable units are and where one omits, for the sake of simplicity, the electromagnetic field), we have, for example,
The kinetic energy is represented here by the elementary Laplacian ▵, and the dynamics can be maximally reduced to the mere scalar mass term, which may be made position-dependent, .
In the simplest non-stationary WDW model, the analogue of the mass term would be a time-dependent function (cf., e.g., Section 3.5 of review [7] for further references). The KG–WDW analogy enables us to use the same mathematical tools. The relevant literature is fairly extensive but, for our present purposes, it is sufficient to cite the paper by Feshbach and Villars ([35], cf. also Ref. [36]) in which the change of variables
was shown to lead to a replacement of the hyperbolic partial differential Equation (4) by the Schrödinger-like parabolic equation for the two-component wave function (5),
This equation can be interpreted as controlling the unitary evolution of the system via the generator alias FV Hamiltonian
Such an operator is, in the FV Hilbert space
manifestly non-Hermitian, . Pauli with Weisskopf [37] noticed that the same operator can in fact be treated as selfadjoint with respect to another, indefinite inner product,
i.e., that it is selfadjoint in another, ad hoc Krein space. In the modern terminology, one would say that this operator is non-Hermitian but -symmetric [38].
Decisive progress achieved under the stationarity assumption (or, more precisely, after its generalized form, called the quasi-stationarity assumption) is due to Mostafazadeh. In his papers [8,39], he imagined that the FV pseudometric could be replaced by the positive definite metric , converting the Krein-space physics (in which, during evolution, the usual norm is not conserved) into the fully standard and norm-conserving Hilbert-space physics. In essence, only a straightforward change in the inner product was needed,
This opened the way towards a consistent picture of unitary physics in which the stationary Hamiltonian controls the NSP quantum evolution, which is, with respect to the amended inner product (9), unitary.
After either the KG or the WDW interpretation of Equation (4) in the stationary case, the Hilbert-space metrics in (9) can be given a formal block-diagonal-operator structure
This leads to the first quantization of both of these systems.
3. Fine-Tuned Nature of the Quantum Big Bang
The conventional mental operation called “quantization of the classical theory” does really very naturally lead to the conclusion that the singularity is “smeared out” near due to “quantum effects” [40,41] (see also the four-by-four Hermitian matrix (2)). In our text, we pointed out that the support of such a regularization hypothesis is only unavoidable in the conventional “textbook” quantum mechanics. In a more general, hiddenly Hermitian theory, such an assumption is artificial and unfounded (cf. Appendix A or toy model (3)). Once one overcomes the mental barrier, one reveals that the inner product may start playing the central descriptive role.
3.1. The N-Grid-Point Toy Model of Kinematics
In the literature, the manifestly non-Hermitian but Hermitizable Wheeler-DeWitt equation has only been considered in the stationary (or, better, quasi-stationary) mathematical NSP regime (cf. [7] or Section 2.2 above). In Section 4, we will turn attention to the conceptual necessity of keeping the WDW-related Hilbert space time-dependent. In the overall context of the canonical quantization of gravity, we have to be prepared to address, therefore, a number of purely technical questions and tasks.
In the first one, the point-like Big Bang must be made compatible with a consequent theoretical unitary evolution scenario. Thus, we have to complement the abstract argumentation of Section 2 with a detailed description of a suitable concrete toy model. In the model, the measurable values of the spatial grid points (say, the necessarily real and time-dependent values with ) will have to be assumed obtainable, in principle at least, as eigenvalues of a suitable non-Hermitian geometry-representing “effective kinematical input” operator (say, ).
Secondly, we have to keep in mind that, in a way indicated by our four-by-four matrix (3), we may assume that the general N by N matrix will still be real and tridiagonal. Indeed, in a way explained in [42], the reality and tridiagonality is an important merit of any candidate for an observable because it enables one to construct the metric algebraically, in a recurrent manner. In this sense, we may recall the existing results in linear algebra [43] and choose the one-parametric family of our N by N toy model “effective kinematics” as follows:
The non-triviality of this matrix and the arbitrariness of its dimension N in combination with its non-numerical tractability [44] will enable us to show how the requirement of the existence of the quantum Big Bang singularity becomes supported by a consistent reconstruction of the related physical time-dependent Hilbert-space metric. As long as can be any suitable function of time, we may restrict our considerations to the interval of in the interior of which the grid-point-coordinate spectrum of remains non-degenerate, real, and discrete, and at the boundaries of which one can visualize the realization of the Big Bang. Thus, after the simplest choice of , we obtain an immediate level analogue of the graphical evolution pattern of Equation (2), where we had .
One of the main constraints imposed upon our toy model “geometry operator” (11) is its compatibility with the unitarity of the quantum evolution, i.e., with the existence of the Hilbert-space metric. Naturally, the process of the evolution of the corresponding schematic Universe will have to start at the Big Bang single-point-degeneracy singularity, which is such that
On the technical level, one can really speak about a challenge because even the purely formal construction of a highly schematic “Big-Banging” model of the quantum Universe must remain compatible with the basic theoretical requirement of compatibility between the kinematical input information (12) and the dynamical input information as represented by the WDW Hamiltonian operator. The details will be discussed below. For the time being, let us only assume that with the kinematical spatial-grid input (12) adapted to any phenomenological requirements, the dynamics of the WDW-related Universe will remain reflected by a suitable non-stationary form of the operator D in its form entering the non-stationary analogue of the stationary (or, if you wish, adiabatic) form (10) of the WDW Hilbert-space metric.
3.2. The Fine-Tuned Nature of the Hilbert-Space Metric
One of our most important WDW-related model-building tasks can be seen in the generalization of the qualitative and consistent picture of the quantum Big Bang singularity as mediated by its grid-point realization via Equation (3) above (cf. also Figure 2). In such a project, we encounter the two main technical obstacles. The first one lies in the necessity of the guarantee of the existence of the metric at all times (i.e., in our model, at all of the sufficiently small positive times) up to the very Big Bang birth-of-the-Universe EP limit . In our toy model, due to its exact solvability [43], such a guarantee will have an exact, non-numerical form.
The means of circumventing the second technical obstacle (viz., the necessity of a guarantee that the Hilbert-space metric remains, at all of the relevant times, non-singular and positive definite) is equally difficult to find. In our model, we shall see that, for the model in question, this goal can be achieved by non-numerical means as well.
The respective solutions of both of the above-mentioned problems are closely interrelated. Their essence can be identified with the necessity of the coexistence of the singularity in the grid with the singularity-free nature of the metric . The most universal approach to this problem has been promoted by Scholtz et al. [22], who proposed to use the complete information about the set of the observables , , …. Such an “extreme” model-building strategy yielded a unique physical metric . In principle, its applicability is strongly N-dependent of course. Thus, our methodical considerations will only concern the systems with the smallest dimensions.
3.2.1. The Eligible Hilbert-Space Metrics at
At , the grid-point operator (11) reads
with the four real parameters and , with, for the sake of definiteness, positive , and with the general ansatz
For the Hilbert-space metric, the condition of quasi-Hermiticitiy degenerates to the two elementary relations,
and without any loss of generality, we may set and evaluate the eigenvalues of matrix of Equation (14),
Thus, this matrix may be declared acceptable as a metric if and only if it is positive definite, i.e., if and only if
This relation clearly indicates that near the EP limit , the range of variability of the admissible parameter (numbering the admissible Hilbert-space metrics) becomes extremely narrow. Moreover, whenever the dynamics-controlling parameter z moves closer to the EP singularity, the interval quickly shrinks so that our choice of the metric must be, in the Big Bang vicinity, very precisely “fine-tuned”.
Equation (15) becomes further simplified when we reparametrize the strength of the non-Hermiticity in terms of the new variable . Now, the Hermitian limit corresponds to while the singular EP (or, if you wish, Big Bang or Big Crunch) extreme is reached at . Ultimately, formula
defines, up to an inessential overall factor, all of the eligible correct metric operators at .
3.2.2. and the Requirement of Positivity
Once we move to the next geometry operator (11) with , the general ansatz for the metric may be reduced to a six-parametric Hermitian matrix
This reveals that the construction of the metric remains a purely routine linear-algebraic problem. At the same time, the weakness of the construction is found to lie in the less easy determination of the domain of parameters for which the metric operator remains positive definite. Although the domain of positivity of the metric is still implicitly defined by the secular determinant and by the relation
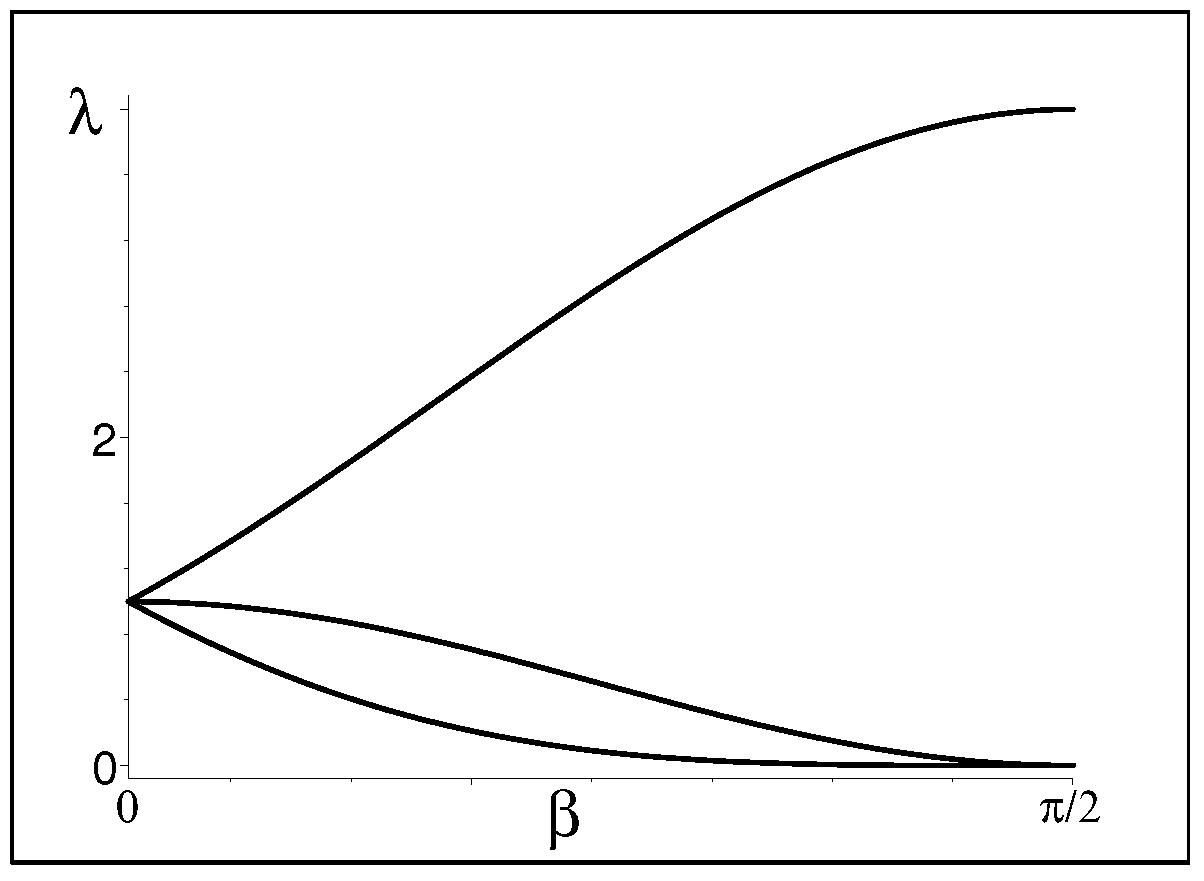
the analogue of the Equation (16) would be complicated for an explicit display. The task still remains non-numerical because the secular polynomial remains linear in the parameters , f, and/or . This still allows the determination of the range of the admissible parameters to be straightforward. A typical example of such a determination is provided by Figure 3.
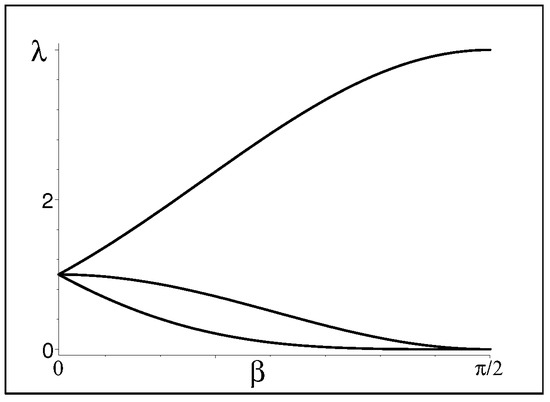
Figure 3.
Eigenvalues of our singularity-free metric (17) as functions of one of the parameters at .
In this illustrative picture, we see that the eigenvalues of the metric remain real and non-degenerate in a large interval of one of the dynamical parameters . In a small vicinity of the singular EP/BB limit , we may deduce that the rank of the metric becomes approximately equal to one. The picture even shows the confluence of the eigenvalues of the metric in the trivial-metric Hermitian-system limit , i.e., very far from the EP/BB dynamical regime.
Naturally, the technical difficulties will grow with the dimension. At the larger N, the construction has to be given an alternative, purely graphical form. This strategy has been used in paper [45], where it has been shown that the use of the graphical method remains feasible even for the higher-order secular polynomials (cf. Figures 16 and 17 in loc. cit.). Nonetheless, one has to expect that at the truly large matrix dimensions, the construction becomes purely numerical.
3.3. Candidates for the Other Observables
For any given non-Hermitian grid-point operator with the real and nondegenerate spectrum , one can construct the arbitrarily normalized eigenvectors,
For the same spectrum, the arbitrarily normalized double-bra-marked left eigenvectors may be also defined as the standard right eigenvectors of a Hermitian conjugate operator,
It is easy to deduce that for . In the generic case, the overlaps will be real and non-vanishing. Whenever N is finite, the resulting biorthogonal basis can be used in a generalized spectral representation of the operator
We may conclude that the general (though not necessarily invertible or positive definite) N-parametric Hilbert-space metric can be then defined by formula
The parameters must be all real. The acceptability of the matrix in the role of the physical Hilbert-space metric (i.e., the necessary invertibility and positivity properties) is then guaranteed if and only if at all n [46]. In such a setting, one can easily use an analogous generalized spectral representation to define also any other operator of an acceptable quantum observable.
4. Mathematics: Non-Hermitian Interaction Picture (NIP)
Naturally, the (quasi-) stationarity restriction becomes, in the WDW case, hardly acceptable, especially if one tries to deal with the quantum dynamics near a singularity such as the Big Bang. In such a case, a much deeper modification of the formalism of the non-Hermitian quantum theory is needed.
After one decides to relax the assumptions of stationarity, an increase in the complexity of the system of equations is partially compensated by the clarification of several conceptual problems. In this sense, our main methodical recommendation is that, in analogy with the Hermitian interaction picture of textbooks, one still keeps in mind the necessity of the description of the dynamics in terms of both the operators and wave functions. In other words, it is necessary to avoid several existing and widespread misunderstandings that can be found in the current literature. Paradoxically, the root of these misunderstandings may be seen in an insufficiently careful use of the terminology (see, e.g., the explanatory “Rosetta-stone-like” Table 1 in [12]). Indeed, once we replace a stationary NSP model by its non-stationary IP and/or NIP alternative and extension, the concept of quantum Hamiltonian ceases to be unique and adequate.
4.1. Non-Stationary Quantum Systems
In the non-stationary quantum theory, the use of the time-dependent metric is known to lead to the loss of the unitarity of the evolution or to the loss of the observability of the NSP Hamiltonian [7]. In fact [9], the puzzle is artificial and purely terminological. The problem disappears when one employs the non-Hermitian version of Dirac’s interaction picture (NIP, [12]).
4.1.1. Evolution Law for the NIP Ket Vectors
In the non-stationary non-Hermitian cases, there is no need for the observability of the generator of the evolution of the ket vectors [47,48,49,50]. Easily, the stationary version of the Dyson map (A3) can be replaced by its time-dependent generalization
In , similarly, Schrödinger Equation (A4) acquires the form
in which the generator is only one of the two unobservable components of the observable instantaneous-energy operator
Only the sum will be called Hamiltonian in what follows. The other component of the Hamiltonian can be defined directly in terms of the Dyson map,
(see [10,11,12] for details).
In the unitary evolution case, the observable version of the non-Hermitian but Hermitizable Hamiltonian (24) is connected with its selfadjoint partner by formula
In , operator (26) has the property of quasi-Hermiticity,
In an internally consistent theory of a unitary (or hidden unitary) quantum system, the Hamiltonian still has to have the real and discrete spectrum representing the instantaneous (but still observable) bound-state energies.
It is unfortunate that, in the literature, only too many people assign the name of a Hamiltonian also to both of the other operators and , neither of which represents an observable quantity [9,11,49]. We prefer calling operator a “generator” (which does not represent an observable, while still controlling and generating the evolution of the IP/NIP wave functions). In parallel, we would also propose calling operator , say, a “Coriolis force”.
4.1.2. Evolution Law for the NIP Bra Vectors
Equation (22) has a dual-space alternative
This enables us to treat the new states as solutions of another Schrödinger equation in [10,11],
The process of the solution of the two Schrödinger equations is maximally economical. The key merit of this recipe (see also more commentaries in [12]) is that it circumvents the necessity of the technically much more complicated direct construction of the metric as used, e.g., in papers [49,51,52,53,54].
The present version of the process must be initiated by the specification of the respective states and at . Thus, Equations (23) and (29) have to be complemented by the specification of the initial values represented by the kets and . Naturally, such values must obey constraints (22) and (28) at . This, in turn, is closely connected with the experiment and with the preparation of the system in question.
4.2. Non-Hermitian Operators in Interaction Picture
It is well known that even in the conventional Hermitian version of IP, the Coriolis-force operators obey the Heisenberg-type equations. These equations control the evolution of every relevant operator of an observable.
In the non-Hermitian NIP formalism, the role of is analogous. In both of the IP and NIP cases, the ultimate goal of the theory lies in the derivation of the predictions of the results of measurements. In our present version of the recipe, this merely requires the evaluation of the overlaps
Due to the identity
or due to its alternative version (cf. Equation (27)),
the NIP formalism is internally consistent, indeed. At the same time, one has to keep in mind that the operators of the IP or NIP observables are manifestly time-dependent and that their time dependence is not arbitrary.
4.2.1. Evolution Law for the Density Matrices
In the non-Hermitian but unitary pure-state quantum systems of our present interest, the state is defined by a pair of the ket vectors, i.e., by the projectors
Alternatively, one can speak about the non-Hermitian density matrix
4.2.2. The Evolution of Observables
The requirement
guarantees the observability status of any operator . This relation is equivalent, due to Equation (A7), to the NSP Hermiticity of in since
The Heisenberg-type evolution equation follows:
It is recommendable to assume that the partial derivatives vanish so that the related operator would be vanishing as well, making the process of the solution of Equation (38) more user-friendly.
Given the generator , the choice of the Coriolis force is far from arbitrary. First of all, it is constrained by the experiment-related initial state vectors. Secondly, it must be compatible with its relation (24) to the initial instant energy and to its evolution law
or, equivalently,
Next, one will also frequently decide to accept the important simplification obtained for the vanishing NSP-time-derivative operators
As long as , there remains no freedom left. In particular, as long as we have the definition
the only ambiguity of is contained in its initial-value specification.
5. The Construction of Non-Stationary WDW Universe Admitting Big Bang
In our present study of the applicability of the NIP approach to the various models in cosmology, we felt particularly interested in a guarantee of the Big Bang degeneracy property
which, in the formal context of quantum mechanics, prescribes and restricts the behavior of certain time-dependent eigenvalues of a suitable operator characterizing the spatial geometry (or at least the size) of the Universe, sampled, say, by of Equation (37), or of Equation (3), with the spectrum as sampled in Figure 2. For this purpose, let us now return to some less general, simplified WDW models.
5.1. The Evolution of the WDW Ket Vectors
Even in the non-stationary cases, many KG and WDW models remain formally equivalent. For this reason, let us now return to Equation (4), replaced by its non-stationary generalization
Using the same amendment of the wave functions as before,
we are able to replace Equation (43) by an analogue of Equation (23), i.e., by the correct NIP Schrödinger equation
Here, the spectrum of the WDW generator need not be real of course (see, for example, an elementary illustrative example as given in [11]).
5.2. The Evolution of the WDW Bra Vectors
It is obvious that the time dependence of the metric may be highly sensitive to its initial value at [49,51,52,55]. Unfortunately, the direct analysis of this dependence via the solution of Equation (32) is complicated. For this reason, we recommended, in [12], to follow the guidance of papers [47,55] and to circumvent the solution of the auxiliary operator evolution Equation (32) (which was characterized, in [49], as the “time-dependent quasi-Hermiticity relation”) and to solve the second Schrödinger equation (for the mere bra vectors) instead.
This leads to the implementation of the NIP recipe with the evolution of
controlled by Schrödinger Equation (29),
Here, it is necessary to emphasize that once we identified the NIP generator with the WDW generator in Equations (45) and (47), we made, in effect, a certain highly nontrivial decision. It has two aspects. In the phenomenological context, such a decision implies that the WDW generator does not represent an observable. We believe that there are many reasons for such a preference, especially in the context of the possible quantization of gravity, because, in such a context, the WDW eigenstates are usually treated as a means of specification of the Hilbert space, rather than as the observable states that would be directly connected with the energy [5].
5.3. Reconstruction of the Metric from the Generator
In the NIP framework, it is sufficient to admit that only the sum (24) of the generator and of the Coriolis force (of a purely kinematical origin) can be interpreted as the observable Hamiltonian. In such a non-stationary NIP scenario, several open questions emerge and have to be resolved, of course.
5.3.1. Big Bang Rendered Possible by the Time Dependence of the Metric
Let us now accept the model-building strategy in which one is given the kinematical input operator . Then, the general non-Hermitian interaction picture can be declared exceptional because only this picture is in fact a candidate for a realization of the quantum Big-Bang-like phase transitions via a unitary evolution process [43,56,57]. Naturally, the details of such a realization remain nontrivial even when we restrict our attention to the Wheeler-DeWitt form of the most elementary differential-operator generators and to the Big-Bang-like quantum phase transitions. Nevertheless, what we achieve is that we avoid and eliminate the danger of the Big-Bounce smearing after quantization. In Hermitian theory, this smearing is unavoidable, caused by an effective level repulsion, as sampled in Figure 1 above. In the quasi-Hermitian NIP context, the Big-Bang-related exceptional-point degeneracy is rendered possible via the “fine-tuning” of the metric: a few non-numerical, exactly solvable simulations of such a fine-tuning may be found described, e.g., in [56].
A complementary word of warning has been formulated in our brief methodical note [47]. We revealed there that in the Heisenberg picture (HP), the Big Bang degeneracy cannot be realized at all. Indeed, the underlying constant choice of vanishing has been shown to imply the stationarity of the HP metric, (recall Equation (32) for the quick proof). The HP form of Equation (24) implies that we have so that only the solution of the Heisenberg Equations (38) is needed. The only advantage of using the HP simplification is that both of the underlying Schrödinger equations remain trivial. Nevertheless, as long as the realization of the Big Bang degeneracy necessarily requires that the Hilbert-space metric has to vary with time, the use of the NIP formalism with nontrivial is unavoidable.
Unfortunately, no help has been reached in an extended Heisenberg picture (EHP, [55]). In a slightly amended formalism, we proposed the use of a constant-operator choice of a non-vanishing generator . We found that the EHP formalism can already describe the evolution equivalent to the one generated by the manifestly time-dependent selfadjoint quantum Hamiltonians (cf. Abstract of Ref. [55] or a rediscovery of this possibility in [54]). Nonetheless, the description of the phase transitions (such as the Big Bang) remains beyond the capacity of the amended EHP approach. The fully fledged NIP is needed.
5.3.2. The Detailed WDW NIP Recipe
In [12], we outlined some of the details of the constructive treatment of the quantum phase transitions. We pointed out that our “dynamical input” knowledge of the non-observable Hamiltonian enables us to solve the pair of our Schrödinger Equations (23) and (29) at any initial conditions. In this sense, every initial N-plet
and
chosen at can be used to construct the time-dependent N-plets of the kets
and
Under an elementary working hypothesis of a finite-, N-dimensional Hilbert space, the additional initial bi-orthonormality assumption
and the completeness
become immediately extended to all times ,
Moreover, the time-dependent metric operator acquires the standard representation in ,
This means that the choice of a suitable generator and of the two suitable initial vector sets (48) and (49) with properties (50) and (51) does not leave too much space for the further requirements concerning the dynamics.
Fortunately, we come to the conclusion that the space left by the NIP formalism is still sufficient for our present purposes. Indeed, in our construction, we started from the assumption of the knowledge of a preselected WDW form of the generator . Such specific “kinematical-like” input information is still not in conflict with the Big Bang dynamics. Indeed, such a version of the general NIP formalism still admits the use of the formal spectral representation of the observables. In this sense, there exist the two most important operators of our present interest. The first one is the “dynamical”, observable-energy-representing operator called Hamiltonian. In its spectral representation of the form
the choice of the energy eigenvalues remains unrestricted.
In the climax of the story, an entirely analogous expansion should be finally introduced in order to define the complementary, “kinematical”, background-representing operator of a suitable “geometry” or “spatial-grid” operator (37). In its analogous spectral representation
we are free to require the validity of the Big Bang constraint (42) imposed upon all of its spatial-background-representing eigenvalues .
6. Discussion
The non-Hermitian innovation of the NSP framework opened, in [8], the way towards a deeper understanding of the KG- and WDW-like quantum systems in stationary approximation. Later, the birth of the more sophisticated non-Hermitian version of Dirac’s interaction picture [10] seemed to be, initially, merely an artificial mathematical exercise. Nobody seemed to be willing to admit that the NIP formalism might find application in quantum gravity. The main reason was that in the most advanced version of quantum gravity (i.e., in the canonical LQG approach), virtually all the results seemed to indicate that the classical Big Bang singularity has to be replaced by its quantized Big Bounce alternative.
Even among mathematicians, it has been firmly believed that the quantization must necessarily smear out the singularities of the classical Einstein’s general relativity [3]. In this sense, before any return to the quantum Big Bang hypothesis, it was necessary to wait for a renewal of its support in the realistic LQG context [20]. Naturally, the problem is technically complicated. In this sense, the present methodical support of the latter hypothesis is also merely schematic and incomplete. In its framework, we had to leave many important phenomenological requirements aside. Let us now mention some of them in the form of brief comments.
6.1. The Background Independence Requirement
In Isham’s foreword preceding Thiemann’s comprehensive 2007 monograph on canonical quantum gravity [3], the Hamiltonian constraint alias “the famous Wheeler-DeWitt equation” is characterized as “arguably one of the most elegant equations in theoretical physics, and certainly one of the most mathematically ill-defined”. In the introductory part of the book itself, one reads, indeed, that the sufficiently rigorous specification of a suitable Hilbert space in which the Wheeler-DeWitt operator would be defined represents one of the most important unresolved theoretical challenges.
The latter Hilbert-space problem may be found thoroughly discussed in Section 9.2 of Mostafazadeh’s 2010 study [7]. Even the authors of the LQG study admit that such an approach does not yet provide a fully consistent description of the physical reality. Nonetheless, their approach addresses, successfully, the necessary background independence of the theory [5]. In some sense, such a requirement should be incorporated into any theory that pretends to be “fundamental” rather than merely “effective”.
From the perspective of our present approach based on the drastically simplified WDW equation, the constructions that would be background-independent were found feasible. In some sense, such a requirement can be perceived as lying in the very center of the NIP approach, in which, admittedly, one starts from the knowledge of the explicit WDW form of the operator , but in which the theory admits the introduction of an “observable background”. Although our present spectral representation definition (55) of such an independent kinematical background may appear rather abstract, a more specific example may be sought, say, in [58], where a nontrivial coordinate/background has constructively been obtained in an elementary dynamical model.
In our considerations, the role of a geometric background has been played by the “dynamical input” operator sampled by a matrix in Equation (3), with the spectrum simulating the “observable” spatial grid points and guaranteeing the existence of the Big Bang singularity at (cf. Equation (42) or Figure 2). In discussion, one only has to emphasize the mathematical subtlety of the correspondence between the hidden Hermiticity of and the fine-tuned nature of the corresponding Hilbert-space metric , which guarantees the unitarity of the system (i.e., of the evolution of the Universe from the very beginning of its observability and existence).
In the latter considerations, the truly drastic simplifications of the picture seem still absolutely necessary at present, skipping, typically, the Lorentz-covariance requirements and working with the models in which the time is a parameter and in which, for methodical reasons, the “Universe” is one-dimensional and discretized via a finite mesh of the time-dependent grid points , . In such a “Universe”, only the degeneracy in the classical physics Big Bang limit is asked for.
6.2. Problems with Terminology
The conventional belief that the avoided crossings of the eigenvalues are generic is equivalent to the (usually, only tacit) assumption of the time independence of the physical inner-product metric . In the opposite direction, once we replace the conventional selfadjoint grid matrix with its isospectral but merely hidden Hermitian partner , we discover the existence of a new freedom in the formalism as carried by the Dyson map . As a consequence, the existence of the singular Big Bang grid-point limit (42) is rendered possible.
In the language of mathematics, the innovation lies in the enhancement of the flexibility of the dynamical laws. One arrives at the less usual, non-Hermitian NIP formulation of quantum mechanics. In its framework, the unitary and closed quantum systems may be defined via structures using more than one inner product, i.e., strictly speaking, more than one Hilbert space.
One of the most welcome consequences is an enhancement of the flexibility, while, on the other hand, one may find terminological misunderstandings. In the phenomenologically oriented literature, several similar terms denote more or less the same theory. Thus, in different papers, one encounters, e.g., a reference to the quasi-Hermitian quantum theory [22,59], to the pseudo-Hermitian quantum theory [7], to the non-Hermitian but -symmetric quantum theory (usually also with = parity and with = time reversal [38]), to the three-Hilbert-space quantum theory [11], or to the crypto-Hermitian quantum theory [60], etc.
6.3. The Danger of an Over-Determination of the Dynamical Input
All of the latter approaches lead to a perceivable gain in flexibility of the realistic models of various quantum systems. This is to be countered merely by the necessity of keeping trace of the more sophisticated forms of Hermitian conjugations. One can conclude that the subject is still relevant. On a model-independent level of discussion, it is worth adding that the consistency of the dynamical input need not in fact be easily guaranteed. In review [22], for example, the authors stressed that in the over-determined cases, the necessary Hilbert-space metric (and, hence, the theory itself) need not exist at all. In [61], such a non-existence has been shown to occur even in some fairly popular realistic models. An abstract analysis of such an unpleasant possibility was presented in [62]. Only recently, more encouraging results were obtained in [25], offering a certain systematic guide to the construction of the mutually compatible non-Hermitian observables.
Once we restrict attention to the applicability of the NIP approach in cosmology, encouragement may be sought in the progress and simplifications of the canonical quantization [3,5]. The latter two reviews of the state of the art differ by the language, with the former one being more mathematically oriented. Nonetheless, both of these monographs share the traditional philosophy interpreting the quantum theory as a result of a modification of its classical predecessor. In our final remark, we would like to point out that one could also try to weaken our dependence on the classical-physics-based intuition by treating, as primary, the tentative quantum hypotheses in a way defended, e.g., by Brody and Hughston [63].
7. Summary
The core of our present message is that the consistency of the quantum-mechanical interpretation of the non-stationary WDW systems requires that the Schrödinger equation ceases to be perceived as offering a complete picture of the evolution. In this sense, it is necessary to add a parallel and fully fledged description of the evolution of the operators of observables using the Heisenberg-like evolution equations. In the natural physical quantum-gravity context, the unitarity of the WDW-controlled evolution can be then guaranteed. The apparently non-unitary evolution of the left and right wave functions (controlled by the respective two Schrödinger-type equations) is precisely compensated by the apparent non-unitarity of the evolution of the operators representing the observables (controlled, in parallel, by non-Hermitian Heisenberg-type equations).
Having accepted such a philosophy, our present paper can be read as a more or less purely methodical return to the question of whether, in the framework of quantum cosmology, the birth of our Universe should be perceived as a point-like Big Bang or as a smeared Big Bounce. In essence, we have presented here a few arguments supporting our persuasion that, in the purely theoretical NIP framework, such a question remains, at present, open.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Two Hilbert Spaces in Quantum Mechanics
In the conventional quantum mechanics of textbooks [21], the predictions of the results of experiments have their mathematical background, in NSP, in the evaluation of matrix elements
The symbol denotes here a selfadjoint operator of the observable in question; usually, this operator is time-independent, . All information about the evolution of the system in time is carried, in the pure state regime, by a ket vector element of a Hilbert space of states . This state is assumed prepared at and measured at . Prediction (A1) is probabilistic and contains only the NSP wave-ket solutions of Schrödinger equation
Due to the Stone theorem, the evolution is unitary if and only if the Hamiltonian is selfadjoint in , [64].
One of many efficient simplifications of the practical solution of Equation (A2) is due to Dyson [65]. He revealed that, in many cases, one has to work with a technically unfriendly Hamiltonian, which can be perceivably simplified via a suitable isospectral preconditioning . This is formally equivalent to the transformation of the ket vector wave functions,
Operator has to be -independent and stationary (). Dyson also recommended to make the choice of non-unitary (). In analogy with the so-called coupled-cluster method based on a similar idea [66], one may also treat the simpler partner of the Hilbert space as formally different, denoted by a different dedicated symbol, say, .
Schrödinger Equation (A2) becomes replaced, in the majority of applications of the Dyson-recommended and -mediated change of space , by a friendlier equation
The transformed Hamiltonian is de-Hermitized since in . In the early review [22] of the procedure, a change in the philosophy has been proposed, resulting in a reformulation of the textbook NSP approach called, in the spirit of the mathematician’s terminology [59], quasi-Hermitian quantum mechanics. In this framework, the model-building process has to start directly from Equation (A4) and from a guarantee of the user-friendliness of the preconditioned Hamiltonian H. Whenever necessary, one may, after all, re-Hermitize the model, say, via a reconstruction of [7].
The non-unitarity of the map implies, for the manifestly auxiliary Hilbert space , the loss of its physical-space status. Fortunately, it appeared sufficient to amend the inner product and to convert into a fully acceptable and physical Hilbert space . By construction, the latter space has to be unitary equivalent to , with the most straightforward method being the reconstruction of the so-called metric . The mathematical details can be found in reviews [22] and [7]. The essence of the trick is that the correct space can be represented via the mere amendment of the bra vectors in ,
In the terminology of functional analysis, the definition of the dual alias bra vector space of the linear functionals is merely amended and transferred back, from to , via formula . In other words, one simply converts the conventional, unphysical bra-ket inner product into its physical alternative,
In light of this relation, it is possible to perform all calculations in . Nonetheless, in practice, the redundancy of the introduction of the manifestly unphysical Hilbert space must be well motivated. The expense must be more than compensated by the simplification of the evaluation of the experimental predictions. Moreover, the loss of the direct connection with has to be taken into account because, in this space, we usually define the operators of observables using the principle of correspondence [21].
One can often pull at least some of the necessary operators from up to the auxiliary Hilbert space (see, e.g., [58]), e.g., whenever one knows the Dyson map, one can define the necessary operators in using formula
References
- DeWitt, B.S. Quantum Theory of Gravity. I. The Canonical Theory. Phys. Rev. 1967, 160, 1113–1148. [Google Scholar] [CrossRef]
- Hamber, H.W.; Williams, R.M. Discrete Wheeler-DeWitt Equation. Phys. Rev. 2011, 84, 104033. [Google Scholar] [CrossRef]
- Thiemann, T. Introduction to Modern Canonical Quantum General Relativity; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Rovelli, C.; Smolin, L. Loop space representation of quantum general relativity. Nucl. Phys. B 1990, 331, 80–152. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ashtekar, A.; Lewandowski, J. Background independent quantum gravity: A status report. Class. Quantum Grav. 2004, 21, R53–R152. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudo-Hermitian Representation of Quantum Mechanics. Int. J. Geom. Meth. Mod. Phys. 2010, 7, 1191–1306. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Quantum mechanics of Klein-Gordon-type fields and quantum cosmology. Ann. Phys. 2004, 309, 1–48. [Google Scholar] [CrossRef]
- Znojil, M. Which operator generates time evolution in Quantum Theory? arXiv 2007, arXiv:0711.0535. [Google Scholar]
- Znojil, M. Time-dependent version of cryptohermitian quantum theory. Phys. Rev. D 2008, 78, 085003. [Google Scholar] [CrossRef]
- Znojil, M. Three-Hilbert-space formulation of Quantum Mechanics. Symm. Integ. Geom. Meth. Appl. SIGMA 2009, 5, 001. [Google Scholar] [CrossRef]
- Znojil, M. Non-Hermitian interaction representation and its use in relativistic quantum mechanics. Ann. Phys. 2017, 385, 162–179. [Google Scholar] [CrossRef]
- Bojowald, M. Absence of a singularity in loop quantum cosmology. Phys. Rev. Lett. 2001, 86, 5227–5230. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum nature of the big bang: Improved dynamics. Phys. Rev. D 2006, 74, 084003. [Google Scholar] [CrossRef]
- Bojowald, M. Quantum nature of cosmological bounces. Gen. Rel. Grav. 2008, 40, 2659–2683. [Google Scholar] [CrossRef]
- Ashtekar, A.; Corichi, A.; Singh, P. Robustness of key features of loop quantum cosmology. Phys. Rev. D 2008, 77, 024046. [Google Scholar] [CrossRef]
- Malkiewicz, P.; Piechocki, W. Turning Big Bang into Big Bounce: II. Quantum dynamics. Class. Quant. Gravity 2010, 27, 225018. [Google Scholar] [CrossRef]
- Bojowald, M.; Paily, G.M. A no-singularity scenario in loop quantum gravity. Class. Quant. Gravity 2012, 29, 242002. [Google Scholar] [CrossRef][Green Version]
- Yang, J.-S.; Zhang, C.; Ma, Y.-G. Loop quantum cosmology from an alternative Hamiltonian. Phys. Rev. D 2019, 100, 064026. [Google Scholar] [CrossRef]
- Wang, C.; Stankiewicz, M. Quantization of time and the big bang via scale-invariant loop gravity. Phys. Lett. B 2020, 800, 135106. [Google Scholar] [CrossRef]
- Messiah, A. Quantum Mechanics; North Holland: Amsterdam, The Netherlands, 1961. [Google Scholar]
- Scholtz, F.G.; Geyer, H.B.; Hahne, F.J.W. Quasi-Hermitian Operators in Quantum Mechanics and the Variational Principle. Ann. Phys. 1992, 213, 74–101. [Google Scholar] [CrossRef]
- Bagarello, F.; Gazeau, J.-P.; Szafraniec, F.; Znojil, M. (Eds.) Non-Selfadjoint Operators in Quantum Physics: Mathematical Aspects; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Bender, C.M. PT Symmetry in Quantum and Classical Physics; World Scientific: Singapore, 2018. [Google Scholar]
- Znojil, M. Feasibility and method of multi-step Hermitization of crypto-Hermitian quantum Hamiltonians. Eur. Phys. J. Plus 2022, 137, 335. [Google Scholar] [CrossRef]
- Rovelli, C.; Smolin, L. Discreteness of area and volume in quantum gravity. Nucl. Phys. B 1995, 442, 593–619. [Google Scholar] [CrossRef]
- Thiemann, T. A length operator for canonical quantum gravity. J. Math. Phys. 1998, 39, 3372–3392. [Google Scholar] [CrossRef]
- Znojil, M. Quantum Big Bang without fine-tuning in a toy-model. J. Phys. Conf. Ser. 2012, 343, 012136. [Google Scholar] [CrossRef]
- Znojil, M. Quantization of Big Bang in crypto-Hermitian Heisenberg picture. In Non-Hermitian Hamiltonians Quantum Physics; Bagarello, F., Passante, R., Trapani, C., Eds.; Springer: Cham, Switzerland, 2016; Volume 184, pp. 383–399. [Google Scholar]
- Brody, D.C.; Hughston, L.P. Quantum measurement of space-time events. J. Phys. A Math. Theor. 2021, 54, 235304. [Google Scholar] [CrossRef]
- Kato, T. Perturbation Theory for Linear Operators; Springer: Berlin/Heidelberg, Germany, 1966. [Google Scholar]
- Znojil, M. Parity-time symmetry and the toy models of gain-loss dynamics near the real Kato’s exceptional points. Symmetry 2016, 8, 52. [Google Scholar] [CrossRef]
- Styer, D.F.; Balkin, M.S.; Becker, K.M.; Burns, M.R.; Dudley, C.E.; Forth, S.T.; Gaumer, J.S.; Kramer, M.A.; Oertel, D.C.; Park, L.H.; et al. Nine formulations of quantum mechanics. Am. J. Phys. 2002, 70, 288–297. [Google Scholar] [CrossRef]
- Moiseyev, N. Non-Hermitian Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Feshbach, H.; Villars, F. Elementary relativistic wave mechanics of spin 0 and spin 1/2 particles. Rev. Mod. Phys. 1958, 30, 24–45. [Google Scholar] [CrossRef]
- Znojil, M. Relativistic supersymmetric quantum mechanics based on Klein-Gordon equation. J. Phys. A Math. Gen. 2004, 37, 9557–9571. [Google Scholar] [CrossRef]
- Pauli, W.; Weisskopf, V. Uber die Quantisierung der skalaren relativistischen Wellengleichung. Helv. Phys. Acta 1934, 7, 709–731. [Google Scholar]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947–1118. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Hilbert space structures on the solution space of Klein-Gordon type evolution equations. Class. Quant. Grav. 2003, 20, 155–171. [Google Scholar] [CrossRef]
- Gielen, S.; Turok, N. Perfect Quantum Cosmological Bounce. Phys. Rev. Lett. 2016, 117, 021301. [Google Scholar] [CrossRef]
- Ashtekar, A.; Bianchi, E. A short review of loop quantum gravity. Rep. Prog. Phys. 2021, 84, 042001. [Google Scholar] [CrossRef] [PubMed]
- Znojil, M. Quantum inner-product metrics via recurrent solution of Dieudonne equation. J. Phys. A Math. Theor. 2012, 45, 085302. [Google Scholar] [CrossRef][Green Version]
- Znojil, M. Tridiagonal PT-symmetric N by N Hamiltonians and a fine-tuning of their observability domains in the strongly non-Hermitian regime. J. Phys. A Math. Theor. 2007, 40, 13131–13148. [Google Scholar] [CrossRef]
- Znojil, M. Maximal couplings in PT-symmetric chain-models with the real spectrum of energies. J. Phys. A Math. Theor. 2007, 40, 4863–4875. [Google Scholar] [CrossRef]
- Znojil, M. N-site-lattice analogues of V(x) = ix3. Ann. Phys. 2012, 327, 893–913. [Google Scholar] [CrossRef]
- Znojil, M. On the role of the normalization factors κn and of the pseudo-metric P in crypto-Hermitian quantum models. Symm. Integ. Geom. Meth. Appl. SIGMA 2008, 4, 001. [Google Scholar] [CrossRef]
- Znojil, M. Non-Hermitian Heisenberg representation. Phys. Lett. A 2015, 379, 2013–2017. [Google Scholar] [CrossRef]
- Miao, Y.-G.; Xu, Z.-M. Investigation of non-Hermitian Hamiltonians in the Heisenberg Picture. Phys. Lett. A 2016, 380, 1805–1810. [Google Scholar] [CrossRef]
- Fring, A.; Moussa, M.H.Y. Unitary quantum evolution for time-dependent quasi-Hermitian systems with non-observable Hamiltonians. Phys. Rev. A 2016, 93, 042114. [Google Scholar] [CrossRef]
- Luiz, F.S.; Pontes, M.A.; Moussa, M.H.Y. Unitarity of the time-evolution and observability of non-Hermitian Hamiltonians for time-dependent Dyson maps. arXiv 2016, arXiv:1611.08286. [Google Scholar] [CrossRef]
- Gong, J.-B.; Wang, Q.-H. Time-dependent PT-symmetric quantum mechanics. J. Phys. A Math. Theor. 2013, 46, 485302. [Google Scholar] [CrossRef]
- Bíla, H. Non-Hermitian Operators in Quantum Physics. Ph.D. Thesis, Charles University, Prague, Czech Republic, 2008. [Google Scholar]
- Bíla, H. Adiabatic time-dependent metrics in PT-symmetric quantum theories. arXiv 2009, arXiv:0902.0474. [Google Scholar]
- Fring, A.; Frith, T. Exact analytical solutions for time-dependent Hermitian Hamiltonian systems from static unobservable non-Hermitian Hamiltonians. Phys. Rev. A 2017, 95, 010102(R). [Google Scholar] [CrossRef]
- Znojil, M. Crypto-unitary forms of quantum evolution operators. Int. J. Theor. Phys. 2013, 52, 2038. [Google Scholar] [CrossRef]
- Znojil, M. Passage through exceptional point: Case study. Proc. Roy. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190831. [Google Scholar] [CrossRef]
- Znojil, M. Horizons of stability. J. Phys. A Math. Theor. 2008, 41, 44027. [Google Scholar] [CrossRef]
- Mostafazadeh, A.; Batal, A. Physical Aspects of Pseudo-Hermitian and PT-Symmetric Quantum Mechanics. J. Phys. A Math. Gen. 2004, 37, 11645–11679. [Google Scholar] [CrossRef]
- Dieudonne, J. Quasi-Hermitian operators. In Proceedings of the International Symposium on Linear Spaces; Pergamon: Oxford, UK, 1961; pp. 115–122. [Google Scholar]
- Smilga, A.V. Cryptogauge symmetry and cryptoghosts for crypto-Hermitian Hamiltonians. J. Phys. A Math. Theor. 2008, 41, 244026. [Google Scholar] [CrossRef]
- Znojil, M.; Semorádová, I.; Rŭžička, F.; Moulla, H.; Leghrib, I. Problem of the coexistence of several non-Hermitian observables in PT-symmetric quantum mechanics. Phys. Rev. A 2017, 95, 042122. [Google Scholar] [CrossRef]
- Krejčiřík, D.; Lotoreichik, V.; Znojil, M. The minimally anisotropic metric operator in quasi-hermitian quantum mechanics. Proc. Roy. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20180264. [Google Scholar] [CrossRef] [PubMed]
- Brody, D.C.; Hughston, L.P. Geometric quantum mechanics. J. Geom. Phys. 2001, 38, 19–53. [Google Scholar] [CrossRef]
- Stone, M.H. On one-parameter unitary groups in Hilbert Space. Ann. Math. 1932, 33, 643–648. [Google Scholar] [CrossRef]
- Dyson, F.J. General Theory of Spin-Wave Interactions. Phys. Rev. 1956, 102, 1217. [Google Scholar] [CrossRef]
- Bishop, R.F.; Znojil, M. The coupled-cluster approach to quantum many-body problem in a three-Hilbert-space reinterpretation. Acta Polytech. 2014, 54, 85–92. [Google Scholar] [CrossRef][Green Version]
- Znojil, M. The cryptohermitian smeared-coordinate representation of wave functions. Phys. Lett. A 2011, 375, 3176–3183. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).