Abstract
An accurate understanding of dissimilarities in geomagnetic variability between quiet and disturbed periods has the potential to vastly improve space weather diagnosis. In this work, we exploit some recently developed methods of dynamical system theory to provide new insights and conceptual ideas in space weather science. In particular, we study the co-variation and recurrence statistics of two geomagnetic indices, SYM-H and AL, that measure the intensity of the globally symmetric component of the equatorial electrojet and that of the westward auroral electrojet, respectively. We find that the number of active degrees of freedom, required to describe the phase space dynamics of both indices, depends on the geomagnetic activity level. When the magnetospheric substorm activity, as monitored by the AL index, increases, the active number of degrees of freedom increases at high latitudes above the dimension obtained through classical time delay embedding methods. Conversely, a reduced number of degrees of freedom is observed during geomagnetic storms at low latitude by analysing the SYM-H index. By investigating time-dependent relations between both indices we find that a significant amount of information is shared between high and low latitude current systems originating from coupling mechanisms within the magnetosphere–ionosphere system as the result of a complex interplay between processes and phenomena of internal origin activated by the triggering of external source processes. Our observations support the idea that the near-Earth electromagnetic environment is a complex system far from an equilibrium.
1. Introduction
The geospace environment, especially the ionosphere and the magnetosphere, is a multi-scale complex system showing variability over a wide range of temporal and spatial scales [1]. It continuously interacts with the solar wind, whose dynamical variability affects its shape and dynamics [2]. Nevertheless, the dynamical behavior of the geospace environment not only passively responds to changes in solar wind conditions but also shows very rich nonlinear dynamics [3,4,5], whose description needs to be asserted in the framework of dissipative dynamical systems [6]. As a consequence of the solar wind–magnetosphere–ionosphere (SMI) interactions, several induced phenomena take place such as aurorae, geomagnetic storms, magnetospheric substorms, and ground geomagnetically induced currents [7,8]. These are responsible for changes in the space weather conditions around Earth, i.e., the dynamical state of the near-Earth geospace environment [9]. The primary element of space weather is the Sun, whose conditions on its surface and its upper atmosphere can cause a multitude of phenomena like solar flares, coronal mass ejections (CMEs), solar energetic proton (SEP) events, and so on [10]. While the Earth’s magnetic field offers us some protection from solar phenomena, under certain circumstances energy and momentum can be transferred into the geospace environment that becomes disturbed with effects felt on both global and local scales [11]. These phenomena can affect numerous sectors of our global economy: From space based communication, terrestrial weather services, and Global Navigation Satellite Systems (GNSSs), to electric power distribution and High Frequency (HF) radio communication. Thus, a lot of effort is needed, through observations, monitoring, analysis and modeling, to understand and forecast the state of the near-Earth geospace environment [12].
In the context of the SMI system a relevant objective of scientific research is the identification of, and the role played by those processes which are related to the internal magnetospheric and ionospheric variability [13] in terms of interactions between geomagnetic storms and magnetospheric substorms. This is one of the most challenging problems in contemporary space physics [14] and has a crucial impact on our forecast capabilities [15]. Despite the considerable amount of literature on the topic, two contrasting views still persist [16,17]. On one hand, geomagnetic storms are considered as originating from a collection of multiple substorms [17,18,19,20,21]; on the other hand, magnetospheric substorms and geomagnetic storms are viewed as independent processes individually driven by the solar wind variability [22,23,24,25]. Both views can be motivated based upon different observations: Intense magnetospheric substorms occur while magnetic storms are developing with the injection of ionospheric oxygen ions into the outer edge of the magnetospheric ring current [19], and enhanced magnetospheric convection driven by the solar wind electric field [22]. Yet, substorms can also occur when the equatorial ring current is in its reference state configuration suggesting that magnetospheric substorms should not be interpreted as a component of a geomagnetic storm. While the more traditional view of interpreting geomagnetic storms as a collection of magnetospheric substorms seems altogether to be more strongly supported by different pieces of evidence, this issue is still far from being solved [2]. One of the main challenges in studying the storm–substorm relationship is the difficulty of direct measurements and of the existence of in situ real time proxies of both phenomena, being indirectly represented via geomagnetic indices (e.g., the SYM-H and AE indices). These proxies are not capable of describing the full structure of the geospace environment, being representative of the large scale structures (magnetospheric and ionospheric currents) but not very sensitive to small scale phenomena. While this poses some constraints on interpreting the results obtained by analysing the variability of geomagnetic indices, at present, these proxies provide the only reliable source of information on long-term variations of the geospace dynamical state.
In this work, we exploit some recently introduced dynamical system measures to study the co-variation and recurrence statistics of the AL and SYM-H geomagnetic indices. We show that the number of active degrees of freedom required to describe the phase space dynamics of both indices depends on the geomagnetic activity level. When the magnetospheric substorm activity increases, the active number of degrees of freedom increases at high latitudes. Conversely, a reduced number of degrees of freedom is observed during geomagnetic storms at low latitudes. By investigating time-dependent relations between the two geomagnetic indices, we demonstrate the existence of concurrent effects between high and low latitude current systems emerging due to coupling mechanisms within the magnetosphere–ionosphere system, which are the result of a complex interplay between processes and phenomena of internal origin activated by the triggering of external source processes [19,22]. Our observations support the idea that the near-Earth electromagnetic environment is a complex system far from an equilibrium.
2. Data
We use two different geomagnetic indices (SYM-H and AL) Iyemori90,Davis66. While the former quantifies the disruptions of the low latitude ring current during a geomagnetic storm, the latter monitors the high latitude westward electroject associated with the impulsive activity of the magnetotail during magnetospheric substorms. Specifically, the use of the high latitude AL index (instead of the more widely studied AE index) is motivated by our intention to investigate the link between geomagnetic storms and magnetospheric substorms, with a special emphasis on the internal magnetotail dynamics. Indeed, as widely reported in the literature, AL is mainly related to the impulsive events taking place in the central plasma sheet (CPS) being representative of the westward electrojet current, which is connected with the closure of the FAC and DP1 ionospheric and substorm current systems [26].
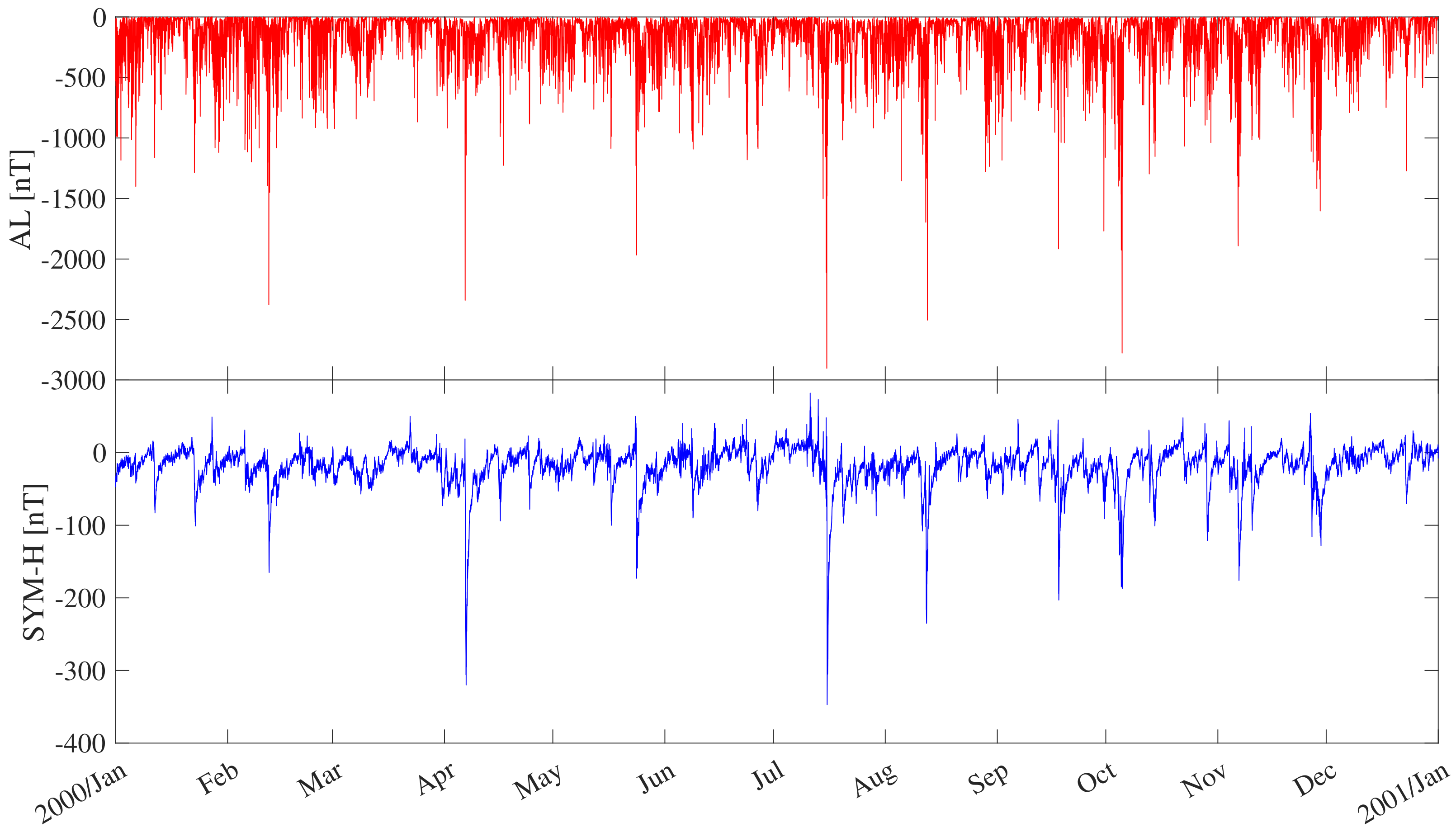
Both indices have a 1 min time resolution and are derived from the H component of the geomagnetic field measured at a longitudinally distributed chain of low (SYM-H) and high (AL) latitude ground based magnetometers. We use time series of one year length during the maximum phase of solar cycle 23, which are shown in Figure 1. The data are freely available from the Kyoto World Data Center (WDC) for Geomagnetism at http://wdc.kugi.kyoto-u.ac.jp/ (accessed on 12 January 2022). Specifically, the studied data set covers the time interval from 1 January to 31 December 2000. Figure 1 displays the time series of the two geomagnetic indices (AL, red line; SYM-H, blue line) for the selected period. Both geomagnetic indices exhibit large excursions, with minimum values of SYM-H of about nT and AL of about nT, corresponding to the famous Bastille Day geomagnetic storm on 14 July 2000.
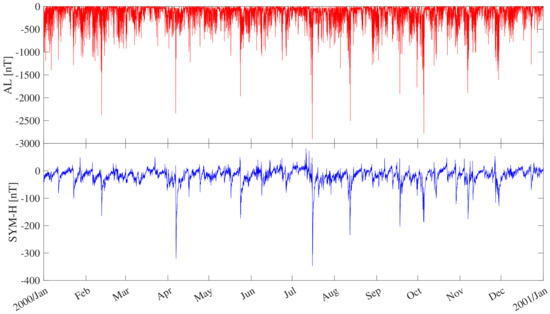
Figure 1.
Time series of the high latitude geomagnetic index AL (upper panel) and low latitude geomagnetic index SYM-H (lower panel) from 1 January to 31 December 2000.
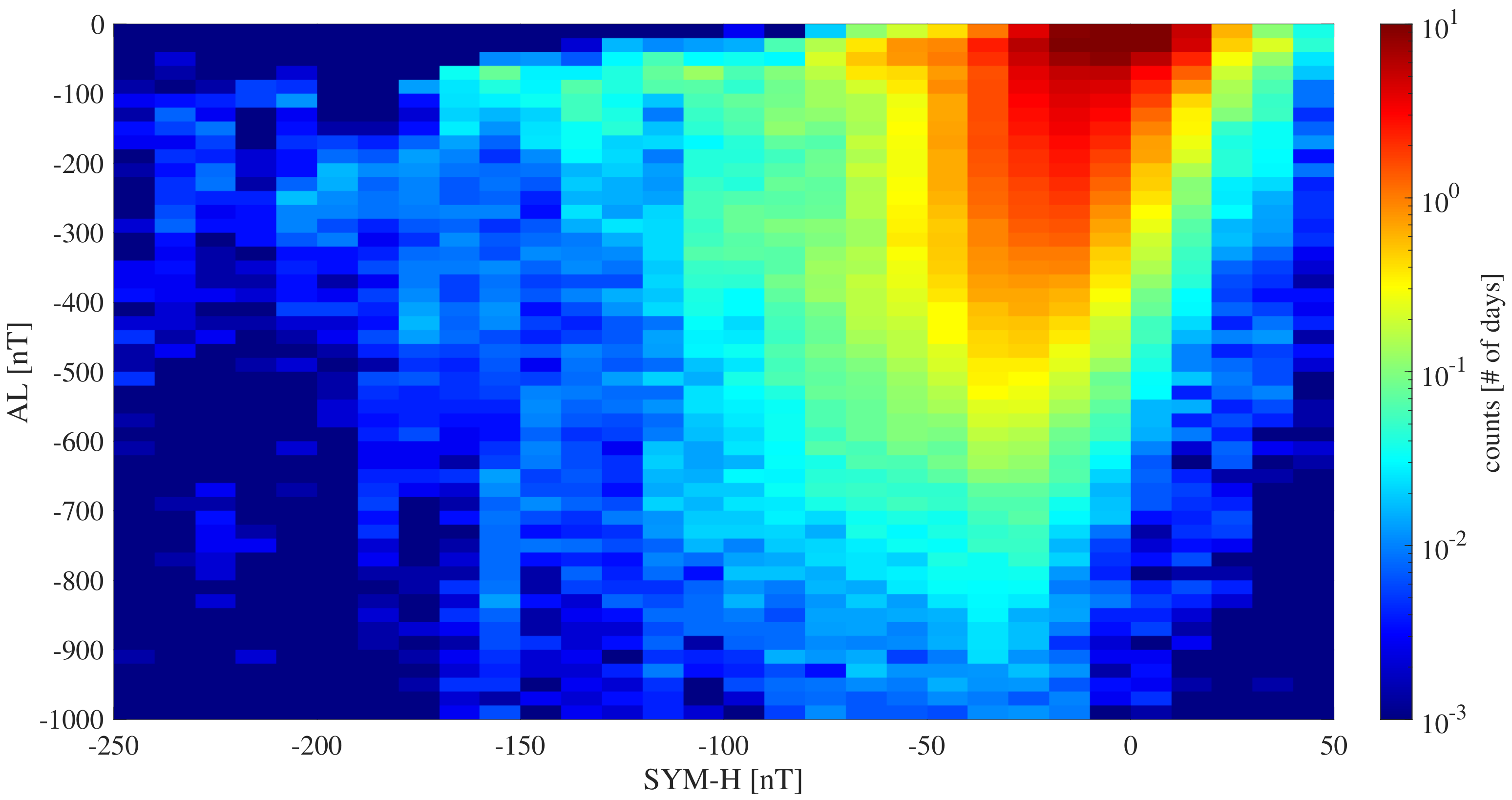
Figure 2 reports the joint distribution (in terms of frequencies of occurrences) of values of both SYM-H and AL geomagnetic indices. It is easy to note that, although different combinations of values exist in our data, they are not all equally likely. Indeed, it is clear that the most probable pairs of values fall in the range nT, with less probable ones at more negative values, usually associated with the occurrence of geomagnetic storms and magnetospheric substorms [26,27]. Notably, despite the fact that large negative values of both indices typically co-occur in time, there is no simple (linear or even nonlinear) statistical relationship between the two applying independent of time or the overall state of the near-Earth eletromagnetic environment as a whole.
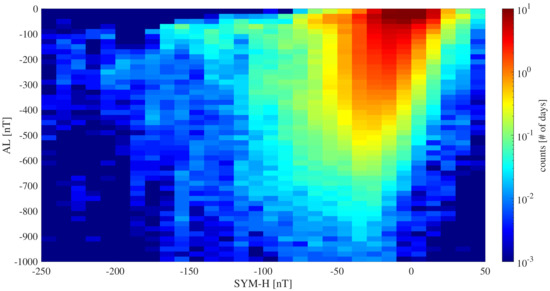
Figure 2.
Joint probability density (frequencies of occurrences) of values of the SYM-H and AL geomagnetic indices.
3. Methods
3.1. Time Delay Embedding
Since our two observables of interest are expressed by univariate geomagnetic index time series that cannot fully capture the dynamical complexity of the complete phase space, additional unobserved components first need to be qualitatively reconstructed from the available data. For this purpose, we utilize the time delay embedding procedure originally proposed by Takens [28], which is an established and widely used concept in nonlinear time series analysis with a solid and well developed theoretical mathematical foundation [28,29,30,31]. Given a univariate time series with , we replace each single value with a multivariate pattern of m values describing distinct multivariate phase space points (state vectors) whose components consist of original observations that are mutually separated by a time delay . Hence, this time delay embedding procedure generates a multivariate time series in which each individual state vector represents both the present value of the univariate observable of interest at time t and the dynamical evolution of the system culminating in the associated observation.
The specific phase space reconstruction obtained by the time delay embedding procedure depends ultimately on the choice of two parameters: The embedding delay and the embedding dimension m. In general, the choice of should be guided by the need for statistically sufficiently independent components (to avoid redundant information stored in the individual components of each state vector). Once a proper value of has been fixed, the embedding dimension m should be taken sufficiently large to fully unfold the phase space geometry represented by the univariate observations while still remaining small enough to let the multivariate state vectors provide a sufficient coverage of the reconstructed phase space. For the purpose of our present work, we select both and m by using two standard approaches that have been widely used in the scientific literature, which are detailed in the following. In both cases, we consider all data points and do not filter for specific values of the studied geomagnetic indices, i.e., we do not exclude any particular space weather events (or periods with an absence of associated geomagnetic perturbations) from our analysis.
The embedding delay is chosen based on the auto-mutual information function [32] of the original univariate time series , which is defined as
where is the joint probability of observing a pair of values of the univariate observable x at a mutual time lag of , i.e., the probability that and simultaneously , and is the probability distribution of the observable x [33]. Since the time series of both geomagnetic indices have been sampled at a finite resolution resulting in T = 527,040 data points, we estimate here the joint and marginal probability distributions via a non-parametric procedure known as kernel density estimation [34]. This approach allows us to reduce data sampling effects and to smooth the distribution via a suitable kernel function. Specifically, we use the Epanechnikov kernel, which is optimal in a mean squared error sense [35].
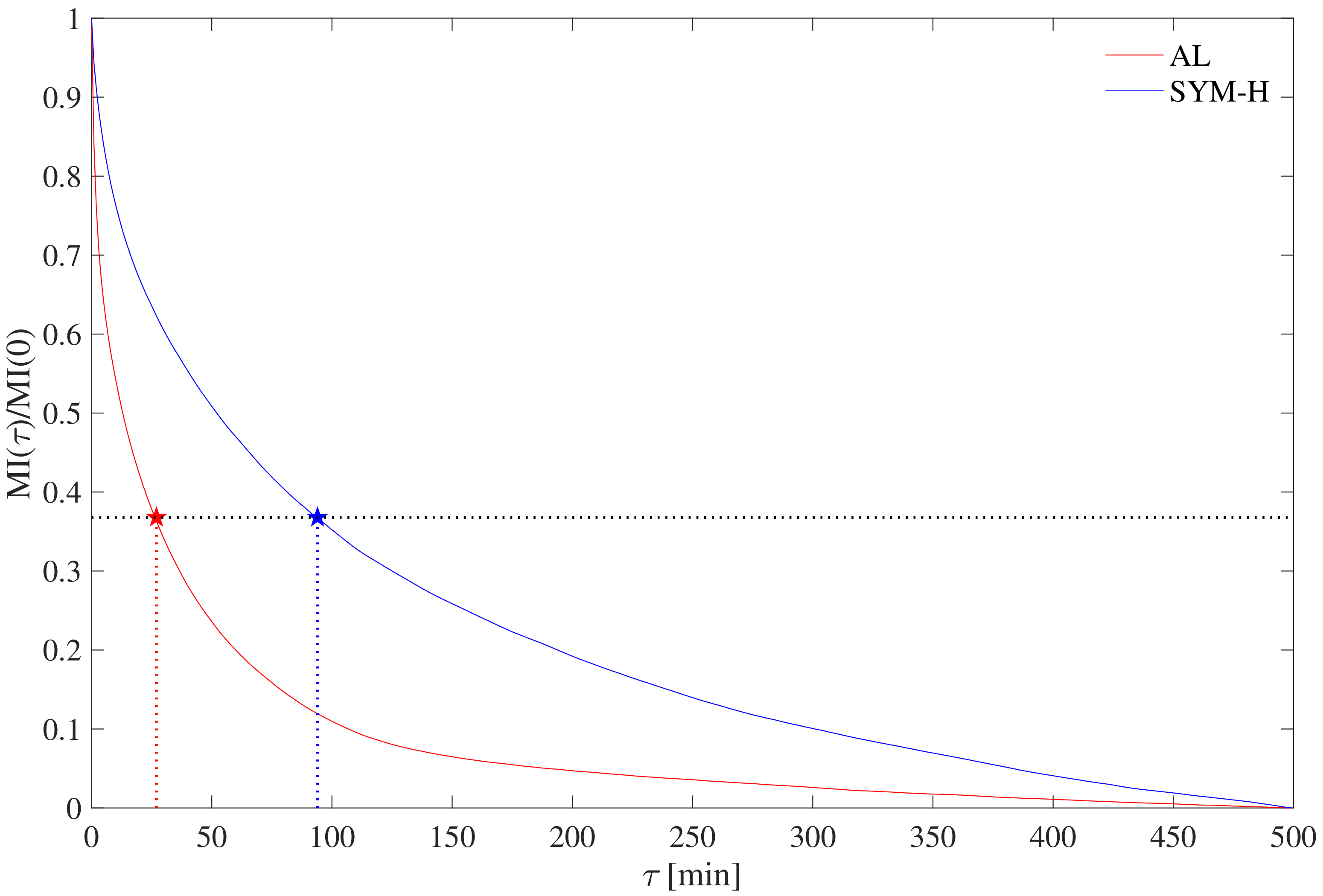
Taking the auto-mutual information function estimated from each time series, we select the embedding delay equal to the value of at which falls for the first time below , i.e., the time lag at which the auto-mutual information function has decayed by a factor of with respect to its initial value at (which corresponds to the Shannon entropy of the signal under study) [36]. As shown in Figure 3, the resulting embedding delays are min for AL and min for SYM-H, respectively, in agreement with previous results [36,37]. We note that the exact values of are typically less relevant for a successful application of time delay embedding, as long as the aforementioned requirement of sufficiently independent components is met. Indeed, we have checked that moderate variations of do not change the results reported below qualitatively (not shown).
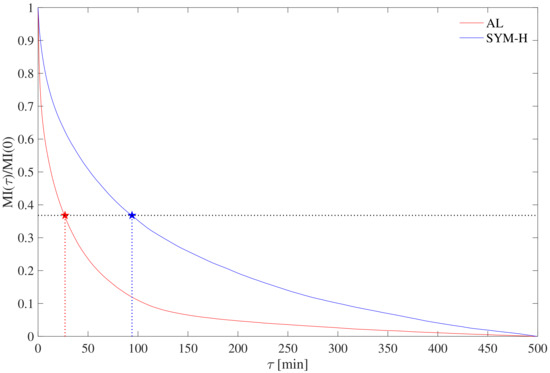
Figure 3.
Normalized auto-mutual information functions for AL (red) and SYM-H (blue), respectively. The stars represent the chosen embedding delays as those values at which , the latter reported by the horizontal dotted line. The two dotted vertical lines from the star symbols visually highlight the choices of .
The embedding dimension m is determined by using the false nearest neighbor (FNN) method [38,39]. Given the correspondence between the univariate time series values and the multivariate state vectors , we have to determine the necessary dimension to completely unfold the univariate time series in the reconstructed phase space. The FNN method examines the nearest neighbors of all state vectors as a function of the embedding dimension m to find the minimum embedding dimension at which most of the nearest neighbors do not move apart significantly if the embedding dimension is increased to , which indicates the absence of projection effects in the lower () dimensional representation of the time series. Specifically, we consider each m-dimensional state vector and determine its nearest neighbor . Then, we compute the spatial distance between both state vectors in the m-dimensional embedding and, by appending another delay component to each state vector, in an -dimensional phase space, and compute the ratio between both as
If exceeds a threshold , this state vector is considered to be associated with a false nearest neighbor in the lower dimensional embedding [39]. By performing this analysis for each state vector, we find the number of false nearest neighbors associated with each embedding dimension m, and select the value of m at which this fraction gets sufficiently close to zero as the desired embedding dimension to be employed in our subsequent analysis.
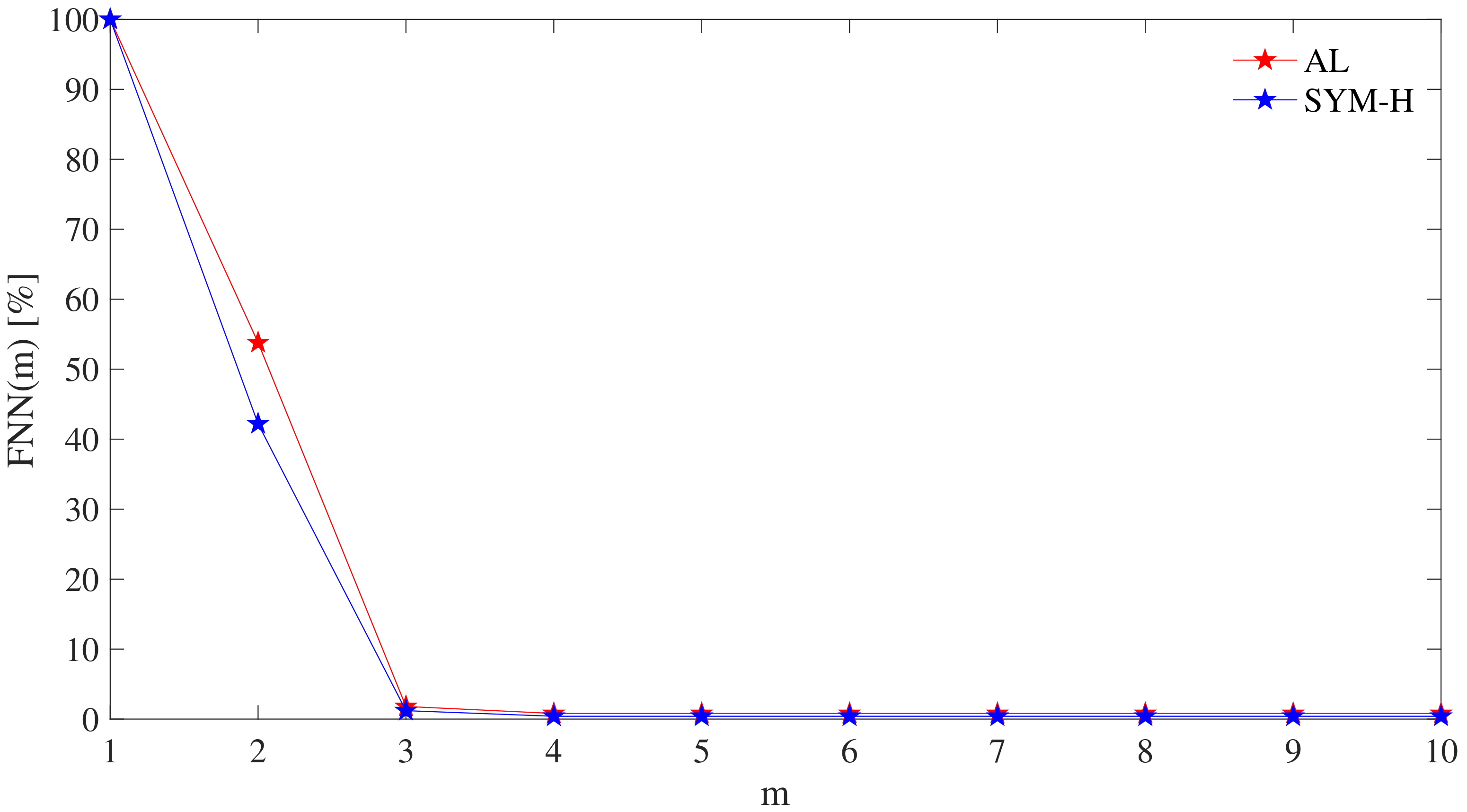
For the two geomagnetic indices studied in this work, Figure 4 displays the fraction of false nearest neighbors as a function of the embedding dimension m. Our results indicate an embedding dimension of 3 as an appropriate choice for both AL and SYM-H. The corresponding result is qualitatively independent of the particular choice of the distance measure applied (e.g., Euclidean or maximum norm, not shown).
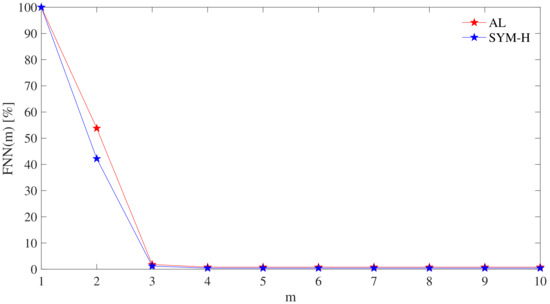
Figure 4.
Percentage of false nearest neighbors as a function of the embedding dimension m.
3.2. Dynamical System Metrics for Univariate Time Series
Characterizing the dynamical features of nonlinear and nonstationary time series is one of the most intensively studied contemporary problems in nonlinear sciences. In the recent past, several techniques based on dynamical system theory have been developed to track the dynamics of, e.g., atmospheric blocking regimes and jets [40,41] via a set instantaneous indicators that track rarity, predictability and persistence of atmospheric jet states and circulation patterns. These instantaneous properties are determined by two quantities: The instantaneous dimension and stability of the state vector being considered. The concept of instantaneous dimension is intuitive: For a given geomagnetic configuration represented by an associated state vector, the instantaneous dimension characterizes the geometric alignment of similar configurations in the reconstructed phase space. Thereby, this property can be related to both the active number of degrees of freedom and the predictability of nearby trajectories. The stability of the state is measured by , defined as the inverse of the average persistence time of trajectories around . If is a fixed point of the dynamics, . For a trajectory that leaves the neighborhood of instantaneously, . In general, the more persistent the configuration , the longer the previous and subsequent states of the system will resemble (i.e., low values of indicate high instantaneous stability).
Mathematically, let be an arbitrary state of interest, i.e., an m-dimensional vector characterized by the components of the multivariate time series at a certain time instant in the reconstructed phase space obtained by time delay embedding as discussed above, and
the logarithmic return. That is, the logarithmic return is defined as the negative logarithmic Euclidean distance in the reconstructed phase space between each point on the trajectory , i.e., each m-dimensional vector characterized by the values at any time instant of , and the considered reference state . To simplify the notation, we omit the time dependence of the logarithmic return in the following. For any given configuration observed at an arbitrary time , we consider the probability that at a different time instant the system has evolved into a state that is located within a ball of radius centered at the point in the reconstructed phase space. If we define to be the q–th empirical percentile of , we can consider neighborhoods in the reconstructed phase space for each state with a radius according to this percentile, so that all these neighborhoods are encountered with the same probability of .
Next, we let denote the exceedances above the selected empirical quantile. In this case, the Freitas–Freitas–Todd theorem [42] modified by Lucarini et al. [43] states that the cumulative distribution of these exceedances converges to the exponential member of the Generalized Pareto family
The two parameters and of this empirical distribution, which are specific to each given reference state and can be estimated using maximum likelihood methods, are formally related to the two dynamical system metrics and D via the relations
3.3. Dynamical System Metrics for Bivariate Time Series
The two relations given in Equation (5) allow us to retain information on a given system in a univariate framework. This means that they permit us to describe the phase space of the system by means of a single multivariate trajectory related to a single variable x (or a single set of variables, represented in our case by the time shifted replications of our geomagnetic index values). This formalism can be extended to the bivariate case by considering two trajectories in the reconstructed phase space, namely and . We can consider the phase space jointly spanned by the state vectors and and define their associated reference state as . The joint logarithmic return of and at the same time t can be now defined as
We need to remark that, since we are considering variables with different ranges (i.e., nT and nT), both geomagnetic indices are first made quantitatively comparable by subtracting their mean and then dividing by their respective standard deviations. This is the standard procedure also used in Faranda et al. [44] to avoid that distances in the subspace representing the variable with the larger spread would dominate the joint returns and, hence, the dynamical system metrics estimated therefrom.
As for the univariate case, based on Equation (6) we compute the co-dimension between the two univariate observables x and y [44]. This means that we are investigating the mutual dependence of x and y in terms of their joint recurrences in the reconstructed phase space, i.e., we are requiring that a given reference state is simultaneously observed in both variables. For this reason, the following relation holds:
meaning that x and y are decoupled when , while they are linked via a deterministic function (i.e., exhibit generalized synchronization) when . As for D, the bivariate persistence can be defined as a weighted average of and [44,45].
Different from the univariate case, an additional new dynamical system metric can be defined in the bivariate case, i.e., the so-called co-recurrence ratio
with being the number of events satisfying the condition . This means that we are computing the ratio between the number of states for which resembles the reference state , given that resembles the reference state , and the number of states when resembles irrespective of . In other words, when then there are no co-recurrences of when we observe ; when then all the co-recurrences of correspond to recurrences of . As noted in Faranda et al. [44], cannot be interpreted in terms of causation but only as mutual relation.
The dynamical system metrics based on extreme value theory as described above have been extensively used in recent years within a broad range of applications [40,41,43,44,46]. These publications have demonstrated that the local dimension and stability metrics provide useful information on the dynamics of a given system: While D is related to the geometry of states in a certain region of the phase space, i.e., informs about the mutual similarity of states, provides us with a measure of the persistence in a specific region, i.e., how long the system can be expected to stay within a certain region of the phase space. Thus, D is connected with the number of active degrees of freedom, i.e., how many variables are needed to describe the dynamics within the different regions, while is related to the predictability horizon of a certain region, i.e., contributing to the question how well we are able to anticipate which state will be approached at the time given that we are in the state at the time t. This means that estimating the dynamical system metrics means retrieving information on the predictability of the system (an explicit connection is provided in Faranda and Vaienti [47]). Numerical codes to evaluate the dynamical system metrics can be found at https://it.mathworks.com/matlabcentral/fileexchange/95768-attractor-local-dimension-and-local-persistence-computation (Matlab version, accessed on 12 January 2022), https://github.com/yrobink/CDSK (Python version, accessed on 12 January 2022), and https://github.com/thaos/dtheta (R version, accessed on 12 January 2022).
For the sake of clarity, we define and as the univariate metrics (i.e., the dynamical systems metrics derived from the univariate time series), while we define as the metrics derived from the bivariate time series consisting of both geomagnetic indices. For all our computations, we fix as quantile threshold, a proper choice for our measurements consisting of T = 527,040 data points. Furthermore, we iterate our procedure by using all points in the reconstructed phase space, thus making a direct connection between the reference state and the values of both indices at the time instance t.
4. Results
4.1. Instantaneous Dimensions
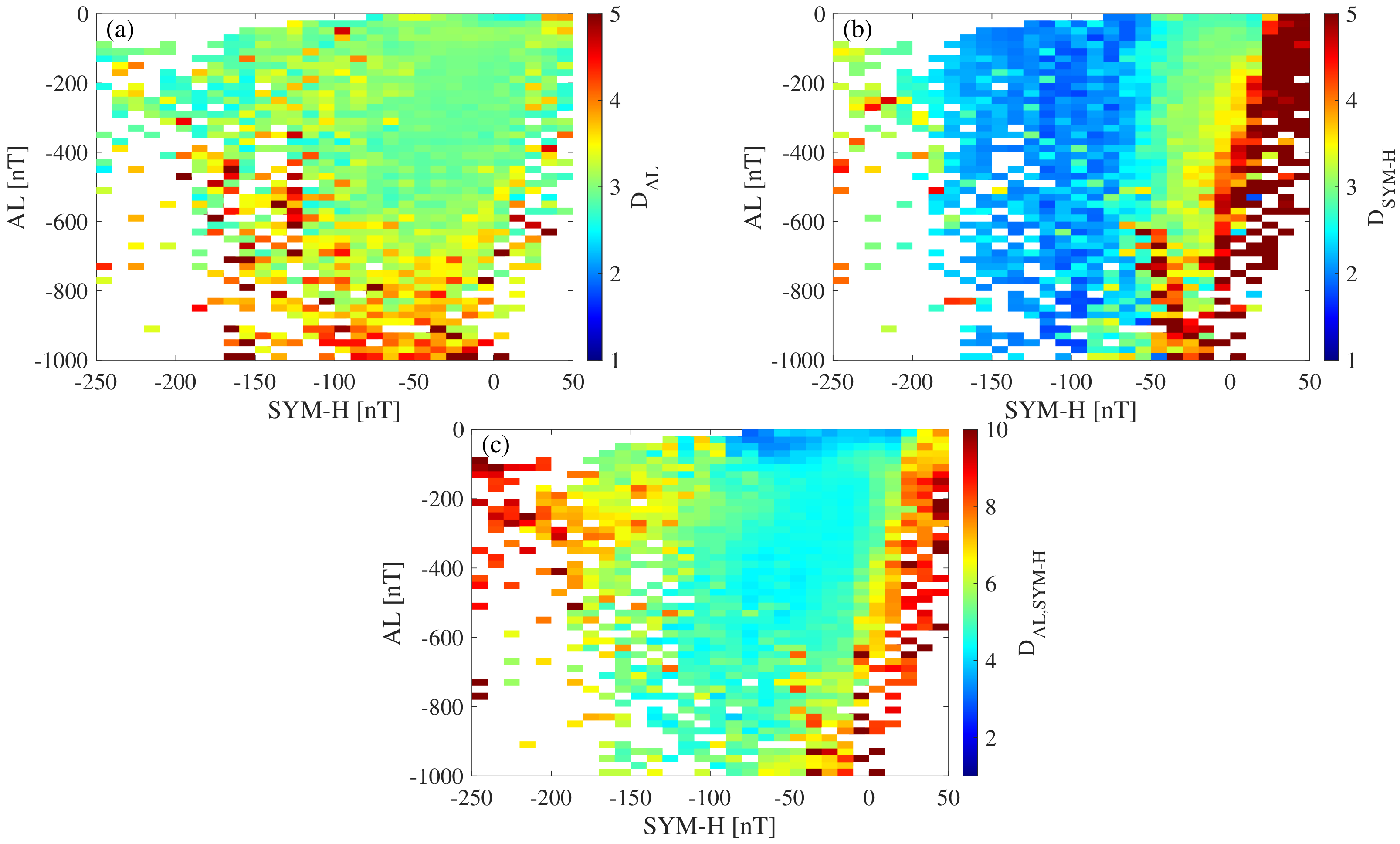
Figure 5 reports the instantaneous dimensions D as a function of the values of both geomagnetic indices, respectively. The values of D have been grouped into equidistant bins of size nT in the range nT and nT. The number of data points in each bin varies between 1420 (∼1 day) and 96882 (∼67 days). Panels (a) and (b) refer to the univariate time series of the two individual indices, while panel (c) corresponds to the bivariate time series comprising both indices.
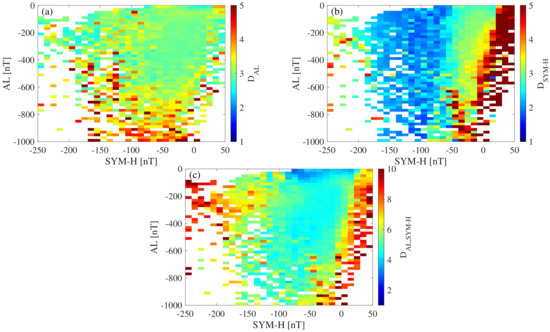
Figure 5.
Instantaneous dimension D as a function of the values of both geomagnetic indices. Panels (a,b) refer to the univariate time series, while panel (c) corresponds to the bivariate one.
When independently considered, the instantaneous dimensions and clearly show different behaviors depending on the values of both indices.
As the magnetospheric substorm activity increases ( nT) tends to increase up to values around 4, independent of SYM-H. This means that the active number of degrees of freedom exceeds the dimension of the phase space (i.e., the embedding dimension ), thus suggesting the existence of an external component driving the intrinsic dynamics of the AL index. During quiet or low auroral activity ( nT) mostly fluctuates around 3. These findings suggest that the dynamics of the westward auroral electroject, as monitored via the AL index, is composed by processes of both internal and external origin. The internal (intrinsic) dynamics is characterized by stochastic fluctuations around a possible fixed point (), unless a strong (external) driving mechanism operates. These features can be related to the dynamics of the Earth’s magnetotail, mostly contributing to the intrinsic dynamics, also describing the internal response to the external solar wind driving effect [6]. Thus, the high latitude variability can be described in terms of a continuously perturbed stochastic system around a non-equilibrium critical point, displaying spatiotemporal coherent features resulting from the solar wind transferring energy to the magnetotail [22].
At low latitudes, decreases as SYM-H decreases, independent of the values of the AL index. Interestingly, larger values are found for positive values of SYM-H, typically related to the so-called Sudden Storm Commencement (SSC) and the initial phase of a geomagnetic storm. These phases of the development of a geomagnetic storm are related to the increase in solar wind dynamic pressure producing an increase of the H component of the geomagnetic field towards positive values. Thus, the excess of the active number of degrees of freedom () during the early stages of a geomagnetic storm seems to be again related to an external driving mechanism due to the solar wind. However, it is remarkable that AL modulates this effect. Indeed, when strongly negative AL values are present (i.e., during magnetospheric substorms), this excess dimension () is also observed for moderately negative SYM-H values—this could indicate a successive coupling between high and low latitudes, i.e., between magnetospheric substorms/high latitude processes and geomagnetic storms/low latitude ones. This behavior seems to be congruent with results based on information theory measures (e.g., [17,21]). By contrast, in the absence of high latitude disruptions ( nT), we instead find an excess dimension of SYM-H only when the index values are strictly positive. Conversely, is usually observed during intermediate levels of geomagnetic activity, likely related to the recovery phase of a geomagnetic storm, suggesting an organized dynamics of processes leading to the recovery of the magnetospheric ring current towards the quiet time level. As for the high latitude variability, the low latitude one is composed by an intrinsic dynamics, related to the equatorial ring current activities, typically stochastically fluctuating around a mean value, and external driving mechanisms. However, the latter are related to both the solar wind activity, during the early stages of a geomagnetic storm, and high latitude processes, mainly due to the outflow of high latitude oxygen ions (O) of ionospheric origin towards the magnetospheric ring current related to the activation of field aligned currents [19].
Taken together, the results of our univariate analysis suggest that the number of active degrees of freedom depends on the level of geomagnetic activity as exploited in terms of magnetospheric substorms and geomagnetic storms, although in a completely different way. The results for SYM-H are qualitatively consistent with previous findings based on so-called recurrence networks, whose transitivity property for SYM-H [37] as well as the conceptually related, yet temporally lower resolution disturbance storm time index (Dst) [36], has been found to rise during magnetic storm periods, thereby indicating a lower dimensional dynamics.
In order to further explore the possible interdependence between AL and SYM-H Figure 5c reports the behavior of the instantaneous co-dimension for the bivariate time series analysis. The observed pattern, as a function of AL and SYM-H values, is a mix of those observed for the individual components’ dimensions, although with a clear difference. takes larger values during the initial and the main phase of a storm, while it reduces to values between 4 and 5 during the recovery phase irrespective of the particular high latitude conditions reflected by AL. Furthermore, during strong depressions of the H component of the geomagnetic field (i.e., nT) , while for moderate depressions (i.e., nT) . These findings will be further discussed in Section 4.4 for a selected geomagnetic storm.
As opposed to the dependence on the SYM-H values, the actual AL conditions play only a marginal role for the co-dimension . The most notable effect takes place for weakly negative SYM-H and AL values close to zero, in which case the co-dimension is reduced to values of about 3–4, i.e., of the order of the individual subsystems’ dimensions, thereby suggesting the existence of a (deterministic) transfer function between both indices in the absence of magnetospheric perturbations, a phenomenon known as generalized synchronization in complex system theory that is often observed in the presence of strongly coupled nonlinear systems. Physically, this can be interpreted as the result of high to low latitude coupling mechanisms acting during quiet periods, thus pointing towards a possible co-variability of the different current systems within the near-Earth electromagnetic environment as a result of a closure of the electric circuit [48]. This seems to point also towards recent findings of low energy (few tens of electron volts) field aligned ionospheric ions flowing out during quiet periods, being a major source of heavy ions for the plasma sheet and lobe [49]. Conversely, the observation that the coupling is stronger during the initial phase (development) of a geomagnetic storm (with the injection of ionospheric oxygen ions into the outer edge of the magnetospheric ring current) points toward a net transfer of variability from the high latitude ionosphere to the low latitude magnetosphere [17,19,21].
4.2. Instantaneous Stability
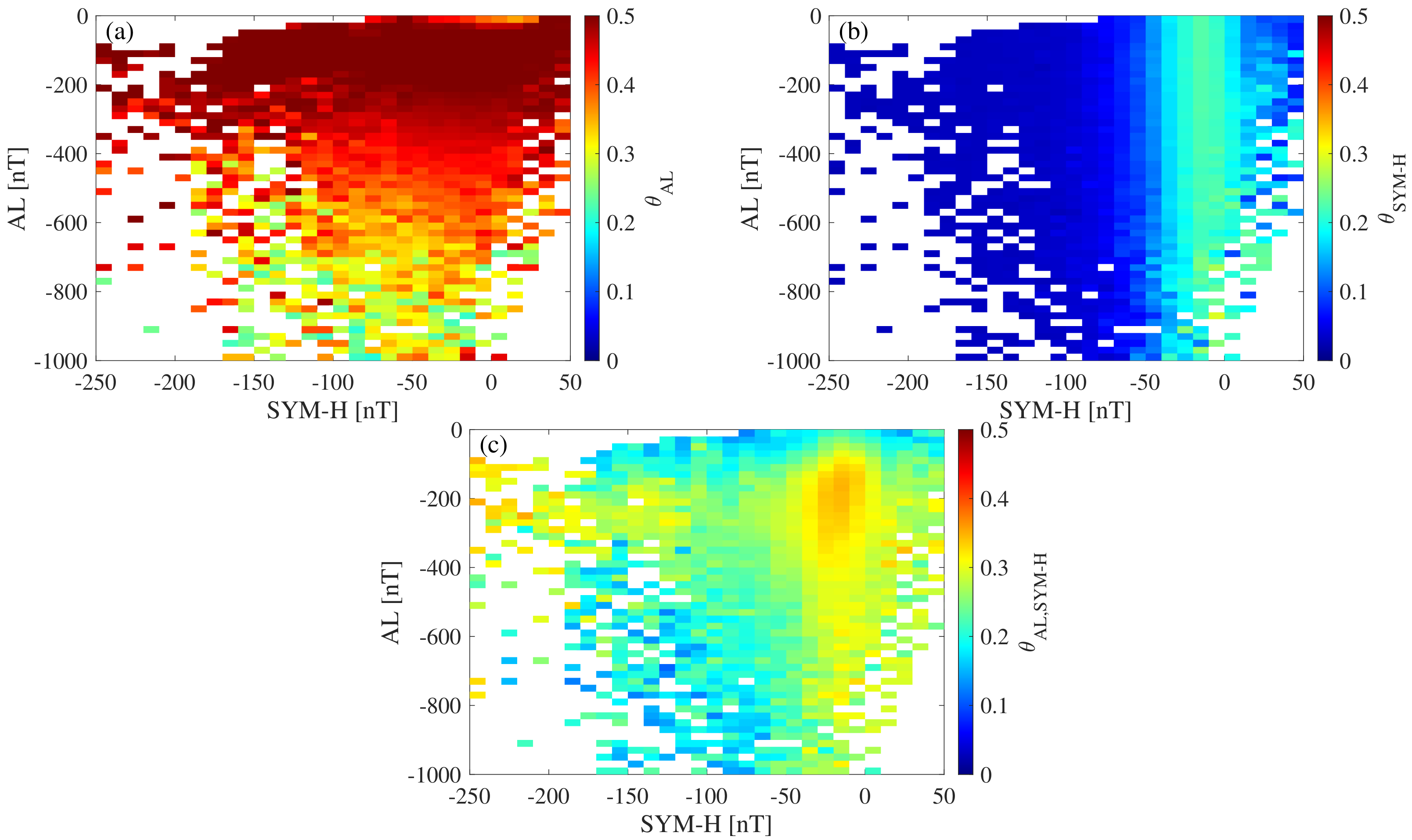
Similar considerations as for the instantaneous dimensions can also be drawn for the instantaneous stability as a function of the values of both geomagnetic indices (see Figure 6). An increased persistence of fluctuations (small ) is observed for AL and SYM-H when the magnetospheric substorm and the geomagnetic storm activity increase, respectively. Indeed, lower values of (indicating more stable conditions) are found in close correspondence with geomagnetically disturbed periods. However, a clear difference emerges in terms of values: While , , thus suggesting an increasingly persistent nature of fluctuations. This behavior can be related to the role of solar wind fluctuations during a geomagnetic storm, making the temporal variability of the SYM-H index more persistent especially during the main and the recovery phases of the storm [46,50,51,52,53]. This can be also associated with a smoother multifractal behavior pointing towards a reduction of stochasticity together with an increase in predictability of the system [40,41]. By further investigating the joint dynamical features of both geomagnetic indices (Figure 6c) we clearly demonstrate that the lower the geomagnetic activity (close to zero values of both SYM-H and AL), the more stochastic the nature of fluctuations (elevated ). As the geomagnetic activity increases, due to either a geomagnetic storm or magnetospheric substorm activity, the persistence of fluctuations increases as well, making the system dynamics more predictable. Thus, our findings suggest that the solar wind driving effect suppresses the stochastic nature of the geomagnetic activity, increasing the predictability of the system during the early phases of a geomagnetic storm, although introducing additional degrees of freedom. By contrast, the recovery phase seems to be mostly related to intrinsic mechanisms, restoring the stochastic near out of equilibrium nature of the magnetosphere–ionosphere system [6].
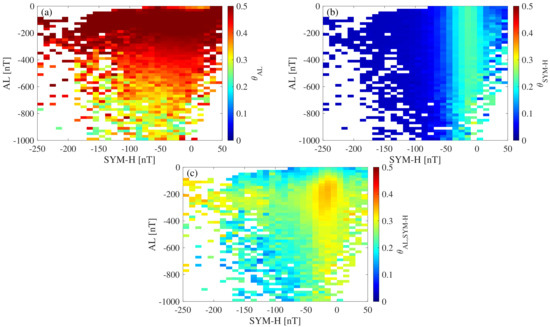
Figure 6.
Instantaneous stability as a function of the values of both geomagnetic indices. Panels (a,b) refer to the individual time series, while panel (c) corresponds to the joint observations. The color map is saturated above 0.5 for visualization purposes.
4.3. Differences between Quiet and Storm Time Conditions
To further analyze possible differences between quiet and storm time conditions in a more systematic manner, we construct the histograms of values of D and for different geomagnetic activity levels. Specifically, we distinguish three different conditions:
- 1.
- Group I: nT;
- 2.
- Group II: nT;
- 3.
- Group III: nT.
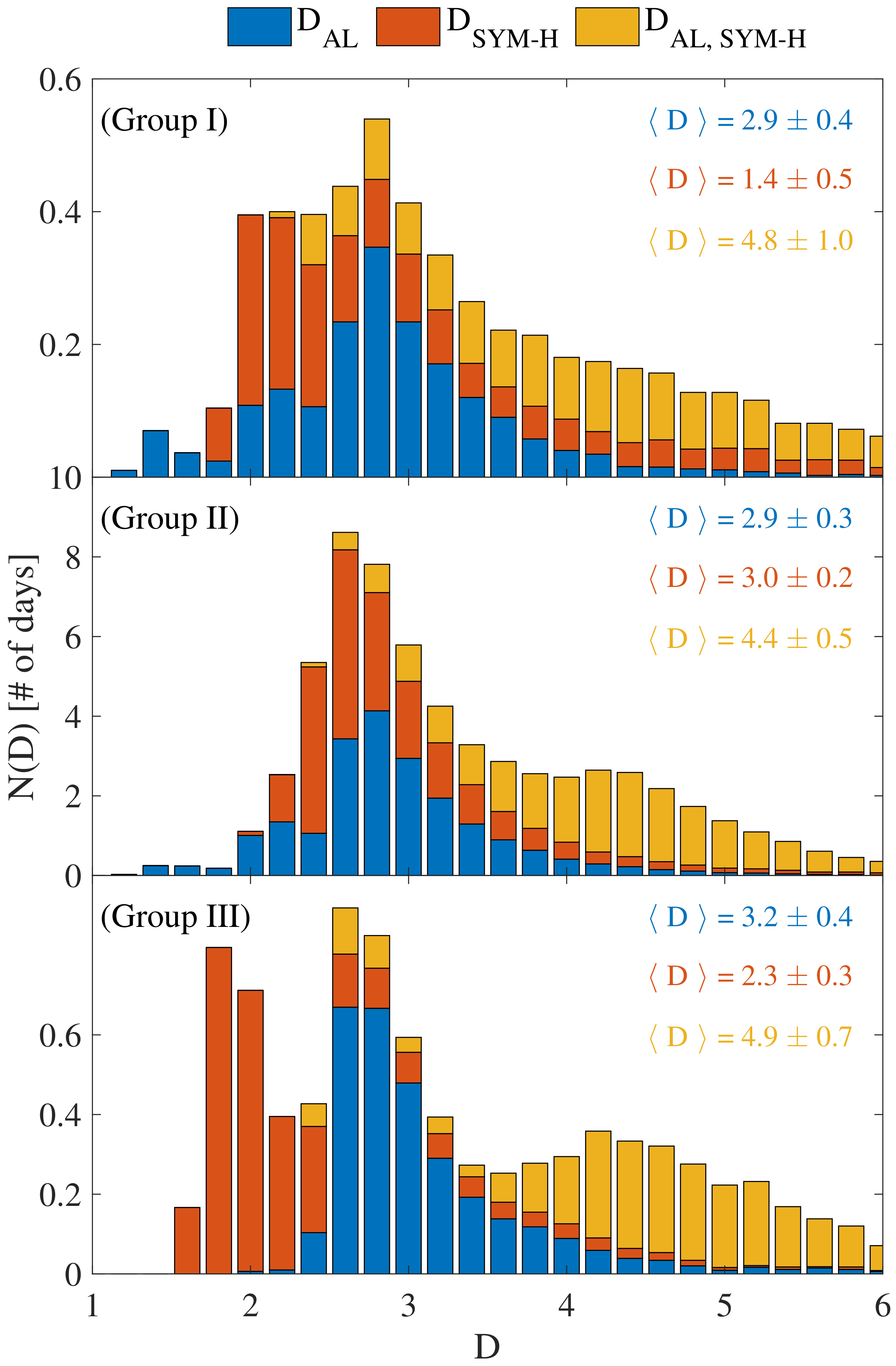
Figure 7 reports the histograms of the instantaneous dimensions D for the three different geomagnetic activity levels. We find no significant dependence of the average values of on the geomagnetic activity level, with , although lower values of the order of are sporadically found during the initial phase of geomagnetic storms and quiet time intervals (i.e., nT). On the other hand, the average values of decrease as the geomagnetic activity level increases, being larger than 3 during the initial phase of geomagnetic storms and quiet periods (Groups I–II), while close to 2 during geomagnetic storms (Group III). This is a clear reflection of the externally driven mechanisms due to the solar wind structure hitting the Earth’s magnetopause during a geomagnetic storm, thus reducing the active number of degrees of freedom and producing an overall self-organization of the magnetospheric dynamics during disturbed periods. A different behavior is observed when both indices are jointly investigated, with being lower during quiet periods than during geomagnetic storms. This appears to be consistent with the common view according to which intense geomagnetic storms are associated with a collection of multiple magnetospheric substorms [17,18,19,20,21]. The increased number of degrees of freedom during the initial phases of a geomagnetic storm could be related to the injection of ionospheric oxygen ions into the outer edge of the magnetospheric ring current [19], thus acting as a driving mechanism for geomagnetic storms.
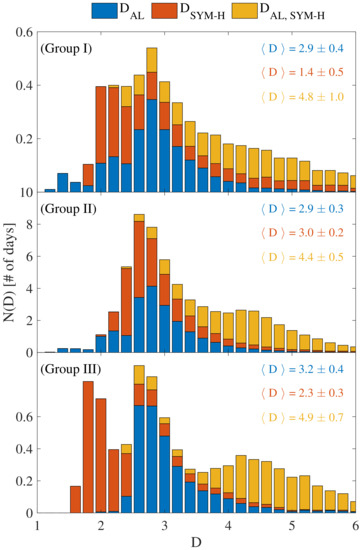
Figure 7.
Histograms of the instantaneous dimensions D as a function of the different geomagnetic activity levels: Group I ( nT), Group II ( nT), Group III ( nT). Blue, orange, and yellow bars refer to , , and , respectively. The average values and their uncertainties are reported in each panel for each D. The values of D have been grouped into equidistant bins of size .
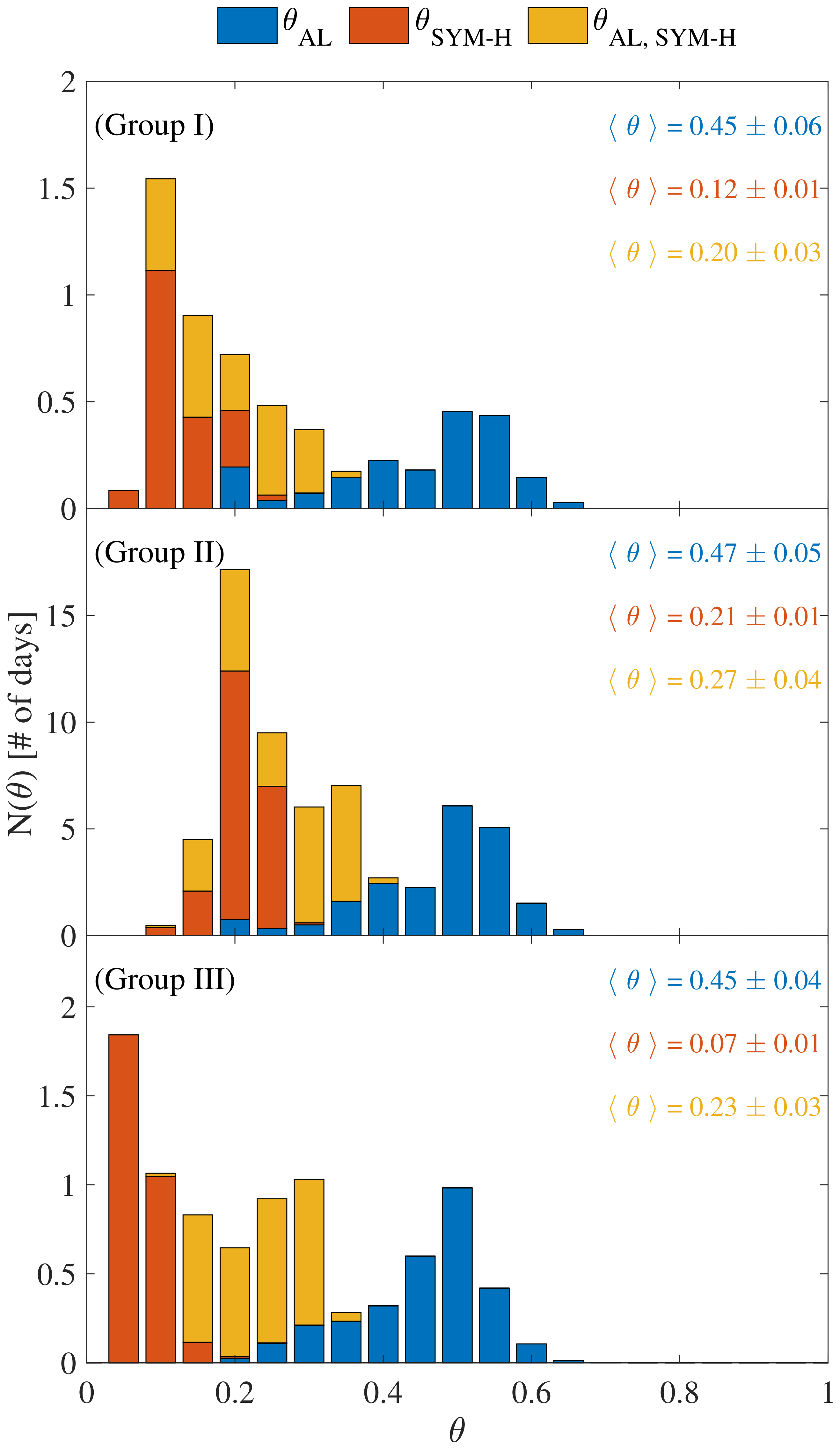
By looking at the histograms of the instantaneous stability (see Figure 8) we can draw similar conclusions. Indeed, while the average values of are almost independent of the geomagnetic activity level, decreases with the geomagnetic activity level. This can be again interpreted as an increasingly persistent nature of fluctuations, reflecting an increased self-organization of the overall magnetospheric activity during geomagnetic storms. This also suggests that the SYM-H index dynamics is characterized by an increased predictability during geomagnetic storms. This finding matches earlier observations [15] on the increase of the forecast horizon during a disturbed period, with a more chaotic nature of fluctuations during quiet periods [37]. Our findings support the theory that the near-Earth electromagnetic environment is a complex system far from an equilibrium.
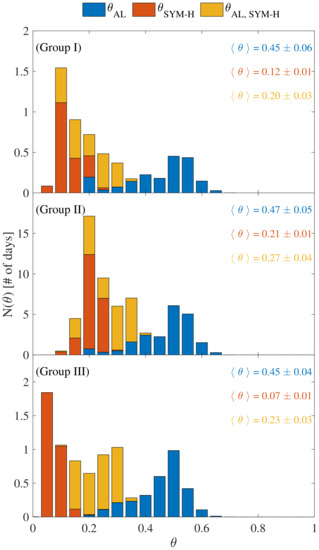
Figure 8.
Histograms of the instantaneous stability as a function of the different geomagnetic activity levels: Group I ( nT), Group II ( nT), Group III ( nT). Blue, orange, and yellow bars refer to , , and , respectively. The average values and their uncertainties are reported in each panel for each . The values of have been grouped into equidistant bins of size .
4.4. Case Study: The Bastille Day Geomagnetic Storm
To further explore the concurrent effects and to disentangle them during the different phases of a geomagnetic storm, we select a specific period from our data set corresponding to the Bastille Day geomagnetic storm. Figure 9 reports the behavior of the co-dimension (upper panel), the co-persistence (middle panel), and the co-recurrence ratio during the selected event, together with the temporal behavior of the AL index. An increase in the co-dimension and in the co-recurrence ratio is evident during the initial and the main phase of the geomagnetic storm, thus suggesting that configurations with higher dimensions typically favor a stronger coupling between high and low latitude magnetospheric fluctuations. This can be linked to the outflow of oxygen ions from the high latitude ionosphere to the low latitude equatorial plasma sheet during the initial and the main phases of the geomagnetic storm, increasing the dimensionality of the global system. This is observed not only during the Bastille Day geomagnetic storm but also during the moderate geomagnetic activity period on 20 July, where an increase of is found in close correspondence to the initial and main phase of SYM-H shifting towards negative values. These findings suggest that there is a non-negligible contribution to the observed variability coming from the internal dynamics of the magnetosphere–ionosphere system as a result of a complex interplay between processes and phenomena of internal origin activated by the triggering of external source processes. In the classical scenario of storm–substorm relations this could be explained via the outflow of high latitude oxygen ions (O) of ionospheric origin towards the magnetospheric ring current related to the activation of field-aligned currents [19]. This further supports the view that geomagnetic storms, although mainly driven by solar wind changes, can also be understood as a collection of substorms [1,18], with the storm time ring current being mainly of terrestrial origin [17,19,21].
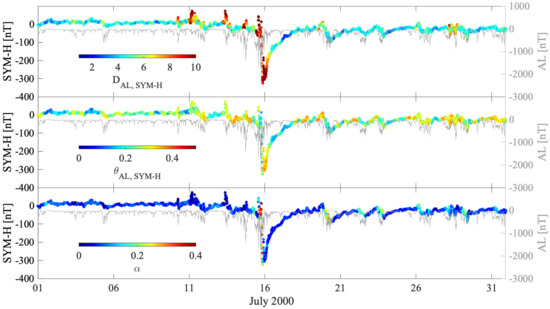
Figure 9.
Behavior of the co-dimension (upper panel), the co-persistence (middle panel), and the co-recurrence ratio during the Bastille Day geomagnetic storm across the SYM-H index. The time behavior of the AL index is reported in gray for comparison.
5. Discussion and Conclusions
This study provides a first attempt to jointly characterize the instantaneous nonlinear dynamical properties of two different geomagnetic indices by using some recently introduced methods of dynamical system theory [40,41]. In particular, we study the co-variation and recurrence statistics of the AL and SYM-H indices. One of the most significant findings emerging from this study is that the number of active degrees of freedom, required to describe the phase space dynamics of both indices, depends on the geomagnetic activity level. In addition, a completely different behavior is observed for high versus low latitude processes.
The univariate time series analysis has shown that when the magnetospheric substorm activity increases ( nT), the active number of degrees of freedom at high latitudes increases clearly above the topological dimension of the considered reconstructed phase space. Conversely, a reduced number of degrees of freedom is observed during a geomagnetic storm at low latitudes. While the latter is the counterpart of a strong driving effect from externally driven fluctuations [13,46], the former is related to fast relaxation processes occurring in the magnetotail as intermittent coherent bursts mainly due to internal magnetospheric conditions [22]. Thus, both the high and the low latitude variability can be described in terms of a continuously perturbed stochastic system fluctuating around a non-equilibrium critical point, displaying spatiotemporal coherent features. The main difference between high and low latitude dynamics is related to the external-driving mechanisms. While the auroral activity is externally driven by the solar wind only, the enhancements of the equatorial ring current during disturbed periods are related to both the solar wind activity, during the early stages of a geomagnetic storm, and high latitude processes, mainly due to the outflow of high latitude oxygen ions (O) of ionospheric origin towards the magnetospheric ring current related to the activation of field aligned currents [19].
The bivariate time series analysis, offering us the opportunity of investigating time-dependent joint relations between both indices, has highlighted an increase of the co-dimension and the co-recurrence ratio during the initial and the main phase of a geomagnetic storm, thus suggesting that configurations with higher individual dimensions typically favor stronger coupling. Thus, a significant contribution to the observed variability comes from coupling mechanisms within the magnetosphere–ionosphere system. This could be the result of a complex interplay between processes and phenomena of internal origin activated by the triggering of external source processes [19,22]. Our findings suggest that the solar wind driving effect suppresses the stochastic nature of the geomagnetic activity, thereby increasing the predictability of the system during the early phases of a geomagnetic storm, although introducing additional degrees of freedom. By contrast, the recovery phase seems to be mostly related to intrinsic mechanisms, restoring the stochastic near out of equilibrium nature of the magnetosphere–ionosphere system [6].
The emerging scenario is that of an increased overall self-organization of the magnetospheric dynamics during disturbed periods due to the externally driven mechanisms of solar wind origin. For instance, during the initial phase of a geomagnetic storm or during the occurrence of intense storms the increase in the active number of degrees of freedom supports the view according to which magnetospheric substorms contribute substantially to geomagnetic storm development [17,18,19,20,21]. The increased number of degrees of freedom, in this case, could be related to the injection of ionospheric oxygen ions into the outer edge of the magnetospheric ring current [19], thus acting as a sort of driving mechanism for geomagnetic storms. Thus, our observations support the idea that the near-Earth electromagnetic environment is a complex system far from an equilibrium.
Our findings can be also reconciled in the space weather framework. Indeed, the dynamical features of the near-Earth geospace depend on the number of considered components. When the geospace environment is described using just a single geomagnetic index we can only access a reduced subspace of the full phase space spanned by multiple variables. Describing the geospace via the SYM-H index means to gain information on low latitude processes, while describing the geospace via the AL index means to retrieve information on the dynamics of the westward electroject. Taking into account both indices allows us to consider both high and low latitude processes and to gain more information on how the geospace conditions depend on different types of independent and coupled processes. This means that a deeper understanding of the role of geospace preconditioning and feedback is required to provide an accurate forecasting of space weather phenomena as well as an accurate estimation of space weather effects on infrastructure. This is only a preliminary step towards fully understanding the dynamics of the geospace environment. Further studies need to be carried out in order to validate the obtained results by analysing a wider set of geomagnetic indices (or even explicitly the ensemble of ground-based magnetometer recordings underlying the definition of these indices) and solar wind parameters, as well as various geomagnetic storms, and by investigating the role of the different scale-dependent components.
Author Contributions
Conceptualization, T.A. and G.C.; methodology, T.A., D.F. and R.V.D.; software, D.F.; formal analysis, T.A. and D.F.; investigation, T.A., G.C., P.D.M. and V.C.; data curation, P.D.M.; writing—original draft preparation, T.A.; writing—review and editing, D.F., G.C., P.D.M., R.V.D. and V.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data used in this study are freely available from the Kyoto World Data Center (WDC) for Geomagnetism at http://wdc.kugi.kyoto-u.ac.jp/ (accessed on 12 January 2022).
Acknowledgments
This work has benefit from discussions within the International Space Science Institute (ISSI) Team #455 “Complex Systems Perspectives Pertaining to the Research of the Near-Earth Electromagnetic Environment”.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CME | Coronal Mass Ejection |
| GNSS | Global Navigation Satellite Systems |
| HF | High Frequency |
| SEP | Solar Energetic proton |
| SMI | Solar wind-magnetosphere–ionosphere |
| SSC | Sudden Storm Commencement |
References
- Akasofu, S.I. A Review of Studies of Geomagnetic Storms and Auroral/Magnetospheric Substorms based on the Electric Current Approach. Front. Astron. Space Sci. 2021, 7, 100. [Google Scholar] [CrossRef]
- Borovsky, J.E. Perspective: Is Our Understanding of Solar-Wind/Magnetosphere Coupling Satisfactory? Front. Astron. Space Sci. 2021, 8, 5. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Sugiura, M.; Iyemori, T.; Goldstein, B.E.; Gonzalez, W.D.; Akasofu, S.I.; Smith, E.J. The nonlinear response of AE to the IMF BS driver: A spectral break at 5 h. Geophys. Res. Lett. 1990, 17, 279–282. [Google Scholar] [CrossRef]
- Vassiliadis, D.V.; Sharma, A.S.; Eastman, T.E.; Papadopoulos, K. Low-dimensional chaos in magnetospheric activity from AE time series. Geophys. Res. Lett. 1990, 17, 1841–1844. [Google Scholar] [CrossRef]
- Klimas, A.J.; Vassiliadis, D.; Baker, D.N.; Roberts, D.A. The organized nonlinear dynamics of the magnetosphere. J. Geophys. Res. 1996, 101, 13089–13114. [Google Scholar] [CrossRef]
- Consolini, G. Chapter 7—Emergence of Dynamical Complexity in the Earth’s Magnetosphere. In Machine Learning Techniques for Space Weather; Camporeale, E., Wing, S., Johnson, J.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 177–202. [Google Scholar] [CrossRef]
- Tsurutani, B.T.; Hajra, R.; Echer, E.; Gjerloev, J.W. Extremely intense (SML ≤-2500 nT) substorms: Isolated events that are externally triggered? Ann. Geophys. 2015, 33, 519–524. [Google Scholar] [CrossRef]
- Tozzi, R.; De Michelis, P.; Coco, I.; Giannattasio, F. A Preliminary Risk Assessment of Geomagnetically Induced Currents over the Italian Territory. Space Weather 2019, 17, 46–58. [Google Scholar] [CrossRef]
- Bothmer, V.; Daglis, I.A. Space Weather—Physics and Effects; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Temmer, M. Space weather: The solar perspective. Living Rev. Sol. Phys. 2021, 18, 4. [Google Scholar] [CrossRef]
- Foullon, C.; Malandraki, O. SpaceWeather of the Heliosphere: Processes and Forecasts. In IAU Symposium Proceedings; Cambridge University Press: Cambridge, UK, 2018; Volume 335. [Google Scholar] [CrossRef]
- Chandorkar, M.; Camporeale, E. Chapter 9—Probabilistic Forecasting of Geomagnetic Indices Using Gaussian Process Models. In Machine Learning Techniques for Space Weather; Camporeale, E., Wing, S., Johnson, J.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 237–258. [Google Scholar] [CrossRef]
- Alberti, T.; Consolini, G.; Lepreti, F.; Laurenza, M.; Vecchio, A.; Carbone, V. Timescale separation in the solar wind-magnetosphere coupling during St. Patrick’s Day storms in 2013 and 2015. J. Geophys. Res. (Space Phys.) 2017, 122, 4266–4283. [Google Scholar] [CrossRef]
- Manshour, P.; Balasis, G.; Consolini, G.; Papadimitriou, C.; Paluš, M. Causality and Information Transfer Between the Solar Wind and the Magnetosphere–Ionosphere System. Entropy 2021, 23, 390. [Google Scholar] [CrossRef]
- Consolini, G.; Alberti, T.; De Michelis, P. On the Forecast Horizon of Magnetospheric Dynamics: A Scale-to-Scale Approach. J. Geophys. Res. (Space Phys.) 2018, 123, 9065–9077. [Google Scholar] [CrossRef]
- Kamide, Y.; Baumjohann, W.; Daglis, I.A.; Gonzalez, W.D.; Grande, M.; Joselyn, J.A.; McPherron, R.L.; Phillips, J.L.; Reeves, E.G.D.; Rostoker, G.; et al. Current understanding of magnetic storms: Storm-substorm relationships. J. Geophys. Res. 1998, 103, 17705–17728. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Materassi, M.; Tozzi, R. An information theory approach to the storm-substorm relationship. J. Geophys. Res. (Space Phys.) 2011, 116, A08225. [Google Scholar] [CrossRef]
- Akasofu, S.I. Polar and Magnetosphere Substorms; Springer: Dordrecht, Germany, 1968; Volume 11. [Google Scholar] [CrossRef]
- Daglis, L.A.; Livi, S.; Sarris, E.T.; Wilken, B. Energy density of ionospheric and solar wind origin ions in the near-Earth magnetotail during substorms. J. Geophys. Res. 1994, 99, 5691–5704. [Google Scholar] [CrossRef]
- Akasofu, S.I. Auroral Substorms: Search for Processes Causing the Expansion Phase in Terms of the Electric Current Approach. Space Sci. Rev. 2017, 212, 341–381. [Google Scholar] [CrossRef]
- Stumpo, M.; Consolini, G.; Alberti, T.; Quattrociocchi, V. Measuring Information Coupling between the Solar Wind and the Magnetosphere-Ionosphere System. Entropy 2020, 22, 276. [Google Scholar] [CrossRef]
- McPherron, R.L.; Baker, D.N.; Bargatze, L.F.; Clauer, C.R.; Holzer, R.E. IMF control of geomagnetic activity. Adv. Space Res. 1988, 8, 71–86. [Google Scholar] [CrossRef]
- Kamide, Y. Is Substorm Occurrence a Necessary Condition for a Magnetic Storm? J. Geomagn. Geoelectr. 1992, 44, 109–117. [Google Scholar] [CrossRef]
- Kamide, Y.; Kokubun, S. Two-component auroral electrojet: Importance for substorm studies. J. Geophys. Res. 1996, 101, 13027–13046. [Google Scholar] [CrossRef]
- Lui, A.T.Y. Dipolarization front and current disruption. Geophys. Res. Lett. 2016, 43, 10050–10058. [Google Scholar] [CrossRef]
- Davis, T.N.; Sugiura, M. Auroral electrojet activity index AE and its universal time variations. J. Geophys. Res. 1966, 71, 785–801. [Google Scholar] [CrossRef]
- Iyemori, T. Storm-time magnetospheric currents inferred from mid-latitude geomagnetic field variations. J. Geomagn. Geoelectr. 1990, 42, 1249–1265. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Springer: Berlin/Heidelberg, Germany, 1981; Volume 898, p. 366. [Google Scholar] [CrossRef]
- Mañé, R. On the dimension of the compact invariant sets of certain non-linear maps. In Dynamical Systems and Turbulence, Warwick 1980; Springer: Berlin/Heidelberg, Germany, 1981; Volume 898, p. 230. [Google Scholar] [CrossRef]
- Packard, N.H.; Crutchfield, J.P.; Farmer, J.D.; Shaw, R.S. Geometry from a Time Series. Phys. Rev. Lett. 1980, 45, 712–716. [Google Scholar] [CrossRef]
- Sauer, T.; Yorke, J.A.; Casdagli, M. Embedology. J. Stat. Phys. 1991, 65, 579–616. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman and Hall: London, UK, 1986. [Google Scholar]
- Epanechnikov, V.A. Non-Parametric Estimation of a Multivariate Probability Density. Theory Probab. Its Appl. 1969, 14, 153–158. [Google Scholar] [CrossRef]
- Donner, R.V.; Stolbova, V.; Balasis, G.; Donges, J.F.; Georgiou, M.; Potirakis, S.M.; Kurths, J. Temporal organization of magnetospheric fluctuations unveiled by recurrence patterns in the Dst index. Chaos 2018, 28, 085716. [Google Scholar] [CrossRef]
- Alberti, T.; Lekscha, J.; Consolini, G.; De Michelis, P.; Donner, R.V. Disentangling nonlinear geomagnetic variability during magnetic storms and quiescence by timescale dependent recurrence properties. J. Space Weather Space Clim. 2020, 10, 25. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef]
- Kennel, M.B.; Buhl, M. Estimating Good Discrete Partitions from Observed Data: Symbolic False Nearest Neighbors. Phys. Rev. Lett. 2003, 91, 084102. [Google Scholar] [CrossRef]
- Faranda, D.; Messori, G.; Yiou, P. Dynamical proxies of North Atlantic predictability and extremes. Sci. Rep. 2017, 7, 41278. [Google Scholar] [CrossRef]
- Faranda, D.; Messori, G.; Alvarez-Castro, M.C.; Yiou, P. Dynamical properties and extremes of Northern Hemisphere climate fields over the past 60 years. Nonlinear Process. Geophys. 2017, 24, 713–725. [Google Scholar] [CrossRef]
- Moreira Freitas, A.C.; Milhazes Freitas, J.; Todd, M. Extremal Index, Hitting Time Statistics and periodicity. arXiv 2010, arXiv:1008.1350. [Google Scholar]
- Lucarini, V.; Faranda, D.; Wouters, J.; Kuna, T. Towards a General Theory of Extremes for Observables of Chaotic Dynamical Systems. J. Stat. Phys. 2014, 154, 723–750. [Google Scholar] [CrossRef]
- Faranda, D.; Messori, G.; Yiou, P. Diagnosing concurrent drivers of weather extremes: Application to warm and cold days in North America. Clim. Dyn. 2020, 54, 2187–2201. [Google Scholar] [CrossRef]
- Abadi, M.; Moreira Freitas, A.C.; Milhazes Freitas, J. Dynamical counterexamples regarding the Extremal Index and the mean of the limiting cluster size distribution. arXiv 2018, arXiv:1808.02970. [Google Scholar] [CrossRef]
- Alberti, T.; Consolini, G.; De Michelis, P. Complexity measures of geomagnetic indices in the last two solar cycles. J. Atmos. Sol.-Terr. Phys. 2021, 217, 105583. [Google Scholar] [CrossRef]
- Faranda, D.; Vaienti, S. Correlation dimension and phase space contraction via extreme value theory. Chaos 2018, 28, 041103. [Google Scholar] [CrossRef]
- Parks, G.K. Physics of Space Plasmas: An Introduction; Addison-Wesley: Redwood City, CA, USA, 1991. [Google Scholar]
- Parks, G.K.; Lee, E.; Fu, S.Y.; Fillingim, M.; Dandouras, I.; Cui, Y.B.; Hong, J.; Rème, H. Outflow of low-energy O+ ion beams observed during periods without substorms. Ann. Geophys. 2015, 33, 333–344. [Google Scholar] [CrossRef][Green Version]
- Wanliss, J. Fractal properties of SYM-H during quiet and active times. J. Geophys. Res. (Space Phys.) 2005, 110, A03202. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.A.; Kapiris, P.; Mandea, M.; Vassiliadis, D.; Eftaxias, K. From pre-storm activity to magnetic storms: A transition described in terms of fractal dynamics. Ann. Geophys. 2006, 24, 3557–3567. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.A.; Papadimitriou, C.; Kalimeri, M.; Anastasiadis, A.; Eftaxias, K. Dynamical complexity in Dst time series using non-extensive Tsallis entropy. Geophys. Res. Lett. 2008, 35, L14102. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G. On the local Hurst exponent of geomagnetic field fluctuations: Spatial distribution for different geomagnetic activity levels. J. Geophys. Res. (Space Phys.) 2015, 120, 2691–2701. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).