Hyperbolic Inflation in the Jordan Frame

Abstract

We consider a multi-scalar field model in the Jordan frame, which can be seen as a two-scalar field model where the Brans–Dicke field interacts in the kinetic part with the second scalar field. This theory under a conformal transformation reduces to the hyperbolic inflation. We show that scaling solutions and the de Sitter universe are provided by the theory. In the study of asymptotic dynamics, we determine an attractor where all the fluid sources contribute in the cosmological fluid. This attractor is always a spiral, and it can be seen as the analogue of the hyperbolic inflation in the Jordan frame.

1. Introduction

Brans and Dicke proposed a scalar field gravitational theory that embodied Mach’s Principle [1]. In Brans–Dicke theory, the presence of the scalar field is essential for the existence of the gravitational field, because the scalar field is non-minimally coupled to gravity. That is, the gravitational theory is defined in the Jordan frame [2]. This gravitational theory has been widely studied before for the description of various epochs of the cosmological history, see for instance [3,4,5,6,7,8,9,10,11] and references therein. The Brans–Dicke theory belongs to the family of modified theories of gravity and the scalar field can attribute dynamical degrees of freedom provided by higher-order theories, such as in the case of the $f\left(R\right)$-theory [12].

On the other hand, General Relativity is a theory defined in the so-called Einstein frame. There exists a geometrical map that connects the Jordan frame to the Einstein one and vice versa [13]. The two frames are related under the action of a conformal transformation [14]. The two frames have different metric tensors, which are conformally related, thus the physical properties of a given theory in the two frames should be compared, and the problem of the selection of the physical frame follows [15]. The latter has been a subject of debate in the last decades and there are various studies on this analysis. The two frames are only mathematically equivalent, while the physical properties of a gravitational theory rarely survives. For instance, a singular solution in the one frame can be read as a solution without singularity in the other frame [16,17,18].

A gravitational model that has drawn the attention of cosmologists over the last years is a multi-scalar field model in the Einstein frame, which provides the hyperbolic inflation [19]. In this theory, the inflation field [20], which drives the dynamics of the rapid expansion of the universe, consists by two scalar fields that interact in the kinetic components of the Lagrangian function [19]. Specifically, the dynamics of the two scalar fields are defined on a two-dimensional hyperbolic space. This model is also known as Chiral theory, and it has been widely studied in the literature before [21,22,23,24,25,26,27,28,29,30]. This two-scalar field model for the exponential scalar field potential admits an attractor, which can provide the asymptotic behavior of the hyperbolic inflation. In particular, it was found that this inflationary solution is described by a stable spiral in terms of dynamical systems [31].

In this study, we propose a new multi-scalar field model defined in the Jordan frame and under the application of a conformal transformation it is equivalent to the hyperbolic inflationary model, or the Chiral model. One of the scalar fields is the Brans–Dicke field while the second scalar field is coupled to the Brans–Dicke field only. The main idea of this study is to investigate if there exists an analogue of the hyperbolic inflation in the Jordan frame and to compare the physical properties of the two-scalar field model in the Einstein and Jordan frames. In order to achieve our goal we apply methods from the dynamical systems and we investigate the stationary points for the field equations and we study their stability criteria. The dynamical analysis is an important mathematical tool for the qualitative study of a gravitational theory. It has been applied in various models in order to test the cosmological viability of theories as also to reconstruct the cosmological history [32,33,34,35,36,37,38]. The plan of the paper is as follows.

In Section 2, we present the multi-field cosmological model of our consideration and we derive the field equations in the case of a spatially flat isotropic and homogeneous geometry. In Section 3, we show the existence of exact solutions of special interest; indeed, we prove that the field equations can be solved explicitly and the scaling and de Sitter solutions are provided by the proposed theory. The main analysis of this study is presented in Section 4. In particular, we perform a detailed analysis of the dynamics of the field equations by using dimensional variables in the Hubble normalization approach. We show that there exists an analogue of the hyperbolic inflation in the Jordan frame. Finally, in Section 5, we draw our conclusions and we extend our discussion in the case of anisotropic spacetimes.

2. Cosmological Model

Consider the multi-scalar field Action Integral:

$$S_A=\int d{x}^4\sqrt{-g}\left[\frac{1}{2}\varphi R+\frac{1}{2}\frac{{\omega }_{BD}}{\varphi }{g}^{\mu \nu }{\varphi }_{;\mu }{\varphi }_{;\nu }+\frac{1}{2}{F}^2\left(\varphi \right)g^{\mu \nu }{\psi }_{;\mu }{\psi }_{;\nu }+V\left(\varphi ,\psi \right)\right],$$

(1)

where $\varphi \left(x^k\right)$ and $\psi \left(x^k\right)$ are two scalar fields that we assume inherit the symmetries of the background space and in general they interact through the function $F\left(\varphi \right)$ and the potential function $V\left(\varphi ,\psi \right)$.

Scalar field $\varphi \left(x^k\right)$ is the Brans–Dicke scalar field [1] coupled to gravity and ${\omega }_{BD}$ is the Brans–Dicke parameter [9], with ${\omega }_{BD}\ne -\frac{3}{2}$. We remark that for ${\omega }_{BD}=0$, the Brans–Dicke field describes the higher-order derivatives of $f\left(R\right)$-gravity [12], while for ${\omega }_{BD}=-\frac{3}{2}$, the Brans–Dicke field does not describe real degrees of freedom.

For the Action Integral (1), the gravitational field equations are

$$\begin{array}{cc}\hfill \varphi G_{\mu \nu }& =\frac{{\omega }_{BD}}{\varphi }\left({\varphi }_{;\mu }{\varphi }_{;\nu }-\frac{1}{2}{g}_{\mu \nu }{g}^{\kappa \lambda }{\varphi }_{;\kappa }{\varphi }_{;\lambda }\right)-\left(g_{\mu \nu }{g}^{\kappa \lambda }{\varphi }_{;\kappa \lambda }-{\varphi }_{;\mu }{\varphi }_{;\nu }\right)\hfill \\ \hfill & +g_{\mu \nu }V\left(\varphi ,\psi \right)-F^2\left(\varphi \right)\left({\psi }_{;\mu }{\psi }_{;\nu }-\frac{1}{2}{g}_{\mu \nu }{g}^{\kappa \lambda }{\psi }_{;\kappa \lambda }\right),\hfill \end{array}$$

(2)

and the equations of motion for the two scalar fields

$$\left(2{\omega }_{BD}+3\right)\left(g^{\mu \nu }{\varphi }_{;\mu \nu }\right)-\varphi V_{,\varphi }+2V-\frac{1}{2}{\left(F^2\right)}_{,\varphi }{\dot{\psi }}^2=0,$$

(3)

$$g^{\mu \nu }\left({\psi }_{;\mu \nu }+{\left(ln\left(F^2\right)\right)}_{,\varphi }{\varphi }_{;\mu }{\psi }_{;\nu }\right)=0.$$

(4)

The gravitational model (1) has not been defined as arbitrary. More specifically, the multi-scalar field Action Integral (1) can be seen as the equivalent of the hyperbolic inflation in the Jordan frame for a specific functional form of $F\left(\varphi \right)$. Indeed, when we perform the conformal transformation $\overline{g}=\varphi g_{ij}$, the Action Integral (1) in the Einstein frame reads

$$S_A=\int d{x}^4\sqrt{-g}\left[\frac{1}{2}R-\frac{1}{2}{g}^{\mu \nu }{\mathsf{\Phi }}_{;\mu }{\mathsf{\Phi }}_{;\nu }-\frac{1}{2}{F}^2\left(\mathsf{\Phi }\right)e^{\overline{\omega }\mathsf{\Phi }}{g}^{\mu \nu }{\psi }_{;\mu }{\psi }_{;\nu }-\overline{V}\left(\mathsf{\Phi },\psi \right)\right],$$

(5)

where $\mathsf{\Phi }\simeq ln\varphi$ is a new scalar field minimally coupled to gravity and $\overline{\omega }=\overline{\omega }\left({\omega }_{BD}\right)$. We observe that the hyperbolic inflation is recovered when $F\left(\mathsf{\Phi }\right)=const$. or $F\left(\mathsf{\Phi }\right)=e^{\overline{\kappa }\mathsf{\Phi }}$, that is, $F\left(\varphi \right)\simeq {\varphi }^{\kappa }$.

In the hyperbolic inflation, for the scalar field potential $\overline{V}\left(\mathsf{\Phi },\psi \right)$ it holds, ${\overline{V}}_{,\psi }=0$ and $\overline{V}\left(\mathsf{\Phi }\right)$ is an exponential function, thus in this work, for the dynamical analysis we shall assume the power-potential $V\left(\varphi \right)=V_0{\varphi }^{\lambda }$. Let us focus in the case where $V\left(\varphi ,\psi \right)=V\left(\varphi \right)$.

We assume the isotropic and homogeneous background space described by the spatially flat Friedmann–Lemaître–Robertson–Walker (FLRW) geometry with line element

$$d{s}^2=-d{t}^2+a^2\left(t\right)\left(d{x}^2+d{y}^2+d{z}^2\right),$$

(6)

in which $a\left(t\right)$ is the scalar factor. The Hubble function is defined as $H=\frac{\dot{a}}{a}$, in which $\dot{a}=\frac{da}{dt}$. The FLRW geometry admits six isometries, the three translations and three rotations of the three-dimensional flat hypersurface. Because we consider the scalar fields to inherit the symmetries of the background space we find $\varphi =\varphi \left(t\right)$ and $\psi =\psi \left(t\right)$.

We derive the Ricciscalar

$$R=6\left[\frac{\ddot{a}}{a}+{\left(\frac{\dot{a}}{a}\right)}^2\right].$$

(7)

By replacing in (2), the modified Friedmann’s equations are derived

$$-3H^2=3H\frac{\dot{\varphi }}{\varphi }-\frac{{\omega }_{BD}}{2}{\left(\frac{\dot{\varphi }}{\varphi }\right)}^2-\frac{1}{2}\frac{F^2\left(\varphi \right)}{\varphi }{\dot{\psi }}^2-\frac{1}{\varphi }V\left(\varphi \right),$$

(8)

$$-\left(3\varphi H^2+2\varphi \dot{H}\right)=2H\dot{\varphi }+\frac{{\omega }_{BD}}{2\varphi }{\dot{\varphi }}^2+\frac{1}{2}{F}^2\left(\varphi \right){\dot{\psi }}^2+\ddot{\varphi }-V\left(\varphi \right)$$

(9)

Furthermore, the equations of motion for the two scalar fields read

$${\omega }_{BD}\left(\ddot{\varphi }-\frac{1}{2}{\left(\frac{\dot{\varphi }}{\varphi }\right)}^2+3H\dot{\varphi }\right)+6H^2\varphi +\varphi \left(3\dot{H}+V_{,\varphi }-\frac{1}{2}{\left(F^2\right)}_{,\varphi }{\dot{\psi }}^2\right)=0,$$

(10)

$$\ddot{\psi }+3H\dot{\psi }+{\left(ln\left(F^2\right)\right)}_{,\varphi }\dot{\varphi }\dot{\psi }=0.$$

(11)

The field Equations (8) and (9) can be written in the equivalent form

$$3H^2={\rho }_{eff},$$

(12)

$$2\dot{H}+3H^2=p_{eff},$$

(13)

where we have defined

$${\rho }_{eff}=-3H\frac{\dot{\varphi }}{\varphi }+\frac{{\omega }_{BD}}{2}{\left(\frac{\dot{\varphi }}{\varphi }\right)}^2+\frac{1}{2}\frac{F^2\left(\varphi \right)}{\varphi }{\dot{\psi }}^2+\frac{1}{\varphi }V\left(\varphi \right),$$

(14)

$$p_{eff}=2H\frac{\dot{\varphi }}{\varphi }+\frac{{\omega }_{BD}}{2}{\left(\frac{\dot{\varphi }}{\varphi }\right)}^2+\frac{1}{2}\frac{F^2\left(\varphi \right)}{\varphi }{\dot{\psi }}^2-\frac{\ddot{\varphi }}{\varphi }-\frac{1}{\varphi }V\left(\varphi \right).$$

(15)

3. Exact Solutions

We investigate the existence of exact solutions of special interest for the cosmological evolution. Indeed, we search for scaling solutions, $a\left(t\right)=a_0{t}^p$, exponential power-law $a\left(t\right)=a_0{e}^{H_{0}t}$. For the analysis in this Section we consider an arbitrary potential function $V\left(\varphi \right)$.

Equation (11) gives the solution

$$\dot{\psi }\left(t\right)={\psi }_0{a}^{-3}{\varphi }^{-2\kappa }.$$

(16)

where in the following we shall assume that ${\psi }_0$ is a non-zero constant, otherwise we end to the usual Brans–Dicke theory.

For the power-law scale factor $a\left(t\right)=a_0{t}^p$, from (8) and (9) with the use of (16), we end with the second-order ordinary differential equation

$$\ddot{\varphi }+{\omega }_{BD}\frac{{\dot{\varphi }}^2}{\varphi }-\frac{p}{t}\dot{\varphi }-\frac{2p}{t^2}\varphi +t^{-6p}{\psi }_0^2{\varphi }^{-2\kappa }=0.$$

(17)

A closed-form solution for the field equations is

$$a\left(t\right)=a_0{t}^p,\varphi ={\varphi }_0{t}^{2\frac{1-3p}{1+2\kappa }},\psi \left(t\right)=\frac{1+2\kappa }{1-2\kappa }\frac{{\psi }_0}{1-3p}{\varphi }_0^{-2\kappa }{t}^{\frac{\left(1-3p\right)\left(1-2\kappa \right)}{1+2\kappa }},$$

(18)

with ${\psi }_0$ given by the expression

$${\psi }_0=\pm \frac{\sqrt{2}{\varphi }_0^{\frac{1}{2}+\kappa }}{\sqrt{1+4\kappa +{\kappa }^{32}}}\sqrt{11p-21p^2-1+2\kappa -6p^2\kappa +4p{\kappa }^2-2{\omega }_{BD}\left(1-6p+9p^2\right)},$$

(19)

and potential function

$$V\left(\varphi \left(t\right)\right)=\frac{\left(1-2\kappa -p\left(17+4\kappa \left(3+\kappa \right)+6p\left(\kappa \left(2\kappa -5\right)-6\right)\right)\right)}{{\left(1+2\kappa \right)}^2}{\varphi }_0{t}^{\frac{2\left(3p+2\kappa \right)}{1+2\kappa }},$$

(20)

that is

$$V\left(\varphi \right)=\frac{\left(1-2\kappa -p\left(17+4\kappa \left(3+\kappa \right)+6p\left(\kappa \left(2\kappa -5\right)-6\right)\right)\right)}{{\left(1+2\kappa \right)}^2}{\varphi }_0^{\frac{1+2\kappa }{1-3p}}{\varphi }^{-\frac{3p+2\kappa }{1-3p}}.$$

(21)

In the special case where $\kappa =-\frac{1}{2}$, it follows $p=\frac{1}{3}$, ${\psi }_0=\sqrt{\frac{2\left(1+2q_1\right)-3q_1^2\left(1-{\omega }_{BD}\right)}{3}}$ and potential function $V\left(\varphi \left(t\right)\right)=-\frac{1}{2}\left(q_1\left(3q_1-10\right)-4\right)t^{-2+q_1}{\varphi }_0$, that is,

$$V\left(\varphi \right)=-\frac{1}{2}\left(q_1\left(3q_1-10\right)-4\right){\left(\frac{\varphi }{{\varphi }_0}\right)}^{1-\frac{2}{q_1}}{\varphi }_0.$$

(22)

Moreover, the de Sitter universe is recovered when

$$\ddot{\varphi }+{\omega }_{BD}\frac{{\dot{\varphi }}^2}{\varphi }-H_0\dot{\varphi }+e^{-6H_{0}t}{\psi }_0^2{\varphi }^{-2\kappa }=0.$$

(23)

We easily find that Equation (23) admits an exponential closed-form solution, thus, the field equations provide

$$a\left(t\right)=a_0{e}^{H_{0}t},\varphi \left(t\right)={\varphi }_0{e}^{-\frac{6H_0}{1+2\kappa }t},\psi \left(t\right)={\psi }_0{\varphi }_0^{-2\kappa }{e}^{-3H_0\frac{1-2\kappa }{1+2\kappa }t},$$

(24)

with

$${\psi }_0=\pm \frac{\sqrt{6}{H}_0\sqrt{-\left(7+2\kappa +6{\omega }_{BD}\right)}}{1+2\kappa },$$

(25)

and potential

$$V\left(\varphi \left(t\right)\right)=6H_0^2\frac{6+\kappa \left(5-2\kappa \right)}{{\left(1+2\kappa \right)}^2}{\varphi }_0{e}^{-\frac{6H_0}{1+2\kappa }t},$$

(26)

that is

$$V\left(\varphi \right)=6H_0^2\frac{6+\kappa \left(5-2\kappa \right)}{{\left(1+2\kappa \right)}^2}\varphi .$$

(27)

However, for $\kappa =-\frac{1}{2}$ we end with the closed-form solution ${\psi }_0=0$ and $\varphi \left(t\right)={\varphi }_0{e}^{{\varphi }_{1}t}$ with linear potential function. This solution is not of special interest because the second scalar field, $\psi$ does not contribute in the cosmological fluid.

4. Dynamical System Analysis

In order to perform the dynamical analysis, we consider the new variables in the H-normalization:

$$x=\frac{\dot{\varphi }}{\varphi H},y^2=\frac{V\left(\varphi \right)}{3\varphi H^2},z=\frac{\dot{\psi }F\left(\varphi \right)}{\sqrt{6\varphi }H},$$

(28)

and

$$\lambda =\varphi {\left(lnV\left(\varphi \right)\right)}_{,\varphi },\kappa =\varphi {\left(lnF\left(\varphi \right)\right)}_{,\varphi },d\tau =Hdt.$$

(29)

Furthermore, we assume the exponential potential $V\left(\varphi \right)=V_0{e}^{\lambda \varphi }$ and the power-law function $F\left(\varphi \right)={\varphi }^{\kappa }$, thus parameters $\lambda$ and $\kappa$ are constants. We proceed with the isotropic background space.

For the spatially flat FLRW spacetime, the field equations in the new variables read

$$1-\left(\frac{3}{2{\omega }_{BD}}\right)-{\left(\sqrt{\frac{{\omega }_{BD}}{6}}x-\frac{\sqrt{6}}{2\sqrt{{\omega }_{BD}}}\right)}^2-y^2-z^2=0$$

(30)

$$\begin{array}{cc}\hfill \left(6+4{\omega }_{BD}\right)\frac{dx}{d\tau }& =6\left(1+\left(3+2\lambda \right)y^2+z^2\left(4\kappa -3\right)\right)-x\left(6{\omega }_{BD}+x\left(7{\omega }_{BD}+6\right)\right)\hfill \\ \hfill & +x\left({\omega }_{BD}\left(1+{\omega }_{BD}\right)x^2+6\left(\lambda -{\omega }_{BD}\right)y^2+6\left(2\kappa +{\omega }_{BD}\right)z^2\right),\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill \frac{\left(3+2{\omega }_{BD}\right)}{y}\frac{dy}{d\tau }& =-\left(3+4{\omega }_{BD}+\lambda \left(3+2{\omega }_{BD}\right)\right)x+{\omega }_{BD}\left(1+{\omega }_{BD}\right)x^2\hfill \\ \hfill & +6\left(2+{\omega }_{BD}+\left(\lambda -{\omega }_{BD}\right)y^2+\left(2\kappa +{\omega }_{BD}\right)z^2\right),\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill \frac{\left(3+2{\omega }_{BD}\right)}{z}\frac{dz}{d\tau }& =-\left(3+4{\omega }_{BD}+\kappa \left(6+4{\omega }_{BD}\right)\right)x+{\omega }_{BD}\left(1+{\omega }_{BD}\right)x^2\hfill \\ \hfill & -6\left(1+{\omega }_{BD}+\left({\omega }_{BD}-\lambda \right)y^2\right)+6\left(2\kappa +{\omega }_{BD}\right)z^2.\hfill \end{array}$$

(33)

From Equation (30) and for ${\omega }_{BD}>0$, variables $\left(x,y,z\right)$ take values on the sphere with radius $1+\left(\frac{3}{2{\omega }_{BD}}\right)$ and center the point $\left(\frac{\sqrt{6}}{2\sqrt{{\omega }_{BD}}},0,0\right)$. However, for ${\omega }_{BD}<0$, variables $\left(x,y,z\right)$ are without boundaries. Thus, for ${\omega }_{BD}<0$ Poincare variables should be used in order to perform a complete analysis.

At this point it is important to mention that the field equations are invariant on the discrete transformations $y\to -y$ and $z\to -z$, thus without loss of generality we select to work on the branch $y>0$.

From (30) we replace variable y and we end with a two-dimensional system on the variables $\left(x,z\right)$.

The stationary points $A=\left(x\left(A\right),z\left(A\right)\right)$ of the reduced system are

$$A_1^{\pm }=\left(-2,\pm \sqrt{-1-\frac{2}{3}{\omega }_{BD}}\right),A_2^{\pm }=\left(\frac{3\pm \sqrt{9+6{\omega }_{BD}}}{{\omega }_{BD}},0\right),$$

$$A_3^{\pm }=\left(\frac{6}{\lambda -2\kappa },\pm \frac{\sqrt{\lambda \left(\lambda +5\right)-3-2\kappa \left(2+\lambda \right)-6{\omega }_{BD}}}{\lambda -2\kappa }\right),$$

$$A_4=\left(\frac{2\left(\lambda +2\right)}{1-\lambda +2{\omega }_{BD}},0\right).$$

Points $A_1^{\pm }$ describe asymptotic solutions where only the kinetic parts of the two scalar fields contribute to the cosmological fluid, that is, $y\left(A_1^{\pm }\right)=0$. The points are real and physically accepted when ${\omega }_{BD}>-\frac{3}{2}$, while the effective equation of state parameter is $w_{eff}\left(A_1^{\pm }\right)=\frac{1}{3}\left(1-4\kappa \right)$. Thus, points $A_1^{\pm }$ describe acceleration when $\kappa >\frac{1}{2}$.

Points $A_2^{\pm }$ are real when ${\omega }_{BD}>-\frac{3}{3}$ while they provide $y\left(A_2^{\pm }\right)=0$, which means that only the kinetic part of the scalar field $\varphi$, contributes to the cosmological solution Moreover, $w_{eff}\left(A_2^{\pm }\right)=\frac{6+3{\omega }_{BD}\pm 2\sqrt{9+6{\omega }_{BD}}}{3{\omega }_{BD}}$, that is, $w_{eff}\left(A_2^{+}\right)<-\frac{1}{3}$ for $-\frac{3}{2}<{\omega }_{BD}<0$.

For the stationary points $A_3^{\pm }$ we calculate $y\left(A_3^{\pm }\right)=\frac{\sqrt{\left(2\kappa -1\right)\left(2\kappa -\lambda -3\right)}}{\lambda -2\kappa }$ and $w_{eff}\left(A_3^{\pm }\right)=1+\frac{2\left(1+2\kappa \right)}{\lambda -2\kappa }$. The points are real when $\left(2\kappa -1\right)\left(2\kappa -\lambda -3\right)>0$ and ${\omega }_{BD}<\frac{1}{6}(\lambda \left(\lambda +5\right)-3-2\kappa \left(2+\lambda \right))$. In these asymptotic solutions, all the components of the scalar fields contribute to the cosmological fluid. Specifically, they can be seen as the set of the hyperbolic inflationary solutions when $w_{eff}\left(A_3^{\pm }\right)<0$, in the Jordan frame.

Finally, point $A_4$ provides $y\left(A_4\right)=\frac{\sqrt{5-\lambda \left(4+\lambda \right)-6{\omega }_{BD}}\sqrt{3+2{\omega }_{BD}}}{\sqrt{3}\left(\lambda -1-2{\omega }_{BD}\right)}$, $w_{eff}\left(A_4\right)=$$\frac{1+\lambda \left(9+2\lambda \right)-6{\omega }_{BD}}{3\left(1-\lambda +2{\omega }_{BD}\right)}$. The point is real for $\left(5-\lambda \left(4+\lambda \right)-6{\omega }_{BD}\right)\left(3+2{\omega }_{BD}\right)\ge 0$.

We proceed with the stability analysis of the stationary points so that we can build the cosmological history.

The eigenvalues of the linearized system around points $A_1^{\pm }$ are

$$e_1\left(A_1^{\pm }\right)=1-2\kappa ,e_2\left(A_1^{\pm }\right)=-2\left(2\kappa -\lambda -3\right),$$

(34)

which means that for $\left\{\lambda <-2,\kappa >\frac{1}{2}\right\}$ and $\left\{\lambda >-2,\kappa >\frac{3+\lambda }{2}\right\}$, the stationary points have negative eigenvalues, which means that they are attractors. For the stationary points $A_2^{\pm }$ we find

$$\begin{array}{cc}\hfill e_1\left(A_2^{\pm }\right)& =\pm \frac{\left(1-2\kappa \right)\left(3+\sqrt{3\left(3+2{\omega }_{BD}\right)}\right)}{2{\omega }_{BD}},\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill e_2\left(A_2^{\pm }\right)& =\pm \frac{3\left(1-\lambda +2{\omega }_{BD}\right)+\left(1-\lambda \right)\sqrt{3\left(3+2{\omega }_{BD}\right)}}{{\omega }_{BD}}.\hfill \end{array}$$

(36)

Hence, point $A_2^{+}$ is an attractor when $\left\{\lambda \le -2,-\frac{3}{2}<{\omega }_{BD}<0,\kappa <\frac{1}{2}\right\}$, $\{-2<\lambda <1,$$\frac{{\lambda }^2+4\lambda -5}{6}<{\omega }_{BD}<0,\kappa <\frac{1}{2}\}$ and $\left\{\lambda >1,0<{\omega }_{BD}<\frac{{\lambda }^2+4\lambda -5}{6},\kappa >\frac{1}{2}\right\}$. On the other hand, point $A_2^{-}$ is an attractor when $\left\{\lambda \le -5,-\frac{3}{2}<{\omega }_{BD}<0,\kappa <\frac{1}{2}\right\}$, $\left\{-5<\lambda <-2,-\frac{3}{2}<{\omega }_{BD}<\frac{{\lambda }^2+4\lambda -5}{6},\kappa <\frac{1}{2}\right\}$.

For the stationary point $A_4$, the eigenvalues are

$$\begin{array}{cc}\hfill e_1\left(A_4\right)& =\frac{5-4\lambda -{\lambda }^2+6{\omega }_{BD}}{\lambda -1-2{\omega }_{BD}},\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill e_2\left(A_4\right)& =\frac{3+4\kappa -5\lambda +2\kappa \lambda -{\lambda }^2+6{\omega }_{BD}}{\lambda -1-2{\omega }_{BD}}.\hfill \end{array}$$

(38)

It follows that the stationary point $A_4$ is an attractor when $\{\lambda <-2,{\omega }_{BD}>\frac{\left(\lambda -1\right)\left(5+\lambda \right)}{6},$$\kappa <\frac{5\lambda -3+{\lambda }^2-6{\omega }_{BD}}{2\left(2+\lambda \right)}\}$, $\left\{\lambda =-2,{\omega }_{BD}>-\frac{3}{2}\right\}$, $\left\{-2<\lambda \le 1,{\omega }_{BD}>\frac{\lambda -1}{2},\kappa >\frac{5\lambda -3+{\lambda }^2-6{\omega }_{BD}}{2\left(2+\lambda \right)}\right\}$ and $\left\{\lambda >1,{\omega }_{BD}>\frac{\left(\lambda -1\right)\left(5+\lambda \right)}{6},\kappa >\frac{5\lambda -3+{\lambda }^2-6{\omega }_{BD}}{2\left(2+\lambda \right)}\right\}$.

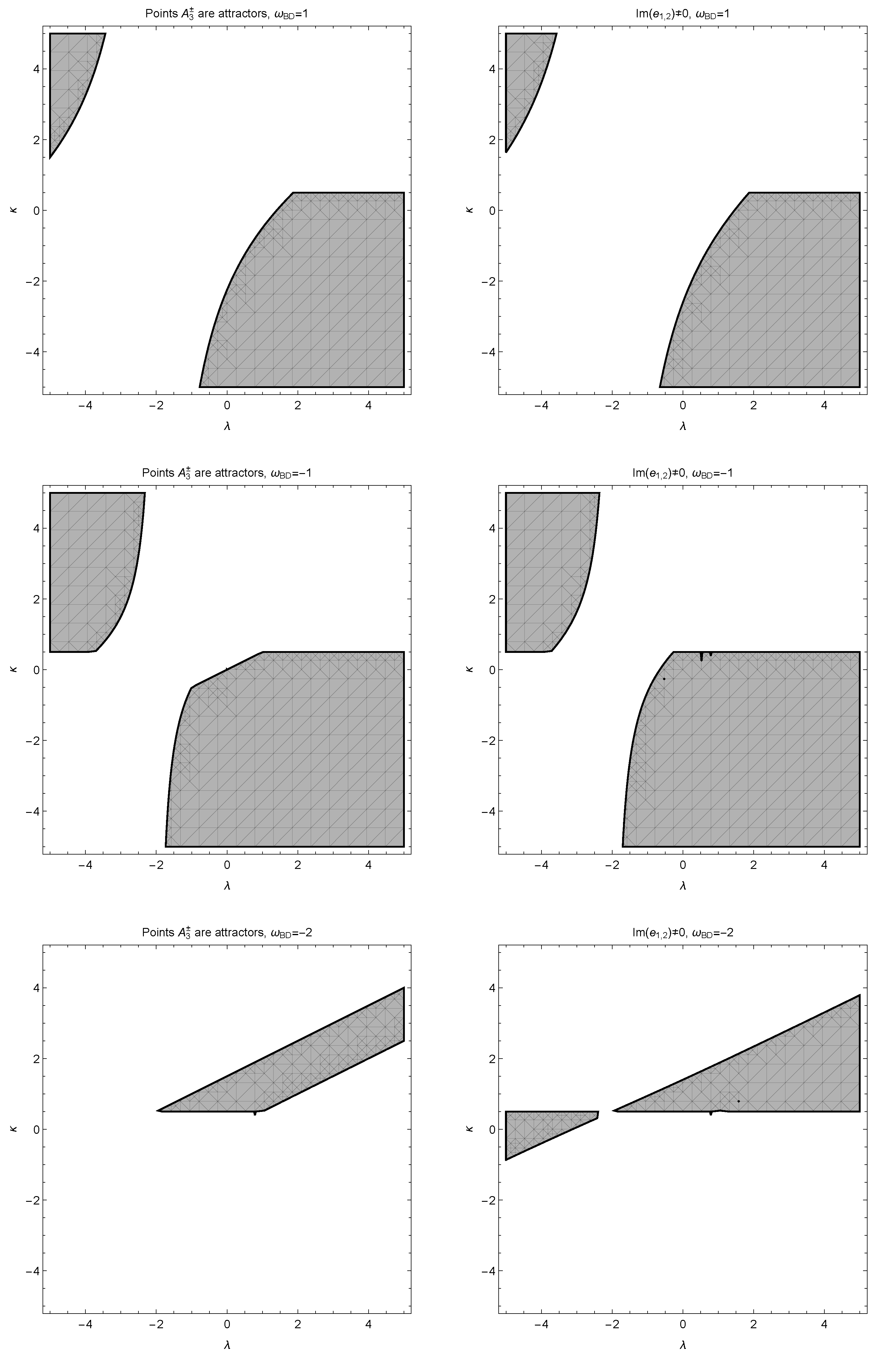
Finally, for the points $A_3^{\pm }$ the eigenvalues $e_{1,2}\left(A_3^{\pm }\right)$ are studied numerically. In Figure 1, we present regions in the two-dimensional plane $\left(\lambda ,\kappa \right)$ for various values of the variable ${\omega }_{BD}$. What is important is that the stationary points, when they are attractors, are spirals, which is in agreement with the hyperbolic inflation in the Einstein frame.

Figure 1. Region plots of the real and imaginary parts of the eigenvalues $e_{1,2}\left(A_3^{\pm }\right)$ in the plane $\left(\lambda ,\kappa \right)$ for ${\omega }_{BD}=1$, ${\omega }_{BD}=-1$ and ${\omega }_{BD}=-2.$ Left column is the region where the eigenvalues have negative real parts and right column is the region where the imaginary parts of the eigenvalues are nonzero.

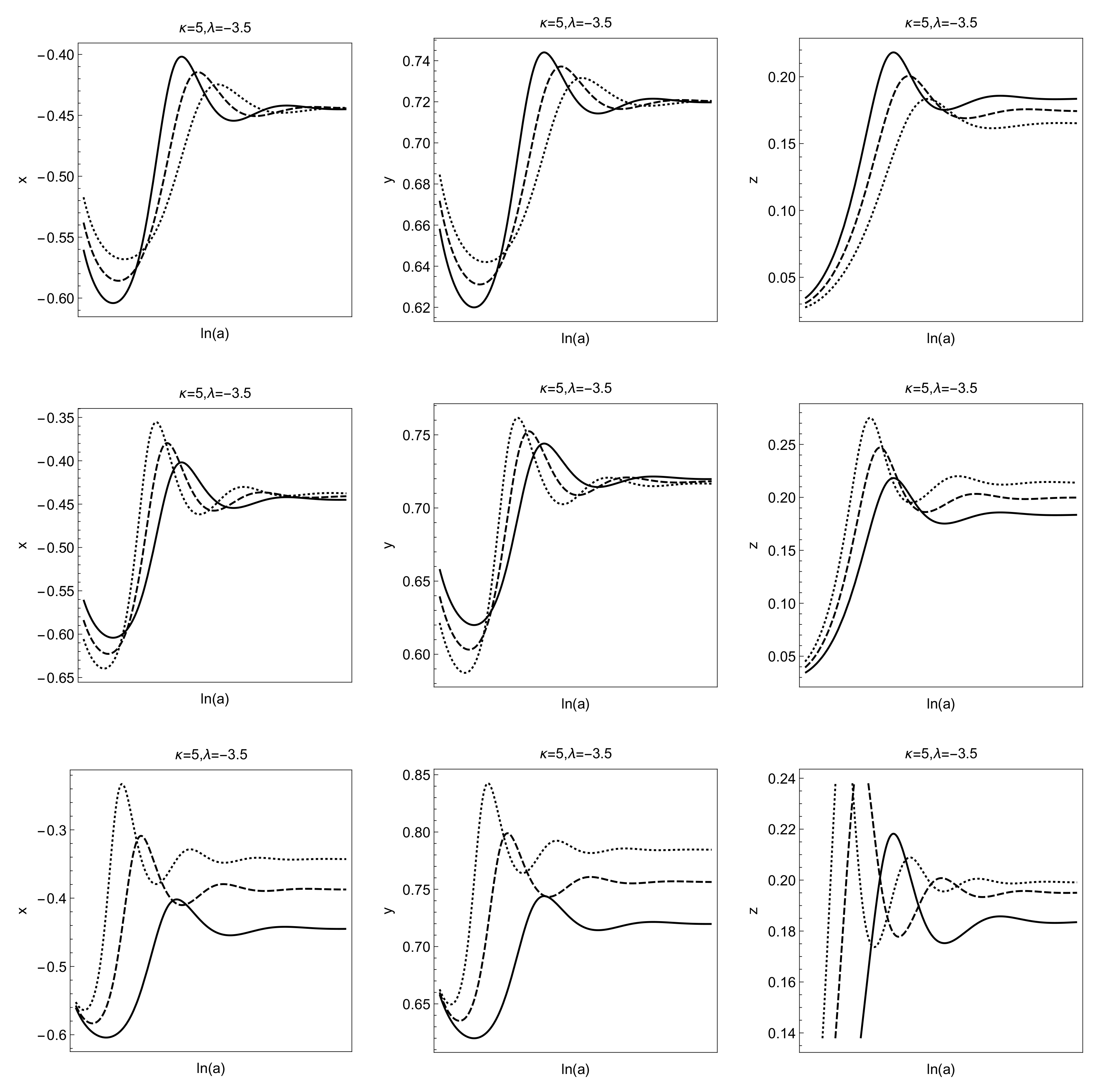
In Figure 2, we present the qualitative evolution for the effective equation of the state parameter for various values of the free parameters $\left({\omega }_{BD},\lambda ,\kappa \right)$ where the hyperbolic inflation is a future attractor. The qualitative evolution of the dimensionless variables $\left(x,y,z\right)$ are presented in Figure 3.

Figure 2. Qualitative evolution of the $w_{eff}$ with a future atractor point $A_3^{+}$. Left Figure is for $\left(\kappa =5,\lambda =-3.5\right)$, and ${\omega }_{BD}=0.1$ (solid line), ${\omega }_{BD}=0.2$ (dashed line) and ${\omega }_{BD}=0.3$ (dotted line). Center Figure is for $\left({\omega }_{BD},\kappa \right)=\left(0.1,5\right)$, $\lambda =-3.5$ (solid line), $\lambda =-3.6$ (dashed line) and $\lambda =-3.7$ (dotted line). Right line is for $\left({\omega }_{BD},\lambda \right)=\left(0.1,-3.5\right)$, $\kappa =-3.5$ (solid line), $\kappa =-3.6$ (dashed line) and $\kappa =-3.7$ (dotted line).

Figure 3. Qualitative evolution of the dimensionless variables $\left(x,y,z\right)$ for various values of the free parameters $\left({\omega }_{BD},\kappa ,\lambda \right)$. First row is for $\left(\kappa =5,\lambda =-3.5\right)$, and ${\omega }_{BD}=0.1$ (solid lines), ${\omega }_{BD}=0.2$ (dashed lines) and ${\omega }_{BD}=0.3$ (dotted lines). Second row is for $\left({\omega }_{BD},\kappa \right)=\left(0.1,5\right)$, $\lambda =-3.5$ (solid lines), $\lambda =-3.6$ (dashed lines) and $\lambda =-3.7$ (dotted lines). Third row is for $\left({\omega }_{BD},\lambda \right)=\left(0.1,-3.5\right)$, $\kappa =-3.5$ (solid lines), $\kappa =-3.6$ (dashed lines) and $\kappa =-3.7$ (dotted lines).

Analysis at Infinity

For negative values of the Brans–Dicke parameter we define the new variables

$$X=\frac{\rho }{\sqrt{1-{\rho }^2}}cos\mathsf{\Theta },y=\frac{\rho }{\sqrt{1-{\rho }^2}}sin\mathsf{\Theta }cos\mathsf{\Phi },z=\frac{\rho }{\sqrt{1-{\rho }^2}}sin\mathsf{\Theta }sin\mathsf{\Phi }$$

where we have replaced $x=\sqrt{\frac{6}{\left|{\omega }_{BD}\right|}}X-\frac{3}{\left|{\omega }_{BD}\right|}$.

Assume now that we work on the region $\rho >1$, that is, in order $y\ge 0$, it follows $\mathsf{\Theta }\in [0,\pi )$ and $\mathsf{\Phi }\in (-\frac{\pi }{2},\frac{\pi }{2}]$

In the new variables the infinity is reached when $\rho \to 1$. Thus, with use of the use of the constraint equation, for $\rho \to 1$ we end with the following system of ordinary differential equations:

$$\dot{\rho }=0$$

(39)

$$\dot{\mathsf{\Phi }}=-\frac{1}{2}\sqrt{\frac{3}{2\left|{\omega }_{BD}\right|}}\left(2\kappa -\lambda \right)cos\mathsf{\Theta }sin\left(2\mathsf{\Phi }\right),\mathsf{\Theta }=\frac{\pi }{4}\mathrm{or}\mathsf{\Theta }=\frac{3\pi }{4}.$$

(40)

The first equation indicates that when the dynamical system lies at the infinity, it stays at $\rho \to 1$. Moreover, from the second equation, it follows that ${\mathsf{\Phi }}_1=0,{\mathsf{\Phi }}_2=\frac{\pi }{2}$.

Hence, the stationary points $B=\left(\mathsf{\Theta }\left(B\right),\mathsf{\Phi }\left(B\right)\right)$ are $B_1=\left(\frac{\pi }{4},0\right)$, $B_2=\left(\frac{\pi }{4},\frac{\pi }{2}\right)$, $B_3=\left(\frac{3\pi }{4},0\right)$ and $B_4=\left(\frac{3\pi }{4},\frac{\pi }{2}\right)$. For the points $B_1$ and $B_3$, we derive $z\left(B_1\right)=0$ and $z\left(B_3\right)=0$, while for the points $B_2$ and $B_4$, we find $y\left(B_2\right)=0$ and $y\left(B_4\right)=0$.

As far as the stability properties of the points are concerned, we find that points $B_1$ and $B_4$ are attractors for $2\kappa -\lambda >0$, otherwise for $2\kappa -\lambda <0$ points $B_2$ and $B_4$ are attractors on the surface $\rho \to 1$.

5. Conclusions

Hyperbolic inflation is a two-scalar field model in the Einstein frame where the two scalar fields lie on a hyperbolic plane. This model admits an attractor, which describes an inflationary solution where the two scalar fields contribute to the cosmological solution.

In this piece of work, we consider a cosmological model of two-scalar fields in the Jordan frame, which recovers the multi-field model of hyperbolic inflation under a conformal transformation. The main motivation of this study is to investigate the nature of the attractor that corresponds to the hyperbolic inflation under conformal transformations.

For our model, which is an extension of the Brans–Dicke, and in the case of a spatially flat FLRW geometry, we performed a detailed analysis of the dynamics of the field equations by using normal variables. The Brans–Dicke theory is recovered, however we found a set of stationary points, namely $A_3^{\pm }$, where all the components of the gravitational Action Integral contribute to the cosmological solution. The asymptotic solutions at the points $A_3^{\pm }$ are scaling solutions, which can describe accelerated universes. Thus, these solutions can be seen as the analogue of the hyperbolic inflation in Jordan frame.

Furthermore, surprisingly, points $A_3^{\pm }$ are stable spirals, which means that they are in the same nature as the attractor of the hyperbolic inflation in the Einstein frame. That is an interesting result because the physical properties and the stability properties of the hyperbolic inflation remain invariant under conformal transformation.

At this point, we wish to briefly discuss the hyperbolic inflationary solution in the presence of anisotropy. We assume the locally rotational Bianchi I spacetime with line element

$$d{s}^2=-d{t}^2+a^2\left(e^{2\sigma }d{x}^2+e^{-\sigma }\left(d{y}^2+d{z}^2\right)\right),$$

(41)

and by using dimensionless-like variables as before, we conclude that the isotropic inflationary solution described by the stationary points $A_3^{\pm }$ exist, with the same physical properties as before, and the same stability properties. Hence, the hyperbolic inflation in the Jordan frame is an isotropic attractor and can solve the isotropization problem as in the case of the Einstein frame. Finally, we conclude that no new anisotropic exact solutions are provided by this model except that of that of the standard Brans–Dicke theory.

In a future work, we plan to investigate in detail the presence of curvature and anisotropy in the initial conditions of the theory.