Density Matrix Formalism for Interacting Quantum Fields
Abstract
1. Introduction
2. Derivation
2.1. Density Matrices in Fock Space
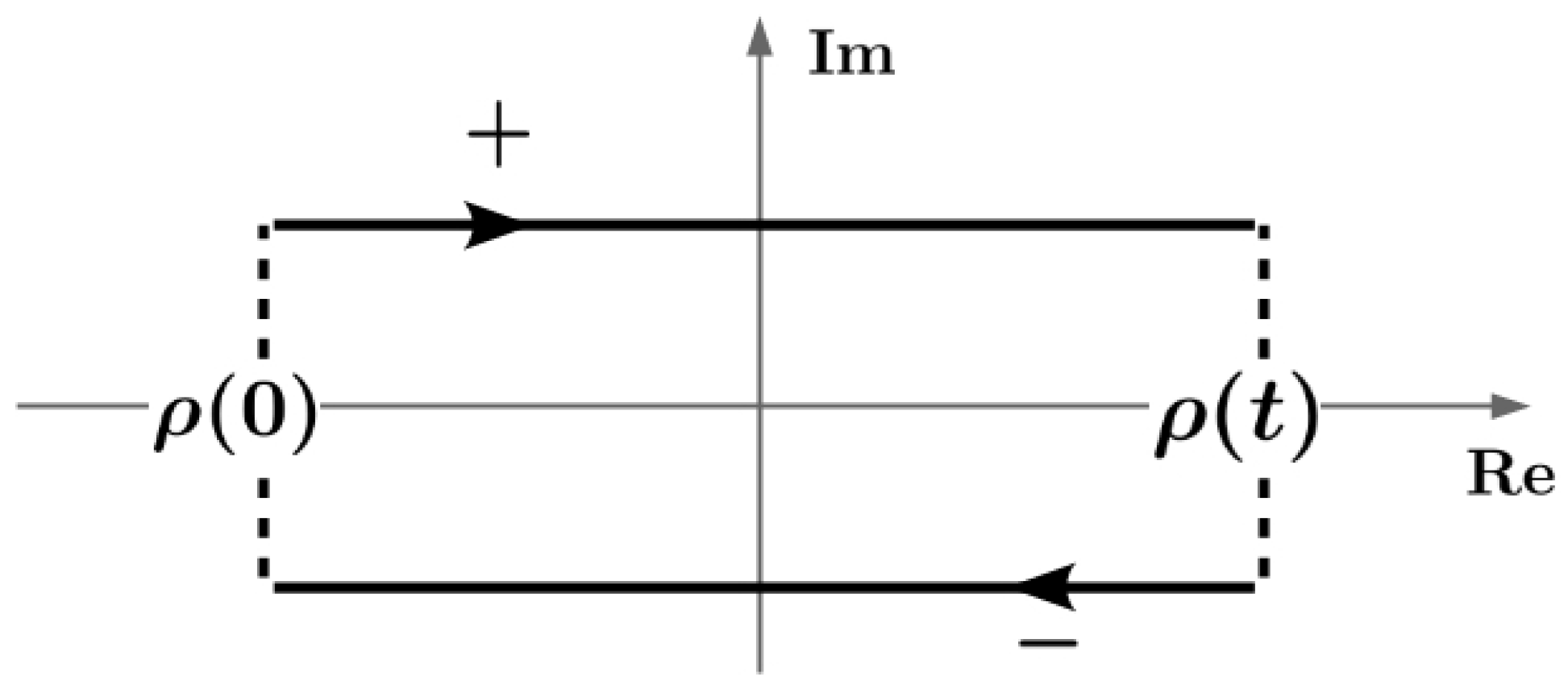
2.2. The Schwinger-Keldysh Formalism
2.3. Thermo-Field Dynamics
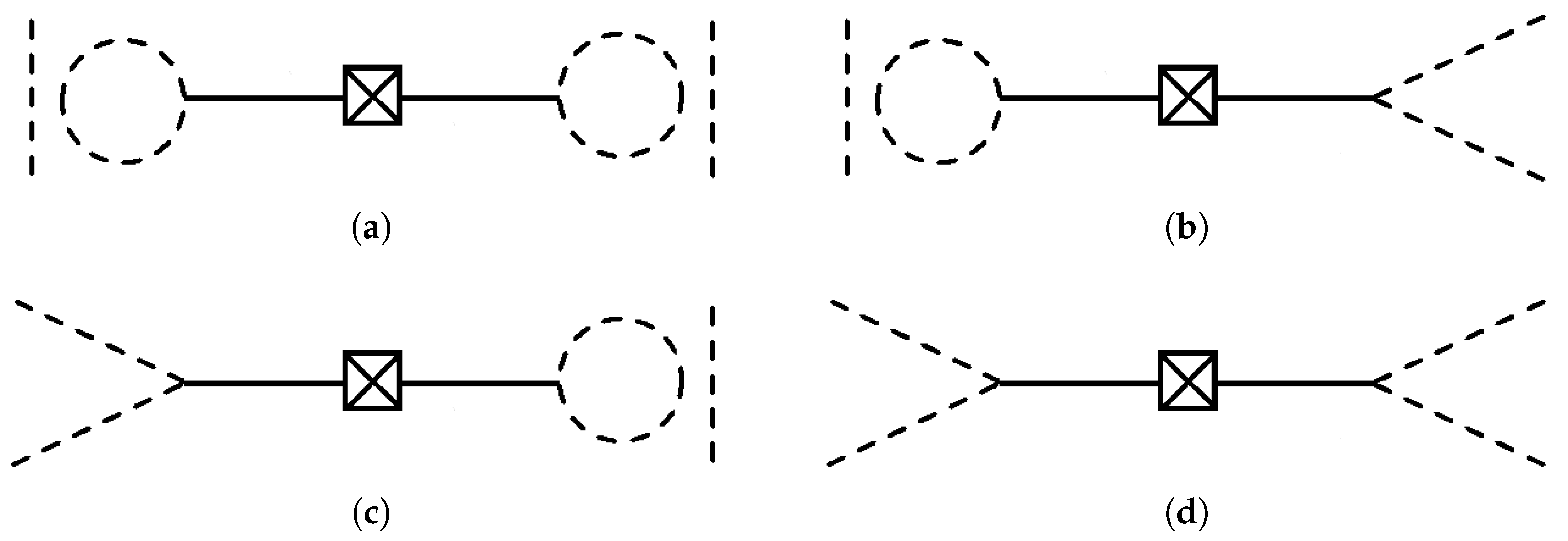
2.4. Density Matrix Elements
3. Example
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LSZ | Lehmann-Szymanzik-Zimmermann |
| TFD | Thermo field dynamics |
| 1 | Later we will also make use of for the 4-momenta. |
| 2 | We use throughout the entire article. |
| 3 | The extension to more field species is straightforward. |
| 4 | Compare it to the influence functional propagator in the literature, e.g., in Ref. [5]. |
References
- Schlosshauer, M. Decoherence and the Quantum-To-Classical Transition; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Calabrese, P.; Cardy, J.L. Entanglement entropy and quantum field theory. J. Stat. Mech. 2004, 2004, P06002. [Google Scholar] [CrossRef]
- Calabrese, P.; Cardy, J.L. Entanglement entropy and quantum field theory: A Non-technical introduction. Int. J. Quant. Inf. 2006, 4, 429. [Google Scholar] [CrossRef]
- Gavrilov, S.P.; Gitman, D.M.; Tomazelli, J.L. Density matrix of a quantum field in a particle-creating background. Nucl. Phys. B 2008, 795, 645–677. [Google Scholar] [CrossRef]
- Calzetta, E.A.; Hu, B.L. Nonequilibrium Quantum Field Theory; Cambridge University Press: Cambridge UK, 2008. [Google Scholar]
- Casini, H.; Huerta, M. Entanglement entropy in free quantum field theory. J. Phys. A 2009, 42, 504007. [Google Scholar] [CrossRef]
- Balasubramanian, V.; McDermott, M.B.; Van Raamsdonk, M. Momentum-space entanglement and renormalization in quantum field theory. Phys. Rev. D 2012, 86, 045014. [Google Scholar] [CrossRef]
- Boyanovsky, D. Effective field theory out of equilibrium: Brownian quantum fields. New J. Phys. 2015, 17, 063017. [Google Scholar] [CrossRef]
- Doyon, B. Nonequilibrium density matrix for thermal transport in quantum field theory. In Strongly Interacting Quantum Systems out of Equilibrium: Lecture Notes of the Les Houches Summer School: Volume 99, August 2012; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Sieberer, L.M.; Buchhold, M.; Diehl, S. Keldysh field theory for driven open quantum systems. Rep. Prog. Phys. 2016, 79, 096001. [Google Scholar] [CrossRef]
- Marino, J.; Diehl, S. Quantum dynamical field theory for nonequilibrium phase transitions in driven open systems. Phys. Rev. B 2016, 94, 085150. [Google Scholar] [CrossRef]
- Baidya, A.; Jana, C.; Loganayagam, R.; Rudra, A. Renormalization in open quantum field theory. Part I. Scalar field theory. JHEP 2017, 11, 204. [Google Scholar] [CrossRef]
- Engelhardt, N.; Fischetti, S. Causal density matrices. Phys. Rev. D 2017, 95, 126012. [Google Scholar] [CrossRef]
- Burrage, C.; Käding, C.; Millington, P.; Minář, J. Open quantum dynamics induced by light scalar fields. Phys. Rev. D 2019, 100, 076003. [Google Scholar] [CrossRef]
- Zhang, J.; Ruggiero, P.; Calabrese, P. Subsystem Trace Distance in Quantum Field Theory. Phys. Rev. Lett. 2019, 122, 141602. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Qi, X.L.; Shangnan, Z.; Yang, Z. Effective entropy of quantum fields coupled with gravity. JHEP 2020, 10, 052. [Google Scholar] [CrossRef]
- Nagy, S.; Polonyi, J. Renormalizing Open Quantum Field Theories. Universe 2022, 8, 127. [Google Scholar] [CrossRef]
- Jana, C. Aspects of Open Quantum Field Theory. Ph.D. Thesis, Tata Institute, Mumbai, India, 2021. [Google Scholar]
- Fogedby, H.C. Field-theoretical approach to open quantum systems and the Lindblad equation. Phys. Rev. A 2022, 106, 022205. [Google Scholar] [CrossRef]
- Emonts, P.; Kukuljan, I. Reduced density matrix and entanglement in interacting quantum field theory with Hamiltonian truncation. Phys. Rev. Res. 2022, 4, 033039. [Google Scholar] [CrossRef]
- Käding, C.; Pitschmann, M. A new method for directly computing reduced density matrices. arXiv 2022, arXiv:2204.08829. [Google Scholar]
- Boyanovsky, D. Thermalization by off-shell processes: The virtues of small virtuality. Phys. Rev. D 2022, 106, 045019. [Google Scholar] [CrossRef]
- Kaplanek, G.; Tjoa, E. Mapping Markov: On effective master equations for two accelerated qubits. arXiv 2022, arXiv:2207.13750. [Google Scholar]
- Lombardo, F.; Mazzitelli, F.D. Coarse graining and decoherence in quantum field theory. Phys. Rev. D 1996, 53, 2001–2011. [Google Scholar] [CrossRef]
- Lombardo, F.C.; Nacir, D.L. Decoherence during inflation: The generation of classical inhomogeneities. Phys. Rev. D 2005, 72, 063506. [Google Scholar] [CrossRef]
- Lombardo, F.C. Influence functional approach to decoherence during inflation. Braz. J. Phys. 2005, 35, 391–396. [Google Scholar] [CrossRef]
- Boyanovsky, D. Effective field theory during inflation: Reduced density matrix and its quantum master equation. Phys. Rev. 2015, D92, 023527. [Google Scholar] [CrossRef]
- Boyanovsky, D. Effective field theory during inflation. II. Stochastic dynamics and power spectrum suppression. Phys. Rev. 2016, D93, 043501. [Google Scholar] [CrossRef]
- Boyanovsky, D. Fermionic influence on inflationary fluctuations. Phys. Rev. 2016, D93, 083507. [Google Scholar] [CrossRef]
- Boyanovsky, D. Imprint of entanglement entropy in the power spectrum of inflationary fluctuations. Phys. Rev. 2018, D98, 023515. [Google Scholar] [CrossRef]
- Burgess, C.P.; Holman, R.; Tasinato, G.; Williams, M. EFT beyond the horizon: Stochastic inflation and how primordial quantum fluctuations go classical. J. High Energy Phys. 2015, 2015, 90. [Google Scholar] [CrossRef]
- Hollowood, T.J.; McDonald, J.I. Decoherence, discord, and the quantum master equation for cosmological perturbations. Phys. Rev. D 2017, 95, 103521. [Google Scholar] [CrossRef]
- Emond, W.T.; Millington, P.; Saffin, P.M. Boltzmann equations for preheating. JCAP 2018, 9, 041. [Google Scholar] [CrossRef]
- Colas, T.; Grain, J.; Vennin, V. Four-mode squeezed states: Two-field quantum systems and the symplectic group Sp(4,R). Eur. Phys. J. C 2022, 82, 6. [Google Scholar] [CrossRef]
- Brahma, S.; Berera, A.; Calderón-Figueroa, J. Universal signature of quantum entanglement across cosmological distances. arXiv 2021, arXiv:2107.06910. [Google Scholar] [CrossRef]
- Brahma, S.; Berera, A.; Calderón-Figueroa, J. Quantum corrections to the primordial tensor spectrum: Open EFTs & Markovian decoupling of UV modes. JHEP 2022, 8, 225. [Google Scholar] [CrossRef]
- Colas, T.; Grain, J.; Vennin, V. Benchmarking the cosmological master equations. arXiv 2022, arXiv:2209.01929. [Google Scholar]
- Yu, H.W.; Zhang, J.; Yu, H.w.; Zhang, J.l. Understanding Hawking radiation in the framework of open quantum systems. Phys. Rev. D 2008, 77, 024031, Erratum in Phys. Rev. D 2008, 77, 029904. [Google Scholar] [CrossRef]
- Lombardo, F.C.; Turiaci, G.J. Dynamics of an Acoustic Black Hole as an Open Quantum System. Phys. Rev. D 2013, 87, 084028. [Google Scholar] [CrossRef]
- Kaplanek, G.; Burgess, C.P. Qubits on the Horizon: Decoherence and Thermalization near Black Holes. JHEP 2021, 1, 098. [Google Scholar] [CrossRef]
- Burgess, C.P.; Holman, R.; Kaplanek, G. Quantum Hotspots: Mean Fields, Open EFTs, Nonlocality and Decoherence Near Black Holes. Fortschritte der Physik 2022, 70, 2200019. [Google Scholar] [CrossRef]
- Kaplanek, G.; Burgess, C.P.; Holman, R. Qubit heating near a hotspot. JHEP 2021, 8, 132. [Google Scholar] [CrossRef]
- Brambilla, N.; Escobedo, M.A.; Soto, J.; Vairo, A. Quarkonium suppression in heavy-ion collisions: An open quantum system approach. Phys. Rev. 2017, D96, 034021. [Google Scholar] [CrossRef]
- Brambilla, N.; Escobedo, M.A.; Soto, J.; Vairo, A. Heavy quarkonium suppression in a fireball. Phys. Rev. 2018, D97, 074009. [Google Scholar] [CrossRef]
- Akamatsu, Y. Quarkonium in quark–gluon plasma: Open quantum system approaches re-examined. Prog. Part. Nucl. Phys. 2022, 123, 103932. [Google Scholar] [CrossRef]
- De Jong, W.A.; Metcalf, M.; Mulligan, J.; Płoskoń, M.; Ringer, F.; Yao, X. Quantum simulation of open quantum systems in heavy-ion collisions. Phys. Rev. D 2021, 104, 051501. [Google Scholar] [CrossRef]
- Yao, X. Open quantum systems for quarkonia. Int. J. Mod. Phys. A 2021, 36, 2130010. [Google Scholar] [CrossRef]
- Brambilla, N.; Escobedo, M.A.; Strickland, M.; Vairo, A.; Vander Griend, P.; Weber, J.H. Bottomonium production in heavy-ion collisions using quantum trajectories: Differential observables and momentum anisotropy. Phys. Rev. D 2021, 104, 094049. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Lehmann, H.; Symanzik, K.; Zimmermann, W. On the formulation of quantized field theories. Nuovo Cim. 1955, 1, 205–225. [Google Scholar] [CrossRef]
- Burrage, C.; Käding, C.; Millington, P.; Minář, J. Influence functionals, decoherence and conformally coupled scalars. J. Phys. Conf. Ser. 2019, 1275, 012041. [Google Scholar] [CrossRef]
- Käding, C. Astro- and Quantum Physical Tests of Screened Scalar Fields. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2019. [Google Scholar]
- Feynman, R.P.; Vernon, F.L. The theory of a general quantum system interacting with a linear dissipative system. Ann. Phys. 1963, 24, 118–173. [Google Scholar] [CrossRef]
- Millington, P.; Pilaftsis, A. Perturbative nonequilibrium thermal field theory. Phys. Rev. 2013, D88, 085009. [Google Scholar] [CrossRef]
- Millington, P.; Pilaftsis, A. Perturbative Non-Equilibrium Thermal Field Theory to all Orders in Gradient Expansion. Phys. Lett. 2013, B724, 56–62. [Google Scholar] [CrossRef]
- Schwinger, J.S. Brownian Motion of a Quantum Oscillator. J. Math. Phys. 1961, 2, 407–432. [Google Scholar] [CrossRef]
- Keldysh, L.V. Diagram technique for nonequilibrium processes. Sov. Phys. JETP 1965, 20, 1018–1026. [Google Scholar]
- Takahasi, Y.; Umezawa, H. Thermo field dynamics. Collect. Phenom. 1975, 2, 55–80. [Google Scholar]
- Arimitsu, T.; Umezawa, H. A General Formulation of Nonequilibrium Thermo Field Dynamics. Prog. Theor. Phys. 1985, 74, 429–432. [Google Scholar] [CrossRef]
- Arimitsu, T.; Umezawa, H. Non-Equilibrium Thermo Field Dynamics. Prog. Theor. Phys. 1987, 77, 32. [Google Scholar] [CrossRef]
- Khanna, F.C.; Malbouisson, A.P.C.; Malbouisson, J.M.C.; Santana, A.E. Thermal Quantum Field Theory: Algebraic Aspects and Applications; World Scientific: Singapore, 2009. [Google Scholar]
- Wick, G.C. The Evaluation of the Collision Matrix. Phys. Rev. 1950, 80, 268–272. [Google Scholar] [CrossRef]
- Käding, C.; Millington, P.; Pitschmann, M. 2023.

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Käding, C.; Pitschmann, M. Density Matrix Formalism for Interacting Quantum Fields. Universe 2022, 8, 601. https://doi.org/10.3390/universe8110601
Käding C, Pitschmann M. Density Matrix Formalism for Interacting Quantum Fields. Universe. 2022; 8(11):601. https://doi.org/10.3390/universe8110601
Chicago/Turabian StyleKäding, Christian, and Mario Pitschmann. 2022. "Density Matrix Formalism for Interacting Quantum Fields" Universe 8, no. 11: 601. https://doi.org/10.3390/universe8110601
APA StyleKäding, C., & Pitschmann, M. (2022). Density Matrix Formalism for Interacting Quantum Fields. Universe, 8(11), 601. https://doi.org/10.3390/universe8110601





