Weak Deflection Angle by Kalb–Ramond Traversable Wormhole in Plasma and Dark Matter Mediums
Abstract
1. Introduction
2. Kalb–Ramond Traversable Wormhole Solution
3. Deflection Angle in the Plasma Medium
4. Graphical Behavior of the Deflection Angle
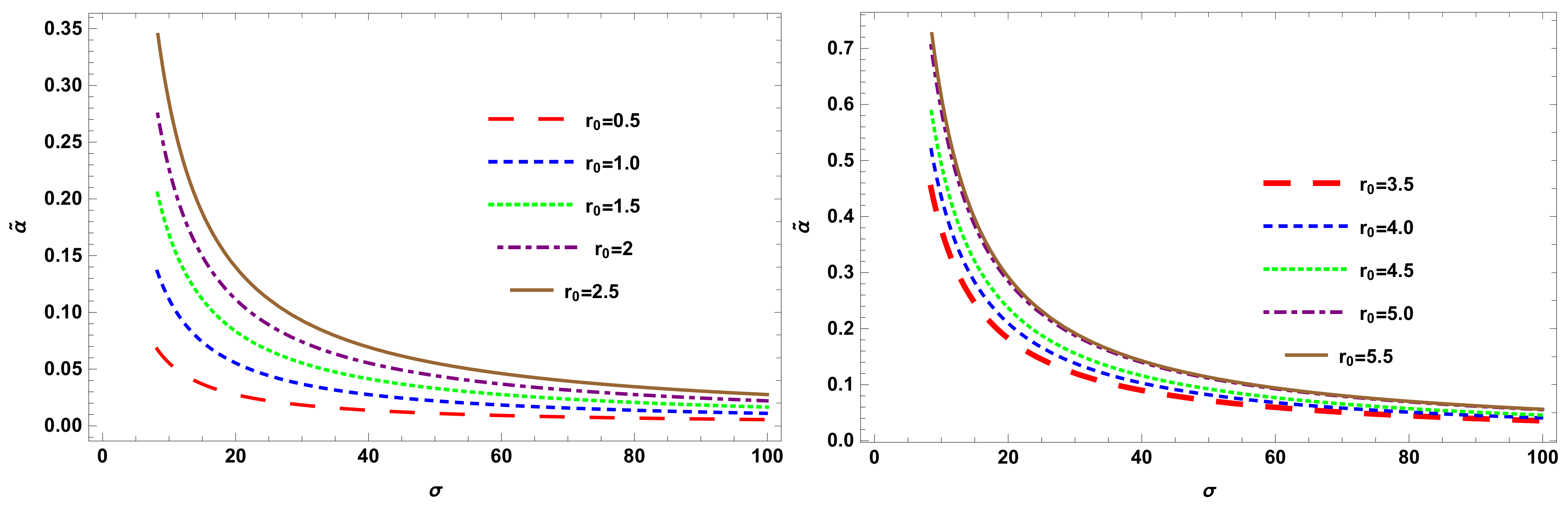
4.1. versus
4.2. versus
5. Deflection Angle Using the Keeton and Petters Method
6. Deflection Angle of a Photon in the Dark Matter Medium
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Javed, W.; Abbas, G.; Ali, R. Charged vector particle tunneling from a pair of accelerating and rotating and 5D gauged super-gravity black holes. Eur. Phys. J. C 2017, 77, 296. [Google Scholar] [CrossRef]
- Einstein, A.; Rosen, N. The Particle Problem in the General Theory of Relativity. Phys. Rev. 1935, 48, 73–77. [Google Scholar] [CrossRef]
- Javed, W.; Khadim, M.B.; Övgün, A.; Abbas, J. Weak gravitational lensing by stringy black holes. Eur. Phys. J. Plus 2020, 135, 314. [Google Scholar] [CrossRef]
- Visser, M. Lorentzian Wormholes: From Einstein to Hawking; American Institute of Physics: New York, NY, USA, 1996. [Google Scholar]
- Wheeler, J.A. Geons. Phys. Rev. 1955, 97, 511–536. [Google Scholar] [CrossRef]
- Fuller, R.W.; Wheeler, J.A. Causality and Multiply Connected Space-Time. Phys. Rev. 1962, 128, 919–929. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S. Wormholes in space-time and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar] [CrossRef]
- Hochberg, D.; Visser, M. The Null energy condition in dynamic wormholes. Phys. Rev. Lett. 1998, 81, 746–749. [Google Scholar] [CrossRef]
- Visser, M. Traversable wormholes: Some simple examples. Phys. Rev. D 1989, 39, 3182–3184. [Google Scholar] [CrossRef] [PubMed]
- Ellis, H.G. Ether flow through a drainhole - a particle model in general relativity. J. Math. Phys. 1973, 14, 104–118. [Google Scholar] [CrossRef]
- Chetouani, L.; Clement, L.G. Geometrical optics in the Ellis geometry. Gen. Relat. Gravit. 1984, 16, 111–119. [Google Scholar] [CrossRef]
- Nakajima, K.; Asada, H. Deflection angle of light in an Ellis wormhole geometry. Phys. Rev. D 2012, 85, 107501. [Google Scholar] [CrossRef]
- Kuhfittig, P.K.F. Gravitational lensing of wormholes in the galactic halo region. Eur. Phys. J. C 2014, 74, 2818. [Google Scholar] [CrossRef]
- Tsukamoto, N.; Gong, Y. Extended source effect on microlensing light curves by an Ellis wormhole. Phys. Rev. D 2018, 97, 084051. [Google Scholar] [CrossRef]
- Tsukamoto, N.; Harada, T. Light curves of light rays passing through a wormhole. Phys. Rev. D 2017, 95, 024030. [Google Scholar] [CrossRef]
- Tsukamoto, N. Strong deflection limit analysis and gravitational lensing of an Ellis wormhole. Phys. Rev. D 2016, 94, 124001. [Google Scholar] [CrossRef]
- Tsukamoto, N.; Gong, Y. Retrolensing by a charged black hole. Phys. Rev. D 2017, 95, 064034. [Google Scholar] [CrossRef]
- Tsukamoto, N. Deflection angle in the strong deflection limit in a general asymptotically flat, static, spherically symmetric spacetime. Phys. Rev. D 2017, 95, 064035. [Google Scholar] [CrossRef]
- Övgün, A.; Sakallı, İ.; Saavedra, J. Shadow cast and Deflection angle of Kerr-Newman-Kasuya spacetime. JCAP 2018, 10, 41. [Google Scholar] [CrossRef]
- Sakalli, I.; Övgün, A. Hawking Radiation and Deflection of Light from Rindler Modified Schwarzschild Black Hole. EPL 2017, 118, 60006. [Google Scholar] [CrossRef]
- Övgün, A.; Jusufi, K.; Sakalli, I. Gravitational lensing under the effect of Weyl and bumblebee gravities: Applications of Gauss–Bonnet theorem. Ann. Phys. 2018, 399, 193–203. [Google Scholar] [CrossRef]
- Övgün, A. Deflection Angle of Photons through Dark Matter by Black Holes and Wormholes Using Gauss–Bonnet Theorem. Universe 2019, 5, 115. [Google Scholar] [CrossRef]
- Övgün, A.; Sakallı, İ.; Saavedra, J. Weak gravitational lensing by Kerr-MOG black hole and Gauss–Bonnet theorem. Ann. Phys. 2019, 411, 167978. [Google Scholar] [CrossRef]
- Övgün, A.; Sakallı, İ. Testing generalized Einstein–Cartan–Kibble–Sciama gravity using weak deflection angle and shadow cast. Class. Quant. Grav. 2020, 37, 225003. [Google Scholar] [CrossRef]
- Jusufi, K.; Werner, M.C.; Banerjee, A.; Övgün, A. Light Deflection by a Rotating Global Monopole Spacetime. Phys. Rev. D 2017, 95, 104012. [Google Scholar] [CrossRef]
- Jusufi, K.; Övgün, A.; Saavedra, J.; Vásquez, Y.; González, P.A. Deflection of light by rotating regular black holes using the Gauss–Bonnet theorem. Phys. Rev. D 2018, 97, 124024. [Google Scholar] [CrossRef]
- Javed, W.; Babar, R.; Övgün, A. The effect of the Brane-Dicke coupling parameter on weak gravitational lensing by wormholes and naked singularities. Phys. Rev. D 2019, 99, 084012. [Google Scholar] [CrossRef]
- Övgün, A. Weak field deflection angle by regular black holes with cosmic strings using the Gauss–Bonnet theorem. Phys. Rev. D 2019, 99, 104075. [Google Scholar] [CrossRef]
- Övgün, A.; Jusufi, K.; Sakallı, İ. Exact traversable wormhole solution in bumblebee gravity. Phys. Rev. D 2019, 99, 024042. [Google Scholar] [CrossRef]
- Övgün, A.; Gyulchev, G.; Jusufi, K. Weak Gravitational lensing by phantom black holes and phantom wormholes using the Gauss–Bonnet theorem. Ann. Phys. 2019, 406, 152–172. [Google Scholar] [CrossRef]
- Li, Z.; Övgün, A. Finite-distance gravitational deflection of massive particles by a Kerr-like black hole in the bumblebee gravity model. Phys. Rev. D 2020, 101, 024040. [Google Scholar] [CrossRef]
- Javed, W.; Abbas, J.; Övgün, A. Deflection angle of photon from magnetized black hole and effect of nonlinear electrodynamics. Eur. Phys. J. C 2019, 79, 694. [Google Scholar] [CrossRef]
- Javed, W.; Abbas, j.; Övgün, A. Effect of the Hair on Deflection Angle by Asymptotically Flat Black Holes in Einstein-Maxwell-Dilaton Theory. Phys. Rev. D 2019, 100, 044052. [Google Scholar] [CrossRef]
- Jusufi, K.; Övgün, A.; Banerjee, A.; Sakallı, İ. Gravitational lensing by wormholes supported by electromagnetic, scalar, and quantum effects. Eur. Phys. J. Plus 2019, 134, 428. [Google Scholar] [CrossRef]
- Javed, W.; Babar, R.; Övgün, A. Effect of the dilaton field and plasma medium on deflection angle by black holes in Einstein-Maxwell-dilaton-axion theory. Phys. Rev. D 2019, 100, 104032. [Google Scholar] [CrossRef]
- Kumaran, Y.; Övgün, A. Weak Deflection Angle of Extended Uncertainty Principle Black Holes. Chin. Phys. C 2020, 44, 025101. [Google Scholar] [CrossRef]
- Övgün, A.; Kumaran, Y.; Javed, W.; Abbas, J. Effect of Horndeski theory on weak deflection angle using the Gauss–Bonnet theorem. Int. J. Geom. Meth. Mod. Phys. 2022, 19, 2250192. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, G.; Övgün, A. Circular Orbit of a Particle and Weak Gravitational Lensing. Phys. Rev. D 2020, 101, 124058. [Google Scholar] [CrossRef]
- Okyay, M.; Övgün, A. Nonlinear electrodynamics effects on the black hole shadow, deflection angle, quasinormal modes and greybody factors. JCAP 2022, 1, 9. [Google Scholar] [CrossRef]
- Javed, W.; Abbas, J.; Övgün, A. Effect of the Quintessential Dark Energy on Weak Deflection Angle by Kerr-Newmann Black Hole. Ann. Phys. 2020, 418, 168183. [Google Scholar] [CrossRef]
- Javed, W.; Hamza, A.; Övgün, A. Effect of nonlinear electrodynamics on the weak field deflection angle by a black hole. Phys. Rev. D 2020, 101, 103521. [Google Scholar] [CrossRef]
- Övgün, A. Weak Deflection Angle of Black-bounce Traversable Wormholes Using Gauss–Bonnet Theorem in the Dark Matter Medium. Turk. J. Phys. 2020, 44, 465–471. [Google Scholar] [CrossRef]
- Javed, W.; Khadim, M.B.; Övgün, A. Weak gravitational lensing by Bocharova–Bronnikov–Melnikov–Bekenstein black holes using Gauss–Bonnet theorem. Eur. Phys. J. Plus 2020, 135, 595. [Google Scholar] [CrossRef]
- Çimdiker, İ.; Demir, D.; Övgün, A. Black hole shadow in symmergent gravity. Phys. Dark Univ. 2021, 34, 100900. [Google Scholar] [CrossRef]
- Kumaran, Y.; Övgün, A. Deriving weak deflection angle by black holes or wormholes using Gauss–Bonnet theorem. Turk. J. Phys. 2021, 45, 247–267. [Google Scholar]
- Javed, W.; Abbas, J.; Kumaran, Y.; Övgün, A. Weak deflection angle by asymptotically flat black holes in Horndeski theory using Gauss–Bonnet theorem. Int. J. Geom. Meth. Mod. Phys. 2021, 18, 2150003. [Google Scholar] [CrossRef]
- Pantig, R.C.; Övgün, A. Dark matter effect on the weak deflection angle by black holes at the center of Milky Way and M87 galaxies. Eur. Phys. J. C 2022, 82, 391. [Google Scholar] [CrossRef]
- Pantig, R.C.; Övgün, A. Dehnen halo effect on a black hole in an ultra-faint dwarf galaxy. JCAP 2022, 8, 56. [Google Scholar] [CrossRef]
- Pantig, R.C.; Rodulfo, E.T. Weak deflection angle of a dirty black hole. Chin. J. Phys. 2020, 66, 691–702. [Google Scholar] [CrossRef]
- Pantig, R.C.; Yu, P.K.; Rodulfo, E.T.; Övgün, A. Shadow and weak deflection angle of extended uncertainty principle black hole surrounded with dark matter. Ann. Phys. 2022, 436, 168722. [Google Scholar] [CrossRef]
- Sharif, M.; Iftikhar, S. Strong gravitational lensing in non-commutative wormholes. Astrophys. Space Sci. 2015, 357, 85. [Google Scholar] [CrossRef]
- Shaikh, R.; Kar, S. Gravitational lensing by scalar-tensor wormholes and the energy conditions. Phys. Rev. D 2017, 96, 044037. [Google Scholar] [CrossRef]
- Sajadi, S.N.; Riazi, N. Gravitational lensing by multi-polytropic wormholes. Can. J. Phys. 2020, 98, 1046–1054. [Google Scholar] [CrossRef]
- Asada, H. Gravitational lensing by exotic objects. Mod. Phys. Lett. A 2017, 32, 1730031. [Google Scholar] [CrossRef]
- Yoo, C.M.; Harada, T.; Tsukamoto, N. Wave Effect in Gravitational Lensing by the Ellis Wormhole. Phys. Rev. D 2013, 87, 084045. [Google Scholar] [CrossRef]
- Tsukamoto, N.; Harada, T.; Yajima, K. Can we distinguish between black holes and wormholes by their Einstein ring systems? Phys. Rev. D 2012, 86, 104062. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Potapov, A.A. Bending of light in Ellis wormhole geometry. Mod. Phys. Lett. A 2010, 25, 2399–2409. [Google Scholar] [CrossRef]
- Liebes, J. Gravitational Lenses. Phys. Rev. 1964, 133, 835. [Google Scholar] [CrossRef]
- Refsdal, S. The gravitational lens effect. Mon. Not. Roy. Astron. Soc. 1964, 128, 295. [Google Scholar] [CrossRef]
- Pantig, R.C.; Mastrototaro, L.; Lambiase, G.; Övgün, A. Shadow, lensing and neutrino propagation by dyonic ModMax black holes. arXiv 2022, arXiv:2208.06664. [Google Scholar]
- Barriola, M.; Vilenkin, A. Gravitational Field of a Global Monopole. Phys. Rev. Lett. 1989, 63, 341. [Google Scholar] [CrossRef]
- Keeton, C.R.; Kochanek, C.S.; Falco, E.E. The Optical properties of gravitational lens galaxies as a probe of galaxy structure and evolution. Astrophys. J. 1998, 509, 561–578. [Google Scholar] [CrossRef]
- Eiroa, E.F.; Romero, G.E.; Torres, D.F. Reissner-Nordstrom black hole lensing. Phys. Rev. D 2002, 66, 024010. [Google Scholar] [CrossRef]
- Uniyal, A.; Pantig, R.C.; Övgün, A. Probing a nonlinear electrodynamics black hole with thin accretion disk, shadow and deflection angle with M87* and Sgr A* from EHT. arXiv 2022, arXiv:2205.11072. [Google Scholar]
- Pantig, R.C.; Övgün, A. Testing dynamical torsion effects on the charged black hole’s shadow, deflection angle and greybody with M87* and Sgr A* from EHT. arXiv 2022, arXiv:2206.02161. [Google Scholar]
- Rayimbaev, J.; Pantig, R.C.; Övgün, A.; Abdujabbarov, A.; Demir, D. Quasiperiodic oscillations, weak field lensing and shadow cast around black holes in Symmergent gravity. arXiv 2022, arXiv:2206.06599. [Google Scholar]
- Mustafa, G.; Atamurotov, F.; Hussain, I.; Shaymatov, S.; Övgün, A. Shadows and gravitational weak lensing by the Schwarzschild black hole in the string cloud background with quintessential field. arXiv 2022, arXiv:2207.07608. [Google Scholar]
- Kuang, X.M.; Övgün, A. Strong gravitational lensing and shadow constraint from M87* of slowly rotating Kerr-like black hole. Ann. Phys. 2022, 447, 169147. [Google Scholar] [CrossRef]
- Javed, W.; Riaz, S.; Övgün, A. Weak Deflection Angle and Greybody Bound of Magnetized Regular Black Hole. Universe 2022, 8, 262. [Google Scholar] [CrossRef]
- Javed, W.; Hussain, I.; Övgün, A. Weak deflection angle of Kazakov–Solodukhin black hole in plasma medium using Gauss–Bonnet theorem and its greybody bonding. Eur. Phys. J. Plus 2022, 137, 148. [Google Scholar] [CrossRef]
- Javed, W.; Khadim, M.B.; Övgün, A. Weak gravitational lensing by Einstein-nonlinear-Maxwell–Yukawa black hole. Int. J. Geom. Meth. Mod. Phys. 2020, 17, 2050182. [Google Scholar] [CrossRef]
- Moumni, H.E.; Masmar, K.; Övgün, A. Weak deflection angle of light in two classes of black holes in nonlinear electrodynamics via Gauss–Bonnet theorem. Int. J. Geom. Meth. Mod. Phys. 2022, 19, 2250094. [Google Scholar] [CrossRef]
- Belhaj, A.; Belmahi, H.; Benali, M.; El, H.M. Light Deflection by Rotating Regular Black Holes with a Cosmological Constant. arXiv 2022, arXiv:2204.10150. [Google Scholar] [CrossRef]
- Belhaj, A.; Belmahi, H.; Benali, M.; Moumni, H.E. Light deflection angle by superentropic black holes. Int. J. Mod. Phys. D 2022, 31, 2250054. [Google Scholar] [CrossRef]
- Belhaj, A.; Benali, M.; Balali, A.E.; Moumni, H.E.; Ennadifi, S.E. Deflection angle and shadow behaviors of quintessential black holes in arbitrary dimensions. Class. Quant. Grav. 2020, 37, 215004. [Google Scholar] [CrossRef]
- Javed, W.; Aqib, M.; Övgün, A. Effect of the magnetic charge on weak deflection angle and greybody bound of the black hole in Einstein-Gauss–Bonnet gravity. Phys. Lett. B 2022, 829, 137114. [Google Scholar] [CrossRef]
- Javed, W.; Hamza, A.; Övgün, A. Weak Deflection Angle and Shadow by Tidal Charged Black Hole. Universe 2021, 7, 385. [Google Scholar] [CrossRef]
- Bozza, V. Gravitational lensing in the strong field limit. Phys. Rev. D 2002, 66, 103001. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Ellis, G.F.R. Schwarzschild black hole lensing. Phys. Rev. D 2000, 62, 084003. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Ellis, G.F.R. Gravitational lensing by naked singularities. Phys. Rev. D 2002, 65, 103004. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Narasimha, D.; Chitre, S.M. Role of the scalar field in gravitational lensing. Astron. Astrophys. 1998, 337, 1–8. [Google Scholar]
- Virbhadra, K.S.; Keeton, C.R. Time delay and magnification centroid due to gravitational lensing by black holes and naked singularities. Phys. Rev. D 2008, 77, 124014. [Google Scholar] [CrossRef]
- Virbhadra, K.S. Relativistic images of Schwarzschild black hole lensing. Phys. Rev. D 2009, 79, 083004. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Werner, M.C. Applications of the Gauss–Bonnet theorem to gravitational lensing. Class. Quant. Grav. 2008, 25, 235009. [Google Scholar] [CrossRef]
- Werner, M.C. Gravitational lensing in the Kerr-Randers optical geometry. Gen. Relativ. Gravit. 2012, 44, 3047–3057. [Google Scholar] [CrossRef]
- Ono, T.; Ishihara, A.; Asada, H. Gravitomagnetic bending angle of light with finite-distance corrections in stationary axisymmetric spacetimes. Phys. Rev. D 2017, 96, 104037. [Google Scholar] [CrossRef]
- Ono, T.; Ishihara, A.; Asada, H. Deflection angle of light for an observer and source at finite distance from a rotating wormhole. Phys. Rev. D 2018, 98, 044047. [Google Scholar] [CrossRef]
- Ono, T.; Ishihara, A.; Asada, H. Deflection angle of light for an observer and source at finite distance from a rotating global monopole. Phys. Rev. D 2019, 99, 124030. [Google Scholar] [CrossRef]
- Takizawa, K.; Ono, T.; Asada, H. Gravitational deflection angle of light: Definition by an observer and its application to an asymptotically nonflat spacetime. Phys. Rev. D 2020, 101, 104032. [Google Scholar] [CrossRef]
- Keeton, C.R.; Petters, A.O. Formalism for testing theories of gravity using lensing by compact objects. I. Static, spherically symmetric case. Phys. Rev. D 2005, 72, 104006. [Google Scholar] [CrossRef]
- Keeton, C.R.; Petters, A.O. Formalism for testing theories of gravity using lensing by compact objects. II. Probing post-post-Newtonian metrics. Phys. Rev. D 2006, 73, 044024. [Google Scholar] [CrossRef]
- Sereno, M.; Luca, F.D. Analytical Kerr black hole lensing in the weak deflection limit. Phys. Rev. D 2006, 74, 123009. [Google Scholar] [CrossRef]
- Jusufi, K.; Övgün, A. Gravitational Lensing by Rotating Wormholes. Phys. Rev. D 2018, 97, 024042. [Google Scholar] [CrossRef]
- Övgün, A. Light deflection by Damour-Solodukhin wormholes and Gauss–Bonnet theorem. Phys. Rev. D 2018, 98, 044033. [Google Scholar] [CrossRef]
- Feng, J.L. Dark Matter Candidates from Particle Physics and Methods of Detection. Ann. Rev. Astron. Astrophys. 2010, 48, 495–545. [Google Scholar] [CrossRef]
- Latimer, D.C. Dispersive Light Propagation at Cosmological Distances: Matter Effects. Phys. Rev. D 2013, 88, 063517. [Google Scholar] [CrossRef]
- Latimer, D.C. Anapole dark matter annihilation into photons. Phys. Rev. D 2017, 95, 095023. [Google Scholar] [CrossRef]
- Lessa, L.A.; Oliveira, R.; Silva, J.E.G.; Almeida, C.A.S. Traversable wormhole solution with a background Kalb–Ramond field. Ann. Phys. 2021, 433, 168604. [Google Scholar] [CrossRef]
- Crisnejo, G.; Gallo, E. Weak lensing in a plasma medium and gravitational deflection of massive particles using the Gauss–Bonnet theorem. A unified treatment. Phys. Rev. D 2018, 97, 124016. [Google Scholar] [CrossRef]
- Jusufi, K.; Övgün, A.; Banerjee, A. Light deflection by charged wormholes in Einstein-Maxwell-dilaton theory. Phys. Rev. D 2017, 96, 084036. [Google Scholar] [CrossRef]
- Arakida, H. Light deflection and Gauss–Bonnet theorem: Definition of total deflection angle and its applications. Gen. Relativ. Gravit. 2018, 50, 48. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javed, W.; Irshad, H.; Pantig, R.C.; Övgün, A. Weak Deflection Angle by Kalb–Ramond Traversable Wormhole in Plasma and Dark Matter Mediums. Universe 2022, 8, 599. https://doi.org/10.3390/universe8110599
Javed W, Irshad H, Pantig RC, Övgün A. Weak Deflection Angle by Kalb–Ramond Traversable Wormhole in Plasma and Dark Matter Mediums. Universe. 2022; 8(11):599. https://doi.org/10.3390/universe8110599
Chicago/Turabian StyleJaved, Wajiha, Hafsa Irshad, Reggie C. Pantig, and Ali Övgün. 2022. "Weak Deflection Angle by Kalb–Ramond Traversable Wormhole in Plasma and Dark Matter Mediums" Universe 8, no. 11: 599. https://doi.org/10.3390/universe8110599
APA StyleJaved, W., Irshad, H., Pantig, R. C., & Övgün, A. (2022). Weak Deflection Angle by Kalb–Ramond Traversable Wormhole in Plasma and Dark Matter Mediums. Universe, 8(11), 599. https://doi.org/10.3390/universe8110599







