Abstract
Radio radiation has been detected across the Hertzsprung Russell diagram. We selected three objects with radio radiation (a semi-detached eclipsing binary V Crt, and two detached binaries WY Cnc and CG Cyg) that show magnetic activity. We made new photometric observations using a SARA 60 cm and NAOC 85 cm optical telescopes. Then, we obtained their orbital and starspot parameters by analyzing our light curves and published radial velocities using the updated Wilson-Devinney program. We revised the ephemeris information for V Crt and WY Cnc by analyzing the orbital minimum times. The orbital periods increased by 2.8 () × d yr for V Crt, which maybe caused by mass transfer. The orbital periods decreased by −8.641 () × d yr for WY Cnc. Orbital period change for CG Cyg was also found and we used a third-body of of 0.14 M and a period of approximately 59.20 (0.36) yr to explain that. We also analysed the possible second period oscillation of CG Cyg with a cycle about 18.31 (0.06) yr. The long period changes of WY Cnc and CG Cyg might be caused by magnetic activity or stellar wind, rather than mass transfer.
1. Introduction
Radio radiation has been detected in all star types across the Hertzsprung–Russell diagram [1]. There exist approximately 150 eclipsing binaries that displayed radio emission. Stellar radio radiation provides the most direct probes of physical processes, including magnetic activity, particle acceleration, stellar disk and mass transport [2]. Early astronomy studies were based on the observation of visible bands because the study of astrophysics is dependent on the capabilities of the detection equipment. Radio technology, such as Very Large Array (VLA) [3], is improving with the advent technology, which allows the nature of radio to be studied. Early radio observations were influenced by many factors, for example, instrumentation and background radiation. Kellermann and Pauliny-Toth [4] observed that the radio signal of the star named Ori about 0.11 ± 0.03 Jy in the 2.8 cm band under such condition. Then, Seaquist [5] obtained the radio intensity of four stars in the 2.85 cm band. Güdel [1] presented a radio Hertzsprung-Russell diagram between 1 and 10 GHz based on a radio catalog with 3021 radio stars [6]. Later, Wendker [7] updated it to 3699 radio stars in 2001, and revealed the ubiquity of stellar radio emissions.
Obtaining the parameters of the eclipsing binaries with radio emissions is required for optical and radio observations. We selected three eclipsing binaries and revised their stellar parameters. The introduction of these three binaries (V Crt, WY Cnc, and CG Cyg) with radio radiations is as follows:
V Crt is a conventional semi-detached eclipsing binary with a period of 0.702 d, and was listed as a variable star [8]. Parthasarathy and Sanwal [9] obtained the light curve of photoelectric photometry in the B and V bands. V Crt was detected at a radio intensity close to 25 mJy at 10,600 MHz [10]. Liu [11] has studied more detail and obtained the orbit parameter of V Crt. Sarma and Vivekananda Rao [12] updated its stellar parameters with a mass ratio of q = 0.4, which is smaller than the result of 0.683 [11].
WY Cnc is an RS CVn type detached eclipsing binary with a period of 0.8293686 d [13], which shows strong photospheric starspot activity and chromospheric activity emissions in the H, and CaII HK lines. It exhibits radio emissions of 0.4 mJy at 4860 MHz and 0.23 mJy at 4885 MHz [7]. It was first defined as an Algol eclipsing system [14]. Rao and Sarma [15] performed preliminary statistics on the total brightness and discovered light curve distortion outside the eclipse. Subsequently, a systematic photometric study was conducted [16,17,18]. Xie et al. [19] analyzed the position of a spot on the photospheric surface, and found a starspot variation outside the eclipse. Helfand et al. [20] obtained a radio intensity of 0.4 to 0.5 mJy using the VLA FIRST survey. Hall et al. [21] observed a decreasing orbital period. Later, Albayrak et al. [22] found that WY Cnc has a third body with a possible light time effect of approximately 85 yr. Recently, many astronomers have obtained more light minimum [23,24,25,26,27,28,29,30,31,32,33,34]. Kjurkchieva et al. [35] revised the orbital parameters based on spectroscopic and photometric observations. Tian et al. [36] analyzed O-C and argued that the periodic change was because of the angular momentum loss of magnetic braking. Chen [37] analyzed the angular momentum loss and suggested that the period change may be due to magnetic braking or circum-binary disk, but also requires too strong magnetic field strength. Long-term photometric monitoring is therefore required to discuss the orbital period of WY Cnc.
CG Cyg is an RS CVn binary consisting of two dwarf components and has a period of 0.6311 d, which was discovered to be a variable star [38]. There is a radio emission of 25 mJy at 10,600 MHz [7]. Naftilan and Milone [39] obtained the spectral type of CG Cyg with G9V and K3V. The remarkable intrinsic variations was observed both outside and within the eclipse [40,41,42,43,44,45,46,47,48,49,50,51], which were explained the starspot models [42,51,52,53,54]. The period of CG Cyg was increased using light curve minima [44]. Later, Albayrak et al. [22] calculated the period variation using a model of a third-body orbit with period of 46.54 yr by fitting the light curve minimum. Afsar et al. [55] revised the period cycle of 51 or 22.5 yrs, which was caused by magnetic activity. Shi et al. [56] estimated that the period increased by 2.48 × 10d yr.
Because V Crt, WY Cnc and CG Cyg are short period eclipsing binaries with magnetic activity and radio radiation, we performed photometric observations using an optical telescope, and revise their orbital parameters. Further, we also collected the light curve minimum times of eclipsing binaries to analyze their period variation and discussed their physical mechanisms.
2. Radio Eclipsing Binaries and Photometric Follow-Up Observations
We found 150 eclipsing binaries from the updated catalogue of 3699 radio stars [7]. We collected their respective stellar parameters, including the coordinate, spectral types, stellar type, radio intensities at different wavelengths (1465 MHz, 1490 MHz, and 4860 MHz) and listed them in Table 1. The full table will be published in electric format. There are different type eclipsing binaries, such as Algol eclipsing binary, X-ray binaries, RS CVn binary, and so on). V Crt is one of the semi-detached binaries and belonged to the Beta Lyr binary type. We calculated the number of spectral types and binary types using the eclipse binaries exhibiting radio emission. The results are shown in Figure 1. As shown in Figure 1, most of the eclipsing binaries with radio emission are B and A spectral-type stars, whose radio radiation might be explained using the stellar wind. By contrast, the radio radiations of eclipsing binaries with spectral-types FGKM are likely caused by stellar magnetic activity [1,2].

Table 1.
Parameter of radio eclipsing binaries [6,7].
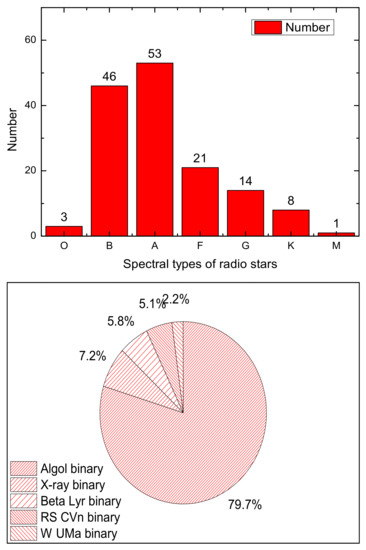
Figure 1.
The number distribution of 152 radio eclipsing binaries, where the top panel is the distribution of their spectral types, and the bottom panel is the distribution of the percentage of types of radio stars.
From the radio eclipsing binaries, we selected three objects (V Crt, CG Cyg, and WY Cnc) with short orbital periods to discuss their physical properties. We analyzed their stellar physical parameters via photometric method using an optical telescope. Our photometric observation for V Crt was conducted using the 60 cm optical telescope at the Southeastern Association for Research in Astronomy (SARA) in Chile on 27 February, 28 May, and 2 March 2020. They were conducted in four BVRI bands using a charge-coupled device (CCD) with resolution of a 1024 × 1024 pixels with BVRI filters of a Bessel system with a 13’ × 13’ field. The limit magnitude with an S/N of 10 is approximately 19 mag of V filter in 10 min [57]. For WY Cnc and CG Cyg, the CCD photometric observation data in BVRI were obtained using 85 cm optical telescope at the Xinglong station of the National Astronomical Observatories of China (NAOC). The detector used 1024 × 1024 pixels [58]. The photometric data of WY Cnc was observed on 25 and 30 December 2009, and 4, 6 and 7 January 2010, while CG Cyg was observed on 1, 2, and 3 October 2009. The CCD photometric images were reduced using the IRAF(IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.) package. The photometric data obtained after processing are listed in Table 2. TYC 6085-1462-1, 2-MASS J11240146-1639367 and NSV 25409 are the comparison stars of V Crt, WY Cnc and CG Cyg, respectively. The magnitude of the light curves of V Crt, CG Cyg, and WY Cnc obtained from our observations are plotted in Figure 2, Figure 3 and Figure 4, respectively.

Table 2.
Some examples of the observational Heliocentric Julian Date (HJD) and different magnitude of V Crt, WY Cnc and CG Cyg.
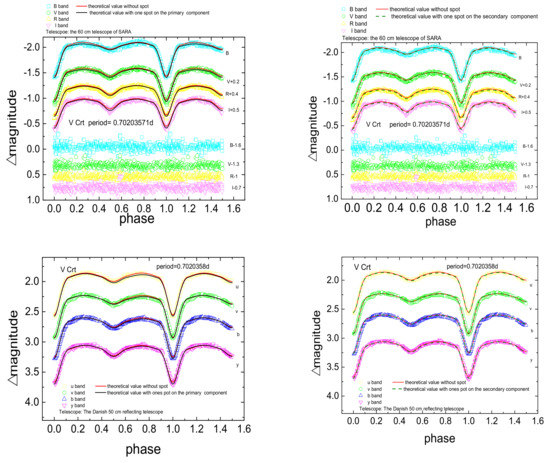
Figure 2.
The theoretical and observational light curves of V Crt, where observations are colored points; model light curves are solid lines.
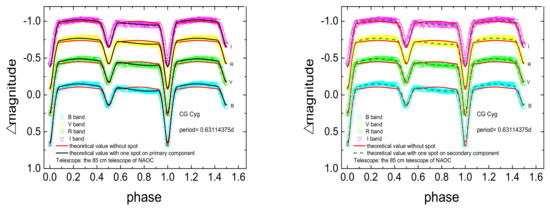
Figure 3.
The theoretical and observational light curves of CG Cyg, where the left panel shows the model with a spot on the primary component, and the right panel shows the model with spot on the secondary component.
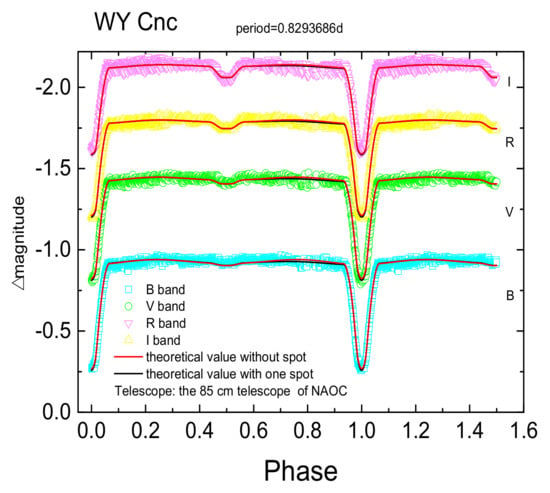
Figure 4.
The theoretical and observational light curves of WY Cnc, where the spot is on the primary component.
3. Period Analyses
It is important to calculate and collect the values of the light minimum time of the eclipsing binaries to determine the period variation and their physical mechanisms. We calculated the new minimum from our observations using the program reported by Nelson et al. [59], which uses polynomial fits [60]. The minimum times are listed in Table 3. Furthermore, we collected all available light minima times for our objects from the Eclipsing Binaries Minimum Times Database (http://var2.astro.cz/ocgate/ (accessed on 8 June 2016)) and previous articles. Table 4 lists the available light minima times, where the minimum times error is set by the mean uncertainties of other data using the same observational method if there are no errors in the literature.

Table 3.
Newly obtained minima times of three eclipsing binaries in BVRI bands.

Table 4.
Minimum times and relevant parameters of period variation of V Crt, WY Cnc and CG Cyg.
3.1. Period Analysis of V Crt
The minima were obtained from the light curves of different observational methods, such as visual (vis), photographic (pg) and CCD. Because different observational methods would lead to different observational errors, we generally assigned weighting factors (1 for vis and pg, 5 for pe, and 10 for more accurate CCD data) [127]. The linear ephemeris formula was obtained as follows:
where 2441397.3311 is the initial time in HJD format, value of orbital period is 0.70203571 d, and decimal in parentheses are the errors. The residuals (O-C)I values of the linear fit are listed in Table 4, and plotted in Figure 5. There appears to be a very weak upward polynomial variation for V Crt. The following is the quadratic ephemeris:
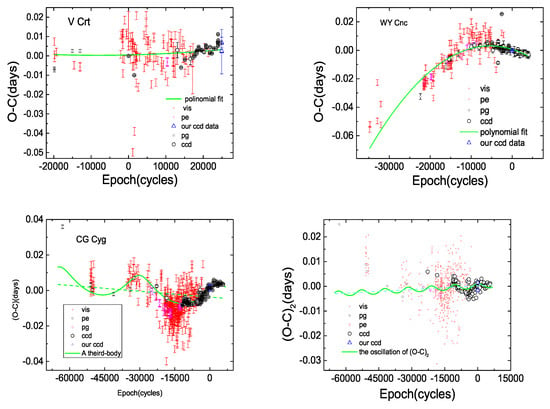
Figure 5.
The fit of the minima times of eclipsing binaries, where the upper-left panel is the polynomial fit of V Crt, and the upper right panel is the polynomial fit of WY Cnc. The bottom left is the fit of third-body of CG Cyg, and the bottom right is the fit of (O-C) II of CG Cyg.
The period may have been increasing, but this is only a 1.3 sigma result. We calculated the rate of increasing as 2.8 () × d yr. The fitting line of V Crt is shown in Figure 5. As the period variation is very weak, more data are required to confirm the obtained results.
3.2. Period Analysis of WY Cnc
The new epoch for WY Cnc was calculated by fitting the light minima as follows by fitting the light minima:
We set HJD2441397.3311 as the initial time and then calculated the new orbital period as 0.70203571 d. The (O-C)I values of the linear fit residuals are listed in Table 4, and ploted in Figure 5, where a downward trend was observed. Following is the quadratic ephemeris:
The value of is the quadratic coefficient of the period change, which means that the period of WY Cnc is decreasing. Therefore, we obtained a variation period of −8.641() × d yr.
3.3. Period Analysis of CG Cyg
Using the same method, a new epoch of CG Cyg was obtained as follows:
The cyclical variation of the orbital periods can be seen in the (O-C)I curve of CG Cyg in the lower left panel of Figure 5. These were explained using a magnetic activity cycle or light-travel time effects (LITE) of the third-body. The conventional method was used to obtain their parameters,
where is the orbital semi-major axis in the binary system of a third body system, and and is the eccentricity, inclination, true anomaly and longitude of the periastron, respectively. We test for a possible fourth body using the O-C diagram, as shown in the lower right panel in Figure 5. Therefore we fitted the minimum time again. The results are plotted in Figure 5. After fitting, the oscillation cycle of the third-body was 59.20 (±0.36) yr. We found that the cycle of the second oscillation was 18.31 (±0.60) yr with a smaller oscillation amplitude. The values of the two possible cycles of period variation were similar to those results of 51 and 22.5 yrs [55].
4. Orbital Parameters and Starspots
We used the updated 2014 Wilson-Devinney program [128,129,130,131] to revise the orbital parameters of the eclipsing binaries. The Wilson-Devinney program is the most widely used for light curve modeling code to obtain the stellar and starspot parameters of eclipsing binary. This program uses a different correction method for parameter adjustment of the observed light and velocity curves by the lease squares criterion, and produced the corresponding theoretical curves. We set V Crt as a semi-detached binary in the WD program according to previous research [11]. We set 7500 K for the primary component, 5000 K for the secondary component, a mass ratio of the secondary component and primary component (q) of 0.683 as the initial value. Further, we also set the bolometric albedo coefficient = = 0.5 [132] and gravity-darkening coefficients = = 0.32 [133]. The bolometric limb-darkening coefficients and limb-darkening coefficients for the four BVRI bands are = 0.469, = 0.429; = 0.558, = 0.864, = 0.471, = 0.725, = 0.375, = 0.599, = 0.294, = 0.489, respectively based on the stellar temperature [134]. We attempted the calculation using several sets of mass ratios to obtain the best rate if the mass ratio was unknown. The temperature was obtained using J-H color index relation [135] or spectral type. We simultaneously adjusted with other parameters: orbital inclination (i), temperature of secondary component (), monochromatic luminosity of the primary component (, , and ), and dimensionless potentials of the two components ( and ). We adjusted each parameters for converge to obtain the best solution by several steps. We used the weighted sum of squares of the residual between the theoretical and observed light curves to judge the best results.
The corresponding orbital parameters obtained from several calculations are listed in Table 5. The theoretical and observed light curves are demonstrated in Figure 2. The stellar structure is displayed in Figure 6. An obvious asymmetry was observed in the light curve. We attempted to add a cold spot on the primary or secondary components to explain this. We assumed the spot shape is circular. The spot longitude, radius and temperature are the free parameters. The starspot parameters were appropriately adjusted until they converge. The weighted sum of squares of the residual between the theoretical and observed light curves was used to judge the best results. Before fitting the spot parameters, we must set the initial value, generally, the latitude is fixed at 90 to simplify the model. The spot temperature factor (Tspot/Tstar) was set to 0.8 because the cold spot was approximately 1000 K below the stellar total surface temperature, and the radius was set equal to the phase range where the deviation of the light curves occurs. The spot longitude was determined using the center of the light curve distortion. The spot radius was estimated by the fitting the observed light curve. Because the spot size is correlated with stellar temperature, and the spot latitude is correlated with spot radius. We have to adjust the spot parameters for many runs to determine the converge solutions. We obtained the best solution with the lowest sum of squares of the residual between the theoretical and observed light curves. The details of the fitting of these parameters have been described in the previous paper [136]. Initially, we added a cold spot at the secondary component but the result is not very good. We suppose that that the primary star is gaining mass because the secondary Roche lobe was filled as a semi-detached binary system. Hence, we changed the spot at primary component. Finally, we obtained the two solutions of a spot on the primary and secondary component. The was 6.614 for the spot on primary component and 7.0947 for the spot on the secondary component. We found that there are no significantly different for the two solutions, as shown in Figure 2. We also attempted to use two spots to explain the light curve distortion. However, there are no significantly improvements of the residual. For our light curve, there were no significant improvements of the residuals. The longitude of the spot on the primary component was . The spot radius was and the spot temperature was 6763 K ± 909 K. The spot parameters are listed in Table 6.

Table 5.
Orbital Parameters of V Crt, WY Cnc and CG Cyg.
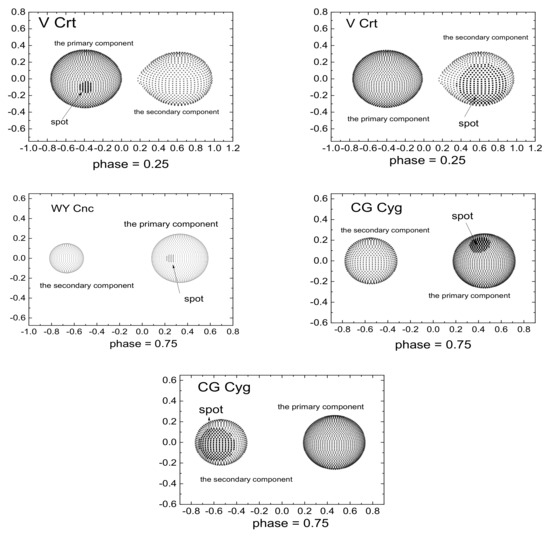
Figure 6.
Spot structures of V Crt, WY Cnc and CG Cyg.

Table 6.
Spot parameters of three eclipsing binaries.
We used a similar method to obtain orbital and starspot parameters for WY Cnc and CG Cyg. We set the temperature of the primary component of WY Cnc to 5500 K and set the secondary temperature to 4000 K [35]. Based on the temperatures of both components, we determined the bolometric limb-darkening coefficients and limb-darkening coefficients for BVRI four bands to be = 0.520, = 0.429; = 0.781, = 0.817, = 0.644, = 0.705, = 0.533, = 0.612, = 0.438, = 0.476, respectively. For CG Cyg, we set the temperature of the primary component to 5200 K and that of the secondary component to 4400 K [51]. The corresponding bolometric limb-darkening coefficients and limb-darkening coefficients for the BVRI bands were = 0.530, = 0.532; = 0.822, = 0.944, = 0.684, = 0.795, = 0.566, = 0.658, = 0.464, = 0.532, respectively. We collected radial velocity values of WY Cnc [35] and CG Cyg [51]. We analyzed the published radial velocities and light curve to obtain orbital parameters using the WD program. The resultant light curves are shown in Figure 3 and Figure 4 for WY Cnc and CG Cyg. The orbital parameters are listed in Table 5 and the spot parameters are listed in Table 6. Further, we plotted the theoretical and observational radial velocity curves in Figure 7. The starspot structures of WY Cnc and CG Cyg are displayed in Figure 6.
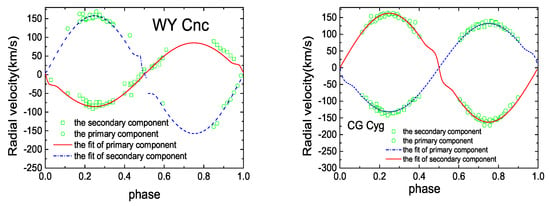
Figure 7.
Theoretical and observational radial velocity curves, where the left panel is the radial velocity of WY Cnc, and right is CG Cyg.
5. Discussions and Conclusions
The photometric orbital parameters of V Crt were obtained using the WD program. The mass ratio and orbital inclination were 0.637 ± 0.004 and 73.629± 0.067, respectively, which are similar to the results of the mass ratio of 0.683 ± 0.002 and inclination of 73.08± 0.05 [11]. The luminosity ratio of the primary component and total intensity of V Crt in the difference BVRI bands were 0.9263 ± 0.0026, 0.8721 ± 0.0035, 0.8221 ± 0.0042 and 0.7759 ± 0.0046, respectively. The dimensionless potential of V Crt was = = 3.489 ± 0.014. The mass of primary component of V Crt was obtained as = 1.68 M based on the relationship between mass and color index. The mass of the secondary component was 1.07 M. The semi-major axis a was obtained using the Kepler’s third law (). We calculated the radius (R) of each component using , where r is the weighted average value of r, r and r. The luminosity was obtained by = (/(/, where T = 5770 K. We calculated the period change of dP/dt = 2.80 () × d yr using the change of parabolic fit with quadratic coefficient terms greater than zero, which may means that the mass was transferred mass from the secondary component to the primary component [137] or magnetic breaking [138]. Because of the semi-detached system, we calculated the mass transfer rate using the following formula [139]:
Finally, we obtained the rate of mass transfer of d/dt = 3.92 () × M yr.
We obtained a rate of mass decrease for WY Cnc as d/dt= −7.31 () × yr. Because WY Cnc is a detached binary system, we opine that the period variation can not explained by the mass transfer. If the change in period contributes to magnetic breaking, we can calculate the angular momentum loss as follows:
where the angular momentum is:
where G is the gravitational constant. We calculated J as , which is similar to the result reported by Chen [37]. The period change of WY Cnc may be caused by the magnetic braking effect [37].
For CG Cyg, a cyclic variation of O-C was observed, as shown in the lower left panel of Figure 5, which might be explained by the light-time effect with a third body. Firstly, the semi-axis of the binary must be calculated:
where i is the orbital inclination, A is the amplitude, and c is the speed of light. The amplitude of the oscillation of the systemic velocity can be calculated as follows [140]:
where , , and are the velocity (km/s), distance from the sun to the earth (Au), and period of third body (yr), respectively. Subsequently, we can calculate the mass () of the third-body as followings:
The value of the third body was smallest when i = 90, as illustrated in Figure 8. Therefore, we obtained the minimum mass of as 0.14 M, which is close to the result of 0.12 M [55]. The parameters of the periodic oscillation are listed in Table 7.
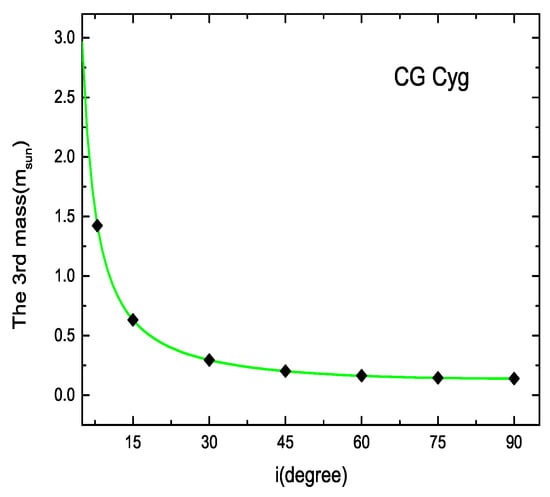
Figure 8.
The mass of the third-body for CG Cyg.

Table 7.
Parameters of the additional bodies of CG Cyg.
Except for the third body, the period oscillation in lower left panel of Figure 5 might be caused by magnetic cycles. The change in quadrupole moment due to magnetic activity in the internal constitution can also cause cyclic oscillations ( P/P). Therefore, we considered the magnetic activity cycles of this system, as following:
where is the period of magnetic activity. The P/P of P of 59.20 yr was calculated to be 1.918 ×. This value is larger than the traditional value of P/P−∼ for magnetic activity in RS CVn and Algol binaries [141]. Therefore, we can conclude that the periodic oscillations might have been caused by the LITE of a third body, not the magnetic cycle. For the second cycle of P of 18.31 yr, the P/P was calculated to be 9.398 × . It is in the range of traditional values, which might be caused by the magnetic activity. There is no direct evidence for the third based on our observation of the telescopes. Therefore, we prefer the magnetic activity cycle than the third body to explain the cyclic variations. However, we cannot rule out that these variations might be caused by the third body. New telescope imaging technology are required to check that in the future.
WY Cnc and CG Cyg are detached and RS CVn eclipsing binaries. Using the obtained light curves, we revised the orbital parameters using the WD program. The derived mass ratio of 0.501 ± 0.002 and orbit inclination of 89.759 ± 0.002 are similar to that obtained in the previous results in regions for a mass ratio of 0.38–0.59 and for an inclination of 86–90 for WY Cnc [35]. The mass ratio of 0.820 ± 0.001 for CG Cyg is similar to 0.862 [53] and 0.825 [51]. The orbit inclination of 82.890 ± 0.029 for CG Cyg is similar to the previous results of 83 ± 0.2 [51] and 82.602 ± 0.099 [35]. We obtained the starspot parameters of WY Cnc and CG Cyg at our observational times, which were different from the previous starspot parameters [35]. We confirm that variation in the light curves variations owing to varying starspot in different seasons [53,142]. Further photometric and spectroscopic observations are required to determine the magnetic activity cycle.
In Figure 9, we plotted the vs. diagrams with many theoretical isochrone [143], and indicated the positions of both primary and second components of V Crt, WY Cnc and CG Cyg. We found that the parameters of the primary and secondary components of WY Cnc and CG Cyg are in agreement with the 0.030 Gyr tracks of the theoretical model. The secondary component of V Crt are in the region of 0.03–0.05 Gyr. Because V Crt is a semi-detached eclipsing binary and the primary component of V Crt is approximately 7500 K, it is difficult to determine its age. However, its age can be determined by investigating additional observations and theoretical models.
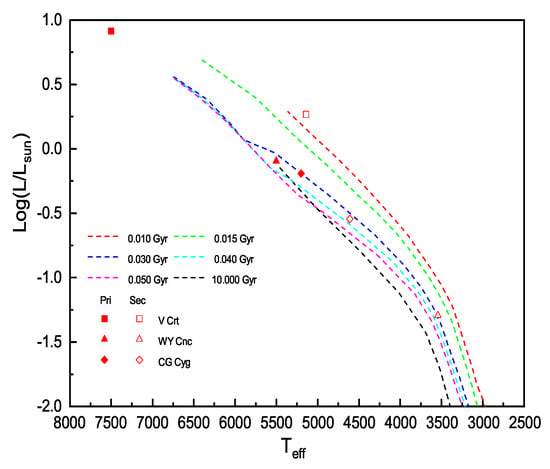
Figure 9.
Position of the components of the three eclipsing in -log diagrams. The dash lines in deferent colors represent different isochrones of the solar chemical composition.
Author Contributions
Data curation, Q.P. and L.J.; Formal analysis, Y.C.; Software, Z.Z., Z.Y. and B.L.; Supervision, L.Z.; Writing—review & editing, X.L.H. and P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Joint Fund of Astronomy of the NSFC and CAS Grant number 11963002, U1631236 and U1431114. We also thank the fostering project of GuiZhou University with No. 201911, Cultivation Project for FAST Scientific Payoff and Research Achievement of CAMS-CAS1. We also acknowledge the science research grants from the China Manned Space Project with No. CMS-CSST-2021-B07. Jiang Linyan thank the Natural Science Foundation of Guizhou province, China (Grant No. 2022164).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Güdel, M. Stellar Radio Astronomy: Probing Stellar Atmospheres from Protostars to Giants. Annu. Rev. Astron. Astrophys. 2002, 40, 217–261. [Google Scholar] [CrossRef]
- Matthews, L.D. Radio Stars: From kHz to THz. Publ. Astron. Soc. Pac. 2019, 131, 016001. [Google Scholar] [CrossRef]
- Heeschen, D.S. The Very Large Array. Sky Telesc. 1975, 49, 344. [Google Scholar]
- Kellermann, K.I.; Pauliny-Toth, I.I.K. A Search for Radio Emission from the Star Alpha Orionis. Astrophys. J. 1966, 145, 953. [Google Scholar] [CrossRef]
- Seaquist, E.R. Radio Emission from Stellar Coronas. Astrophys. J. Lett. 1967, 148, L23. [Google Scholar] [CrossRef]
- Wendker, H.J. Radio continuum emission from stars: A catalogue update. Astron. Astrophys. Suppl. Ser. 1995, 109, 177–179. [Google Scholar]
- Wendker, H.J. VizieR Online Data Catalog: Catalogue of Radio Stars (Wendker, 2001). Vizier Online Data Cat. 2015, 10, VIII/99. [Google Scholar]
- Kreiken, E.A. The Density of Stars of Different Spectral Types. With 1 figure. Z. Astrophys. 1953, 32, 125. [Google Scholar]
- Parthasarathy, M.; Sanwal, N.B. New Light Elements for V Crateris. Inf. Bull. Var. Stars 1972, 719, 1. [Google Scholar]
- Woodsworth, A.W.; Hughes, V.A. Observations of radio stars at 10.6 GHz. Astron. Astrophys. 1977, 58, 105–111. [Google Scholar]
- Liu, Q. Four-colour photometric study of the short-period eclipsing binary V Crateris. Astron. Astrophys. Suppl. Ser. 1993, 101, 49–57. [Google Scholar]
- Sarma, M.B.K.; Vivekananda Rao, P. V Crateris: Photometric Elements. Publ. Astron. Soc. Pac. 1998, 110, 93–97. [Google Scholar] [CrossRef]
- Popper, D.M. Close Binaries with H and K Emission. Inf. Bull. Var. Stars 1976, 1083, 1. [Google Scholar]
- Kippenhahn, R. Mitteilungen über 18 verdächtige und veränderliche Sterne. Astron. Nachrichten 1953, 281, 153. [Google Scholar] [CrossRef]
- Rao, P.V.; Sarma, M.B.K. On the Distortion Wave in the Short Period Rs-Canum Type Eclipsing Binary Wy-Cancri. In Activity in Red-Dwarf Stars; Byrne, P.B., Rodono, M., Eds.; Astrophysics and Space Science Library; Springer: Dordrecht, The Netherlands, 1983; Volume 102, pp. 399–400. [Google Scholar] [CrossRef]
- Chambliss, C.R. The eclipsing binary system WY Cancri. Astron. J. 1965, 70, 741. [Google Scholar] [CrossRef]
- Sarma, M.B.K. Light Curve of WY CANCRI. Bull. Astron. Inst. Czechoslov. 1976, 27, 335. [Google Scholar]
- Awadalla, N.S.; Budding, E. The System WY Cnc and Derivation of Absolute Information at the Lower End of the Main Sequence. Astrophys. Space Sci. 1979, 63, 479–489. [Google Scholar] [CrossRef]
- Xie, X.; Zhai, D.; Chen, H.; Li, Y. Four-color uvby photometry and starspot parameters of WY Cancri. Chin. Astron. Astrophys. 1989, 13, 281–290. [Google Scholar] [CrossRef]
- Helfand, D.J.; Schnee, S.; Becker, R.H.; White, R.L.; McMahon, R.G. The FIRST Unbiased Survey for Radio Stars. Astron. J. 1999, 117, 1568–1577. [Google Scholar] [CrossRef]
- Hall, D.S.; Kreiner, J.M.; Shore, S.N. Period changes and mass loss rates in 34 Rs-Canum type binaries. In Close Binary Stars: Observations and Interpretation; Plavec, M.J., Popper, D.M., Ulrich, R.K., Eds.; Cambridge University Press: Cambridge, UK, 1980; Volume 88, pp. 383–387. [Google Scholar]
- Albayrak, B.; Fikri Özeren, F.; Ekmekçi, F.; Demircan, O. Period Variation of Six RS CVn-Type Binaries with Possible Light-Time Effect. Rev. Mex. Astron. Astrofis. 1999, 35, 3. [Google Scholar]
- Albayrak, B.; Muyesseroglu, Z.; Ozdemir, S. Photoelectric Minima of Some Eclipsing Binary Stars. Inf. Bull. Var. Stars 2000, 4941, 1. [Google Scholar]
- Albayrak, B.; Gurol, B. Photoelectric Minima Times of Some Eclipsing Binaries. Inf. Bull. Var. Stars 2001, 5069, 1. [Google Scholar]
- Pribulla, T.; Vanko, M.; Parimucha, S.; Chochol, D. New Photoelectric and CCD Minima and Updated Ephemerides of Selected Eclipsing Binaries. Inf. Bull. Var. Stars 2002, 5341, 1. [Google Scholar]
- Agerer, F.; Hubscher, J. Photoelectric Minima of Selected Eclipsing Binaries. Inf. Bull. Var. Stars 2003, 5484, 1. [Google Scholar]
- Dvorak, S.W. Times of Minima for Neglected Eclipsing Binaries in 2003. Inf. Bull. Var. Stars 2004, 5502, 1. [Google Scholar]
- Aksu, O.; Ozavci, I.; Yuce, K.; Tanriverdi, T.; Senavci, H.V.; Yilmaz, M.; Kara, A.; Kaya, F.; Helvaci, M.; Cetintas, C.; et al. Photoelectric Minima of Some Eclipsing Binary Stars. Inf. Bull. Var. Stars 2005, 5588, 1. [Google Scholar]
- Hubscher, J.; Paschke, A.; Walter, F. Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2005, 5657, 1. [Google Scholar]
- Hubscher, J. Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2005, 5643, 1. [Google Scholar]
- Hubscher, J. Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2007, 5802, 1. [Google Scholar]
- Zejda, M.; Mikulasek, Z.; Wolf, M. CCD Times of Minima of Selected Eclipsing Binaries. Inf. Bull. Var. Stars 2006, 5741, 1. [Google Scholar]
- Senavci, H.V.; Tanriverdi, T.; Torun, E.; Elmasli, A.; Kilicoglu, T.; Cinar, D.; Sipahioglu, S.; Alan, N.; Colak, T.; Yilmaz, M.; et al. Photoelectric Minima of Some Eclipsing Binary Stars. Inf. Bull. Var. Stars 2007, 5754, 1. [Google Scholar]
- Lewandowski, M.; Niedzielski, A.; Maciejewski, G. CCD Times of Minima of Some Eclipsing Binaries from the SAVS Sky Survey. Inf. Bull. Var. Stars 2007, 5784, 1. [Google Scholar]
- Kjurkchieva, D.; Marchev, D.; Ogloza, W. Spectroscopic and photometric observations of the short-period RS CVn-type star WY CNC. Astron. Astrophys. 2004, 415, 231–239. [Google Scholar] [CrossRef]
- Tian, Y.; Xiang, F.; Xie, W.; Tao, X. Period Change and Possible Magnetic Braking in WY Cancri. Publ. Astron. Soc. Jpn. 2009, 61, 675. [Google Scholar] [CrossRef]
- Chen, W.C. On the Origin of Orbital Period Change in WY Cancri: A Genuine Angular-Momentum Loss? Publ. Astron. Soc. Jpn. 2013, 65, L4. [Google Scholar] [CrossRef]
- Williams, A.S. A new variable star in Cygnus. Mon. Not. R. Astron. Soc. 1922, 82, 300. [Google Scholar] [CrossRef][Green Version]
- Naftilan, S.A.; Milone, E.F. A spectroscopic study of the close binary CG Cygni. Astron. J. 1979, 84, 1218–1222. [Google Scholar] [CrossRef]
- Yu, C.S. Lightcurve and orbit of CG Cygni. Astrophys. J. 1923, 58, 75–85. [Google Scholar] [CrossRef]
- Milone, E.F.; Castle, K.G.; Robb, R.M.; Swadron, D.; Burke, E.W.; Hall, D.S.; Michlovic, J.E.; Zissell, R.E. The changing light curves of CG Cygni. Astron. J. 1979, 84, 417–428. [Google Scholar] [CrossRef]
- Jassur, D.M.Z. Observations and Interpretation of the Close Binary System Cg-Cygni. Astrophys. Space Sci. 1980, 67, 19–30. [Google Scholar] [CrossRef]
- Sowell, J.R.; Wilson, J.W.; Hall, D.S.; Peyman, P.E. CG Cygni: Solutions of 1979 and 1980 light curves. Publ. Astron. Soc. Pac. 1987, 99, 407–419. [Google Scholar] [CrossRef]
- Naftilan, S.A.; Grillmair, C.; Trager, G. Recent Photometry of CG Cygni. Astron. J. 1987, 93, 210. [Google Scholar] [CrossRef]
- Bedford, D.K.; Fuensalida, J.J.; Arevalo, M.J. The BVJK light curves of the short-period eclipsing binary CG Cygni. Astron. Astrophys. 1987, 182, 264–270. [Google Scholar]
- Dapergolas, A.; Kontizas, E.; Kontizas, M. 1987 BV Photoelectric Observations of CG Cyg. Inf. Bull. Var. Stars 1989, 3322, 1. [Google Scholar]
- Zeilik, M.; Cox, D.A.; de Blasi, C.; Rhodes, M.; Budding, E. Long-Term Starspot Activity of Short-Period RS Canum Venaticorum Stars. II. RT Andromedae. Astrophys. J. 1989, 345, 991. [Google Scholar] [CrossRef]
- Zeilik, M.; Ledlow, M.; Rhodes, M.; Summers, D.L.; Jaderlund, E.; Boudreau, K.; Heckert, P.A. 1991 BVR Photometry of CG Cygni. Inf. Bull. Var. Stars 1991, 3663, 1. [Google Scholar]
- Heckert, P.A. 1994 BVRI Photometry of CG Cygni. Inf. Bull. Var. Stars 1994, 4127, 1. [Google Scholar]
- Heckert, P.A. 1997 Photometry of CG Cygni. Inf. Bull. Var. Stars 1998, 4627, 1. [Google Scholar]
- Kjurkchieva, D.P.; Marchev, D.V.; Ogloza, W. Spectroscopic and photometric observations of the short-period RS CVn-type star CG Cyg. Astron. Astrophys. 2003, 400, 623–631. [Google Scholar] [CrossRef]
- Banks, T.; Budding, E. Light Curves for CG Cygni. Inf. Bull. Var. Stars 1989, 3305, 1. [Google Scholar]
- Zeilik, M.; Gordon, S.; Jaderlund, E.; Ledlow, M.; Summers, D.L.; Heckert, P.A.; Budding, E.; Banks, T.S. Long-Term Starspot Activity of Short-Period RS Canum Venaticorum Stars. V. CG Cygni. Astrophys. J. 1994, 421, 303. [Google Scholar] [CrossRef]
- Kozhevnikova, A.V.; Alekseev, I.Y.; Kozhevnikov, V.P.; Svechnikov, M.A. Long-Term Starspot Activity of the Eclipsing Variable System CG Cyg. Astrophysics 2005, 48, 291–303. [Google Scholar] [CrossRef]
- Afşar, M.; Heckert, P.A.; İbanoǧlu, C. Long-term luminosity variations and period changes in CG Cygni. Astron. Astrophys. 2004, 420, 595–604. [Google Scholar] [CrossRef]
- Shi, X.M.; Xiang, F.Y.; Lu, Y. Orbital Period Investigation of the RS CVn-Type Binary CG Cygni. Publ. Astron. Soc. Jpn. 2012, 64, 121. [Google Scholar] [CrossRef]
- Keel, W.C.; Oswalt, T.; Mack, P.; Henson, G.; Hillwig, T.; Batcheldor, D.; Berrington, R.; De Pree, C.; Hartmann, D.; Leake, M.; et al. The Remote Observatories of the Southeastern Association for Research in Astronomy (SARA). Publ. Astron. Soc. Pac. 2017, 129, 015002. [Google Scholar] [CrossRef]
- Zhou, A.Y.; Jiang, X.J.; Zhang, Y.P.; Wei, J.Y. MiCPhot: A prime-focus multicolor CCD photometer on the 85-cm Telescope. Res. Astron. Astrophys. 2009, 9, 349–366. [Google Scholar] [CrossRef]
- Nelson, R.H.; Terrell, D.; Milone, E.F. A critical review of period analyses and implications for mass exchange in W UMa Eclipsing Binaries: Paper 1. New Astron. Rev. 2014, 59, 1–13. [Google Scholar] [CrossRef]
- Kwee, K.K.; van Woerden, H. A method for computing accurately the epoch of minimum of an eclipsing variable. Bull. Astron. Institutes Neth. 1956, 12, 327. [Google Scholar]
- Klimek, Z. Minima of Eclipsing Variables. Inf. Bull. Var. Stars 1973, 779, 1. [Google Scholar]
- Mallama, A.D.; Skillman, D.R.; Pinto, P.A.; Krobusek, B.A. Minima of Eclipsing Variables. Inf. Bull. Var. Stars 1977, 1249, 1. [Google Scholar]
- Results of Observations of Eclipsing Binaries: 1990–1994. In Contributions of the Public Observatory and Planetarium in Brno; ADS: Washington, DC, USA, 1995; Volume 31.
- Diethelm, R. 162-nd List of Minima Timings of Eclipsing Binaries by BBSAG Observers. Inf. Bull. Var. Stars 2003, 5438, 1. [Google Scholar]
- Diethelm, R. Timings of Minima of Eclipsing Binaries. Inf. Bull. Var. Stars 2011, 5992, 1. [Google Scholar]
- Diethelm, R. 163. List of Minima Timings of Eclipsing Binaries by BBSAG Observers. Inf. Bull. Var. Stars 2004, 5543, 1. [Google Scholar]
- Locher, K. Minima Kurt Locher 2004–2005. Open Eur. J. Var. Stars 2005, 3, 1. [Google Scholar]
- Samolyk, G. Recent Minima of 184 Eclipsing Binary Stars. J. Am. Assoc. Var. Star Obs. 2008, 36, 186. [Google Scholar]
- Dvorak, S.W. Photoelectric minima of selected eclipsing binaries in 2008. Inf. Bull. Var. Stars 2009, 5870, 1. [Google Scholar]
- Samolyk, G. Recent CCD Minima of 185 Eclipsing Binary Stars. J. Am. Assoc. Var. Star Obs. 2010, 38, 183. [Google Scholar]
- Samolyk, G. Recent Maxima of 56 Short Period Pulsating Stars. J. Am. Assoc. Var. Star Obs. 2011, 39, 23. [Google Scholar]
- Diethelm, R. Timings of Minima of Eclipsing Binaries. Inf. Bull. Var. Stars 2012, 6029, 1. [Google Scholar]
- Paschke, A. A list of minima and maxima timings, 2015. Open Eur. J. Var. Stars 2017, 181, 1. [Google Scholar]
- Chambliss, C.R. Photoelectric Photometry of WY Cancri. Inf. Bull. Var. Stars 1975, 1029, 1. [Google Scholar]
- Kippenhahn, R. Mitteilungen über 45 verdächtige und veränderliche Sterne. Astron. Nachrichten 1955, 282, 73. [Google Scholar] [CrossRef]
- Dueball, J.; Lehmann, P.B. Beobachtungsergebnisse der Berliner Arbeitsgemeinschaft für Veränderliche Sterne e. V. (BAV). Astron. Nachrichten 1965, 288, 167. [Google Scholar] [CrossRef]
- Pohl, E.; Kizilirmak, A. Beobachtungsergebnisse an Bedeckungsveränderlichen. Astron. Nachrichten 1966, 289, 191. [Google Scholar] [CrossRef]
- Braune, W.; Hübscher, J.; Mundry, E. Beobachtungsergebnisse der Berliner Arbeitsgemeinschaft für veränderliche Sterne e. V. (BAV). Astron. Nachrichten 1970, 292, 185. [Google Scholar] [CrossRef]
- Ahnert, P. Photographic Observations of Eclipsing Variables—Instantaneous Elements of 4 Eclipsing Stars. Inf. Bull. Var. Stars 1973, 786, 1. [Google Scholar]
- Ahnert, P. Photographic Minima of Eclipsing Stars. Inf. Bull. Var. Stars 1976, 1190, 1. [Google Scholar]
- Mullis, C.R.; Faulkner, D.R. A Period Change in WY Cancri. Inf. Bull. Var. Stars 1988, 3206, 1. [Google Scholar]
- Mullis, C.R.; Faulkner, D.R. Epochs of Minimum Light for WY Cancri, AM Leonis, and RR Leporis. Inf. Bull. Var. Stars 1989, 3354, 1. [Google Scholar]
- Mullis, C.R.; Faulkner, D.R. Epochs of Minimum Light for Eight Eclipsing Binary Star Systems. Inf. Bull. Var. Stars 1991, 3593, 1. [Google Scholar]
- Albayrak, B.; Oezeren, F.F.; Ekmekci, F. Photoelectric Minima of Four RS CVn Type Binary Systems: RT And, SV Cam, WY Cnc, and Z Her. Inf. Bull. Var. Stars 1996, 4399, 1. [Google Scholar]
- Pribulla, T.; Chochol, D.; Parimucha, S. Photoelectric Minima of Some Eclipsing Systems. Inf. Bull. Var. Stars 1999, 4751, 1. [Google Scholar]
- Albayrak, B.; Tanriverdi, T.; Aydin, C. Photoelectric Minima of Some Eclipsing Binary Stars. Inf. Bull. Var. Stars 2002, 5300, 1. [Google Scholar]
- Brát, L.; Zejda, M.; Svoboda, P. B.R.N.O. Contributions #34. Open Eur. J. Var. Stars 2007, 74, 1. [Google Scholar]
- Dvorak, S.W. Times of Minima for Neglected Eclipsing Binaries in 2005. Inf. Bull. Var. Stars 2006, 5677, 1. [Google Scholar]
- Hubscher, J.; Steinbach, H.M.; Walter, F. BAV-Results of Observations-Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2009, 201, 1–13. [Google Scholar] [CrossRef]
- Yilmaz, M.; Basturk, O.; Alan, N.; Senavci, H.V.; Tanriverdi, T.; Kilicoglu, T.; Caliskan, S.; Celik, L.; Aydin, G.; Cakan, D.; et al. New Times of Minima of Some Eclipsing Binary Stars and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2009, 5887, 1. [Google Scholar]
- Paschke, A. A list of minima and maxima timings. Open Eur. J. Var. Stars 2009, 116, 1. [Google Scholar]
- Diethelm, R. Timings of Minima of Eclipsing Binaries. Inf. Bull. Var. Stars 2009, 5894, 1. [Google Scholar]
- Hubscher, J.; Lehmann, P.B.; Monninger, G.; Steinbach, H.M.; Walter, F. BAV-Results of Observations-Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2010, 5918, 1. [Google Scholar] [CrossRef]
- Parimucha, S.; Dubovsky, P.; Vanko, M.; Pribulla, T.; Kudzej, I.; Barsa, R. Minima Times of Selected Eclipsing Binaries. Inf. Bull. Var. Stars 2011, 5980, 1. [Google Scholar]
- Hubscher, J.; Lehmann, P.B.; Walter, F. BAV-Results of observations-Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2012, 220, 1. Available online: https://ui.adsabs.harvard.edu/abs/2012BAVSM.220....1H/abstract (accessed on 8 June 2016). [CrossRef]
- Hubscher, J. BAV-Results of observations-Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2013, 6084, 1. [Google Scholar] [CrossRef]
- Hubscher, J.; Lehmann, P.B. BAV-Results of observations-Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2015, 6149, 1. [Google Scholar] [CrossRef]
- Hubscher, J. BAV-Results of observations-Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2017, 6196, 1. [Google Scholar] [CrossRef]
- Pagel, L. BAV-Results of observations-Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2018, 6244, 1. [Google Scholar] [CrossRef]
- Dapergolas, A.; Kontizas, E.; Kontizas, M. 1989 BV Photoelectric Observations of CG Cyg. Inf. Bull. Var. Stars 1989, 3380, 1. [Google Scholar]
- Dapergolas, A.; Kontizas, E.; Kontizas, M. 1990 BV Photoelectric Observations of CG Cyg. Inf. Bull. Var. Stars 1991, 3609, 1. [Google Scholar]
- Dapergolas, A.; Kontizas, E.; Kontizas, M. 1991 BV Photoelectric Observations of CG Cyg. Inf. Bull. Var. Stars 1992, 3719, 1. [Google Scholar]
- Dapergolas, A.; Kontizas, E.; Kontizas, M. 1992, 1993 BV Photoelectric Observations of CG Cyg. Inf. Bull. Var. Stars 1994, 4051, 1. [Google Scholar]
- Hegedus, T.; Biro, I.B.; Borkovits, T.; Paragi, Z. Photoelectric minima of 30 eclipsing binary systems. Inf. Bull. Var. Stars 1996, 4340, 1. [Google Scholar]
- Dapergolas, A.; Kontizas, E.; Kontizas, M. 1994 BV Photoelectric Observations of CG Cyg. Inf. Bull. Var. Stars 2000, 5011, 1. [Google Scholar]
- Agerer, F.; Hubscher, J. Photoelectric Maxima/minima of Selected Variables. Inf. Bull. Var. Stars 1995, 4222, 1. [Google Scholar]
- Nelson, R.H. CCD Minima of Selected Eclipsing Binaries in 1999. Inf. Bull. Var. Stars 2000, 4840, 1. [Google Scholar]
- Agerer, F.; Hubscher, J. Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2002, 5296, 1. [Google Scholar]
- Derman, E.; Kalci, R. Photoelectric Minimum Times of Some Eclipsing Binary Stars. Inf. Bull. Var. Stars 2003, 5439, 1. [Google Scholar]
- Tanriverdi, T.; Kutdemir, E.; Elmasli, A.; Senavci, H.V.; Albayrak, B.; Selam, S.O.; Aydin, C.; Aksu, O.; Bulca, I.; Cinar, D.; et al. Photoelectric Minima of Some Eclipsing Binary Stars. Inf. Bull. Var. Stars 2003, 5407, 1. [Google Scholar]
- Sarounova, L.; Wolf, M. Precise CCD Times of Minima of Selected Eclipsing Binaries. Inf. Bull. Var. Stars 2005, 5594, 1. [Google Scholar]
- Kotkova, L.; Wolf, M. Precise CCD Times of Minima of Selected Eclipsing Binaries. Inf. Bull. Var. Stars 2006, 5676, 1. [Google Scholar]
- Pribulla, T.; Baludansky, D.; Chochol, D.; Chrastina, M.; Parimucha, S.; Petrik, K.; Szasz, G.; Vanko, M.; Zboril, M. New Minima of Selected Eclipsing Close Binaries. Inf. Bull. Var. Stars 2005, 5668, 1. [Google Scholar]
- Krajci, T. Photoelectric Minima of Some Eclipsing Binary Stars. Inf. Bull. Var. Stars 2005, 5592, 1. [Google Scholar]
- Cook, J.M.; Divoky, M.; Hofstrand, A.; Lamb, J.; Quarderer, N. CCD Observations of Times of Minima of Eclipsing Binaries. Inf. Bull. Var. Stars 2005, 5636, 1. [Google Scholar]
- Parimucha, S.; Dubovsky, P.; Baludansky, D.; Pribulla, T.; Hambalek, L.; Vanko, M.; Ogloza, W. Minima Times of Selected Eclipsing Binaries. Inf. Bull. Var. Stars 2009, 5898, 1. [Google Scholar]
- Hubscher, J.; Steinbach, H.M.; Walter, F. BAV-Results of observations-Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2008, 5830, 1. [Google Scholar] [CrossRef]
- Samolyk, G. Recent Minima of 154 Eclipsing Binary Stars. J. Am. Assoc. Var. Star Obs. 2009, 37, 44. [Google Scholar]
- Erkan, N.; Erdem, A.; Akin, T.; Alicavus, F.; Soydugan, F. New Times of Minima of Some Eclipsing Binary Stars. Inf. Bull. Var. Stars 2010, 5924, 1. [Google Scholar]
- Hubscher, J.; Lehmann, P.B.; Walter, F. BAV-Results of observations-Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2012, 6010, 1. Available online: https://ui.adsabs.harvard.edu/abs/2012IBVS.6010....1H/abstract (accessed on 8 June 2016). [CrossRef]
- Zasche, P.; Uhlar, R.; Kucakova, H.; Svoboda, P. Collection of minima. Inf. Bull. Var. Stars 2011, 6007, 1. [Google Scholar]
- Hubscher, J.; Lehmann, P.B.; Monninger, G.; Steinbach, H.M.; Walter, F. BAV-Results of Observations-Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2010, 5941, 1. [Google Scholar] [CrossRef]
- Hubscher, J. BAV Results of observations-Photoelectric Minima of Selected Eclipsing Binaries and Maxima of Pulsating Stars. Inf. Bull. Var. Stars 2014, 6118, 1. [Google Scholar] [CrossRef]
- Zasche, P.; Uhlar, R.; Svoboda, P.; Kucakova, H.; Masek, M.; Jurysek, J. Collection of Minima of Eclipsing Binaries, part III. Inf. Bull. Var. Stars 2017, 6204, 1. [Google Scholar] [CrossRef]
- Hubscher, J. BAV-Results of observations-Photoelectric Minima of Selected Eclipsing Binaries. Inf. Bull. Var. Stars 2016, 6157, 1. [Google Scholar]
- Bahar, E.; Yorukoglu, O.; Esmer, E.M.; Kilicoglu, T.; Ozturk, D.; Dogruel, M.B.; Ozuyar, D.; Gumus, D.; Izci, D.D.; Keten, B.; et al. Times of Minima of Some Eclipsing Binaries. Inf. Bull. Var. Stars 2017, 6209, 1. [Google Scholar] [CrossRef]
- Yang, Y.G.; Lü, G.L.; Yin, X.G.; Zhu, C.H.; Nakajima, K. Orbital Period Changes and Their Evolutionary Status for Weak-Contact Binaries. II. CC Comae Berenices and BV Draconis. Astron. J. 2009, 137, 236–245. [Google Scholar] [CrossRef][Green Version]
- Wilson, R.E.; Devinney, E.J. Realization of Accurate Close-Binary Light Curves: Application to MR Cygni. Astrophys. J. 1971, 166, 605. [Google Scholar] [CrossRef]
- Wilson, R.E. Eccentric orbit generalization and simultaneous solution of binary star light and velocity curves. Astrophys. J. 1979, 234, 1054–1066. [Google Scholar] [CrossRef]
- Wilson, R.E. Accuracy and Efficiency in the Binary Star Reflection Effect. Astrophys. J. 1990, 356, 613. [Google Scholar] [CrossRef]
- Wilson, R.E. Binary Star Light-Curve Models. Publ. Astron. Soc. Pac. 1994, 106, 921. [Google Scholar] [CrossRef]
- Ruciński, S.M. The W UMa-type Systems as Contact Binaries. I. Two Methods of Geometrical Elements Determination. Degree of Contact. Acta Astron. 1973, 23, 79. [Google Scholar]
- Lucy, L.B. Gravity-Darkening for Stars with Convective Envelopes. Z. Astrophys. 1967, 65, 89. [Google Scholar]
- Van Hamme, W. New Limb-Darkening Coefficients for Modeling Binary Star Light Curves. Astron. J. 1993, 106, 2096. [Google Scholar] [CrossRef]
- Collier Cameron, A.; Wilson, D.M.; West, R.G.; Hebb, L.; Wang, X.B.; Aigrain, S.; Bouchy, F.; Christian, D.J.; Clarkson, W.I.; Enoch, B.; et al. Efficient identification of exoplanetary transit candidates from SuperWASP light curves. Mon. Not. R. Astron. Soc. 2007, 380, 1230–1244. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Gu, S.H. Photometric study of the short-period RS Canum Venaticorum binary RT Andromedae. Astron. Astrophys. 2007, 471, 219–226. [Google Scholar] [CrossRef]
- Hoffman, D.I.; Harrison, T.E.; McNamara, B.J.; Vestrand, W.T.; Holtzman, J.A.; Barker, T. The Case for Third Bodies as the Cause of Period Changes in Selected Algol Systems. Astron. J. 2006, 132, 2260–2267. [Google Scholar] [CrossRef]
- Applegate, J.H. A Mechanism for Orbital Period Modulation in Close Binaries. Astrophys. J. 1992, 385, 621. [Google Scholar] [CrossRef]
- Singh, M.; Chaubey, U.S. Mass Loss from Wolf-Rayet Stars. Astrophys. Space Sci. 1986, 124, 389–396. [Google Scholar] [CrossRef]
- Mayer, P. Eclipsing Binaries with Light-time Effect. Bull. Astron. Inst. Czechoslov. 1990, 41, 231. [Google Scholar]
- Lanza, A.F. Internal magnetic fields, spin-orbit coupling, and orbital period modulation in close binary systems. Mon. Not. R. Astron. Soc. 2020, 491, 1820–1831. [Google Scholar] [CrossRef]
- Kozhevnikova, A.V.; Kozhevnikov, V.P.; Alekseev, I.Y.; Yushkov, I.A.; Dorogov, A.A. Spot activity of the binary CG Cyg: Observations during maximum spottedness. Astron. Rep. 2012, 56, 281–289. [Google Scholar] [CrossRef]
- Baraffe, I.; Homeier, D.; Allard, F.; Chabrier, G. New evolutionary models for pre-main sequence and main sequence low-mass stars down to the hydrogen-burning limit. Astron. Astrophys. 2015, 577, A42. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).