Abstract
We study the capture cross-section of massless (photon) and massive test particles by the Schwarzschild–Tangherlini black hole, which is a solution of pure general relativity in higher dimensional spacetime with topology. It is shown that an extra dimension weakens the gravitational attraction of a black hole, and consequently, radii of all the characteristic circular orbits, such as the radius of a photonsphere decrease in the higher dimensions. Furthermore, it is shown that in higher dimensions, there are no stable and bounded circular orbits. The critical impact parameters and capture cross-sections of photons and massive particles are calculated for several higher dimensions and it is shown that they also decrease with increasing dimension. Moreover, we calculate the capture cross-section of relativistic and non-relativistic test particles in the higher dimensions.
1. Introduction
The direct discovery of gravitational waves from the coalescence of black holes in close binary systems by LIGO-VIRGO collaboration [1,2,3,4,5], detection of the first image of a supermassive black hole in the center of the elliptic galaxy Messier 87 (M87) by the Event Horizon Telescope (EHT) [6], measurement of general relativistic effects through observation of S2 star [7,8] and hot spots [9] orbiting Sagittarius A* in the center of our galaxy by GRAVITY consortium make the study of black holes in various theories of gravity a hot topic in relativistic astrophysics.
On the other hand, there is great interest in the alternate theories of gravity including higher dimensional gravitational field theories. One of these is pure general relativity in higher dimensional spacetime with topology which allows exact black hole solutions, e.g., spherical symmetric vacuum Schwarzschild–Tangherlini black hole solution [10]. One of the most astrophysically important features of the black hole spacetimes is to study the test particle’s motion in the close environment of a black hole and extract information about the central object through the dynamics of the test particles. As a black hole is well-known for being the most massive gravitating object with a strong field, its gravitation increases towards the central black hole and at the radius of the so-called event horizon, even light rays cannot escape from it. Beyond the event horizon of the black hole, the particle still has a chance to escape from the black hole, depending on its energy and angular momentum [11]. The capture (or absorption) cross-section of the particle is determined to estimate this chance. In this paper, we aim to study the capture cross-section of massive and massless (photon) particles by the Schwarzschild–Tangherlini black hole. The capture cross-section can be explained geometrically as the area under the critical impact parameter of the particle1. In the case of a massless particle, the capture cross-section is determined through a radius of unstable circular null geodesics (light ring), which is a boundary for the escape and capture scenarios. The capture of the massless particle (photon) by the Schwarzschild–Tangherlini black hole has been studied by several authors via different means. For example, in [12,13,14,15], the authors studied the radius of a photonsphere (light ring) or critical impact parameter of a light ray in the Schwarzschild–Tangherlini black hole spacetime via the analysis of geodesic equations. Moreover, in [16,17], the capture cross-section of a massless particle is determined by studying the absorption cross-section of a massless scalar field in the high energy limit, via the fact that in this limit, the absorption cross-section of a massless scalar field by a black hole tends to and oscillates around a geometrical cross-section of the massless particle [18,19,20,21]. Furthermore, other properties related to the massless particle’s motion around Schwarzschild–Tangherlini black holes have been studied in [22,23]. On the other hand, the capture cross-section of a massive test particle by the Schwarzschild–Tangherlini black hole has not been studied in the literature. Therefore, even if part of the research related to the cross-section of a massless particle presented in our paper partially discusses the problems treated in the above given references, they play an important role by providing a comparison with the massive particle’s capture cross section, and are presented as a separate section here.
The paper is organized as follows. Section 2 is devoted to the description of pure general relativity in higher dimensional spacetime with topology, to its Schwarzschild–Tangherlini black hole solution, and massless (photon) and massive test particles motion in the higher dimensional spacetime. In Section 3, a motion of a photon and its capture by the Schwarzschild–Tangherlini black hole is discussed. In Section 4, we study the capture cross-section of a massive test particle by the Schwarzschild–Tangherlini black hole. Section 5 summarizes the main results obtained in the paper.
2. Basic Equations
The general relativity in higher dimension is described by the generalized Einstein–Hilbert action
Without the loss of generality, we adopted units such that the gravitational constant and speed of the light are equal to unity, i.e., . After applying the least action principle to the action (1), we obtain Einstein field equations for the higher dimensional spacetimes as
where , R, and are Ricci tensor, Ricci scalar and metric tensor, respectively. Note that the Greek indices run within .
By solving the Einstein field Equation (2) for the spacetime with topology , one can obtain the following higher dimensional Schwarzschild solution, aslo known as the Schwarzschild–Tangherlini solution [10]:
where is a metric on a -dimensional unit sphere that is given by
and is a mass parameter that is related to the black hole mass M through a relation
For simplicity, we introduce dimensionless coordinates implementing the following transformations: and so that the metric function of the spacetime (3) takes the following form:
and hereafter, we refer to the new rescaled radial and time coordinates.
At this point, we start to study the test particle’s motion in the spacetime of the Schwarzschild–Tangherlini black hole and assume that the motion is confined at the equatorial plane of the spacetime so as . Then, one can easily notice from the symmetry of the spacetime metric (3) that the momenta corresponding to the time, t, and azimuthal coordinate, , are conserved due to the stationarity and spherical symmetry of the spacetime, and these conserved momenta are called energy, E, and angular momentum, L, of the particle, respectively, as
From the normalization condition , we obtain the following equation for the radial velocity of the particle:
where is the mass of the test particle and it is either or for the massive and massless (photon) particles, respectively.
One can see from Figure 1 that with increasing the dimension of the spacetime, height of the effective potential increases; however, the maximum of the effective potential, which corresponds to the unstable circular photon orbit, shifts towards the central black hole. Now, by using the conditions that the particle revolving around the black hole has no radial velocity and its orbit corresponds to the extrema of the effective potential, respectively, as
one can find the specific energy and specific angular momentum of the particle moving along the circular orbit around Schwarzschild–Tangherlini black hole as
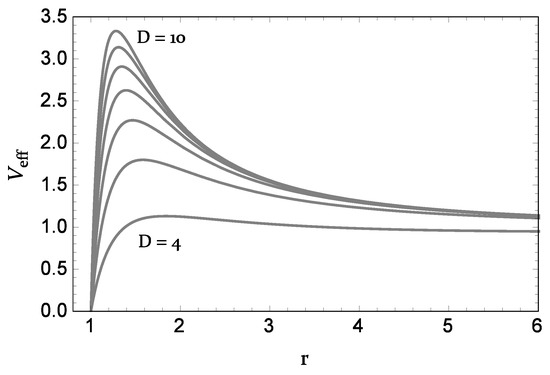
Figure 1.
Radial profile of the effective potential of a test particle in the Schwarzschild–Tangherlini black hole’s spacetime for and the dimension is in the range .
Note that the specific energy (or angular momentum) of the particle defines the energy (or angular momentum) per mass of the particle as (or ). Considering the fact that the energy and angular momentum of the photon in the circular orbit diverge, one can easily find the radius of the photonsphere in the Schwarzschild–Tangherlini black hole spacetime as
In Figure 2, the radius of the photonsphere for several dimensions of the spacetime is presented. In the case of a standard Schwarzschild black hole, one recovers the photonsphere at .
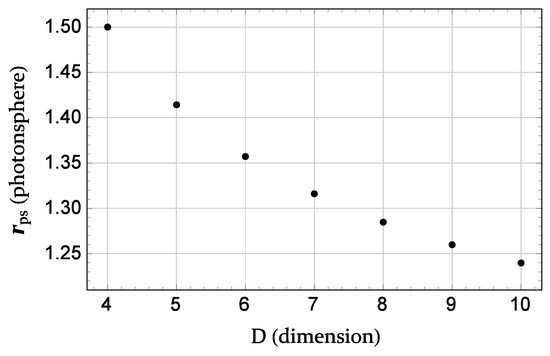
Figure 2.
Radii of the photonsphere as a function of dimension of the Schwarzschild–Tangherlini black hole’s spacetime.
One can see from Equation (12) and Figure 2 that an extra dimension in the spacetime weakens the gravitational attraction of the black hole and consequently, the radius of the photonsphere decsreases.
Another orbit, which is one of the most astrophysically important orbits around the black hole are the marginally stable circular orbits (MSCO). It is obvious that the stability of the orbit is ensured by positivity of the second derivative of the effective potential with respect to a radial coordinate that provides the effective potential to be concave upward. The marginally stable orbits are located at the following inflection point, where the concavity of the effective potential changes:
To find the MSCOs, one must solve Equation (14) together with the circularity conditions Equation (9). By solving them, we determine that the MSCO is bounded only from the inner side. Therefore, we call this orbit the innermost stable circular orbit (ISCO) and it is located at
In the case of a standard 4D Schwarzschild black hole, one recovers the ISCO radius at . Interestingly, one can see from (14) that the ISCO exists only in the case of 4-dimensional spacetime. In higher dimensional Schwarzschild–Tangherlini spacetime, there is no ISCO, which indicates absence of stable circular orbits as in the case of the higher dimensional Majumdar-Papapetrou spacetime [24]. It may be treated as strong evidence that the higher dimensions do not play a role in our Universe, which consists of bounded systems.
The next orbit of the test particle we want to mention here is the marginally bound circular orbit (MBCO). The MBCO represents the innermost circular orbit of a massive particle, which is energetically bounded to the central black hole. This radius is located closer to the black hole than ISCO and between these two orbits, there are circular orbits which are all unstable. Since the spacetime we are considering in this paper is asymptotically flat, the MBCO is determined as the solution to the equation of . By solving this equation, we find the radius of MBCO at
Again, similar to the case of the ISCO, the MBCO exists only in the 4-dimensional standard Schwarzschild black hole spacetime at . By summing all results obtained from the circular orbits, we conclude that the effective potential of the massive test particle does not have region beyond the photonsphere in higher dimensions ().
3. Capture of Photon
In this section, we study a motion of a photon and its capture by the Schwarzschild–Tangherlini black hole, whose line element is given by (3) with metric function (6). Prior to turning to the study, we introduce a notion of impact parameter, denoted by b, that defines the possible closest approach distance of a photon to the black hole before reaching an observer at infinity. It is well-known that the photon passing through the black hole spacetime can approach the black hole until the photonsphere, beyond which it moves along the photonsphere or is captured by the black hole. Therefore, the photonsphere is a boundary between capture and escape scenarios. Therefore, our main task in this section is to find the impact parameter, b, of the photon.
As Figure 3 shows that the effective potential of the photon tends to zero at infinity, the impact parameter is defined by
with being the critical angular momentum of a photon. For simplicity, one can rewrite the radial equation of motion (8) for the photon () by applying the transformation for the affine parameter in the following polynomial form:

Figure 3.
Radial profile of the effective potential of a photon in the Schwarzschild–Tangherlini spacetime for and the dimension in the range .
In order for the right-hand side of Equation (17) to take the monic polynomial form, we multiply both sides of equation by as
The zeros of the right-hand side of Equation (18) represent the turning points. A shape of the effective potential indicates that in this case, there are three possible scenarios in terms of the numbers of turning points: (i) no turning point with , which characterizes the cases that either the photon coming from infinity falls into a black hole, or if a photon that was emitted from near the horizon escapes to infinity; (ii) one turning point with that characterizes the case that the photon coming from infinity or emitted just outside the event horizon of the black hole is captured by the photonsphere at ; (iii) two turning points with characterize the cases that either the photon coming from infinity reaches the periastron () and again escapes to infinity, or if the photon emitted from near the horizon reaches an apastron () and falls back to the black hole.
Thus, we are interested in the second scenario in which the critical impact parameter corresponds to the maximum of the effective potential where two turning points merge into one. To find the value of b for one turning point, we must find the value of b that forms the discriminant of the polynomial on the right hand side of (18). To find the discriminant, we apply a determinant of the Sylvester matrix for the resultant of the polynomial. Since the discriminant of this polynomial strongly depends on the dimension D, we determine the discriminant after specifying the dimension below.
Moreover, to estimate the likelihood of a photon being captured by the black hole, we study the capture cross-section of a photon by the black hole. From the geometrical point of view, the capture cross-section of a photon is determined through the photonsphere at the given plane as
3.1. : Schwarzschild Black Hole
Despite the fact that the capture cross-section of a photon by the Schwarzschild black hole has already been studied in [25,26,27,28,29,30,31], in order to keep sequences for all dimensions, we also present the results here. Thus, in this case, the equation takes the form
The determinant of the polynomial on the right-hand side of (20) is determined by the following Sylvester matrix:
By solving the above equation with respect to the impact parameter, we found the critical value of impact parameter as
and the capture cross-section of the photon by the Schwarzschild black hole is equal to
3.2. : Schwazrschild-Tangherlini Black Hole
For the 5-dimensional Schwazrschild-Tangherlini black hole, Equation (18) takes the following form:
The determinant of the polynomial on the right-hand side of (24) is determined by the following Sylvester matrix:
By solving the above equation with respect to the impact parameter, we found the critical value of impact parameter as
The capture cross-section of a photon by the 5-dimensional Schwarzschild–Tangherlini black hole is equal to
3.3. Generic Case
As we have already stated that the critical impact parameter of a photon is determined by the ratio (16) with the given energy in (10) and angular momentum at the photonsphere at (12). Thus, the impact parameter of a photon in the arbitrary dimensional Schwarzschild–Tangherlini black hole spacetime is determined by
The capture cross-section of a photon by the generic Schwarzschild–Tangherlini black hole is given by
In order to present them quantitatively, we have presented Figure 4 and in Table 1 for the dimension of the spacetime in the range .
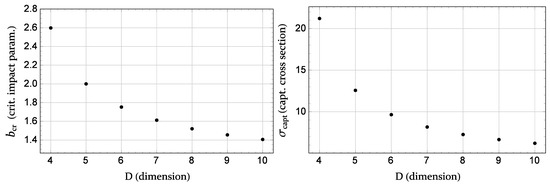
Figure 4.
The critical impact parameter (Left panel) and capture cross-section (Right panel) of a photon in the Schwarzschild–Tangherlini black hole spacetime for the dimension in the range .

Table 1.
The critical impact parameter and capture cross-section of a photon by the Schwarzschild–Tangherlini black hole for several values of spacetime dimension.
Moreover, we study the capture (or escape) of the photon as a function of propagation direction as in [25]. An observer at rest in the field of the Schwarzschild–Tangherlini black hole measures the following velocities of the photon relative to his orthonormal frame:
where + and − signs before the square root indicate the direction of motion of a photon, whether it is coming from or toward a black hole, respectively. The components of the velocity satisfy .
This condition can be written in terms of the trigonometric functions of the angle between radial and propagation directions, , as , with and .
From the effective potential in Figure 3, it can be seen that there is always possibility for a photon to be captured by (or escape from) the black hole. Below, let us analyse the capture of the photon by the black hole cases separately.
- (i)
- The photon is inside the photonsphere (). At the event horizon at , the photon has no chance to escape and it is captured by the black hole (). Beyond the event horizon, the chance to escape from (capture by) the black hole increases (decreases) and at the photonsphere at , the escape and capture are equally likely (). Therefore, in Figure 5, escape and capture curves intersect at the photonsphere, where they are equally likely. In this region, the escape can happen only if and .
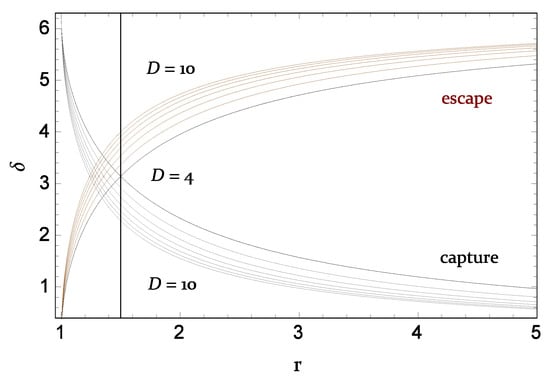 Figure 5. The angle between radial and propagation directions of captured photon by (gray) and escaped photon from (brown) the Schwarzschild–Tangherlini black hole spacetime as a function of radial coordinate for the dimension in the range . Where the vertical line corresponds to the photonsphere of the standard Schwarzschild black hole (black line).
Figure 5. The angle between radial and propagation directions of captured photon by (gray) and escaped photon from (brown) the Schwarzschild–Tangherlini black hole spacetime as a function of radial coordinate for the dimension in the range . Where the vertical line corresponds to the photonsphere of the standard Schwarzschild black hole (black line). - (ii)
- The photon is outside the photonsphere (). In this case, as r increases, a chance for the photon to escape increases and to capture decreases. In this region, escape can happen in two cases: (1) ensures the photon escapes; (2) and ensure the particle moves towards the black hole and reaches the periastron (bigger turning point) and bounces back to infinity.
These two cases are calculated and summed for the photon in the Schwrazschild-Tangherlini black hole spacetime in Figure 5. One can see that in higher dimensional black holes, at the given radius, a photon is more likely to escape rather than the ones with fewer dimensions. This is one more indication that the extra dimension of the Schwrazschild-Tangherlini spacetime weakens the gravitational attraction of the black hole.
4. Capture of Massive Particle
In this section, we study the capture cross-section of a massive test particle by the Schwarzschild–Tangherlini black hole. Similar to the previous section, to study the capture cross-section of a massive particle by the black hole, one must first determine the critical impact parameter of the particle. However, since the effective potential of the massive particle tends to one in Figure 1, not to zero as in the case of photon in Figure 3, at spatial infinity, the critical impact parameter is defined quite differently to the case of photon (16), as follows:
As it is seen from (31), our main task is to find the critical specific angular momentum of the particle. To find it, we first rewrite the radial equation of motion (8) in the following form:
The zeros of a polynomial on the right-hand side of (32) represent the turning points. As in the case of the capture of photon in the previous section, from a shape of the effective potential in Figure 1 it is easy to realize that depending on the energy of the particle, there can be up to two turning points and one of the three scenarios presented in the previous section can occur. Again, the critical impact parameter corresponds to the case with one turning point where two turning points merge. The two turning points merge only if the discriminant of the polynomial on the right-hand side of (32) vanishes. Again, to find the discriminant, we apply the Sylvester matrix for the resultant polynomial. In our case, the Sylvester matrix is the one with a size of . Unfortunately, we could not solve the determinant of this matrix for the arbitrary dimension. Therefore, we solve them by specifying the dimensions of the spacetime below.
4.1. : Schwarzschild Black Hole
In the case of the capture of a massive test particle by the standard Schwarzschild black hole, the radial equation of motion (32) takes the following form:
The Sylvester matrix for this case is written as
that gives the following equation:
By solving this equation, we obtain the following expression for the specific angular momentum:
By inserting expression (36) into (31), one obtains the critical impact parameter and consequently, the capture of the massive particle with energy per mass . Let us check the capture cross-section for some limiting cases.
Let us consider the test particle is relativistic or a highly energetic particle. In this case, the capture cross-section is given by
that is identical with the one in [25].
Now, let us consider a non-relativistic particle with energy , where is a ratio of the velocity of the particle and speed of light as . In this case, the capture cross-section is given by
4.2. : Schwarzschild–Tangherlini Black Hole
In the case of the capture of a massive test particle by the 5-dimensional Schwarzschild–Tangherlini black hole, the radial equation of motion (32) takes the following form:
The Sylvester matrix for this case is and written as
that gives the following equation:
By solving this equation, we obtain the following expression for the specific angular momentum:
By inserting expression (42) into (31), one obtains the critical impact parameter and consequently, the capture of the massive particle with energy per mass . Let us check the capture cross-section for some limiting cases.
Let us consider the test particle is a relativistic or highly energetic particle. In this case, the capture cross-section is given by
For the non-relativistic particle, the capture cross-section is given by
For other dimensions of the spacetime, the same calculations can be repeated. As the dimension of the spacetime increases, the order of the polynomial together with a size of the Sylvester matrix, its determinant and expression of the critical angular momentum all increase. Due to their long forms, we do not report them here, instead, in Table 2, we present the capture cross-section of the test particle that is relativistic and non-relativistic cases for the dimension of the Schwarzschild–Tangherlini black hole spacetime in the range .

Table 2.
The capture cross-section of relativistic and non-relativistic particles by the Schwarzschild–Tangherlini black hole for several values of dimension of the spacetime.
5. Conclusions
In this paper, we have studied the characteristic circular orbits of the massive and massless particles around a Schwrazschild–Tangherlini black hole that is a solution of pure general relativity in higher dimensional spacetime with a topology. By studying the circular orbits of test particles, we have determined the extra dimension of the spacetime weakens the gravitational attraction of the black hole and, consequently, radii of all the characteristic circular orbits, such as radii of the photonsphere, innermost stable and marginally bound circular orbits, decrease in the higher dimensions. Moreover, we have shown that in the Schwarzschild–Tangherlini spacetime there are stable circular orbits only in the four-dimensional standard Schwarzschild spacetime. In higher dimensions, there are no stable circular orbits which contradict the astronomical and cosmological observations of gravitationally bounded systems. It may work in our favor that our Universe, consisting of galaxies that contain stars, is most probably four-dimensional.
We studied the capture cross-section of massless (photon) and massive test particles by the Schwarzschild–Tangherlini black hole. The critical impact parameters and capture cross-sections of a photon and massive particles are calculated for several higher dimensions and it is shown that they also decrease with increasing dimension. Moreover, we have calculated the capture cross-section of relativistic and non-relativistic test particles in the higher dimensions.
Author Contributions
Conceptualization, B.A. and B.T.; methodology, B.T. and O.R.; software, B.T. and O.R.; validation, B.A., B.T. and O.R.; formal analysis, O.R. and B.T.; investigation, B.T.; resources, B.A.; data curation, O.R.; writing—original draft preparation, B.T. and O.R.; writing—review and editing, B.A. and B.T.; visualization, O.R.; supervision, B.A.; project administration, B.T. and B.A.; funding acquisition, B.A. All authors have read and agreed to the published version of the manuscript.
Funding
Authors acknowledge the support of Ministry of Innovative Development of the Republic of Uzbekistan. This research was funded by the Abdus Salam International Centre for Theoretical Physics through Grant No. OEA-NT-01.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
Authors acknowledge the support of Ministry of Innovative Development of the Republic of Uzbekistan and Abdus Salam International Centre for Theoretical Physics through Grant No. OEA-NT-01.
Conflicts of Interest
The authors declare no conflict of interest.
Note
| 1 | Therefore, sometimes in the literature, this quantity is called the geometrical capture cross-section |
References
- The LIGO Scientific Collaboration and the Virgo Collaboration. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- The LIGO Scientific Collaboration and the Virgo Collaboration. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration and the Virgo Collaboration. GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration and the Virgo Collaboration. GW170608: Observation of a 19 Solar-mass Binary Black Hole Coalescence. Astrophys. J. Lett. 2017, 851, L35. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration and the Virgo Collaboration. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. 2019, 875, L1. [Google Scholar] [CrossRef]
- Gravity Collaboration. Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2018, 615, L15. [Google Scholar] [CrossRef]
- Gravity Collaboration. Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2020, 636, L5. [Google Scholar] [CrossRef]
- Tursunov, A.; Zajaček, M.; Eckart, A.; Kološ, M.; Britzen, S.; Stuchlík, Z.; Czerny, B.; Karas, V. Effect of Electromagnetic Interaction on Galactic Center Flare Components. Astrophys. J. 2020, 897, 99. [Google Scholar] [CrossRef]
- Tangherlini, F.R. Schwarzschild field inn dimensions and the dimensionality of space problem. Nuovo Cim. 1963, 27, 636–651. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Kovář, J.; Slaný, P.; Tursunov, A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe 2020, 6, 26. [Google Scholar] [CrossRef]
- Connell, P.; Frolov, V.P. Ray-tracing in four and higher dimensional black hole spacetimes: An analytical approximation. Phys. Rev. D 2008, 78, 024032. [Google Scholar] [CrossRef]
- Tsukamoto, N.; Kitamura, T.; Nakajima, K.; Asada, H. Gravitational lensing in Tangherlini spacetime in the weak gravitational field and the strong gravitational field. Phys. Rev. D 2014, 90, 064043. [Google Scholar] [CrossRef]
- Pratap Singh, B.; Ghosh, S.G. Shadow of Schwarzschild-Tangherlini black holes. arXiv 2017, arXiv:1707.07125. [Google Scholar]
- Bugden, M. Trapped photons in Schwarzschild-Tangherlini spacetimes. Class. Quantum Gravity 2020, 37, 015001. [Google Scholar] [CrossRef]
- Décanini, Y.; Folacci, A.; Raffaelli, B. Unstable circular null geodesics of static spherically symmetric black holes, Regge poles, and quasinormal frequencies. Phys. Rev. D 2010, 81, 104039. [Google Scholar] [CrossRef]
- Décanini, Y.; Folacci, A.; Raffaelli, B. Fine structure of high-energy absorption cross sections for black holes. Class. Quantum Gravity 2011, 28, 175021. [Google Scholar] [CrossRef]
- Glampedakis, K.; Andersson, N. Scattering of scalar waves by rotating black holes. Class. Quantum Gravity 2001, 18, 1939–1966. [Google Scholar] [CrossRef]
- Macedo, C.F.B.; Leite, L.C.S.; Oliveira, E.S.; Dolan, S.R.; Crispino, L.C.B. Absorption of planar massless scalar waves by Kerr black holes. Phys. Rev. D 2013, 88, 064033. [Google Scholar] [CrossRef]
- Benone, C.L.; de Oliveira, E.S.; Dolan, S.R.; Crispino, L.C.B. Absorption of a massive scalar field by a charged black hole. Phys. Rev. D 2014, 89, 104053. [Google Scholar] [CrossRef]
- Toshmatov, B.; Stuchlík, Z.; Schee, J.; Ahmedov, B. Quasinormal frequencies of black hole in the braneworld. Phys. Rev. D 2016, 93, 124017. [Google Scholar] [CrossRef]
- Ivashchuk, V.D.; Melnikov, V.N. Multi-temporal generalization of the Tangherlini solution. Class. Quantum Gravity 1994, 11, 1793–1805. [Google Scholar] [CrossRef]
- Casey, S. Optical 2-metrics of Schwarzschild-Tangherlini spacetimes and the Bohlin-Arnold duality. Class. Quantum Gravity 2012, 29, 237001. [Google Scholar] [CrossRef][Green Version]
- Igata, T.; Tomizawa, S. Stable circular orbits in higher-dimensional multi-black-hole spacetimes. Phys. Rev. D 2020, 102, 084003. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon Press: Oxford, UK, 1975. [Google Scholar]
- Zakharov, A.F. Capture of photons and slow uncharged particles by a spherically symmetric charged compact body in the relativistic theory of gravitation. Theor. Math. Phys. 1992, 90, 97–101. [Google Scholar] [CrossRef]
- Zakharov, A.F. Particle capture cross sections for a Reissner–Nordström black hole. Class. Quantum Gravity 1994, 11, 1027–1033. [Google Scholar] [CrossRef]
- Rahimov, O.G.; Abdujabbarov, A.A.; Ahmedov, B.J. Magnetized Particle Capture Cross Section for Braneworld Black Hole. Astrophys. Space Sci. 2011, 335, 499–504. [Google Scholar] [CrossRef][Green Version]
- Abdujabbarov, A.; Ahmedov, B.; Rahimov, O.; Salikhbaev, U. Magnetized particle motion and acceleration around a Schwarzschild black hole in a magnetic field. Phys. Scr. 2014, 89, 084008. [Google Scholar] [CrossRef]
- Ahmedov, B.; Rahimov, O.; Toshmatov, B. Capture of massless and massive particles by parameterized black holes. Galaxies 2021, submitted. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).