General Relativistic Aberration Equation and Measurable Angle of Light Ray in Kerr–de Sitter Spacetime
Abstract
1. Introduction
2. Light Trajectory in Kerr–de Sitter Spacetime
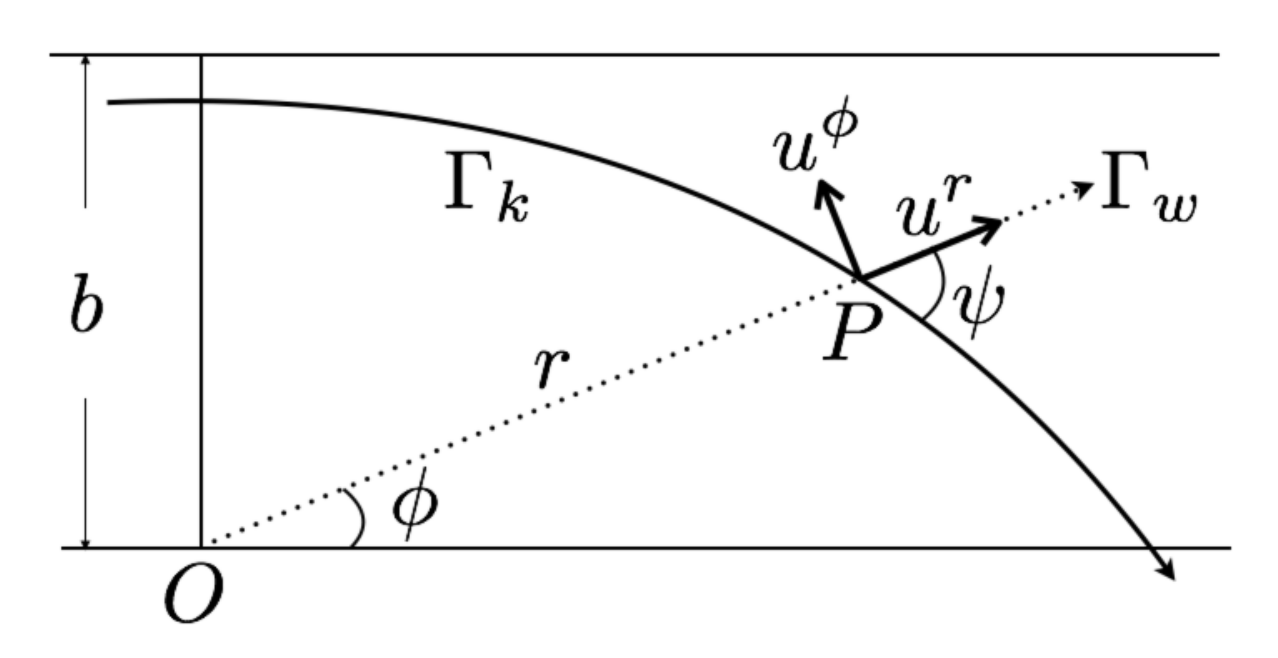
3. Measurable Angle in Kerr–de Sitter Spacetime
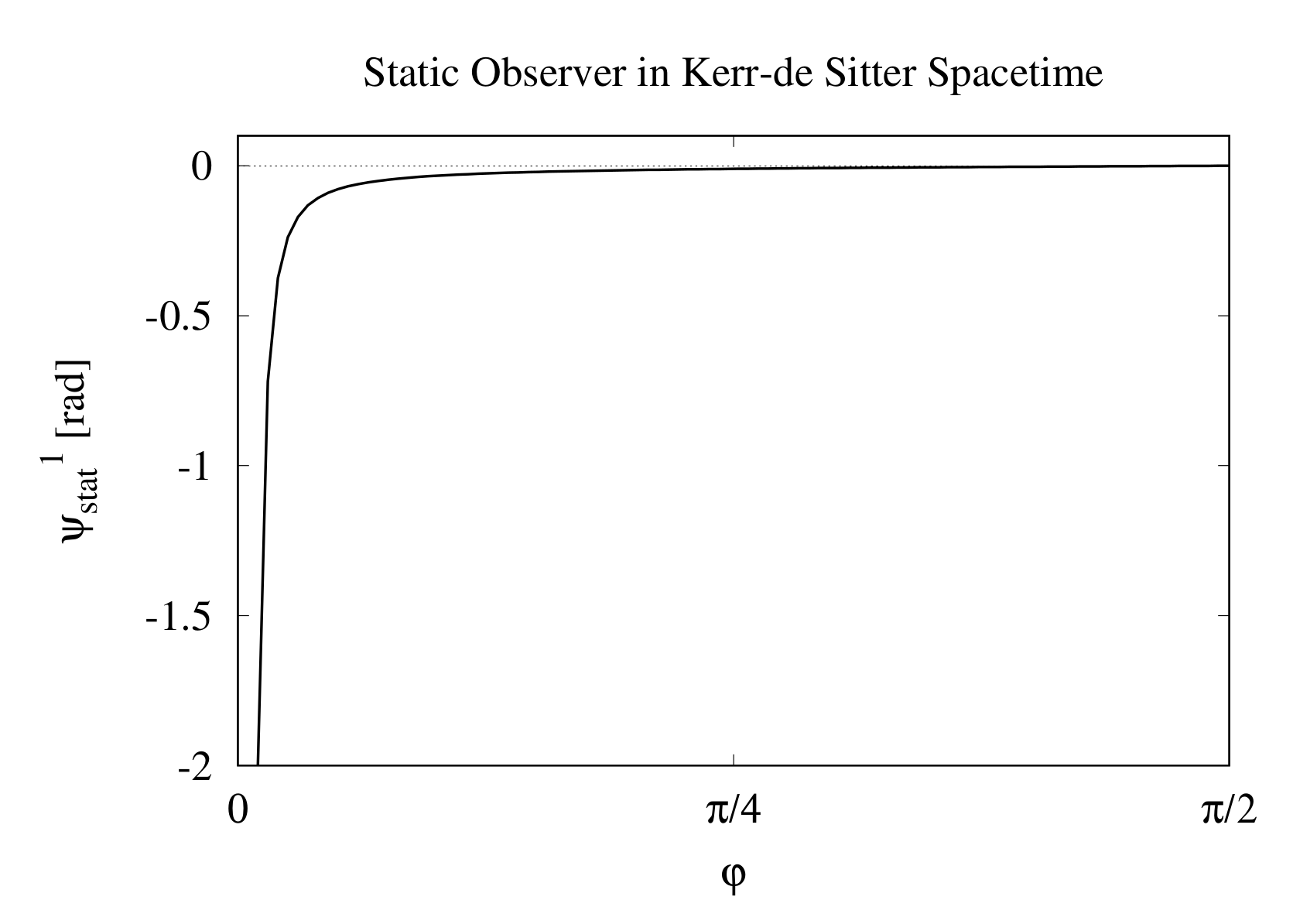
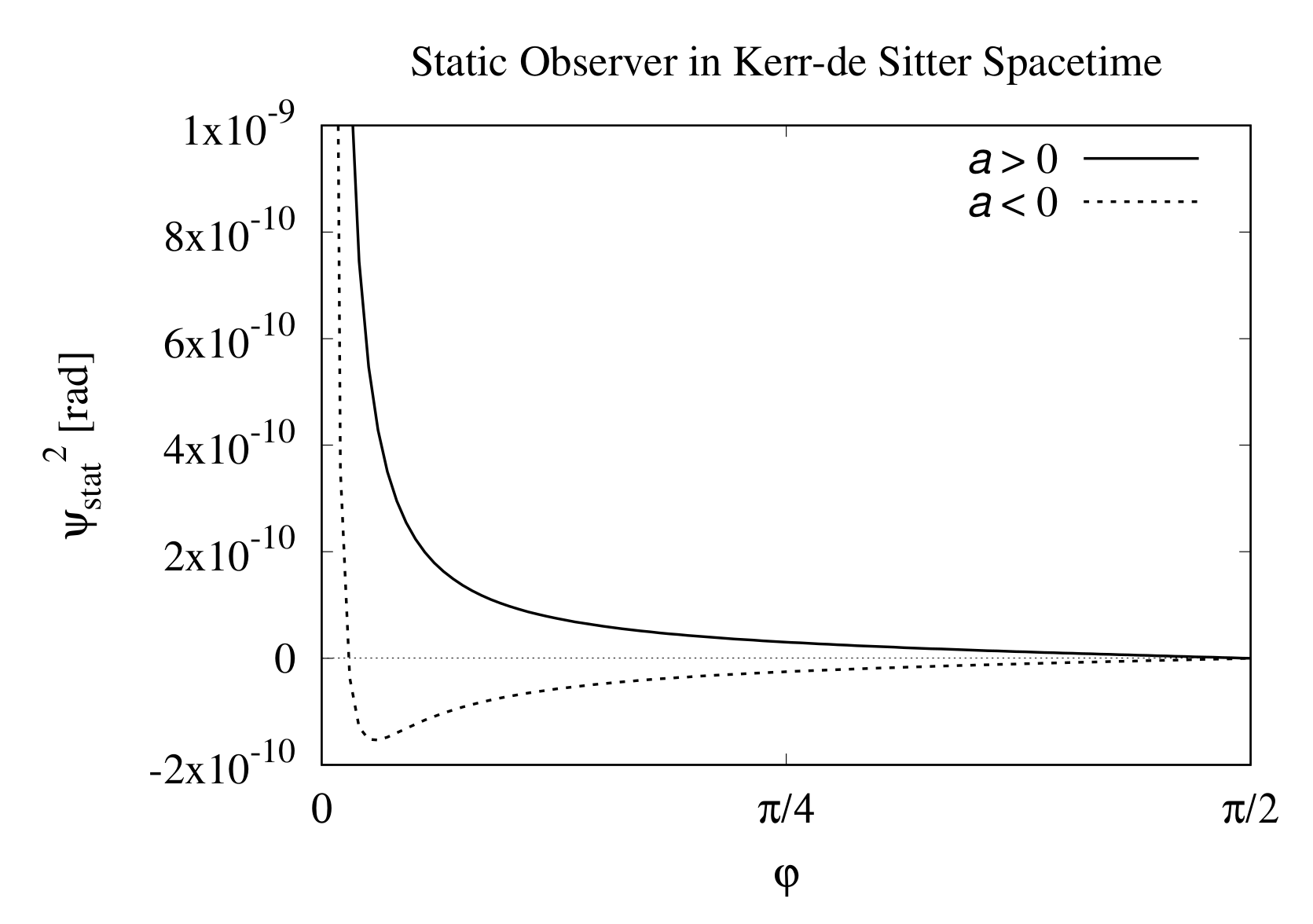
3.1. Measurable Angle by Static Observer
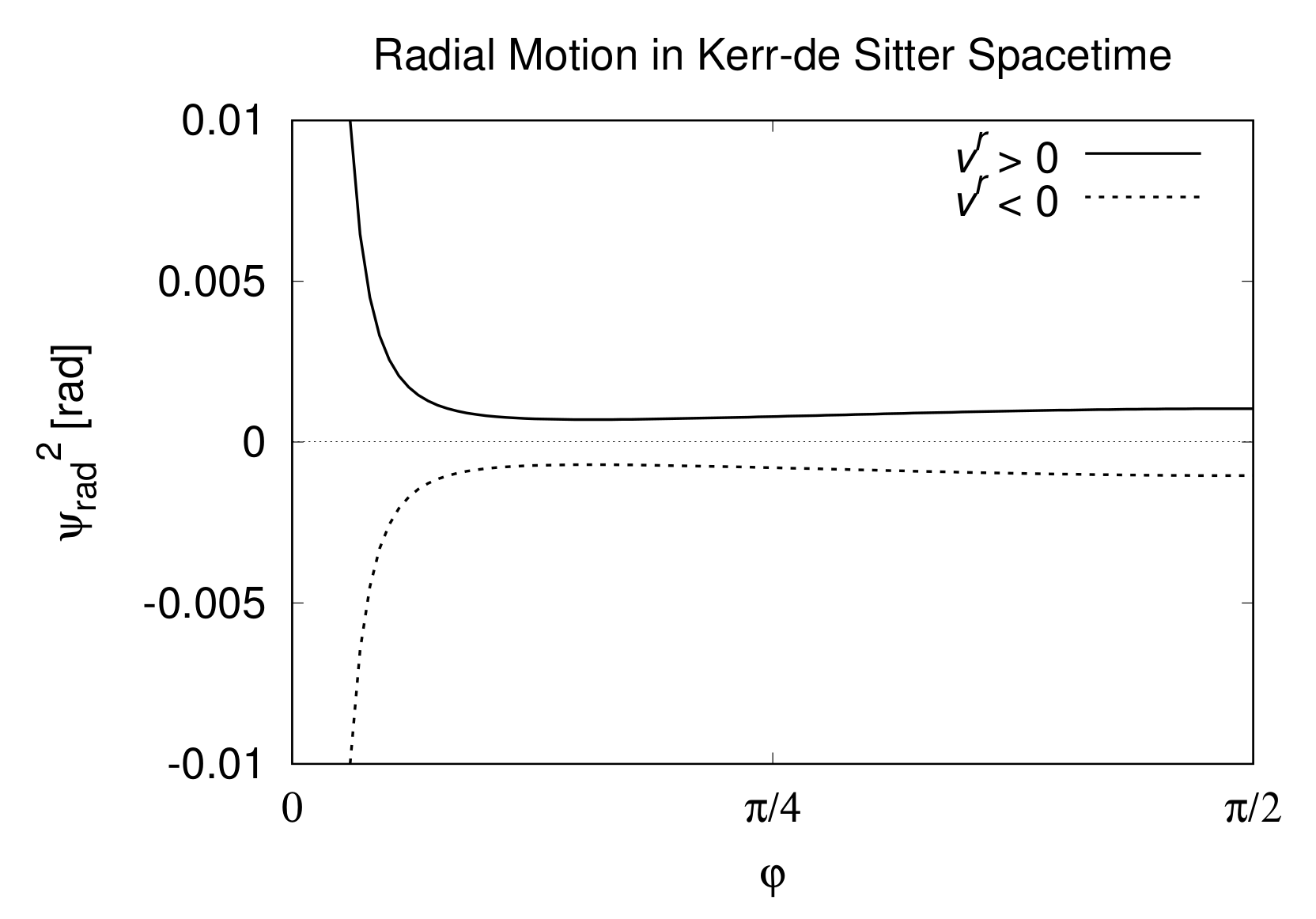
3.2. Measurable Angle by Observer in Radial Motion
3.3. Measurable Angle by Observer in Transverse Motion
3.4. Comparison of Static, Radial and Transverse Cases and Their Properties
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
| 1 | |
| 2 | The motion of an observer in Kerr–de Sitter spacetime, especially in the radial direction, can be characterized by the static radius [46,47,48] at which the gravitational interaction due to the central object and the expansion (repulsion) of the universe are balanced. At the position of the static radius , it is possible for the observer to remain stationary. However the observer at the static radius is in unstable equilibrium (the maximum of the effective potential), then observer begins to accelerate up to the velocity which is related to the boundary of the vacuola of Kerr–de Sitter spacetime (In fact, without rotation , Kerr-de Sitter spacetime can be regarded as the Einstein–Strauss–de Sitter vacuola model of the Universe, see, e.g., [49]). Therefore, there is a region where the observer’s velocity v is ; however, because we are now considering cosmological gravitational lensing in a region far enough from the lens object, we assume the observer’s velocity to be in this paper. |
References
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Carroll, S. The cosmological constant. Living Rev. Relativ. 2001, 4, 1–56. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Schmidt, B.P.; Suntzeff, N.B.; Phillips, M.M.; Schommer, R.A.; Clocchiatti, A.; Kirshner, R.P.; Garnavich, P.; Challis, P.; Leibundgut, B.; Spyromilio, J.; et al. The High-Z Supernova Search: Measuring Cosmic Deceleration and Global Curvature of the Universe Using Type Ia Supernovae. Astrophys. J. 1998, 507, 46–63. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Schneider, P.; Ehlers, J.; Falco, E.E. Gravitational Lenses; Springer: Berlin/Heisenberg, Germany; New York, NY, USA, 1999. [Google Scholar]
- Schneider, P.; Kochanek, C.; Wambsganss, J. Gravitational Lensing: Strong, Weak and Micro; Springer: Berlin/Heisenberg, Germany; New York, NY, USA, 2006. [Google Scholar]
- Islam, J.N. The cosmological constant and classical tests of general relativity. Phys. Lett. A 1983, 97, 239–241. [Google Scholar] [CrossRef]
- Lake, K. Bending of light and the cosmological constant. Phys. Rev. D 2002, 65, 087301. [Google Scholar] [CrossRef]
- Rindler, W.; Ishak, M. Contribution of the cosmological constant to the relativistic bending of light revisited. Phys. Rev. D 2007, 76, 043006. [Google Scholar] [CrossRef]
- Park, M. Rigorous approach to gravitational lensing. Phys. Rev. D 2008, 78, 023014. [Google Scholar] [CrossRef]
- Khriplovich, I.B.; Pomeransky, A.A. Does the Cosmological Term Influence Gravitational Lensing? Int. J. Mod. Phys. D 2008, 17, 2255–2259. [Google Scholar] [CrossRef]
- Ishak, M.; Rindler, W. The relevance of the cosmological constant for lensing. Gen. Rel. Grav. 2010, 42, 2247–2268. [Google Scholar] [CrossRef]
- Simpson, F.; Peacock, J.A.; Heavens, A.F. On lensing by a cosmological constant. MNRAS 2010, 402, 2009–2016. [Google Scholar] [CrossRef]
- Bhadra, A.; Biswas, S.; Sarkar, K. Gravitational deflection of light in the Schwarzschild–de Sitter space-time. Phys. Rev. D 2010, 82, 063003. [Google Scholar] [CrossRef]
- Miraghaei, H.; Nouri-Zonoz, M. Classical tests of general relativity in the Newtonian limit of the Schwarzschild–de Sitter spacetime. Gen. Rel. Grav. 2010, 42, 2947–2956. [Google Scholar] [CrossRef]
- Biressa, T.; de Freitas Pacheco, J.A. The cosmological constant and the gravitational light bending. Gen. Rel. Grav. 2011, 43, 2649–2659. [Google Scholar] [CrossRef]
- Arakida, H.; Kasai, M. Effect of the cosmological constant on the bending of light and the cosmological lens equation. Phys. Rev. D 2012, 85, 023006. [Google Scholar] [CrossRef]
- Hammad, F. A note on the effect of the cosmological constant on the bending of light. Mod. Phys. Lett. A 2013, 28, 1350181. [Google Scholar] [CrossRef]
- Lebedev, D.; Lake, K. On the influence of the cosmological constant on trajectories of light and associated measurements in Schwarzschild de Sitter space. arXiv 2013, arXiv:1308.493. [Google Scholar]
- Batic, D.; Nelson, S.; Nowakowski, M. Light on curved backgrounds. Phys. Rev. D 2015, 91, 104015. [Google Scholar] [CrossRef]
- Arakida, H. Effect of the Cosmological Constant on Light Deflection: Time Transfer Function Approach. Universe 2016, 2, 5. [Google Scholar] [CrossRef]
- Ishihara, A.; Suzuki, Y.; Ono, T.; Kitamura, T.; Asada, H. Gravitational bending angle of light for finite distance and the Gauss–Bonnet theorem. Phys. Rev. D 2016, 94, 084015. [Google Scholar] [CrossRef]
- Arakida, H. Light deflection and Gauss–Bonnet theorem: Definition of total deflection angle and its applications. Gen. Rel. Grav. 2018, 50, 48. [Google Scholar] [CrossRef]
- Kraniotis, G.V. Frame dragging and bending of light in Kerr and Kerr (anti) de Sitter spacetimes. Class. Quant. Grav. 2005, 22, 4391–4424. [Google Scholar] [CrossRef]
- Kraniotis, G.V. Precise analytic treatment of Kerr and Kerr-(anti) de Sitter black holes as gravitational lenses. Class. Quant. Grav. 2011, 28, 085021. [Google Scholar] [CrossRef]
- Sultana, J. Contribution of the cosmological constant to the bending of light in Kerr-de Sitter spacetime. Phys. Rev. D 2013, 88, 042003. [Google Scholar] [CrossRef]
- Charbulák, D.; Stuchlík, Z. Photon motion in Kerr–de Sitter spacetimes. Eur. Phys. J. C 2017, 77, 897. [Google Scholar] [CrossRef]
- Goicoechea, L.J.; Mediavilla, E.; Buitrago, J.; Atrio, F. A second-order approximation to equatorial null geodesics in the Kerr metric—Application to light deflection in eclipsing compact binaries. Mon. Not. R. Astron. Soc. 1992, 259, 281–292. [Google Scholar] [CrossRef]
- Iyer, S.V.; Hansen, E.C. Light’s bending angle in the equatorial plane of a Kerr black hole. Phys. Rev. D 2009, 80, 124023. [Google Scholar] [CrossRef]
- Kraniotis, G.V. Gravitational lensing and frame dragging of light in the Kerr–Newman and the Kerr–Newman (anti) de Sitter black hole spacetimes. Gen. Rel. Grav. 2014, 46, 1818. [Google Scholar] [CrossRef]
- He, G.; Lin, W. Gravitational deflection of light and massive particles by a moving Kerr–Newman black hole. Class. Quant. Grav. 2016, 33, 095007. [Google Scholar] [CrossRef]
- He, G.; Lin, W. Addendum to ‘Gravitational deflection of light and massive particle by a moving Kerr–Newman black hole’. Class. Quant. Grav. 2017, 34, 029401. [Google Scholar] [CrossRef]
- He, G.; Lin, W. Analytical derivation of second-order deflection in the equatorial plane of a radially moving Kerr–Newman black hole. Class. Quant. Grav. 2017, 34, 105006. [Google Scholar] [CrossRef]
- Jiang, C.; Lin, W. Post–Newtonian light propagation in Kerr–Newman spacetime. Phys. Rev. D 2018, 97, 024045. [Google Scholar] [CrossRef]
- Uniyal, R.; Nandan, H.; Jetzer, P. Bending angle of light in equatorial plane of Kerr-Sen Black Hole. Phys. Lett. B 2018, 782, 185–192. [Google Scholar] [CrossRef]
- Arakida, H. General Relativistic Aberration Equation and Measurable Angle of Light Ray in Kerr Spacetime. arXiv 2021, arXiv:1808.03418. [Google Scholar]
- Pechenick, K.R.; Ftaclas, C.; Cohen, J.M. Hot spots on neutron stars—The near-field gravitational lens. ApJ 1983, 274, 846–857. [Google Scholar] [CrossRef]
- Lebedev, D.; Lake, K. Relativistic Aberration and the Cosmological Constant in Gravitational Lensing I: Introduction. arXiv 2016, arXiv:1609.05183. [Google Scholar]
- Stuchlík, Z.; Hledík, S. Equatorial photon motion in the Kerr–Newman spacetimes with a non-zero cosmological constant. Class. Quantum Grav. 2000, 17, 4541–4576. [Google Scholar] [CrossRef][Green Version]
- Stuchlík, Z.; Charbulák, D.; Schee, J. Light escape cones in local reference frames of Kerr–de Sitter black hole spacetimes and related black hole shadow. Eur. Phys. J. C 2018, 78, 180. [Google Scholar] [CrossRef]
- Takizawa, K.; Ono, T.; Asada, H. Gravitational deflection angle of light: Definition by an observer and its application to an asymptotically nonflat spacetime. Phys. Rev. D 2020, 101, 104032. [Google Scholar] [CrossRef]
- Arakida, H. The optical geometry definition of the total deflection angle of a light ray in curved spacetime. arXiv 2020, arXiv:2006.13435. [Google Scholar]
- Carter, B. Black hole equilibrium states. In Black Holes/Les Astres Occlus; Gordon and Breach: New York, NY, USA, 1972; pp. 57–214. [Google Scholar]
- Karachentsev, I. Double Galaxies; Izdatel’stvo Nauka: Moscow, Russia, 1987; Available online: https://ned.ipac.caltech.edu/level5/Sept02/Keel/frames.html (accessed on 3 May 2021).
- Stuchlík, Z. The Motion of Test Particles in Black-Hole Backgrounds with Non-Zero Cosmological Constant. Bull. Astron. Inst. Czechosl. 1983, 34, 129–149. [Google Scholar]
- Stuchlík, Z.; Hledík, S. Some properties of the Schwarzschild–de Sitter and Schwarzschild–anti-de Sitter spacetimes. Phys. Rev. D 1999, 60, 044006. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Kovář, J.; Slaný, P.; Tursunov, A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe 2020, 6, 26. [Google Scholar] [CrossRef]
- Stuchlík, Z. An Einstein–Strauss-de Sitter Model of the Universe. Bull. Astron. Inst. Czechosl. 1984, 35, 205–215. [Google Scholar]
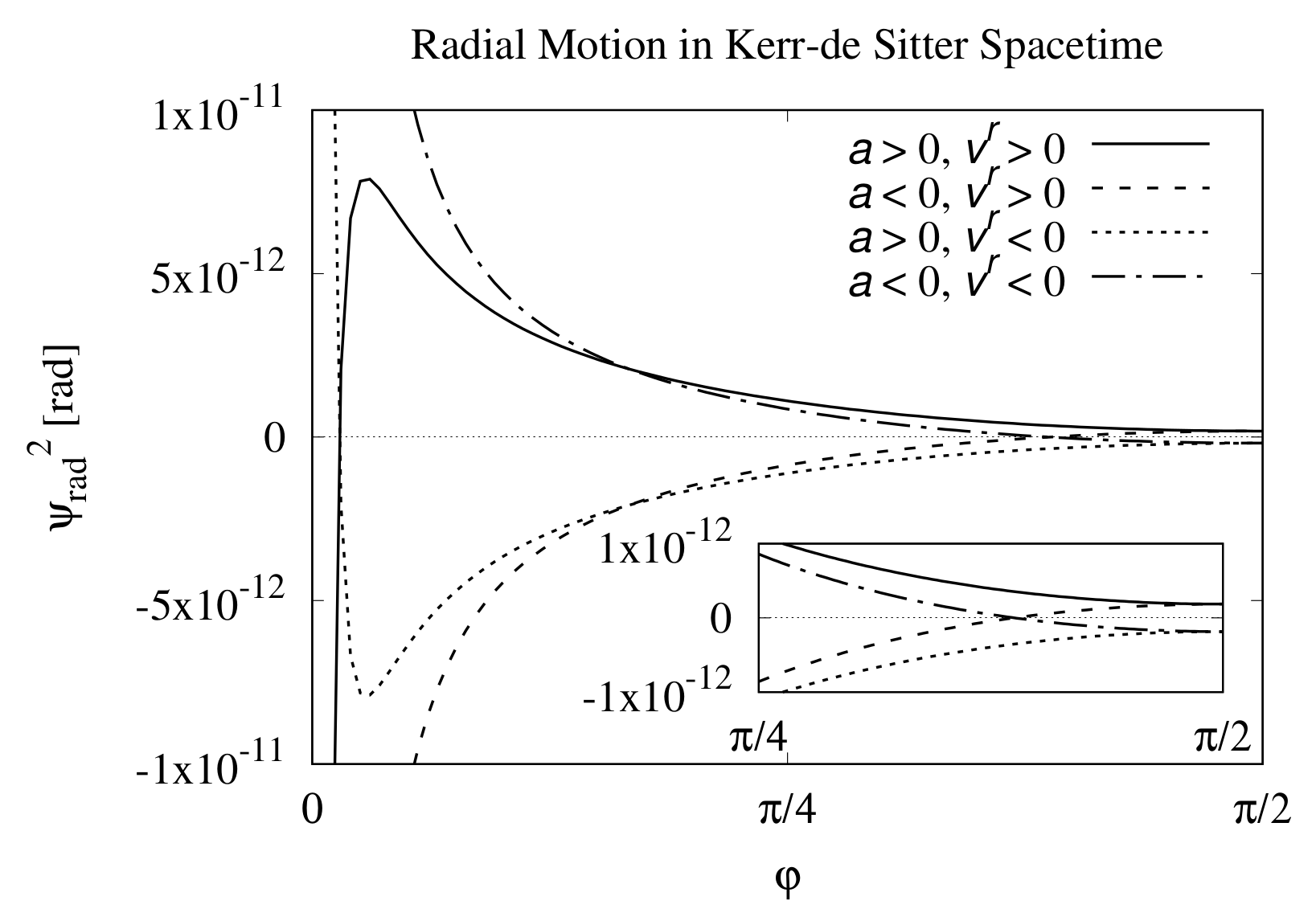
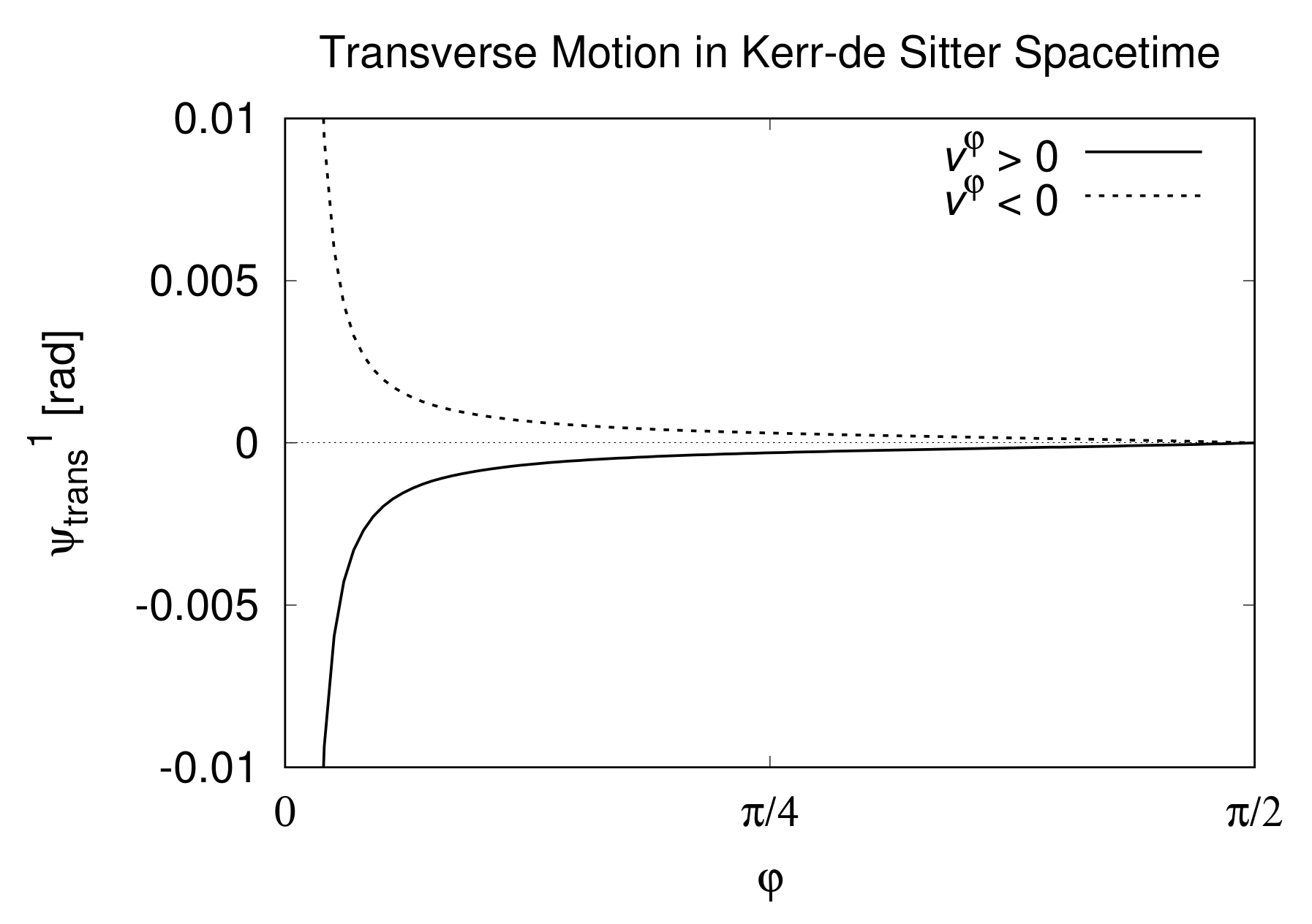

| Name | Symbol | Value |
|---|---|---|
| Mass of the Galaxy | ||
| m | ||
| Impact Parameter | m | |
| Angular Momentum of the Galaxy [45] | kg m/s | |
| Spin Parameter | m | |
| Cosmological Constant | m | |
| Hubble Constant | ||
| Distance from Lens Object | ||
| Recession Velocity | ||
| Radial Velocity | ||
| Transverse Velocity |
| Motion of Observer | Equation Number | |||
|---|---|---|---|---|
| Static | Equation (43) | Negative | 0 | |
| Equation (44) | ∞ | 0 | ||
| Mostly Negative for | ||||
| Radial | Equation (45) | ∞ for | Positive for | |
| for | Negative for | |||
| Equation (46) | for | Mostly Positive for | ||
| Mostly Negative for | ||||
| ∞ for | Mostly Negative for | |||
| Mostly Positive for | ||||
| Transverse | Equation (48) | for | Negative for | 0 |
| ∞ for | Positive for | |||
| Equation (49) | ∞ for | Positive for | ||
| Mostly Negative for | ||||
| for | Negative for | |||
| Mostly Positive for |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arakida, H. General Relativistic Aberration Equation and Measurable Angle of Light Ray in Kerr–de Sitter Spacetime. Universe 2021, 7, 173. https://doi.org/10.3390/universe7060173
Arakida H. General Relativistic Aberration Equation and Measurable Angle of Light Ray in Kerr–de Sitter Spacetime. Universe. 2021; 7(6):173. https://doi.org/10.3390/universe7060173
Chicago/Turabian StyleArakida, Hideyoshi. 2021. "General Relativistic Aberration Equation and Measurable Angle of Light Ray in Kerr–de Sitter Spacetime" Universe 7, no. 6: 173. https://doi.org/10.3390/universe7060173
APA StyleArakida, H. (2021). General Relativistic Aberration Equation and Measurable Angle of Light Ray in Kerr–de Sitter Spacetime. Universe, 7(6), 173. https://doi.org/10.3390/universe7060173






