Initial State Interaction for the 20Ne + 130Te and 18O + 116Sn Systems at 15.3 AMeV from Elastic and Inelastic Scattering Measurements
Abstract
1. Introduction
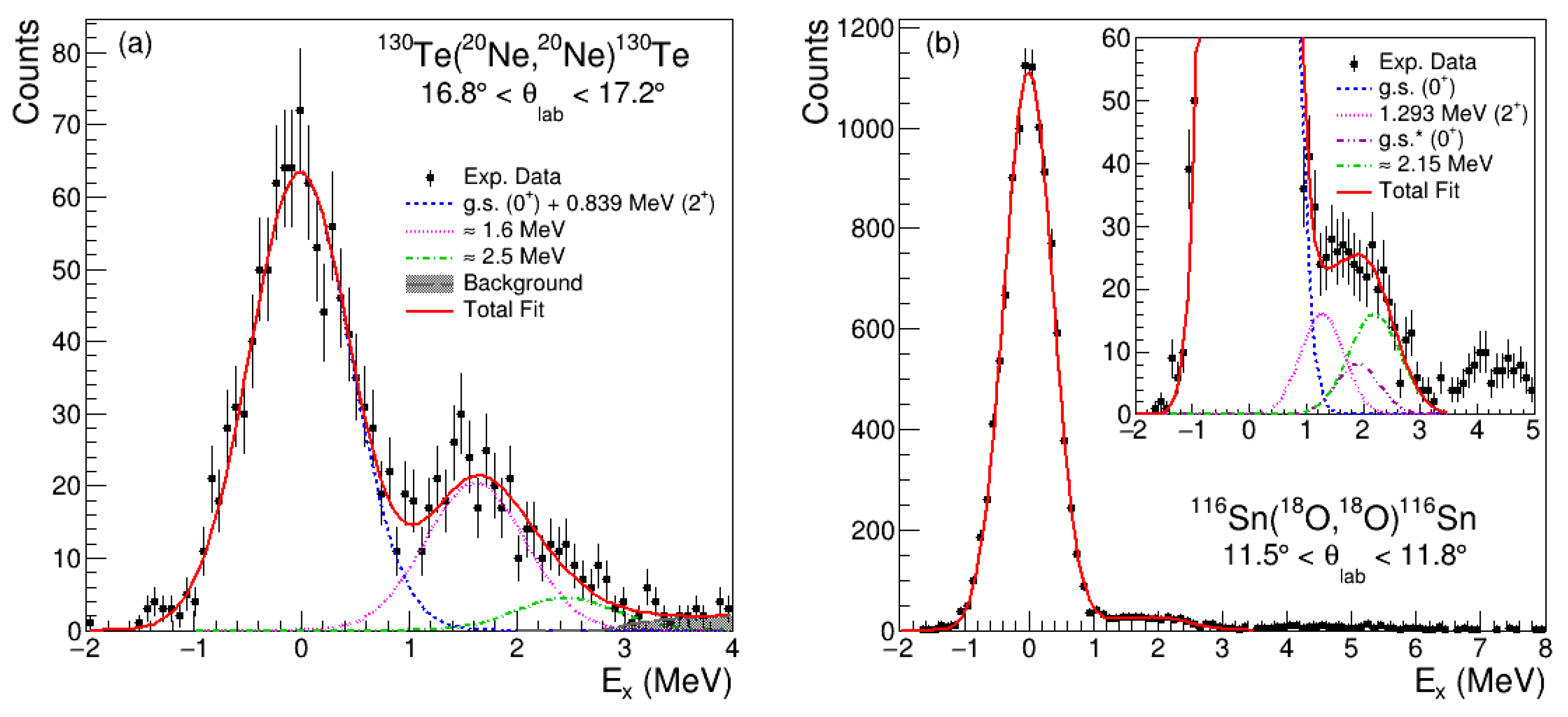
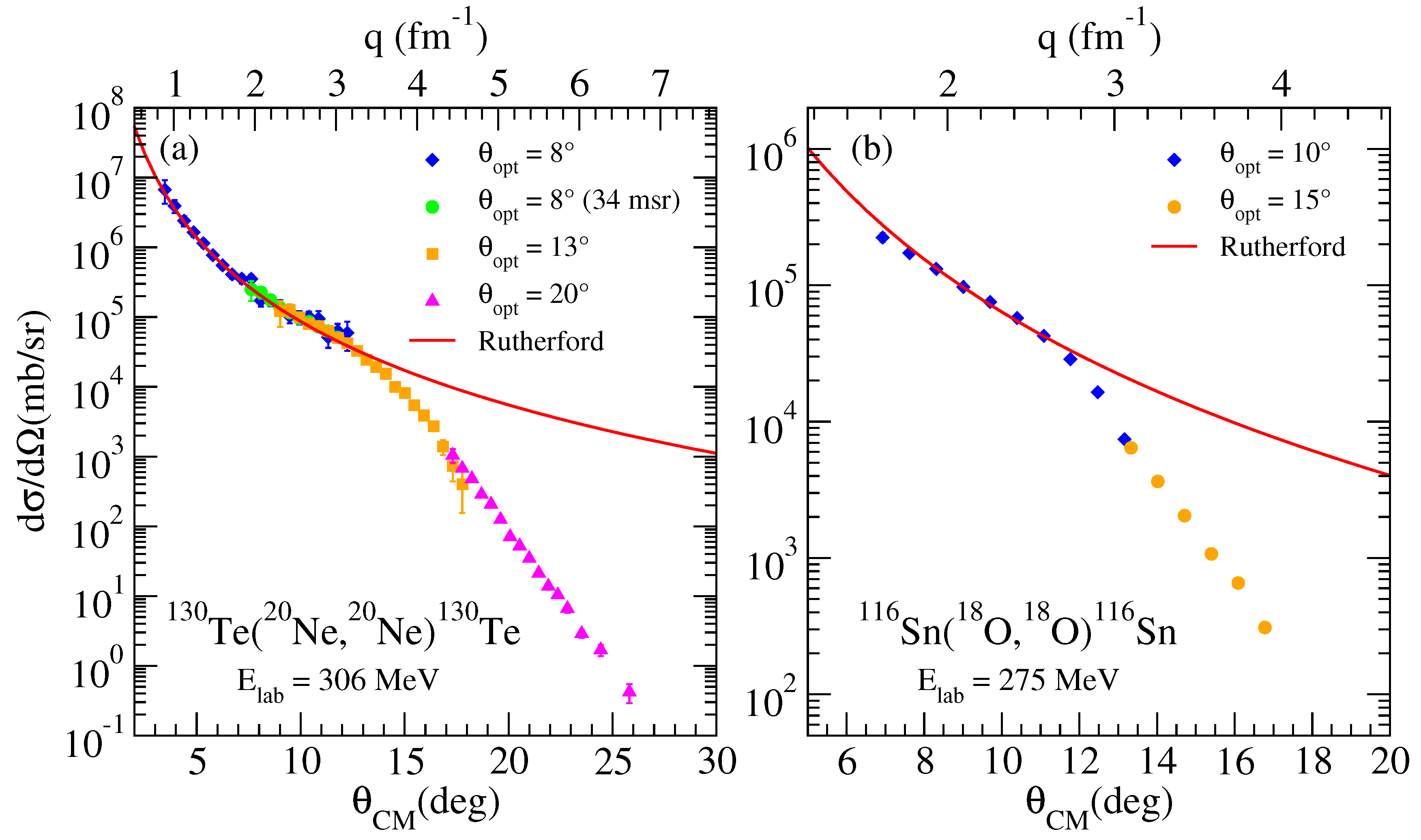
2. Experimental Setup and Results
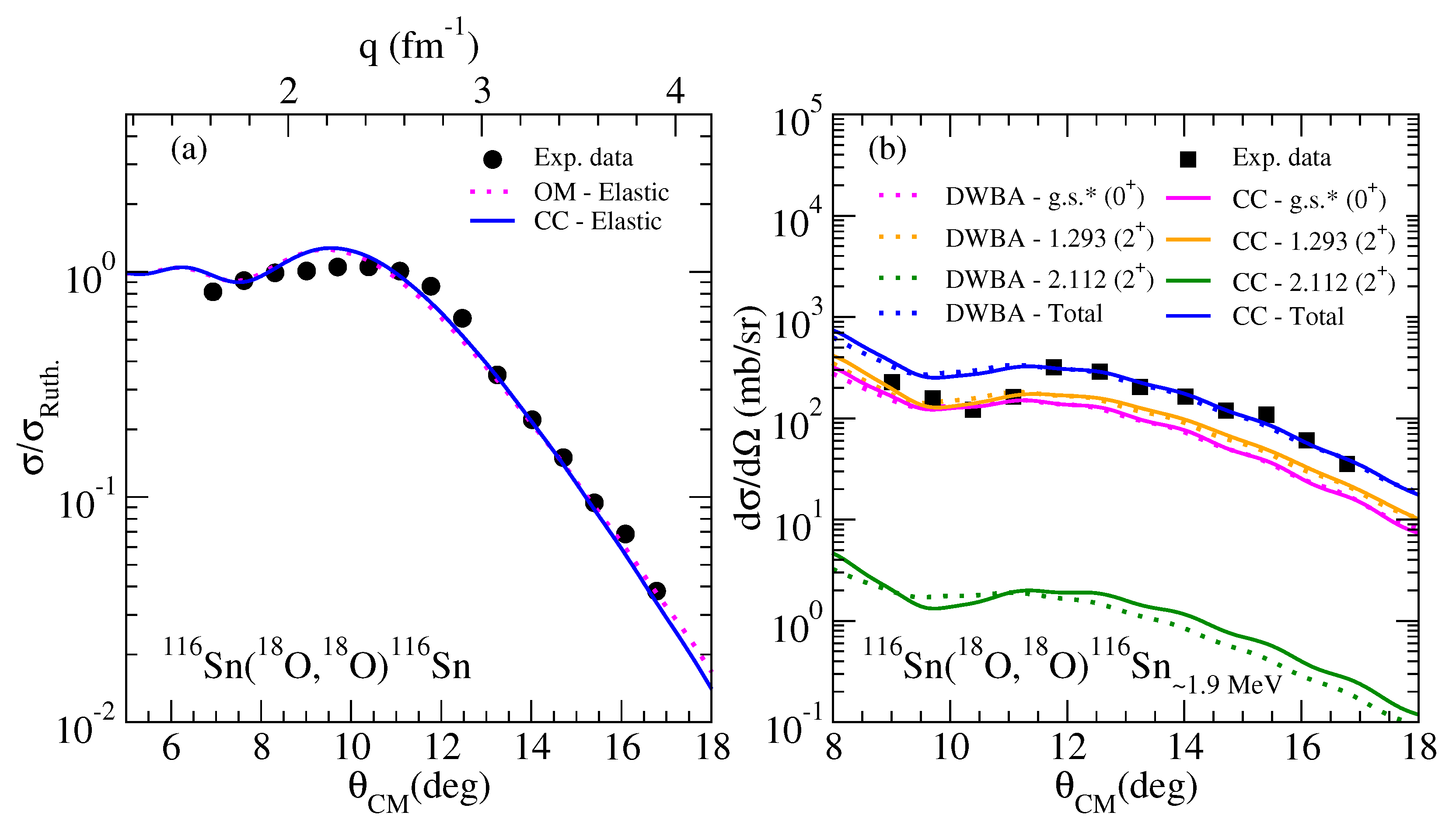
3. Theoretical Analysis
4. Discussion
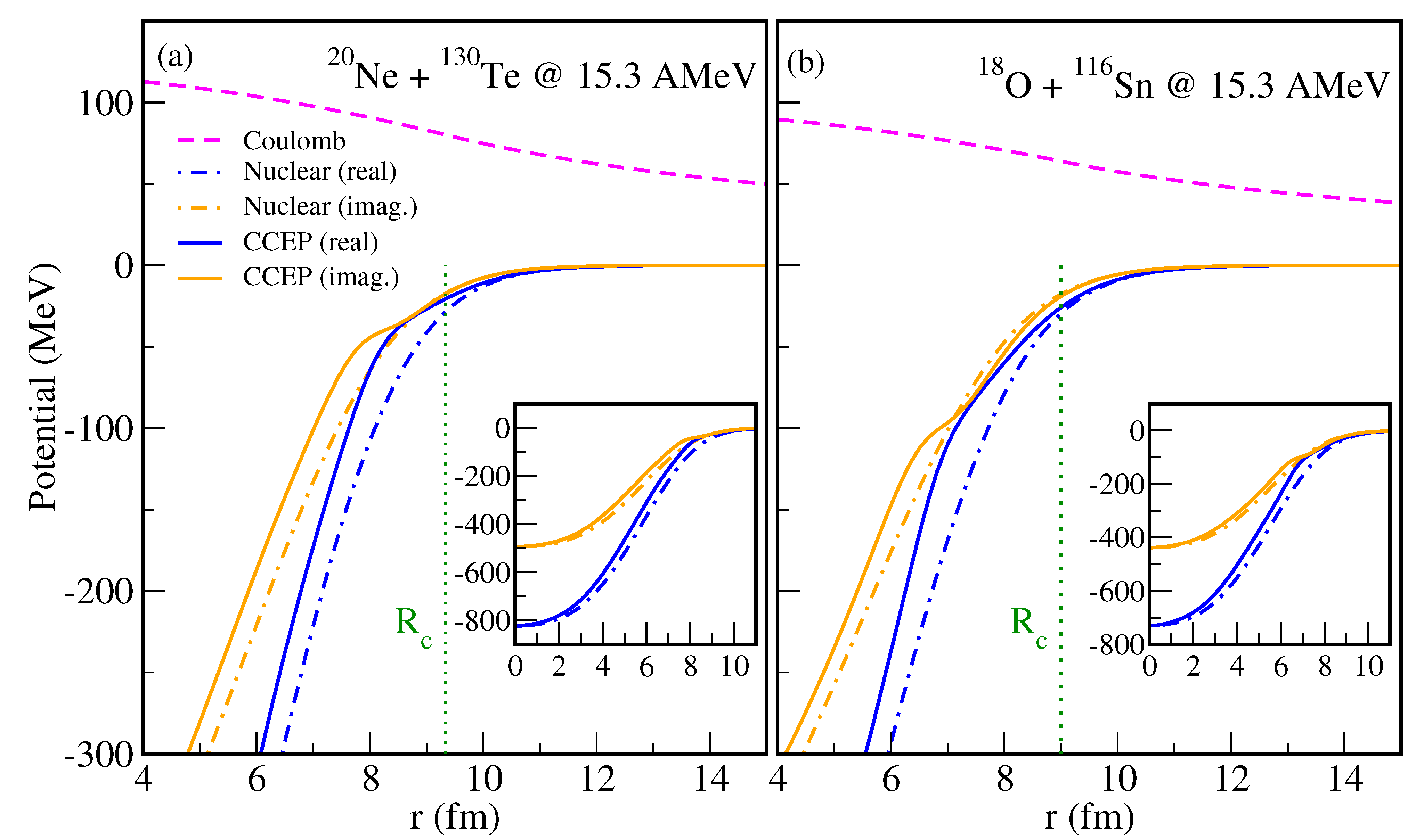
4.1. The 20Ne+130Te System
4.2. The 18O+116Sn System
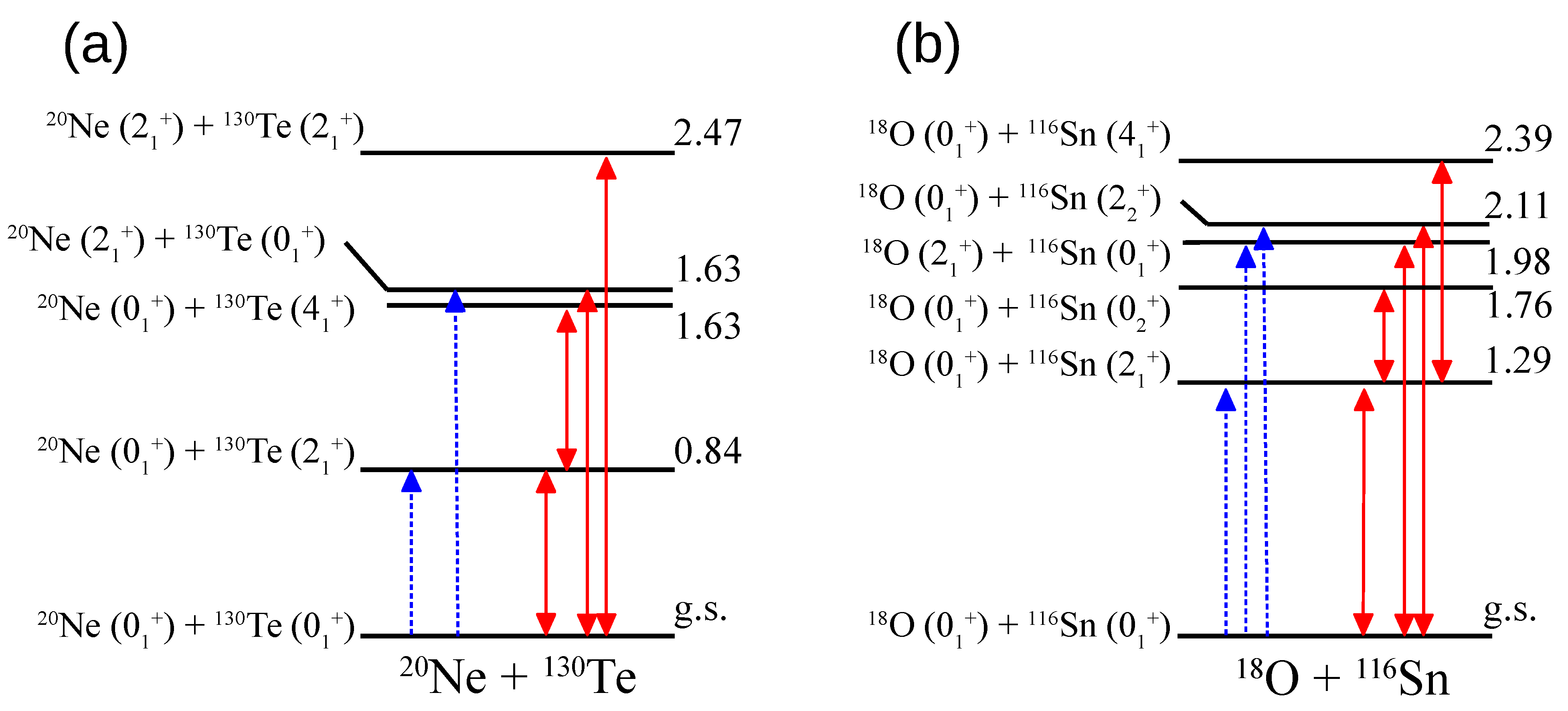
4.3. Initial State Interactions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Majorana, E. Teoria simmetrica dell’elettrone e del positrone. Nuovo C. 1937, 14, 171–184. [Google Scholar] [CrossRef]
- Dell’Oro, S.; Marcocci, S.; Viel, M.; Vissani, F. Neutrinoless double beta decay: 2015 review. Adv. High Energy Phys. 2016, 2016, 2162659. [Google Scholar] [CrossRef]
- Dolinski, M.J.; Poon, A.W.; Rodejohann, W. Neutrinoless Double-Beta Decay: Status and Prospects. Annu. Rev. Nucl. Part. Sci. 2019, 69, 219–251. [Google Scholar] [CrossRef]
- Agostini, M.; Araujo, G.R.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; Bettini, A.; et al. Final Results of GERDA on the Search for Neutrinoless Double-β Decay. Phys. Rev. Lett. 2020, 125, 252502. [Google Scholar] [CrossRef]
- Ejiri, H.; Suhonen, J.; Zuber, K. Neutrino–nuclear responses for astro-neutrinos, single beta decays and double beta decays. Phys. Rept. 2019, 797, 1–102. [Google Scholar] [CrossRef]
- Ejiri, H. Neutrino-Mass Sensitivity and Nuclear Matrix Element for Neutrinoless Double Beta Decay. Universe 2020, 6, 225. [Google Scholar] [CrossRef]
- Menéndez, J. Neutrinoless ββ decay mediated by the exchange of light and heavy neutrinos: The role of nuclear structure correlations. J. Phys. G Nucl. Part. Phys. 2017, 45, 014003. [Google Scholar] [CrossRef]
- Cappuzzello, F.; Agodi, C.; Cavallaro, M.; Carbone, D.; Tudisco, S.; Lo Presti, D.; Oliveira, J.R.B.; Finocchiaro, P.; Colonna, M.; Rifuggiato, D.; et al. The NUMEN project: NUclear Matrix Elements for Neutrinoless double beta decay. Eur. Phys. J. A 2018, 54, 72. [Google Scholar] [CrossRef]
- Cavallaro, M.; Aciksoz, E.; Acosta, L.; Agodi, C.; Auerbach, N.; Bellone, J.; Bijker, R.; Bianco, S.; Bonanno, D.; Bongiovanni, D.; et al. NURE: An ERC project to study nuclear reactions for neutrinoless double beta decay. In Proceedings of the 55th International Winter Meeting on Nuclear Physics—PoS(BORMIO2017), Bormio, Italy, 23–27 January 2017; p. 015. [Google Scholar]
- Agodi, C.; Cappuzzello, F.; Cavallaro, M.; Bondì, M.; Carbone, D.; Cunsolo, A.; Foti, A. Heavy Ions Double Charge Exchange reactions: Towards the 0νββ Nuclear Matrix Element determination. Nucl. Part. Phys. Proc. 2015, 265-266, 28–30. [Google Scholar] [CrossRef]
- Agodi, C.; Russo, A.D.; Calabretta, L.; D’Agostino, G.; Cappuzzello, F. NUMEN project towards new experiments with high intensity beams. Universe. submitted.
- Cappuzzello, F.; Cavallaro, M.; Agodi, C.; Bondì, M.; Carbone, D.; Cunsolo, A.; Foti, A. Heavy-ion double charge exchange reactions: A tool toward 0νββ nuclear matrix elements. Eur. Phys. J. A 2015, 51, 145. [Google Scholar] [CrossRef]
- Kisamori, K.; Shimoura, S.; Miya, H.; Michimasa, S.; Ota, S.; Assie, M.; Baba, H.; Baba, T.; Beaumel, D.; Dozono, M.; et al. Candidate Resonant Tetraneutron State Populated by the 4He(8He,8 Be) Reaction. Phys. Rev. Lett. 2016, 116, 052501. [Google Scholar] [CrossRef] [PubMed]
- Matsubara, H.; Takaki, M.; Uesaka, T.; Shimoura, S.; Aoi, N.; Dozono, M.; Fujii, T.; Hatanaka, K.; Hashimoto, T.; Kawabata, T.; et al. Spectroscopic Measurement in 9He and 12Be. Few Body Syst. 2013, 54, 1433–1436. [Google Scholar] [CrossRef]
- Takahisa, K.; Ejiri, H.; Akimune, H.; Fujita, H.; Matumiya, R.; Ohta, T.; Shima, T.; Tanaka, M.; Yosoi, M. Double charge exchange (11B,11Li) reaction for double beta decay response. arXiv 2017, arXiv:1703.08264. [Google Scholar]
- Carbone, D.; Ferreira, J.L.; Calabrese, S.; Cappuzzello, F.; Cavallaro, M.; Hacisalihoglu, A.; Lenske, H.; Lubian, J.; Agodi, C.; Borello-Lewin, T.; et al. Analysis of two-nucleon transfer reactions in the 20Ne+116 Cd system at 306 MeV. Phys. Rev. C 2020, 102, 044606. [Google Scholar] [CrossRef]
- Ferreira, J.; Carbone, D.; Cavallaro, M.; Deshmukh, N.; Agodi, C. Analysis of two-proton transfer in the 40Ca(18O,20Ne)38Ar reaction at 270 MeV incident energy. Phys. Rev. C. accepted.
- Lenske, H.; Bellone, J.I.; Colonna, M.; Lay, J.A. Theory of Single Charge Exchange Heavy Ion Reactions. Phys. Rev. C 2018, 98, 044620. [Google Scholar] [CrossRef]
- Santopinto, E.; García-Tecocoatzi, H.; Magaña Vsevolodovna, R.; Ferretti, J. Heavy-ion double-charge-exchange and its relation to neutrinoless double-β decay. Phys. Rev. C 2018, 98, 061601. [Google Scholar] [CrossRef]
- Lenske, H. Probing Double Beta-Decay by Heavy Ion Charge Exchange Reactions. J. Phys. Conf. Ser. 2018, 1056, 012030. [Google Scholar] [CrossRef]
- Lenske, H.; Cappuzzello, F.; Cavallaro, M.; Colonna, M. Heavy ion charge exchange reactions as probes for nuclear β-decay. Prog. Part. Nucl. Phys. 2019, 109, 103716. [Google Scholar] [CrossRef]
- Bellone, J.I.; Burrello, S.; Colonna, M.; Lay, J.A.; Lenske, H. Two-step description of heavy ion double charge exchange reactions. Phys. Lett. B 2020, 807, 135528. [Google Scholar] [CrossRef]
- Hodgson, P.E. Nuclear Reactions and Nuclear Structure; Clarendon Press: Oxford, UK, 1971. [Google Scholar]
- Satchler, G.R. Direct Nuclear Reactions; Oxford University Press: Oxford, UK, 1983. [Google Scholar]
- Glendenning, N.K. Direct Nuclear Reactions; Academic Press, Inc.: London, UK, 1983. [Google Scholar]
- Cage, M.; Cole, A.; Pyle, G. Ambiguities and systematics in the real central part of the optical-model potential. Nucl. Phys. A 1973, 201, 418–432. [Google Scholar] [CrossRef]
- Ohkubo, S.; Hirabayashi, Y. Evidence for a secondary bow in Newton’s zero-order nuclear rainbow. Phys. Rev. C 2014, 89, 051601. [Google Scholar] [CrossRef]
- Oliveira, J.R.B.; Cappuzzello, F.; Chamon, L.C.; Pereira, D.; Agodi, C.; Bondí, M.; Carbone, D.; Cavallaro, M.; Cunsolo, A.; De Napoli, M.; et al. Study of the rainbow-like pattern in the elastic scattering of 16O on 27Al at Elab.= 100 MeV. J. Phys. G Nucl. Part. Phys. 2013, 40, 105101. [Google Scholar] [CrossRef]
- Pereira, D.; Linares, R.; Oliveira, J.; Lubian, J.; Chamon, L.; Gomes, P.; Cunsolo, A.; Cappuzzello, F.; Cavallaro, M.; Carbone, D.; et al. Nuclear rainbow in the 16O +27 Al system: The role of couplings at energies far above the barrier. Phys. Lett. B 2012, 710, 426–429. [Google Scholar] [CrossRef]
- Cappuzzello, F.; Nicolosi, D.; Linares, R.; Oliveira, J.R.B.; Lubian, J.; Agodi, C.; Carbone, D.; Cavallaro, M.; de Faria, P.N.; Foti, A.; et al. Interplay of the elastic and inelastic channels in the 16O + 27Al scattering at Elab.=280 MeV. Eur. Phys. J. A 2016, 52, 169. [Google Scholar] [CrossRef]
- Zagatto, V.A.B.; Cappuzzello, F.; Lubian, J.; Cavallaro, M.; Linares, R.; Carbone, D.; Agodi, C.; Foti, A.; Tudisco, S.; Wang, J.S.; et al. Important role of projectile excitation in 16O + 60Ni and 16O + 27Al scattering at intermediate energies. Phys. Rev. C 2018, 97, 054608. [Google Scholar] [CrossRef]
- Spatafora, A.; Cappuzzello, F.; Carbone, D.; Cavallaro, M.; Lay, J.A.; Acosta, L.; Agodi, C.; Bonanno, D.; Bongiovanni, D.; Boztosun, I.; et al. 20Ne +76 Ge elastic and inelastic scattering at 306 MeV. Phys. Rev. C 2019, 100, 034620. [Google Scholar] [CrossRef]
- Calabrese, S.; Cappuzzello, F.; Carbone, D.; Cavallaro, M.; Agodi, C.; Acosta, L.; Bonanno, D.; Bongiovanni, D.; Borello-Lewin, T.; Boztosun, I.; et al. First measurement of the 116Cd(20Ne,20 O)116Sn reaction at 15 AMeV. Acta Phys. Pol. B 2018, 49, 275–280. [Google Scholar] [CrossRef]
- Burrello, S. Analysis of two-step transfer mechanisms in 116Cd (20Ne, 20F) 116In at 306 MeV within the NUMEN project. in preparation.
- La Fauci, L.; Spatafora, A.; Cappuzzello, F.; Agodi, C.; Carbone, D.; Cavallaro, M.; Lubian, J.; Acosta, L.; Amador-Valenzuela, P.; Borello-Lewin, T.; et al. 18O+76Se elastic and inelastic scattering at 275 MeV. Phys. Rev. C. submitted.
- Cavallaro, M.; Bellone, J.I.; Calabrese, S.; Agodi, C.; Burrello, S.; Cappuzzello, F.; Carbone, D.; Colonna, M.; Deshmukh, N.; Lenske, H.; et al. A constrained analysis of the 40Ca(18O,18F)40K direct charge exchange reaction mechanism at 275 MeV. Front. Astron. Space Sci. accepted.
- Chamon, L.C.; Carlson, B.V.; Gasques, L.R.; Pereira, D.; De Conti, C.; Alvarez, M.A.G.; Hussein, M.S.; Cândido Ribeiro, M.A.; Rossi, E.S., Jr.; Silva, C.P. Toward a global description of the nucleus-nucleus interaction. Phys. Rev. C 2002, 66, 014610. [Google Scholar] [CrossRef]
- Caminata, A.; Adams, D.; Alduino, C.; Alfonso, K.; Avignone, F.I.; Azzolini, O.; Bari, G.; Bellini, F.; Benato, G.; Bersani, A.; et al. Results from the Cuore Experiment. Universe 2019, 5, 10. [Google Scholar] [CrossRef]
- Ebert, J.; Fritts, M.; Rajek, S.; Heidrich, N.; Neddermann, T.; Gehre, D.; Oldorf, C.; Quante, T.; Gopfert, T. Current Status and Future Perspectives of the COBRA Experiment. Adv. High Energy Phys. 2013, 2013, 703572. [Google Scholar] [CrossRef]
- Barabash, A.; Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V. Final results of the Aurora experiment to study 2β decay of 116Cd with enriched 116CdWO4 crystal scintillators. Phys. Rev. D 2018, 98, 092007. [Google Scholar] [CrossRef]
- Sgouros, O.; Soukeras, V.; Pakou, A.; Patronis, N.; Zerva, K.; Keeley, N.; Strojek, I.; TrzciŃSKA, A.; Piasecki, E.; Rusek, K.; et al. Backward angle structure in the 20Ne+28Si quasielastic scattering. Int. J. Mod. Phys. E 2013, 22, 1350073. [Google Scholar] [CrossRef]
- Belery, P.; Delbar, T.; Grégoire, G.; Grotowski, K.; Wall, N.S.; Kozik, T.; Micek, S. Elastic scattering of 20Ne+24Mg at Elab=50, 60, 80, 90, and 100 MeV. Phys. Rev. C 1981, 23, 2503–2512. [Google Scholar] [CrossRef]
- Palumbo, A.; Tan, W.P.; Best, A.; Couder, M.; Crowter, R.; de Boer, R.J.; Falahat, S.; LeBlanc, P.J.; Lee, H.Y.; Strandberg, E. Systematic study of the α-optical potential via elastic scattering near the Z = 50 region for p-process nuclei. Phys. Rev. C 2012, 85, 035808. [Google Scholar] [CrossRef]
- De, T.K.; Goswami, A.; Baliga, B.B. Scattering of alpha-particles from 130Te at 40 and 50 MeV. Il Nuovo Cimento 1990, 103A, 1427–1434. [Google Scholar] [CrossRef]
- Chen, X.; Lui, Y.W.; Clark, H.; Tokimoto, Y.; Youngblood, D. Folding model analysis of 240-MeV Li-6 elastic scattering on Sn-116 and inelastic scattering to low-lying states of Sn-116. Phys. Rev. C 2007, 76, 054606. [Google Scholar] [CrossRef]
- Robertson, B.C.; Sample, J.T.; Goosman, D.R.; Nagatani, K.; Jones, K.W. Elastic Scattering of 16,18O by 116,120Sn at Energies near the Coulomb Barrier. Phys. Rev. C 1971, 4, 2176–2180. [Google Scholar] [CrossRef]
- Rifuggiato, D.; Calabretta, L.; Celona, L.; Chines, F.; Cosentino, L.; Cuttone, G.; Finocchiaro, P.; Pappalardo, A.; Re, M.; Rovelli, A. Radioactive ion beam facilities at INFN LNS. J. -Phys. Conf. Ser. 2011, 267, 012007. [Google Scholar] [CrossRef]
- Cavallaro, M.; Santagati, G.; Cappuzzello, F.; Carbone, D.; Linares, R.; Torresi, D.; Acosta, L.; Agodi, C.; Bonanno, D.; Bongiovanni, D.; et al. Charge-state distributions of 20Ne ions emerging from thin foils. Results Phys. 2019, 13, 102191. [Google Scholar] [CrossRef]
- Cappuzzello, F.; Carbone, D.; Cavallaro, M.; Cunsolo, A. MAGNEX: An innovative large acceptance magnetic spectrometer for nuclear reaction studies. In Magnets: Types, Uses and Safety; Akitsu, T., Ed.; Nova Science Publishers, Inc.: New York, NY, USA, 2011. [Google Scholar]
- Cappuzzello, F.; Agodi, C.; Carbone, D.; Cavallaro, M. The MAGNEX spectrometer: Results and perspectives. Eur. Phys. J. A 2016, 52, 167. [Google Scholar] [CrossRef]
- Cavallaro, M.; Cappuzzello, F.; Carbone, D.; Cunsolo, A.; Foti, A.; Khouaja, A.; Rodrigues, M.; Winfield, J.; Bondì, M. The low-pressure focal plane detector of the MAGNEX spectrometer. Eur. Phys. J. A 2012, 48, 59. [Google Scholar] [CrossRef]
- Torresi, D.; Sgouros, O.; Soukeras, V.; Cavallaro, M.; Cappuzzello, F.; Carbone, D.; Agodi, C.; Brischetto, G.; Calabrese, S.; Ciraldo, I.; et al. An upgraded focal plane detector for the MAGNEX spectrometer. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometer Detect. Assoc. Equip. 2021, 989, 164918. [Google Scholar] [CrossRef]
- Cappuzzello, F.; Cavallaro, M.; Cunsolo, A.; Foti, A.; Carbone, D.; Orrigo, S.; Rodrigues, M. A particle identification technique for large acceptance spectrometers. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2010, 621, 419–423. [Google Scholar] [CrossRef]
- Cappuzzello, F.; Agodi, C.; Bondì, M.; Carbone, D.; Cavallaro, M.; Cunsolo, A.; De Napoli, M.; Foti, A.; Nicolosi, D.; Tropea, S.; et al. A broad angular-range measurement of elastic and inelastic scatterings in the 16O on 27Al reaction at 17.5 MeV/u. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometer Detect. Assoc. Equip. 2014, 763, 314–319. [Google Scholar] [CrossRef]
- Carbone, D. Signals of the Giant Pairing Vibration in 14C and 15C nuclei populated by (18O,16O) two-neutron transfer reactions. Eur. Phys. J. Plus 2015, 130, 143. [Google Scholar] [CrossRef]
- Cappuzzello, F.; Carbone, D.; Cavallaro, M. Measuring the ions momentum vector with a large acceptance magnetic spectrometer. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers, Detect. Assoc. Equip. 2011, 638, 74–82. [Google Scholar] [CrossRef]
- Cavallaro, M.; Cappuzzello, F.; Carbone, D.; Cunsolo, A.; Foti, A.; Linares, R. Transport efficiency in large acceptance spectrometers. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers, Detect. Assoc. Equip. 2011, 637, 77–87. [Google Scholar] [CrossRef]
- Thompson, I.J. Coupled reaction channels calculations in nuclear physics. Comput. Phys. Rep. 1988, 7, 167–212. [Google Scholar] [CrossRef]
- Crema, E.; Otomar, D.; Simoes, R.; Barioni, A.; Monteiro, D.; Ono, L.; Shorto, J.; Lubian, J.; Gomes, P. Near-barrier quasielastic scattering as a sensitive tool to derive nuclear matter diffuseness. Phys. Rev. C 2011, 84, 024601. [Google Scholar] [CrossRef]
- Crema, E.; Zagatto, V.A.B.; Shorto, J.M.B.; Paes, B.; Lubian, J.; Simões, R.F.; Monteiro, D.S.; Huiza, J.F.P.; Added, N.; Morais, M.C.; et al. Reaction mechanisms of the 18O + 63 Cu system at near-barrier energies. Phys. Rev. C 2018, 98, 044614. [Google Scholar] [CrossRef]
- Fonseca, L.M.; Linares, R.; Zagatto, V.A.B.; Cappuzzello, F.; Carbone, D.; Cavallaro, M.; Agodi, C.; Lubian, J.; Oliveira, J.R.B. Elastic and inelastic scattering of 16O on 27Al and 28Si at 240 MeV. Phys. Rev. C 2019, 100, 014604. [Google Scholar] [CrossRef]
- Alvarez, M.A.G.; Chamon, L.C.; Hussein, M.S.; Pereira, D.; Gasques, L.R.; Rossi, E.S., Jr.; Silva, C.P. A parameter-free optical potential for the heavy-ion elastic scattering process. Nuclear Physics A 2003, 723, 93–103. [Google Scholar] [CrossRef]
- Khoa, D.T.; Satchler, G. Generalized folding model for elastic and inelastic nucleus–nucleus scattering using realistic density dependent nucleon–nucleon interaction. Nucl. Phys. A 2000, 668, 3–41. [Google Scholar] [CrossRef]
- Chamon, L.; Carlson, B. Systematics of nuclear densities, deformations and excitation energies within the context of the generalized rotation–vibration model. Nucl. Phys. A 2010, 846, 1–30. [Google Scholar] [CrossRef]
- Pritychenko, B.; Birch, M.; Singh, B.; Horoi, M. Tables of E2 transition probabilities from the first 2+ states in even–even nuclei. At. Data Nucl. Data Tables 2016, 107, 1–139. [Google Scholar] [CrossRef]
- Raman, S.; Nestor, C., Jr.; Tikkanen, P. Transition probability from the ground to the first-excited 2+ state of even–even nuclides. At. Data Nucl. Data Tables 2001, 78, 1. [Google Scholar] [CrossRef]
- Jonsson, N.G.; Bäcklin, A.; Kantele, J.; Julin, R.; Luontama, M.; Passoja, A. Collective states in even Sn nuclei. Nucl. Phys. A 1981, 371, 333–348. [Google Scholar] [CrossRef]
- Bäcklin, A.; Jonsson, N.; Julin, R.; Kantele, J.; Luontama, M.; Passoja, A.; Poikolainen, T. 0+ states and E0 and E2 transition rates in even Sn nuclei. Nucl. Phys. A 1981, 351, 490–508. [Google Scholar] [CrossRef]
- Thompson, I.J.; Nagarajan, M.A.; Lilley, J.S.; Smithson, M.J. The threshold anomaly in 16O + 208Pb scattering. Nucl. Phys. A 1989, 505, 84. [Google Scholar] [CrossRef]
- Rangel, J.; Lubian, J.; Canto, L.F.; Gomes, P.R.S. Effect of Coulomb breakup on the elastic cross-section of the 8B proton-halo projectile on a heavy, 208Pb target. Phys. Rev. C 2016, 93, 054610. [Google Scholar] [CrossRef]


| System | (fm) | J (MeV fm3) | J (MeV fm3) | J (MeV fm3) |
|---|---|---|---|---|
| Ne+Te | 5.66 | −339.6 | −264.9 | −203.8 |
| O+Sn | 5.45 | −339.8 | −265.0 | −203.9 |
| Nuclei | Transition | Initial State | Final State | Ref. | ||
|---|---|---|---|---|---|---|
| (MeV) | (MeV) | () | (fm) | |||
| O | 0.00 | 1.98 | 0.0043 | 0.63 | [65] | |
| Ne | 0.00 | 1.63 | 0.034 | 1.35 | [66] | |
| Sn | 0.00 | 1.29 | 0.209 | 0.70 | [66] | |
| Sn | 0.00 | 2.11 | 0.0021 | 0.07 | [67] | |
| Sn | 1.29 | 1.76 | 0.060 | 0.84 | [68] | |
| Sn | 1.29 | 2.39 | 0.076 | 0.95 | [67] | |
| Te | 0.00 | 0.84 | 0.295 | 0.77 | [66] | |
| Te | 0.84 | 1.63 | 0.059 | 0.35 | [66] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carbone, D.; Linares, R.; Amador-Valenzuela, P.; Calabrese, S.; Cappuzzello, F.; Cavallaro, M.; Firat, S.; Fisichella, M.; Spatafora, A.; Acosta, L.; et al. Initial State Interaction for the 20Ne + 130Te and 18O + 116Sn Systems at 15.3 AMeV from Elastic and Inelastic Scattering Measurements. Universe 2021, 7, 58. https://doi.org/10.3390/universe7030058
Carbone D, Linares R, Amador-Valenzuela P, Calabrese S, Cappuzzello F, Cavallaro M, Firat S, Fisichella M, Spatafora A, Acosta L, et al. Initial State Interaction for the 20Ne + 130Te and 18O + 116Sn Systems at 15.3 AMeV from Elastic and Inelastic Scattering Measurements. Universe. 2021; 7(3):58. https://doi.org/10.3390/universe7030058
Chicago/Turabian StyleCarbone, Diana, Roberto Linares, Paulina Amador-Valenzuela, Salvatore Calabrese, Francesco Cappuzzello, Manuela Cavallaro, Suna Firat, Maria Fisichella, Alessandro Spatafora, Luis Acosta, and et al. 2021. "Initial State Interaction for the 20Ne + 130Te and 18O + 116Sn Systems at 15.3 AMeV from Elastic and Inelastic Scattering Measurements" Universe 7, no. 3: 58. https://doi.org/10.3390/universe7030058
APA StyleCarbone, D., Linares, R., Amador-Valenzuela, P., Calabrese, S., Cappuzzello, F., Cavallaro, M., Firat, S., Fisichella, M., Spatafora, A., Acosta, L., Agodi, C., Boztosun, I., Brischetto, G. A., Calvo, D., Chávez Lomelí, E. R., Ciraldo, I., Cutuli, M., Delaunay, F., Deshmukh, N., ... Zagatto, V. A. B., for the NUMEN collaboration. (2021). Initial State Interaction for the 20Ne + 130Te and 18O + 116Sn Systems at 15.3 AMeV from Elastic and Inelastic Scattering Measurements. Universe, 7(3), 58. https://doi.org/10.3390/universe7030058













