Spectral Problems for Quasinormal Modes of Black Holes
Abstract
:1. Introduction
2. A Quantum Mechanical Approach to Spectral Problems
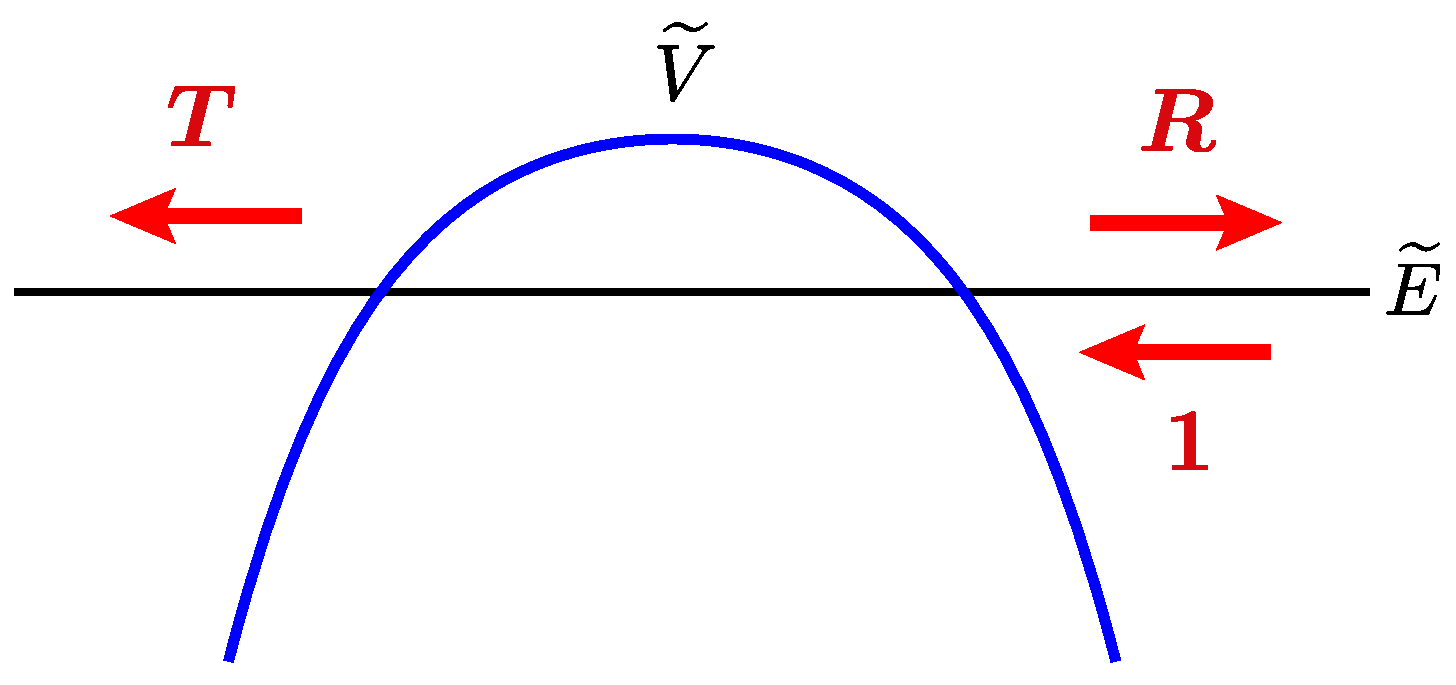
2.1. Bound States and Resonant States
2.2. Lessons from an Exactly Solvable Model
2.3. Numerical Methods
2.3.1. Milne’s Method
2.3.2. Wronskian Method
2.4. Perturbation Theory
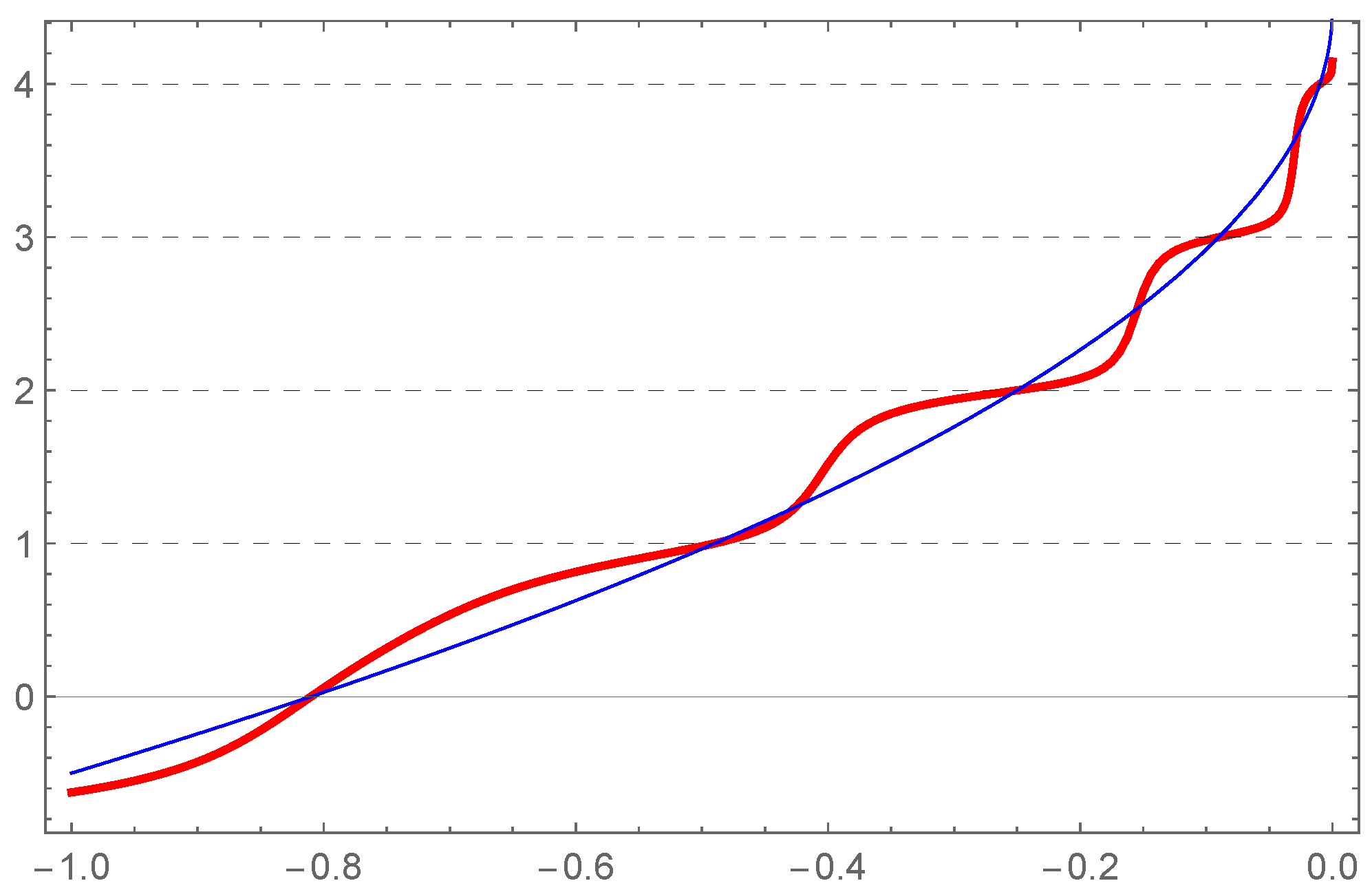
2.5. The WKB Method
2.5.1. Standard WKB
2.5.2. Uniform WKB
3. Applications to Black Hole Perturbation Theory
3.1. Quasinormal Modes of Schwarzschild Black Holes
3.1.1. Wronskian Method
3.1.2. WKB Method
3.1.3. Perturbative Method
3.1.4. Comments on Even Parity Perturbation
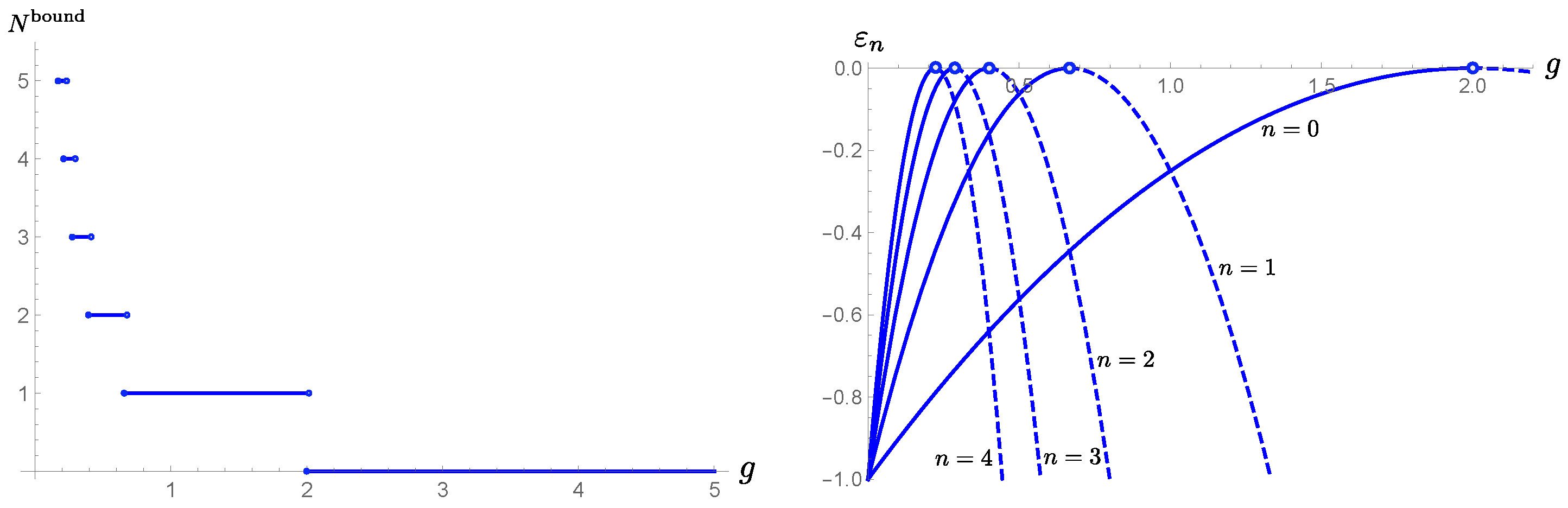
3.2. Mode Stability Analysis: Gregory–Laflamme Instability for Black Strings
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Master Equations around the Four-Dimensional Schwarzschild Spacetime
Appendix A.1. Four-Dimensional Schwarzschild Spacetime and Killing Vectors
Appendix A.2. Massless Klein–Gordon Equation
Appendix A.2.1. Killing Vector and Separation of Variable
Appendix A.2.2. Separation of Variable Using SO(3) Symmetry
Appendix A.2.3. Explicit Calculation
Appendix A.3. Vector Harmonics on S2
Appendix A.3.1. Helmholtz–Hodge Decomposition
Appendix A.3.2. Vector Harmonics
Appendix A.4. Einstein Equations
Appendix A.4.1. Linear Metric Perturbation
Appendix A.4.2. Parity Transformation
Appendix A.4.3. Gauge Transformation
Appendix A.4.4. Remarks on Complete Gauge Fixing and Gauge Invariant Quantities
Appendix A.4.5. Odd Parity Perturbation
Appendix A.4.6. Even Parity Perturbation
Appendix A.4.7. Relation between the Regge–Wheeler and Zerilli Equations
Appendix A.5. Maxwell Equations
Appendix A.6. Master Equations for Different Spins
Appendix B. Some Basics on Second Order Ordinary Differential Equations
Appendix B.1. Regular Singular Points
Appendix B.2. Irregular Singular Points
Appendix B.3. Borel Summations and Stokes Phenomena

Appendix C. Padé Approximants
Appendix C.1. Convergent Series
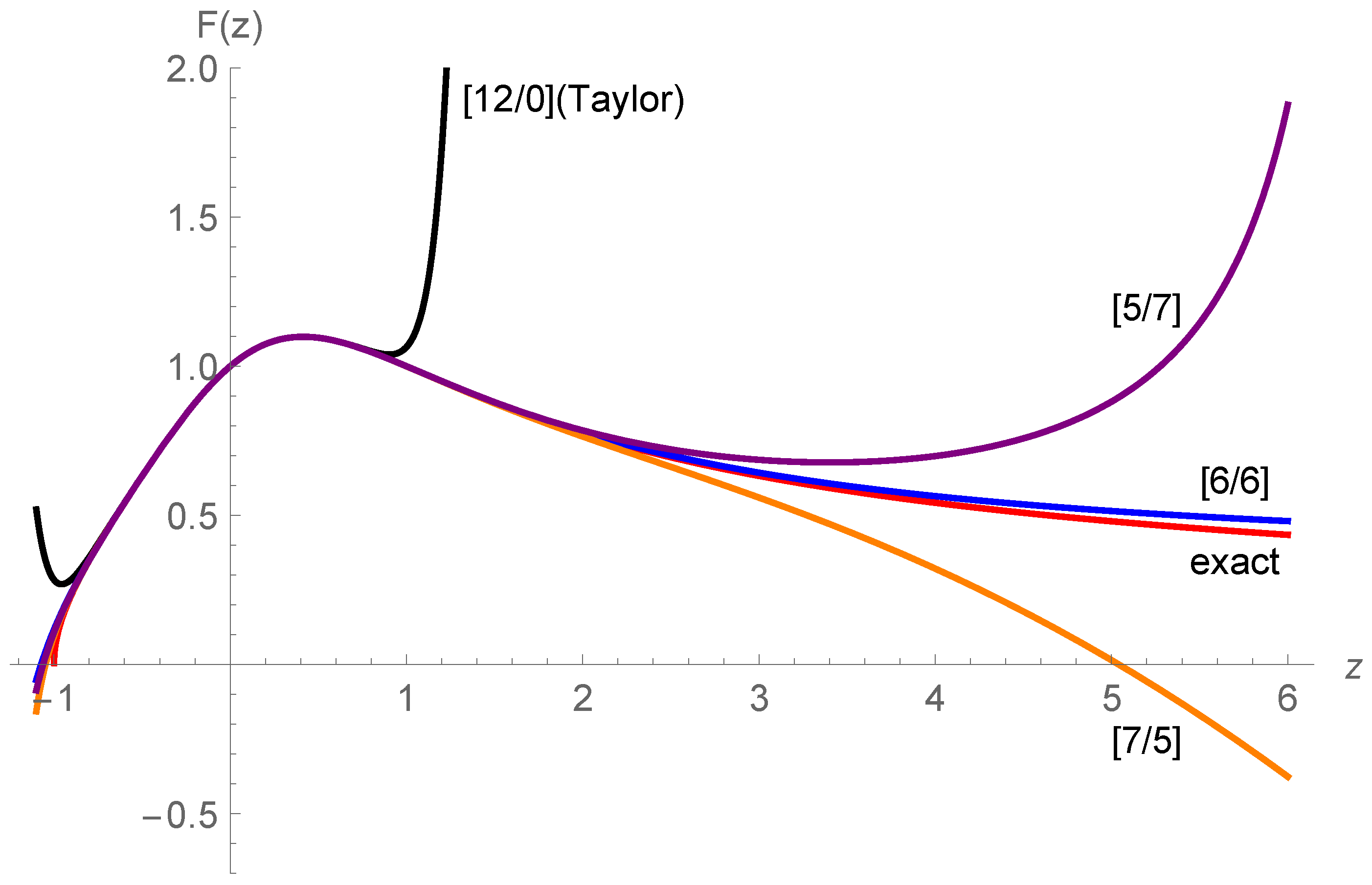

Appendix C.2. Divergent Series
| m | |||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 | |||

| 1 | We note that there is also a branch cut contribution, which corresponds to the power law tails. We do not discuss this contribution in the present article. |
| 2 | In this section, we use for resonant state problems to distinguish them from bound state problems. |
| 3 | We have the freedom to set , and it leads to another branch of the resonance. Since these two branches are symmetric, it is sufficient to consider either of them. |
| 4 | Concerning boundary conditions, one can see the following observation. If the wave function behaves as in , then it satisfies the bound state condition in . After the analytic continuation, the wave function behaves as , and satisfies the resonant boundary condition. |
| 5 | Strictly, there is a subtlety on the number of the allowed bound states. This point is discussed in the next section. This relation is also based on an assumption that the potential has bound states. In the case of the cubic potential for example, both and have only the resonant states, and the relation (7) should be modified for these eigenvalues. |
| 6 | In fact, this state satisfies the boundary condition such that there is no contamination of the decaying mode in . That is, the solution purely grows in . |
| 7 | Moreover the infinite number of the resonant states is “doubled” by the other analytic continuation . This corresponds to including . |
| 8 | We are not sure whether this is strictly proved or not. As far as we checked for many models, it indeed holds. |
| 9 | |
| 10 | However, up to the optimal order, the truncated sum gives a very good approximate value. This is why perturbation theory in physics is a successful approximation method |
| 11 | If one puts the ansatz , one obtains the Riccati equation for . It is solved order by order in ℏ. The odd order part in the perturbative solution can be expressed by a derivative of the even order part, and it finally leads to (59). Hence has only the even order corrections as in (61). See [33,34] for a rigorous proof |
| 12 | We notice that this equation is formally equivalent to Milne’s non-linear Equation (28) if identifying . |
| 13 | |
| 14 | A turning point a is defined by |
| 15 | Since has a square root branch cut, it comes back to the same value when going around the two turning points. However changes its sign. |
| 16 | The case of corresponds to another analytic continuation in our framework. |
| 17 | At this moment, we assume that and are real numbers such that , but for the resonant eigenvalues these are actually complex. We easily perform an analytic continuation in this case. If we cannot evaluate the integral analytically, things are more delicate. |
| 18 | This transformation is not always necessary. We do it in order to map the problem into a known differential equation. |
| 19 | Note that the mode exists only for . |
| 20 | For instance, the branch cut of in Mathematica is along the negative real axis. This is not useful in evaluating the contour complex integral (134) numerically. |
| 21 | In the original variable E, the differential equation is also hypergeometric-type, but two of the solutions near are expressed in terms of so-called Meijer’s G-functions |
| 22 | For , we get the complex conjugate to the right hand side in (168). Because of the physical requirement of the QNMs, we have to choose a branch of the square root of so that the imaginary part of must be negative. Therefore the two possible values of finally lead to two branches of whose real parts have opposite signs to each other. |
| 23 | |
| 24 | |
| 25 | This conclusion holds even if we do not use the global spherical symmetry of the spacetime. Because the only non-trivial operator which commutes with all Killing vectors is the Casimir operator , the derivatives with respect to the angular coordinates in □ should be proportional to . Thus, assuming where the function Y satisfies with a separation constant , should take the form of . |
| 26 | We can easily calculate the explicit form of by using Mathematica. |
| 27 | Generalization to compact Riemannian (Einstein) manifolds can be seen in [86]. |
| 28 | The homogeneous equation has a constant solution, and this gives an ambiguity of the solution for mode. However, it does not affect . |
| 29 | While one may think that there might exitst a tensor part which satisfies with trace free and divergence free conditions , such a term does not exist for . If we assume that a tensor part exists, we can consider a perturbed metric , where is the metric of a unit two sphere. Using the conditions , we can show that the Ricci scalar of becomes . This implies that is the metric of a unit two sphere at this order, and the metric can be transformed into the same form as Equation (A31) by a gauge transformation at . Thus, should be with some vector field . If we write with , the conditions implies , and then we conclude . |
| 30 | While there are homogeneous solutions in for and 1 modes, these do not affect . |
| 31 | The proof of the completeness can be seen in [84]. |
| 32 | The second equation can also be written as . |
| 33 | If we use the differential form, becomes . |
| 34 | See [87] for the case with source terms. |
| 35 | We define the parity transformation of the tensor fields as the components of the tensor after performing the coordinate transformation Equation (A59) to the whole tensor which includes the coordinate basis, where ⊗ denotes the tensor product. |
| 36 | Because the ladder operators are constructed from the Killing vector on , Equation (A21) shows that different m modes can be generated by the infinitesimal coordinate transformation associated with the Killing vectors on . |
| 37 | We assume that the Einstein equations can be decouposed into some modes which can be separately duscussed by each mode, for example, even and odd parity modes for the Schwarzschild case, and we focus on one of the modes where the generator of the gauge transformation contains n functional degrees of freedom. At each mode, we can completely fix the gauge iff n independent components of can be set as zero for any by algebraically choosing . Then, is expressed as linear combinations of n components of , which will be set to be zero after the gauge choice, and their derivatives. |
| 38 | If a pure gauge is possible, the perturbed metric becomes with some non-trivial vector field . From the assumption, we already completely fixed the gauge and n independent components of vanish, where n is a functional degrees of freedom of the gauge transformation in the mode which we focus on. If we focus on such n components of the equation , we can solve them algebraically with respect to . The vector is expressed as linear combinations of four components of , which are already set to be zero, and their derivatives. This implies . |
| 39 | Similar to the case of the Klein-Gordon equation, we can compute the components of the linearized Einstein equations by using Mathematica. |
| 40 | See [88] for the other possible choices of the master variables and the effective potentials. |
| 41 | We note that two solutions with the form of Equation (A127) are linearly dependent when is non-zero. |
| 42 | Note that since we can shift the exponents to by a transformation , the monodromy matrix can be always reduced to by . In the new function , the singular point is now apparent. |
| 43 | The definition of the Poincaré rank seems different in the literature. In this article, we follow [48]. |
References
- Nakamura, T.; Oohara, K.; Kojima, Y. General Relativistic Collapse to Black Holes and Gravitational Waves from Black Holes. Prog. Theor. Phys. Suppl. 1987, 90, 1–218. [Google Scholar] [CrossRef]
- Kokkotas, K.D.; Schmidt, B.G. Quasi-Normal Modes of Stars and Black Holes. Living Rev. Rel. 1999, 2, 2. [Google Scholar] [CrossRef] [Green Version]
- Nollert, H.P. Quasinormal Modes: The Characteristic ‘sound’ of Black Holes and Neutron Stars. Class. Quantum Gravit. 1999, 16, R159–R216. [Google Scholar] [CrossRef]
- Ferrari, V.; Gualtieri, L. Quasi-Normal Modes and Gravitational Wave Astronomy. Gen. Relativ. Gravit. 2008, 40, 945–970. [Google Scholar] [CrossRef] [Green Version]
- Berti, E.; Cardoso, V.; Starinets, A.O. Quasinormal Modes of Black Holes and Black Branes. Class. Quantum Gravit. 2009, 26, 163001. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Quasinormal Modes of Black Holes: From Astrophysics to String Theory. Rev. Mod. Phys. 2011, 83, 793–836. [Google Scholar] [CrossRef] [Green Version]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Clarendon Press: Oxford, UK, 1998. [Google Scholar]
- Maggiore, M. Gravitational Waves: Volume 2: Astrophysics and Cosmology; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Andersson, N. Gravitational-Wave Astronomy: Exploring the Dark Side of the Universe; Oxford University Press: Oxford, UK, 2020. [Google Scholar]
- Ferrari, V.; Gualtieri, L.; Pani, P. General Relativity and Its Applications: Black Holes, Compact Stars and Gravitational Waves; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Leaver, E.W. Spectral Decomposition of the Perturbation Response of the Schwarzschild Geometry. Phys. Rev. D 1986, 34, 384–408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nollert, H.P.; Schmidt, B.G. Quasinormal Modes of Schwarzschild Black Holes: Defined and Calculated via Laplace Transformation. Phys. Rev. D 1992, 45, 2617–2627. [Google Scholar] [CrossRef]
- Andersson, N. Excitation of Schwarzschild Black-Hole Quasinormal Modes. Phys. Rev. D 1995, 51, 353–363. [Google Scholar] [CrossRef]
- Andersson, N. Evolving Test Fields in a Black-Hole Geometry. Phys. Rev. D 1997, 55, 468–479. [Google Scholar] [CrossRef] [Green Version]
- Berti, E.; Cardoso, V. Quasinormal Ringing of Kerr Black Holes: The Excitation Factors. Phys. Rev. D 2006, 74, 104020. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; LIGO Scientific and Virgo Collaborations; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; et al. Tests of General Relativity with GW150914. Phys. Rev. Lett. 2016, 116, 221101. [Google Scholar] [CrossRef]
- Giesler, M.; Isi, M.; Scheel, M.A.; Teukolsky, S.A. Black Hole Ringdown: The Importance of Overtones. Phys. Rev. X 2019, 9, 041060. [Google Scholar] [CrossRef] [Green Version]
- Barack, L.; Cardoso, V.; Nissanke, S.; Sotiriou, T.P.; Askar, A.; Belczynski, C.; Bertone, G.; Bon, E.; Blas, D.; Brito, R.; et al. Black Holes, Gravitational Waves and Fundamental Physics: A Roadmap. Class. Quantum Gravit. 2019, 36, 143001. [Google Scholar] [CrossRef] [Green Version]
- Konishi, K.; Paffuti, G. Quantum Mechanics: A New Introduction; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Hatsuda, Y. Quasinormal Modes of Black Holes and Borel Summation. Phys. Rev. D 2020, 101, 024008. [Google Scholar] [CrossRef] [Green Version]
- Eniceicu, D.S.; Reece, M. Quasinormal Modes of Charged Fields in Reissner-Nordstrom Backgrounds by Borel-Pade Summation of Bender-Wu Series. Phys. Rev. D 2020, 102, 044015. [Google Scholar] [CrossRef]
- Ferrari, V.; Mashhoon, B. Oscillations of a Black Hole. Phys. Rev. Lett. 1984, 52, 1361–1364. [Google Scholar] [CrossRef]
- Ferrari, V.; Mashhoon, B. New Approach to the Quasinormal Modes of a Black Hole. Phys. Rev. D 1984, 30, 295–304. [Google Scholar] [CrossRef]
- Zaslavskii, O.B. Black-Hole Normal Modes and Quantum Anharmonic Oscillator. Phys. Rev. D 1991, 43, 605–608. [Google Scholar] [CrossRef] [PubMed]
- Cooper, F.; Khare, A.; Sukhatme, U. Supersymmetry and Quantum Mechanics. Phys. Rep. 1995, 251, 267–385. [Google Scholar] [CrossRef] [Green Version]
- Milne, W.E. The Numerical Determination of Characteristic Numbers. Phys. Rev. 1930, 35, 863–867. [Google Scholar] [CrossRef] [Green Version]
- Hartman, P. Ordinary Differential Equations, 2nd ed.; SIAM: Philadelphia, PA, USA, 1982. [Google Scholar]
- Courant, R.; Hilbert, D. Methods of Mathematical Physics; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Messiah, A. Quantum Mechanics; Courier Corporation: Washington, DC, USA, 2014. [Google Scholar]
- Mariño, M. Lectures on Non-Perturbative Effects in Large N Gauge Theories, Matrix Models and Strings. Fortsch. Phys. 2014, 62, 455–540. [Google Scholar] [CrossRef]
- Bender, C.M.; Wu, T.T. Anharmonic Oscillator. Phys. Rev. 1969, 184, 1231–1260. [Google Scholar] [CrossRef]
- Sulejmanpasic, T.; Ünsal, M. Aspects of Perturbation Theory in Quantum Mechanics: The BenderWu Mathematica Package. Comput. Phys. Commun. 2018, 228, 273–289. [Google Scholar] [CrossRef]
- Fröman, N.F.; Fröman, P.O. Phase-Integral Method: Allowing Nearlying Transition Points; Springer: New York, NY, USA, 1996. [Google Scholar]
- Kawai, T.; Takei, Y. Algebraic Analysis of Singular Perturbation Theory; American Mathematical Society: Providence, RI, USA, 2005. [Google Scholar]
- Fröman, N.; Fröman, P.O.; Andersson, N.; Hökback, A. Black-Hole Normal Modes: Phase-Integral Treatment. Phys. Rev. D 1992, 45, 2609–2616. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory; Elsevier: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Voros, A. The Return of the Quartic Oscillator. The Complex WKB Method. Ann. IHP Phys. Théorique 1983, 39, 211–338. [Google Scholar]
- Dunham, J.L. The Wentzel-Brillouin-Kramers Method of Solving the Wave Equation. Phys. Rev. 1932, 41, 713–720. [Google Scholar] [CrossRef]
- Balian, R.; Parisi, G.; Voros, A. Discrepancies from Asymptotic Series and Their Relation to Complex Classical Trajectories. Phys. Rev. Lett. 1978, 41, 1141–1144. [Google Scholar] [CrossRef]
- Delabaere, E.; Pham, F. Resurgent Methods in Semi-Classical Asymptotics. Ann. IHP Phys. Théorique 1999, 71, 1–94. [Google Scholar]
- Álvarez, G. Langer–Cherry Derivation of the Multi-Instanton Expansion for the Symmetric Double Well. J. Math. Phys. 2004, 45, 3095–3108. [Google Scholar] [CrossRef]
- Dunne, G.V.; Ünsal, M. Uniform WKB, Multi-Instantons, and Resurgent Trans-Series. Phys. Rev. D 2014, 89, 105009. [Google Scholar] [CrossRef] [Green Version]
- Mashhoon, B. Quasi-Normal Modes of a Black Hole. In Proceedings of the Third Marcel Grossmann Meeting on General Relativity, Shanghai, China, 30 August–3 September 1982; Volume 18, pp. 599–608. [Google Scholar]
- Schutz, B.F.; Will, C.M. Black Hole Normal Modes—A Semianalytic Approach. Astrophys. J. 1985, 291, L33–L36. [Google Scholar] [CrossRef] [Green Version]
- Iyer, S.; Will, C.M. Black-Hole Normal Modes: A WKB Approach. I. Foundations and Application of a Higher-Order WKB Analysis of Potential-Barrier Scattering. Phys. Rev. D 1987, 35, 3621–3631. [Google Scholar] [CrossRef] [PubMed]
- Teukolsky, S.A. Rotating Black Holes: Separable Wave Equations for Gravitational and Electromagnetic Perturbations. Phys. Rev. Lett. 1972, 29, 1114–1118. [Google Scholar] [CrossRef] [Green Version]
- Hatsuda, Y. An Alternative to the Teukolsky Equation. Gen. Relativ. Gravit. 2021, 53, 93. [Google Scholar] [CrossRef]
- Ronveaux, A. Heun’s Differential Equations; Oxford University Press: Oxford, NY, USA, 1995. [Google Scholar]
- Fiziev, P.P. Exact Solutions of Regge–Wheeler Equation and Quasi-Normal Modes of Compact Objects. Class. Quantum Gravit. 2006, 23, 2447–2468. [Google Scholar] [CrossRef] [Green Version]
- Leaver, E.W. An Analytic Representation for the Quasi-Normal Modes of Kerr Black Holes. Proc. R. Soc. Lond. A 1985, 402, 285–298. [Google Scholar]
- Leaver, E.W. Quasinormal Modes of Reissner-Nordstrom Black Holes. Phys. Rev. D 1990, 41, 2986–2997. [Google Scholar] [CrossRef] [Green Version]
- Onozawa, H.; Mishima, T.; Okamura, T.; Ishihara, H. Quasinormal Modes of Maximally Charged Black Holes. Phys. Rev. D 1996, 53, 7033–7040. [Google Scholar] [CrossRef] [Green Version]
- Clemens, C.H. A Scrapbook of Complex Curve Theory; American Mathematical Society: Providence, RI, USA, 2002. [Google Scholar]
- Konoplya, R.A. Quasinormal Behavior of the D-Dimensional Schwarzschild Black Hole and the Higher Order WKB Approach. Phys. Rev. D 2003, 68, 024018. [Google Scholar] [CrossRef] [Green Version]
- Dolan, S.R.; Ottewill, A.C. On an Expansion Method for Black Hole Quasinormal Modes and Regge Poles. Class. Quantum Gravit. 2009, 26, 225003. [Google Scholar] [CrossRef]
- Matyjasek, J.; Opala, M. Quasinormal Modes of Black Holes: The Improved Semianalytic Approach. Phys. Rev. D 2017, 96, 024011. [Google Scholar] [CrossRef] [Green Version]
- Konoplya, R.A.; Zhidenko, A.; Zinhailo, A.F. Higher Order WKB Formula for Quasinormal Modes and Grey-Body Factors: Recipes for Quick and Accurate Calculations. Class. Quantum Gravit. 2019, 36, 155002. [Google Scholar] [CrossRef] [Green Version]
- Matyjasek, J.; Telecka, M. Quasinormal Modes of Black Holes. II. Padé Summation of the Higher-Order WKB Terms. Phys. Rev. D 2019, 100, 124006. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, V.; Kimura, M.; Maselli, A.; Berti, E.; Macedo, C.F.B.; McManus, R. Parametrized Black Hole Quasinormal Ringdown: Decoupled Equations for Nonrotating Black Holes. Phys. Rev. D 2019, 99, 104077. [Google Scholar] [CrossRef] [Green Version]
- McManus, R.; Berti, E.; Macedo, C.F.B.; Kimura, M.; Maselli, A.; Cardoso, V. Parametrized Black Hole Quasinormal Ringdown. II. Coupled Equations and Quadratic Corrections for Nonrotating Black Holes. Phys. Rev. D 2019, 100, 044061. [Google Scholar] [CrossRef] [Green Version]
- Kimura, M. Note on the Parametrized Black Hole Quasinormal Ringdown Formalism. Phys. Rev. D 2020, 101, 064031. [Google Scholar] [CrossRef] [Green Version]
- Hatsuda, Y.; Kimura, M. Semi-Analytic Expressions for Quasinormal Modes of Slowly Rotating Kerr Black Holes. Phys. Rev. D 2020, 102, 044032. [Google Scholar] [CrossRef]
- Kodama, H.; Ishibashi, A. A Master Equation for Gravitational Perturbations of Maximally Symmetric Black Holes in Higher Dimensions. Prog. Theor. Phys. 2003, 110, 701–722. [Google Scholar] [CrossRef] [Green Version]
- Ishibashi, A.; Kodama, H. Stability of Higher-Dimensional Schwarzschild Black Holes. Prog. Theor. Phys. 2003, 110, 901–919. [Google Scholar] [CrossRef] [Green Version]
- Kimura, M. A Simple Test for the Stability of a Black Hole by S -Deformation. Class. Quantum Gravit. 2017, 34, 235007. [Google Scholar] [CrossRef]
- Kimura, M.; Tanaka, T. Robustness of the S -Deformation Method for Black Hole Stability Analysis. Class. Quantum Gravit. 2018, 35, 195008. [Google Scholar] [CrossRef] [Green Version]
- Amann, H.; Quittner, P. A Nodal Theorem for Coupled Systems of Schrödinger Equations and the Number of Bound States. J. Math. Phys. 1995, 36, 4553–4560. [Google Scholar] [CrossRef]
- Pani, P. Advanced Methods in Black-Hole Perturbation Theory. Int. J. Mod. Phys. A 2013, 28, 1340018. [Google Scholar] [CrossRef] [Green Version]
- Kimura, M. Stability Analysis of Schwarzschild Black Holes in Dynamical Chern-Simons Gravity. Phys. Rev. D 2018, 98, 024048. [Google Scholar] [CrossRef] [Green Version]
- Pierini, L.; Gualtieri, L. Quasinormal Modes of Rotating Black Holes in Einstein-Dilaton Gauss-Bonnet Gravity: The First Order in Rotation. Phys. Rev. D 2021, 103, 124017. [Google Scholar] [CrossRef]
- Wagle, P.; Yunes, N.; Silva, H.O. Quasinormal Modes of Slowly-Rotating Black Holes in Dynamical Chern-Simons Gravity. arXiv 2021, arXiv:2103.09913. [Google Scholar]
- Srivastava, M.; Chen, Y.; Shankaranarayanan, S. Analytical Computation of Quasinormal Modes of Slowly Rotating Black Holes in Dynamical Chern-Simons Gravity. Phys. Rev. D 2021, 104, 064034. [Google Scholar] [CrossRef]
- Cano, P.A.; Fransen, K.; Hertog, T.; Maenaut, S. Gravitational Ringing of Rotating Black Holes in Higher-Derivative Gravity. arXiv 2021, arXiv:2110.11378. [Google Scholar]
- Aminov, G.; Grassi, A.; Hatsuda, Y. Black Hole Quasinormal Modes and Seiberg-Witten Theory. arXiv 2020, arXiv:2006.06111. [Google Scholar]
- Bianchi, M.; Consoli, D.; Grillo, A.; Morales, J.F. QNMs of Branes, BHs and Fuzzballs from Quantum SW Geometries. arXiv 2021, arXiv:2105.04245. [Google Scholar]
- Novaes, F.; da Cunha, B.C. Isomonodromy, Painlevé Transcendents and Scattering off of Black Holes. J. High Energy Phys. 2014, 2014, 132. [Google Scholar] [CrossRef] [Green Version]
- da Cunha, B.C.; Novaes, F. Kerr Scattering Coefficients via Isomonodromy. J. High Energy Phys. 2015, 2015, 144. [Google Scholar] [CrossRef] [Green Version]
- Carneiro da Cunha, B.; Cavalcante, J.P. Confluent Conformal Blocks and the Teukolsky Master Equation. Phys. Rev. D 2020, 102, 105013. [Google Scholar] [CrossRef]
- Bonelli, G.; Iossa, C.; Lichtig, D.P.; Tanzini, A. Exact Solution of Kerr Black Hole Perturbations via CFT(2) and Instanton Counting. Greybody Factor, Quasinormal Modes and Love Numbers. arXiv 2021, arXiv:2105.04483. [Google Scholar]
- Carneiro da Cunha, B.; Cavalcante, J.P. Teukolsky Master Equation and Painlevé Transcendents: Numerics and Extremal Limit. Phys. Rev. D 2021, 104, 084051. [Google Scholar] [CrossRef]
- Alday, L.F.; Gaiotto, D.; Tachikawa, Y. Liouville Correlation Functions from Four-Dimensional Gauge Theories. Lett. Math. Phys. 2010, 91, 167–197. [Google Scholar] [CrossRef] [Green Version]
- Regge, T.; Wheeler, J.A. Stability of a Schwarzschild Singularity. Phys. Rev. 1957, 108, 1063–1069. [Google Scholar] [CrossRef]
- Zerilli, F.J. Gravitational Field of a Particle Falling in a Schwarzschild Geometry Analyzed in Tensor Harmonics. Phys. Rev. D 1970, 2, 2141–2160. [Google Scholar] [CrossRef]
- Ishibashi, A.; Kodama, H. Chapter 6 Perturbations and Stability of Static Black Holes in Higher Dimensions. Prog. Theor. Phys. Suppl. 2011, 189, 165–209. [Google Scholar] [CrossRef] [Green Version]
- Jansen, A.; Rostworowski, A.; Rutkowski, M. Master Equations and Stability of Einstein-Maxwell-Scalar Black Holes. J. High Energy Phys. 2019, 2019, 36. [Google Scholar] [CrossRef] [Green Version]
- Ishibashi, A.; Wald, R.M. Dynamics in Non-Globally-Hyperbolic Static Spacetimes: III. Anti-de Sitter Spacetime. Class. Quantum Gravit. 2004, 21, 2981–3013. [Google Scholar] [CrossRef] [Green Version]
- Martel, K.; Poisson, E. Gravitational Perturbations of the Schwarzschild Spacetime: A Practical Covariant and Gauge-Invariant Formalism. Phys. Rev. D 2005, 71, 104003. [Google Scholar] [CrossRef] [Green Version]
- Lenzi, M.; Sopuerta, C.F. Master Functions and Equations for Perturbations of Vacuum Spherically-Symmetric Spacetimes. Phys. Rev. D 2021, 104, 084053. [Google Scholar] [CrossRef]
- Coddington, E.A.; Levinson, N. Theory of Ordinary Differential Equations; McGraw-Hill: New York, NY, USA, 1955. [Google Scholar]
- Wasow, W. Asymptotic Expansions for Ordinary Differential Equations; Courier Dover Publications: New York, NY, USA, 2018. [Google Scholar]
- Delabaere, E.; Loday-Richaud, M.; Mitschi, C.; Sauzin, D. Divergent Series, Summability and Resurgence I-III; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Baker, G.A., Jr.; Graves-Morris, P. Pade Approximants: Encyclopedia of Mathematics and It’s Applications; Cambridge University Press: Cambridge, UK, 1996; Volume 59. [Google Scholar]



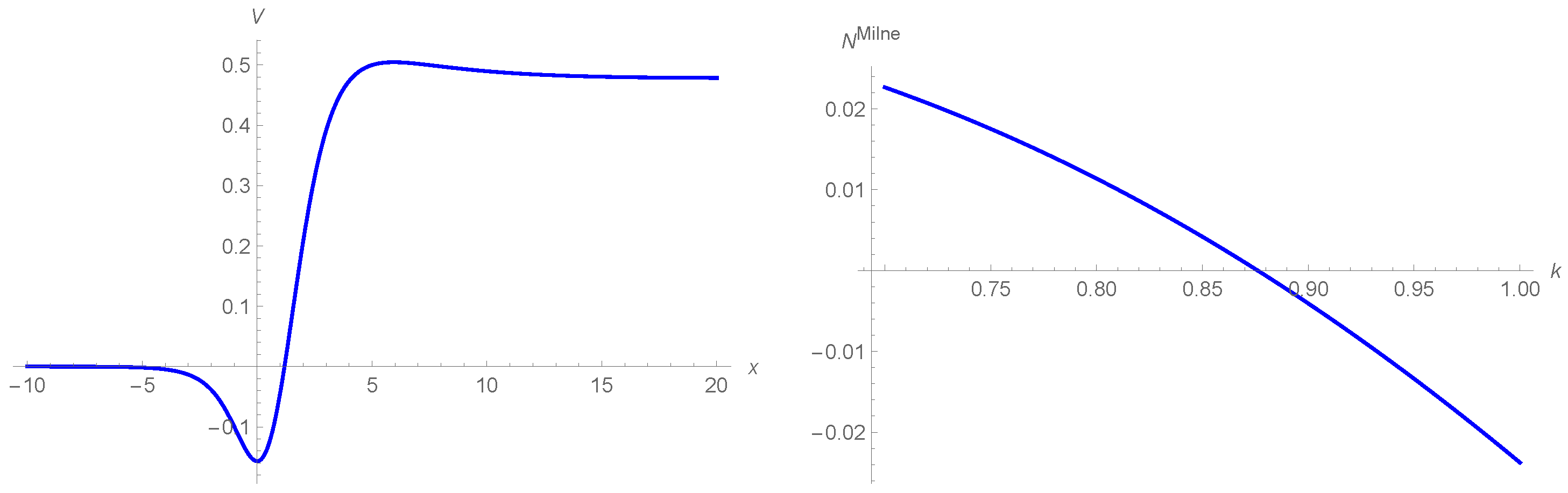
| Order | WKB | Perturbation/Uniform WKB |
|---|---|---|
| Padé | ||
| Wronskian |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatsuda, Y.; Kimura, M. Spectral Problems for Quasinormal Modes of Black Holes. Universe 2021, 7, 476. https://doi.org/10.3390/universe7120476
Hatsuda Y, Kimura M. Spectral Problems for Quasinormal Modes of Black Holes. Universe. 2021; 7(12):476. https://doi.org/10.3390/universe7120476
Chicago/Turabian StyleHatsuda, Yasuyuki, and Masashi Kimura. 2021. "Spectral Problems for Quasinormal Modes of Black Holes" Universe 7, no. 12: 476. https://doi.org/10.3390/universe7120476
APA StyleHatsuda, Y., & Kimura, M. (2021). Spectral Problems for Quasinormal Modes of Black Holes. Universe, 7(12), 476. https://doi.org/10.3390/universe7120476







