1. Introduction
Spatial correlations of quantum and thermal fluctuations of polarization and magnetization of condensed bodies, as well as a vacuum electromagnetic field, lead to the appearance of fluctuating electromagnetic forces between polarizable particles, atoms, and macroscopic bodies. In particular, an attractive force arises between electrically neutral thick metallic or dielectric plates (half-spaces) located at a distance
from each other—the Casimir-Lifshitz force [
1,
2]. Fluctuation-electromagnetic forces in various systems are usually called van der Waals forces [
3]. Upon the relative motion of the plates with velocity
V, in addition to an attractive force, a dissipative tangential force (quantum friction force at
) arises between them [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16]. At nonrelativistic velocities
and temperature
, this force is proportional to
and to higher odd powers of
− at
.
For several decades, the calculation of the van der Waals dissipative force has been the subject of intense theoretical research and discussion by numerous groups of authors, with widely differing results. In particular, the expressions for this force, obtained in the first works [
4,
5,
6,
7], were considered either inaccurate or lacked sufficient details, while correct expressions, in the cases
and
were first obtained in [
8,
9,
10]. However, as has recently been shown [
17], basic results obtained earlier by Polevoi (Equations (1)–(4) in [
6]) make it possible to correctly reproduce all generally accepted expressions for the dissipative van der Waals force between parallel plates. In addition, a more transparent formula for this force, obtained on the basis of these results in [
17], makes it possible to significantly simplify the analysis of its low-temperature dependence. As we have noted in [
17], dissipative tangential force
between metallic (Au) plates increases sharply with decreasing temperature and decreasing electrical resistance. This unexpected result is associated with a significant increase of the contribution from low-frequency electromagnetic modes with frequencies
, with
being the relaxation frequency, which, although small, is finite at
. At the same time, at
, the force
becomes negligibly small.
Along with these results, a general consensus has emerged between several theoretical approaches to the problem of dissipative van der Waals interactions on the whole, reflected, for example, in [
11,
18,
19,
20]. These developments and the results obtained and shown below open up much more optimistic prospects for conducting appropriate experiments to measure van der Waals friction, despite its smallness at ordinary (room) temperatures that hampers experimental studies.
Unlike dissipative van der Waals forces, precise experimental measurements of attractive Casimir-Lifshitz force
have been carried out for more than 20 years [
21,
22,
23], having achieved a high accuracy of
, but at temperatures of
thermal corrections to
are small compared to a “cold” part. This fact greatly complicates experimental measurements of entropy and, accordingly, the resolution of another long-standing problem––the so-called Casimir puzzle and Casimir conundrum [
23,
24,
25,
26] in the case of metallic and dielectric plates: violating the Nernst heat theorem when calculating the force of attraction between the plates in the framework of the Lifshitz theory using conventional, well-tested dielectric functions of materials. A recent comprehensive review on this issue is given in [
27]. In contrast, the van der Waals friction force with a linear dependence on velocity turns out to be most sensitive precisely to the low-temperature dielectric properties of materials, and its measurement can also give a new impetus in solving the Casimir puzzle.
In addition to fundamental interest, exploring van der Waals friction can be of great practical importance for microtechnology and for description of micromechanical systems operation [
28]. There is also reason to guess that van der Waals friction can manifest itself under astrophysical conditions during conglomeration of dust particles [
19,
29].
Taking all the above into account, this work aims at a more detailed analytic and numerical analysis of the low-temperature behavior of the van der Waals friction force between metallic plates, based on the theory by Levin-Polevoi-Rytov [
6,
30] and its development in [
17]. This enables us to confirm our previous conclusions [
17] both analytically and numerically. Namely, van der Waals friction force between the plates of gold increases by 6–7 orders of magnitude when the temperature drops down from 100 to 1 K, provided that the dielectric permittivity is described by the Drude function, with the temperature dependence of relaxation frequency obeying the Bloch-Grüneisen formula or close to it. A simple analytic expression for the friction force is also obtained, and the conditions are discussed for its experimental measurement in the sphere-plate configuration, commonly used when measuring attractive Casimir force. This creates a favorable prospect in measuring van der Waals dissipative friction.
2. Theoretical Background
Let us consider the standard Casimir-Lifshitz configuration of a system of two metallic plates 1 and 2 (
Figure 1) at a temperature
, separated by a vacuum gap
, where plate 1 moves with a nonrelativistic velocity
relative to a fixed plate 2. Recall the original expression for the fluctuation-electromagnetic friction force
per unit area of the vacuum contact of two plates obtained in [
17] in a linear approximation in the velocity
(a more general formula is also given in [
17]).
where
;
and
are the frequency-dependent dielectric permittivity and magnetic permeability of materials of plate 1 and 2,
,
, and
In (1), the Planck constant and the speed of light in vacuum are denoted by ħ and
c, and temperature
is expressed in energy units. The linear approximation in velocity corresponds to the condition
, which at a nonrelativistic velocity
is met both in the case of inhomogeneous (evanescent) electromagnetic waves (
) and in the case of propagating (traveling) waves (
). As shown in [
17], formula (1) fully agrees with the general relativistic expression for the dissipative force
, obtained by Polevoi [
6] within the framework of the fluctuation-electromagnetic theory [
30]. It can also be cast to a more familiar expression with Fresnel’s reflection coefficients of electromagnetic waves [
10,
11] (see
Appendix A). However, formula (1) is much more convenient when analyzing the low-temperature behavior of the force
due to a more transparent dependence on dielectric permittivity.
We will further consider the case of plates of the same nonmagnetic metals with
. Then (1) takes the simpler form
In obtaining (4), we have taken into account the identity . The modification of (2) and (3) for is obvious (keeping the general definition for ).
When studying the low-temperature behavior of the attractive Casimir-Lifshitz force
between metallic plates, the Drude approximation for
is usually used:
where
and
are plasma and relaxation frequencies. Meanwhile, for an ideal metal without impurities and other defects, dependence
obeys the Bloch-Grüneisen law [
31,
32].
where
is the Debye temperature. In the presence of impurities and other physical defects that contribute to the formation of residual resistance, it seems natural to use the expression
with
being the constant and
at
(
. The role of the relaxation frequency at zero temperature and the corresponding mechanisms were discussed in [
32,
33,
34,
35,
36].
As can be easily seen from (4), only traveling waves
can contribute to the friction force
at
. The resulting friction force
in this case is extremely small for measurement at present. Therefore, direct experimental measurements of
at small distances between the plates, when inhomogeneous waves
dominate, would not only be a direct validation of the presence of finite residual resistance but would also enable us to quantitatively assess its magnitude. In view of the above, we will further assume that function
is always nonzero and introduce the frequency parameterization
. For wave vector
, we use the parametrization
(with
in the case
, and
in the case
. Then, for
and
in (4), we obtain
,
in the former case and
,
in the latter case. Accordingly, formula (4) takes the form
where
,
, and functions
are given by
In (9) and (10), we also introduced the quantities
,
,
and
Let us analyze the role of individual terms in (8) as
, when the parameter
is small. If
is defined by (6), then
for
K and
for
K. Moreover, up to high temperatures
, the relation
holds. Parameter
does not depend on temperature. In particular, for gold (
) at
nm, we obtain
. The presence of the hyperbolic sine squared in (8) enhances the role of low-frequency modes with
, when
. Accordingly, a significant temperature effect should manifest itself at
. To allocate the dependence of the force
on
(and on temperature) more clearly, we write (8) in the form
where the integral terms in square brackets are given by
The temperature dependence of
also manifests itself through a small parameter
An analysis of (16)–(19) shows that, in the most important range of nanometer distances,
between the plates, the main contribution is made by the integral
, corresponding to inhomogeneous waves. When calculating
,
takes characteristic values
. Then for
and
, one obtains
. On the other hand, regardless of the relation between
and
, it follows that
Accordingly, for
and
, one obtains
and
while (16) takes the form
where
. Calculating integral (17) yields,
with
being the integral exponential function [
37]. Moreover, the presence of a small parameter
in the second term of (22) makes it negligible in comparison with the first term. In the case when
, from (11) and (20) it follows that
and when this expression is substituted into (16), the result does not depend on
, but it is negligible due to the smallness of the upper limits of integration. In other regions of integration, integral
turns out to be proportional to
or
, so its contribution at
can also be neglected. The rest of the integral terms in (15) are also small. In particular, integral
is cut off due to the large modulus value of the dielectric constant ε (
in (9)), and the contributions
and
from traveling waves are small due to the additional dependence on
Thus, taking into account (18), it follows from (15) that at
force,
increases proportionally to
if
is described by (6). This conclusion is also confirmed by direct numerical calculations in
Section 3.
3. Numerical Results
As an example, we calculated the van der Waals force between two Au plates. The dielectric function was taken in Drude approximation (5) with the relaxation frequency defined by (6) or (7). When using (7), parameter
was varied in such a way that the equality
was fulfilled for values of
in the range from
to
. This made it possible to estimate the residual resistance of the plate material,
. Accordingly, parameter
in (15)–(19) was calculated by
In
Table 1, we compare different contributions to the friction force (
in Equation (15). One can see that integrals
are small compared to
and can be neglected. The resultant friction forces at
are shown in
Table 2. The upper-row values of
for each temperature
and a gap width
were obtained by direct numerical integration of (16). The lower-row values of
were calculated by formula (22) with parameter
depending on
. Since the temperature dependence of integral
was very weak, a good approximation for
at each value of
was obtained when equating (22) and the result of numerical integration in (16) for
. The resultant dependence
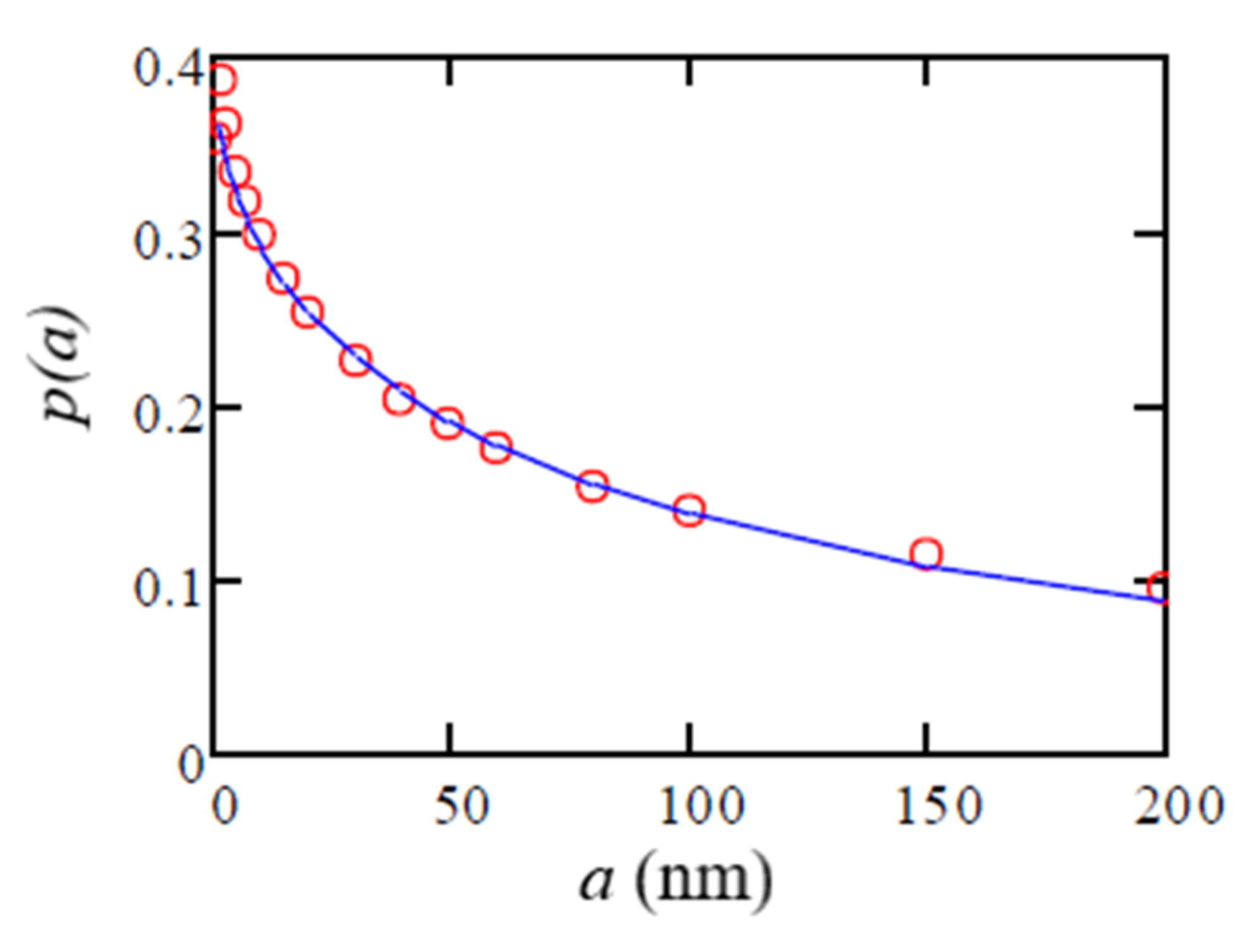
is shown by the solid curve in
Figure 2. The dashed curve was obtained using the fitting function
As follows from the data in
Table 2, the use of (22) in combination with (23) provides a fair description of the friction force. Approximation errors gradually increase from 0–3% for
nm to 3–10% for
nm. Errors are associated with increasing errors of Equation (23) at large values of
Omitting the small second term in (22) and inserting (22) into (15), we obtain an approximate expression for the friction force of the form
where
is given by (23) or it can be taken from
Figure 2 (circles) and
Table 3.
As follows from (24) and the data shown in
Table 2, at
friction force
scales as
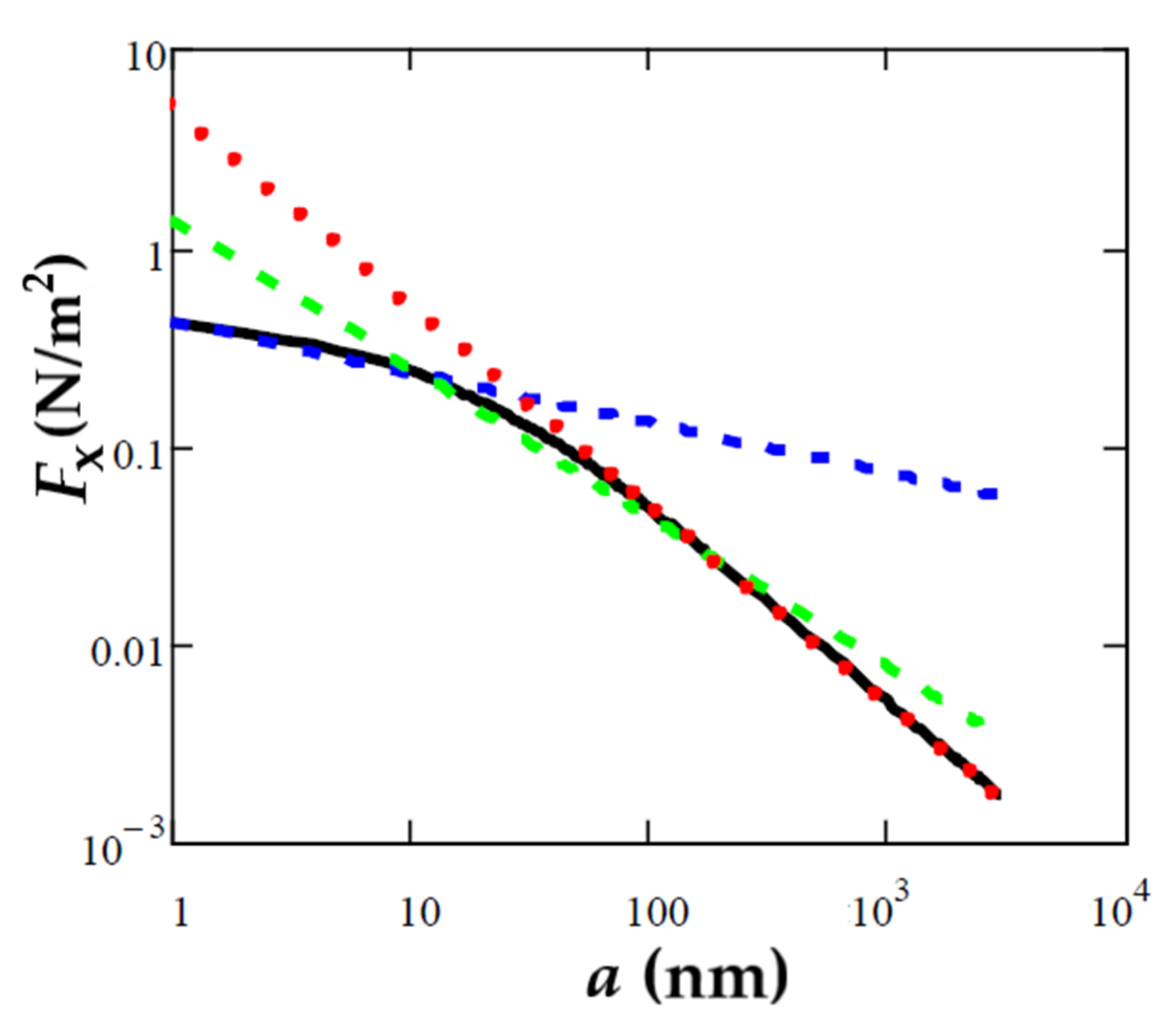
. This is caused by dependence (6). Another striking result is that in the range of distances under consideration (see
Figure 3).
The dependence of on distance (gap width) is relatively weak: for nm, for nm, and for nm. This is in drastic contrast to the behavior of the attractive Casimir force ( for in this range of separations).
As the next step, we calculated dependence
at different values of
. The results are shown in
Figure 4 and
Figure 5 for
nm and
nm.
The formation of a plateau on the plots at
was caused by the finite values of
and residual resistance
. The smaller
, the higher the growth of
with decreasing temperature. A plateau was formed at a temperature
, corresponding to the equality
and the corresponding values of
were proportional to
. Another plateau on the curves, where the friction force barely does not depend on temperature, was observed at
in the range of room and higher temperatures, in agreement with our previous calculations [
17].
4. Discussion
The results obtained fully confirm our earlier conclusion [
17] that van der Waals friction force between metallic plates of gold should increase significantly at temperatures
T < 50 K (see
Figure 4 and
Figure 5). The character of this dependence (
is due to the low-temperature behavior of the relaxation frequency
at
, since
. In the presence of defects and impurities in the metal, the quantity
is associated with the residual resistance of the metal,
. With decreasing temperature below the value
determined by the relation
, the height of the plateau forming on the dependence of the friction force on temperature is proportional to
. Correspondingly, knowing the height of the plateau allows one to find
since
. At first glance, an unexpected increase in friction at
(69 K for gold) had a fairly simple physical justification. In accordance with the Planck distribution, the density of fluctuation modes increased significantly at low frequencies
. However, under normal conditions and a sufficiently high resistance of the metal, the relationship
(
) was satisfied, and the characteristic absorption frequency was the Wien frequency. Accordingly, friction force decreased with decreasing temperature (
. With decreasing temperature
, the relaxation frequency decreased faster than the Wien frequency, the ratio between them changed (
), and the characteristic absorption frequency shifted towards low frequencies with a high density of electromagnetic modes. At the same time, the penetration depth of S-modes increased. Although the mean free path of electrons increased and the resistance to direct current dropped down, an increasing number of electrons underwent small-angle scattering under the action of numerous small-scale local fluctuations of the electromagnetic field and charge density. As a result, Joule dissipation and friction grew up to the saturation threshold due to residual resistance. In general, these processes were controlled by parameter α. Within the framework of this scheme, the sharp drop in the friction force in the limit
is also easily explained: the S-wave field was transformed into a constant magnetic field that freely penetrated into the sample, and the dissipation of energy of electrons disappeared.
Thus, no less important result is that the dominant contribution to the friction force (up to distances
) was due to inhomogeneous S-polarized electromagnetic waves. Meanwhile, it was the low-temperature behavior of the S-modes and their contribution to the magnitude of the thermal part of the Casimir force that played a key role in resolving the Casimir paradox associated with a possible violation of the Nernst theorem, since theoretically consistent models of dielectric response for real metals at low frequencies should agree with the behavior of the Casimir entropy at
. According to [
32], the most promising route for exploring the finite temperature correction to the Casimir pressure and entropy in the standard setup with two parallel plates appears to be the case of large separations around 2 µm. Then the corresponding (relative) temperature correction will be on the level of 1%. However, at such separations, the Casimir pressure itself is small (it is
1.6
times less than at separations of 100 nm). At the same time, if van der Waals friction increases by
times at
, the level of thermal correction to Casimir pressure will be inferior to the magnitude of the van der Waals friction. For ideal metal plates, at
µm,
, the thermal Casimir force
turns out to be
N/m
2, whereas the corresponding friction force was
N/m
2 (at
m/s,
K), i.e., much higher.
Also noteworthy was the very slow decrease in the friction force with distance: even at
we obtained the dependence
, while at smaller distances we had
with
(
Figure 3). This is in drastic contrast to the Casimir attraction force, where
with
. Such a weak dependence lead to an increase in the effective area of interaction in experiments, in which a probing body was a metallized sphere of radius
In addition, the role of surface roughness in this case also turned out to be less important.
The calculated values of the van der Waals friction force seem to be quite achievable in a setup based on an atomic force microscope (AFM), where an Au-coated sphere of radius
is attached to the AFM cantilever and interacts with an Au-coated plate of the substrate material. Thus, for
µm,
nm,
, and
we obtained
and
(at
nm and the same other conditions). Then, with an effective area of interaction
, the calculated friction parameter will be
in the former case and
in the latter. Close to such experimental conditions were those implemented in [
38]. In that experiment, a configuration with the AFM cantilever oriented perpendicular to the surface was applied. Due to the high stiffness of the cantilever in the transverse direction, the distance
between the sphere and the surface could be controlled with an accuracy of several nm. The measured values of the friction parameter
(at
) were
at
and
at
, with the distance dependence
(
. However, the dissipation mechanism in [
38] was not clearly elucidated. However, in the opinion of the authors, the dissipation is electrical in origin, and they did not exclude the influence of adsorbates and other surface defects, causing the appearance of parasitic electric fields. To a greater extent, such effects were likely even more significant in the experiment [
39], with a parallel orientation of the cantilever (in the range of room temperatures). As compared to our expectations, the key points, which likely exclude the relevance of these experiments to the quantitative estimates of the van der Waals friction, are related with the decreasing temperature dependence (with reducing temperature). In addition, the level of the van der Waals friction of order
is expected at temperatures
, which were not reached in [
34].
New fascinating experimental possibilities in precision measurements of Casimir forces and quantum friction forces between plates and in close geometry are opening up with recent experiments [
36,
40,
41]. In particular, in [
41], the Casimir force between interpenetrated rectangular gratings was measured at
K.
Another point that seems to be worth touching on briefly is the possible role of nonlocal corrections to the dielectric constant at low temperatures. In our recent paper [
42], the calculated nonlocal correction to friction force becomes significant at separations
nm, but it affects only the contribution from P-polarized waves, which is much less than the contribution from S-waves (
Table 1). In addition, this nonlocal correction scales with temperature and distance as
. The effect of nonlocality was also negligible in calculating the contribution from S-waves to Casimir pressure [
43,
44]. One more nonlocal modification of Drude function (5) (compared to [
43,
44]) was recently proposed in [
45]. In its essential point, as far as concerned the friction force, the second term in (5) had an additional factor
. In the case of interest,
, this factor either did not change the Drude-like low-temperature behavior of dielectric permittivity,
(
) or lead to the plasma-like dependence. In the latter case, the friction force receded. A more confident judgement needs additional analysis.