Cosmological Perturbations via Quantum Corrections in M-Theory
Abstract
1. Introduction
2. Effective Action and Inflationary Solution in M-Theory
3. Tensor Perturbations in M-Theory
3.1. Equations of Motion for the Tensor Perturbations
3.2. Effective Action for the Tensor Perturbations
4. Solution for the Tensor Perturbations
5. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Scalar Perturbations
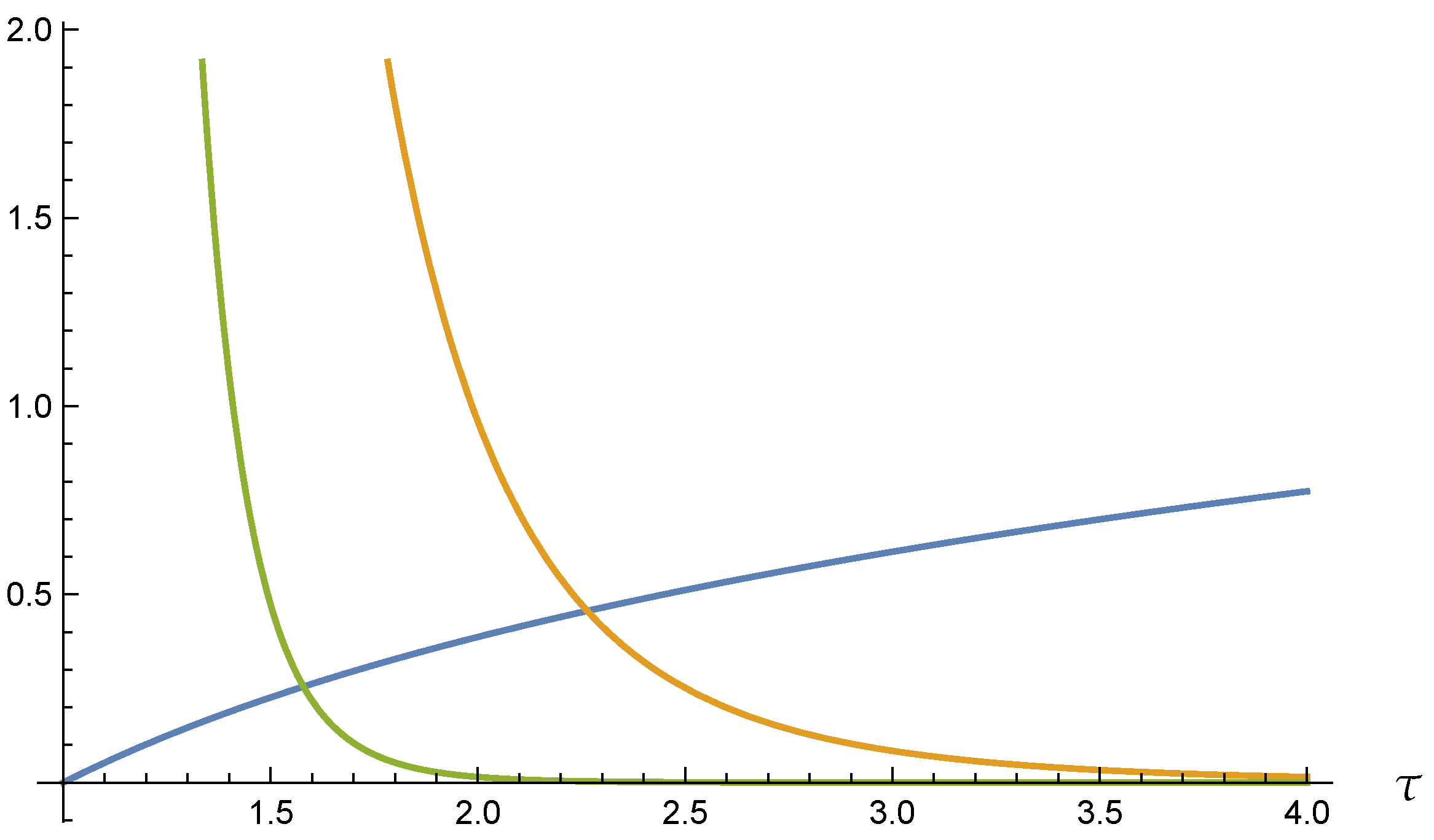
Appendix B. Numerical Analyses for Scalar and Tensor Perturbations


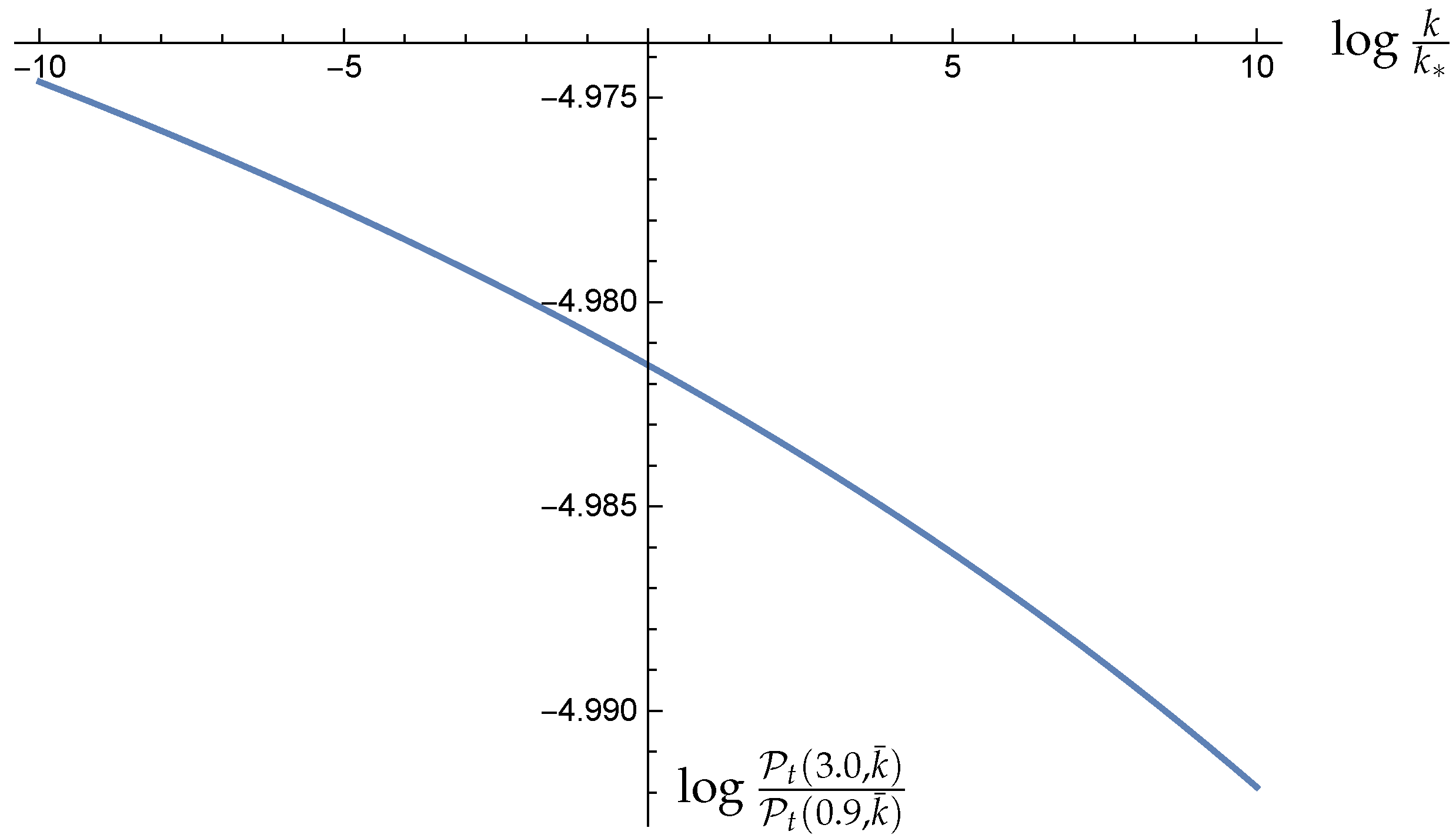
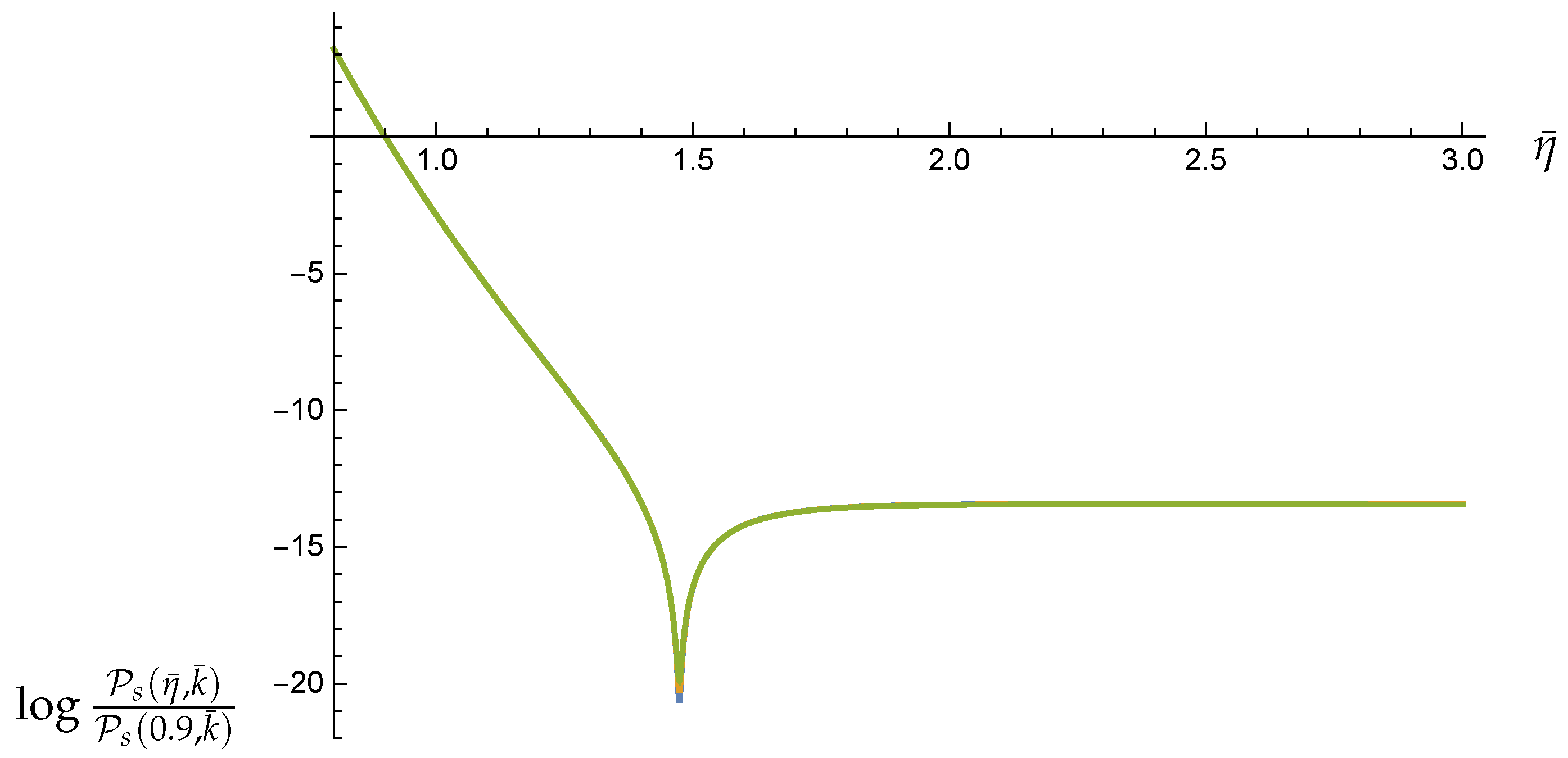
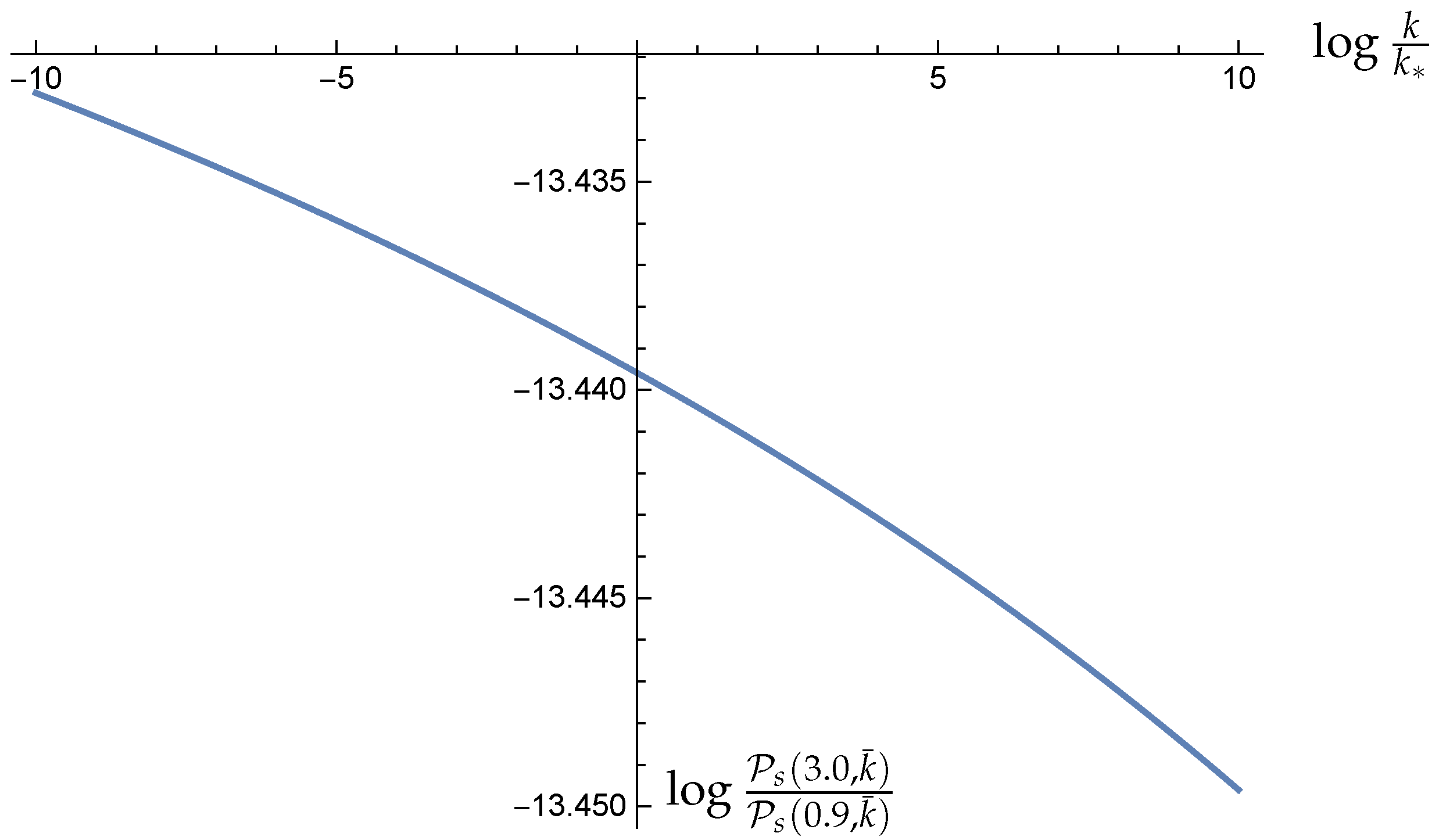
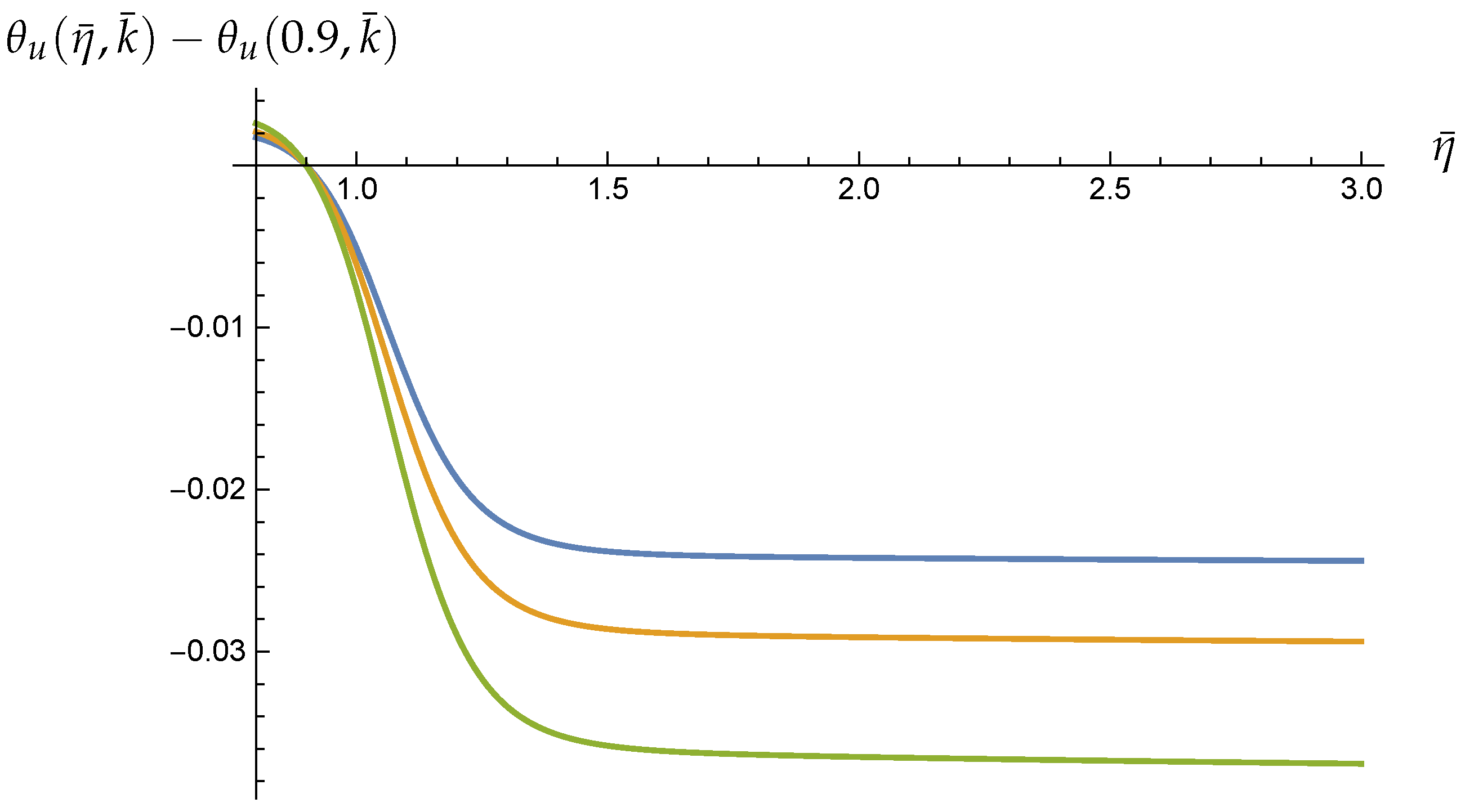
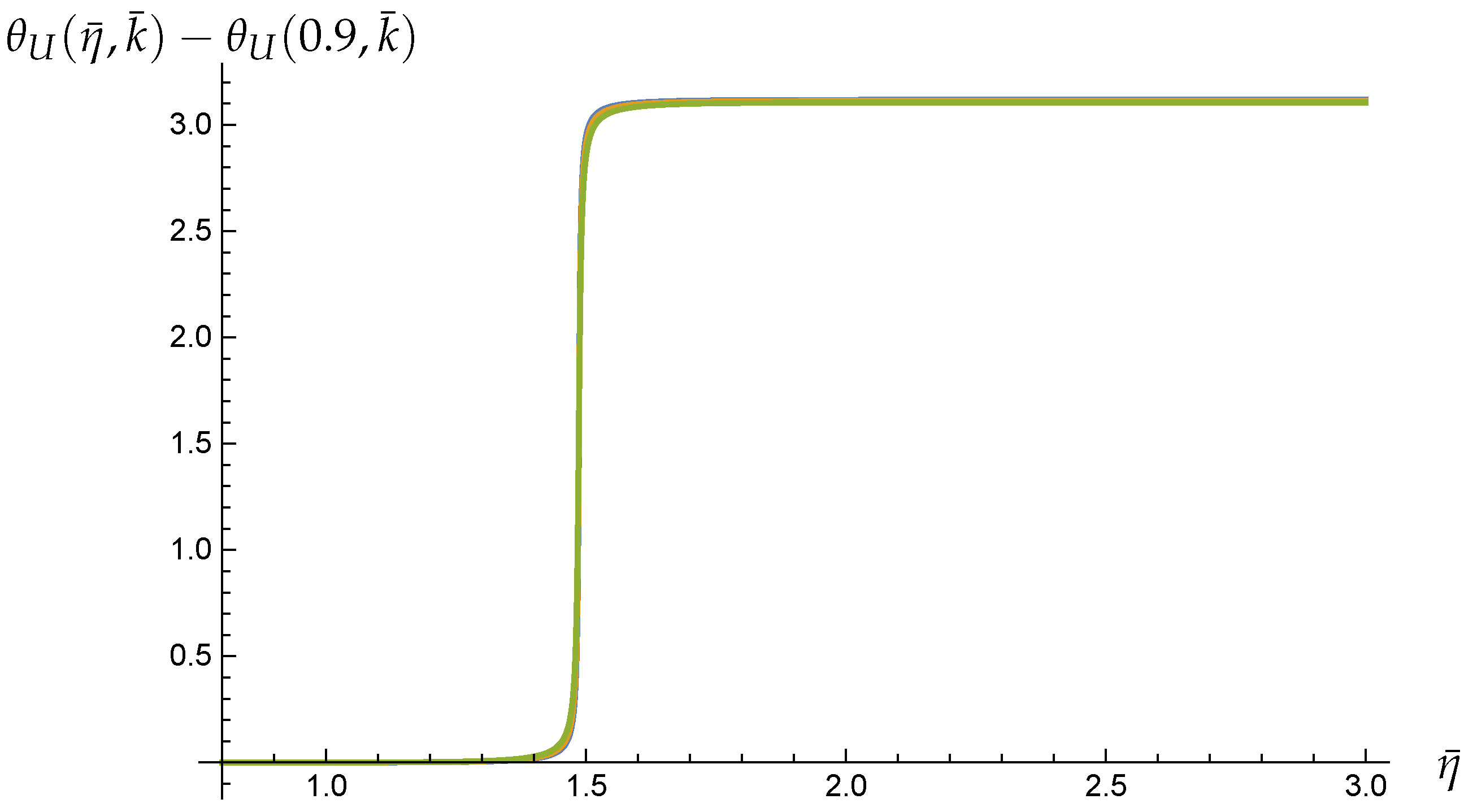
Appendix C. Plots of θu and θU
| 1 | |
| 2 | It is possible to make the Riemann tensor to a Weyl tensor by using field redefinition ambiguity. A more general case is discussed in [35]. |
| 3 | The action contains linear term on 3-form field A which is proportional to
|
| 4 | For example, corresponds to () [36]. Higher derivative terms which are not considered in this paper will also affect the explicit value of . |
| 5 | Some thoughts on this point are given in the appendix in [36]. |
| 6 | A sum of physical degrees of freedom are included in . As discussed in the Section 2, we choose and define a pivot scale as . |
References
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. 1980, 91B, 99. [Google Scholar] [CrossRef]
- Guth, A.H. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 1981, 23, 347. [Google Scholar] [CrossRef]
- Kazanas, D. Dynamics of the Universe and Spontaneous Symmetry Breaking. Astrophys. J. 1980, 241, L59. [Google Scholar] [CrossRef]
- Sato, K. First Order Phase Transition of a Vacuum and Expansion of the Universe. Mon. Not. Roy. Astron. Soc. 1981, 195, 467. [Google Scholar] [CrossRef]
- Linde, A.D. Chaotic Inflation. Phys. Lett. 1983, 129B, 177. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Ahmed, Z.; Aikin, R.W.; Alexander, K.D.; Arnaud, M.; Aumont, J.; Baccigalupi, C.B.; Ay, A.J.; Barkats, D.; et al. Joint Analysis of BICEP2/Keck Array and Planck Data. Phys. Rev. Lett. 2015, 114, 101301. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Ahmed, Z.; Aikin, R.W.; Alexander, K.D.; Barkats, D.; Benton, S.J.; Bischoff, C.A.; Bock, J.J.; Bowens-Rubin, R.; Brevik, J.A.; et al. Improved Constraints on Cosmology and Foregrounds from BICEP2 and Keck Array Cosmic Microwave Background Data with Inclusion of 95 GHz Band. Phys. Rev. Lett. 2016, 116, 031302. [Google Scholar] [CrossRef] [PubMed]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar]
- Kolb, E.W.; Turner, M.S. The Early Universe. Front. Phys. 1990, 69, 1. [Google Scholar]
- Liddle, A.R.; Lyth, D.H. Cosmological Inflation and Large Scale Structure; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Dodelson, S. Modern Cosmology; Academic Press: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Linde, A. Inflationary Cosmology after Planck 2013. arXiv 2013, arXiv:1402.0526. [Google Scholar]
- Baumann, D.; McAllister, L. Inflation and String Theory; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Felice, A.D.; Tsujikawa, S. f(R) theories. Living Rev. Rel. 2010, 13, 3. [Google Scholar]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1. [Google Scholar] [CrossRef]
- Freese, K.; Frieman, J.A.; Olinto, A.V. Natural inflation with pseudo - Nambu-Goldstone bosons. Phys. Rev. Lett. 1990, 65, 3233. [Google Scholar] [CrossRef] [PubMed]
- Linde, A.D. Hybrid inflation. Phys. Rev. D 1994, 49, 748. [Google Scholar] [CrossRef] [PubMed]
- Boubekeur, L.; Lyth, D.H. Hilltop inflation. J. Cosmol. Astropart. Phys. 2005, 0507, 010. [Google Scholar] [CrossRef]
- Bezrukov, F.L.; Shaposhnikov, M. The Standard Model Higgs boson as the inflaton. Phys. Lett. B 2008, 659, 703. [Google Scholar] [CrossRef]
- Gibbons, G.W. Aspects Of Supergravity Theories. In Supersymmetry, Supergravity, and Related Topics; World Scientific Publishing: Singapore, 1985. [Google Scholar]
- Maldacena, J.M.; Nunez, C. Supergravity description of field theories on curved manifolds and a no go theorem. Int. J. Mod. Phys. A 2001, 16, 822. [Google Scholar] [CrossRef]
- Gibbons, G.W. Thoughts on tachyon cosmology. Class. Quant. Grav. 2003, 20, S321. [Google Scholar] [CrossRef]
- Obied, G.; Ooguri, H.; Spodyneiko, L.; Vafa, C. De Sitter Space and the Swampland. arXiv 2018, arXiv:1806.08362. [Google Scholar]
- Garg, S.K.; Krishnan, C. Bounds on Slow Roll and the de Sitter Swampland. J. High Energy Phys. 2019, 11, 075. [Google Scholar] [CrossRef]
- Ooguri, H.; Palti, E.; Shiu, G.; Vafa, C. Distance and de Sitter Conjectures on the Swampland. Phys. Lett. B 2019, 788, 180–184. [Google Scholar] [CrossRef]
- Kachru, S.; Kallosh, R.; Linde, A.D.; Trivedi, S.P. De Sitter vacua in string theory. Phys. Rev. D 2003, 68, 046005. [Google Scholar] [CrossRef]
- Blumenhagen, R.; Brinkmann, M.; Klaewer, D.; Makridou, A.; Schlechter, L. KKLT and the Swampland Conjectures. arXiv 2020, arXiv:2004.09285. [Google Scholar]
- Ishihara, H. Cosmological Solutions of the Extended Einstein Gravity With the Gauss-Bonnet Term. Phys. Lett. B 1986, 179, 217. [Google Scholar] [CrossRef]
- Ohta, N. Accelerating cosmologies and inflation from M/superstring theories. Int. J. Mod. Phys. A 2005, 20, 1. [Google Scholar] [CrossRef]
- Maeda, K.I.; Ohta, N. Inflation from M-theory with fourth-order corrections and large extra dimensions. Phys. Lett. B 2004, 597, 400. [Google Scholar] [CrossRef][Green Version]
- Maeda, K.i.; Ohta, N. Inflation from superstring /M theory compactification with higher order corrections. I. Phys. Rev. D 2005, 71, 063520. [Google Scholar] [CrossRef]
- Akune, K.; Maeda, K.i.; Ohta, N. Inflation from superstring/M-theory compactification with higher order corrections. II. Case of quartic Weyl terms. Phys. Rev. D 2006, 73, 103506. [Google Scholar] [CrossRef]
- Hiraga, K.; Hyakutake, Y. Inflationary Cosmology via Quantum Corrections in M-theory. Prog. Theor. Exp. Phys. 2018, 2018, 113B03. [Google Scholar] [CrossRef]
- Hiraga, K.; Hyakutake, Y. Review of inflationary cosmology via quantum corrections in M-theory. Int. J. Mod. Phys. A 2019, 34, 1930016. [Google Scholar] [CrossRef]
- Hiraga, K.; Hyakutake, Y. Scalar Cosmological Perturbations in M-theory with Higher Derivative Corrections. Prog. Theor. Exp. Phys. 2020, 2020, 113B03. [Google Scholar] [CrossRef]
- Gross, D.J.; Witten, E. Superstring Modifications of Einstein’s Equations. Nucl. Phys. B 1986, 277, 1. [Google Scholar] [CrossRef]
- Gross, D.J.; Sloan, J.H. The Quartic Effective Action for the Heterotic String. Nucl. Phys. B 1987, 291, 41. [Google Scholar] [CrossRef]
- Grisaru, M.T.; Ven, A.E.M.v.; Zanon, D. Four Loop beta Function for the N=1 and N=2 Supersymmetric Nonlinear Sigma Model in Two-Dimensions. Phys. Lett. B 1986, 173, 423. [Google Scholar] [CrossRef]
- Grisaru, M.T.; Zanon, D. σ Model Superstring Corrections to the Einstein-hilbert Action. Phys. Lett. B 1986, 177, 347. [Google Scholar] [CrossRef]
- Tseytlin, A.A. R4 terms in 11 dimensions and conformal anomaly of (2,0) theory. Nucl. Phys. B 2000, 584, 233. [Google Scholar] [CrossRef]
- Becker, K.; Becker, M. Supersymmetry breaking, M theory and fluxes. J. High Energy Phys. 2001, 0107, 038. [Google Scholar] [CrossRef][Green Version]
- De Roo, M.; Suelmann, H.; Wiedemann, A. Supersymmetric R**4 actions in ten-dimensions. Phys. Lett. B 1992, 280, 39. [Google Scholar] [CrossRef]
- De Roo, M.; Suelmann, H.; Wiedemann, A. The Supersymmetric effective action of the heterotic string in ten-dimensions. Nucl. Phys. B 1993, 405, 326. [Google Scholar] [CrossRef][Green Version]
- Suelmann, H. Supersymmetry and String Effective Actions. Ph.D. Thesis, Groningen University, Groningen, The Netherlands, 1994. [Google Scholar]
- Peeters, K.; Vanhove, P.; Westerberg, A. Supersymmetric higher derivative actions in ten-dimensions and eleven-dimensions, the associated superalgebras and their formulation in superspace. Class. Quant. Grav. 2001, 18, 843. [Google Scholar] [CrossRef][Green Version]
- Hyakutake, Y.; Ogushi, S. R4 corrections to eleven dimensional supergravity via supersymmetry. Phys. Rev. D 2006, 74, 025022. [Google Scholar] [CrossRef]
- Hyakutake, Y.; Ogushi, S. Higher derivative corrections to eleven dimensional supergravity via local supersymmetry. J. High Energy Phys. 2006, 0602, 068. [Google Scholar] [CrossRef][Green Version]
- Hyakutake, Y. Toward the Determination of R3F2 Terms in M-theory. Prog. Theor. Phys. 2007, 118, 109. [Google Scholar] [CrossRef]
- Hyakutake, Y. Quantum near-horizon geometry of a black 0-brane. Prog. Theor. Exp. Phys. 2014, 2014, 033B04. [Google Scholar] [CrossRef]
- Weinberg, S. Effective Field Theory for Inflation. Phys. Rev. D 2008, 77, 123541. [Google Scholar] [CrossRef]
- Hwang, J.C.; Noh, H. Cosmological perturbations in generalized gravity theories. Phys. Rev. D 1996, 54, 1460. [Google Scholar] [CrossRef]
- Felice, A.D.; Suyama, T. Vacuum structure for scalar cosmological perturbations in Modified Gravity Models. J. Cosmol. Astropart. Phys. 2009, 0906, 034. [Google Scholar] [CrossRef]
- Mathematica Codes Are Located. Available online: http://yoshi.sci.ibaraki.ac.jp/arXiv20210316.html (accessed on 7 November 2021).
- Hohm, O.; Zwiebach, B. Duality invariant cosmology to all orders in α’. Phys. Rev. D 2019, 100, 126011. [Google Scholar] [CrossRef]
- Brandhuber, A.; Gomis, J.; Gubser, S.S.; Gukov, S. Gauge theory at large N and new G(2) holonomy metrics. Nucl. Phys. B 2001, 611, 179. [Google Scholar] [CrossRef]
- Brandle, M.; Lukas, A.; Ovrut, B.A. Heterotic M theory cosmology in four-dimensions and five-dimensions. Phys. Rev. D 2001, 63, 026003. [Google Scholar] [CrossRef]
- Antoniadis, I.; Cotsakis, S. Infinity in string cosmology: A review through open problems. Int. J. Mod. Phys. D 2016, 26, 1730009. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Where new gravitational physics comes from: M-Theory? Phys. Lett. B 2003, 576, 5. [Google Scholar] [CrossRef]
- Carroll, S.M.; Duvvuri, V.; Trodden, M.; Turner, M.S. Is cosmic speed—up due to new gravitational physics? Phys. Rev. D 2004, 70, 043528. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Sebastiani, L.; Vagnozzi, S. Inflation in f(R,ϕ) -theories and mimetic gravity scenario. Eur. Phys. J. C 2015, 75, 444. [Google Scholar] [CrossRef]
- Sebastiani, L.; Vagnozzi, S.; Myrzakulov, R. Mimetic gravity: A review of recent developments and applications to cosmology and astrophysics. Adv. High Energy Phys. 2017, 2017, 3156915. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hiraga, K.; Hyakutake, Y. Cosmological Perturbations via Quantum Corrections in M-Theory. Universe 2021, 7, 425. https://doi.org/10.3390/universe7110425
Hiraga K, Hyakutake Y. Cosmological Perturbations via Quantum Corrections in M-Theory. Universe. 2021; 7(11):425. https://doi.org/10.3390/universe7110425
Chicago/Turabian StyleHiraga, Kazuho, and Yoshifumi Hyakutake. 2021. "Cosmological Perturbations via Quantum Corrections in M-Theory" Universe 7, no. 11: 425. https://doi.org/10.3390/universe7110425
APA StyleHiraga, K., & Hyakutake, Y. (2021). Cosmological Perturbations via Quantum Corrections in M-Theory. Universe, 7(11), 425. https://doi.org/10.3390/universe7110425






