Investigation of the Elliptic Flow Fluctuations of the Identified Particles Using the a Multi-Phase Transport Model
Abstract
1. Introduction
2. Method
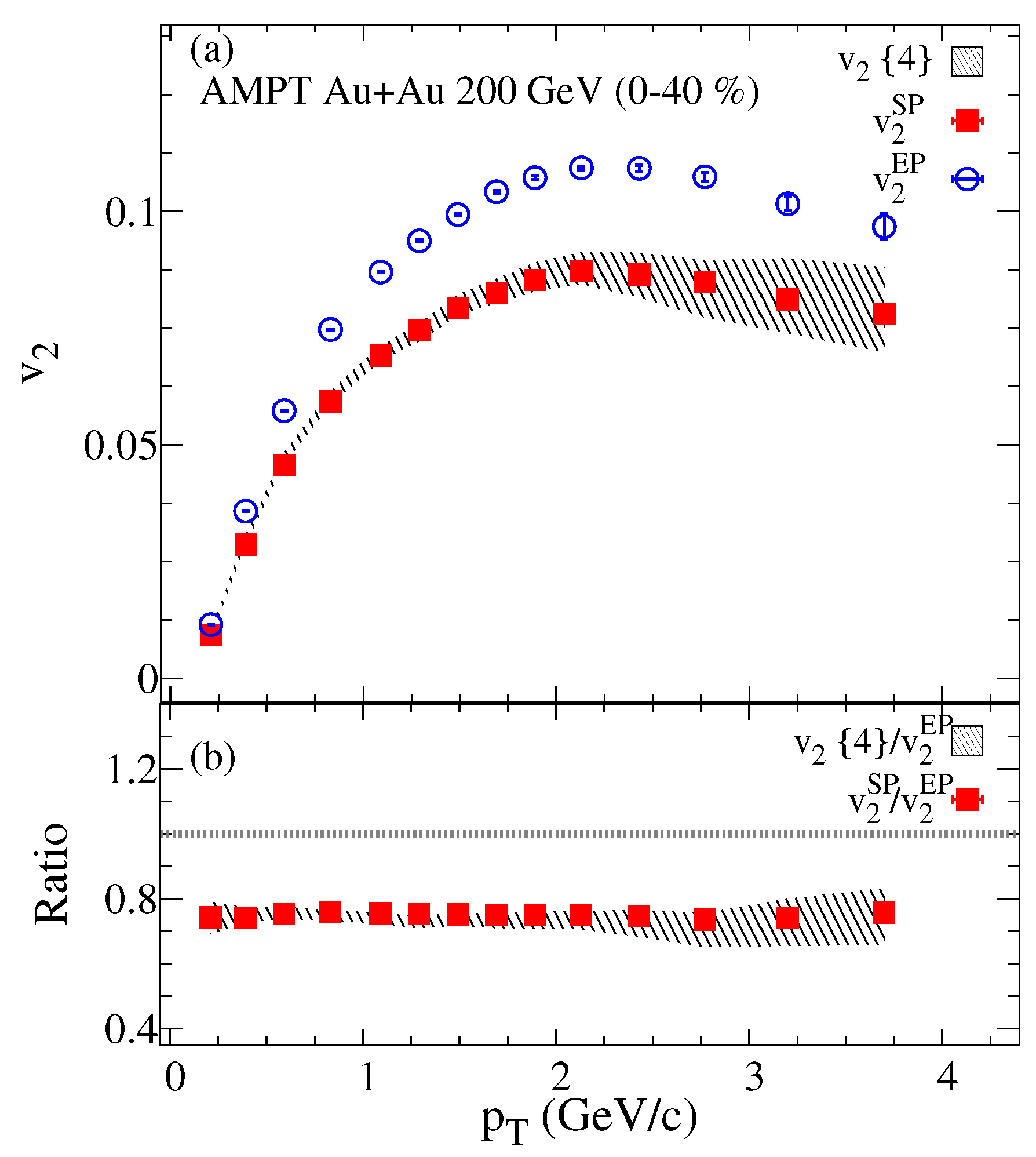
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Heinz, U.W.; Kolb, P.F. Early thermalization at RHIC. Nucl. Phys. 2002, A702, 269–280. [Google Scholar] [CrossRef]
- Hirano, T.; Heinz, U.W.; Kharzeev, D.; Lacey, R.; Nara, Y. Hadronic dissipative effects on elliptic flow in ultrarelativistic heavy-ion collisions. Phys. Lett. 2006, B636, 299–304. [Google Scholar] [CrossRef]
- Huovinen, P.; Kolb, P.F.; Heinz, U.W.; Ruuskanen, P.V.; Voloshin, S.A. Radial and elliptic flow at RHIC: Further predictions. Phys. Lett. 2001, B503, 58–64. [Google Scholar] [CrossRef]
- Hirano, T.; Tsuda, K. Collective flow and two pion correlations from a relativistic hydrodynamic model with early chemical freeze out. Phys. Rev. 2002, C66, 054905. [Google Scholar] [CrossRef]
- Romatschke, P.; Romatschke, U. Viscosity Information from Relativistic Nuclear Collisions: How Perfect is the Fluid Observed at RHIC? Phys. Rev. Lett. 2007, 99, 172301. [Google Scholar] [CrossRef] [PubMed]
- Luzum, M. Flow fluctuations and long-range correlations: Elliptic flow and beyond. J. Phys. 2011, G38, 124026. [Google Scholar] [CrossRef]
- Song, H.; Bass, S.A.; Heinz, U.; Hirano, T.; Shen, C. 200 A GeV Au+Au collisions serve a nearly perfect quark-gluon liquid. Phys. Rev. Lett. 2011, 106, 192301. [Google Scholar] [CrossRef] [PubMed]
- Qian, J.; Heinz, U.W.; Liu, J. Mode-coupling effects in anisotropic flow in heavy-ion collisions. Phys. Rev. 2016, C93, 064901. [Google Scholar] [CrossRef]
- Magdy, N. Beam energy dependence of the anisotropic flow coefficients vn. PoS 2018, CPOD2017, 005. [Google Scholar]
- Magdy, N. Viscous Damping of Anisotropic Flow in 7.7–200 GeV Au+Au Collisions. J. Phys. Conf. Ser. 2017, 779, 012060. [Google Scholar] [CrossRef]
- Schenke, B.; Jeon, S.; Gale, C. Anisotropic flow in = 2.76 TeV Pb+Pb collisions at the LHC. Phys. Lett. 2011, B702, 59–63. [Google Scholar] [CrossRef]
- Teaney, D.; Yan, L. Non linearities in the harmonic spectrum of heavy ion collisions with ideal and viscous hydrodynamics. Phys. Rev. 2012, C86, 044908. [Google Scholar] [CrossRef]
- Gardim, F.G.; Grassi, F.; Luzum, M.; Ollitrault, J.Y. Anisotropic flow in event-by-event ideal hydrodynamic simulations of = 200 GeV Au+Au collisions. Phys. Rev. Lett. 2012, 109, 202302. [Google Scholar] [CrossRef] [PubMed]
- Lacey, R.A.; Reynolds, D.; Taranenko, A.; Ajitanand, N.N.; Alexander, J.M.; Liu, F.H.; Gu, Y.; Mwai, A. Acoustic scaling of anisotropic flow in shape-engineered events: Implications for extraction of the specific shear viscosity of the quark gluon plasma. J. Phys. 2016, G43, 10LT01. [Google Scholar] [CrossRef]
- Voloshin, S.; Zhang, Y. Flow study in relativistic nuclear collisions by Fourier expansion of Azimuthal particle distributions. Z. Phys. C 1996, 70, 665–672. [Google Scholar] [CrossRef]
- Poskanzer, A.M.; Voloshin, S.A. Methods for analyzing anisotropic flow in relativistic nuclear collisions. Phys. Rev. 1998, C58, 1671–1678. [Google Scholar] [CrossRef]
- Magdy, N. Beam-energy dependence of the azimuthal anisotropic flow from RHIC. arXiv 2019, arXiv:1909.09640. [Google Scholar]
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Anderson, D.M.; Aoyama, R.; et al. Azimuthal Harmonics in Small and Large Collision Systems at RHIC Top Energies. Phys. Rev. Lett. 2019, 122, 172301. [Google Scholar] [CrossRef]
- Magdy, N. Collision system and beam energy dependence of anisotropic flow fluctuations. Nucl. Phys. 2019, A982, 255–258. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Ajitanand, N.N.; Alekseev, I.; Anderson, D.M.; Aoyama, R.; et al. Azimuthal anisotropy in Cu+Au collisions at = 200 GeV. Phys. Rev. 2018, C98, 014915. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Ajitanand, N.N.; Alekseev, I.; Anderson, D.M.; Aoyama, R.; Aparin, A.; et al. Harmonic decomposition of three-particle azimuthal correlations at energies available at the BNL Relativistic Heavy Ion Collider. Phys. Rev. 2018, C98, 034918. [Google Scholar] [CrossRef]
- Alver, B.; Roland, G. Collision geometry fluctuations and triangular flow in heavy-ion collisions. Phys. Rev. 2010, C81, 054905. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Eroe, J.; Fabjan, C.; Friedl, M.; et al. Measurement of higher-order harmonic azimuthal anisotropy in PbPb collisions at = 2.76 TeV. Phys. Rev. 2014, C89, 044906. [Google Scholar] [CrossRef]
- Alver, B.; Back, B.B.; Baker, M.D.; Ballintijn, M.; Barton, D.S.; Betts, R.R.; Bindel, R.; Busza, W.; Chetluru, V.; Garcia, E.; et al. Importance of correlations and fluctuations on the initial source eccentricity in high-energy nucleus-nucleus collisions. Phys. Rev. 2008, C77, 014906. [Google Scholar] [CrossRef]
- Alver, B.; Roland, C.; Seals, H.; Wolfs, F.L.H.; Roland, G.; Verdier, R.; Loizides, C.; Holynski, R.; Manly, S.; Li, W.; et al. Non-flow correlations and elliptic flow fluctuations in gold-gold collisions at = 200 GeV. Phys. Rev. 2010, C81, 034915. [Google Scholar] [CrossRef]
- Ollitrault, J.Y.; Poskanzer, A.M.; Voloshin, S.A. Effect of flow fluctuations and nonflow on elliptic flow methods. Phys. Rev. 2009, C80, 014904. [Google Scholar] [CrossRef]
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Ajitanand, N.N.; Alekseev, I.; Anderson, D.M.; et al. Correlation Measurements Between Flow Harmonics in Au+Au Collisions at RHIC. Phys. Lett. 2018, B783, 459–465. [Google Scholar] [CrossRef]
- Qiu, Z.; Heinz, U.W. Event-by-event shape and flow fluctuations of relativistic heavy-ion collision fireballs. Phys. Rev. 2011, C84, 024911. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Aoki, K.; Aramaki, Y.; Atomssa, E.T.; et al. Measurements of Higher-Order Flow Harmonics in Au+Au Collisions at = 200 GeV. Phys. Rev. Lett. 2011, 107, 252301. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Aben, R.; Abi, B.; Abolins, M.; AbouZeid, O.S.; Abramowicz, H.; Abreu, H.; et al. Measurement of event-plane correlations in = 2.76 TeV lead-lead collisions with the ATLAS detector. Phys. Rev. 2014, C90, 024905. [Google Scholar] [CrossRef]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Aben, R.; Abi, B.; Abolins, M.; AbouZeid, O.S.; et al. Measurement of the correlation between flow harmonics of different order in lead-lead collisions at = 2.76 TeV with the ATLAS detector. Phys. Rev. 2015, C92, 034903. [Google Scholar] [CrossRef]
- Niemi, H.; Denicol, G.S.; Holopainen, H.; Huovinen, P. Event-by-event distributions of azimuthal asymmetries in ultrarelativistic heavy-ion collisions. Phys. Rev. 2013, C87, 054901. [Google Scholar] [CrossRef]
- Gardim, F.G.; Noronha-Hostler, J.; Luzum, M.; Grassi, F. Effects of viscosity on the mapping of initial to final state in heavy ion collisions. Phys. Rev. 2015, C91, 034902. [Google Scholar] [CrossRef]
- Fu, J. Centrality dependence of mapping the hydrodynamic response to the initial geometry in heavy-ion collisions. Phys. Rev. 2015, C92, 024904. [Google Scholar] [CrossRef]
- Holopainen, H.; Niemi, H.; Eskola, K.J. Event-by-event hydrodynamics and elliptic flow from fluctuating initial state. Phys. Rev. 2011, C83, 034901. [Google Scholar] [CrossRef]
- Qin, G.Y.; Petersen, H.; Bass, S.A.; Muller, B. Translation of collision geometry fluctuations into momentum anisotropies in relativistic heavy-ion collisions. Phys. Rev. 2010, C82, 064903. [Google Scholar] [CrossRef]
- Gale, C.; Jeon, S.; Schenke, B.; Tribedy, P.; Venugopalan, R. Event-by-event anisotropic flow in heavy-ion collisions from combined Yang-Mills and viscous fluid dynamics. Phys. Rev. Lett. 2013, 110, 012302. [Google Scholar] [CrossRef]
- Liu, P.; Lacey, R.A. Acoustic scaling of linear and mode-coupled anisotropic flow; implications for precision extraction of the specific shear viscosity. arXiv 2018, arXiv:1802.06595. [Google Scholar] [CrossRef]
- Borghini, N.; Dinh, P.M.; Ollitrault, J.Y. A New method for measuring azimuthal distributions in nucleus-nucleus collisions. Phys. Rev. 2001, C63, 054906. [Google Scholar] [CrossRef]
- Miller, M.; Snellings, R. Eccentricity fluctuations and its possible effect on elliptic flow measurements. arXiv 2003, arXiv:0312008. [Google Scholar]
- Manly, S.; Phobos, C. System size, energy and pseudorapidity dependence of directed and elliptic flow at RHIC. Nucl. Phys. 2006, A774, 523–526. [Google Scholar] [CrossRef]
- Voloshin, S.A. Toward the energy and the system size dependece of elliptic flow: Working on flow fluctuations. In Proceedings of the 22nd Winter Workshop on Nuclear Dynamics (WWND 2006), La Jolla, CA, USA, 11–19 March 2006. [Google Scholar]
- Gardim, F.G.; Grassi, F.; Hama, Y.; Luzum, M.; Ollitrault, J.Y. Directed flow at mid-rapidity in event-by-event hydrodynamics. Phys. Rev. 2011, C83, 064901. [Google Scholar] [CrossRef]
- Schenke, B.; Shen, C.; Tribedy, P. Hybrid Color Glass Condensate and hydrodynamic description of the Relativistic Heavy Ion Collider small system scan. Phys. Lett. B 2020, 803, 135322. [Google Scholar] [CrossRef]
- Werner, K. Strings, pomerons, and the venus model of hadronic interactions at ultrarelativistic energies. Phys. Rep. 1993, 232, 87–299. [Google Scholar] [CrossRef]
- Shen, C.; Schenke, B. Dynamical initial state model for relativistic heavy-ion collisions. Phys. Rev. C 2018, 97, 024907. [Google Scholar] [CrossRef]
- Akamatsu, Y.; Asakawa, M.; Hirano, T.; Kitazawa, M.; Morita, K.; Murase, K.; Nara, Y.; Nonaka, C.; Ohnishi, A. Dynamically integrated transport approach for heavy-ion collisions at high baryon density. Phys. Rev. C 2018, 98, 024909. [Google Scholar] [CrossRef]
- Mohs, J.; Ryu, S.; Elfner, H. Particle Production via Strings and Baryon Stopping within a Hadronic Transport Approach. J. Phys. G 2020, 47, 065101. [Google Scholar] [CrossRef]
- Steinheimer, J.; Mitrovski, M.; Schuster, T.; Petersen, H.; Bleicher, M.; Stoecker, H. Strangeness fluctuations and MEMO production at FAIR. Phys. Lett. B 2009, 676, 126–131. [Google Scholar] [CrossRef]
- Martinez, M.; Sievert, M.D.; Wertepny, D.E.; Noronha-Hostler, J. Initial state fluctuations of QCD conserved charges in heavy-ion collisions. arXiv 2019, arXiv:1911.10272. [Google Scholar]
- Giacalone, G.; Noronha-Hostler, J.; Ollitrault, J.Y. Relative flow fluctuations as a probe of initial state fluctuations. Phys. Rev. C 2017, 95, 054910. [Google Scholar] [CrossRef]
- Alba, P.; Mantovani Sarti, V.; Noronha, J.; Noronha-Hostler, J.; Parotto, P.; Vazquez, I.P.; Ratti, C. Effect of the QCD equation of state and strange hadronic resonances on multiparticle correlations in heavy ion collisions. arXiv 2017, arXiv:1711.05207. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Aparin, A.; Arkhipkin, D.; Aschenauer, E.C.; Averichev, G.S.; et al. Centrality and transverse momentum dependence of elliptic flow of multistrange hadrons and ϕ meson in Au+Au collisions at = 200 GeV. Phys. Rev. Lett. 2016, 116, 062301. [Google Scholar] [CrossRef] [PubMed]
- Adler, C.; Strobele, H.; Denisov, A.; Garcia, E.; Murray, M.; White, S. The RHIC zero-degree calorimeters. Nucl. Instrum. Methods 2001, A461, 337–340. [Google Scholar] [CrossRef]
- Adams, J.; Ewigleben, A.; Garrett, S.; He, W.; Huang, T.; Jacobs, P.M.; Ju, X.; Lisa, M.A.; Lomnitz, M.; Pak, R.; et al. The STAR Event Plane Detector. arXiv 2019, arXiv:1912.05243. [Google Scholar]
- Lin, Z.W.; Ko, C.M.; Li, B.A.; Zhang, B.; Pal, S. A Multi-phase transport model for relativistic heavy ion collisions. Phys. Rev. 2005, C72, 064901. [Google Scholar] [CrossRef]
- Ma, G.L.; Lin, Z.W. Predictions for = 5.02 TeV Pb+Pb Collisions from a Multi-Phase Transport Model. Phys. Rev. 2016, C93, 054911. [Google Scholar] [CrossRef]
- Ma, G.L. Decomposition of the jet fragmentation function in high-energy heavy-ion collisions. Phys. Rev. 2013, C88, 021902. [Google Scholar] [CrossRef]
- Ma, G.L. Medium modifications of jet shapes in Pb+Pb collisions at = 2.76 TeV within a multiphase transport model. Phys. Rev. 2014, C89, 024902. [Google Scholar] [CrossRef]
- Bzdak, A.; Ma, G.L. Elliptic and triangular flow in p+Pb and peripheral Pb+Pb collisions from parton scatterings. Phys. Rev. Lett. 2014, 113, 252301. [Google Scholar] [CrossRef]
- Nie, M.W.; Huo, P.; Jia, J.; Ma, G.L. Multiparticle azimuthal cumulants in p+Pb collisions from a multiphase transport model. Phys. Rev. 2018, C98, 034903. [Google Scholar] [CrossRef]
- Magdy, N.; Nie, M.W.; Huang, L.; Ma, G.L.; Lacey, R. An extended (ΔS2) correlator for detecting and characterizing the Chiral Magnetic Wave. arXiv 2020, arXiv:2003.02396. [Google Scholar]
- Wang, X.N.; Gyulassy, M. HIJING: A Monte Carlo model for multiple jet production in p p, p A and A A collisions. Phys. Rev. 1991, D44, 3501–3516. [Google Scholar] [CrossRef]
- Zhang, B. ZPC 1.0.1: A Parton cascade for ultrarelativistic heavy ion collisions. Comput. Phys. Commun. 1998, 109, 193–206. [Google Scholar] [CrossRef]
- Li, B.A.; Ko, C.M. Formation of superdense hadronic matter in high-energy heavy ion collisions. Phys. Rev. 1995, C52, 2037–2063. [Google Scholar] [CrossRef] [PubMed]
- Bilandzic, A.; Snellings, R.; Voloshin, S. Flow analysis with cumulants: Direct calculations. Phys. Rev. 2011, C83, 044913. [Google Scholar] [CrossRef]
- Bilandzic, A.; Christensen, C.H.; Gulbrandsen, K.; Hansen, A.; Zhou, Y. Generic framework for anisotropic flow analyses with multiparticle azimuthal correlations. Phys. Rev. 2014, C89, 064904. [Google Scholar] [CrossRef]
- Jia, J.; Zhou, M.; Trzupek, A. Revealing long-range multiparticle collectivity in small collision systems via subevent cumulants. Phys. Rev. 2017, C96, 034906. [Google Scholar] [CrossRef]
- Gajdošová, K. Investigations of anisotropic collectivity using multi-particle correlations in pp, p–Pb and Pb–Pb collisions. Nucl. Phys. 2017, A967, 437–440. [Google Scholar] [CrossRef]
- Snellings, R. Elliptic Flow: A Brief Review. New J. Phys. 2011, 13, 055008. [Google Scholar] [CrossRef]
- Voloshin, S.A.; Poskanzer, A.M.; Tang, A.; Wang, G. Elliptic flow in the Gaussian model of eccentricity fluctuations. Phys. Lett. 2008, B659, 537–541. [Google Scholar] [CrossRef]
- Wang, G. Anisotropic flow in Au Au and Cu Cu at 62-GeV and 200-GeV. Nucl. Phys. A 2006, 774, 515–518. [Google Scholar] [CrossRef][Green Version]
- Ma, L.; Ma, G.; Ma, Y. Anisotropic flow and flow fluctuations for Au + Au at = 200 GeV in a multiphase transport model. Phys. Rev. C 2014, 89, 044907. [Google Scholar] [CrossRef]
- Ma, G.L.; Bzdak, A. Long-range azimuthal correlations in proton–proton and proton–nucleus collisions from the incoherent scattering of partons. Phys. Lett. B 2014, 739, 209–213. [Google Scholar] [CrossRef]
- Singha, S.; Nasim, M. Scaling of elliptic flow in heavy-ion collisions with the number of constituent quarks in a transport model. Phys. Rev. C 2016, 93, 034908. [Google Scholar] [CrossRef]
- Nayak, K.; Singha, S.; Nasim, M.; Mohanty, B. Study of re-scattering effect on elliptic flow and production of resonances using AMPT. DAE Symp. Nucl. Phys. 2017, 62, 962–963. [Google Scholar]
- Magdy, N. Collision System Dependence of Anisotropic Flow, Flow Fluctuations and Mixed Harmonic Correlations at STAR Energies; Quark Matter; Quark Matter; Stony Brook University: Stony Brook, NY, USA, 2018. [Google Scholar]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magdy, N.; Sun, X.; Ye, Z.; Evdokimov, O.; Lacey, R. Investigation of the Elliptic Flow Fluctuations of the Identified Particles Using the a Multi-Phase Transport Model. Universe 2020, 6, 146. https://doi.org/10.3390/universe6090146
Magdy N, Sun X, Ye Z, Evdokimov O, Lacey R. Investigation of the Elliptic Flow Fluctuations of the Identified Particles Using the a Multi-Phase Transport Model. Universe. 2020; 6(9):146. https://doi.org/10.3390/universe6090146
Chicago/Turabian StyleMagdy, Niseem, Xu Sun, Zhenyu Ye, Olga Evdokimov, and Roy Lacey. 2020. "Investigation of the Elliptic Flow Fluctuations of the Identified Particles Using the a Multi-Phase Transport Model" Universe 6, no. 9: 146. https://doi.org/10.3390/universe6090146
APA StyleMagdy, N., Sun, X., Ye, Z., Evdokimov, O., & Lacey, R. (2020). Investigation of the Elliptic Flow Fluctuations of the Identified Particles Using the a Multi-Phase Transport Model. Universe, 6(9), 146. https://doi.org/10.3390/universe6090146





