1. Introduction
Neutrinos are currently the most elusive known particles, even though during the last decades we have painfully started to know them better by means of bigger and bigger experiments with increased sensitivity [
1,
2,
3,
4]. However, several paramount questions about their intrinsic nature are still open and in need of clear answers in order to shed some light on their peculiarities like the absolute masses, the mass hierarchy, their intrinsic nature of Majorana or Dirac particles [
5,
6,
7,
8,
9,
10,
11,
12,
13]. The discovery of the Neutrinoless Double-Beta Decay (NDBD) would demonstrate that neutrinos are Majorana particles, i.e., each neutrino being its own antiparticle, with relevant consequences on the understanding of the universe [
13,
14,
15]. An important ingredient of the NDBD is the so-called Nuclear Matrix Element (NME), which links the states of the decaying nucleus before and after the decay and enters the expression of the half-life
T1/2 of the NDBD, thus possibly providing a handle on the Majorana effective neutrino mass determination. Indeed, the NDBD decay rate can be expressed as a factorization of three terms: the phase-space factor
G0
ν, the NME
M0
ν, and the term
f (mi, Uei, ξi) containing a combination of the masses
mi, the mixing coefficients
Uei, and the Majorana phases ξ
i of the neutrino species
M0
ν represents the transition amplitude from the initial state
to the final state
by means of the NDBD operator
ONDBD From Equation (1), one can deduce that if the NMEs are established with sufficient precision, the neutrino masses and the mixing coefficients can be extracted from NDBD decay rate measurements. Thus, the determination of the NDBD NMEs is of crucial importance for physics beyond the standard model. The evaluation of the NMEs is presently limited to state-of-the-art model calculations based on different methods (QRPA, shell model, IBM, EDF, etc.). However, the ambiguities in the models are still too large and the constraints too loose to reach accurate values of the NMEs. This is basically because the determination of the NMEs requires the knowledge of the many-body nuclear wave functions. Discrepancy larger than a factor of two between the different models are presently reported in literature.
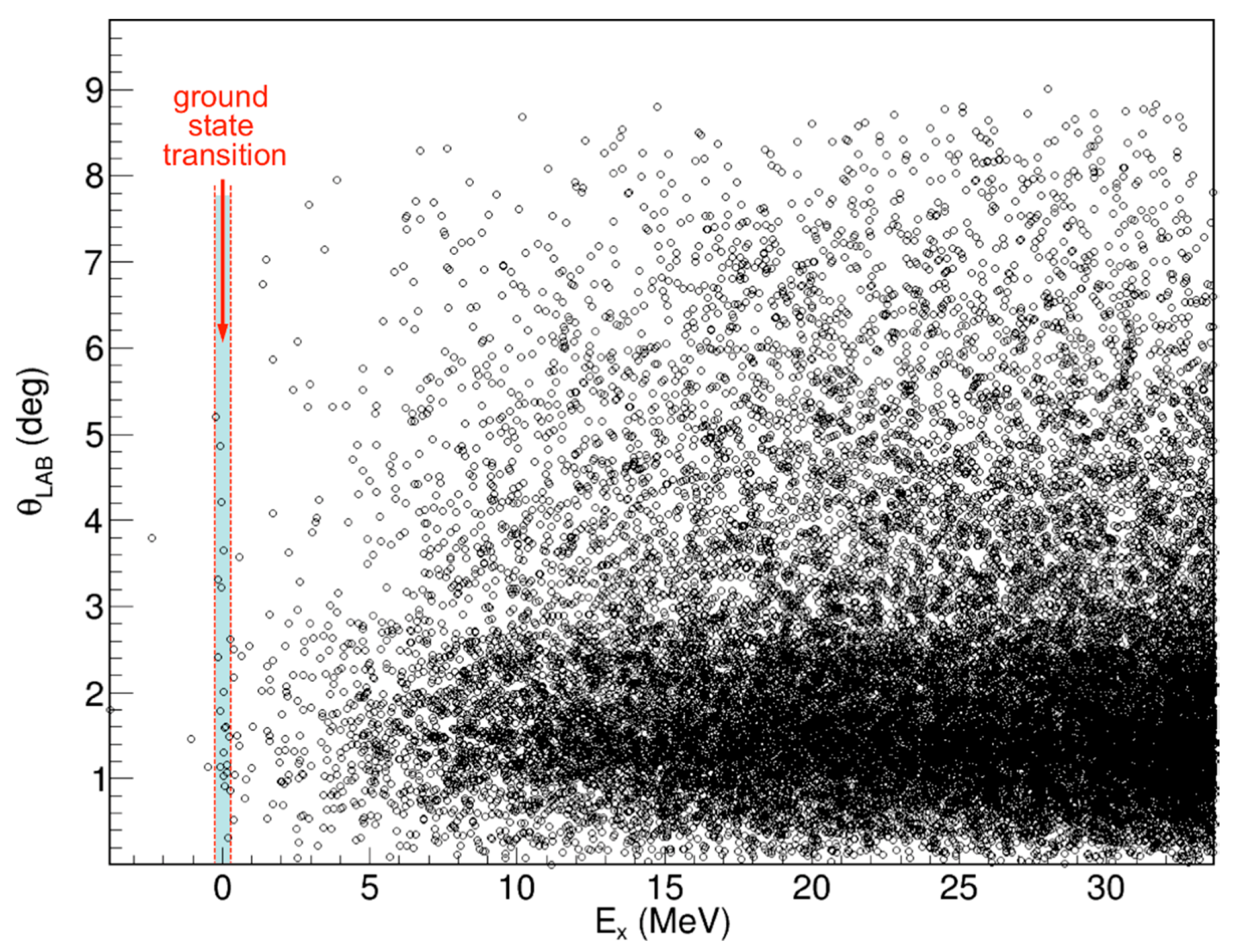
In this framework, the experimental study of different nuclear transitions where the nuclear charge is changed by two units leaving the mass number unvaried, i.e., where the nuclear wave functions involved are the same as in NDBD, could provide relevant information. NUMEN proposes an innovative technique to access information about the NME, by measuring the differential cross section of heavy-ion induced Double Charge Exchange (DCE) reactions, which is basically proportional to the square of the NME. The two processes are characterized by a number of similarities (same initial and final nuclear wave functions, similar mathematical structure of the involved transition operators and other similarities), provided that the transition occurs from ground state to ground state, as reported in detail in [
16].
The main goal of NUMEN is to establish an alternative experimental path to the determination of NDBD NMEs. A campaign of measurements to assess the behavior of the NMEs will be done on different nuclear systems with variable kinetic energy of the projectile.
From the theoretical standpoint, the reaction mechanism can be expressed as the product of three factors, respectively related to the reaction and to the nuclear structure, this last term being the product of projectile and target matrix elements. A microscopic description of the DCE reaction is currently being developed: the nuclear structure part makes use of the Distorted Wave Born Approximation (DWBA), or of Coupled Reaction Channel (CRC) cross sections, in which the reaction part is described in a full quantum scattering picture.
From the experimental standpoint, a systematic set of data will have to face the challenges of the low cross sections and the subsequent requirements of high sensitivity and resolution, in order to pick out the DCE signal in the huge background. The measurement of DCE cross sections foreseen in NUMEN could provide a significant input to the nuclear structure theories of NDBD.
Moreover, NUMEN can provide useful information on the relative weight of the NMEs between different candidate isotopes of interest for the NDBD; indeed, the ratio between the measured cross sections is probably a model-independent way to compare the sensitivity of half-life experiments to different candidate nuclei. This is likely true also in the presence of large systematic uncertainties in the measured cross sections and, consequently, in the DCE matrix elements, as such uncertainties would be mostly cancelled in the ratio. Such a comparative analysis may affect the future experimental developments in the field, possibly driving the choice of the best isotope candidates for NDBD.
Preliminary experimental results obtained at INFN-LNS for the
40Ca(
18O,
18Ne)
40Ar reaction, where
18O projectiles at 270 MeV kinetic energy impinge on a
40Ca target, the
18Ne ejectiles are detected and the
40Ar residuals go undetected, provided an encouraging indication on the capability of the proposed technique to access relevant quantitative information by selecting a zero missing mass in the output channel [
16]. Indeed, if the ejectile is identified and its emission angle and energy are measured, the kinematics are completely determined. A detailed description of the NUMEN physics can be found in [
17,
18,
19] and in a dedicated article in this same issue.
The basic tools needed for the NUMEN experiments are the K800 Superconducting Cyclotron and the MAGNEX spectrometer [
20,
21]. The accelerator has to provide the required heavy-ion beams with excellent energy resolution and low emittance, whereas the large acceptance magnetic spectrometer is essential for the detection, identification, selection, and measurement of the ejectiles. MAGNEX relies on a high-order trajectory reconstruction technique, which makes it possible to reach the experimental resolution and sensitivity necessary for the challenging measurement at forward angles of the DCE cross sections. Unfortunately, the tiny values of such cross sections demand beam intensities much higher than those manageable with the present facility.
The ambitious goal of providing accurate values of the Nuclear Matrix Elements to the neutrino community requires the overcoming of two main limits, i.e., the maximum beam intensity deliverable by the accelerator and the maximum counting rate of the detectors associated with the MAGNEX spectrometer. This gave rise to the POTLNS project, aimed at a challenging upgrade of the LNS cyclotron and at the design and construction of new high-performance detection system for MAGNEX. The project, starting in the second half of 2020, was approved and funded in the frame of a national program aimed at strengthening the research infrastructures identified as priorities, according to the European Strategy Forum on Research Infrastructures (ESFRI).
The tiny cross sections to be measured, even down to few nb, and the consequently needed high beam intensity require very high performance for the whole experimental apparatus. On the one hand, it has to be capable of catching high-resolution data in a stifling rate of nuclear reaction products; on the other hand, it has to respect severe physical and mechanical constraints still withstanding the very high neutron and gamma radiation fields. Moreover, for some of the nuclear systems to be explored by the NUMEN project, the typical energy resolution of MAGNEX with beams provided by the cyclotron is not sufficient to discriminate between the ground state and the first excited states [
16]. In such cases, a gamma detector array will be coupled to the magnetic spectrometer to provide the required discrimination between nearby energy states. Designing and building the experimental setup required by NUMEN represents a technological challenge, from the target to the scattering chamber, from the detection systems to the electronics and the radiation shielding.
2. Materials and Methods
Ideally, the DCE reactions to be studied are quite simple: one sends a beam of a suitable nuclear species, typically 18O or 20Ne, on a target made of a NDBD candidate nuclear species, namely one among 48Ca, 76Ge, 76Se, 82Se, 96Zr, 100Mo, 106Cd, 110Pd, 116Cd, 110Sn, 124Sn, 128Te, 130Te, 136Xe, 130Xe, 148Nd, 150Nd, 154Sm, 160Gd, 198Pt. Oxygen and neon were chosen as the most suitable projectiles because they are the lightest even-even stable nuclei with a reasonably high DCE cross section due to super-allowed transitions. Moreover, the requirement of employing very thin targets to preserve the needed energy resolution, as will be discussed later, imposes to employ as light as possible projectiles. The reaction of interest changes two neutrons into two protons in the projectile, and consequently, two protons into two neutrons in the target, or vice versa. Moreover, the reaction must proceed by leaving both projectile and target in their ground or excited states. Such a small energy exchange implies that the reaction must be very peripheral; thus, the scattered projectile comes out at very forward angles with a quite small cross section down to a few nb. In order to disentangle the reactions of interest from the overwhelming amount of forward-going ions produced by all the other nuclear reactions, the solution is to use a high resolution and large acceptance magnetic spectrometer, capable of selecting outcoming particles in a very small range of kinetic energy, mass, and charge, while deflecting away all the rest, i.e., MAGNEX. However, this is not enough due to the tiny cross sections involved, in most cases one needs to increase the reaction rate. This cannot be done by increasing the target thickness, as it would produce an energy degradation of the projectile and of the outcoming product. A thick target would prevent the correct measurement of the energy balance of the reaction and the identification in mass and charge of the detected product due to the mix-up of the expected trajectories inside the magnet. Therefore, the only solution is to increase the beam intensity. An additional complication is due to the need of rotating the whole spectrometer in order to choose its most convenient angular arrangement around zero degrees with respect to the beam direction, in order to cover for each particular reaction most of the useful solid angle.
Notwithstanding the strong magnetic selection, the expected output particle rate from the spectrometer is of the order of 5 × 106 particles per second (pps), distributed over an area of 100 × 15 cm, which requires the setting up of a challenging detection system capable of measuring for each detected particle its position, impinging direction, energy, mass, charge. In addition, in many cases one would also need to measure a gamma ray in coincidence, as a signature of a DCE reaction proceeding through the first or second excited level of the projectile or the target, which is yet a more challenging issue.
In the following the overall framework will be shortly described, consisting of the cyclotron upgrade and the MAGNEX spectrometer, followed by a more detailed description of the setup and of the heavy ion multidetector, currently being developed, consisting of a gas tracker and a Particle Identification Detector (PID) in the focal plane, which together constitute the Focal Plane Detector (FPD) and a Gamma Detector Array (GDA) around the target. For better clarity, the description has been divided into several sections, each one dedicated to a subsystem.
2.1. The Cyclotron Upgrade
The LNS Superconducting Cyclotron is a three-sector compact accelerator. Two pairs of superconducting coils allow to produce a magnetic field tunable between 2.2 and 4.8 T on the mid-plane. Twenty trim coils, wound on each of the six sectors (120 in total), allow to achieve the isochronous magnetic field requested for the acceleration of all the ions, from the singly ionized molecular hydrogen up to uranium, in a wide range of energies, between 10 and 80 MeV/amu [
22]. As a consequence of the cyclotron compactness, the orbit separation at the outer turns is small. This limits the extraction efficiency, which is of 50–60%. Most of the accelerated beam is stopped by the septum of the first electrostatic deflector, and despite being water-cooled, serious thermal issues occur when the extracted power exceeds 100 W. The NUMEN experiment plans to use mainly beams of oxygen and neon with intensity up to 10
13 pps. The required energies are in the range 15–60 MeV/amu, and the beam power in the range 1–10 kW. Therefore, the extraction of 1–10 kW beams is not feasible using electrostatic deflection. Moreover, the existing extraction channel has small transversal size and no thermal shields to dissipate the beam power coming from beam halos. This is why the cyclotron is going to be upgraded, modifying its magnetic configuration and designing a new channel for the extraction by stripping [
23,
24,
25,
26].
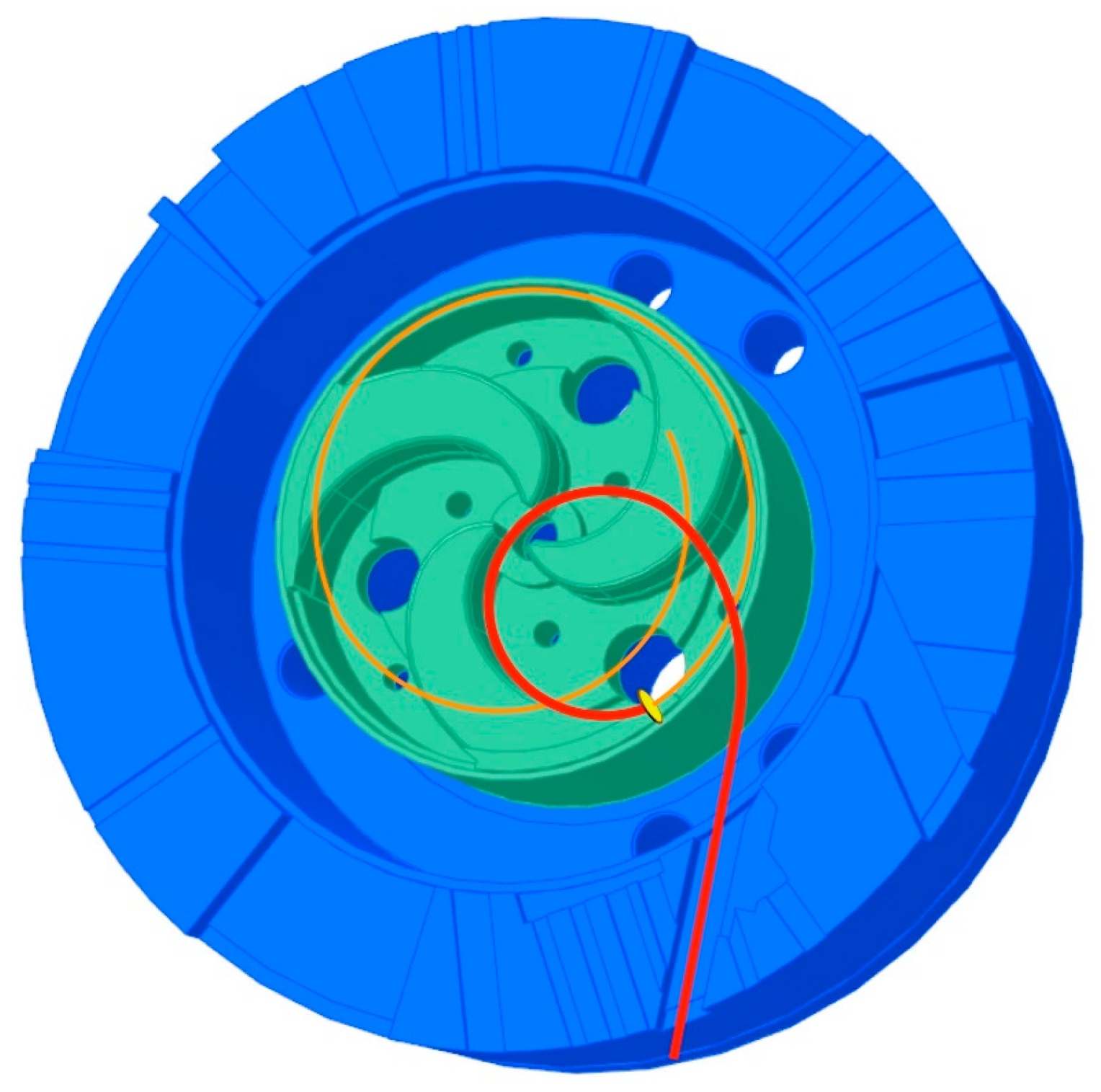
In such a scheme the ions are initially accelerated with a charge state q between (Z-2) and (Z-5). Then, after crossing a stripper foil suitably placed near the maximum radius of the machine, they become fully stripped. The curvature radius of their trajectory becomes abruptly smaller and it runs through the cyclotron pole toward a suitable extraction channel (
Figure 1). Using this technique, all the ions of interest, with mass number A ≤ 40 and energy E ≥ 15 MeV/amu, can be fully stripped with efficiency higher than 99% [
27] and beams can be efficiently accelerated at the desired intensity. In
Figure 1 a pictorial sketch is shown of the inner part of the upgraded cyclotron, with an example of trajectory for an accelerated ion before and after being stripped and extracted.
2.2. The MAGNEX Spectrometer
MAGNEX is a large acceptance magnetic device consisting of a large aperture vertically focusing quadrupole and a horizontally bending dipole magnet. It allows the identification of heavy ions with quite high mass (ΔA/A ≈ 1/160), angular (Δθ ≈ 0.2°) and energy resolution (ΔE/E ≈ 1/1000), within a large solid angle (Ω ≈ 50 msr) and momentum range (−14% < Δ
p/
p < +10%) [
28,
29]. High-resolution measurements for quasi-elastic processes, characterized by differential cross sections falling down to tens of nb/sr, were already performed by this setup [
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42]. A crucial feature is the implementation of a technique of trajectory reconstruction, based on differential algebraic methods, which make possible the solving of the equation of motion of each detected particle to the 10th order [
28,
29].
Figure 2 shows a global view of the MAGNEX spectrometer in the current configuration, whereas
Figure 3 is a 3D representation of the NUMEN multidetector to be installed on the MAGNEX spectrometer, with the new scattering chamber, the gamma detector array, the input quadrupole, the dipole magnet, the focal plane gas tracker detector, and the particle identification detector.
2.3. Target, Cooling System, and Robotic Handling
The main constraints in the design of the NUMEN targets come from:
The heat deposited by the beam in the target;
The energy resolution of the DCE reaction products;
The required compactness of the whole target/cooling system.
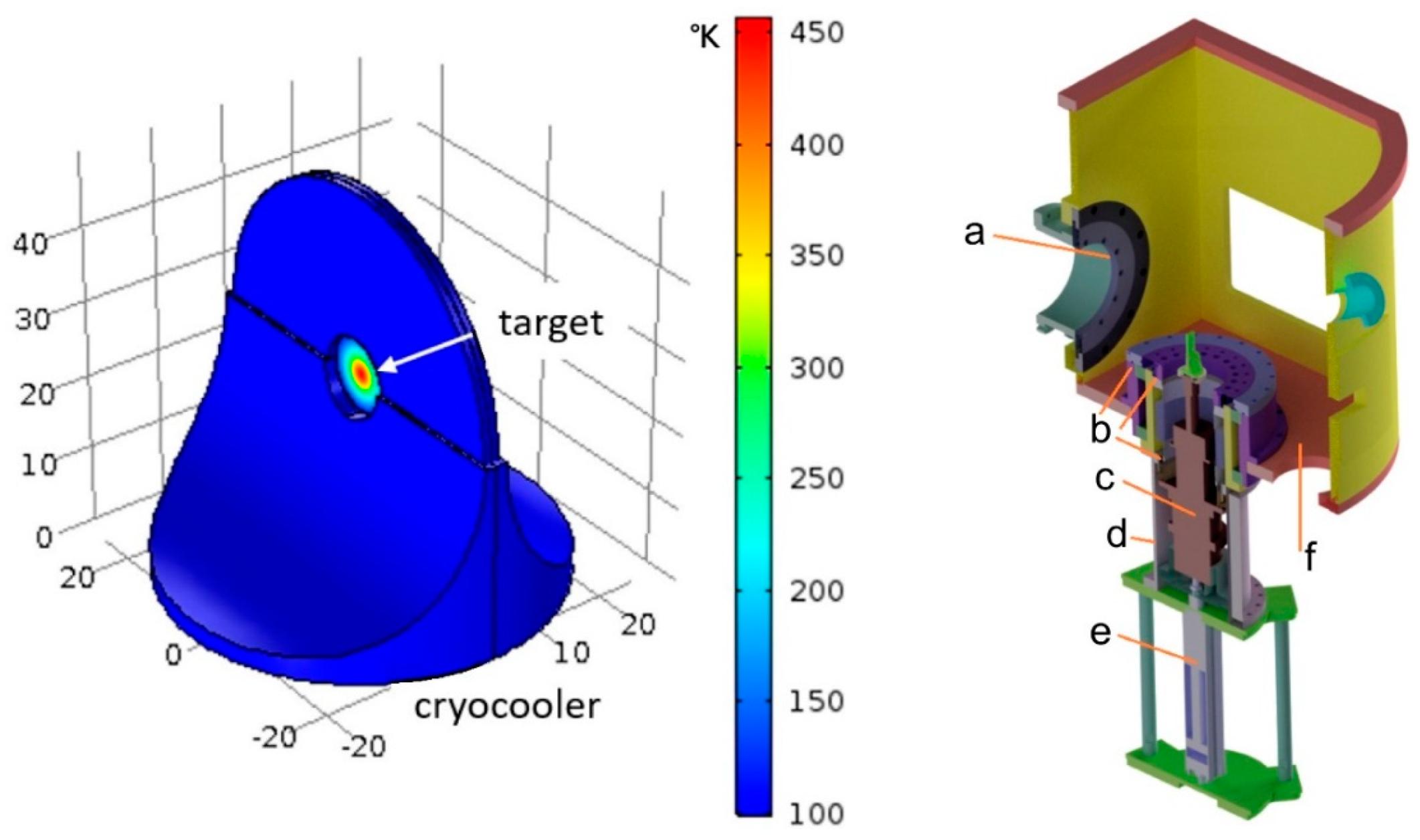
The first issue is related to the very intense heavy-ion beams to be employed. It is planned to use 18O and 20Ne beams with an intensity up to 60 μA, with energies ranging from 15 to 60 MeV/amu. Assuming a gaussian beam spot with a standard deviation of 1 mm, the highest deposited power density in the target will be of the order of 105 W/cm3 for the lowest beam energy (2 to 3 W deposited in a 400-nm thick target). This amount of power would inevitably melt the target material. To prevent such a damage, a dedicated cooling system has been designed.
As for the energy resolution, the kinematics of the DCE reactions will be reconstructed from the energy and scattering angle of the reaction products measured with the MAGNEX spectrometer. In order to disentangle the transitions to the ground state from those to the first excited state of one or both the participant nuclei, the energy resolution should be lower than the energy difference between the two states, usually in the order of 500 keV. In order to attain such a resolution, the targets must be thin (a fraction of a µm) and uniform. Finally, the target system must be as compact as possible, as well as the scattering chamber, thus minimizing the distance between the target itself and the gamma ray calorimeter installed outside on top of the chamber (described in a following section). The first isotopes that have been considered for the target production process are 116Sn, 76Ge, 130Te, chosen as result of a trade-off between scientific priority and technical feasibility, i.e., between the energy resolution and the availability of isotopically enriched material.
Thermal radiation alone is not sufficient to cool down the target, and analytical calculations showed that simply clamping the target with a cold frame does not guarantee its integrity [
43,
44,
45]. The heat dissipation can be enhanced by depositing the target material onto a highly thermally conductive thin substrate. The choice fell on Highly Oriented Pyrolytic Graphite (HOPG), an artificial graphite made by a stack of graphene layers with parallel orientation, which can be produced in thin foils at room temperature. It has an in-plane thermal conductivity of 1950 Wm
−1K
−1, while the transverse conductivity is about 6 Wm
−1K
−1. Thanks to the very high in-plane conductivity, heat can quickly flow from the hot beam spot to a cold frame clamping the HOPG substrate and cooled by a dedicated cryorefrigerator (
Figure 4). The thin target isotope, typically 400 to 800 nm thickness and 1 cm diameter, will be deposited on a 5-cm diameter and <5-µm thick substrate.
Due to the huge activation following a beam session, the target cannot be handled for quite some time, nor can an operator get close to the scattering chamber. This is why a robotic system was designed for insertion, removal, and replacement of the target [
46].
Figure 5 shows the 3D drawing of the robotic arm clamping a target, along with the details of the target hosted on the cold finger of the cryocooler.
Figure 6 shows the 3D drawing of the robotic arm while extracting a target through the suitable vacuum valve, and then placing it on the target parking rack outside the chamber.
2.4. Focal Plane: The Gas Tracker
The FPD tracker requires a good resolution of the phase space parameters at the focal plane (X
foc, Y
foc, θ
foc, φ
foc), respectively the XY transverse coordinates and the horizontal and vertical angles of the trajectory. Indeed the precise and accurate particle trajectory reconstruction is fundamental for the determination of the momentum vector at the target position [
28,
29,
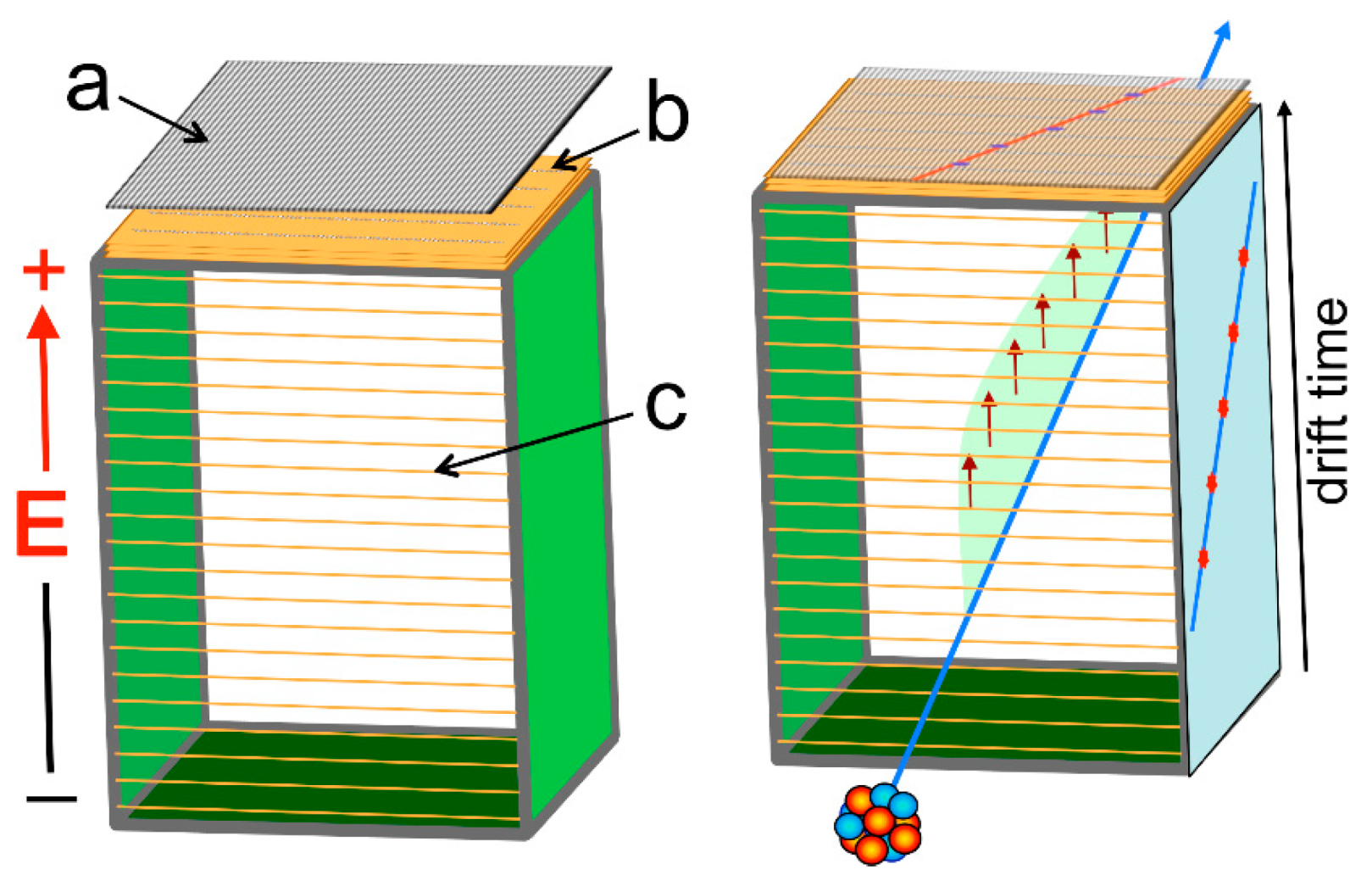
47], which in turn is needed for the particle identification with MAGNEX. Therefore, the particle identification and discrimination are strongly affected by the resolution of the mentioned parameters. Moreover, the FPD must be capable of operating at high speed due to the expected rate of ≈50 kHz/cm following the accelerator upgrade. The structure of the tracker consists of:
a thin entrance window made of mylar;
a vertical drift region, polarized with a bottom-up direction uniform electric field, that is the active volume of the detector, which is crossed by the ejectiles of interest;
an electron multiplication stage, consisting of three layers of Micro-Pattern Gas Detectors (MPGD) in the multiple thick-GEM (M-THGEM) configuration [
48], each one being an insulator plane between two conductor layers with a large number of microscopic holes; close to the holes, the electric field can be very high, thus funneling the arriving electrons and triggering their avalanche multiplication;
a segmented multistrip read-out electrode.
The incident charged particles exiting the MAGNEX dipole cross the thin mylar window, whose thickness is typically chosen between 1.5 and 6 μm according to the beam type and energy. They leave a track of ionized atoms and electrons in the low-pressure gas between the cathode and the electron multiplication stage. Under the uniform electric field, the electrons drift with constant velocity toward the MPGD. As soon as reaching the multiplication element, electrons are conveyed into the holes by the strong electric field. The produced electron avalanches reach the segmented read-out electrode, where the projection of the particle trajectory on the horizontal plane is reconstructed.
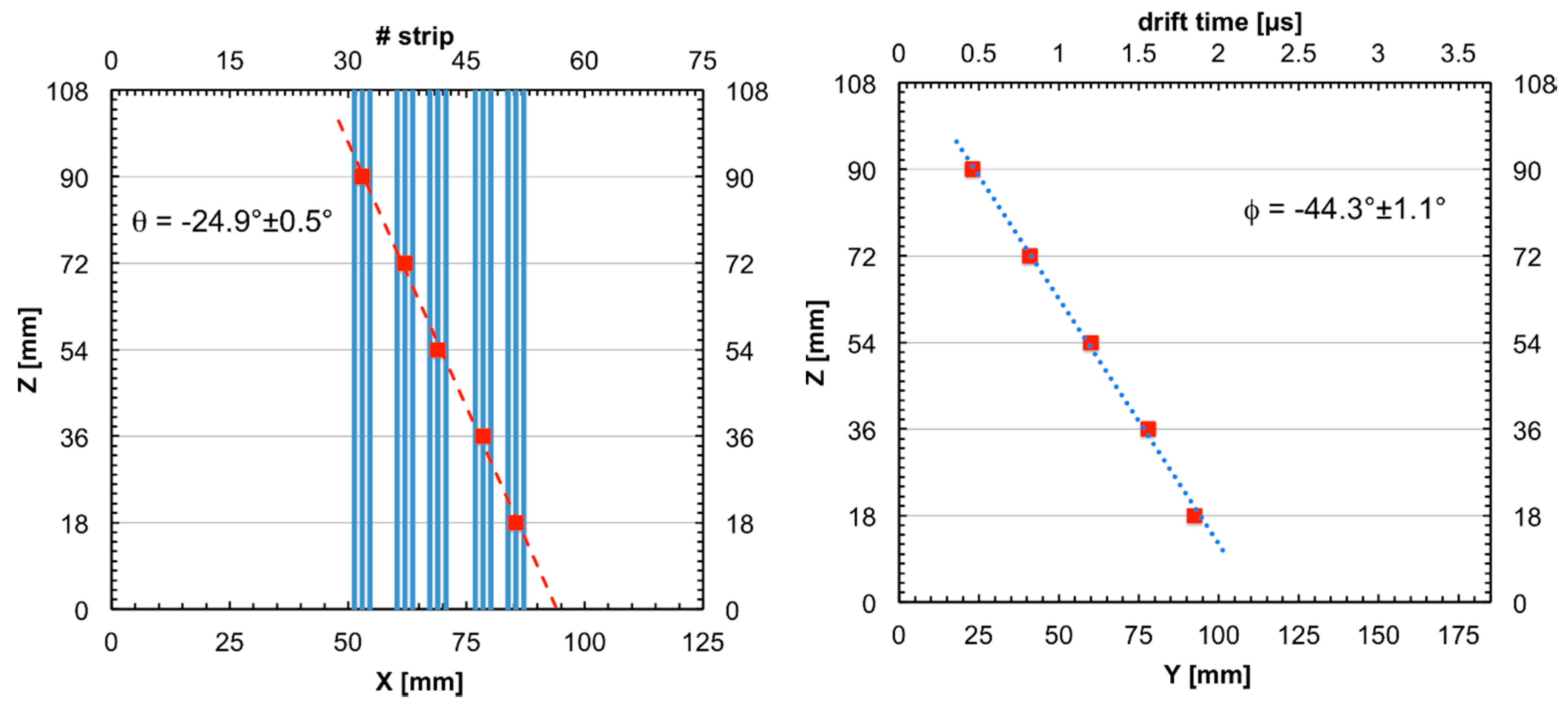
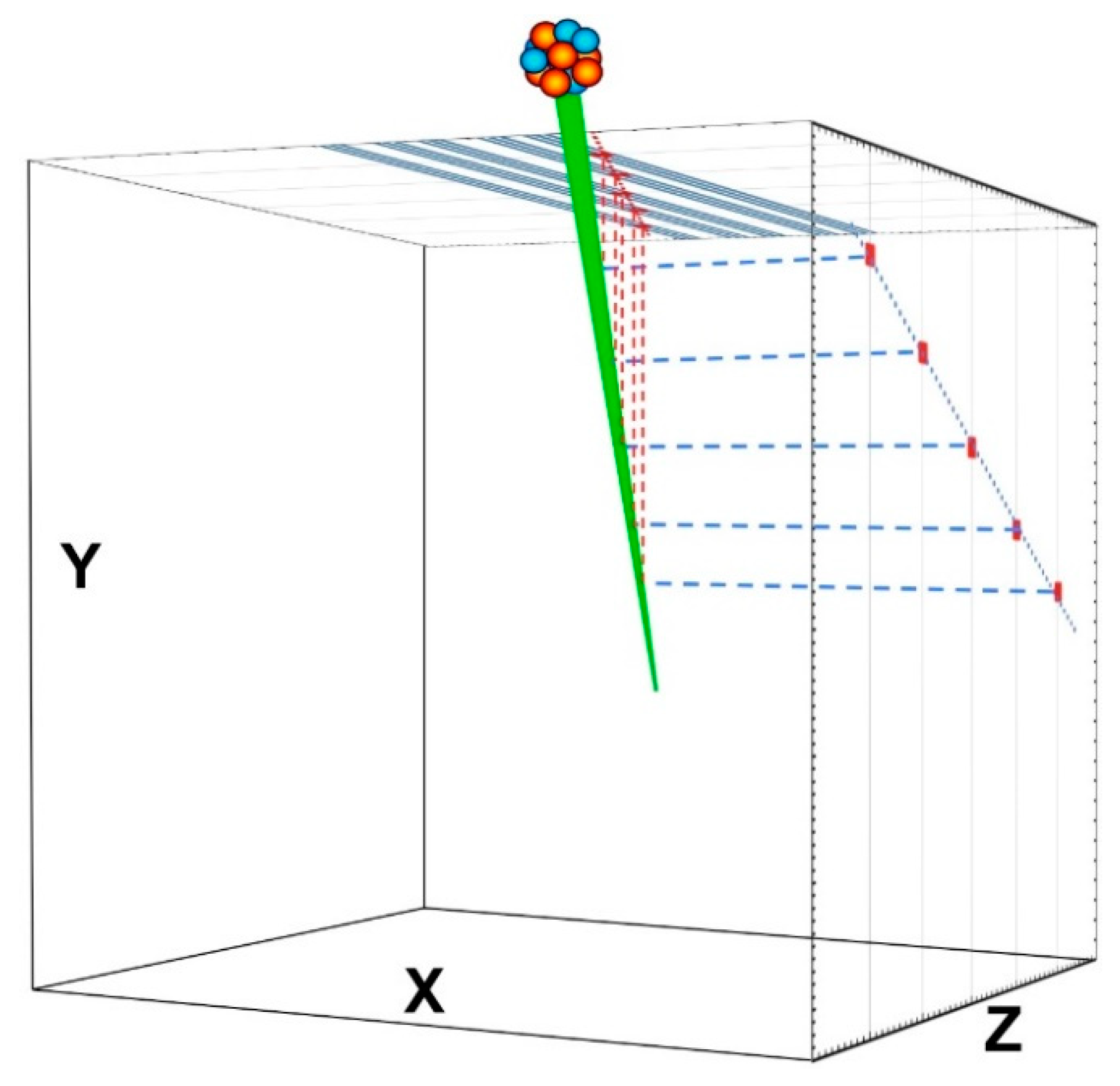
By also measuring the drift time of the electrons in the gas, one can reconstruct the projection of the trajectory on the vertical plane. From the two projections, the full track of the ion can be reconstructed (i.e., XY impact point coordinates and incidence angle at the focal plane). However, in order to minimize the number of parameters to be acquired, as well as the corresponding electronic channels, the three MPGD planes only contain five spaced rows of holes (
Figure 7), and the segmented read-out electrode consists of a set of finely spaced strips orthogonal to these rows. This way, each particle track produces five points on the XZ plane and five on the YZ plane, whose linear fits give rise to the desired quantities. The operating principle is illustrated in
Figure 8.
The tracker has an active volume of 1122 × 185 × 108 mm
3 and is made of eight modules joined together. One of these modules has been used as prototype for testing purposes, and the test results will be described in detail in the Results section (
Figure 9). This prototype, with mechanical and electrical features very similar to the final FPD but only being smaller in the horizontal direction, allowed easier tests in a smaller chamber. The applied voltages, the gas pressure and flowing system, the multiplication technology, and the front-end and read-out electronics are among the main features tested with the smaller size prototype.
The drift region, which extends vertically for 18 cm, is delimited by the cathode on the bottom and the MPGD multiplication stage on top, and was designed to produce a uniform electric field of about 50 V/cm. The left and right sides of the field cage are made of printed circuit boards, whereas the front and back are double rows of gold-plated tungsten wires, 50-μm thick, connecting the two lateral walls and arranged in steps of 5 mm. Electrostatic simulations based on the Poisson Superfish code [
49] have been performed in order to model and design the field cage in the drift region, taking into account the presence of a much stronger electric field in the electron multiplication region (MPGD + anode strips) of the mylar entrance window at ground potential and of high voltage PID-wall elements (see later) very close to the drift region on its exit side. With such a simulation, the static electric field in the detector geometry was calculated by iteratively solving the field equations, minimizing the possible perturbations of the uniform drift field.
The chosen gas is pure isobutane (C4H10), which is also a quencher and is excellent for operations with heavy ions at low pressure, even though the use of different gas mixtures is not excluded in the future. The operational pressure is in the range 10–100 mbar, to be set depending on the different experimental conditions (ions of interest and their kinetic energy). Isobutane features a high drift velocity, which is in the saturated regime with the chosen electrical field and pressure values.
The intrinsic rate capability of the M-THGEM is higher than 10
6 Hz/mm
2, much higher than needed for NUMEN, with a sub-millimeter spatial resolution and few ns time resolution (see [
50] and references therein). The electron multiplication process occurs by means of an avalanche within the holes along the successive multiplication stages, under the action of the strong electric fields resulting from the application of suitable voltages between the electrodes. The intrinsically robust confinement of the avalanche volume within the M-THGEM holes provides an efficient reduction of the photon-induced secondary effects, resulting in a high-gain capability over a broad pressure range, including low pressure operation. An ad hoc M-THGEM was developed for the NUMEN tracker, with the holes arranged in five equidistant rows orthogonal to the strips on the readout board.
2.5. Focal Plane: The Particle Identification Detector
The gas tracker does not provide accurate information on the ion energy loss, thus the particle identification for NUMEN is demanded to a dedicated wall of telescope detectors downstream from the tracker. It must allow the unambiguous identification of atomic species and their isotopes in the region of O, F, and Ne. The most relevant aspects considered in the design of such detection system are related to:
The radiation hardness, since the expected overall heavy-ion fluency will be of the order of 1011 ions/(cm2·yr).
The energy resolution ΔE/E, which must be better than ≈2%, in order to provide identification of atomic number and mass of the same quality as in the present configuration (ΔZ/Z ≈ 1/48 and ΔA/A ≈ 1/160 [
28,
29]) or at least to allow an unambiguous identification of the ejectiles of interest, characterized by an atomic number Z ≈ 10 and mass number A ≈ 20. The energy resolution has to be good enough to attain sufficient sensitivity in the cross-section measurements, which is limited by the spurious events falling inside the identification graphical cuts.
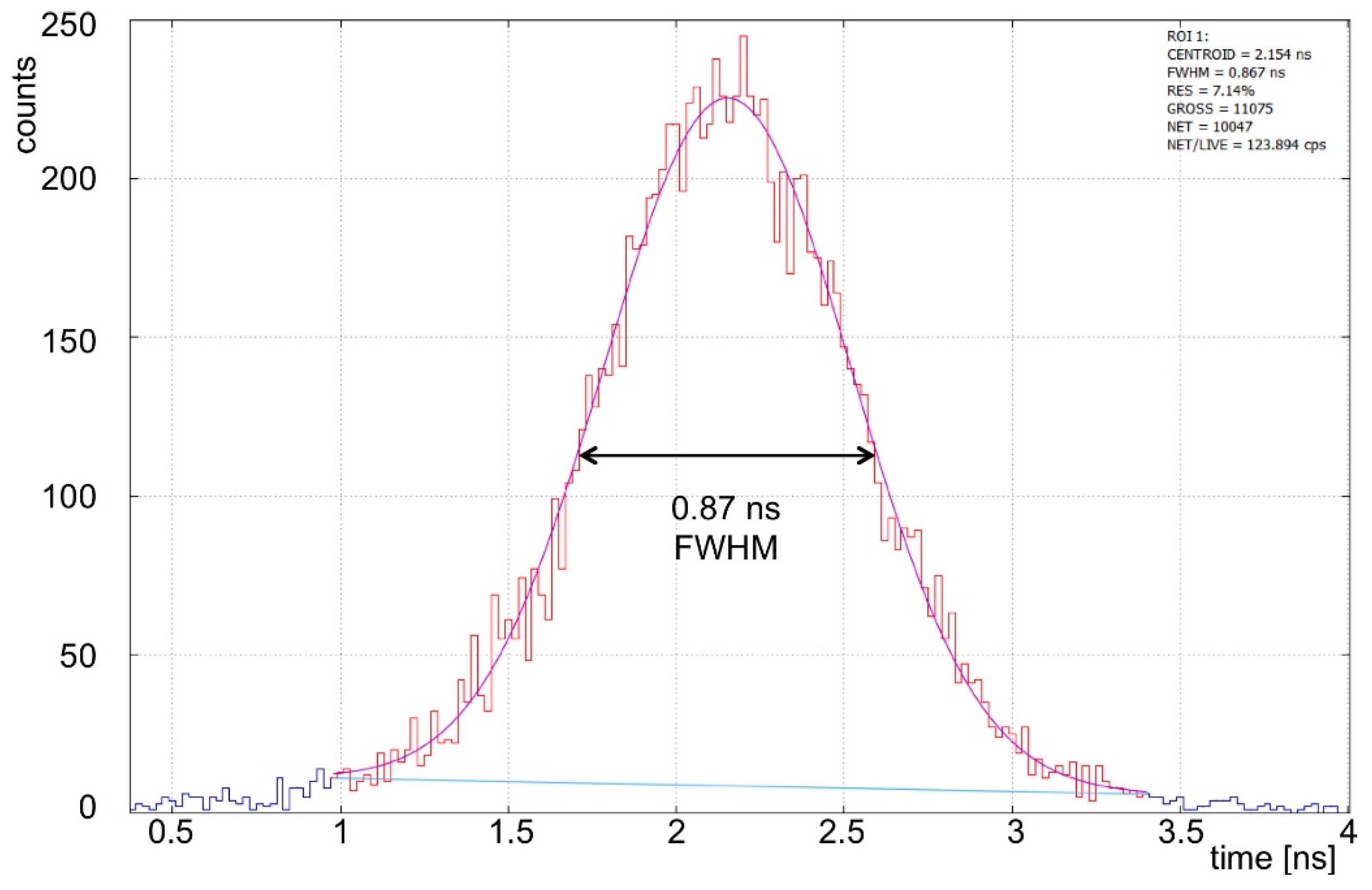
The time resolution in the measurement of Time Of Flight (TOF) of the ejectiles from the target to the focal plane and of the drift time of primary electrons in the gas tracker. A TOF measurement with resolution better than 2–3 ns [
32] is necessary to effectively suppress the background in the coincidence events with the Gamma Detector Array (see later). As seen before, the drift time is required to reconstruct the YZ projection of the tracks, and a time resolution of the order of 5 ns is needed [
51].
The degree of segmentation needed in order to keep the double-hit probability below 3% requires elementary detection cells not larger than 1.5 × 1.5 cm2.
The scalability, so that a large number of detectors can be built, assembled and managed at a reasonable cost also in terms of time required for the calibration procedures and data analysis.
The physical coupling with the tracker, which requires that the PID wall work in a low-pressure gas environment, where the presence of high voltages is also to be considered.
Several nuclear physics experiments [
52,
53,
54] have adopted the telescope solution to identify and study reaction products. It consists of two detectors chosen and assembled in order for the particles of interest to cross the first one and stop into the second one. The correlation between the energy ΔE lost in the thin detector and the residual energy E
r deposited in the stopping one is a function of the atomic number Z of the detected ion through the Bethe-Bloch formula [
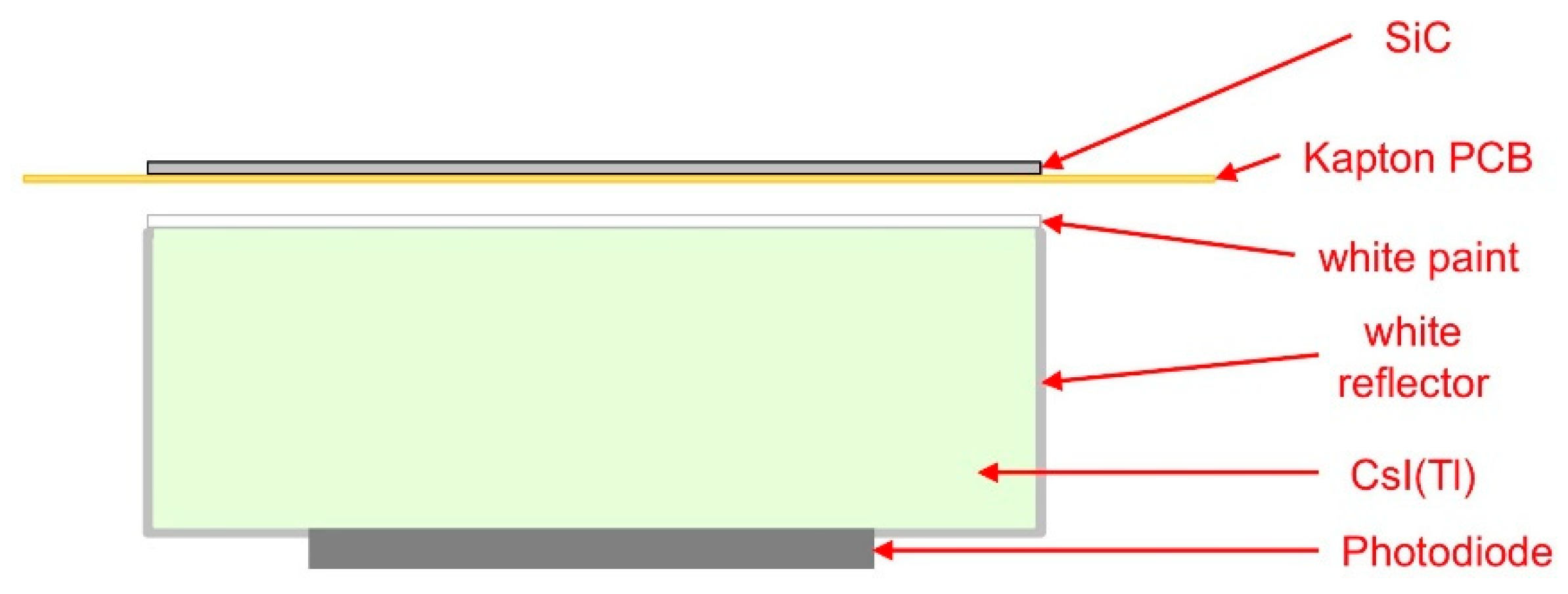
55]. Due to their good energy resolution and linearity, a thin silicon detector or even a gas detector is typically used as ΔE stage, followed by a thicker silicon. This configuration easily provides a good Z identification and energy resolution with an acceptable stopping efficiency, but is limited by the radiation hardness of silicon. Telescopes based on thin silicon carbide (SiC) detectors and thicker inorganic scintillators made of thallium-doped caesium iodide (CsI(Tl)) were chosen and tested as the NUMEN solution for particle identification.
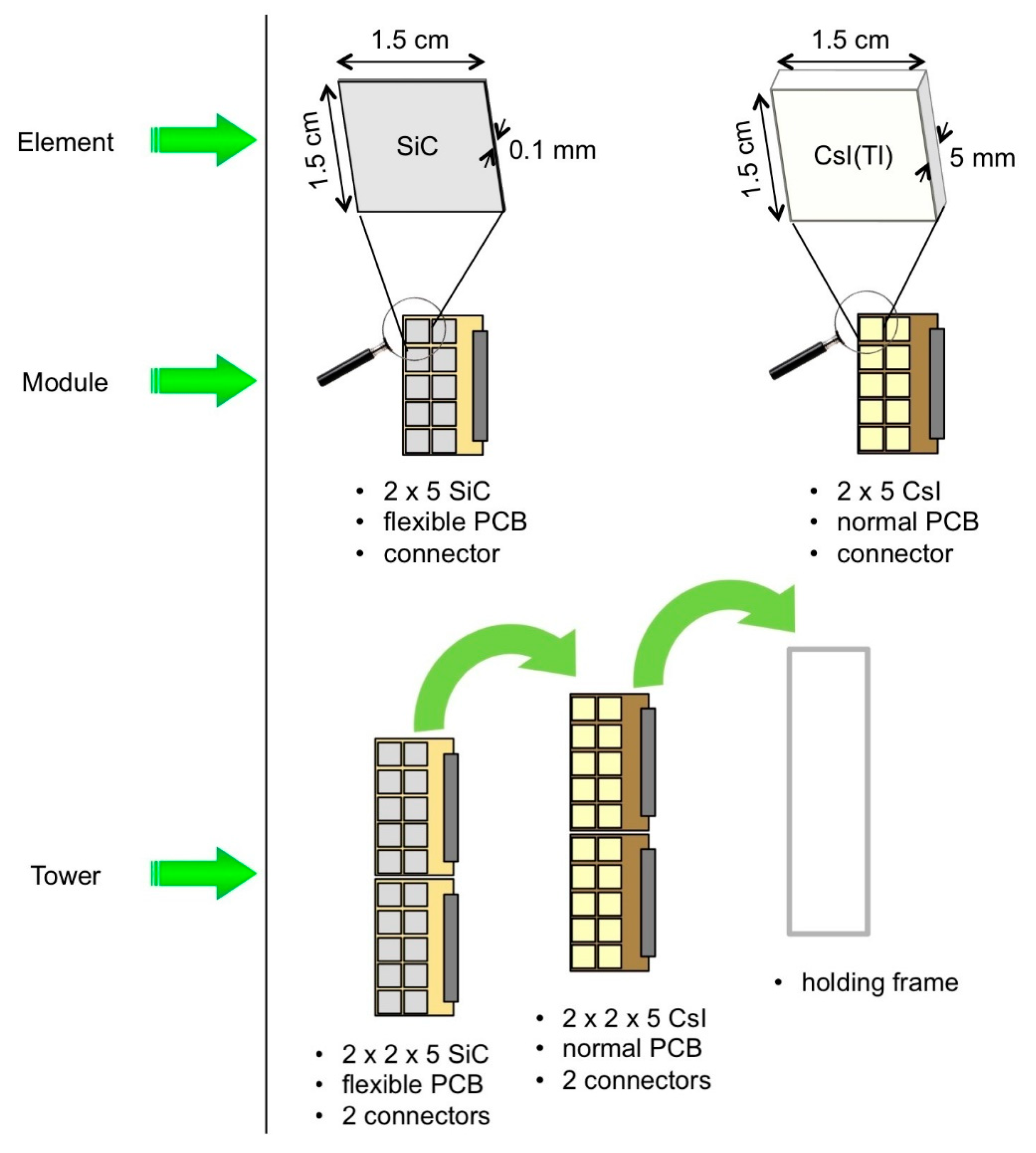
Figure 10 shows the scheme of such an elementary telescope cell, which is the basis of the PID system.
The PID, expected to withstand a counting rate of ≈5 kHz/cm
2, is an array of 820 tiny identical Δ
E-Er telescopes covering the focal plane of the spectrometer. Each detector cell covers an active area of 1.5 × 1.5 cm, with a 0.2-mm dead space between cells. The thickness of the SiC Δ
E layer is 100 µm, whereas with the CsI(Tl)
Er layer, all the particles are stopped, is 5-mm thick, and is coupled to a Hamamatsu S3590 photodiode of 1 × 1 cm active area [
56]. The single detector cell must be capable to handle such a rate and to withstand the corresponding radiation damage, also considering that the impinging particles will be heavy ions. As a reference, the useful energy range for a
16O ion is minimum 10 MeV/amu to reach the
Er stage and maximum 75 MeV/amu to be stopped in there.
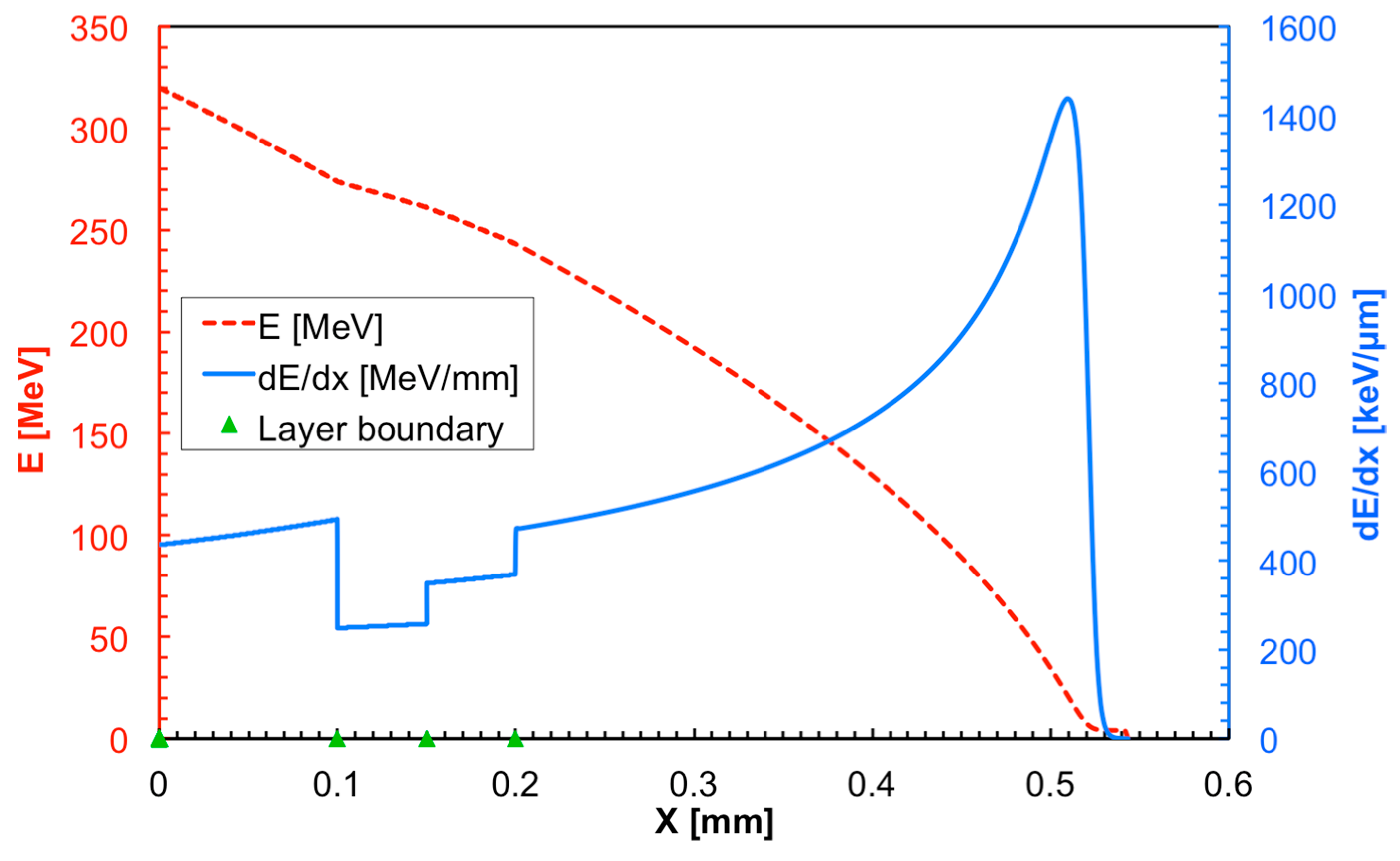
Figure 11 shows a calculation of the energy loss profile in the telescope for an impinging
16O ion with 20 MeV/amu kinetic energy, taking into account also the dead layers, i.e., the SiC backing and the front reflector of the scintillator.
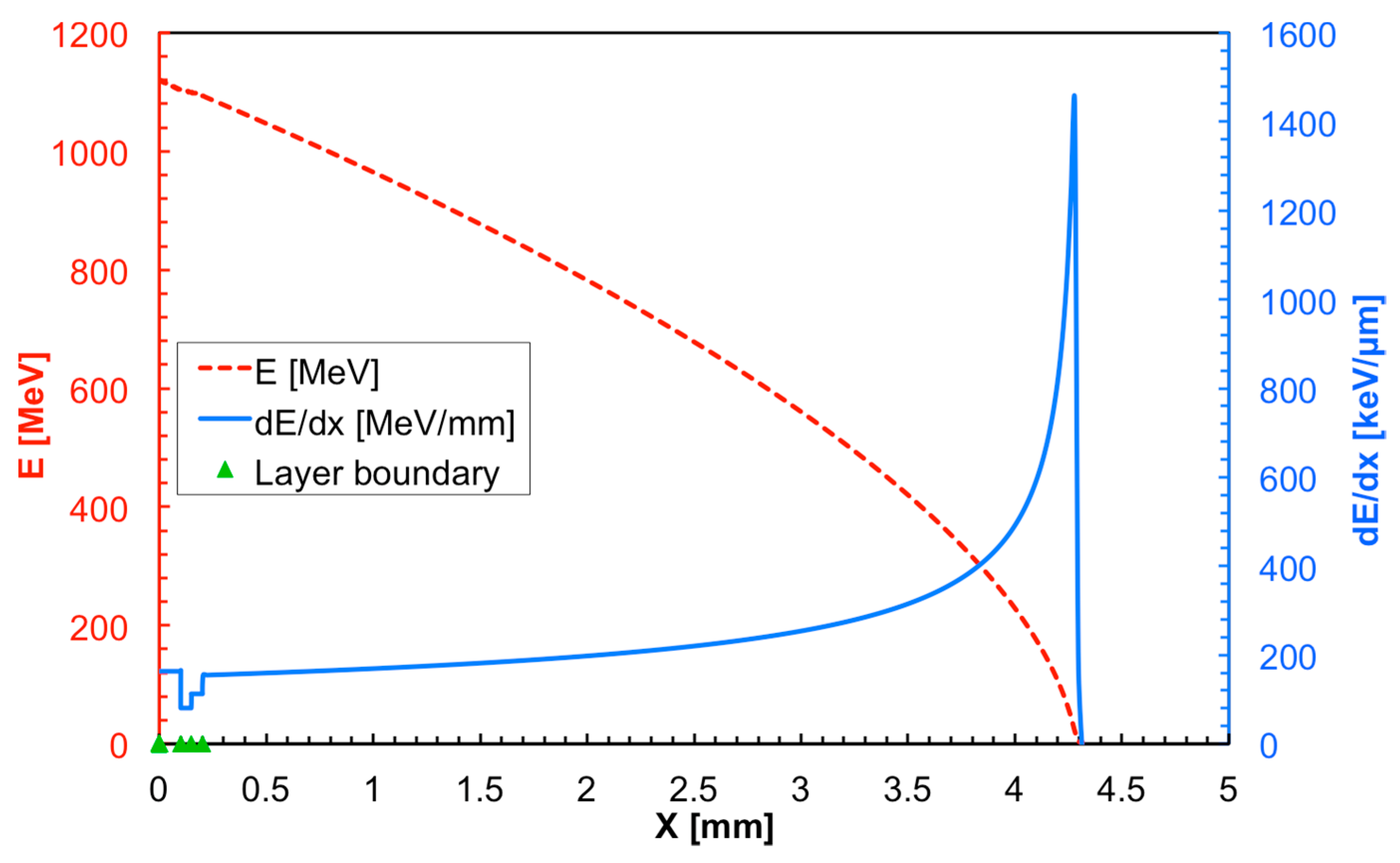
Figure 12 shows the same calculation for an
16O ion with 70 MeV/amu.
SiC was chosen among the “robust” radiation-hard materials also thanks to the technological improvements achieved within the SiCILIA project [
57]. SiC is a compound semiconductor characterized by an energy bandgap of 3.23 eV. It is thermally stable up to about 2000 °C, even in oxidizing and aggressive environments [
58]. Some of its main physical properties as compared to those of Silicon at room temperature are listed in
Table 1.
The first requirement for the PID wall is the radiation hardness, i.e., the tolerance of its detectors to high doses of heavy ions. This is strictly related to the damage created in the lattice by the impinging particles [
59]. Due to the strength of its chemical bonds (higher average energy required to displace an atom), SiC is a very valid alternative to Si for the production of radiation hard detectors. Its wider band gap reduces significantly the rate of thermal noise whereas, on the other hand, it also represents a disadvantage: the consequently higher average energy required for the generation of an electron-hole pair produces less than half the charge signal than silicon. As for the time resolution, due to the high bias voltage, the charge collection time is much faster than on silicon, thus easily allowing a sub-nanosecond timing.
Nonetheless, the heavy ions to be detected in NUMEN give rise to a large number of primary e-h pairs so that the statistical fluctuations are not an issue. Moreover, SiC detectors can withstand much higher temperatures than silicon detectors, still keeping a high signal to noise ratio. The chosen thickness of 100 µm is such that the expected range of energy loss under typical experimental conditions is ΔE ≈ 15–50 MeV.
As for the Er detector, when hit by radiation it produces scintillation light with a spectrum centered around 540 nm and a decay time constant τ ≈ 3 µs, whose readout is performed by means of a PIN photodiode. The suitability of such a scintillator for the particle identification task in NUMEN requires an energy resolution around 2% for the ion species at the energies of interest. As will be shown in the Results section, such a resolution (or even better) is feasible, as well as a satisfactory radiation hardness.
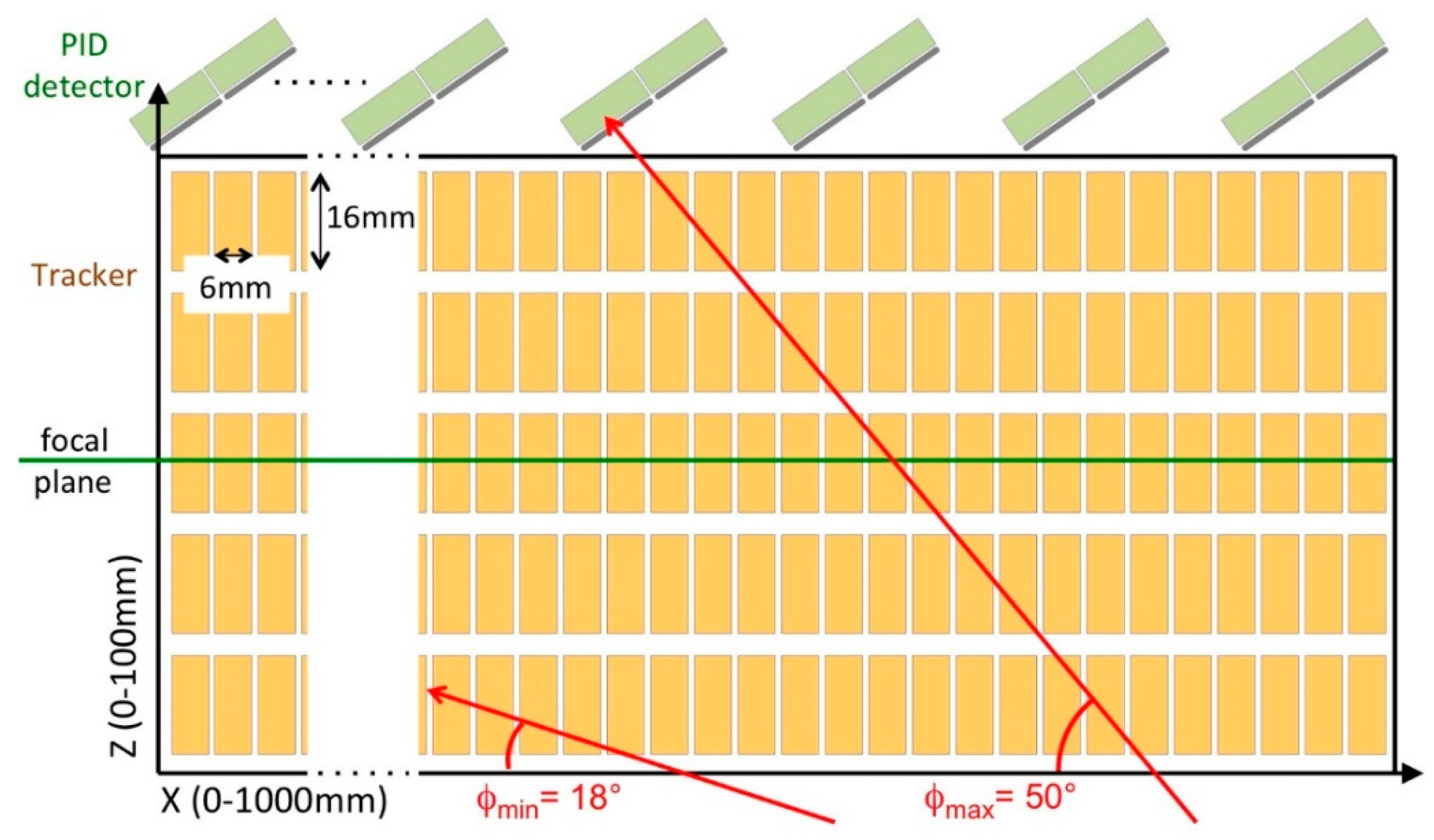
In order to keep a reasonable modularity, it was decided to arrange the elementary cells into independent
modules, each one consisting of 10 telescopes (
elements). The modules are arranged in groups of two into
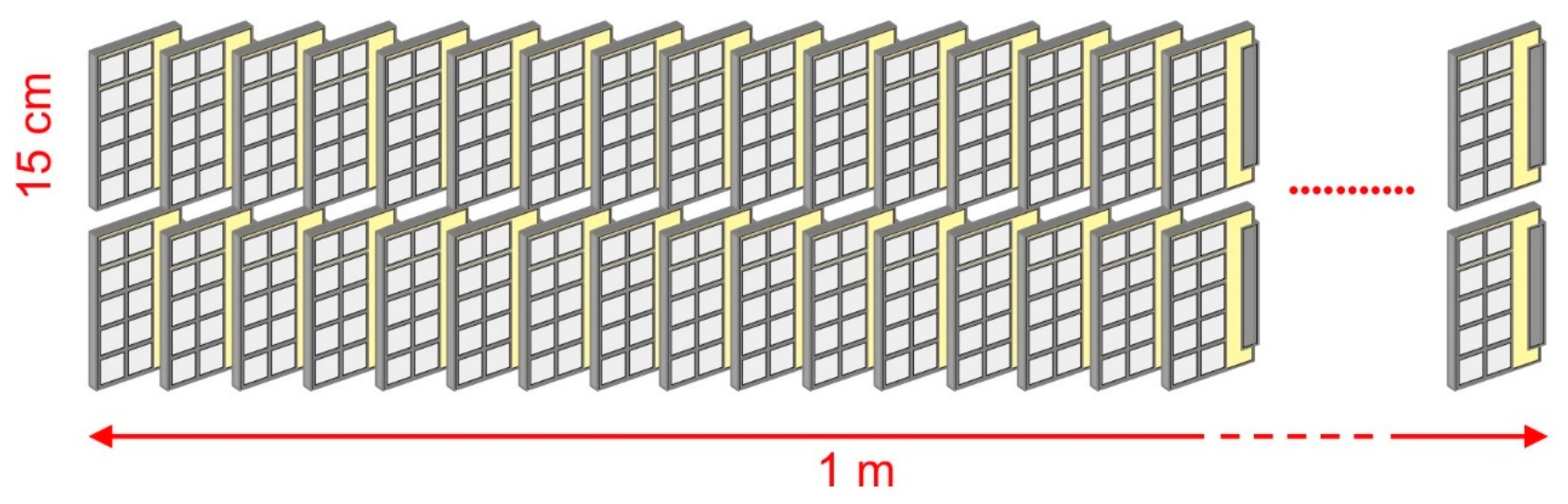
towers (
Figure 13). The full width of the MAGNEX focal plane (1 m), will be covered by 41 towers rotated by about 35° with respect to the vertical axis to make up for the tilting angle of the focal plane with respect to the dipole magnet output (
Figure 14).
2.6. The Gamma Detector Array
The nuclear transitions to be studied in the NUMEN project entail the production of deformed and non-deformed nuclei by means of the DCE or competing reactions. The energy resolution of MAGNEX with the beams provided by the cyclotron, ΔE/E ≈ 0.2%, is adequate to discriminate between the ground state (Iπ = 0+) and first excited states (Iπ = 2+) of both projectile-like and target-like species only for the cases of non-deformed target nuclei and at low incident energy. For nuclei of interest in moderately and strongly deformed mass regions, such as 110Pd, 150Nd, and 160Gd, and in all the cases of higher incident energy, the spectra at the focal plane alone cannot resolve between states of the reaction products. In such cases, a gamma detector array close to the target region has been considered as an ancillary device to the magnetic spectrometer, to be used in coincidence with projectile-like fragments in the FPD in order to provide the necessary discrimination between nearby energy states.
Due to the high beam intensities to be used in the DCE experiments, the target region will become a very strong source of radiation, mostly gamma rays, fast neutrons, and electrons, but also light and heavy ions. The charged particles as well as the low energy X-rays can be absorbed by a sufficient amount of solid material between the target and the array. The expected rate of gamma rays and neutrons is such that no solid state detector could be reasonably employed, both for reasons of radiation hardness and speed. Indeed, the total gamma emission rate expected for the typical NUMEN experiments can easily reach 108–109 gamma/s. In addition to that, a comparable amount of neutrons can be expected, which could also produce signals in the gamma detectors.
This means that the solid angle covered by each individual detector element has to be kept small in order to minimize the pulse pile-up probability, whereas in contrast to that, the DCE cross sections are extremely small. In light of all this the resulting requirements for the GDA are:
large total solid angle;
small solid angle of the individual detectors;
high granularity;
speed, with signal duration ≤100 ns;
good energy resolution, <10% FWHM in the hundreds of keV region;
high photopeak efficiency;
reasonable radiation hardness.
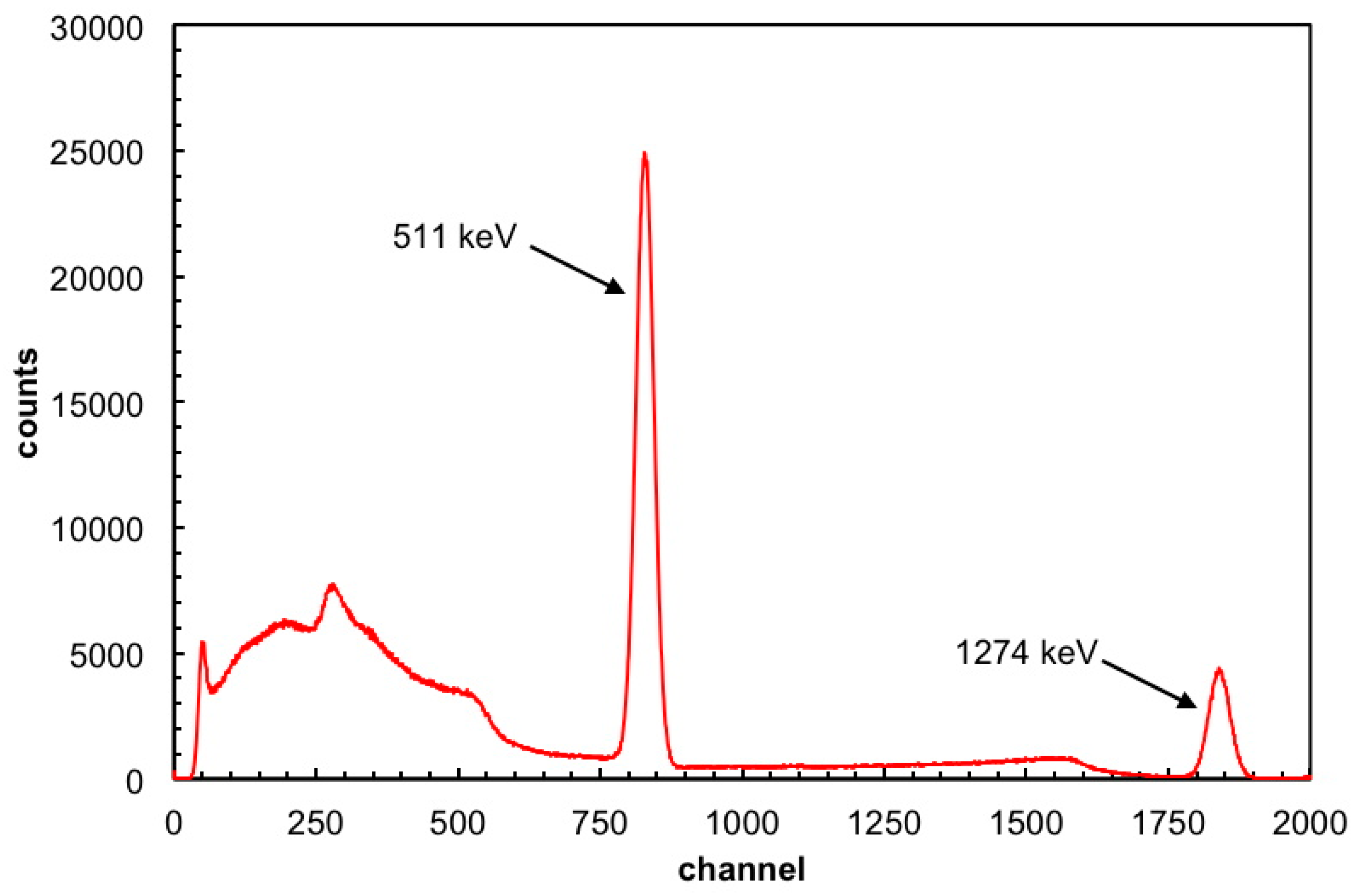
Inorganic scintillators are normally quite tolerant to gamma and neutron radiation, and among them the LaBr
3(Ce) (from now on simply abbreviated as LaBr) was chosen to be employed in the gamma array due to its special features, which fulfil all of the mentioned requirements [
60,
61,
62]. The proposed configuration for the GDA, sketched in
Figure 15, consists of 139 LaBr cylindrical scintillators, 38 mm diameter and 50 mm length, readout by means of photomultiplier tubes (PMT). They are arranged in six concentric rings to be positioned upon the scattering chamber, pointing at the target at 25 cm distance and covering ≈20% of the total solid angle.
The typical energy resolution of LaBr is ≈3% with gamma rays of 662 keV (from a reference 137Cs source), the decay constant of the scintillation light is ≈30 ns, which gives access to subnanosecond time resolution, and the expected photopeak efficiency for the GDA crystals of the chosen size is ≈33%. These features make possible to set narrow energy windows on the measured gamma spectra, corresponding to the first or second excited levels of the residual nucleus, along with a suitable narrow time window in coincidence with the ejectile, thus rejecting a huge amount of background events.
2.7. Electronics and Data Acquisition
The primary task of the NUMEN front end and data acquisition system (DAQ) is to cope with the huge analog data rate coming from the detector subsystems. Then, data have to be converted to digital and finally transferred to a storage system via large bandwidth channels. Apparently, this sounds like a standard procedure; however, there are a few constraints that make it difficult, if not challenging.
Due to the intrinsic nature of the MAGNEX magnetic spectrometer, the tracking algorithm is quite complex and consequently slow. Indeed, it requires to sample the signals from many strips in the tracker and to recognize those that belong to a track, performing weighted averages of signals from neighboring wires and matching them to signals from telescopes in the PID detector system. Together with the 90 k events/s/strip maximum expected counting rate, this prevents any real time selection, event building, and processing. Only typical noise suppression by means of thresholds on individual signals can be realistically foreseen.
Concerning the PID, the expected event rate is a few thousand events/s/telescope. In this case, one can think of performing a noise reduction by means of thresholds and elementary ΔE−E coincidences. The GDA will face a huge incoming event rate whose handling will presumably be possible only during dedicated runs with a reduced beam current.
The basic DAQ requirements for the three subsystems can be summarized as follows.
Tracker: medium energy resolution, ≈1ns time resolution, very high speed.
PID: high energy resolution, ≈1 ns time resolution, high speed.
GDA: high energy resolution, ≈1 ns time resolution, very high speed.
An originally proposed solution based on an existing ASIC, not well tailored to the NUMEN needs, was discarded in favor of a better suited solution based on commercial products. This sounds quite beneficial from the point of view of the maintenance and repair, hardware/firmware updates, backward compatibility in case of new developments and products. Obviously, the question was whether a feasible commercial solution existed, and it sounded reasonable to try opting for a waveform digitizer approach with underlying FPGA firmware/hardware. Such an approach looks powerful and flexible, as it is open to tuning and rearrangements that in case of more traditional electronics would require hardware replacements. However, within a digitizer framework, the idea of recording the waveforms is not suitable at all, due to the large number of channels and to the continuous mode of operation of the accelerator (in other facilities, with 1–2 s long duty cycles and smaller number of detectors, there is time between beam bursts to store the acquired waveforms).
The solution was found in a new high-performance 64-channel digitizer with 125 MHz sampling rate (VX2740 [
63]), which has also been chosen by the Darkside experiment [
64]. Such a module will provide several advantages:
uniform front end and readout hardware architecture;
reduction and simplification of the spares;
programmable signal handling algorithm, tailorable to each detector type;
very good energy resolution, 16-bit conversion;
very good timing capabilities, in 8-ps steps;
pile-up detection and tagging;
high data throughput, nominally up to 10 Gbit/s;
cost reduction due to purchasing only one model for all the detector subsystems.
The VX2740 digitizer development is still being finalized: the hardware is ready whereas the firmware for the FPGA is still being tuned in order to accommodate also some special requests from the Darkside experiment. The new generation FPGA has quite a higher number of gates with respect to previous digitizers, thus allocating more hardware-emulating algorithms and a quad-core processor hosting a real time Linux operating system.
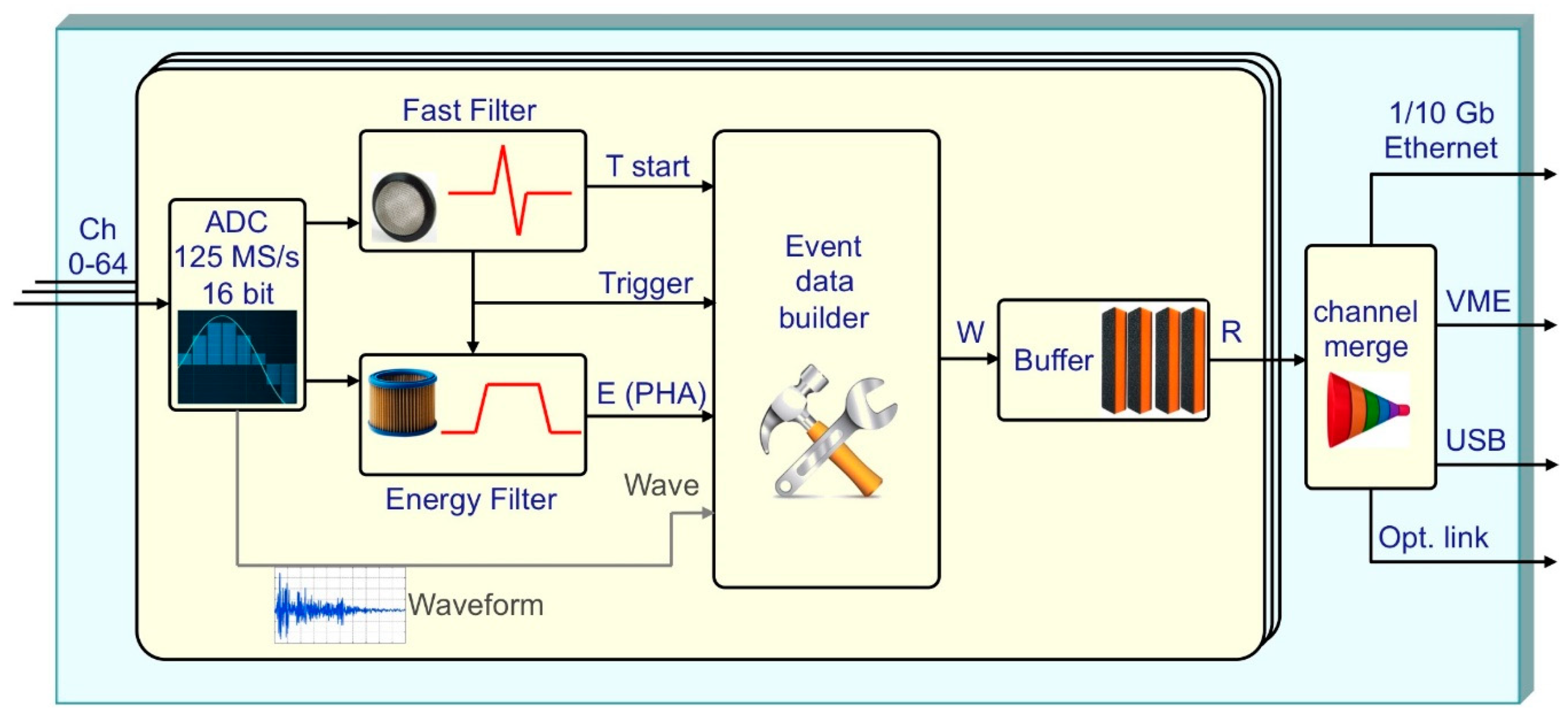
All the signals from the tracker and the PID will be handled by charge-sensitive preamplifiers, and their outputs will go directly to the VX2740 inputs. Here, a fast flash-AD conversion occurs at 125 Msample/s, the FPGA operates a suitable recursive numerical transform implementing a CR-RC2 filter, producing a bipolar signal whose zero crossing time, interpolated at 8-ps steps, is used as detection time. In parallel, a different recursive numerical transform on the digitized input signal produces a trapezoidal shape, whose flat-top height is proportional to the original signal amplitude. These operations are performed on-the-fly in real time and independently for the 64 channels by the on-board FPGA, not introducing additional dead time and therefore resolving or tagging the signal pile-up depending on the relative delay between two consecutive signals. The same numerical analysis is performed for the GDA signals, with the only difference that they do not need to be preamplified because they are produced by PMTs. The block scheme of the operational features of the VX2740 module is depicted in
Figure 16.
A simple on-board logic operation will help reducing the noise on the PID telescopes, mainly due to gamma rays triggering the scintillating stage made of CsI(Tl): by coupling ΔE and Er signals on the same module, the FPGA can easily discard the uncorrelated hit and only accept those with valid coincidences.
The DAQ will operate in free-running mode and the event building will be done at a later stage. The data will be produced in form of hits, each one taking nine bytes according to scheme of
Figure 17 and freely flowing out of each module via a 10 Gbit/s Ethernet interface through concentrators toward the storage system.
The overall data output rate depends on the NUMEN running mode. Two main modes are foreseen: inclusive and exclusive. The inclusive mode, for shorter periods at high beam current (nominal 1013 pps), does not consider coincident GDA data whose rate would be prohibitive. The exclusive mode, in coincidence with the GDA, is only feasible with lower beam current (nominal ≈1012 pps). In both cases the maximum expected output data rate is of the order of 50–60 MBytes/s.
4. Discussion
The aim of NUMEN is to investigate the nuclear response to DCE reactions for all the isotopes explored by present and future studies of 0νββ-decay. Several aspects of the project required the development of innovative techniques for the detection system, the experiment set-up, the theoretical interpretation of the collected data, and also the major upgrade of the INFN-LNS facility. Indeed, following the upgrade, the facility is likely to become unique for this research in a worldwide context.
The complex multidetector, currently under construction, will produce data at such a high rate that the storage in an event-based fashion is not feasible, because the typical response time of the three detection systems is quite different. Indeed, the GDA, fast and close to the target, responds in few nanoseconds; the gas tracker needs up to a couple of microseconds to collect the charge produced by the impinging ion along the track; the PID responds in several hundred nanoseconds (ΔE) and in few microseconds (Er); both tracker and PID pay a variable delay of few hundred nanoseconds due to the different flight paths followed by different ions with different kinetic energies. The solution is to acquire data in asynchronous mode, with each detector channel running independently and simply triggered by a threshold crossing (the only exceptions are the ΔE−Er elements, for which the logical condition of coincidence can be imposed). This is why a global synchronization is required, with each readout channel embedding a global time stamp in its data for a later offline event reconstruction. However, a rough online reconstruction to be used for second level triggering purposes is not excluded a priori, and this possibility is currently under study. Indeed, a rather complex data analysis will make possible a high precision reconstruction of tracks with the identification in mass, nuclear charge and atomic charge state, the measurement of the kinetic energy of the ejectile, and the determination of the final excitation state of both the ejectile and the residual nuclei.
NUMEN is not only a challenging project at the intersection of nuclear and neutrino physics, driven by an important physics case and opening interesting scientific scenarios on our current understanding of fundamental physics: it also opens potential technological spillovers, as is the case for instance with the SiC technology. Due to its radiation hardness and resistance to high temperatures, SiC can replace silicon for several applications in harsh environments: it can easily be employed in dosimeters, or as a lower cost and larger area replacement of diamond detectors in nuclear industry, not to mention the enormous potential envisaged in the automotive sector. Similarly, other technological developments done during the NUMEN R&D activity can be useful for different applications outside the fundamental research field, as for instance the thin targets production techniques, cryogenics, robotic manipulation, electronics, and high throughput data handling.
The final detector assembly and the cyclotron upgrade are foreseen to be complete by October 2023, when the system commissioning will start. The experiments will start by mid 2024 on the 76Ge - 76Se system, and will continue on the other systems according to the availability of the needed thin targets.
In conclusion, the NUMEN experiment will provide access to the DCE cross section for many nuclear systems, which in most cases is in the range of a few nanobarn, likely opening a doorway to a better understanding of the somewhat mysterious and perhaps controversial neutrino properties.