1. Introduction
1.1. Einstein’s Hypothesis
In the Schwarzschild static solution [
1], there is a hypersphere
where the components of the metric tensor
and
“exchange signs”. On this hypersurface,
The vanishing of
means that the infinite small coordinate length in the radial direction corresponds to the finite “natural” length. This circumstance was not unnoticed by Einstein. Here is an excerpt from his article [
2]:
“If it turns out that in some place of the four-dimensional continuum det
vanishes, then it means that at this place the infinite small “natural” volume corresponds to the finite coordinate volume. We assume that this is nowhere to be found.
In this case, det cannot change its sign; we will accept, in accordance with the special theory of relativity, that det
always has a finite and negative value. This assumption is a hypothesis about the physical nature of the considered continuum and, at the same time, a rule concerning the choice of a coordinate system.” (see [
2], below Equation (18a)).
The point of this quote is that is negative provided that a singularity is nowhere to be found. Forgetting “nowhere to be found”, people use the condition unhesitatingly and everywhere. In the Schwarzschild metric, is positive at , and there is an inevitable singularity in the center . At a regular center, the ratio of the circumference to diameter tends to as ; wherein The assumption “nowhere to be found” is violated in the center. For a real physical object of arbitrary high mass with a Schwarzschild gravitational field outside and a regular center, at least one more gravitational radius should exist inside the gravitating body.
The sign of the determinant is not an invariant. If changes sign on some hypersurface, while all invariants of are finite, then this “singularity” is removable, and there exists a regular solution. The condition of regularity (all invariants of are finite) is weaker than the requirement
In the 1930s, in line with Einstein’s hypothesis, the existence of a critical mass
for gravitating, spherically symmetric Fermi systems was established in the fundamental papers by Chandrasekhar [
3], Landau [
4], and Oppenheimer and Volkoff [
5]. The critical mass
is of the order of the solar mass
for a degenerate Fermi gas of neutrons. It was shown [
5] that the equation of state of a relativistic Fermi gas is still far from the ultrarelativistic limit even at the maximum possible mass. It was concluded [
6] that above the critical mass, the dominant forces of gravitational attraction make the contraction of matter unbounded. The state of matter in the process of unbounded gravitational contraction (collapse) is referred to as a black hole.
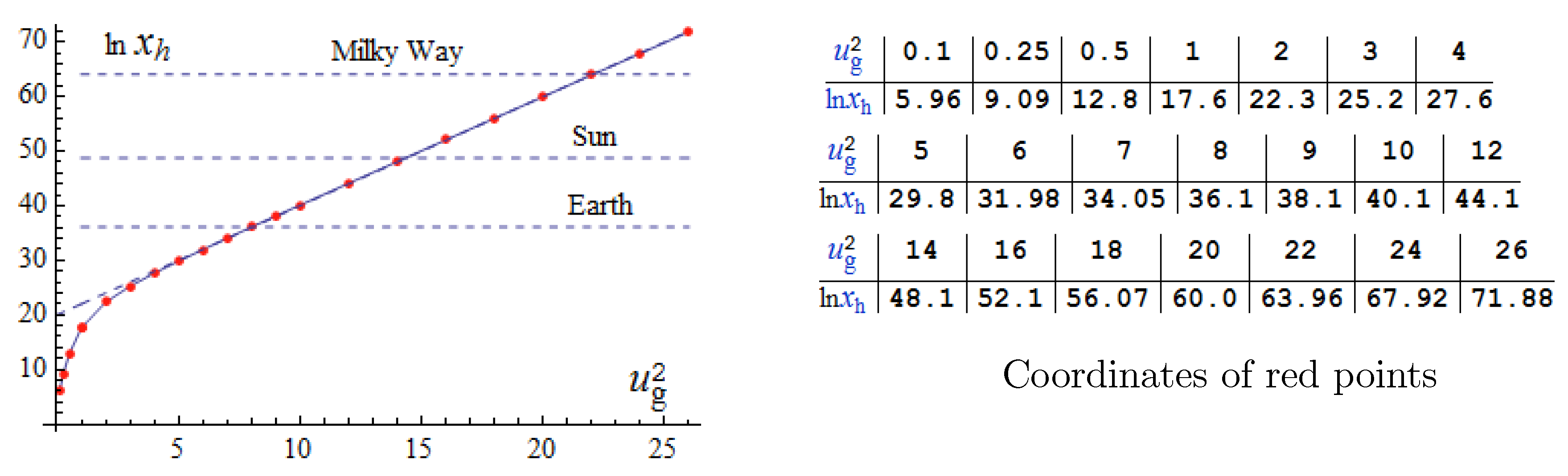
Astrophysical observations point to the existence of supermassive objects at the centers of galaxies. In our Milky Way Galaxy, there is an invisible object located at the same place where the radio source Sagittarius A is. Astronomers estimate its mass from the orbital motion of stars to be as high as
and its radius to be less than
light years [
7]. The mass of the Sun is
g. Since the mass of the object at the galactic center exceeds the critical equilibrium mass
of a neutron star by six orders of magnitude, black holes are considered as the most likely candidates for supermassive objects at the centers of galaxies.
We have no direct opportunity to observe what is happening beyond the horizon. Nevertheless, it is natural to assume that during unlimited contraction, the pressure rises indefinitely, and the energy per particle will inevitably reach the binding energy of atoms, nuclei, neutrons, and further, step-by-step, “elementary particles”. At the same time, the lifetime of galaxies (and, hence, the black holes in their centers) is of the order of the lifetime of the Universe. Since a black hole evolves relatively slowly, local equilibrium concentrations of particles, that enter into “chemical reactions” of transformation into one another, depend on temperature and pressure and are not dependent on specific reaction channels (see [
8], §101). One of the most important, but still unclear questions is the inverse influence of the transformation of particles into one another in the process of gravitational self-contraction. The fact that the lifetime of a galaxy (with a collapsing object in the center) is of the order of the lifetime of the Universe suggests that the transformations of particles into one another can slow down the contraction process or even completely stop it. That is why it makes sense to search for and analyze static configurations of gravitating objects in general relativity.
Black holes, neutron stars, and currently, exotic quark [
9,
10] and boson [
11,
12,
13,
14] stars are considered as the objects whose structure is determined by the equilibrium state in their own gravitational field. In the process of gravitational collapse, the density of matter increases continuously. At a relatively small pressure, due to additional elasticity in view of the Pauli exclusion principle, Fermi systems look more capable of resisting the gravitational contraction. However, in the process of unbounded contraction, the stage when massive Bose particles (Z bosons, W bosons, Higgs scalar bosons, and/or coupled pairs of fermions) are dominating is inevitable. At low temperatures, a degenerate Bose gas is energetically more beneficial than a degenerate Fermi gas. At zero temperature, bosons are located at the ground level. This state of bosonic matter is named the Bose–Einstein condensate.
1.2. Gravitating Bose–Einstein Condensate
In the frames of the Einstein hypothesis (always
), the properties of the equilibrium state of a gravitating Bose–Einstein condensate (in comparison with a degenerate Fermi gas) were summarized in my review article [
15]. There is a specific feature of a gravitating Bose–Einstein condensate. The energy spectrum of gravitating bosons is a function of the wave function of the entire condensate. The very presence of a level depends on its population. In particular, at zero temperature for each level, there is a critical total mass
above which an equilibrium configuration (and, hence, this level itself) does not exist. For bosons with a rest mass
100
, the critical mass
at the zeroth quantum level is about one million tons. The critical mass
increases proportionally to the level number
n. At
, the next level
acts as the ground state. The concept of the ground state of a boson system is modified. The radius of the sphere occupied by the condensate also increases proportionally to the level number. Therefore, the density does not grow with increasing condensate mass. As long as the spacing between nearby energy levels is large compared to the temperature, no constraints on the total mass arise. However, an equilibrium state on a high energy level
is metastable. One bunch of bosons at a high quantum level with a large mass is energetically less favorable than several isolated centers, with a condensate at the zeroth quantum level being in each of them [
15].
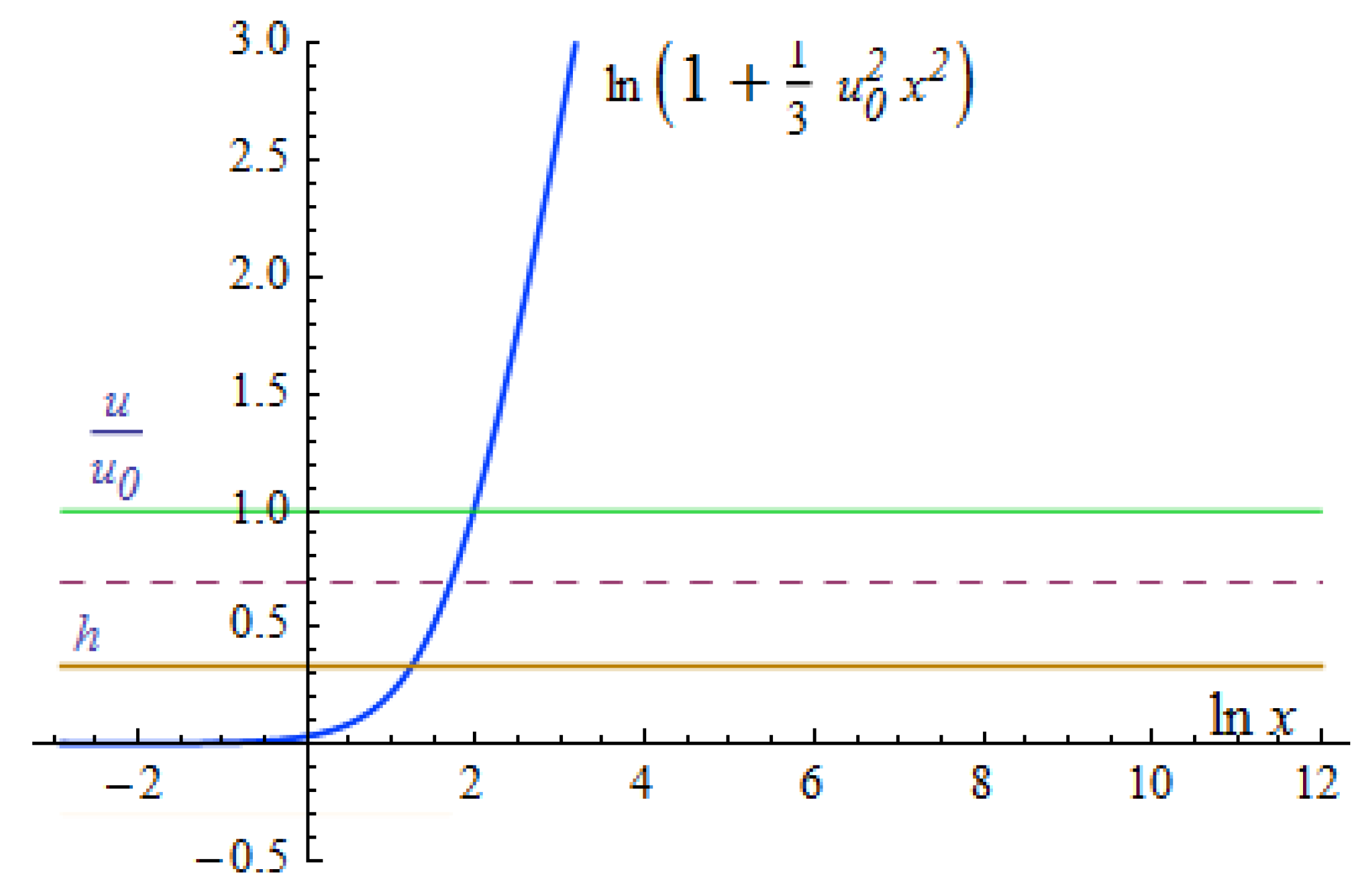
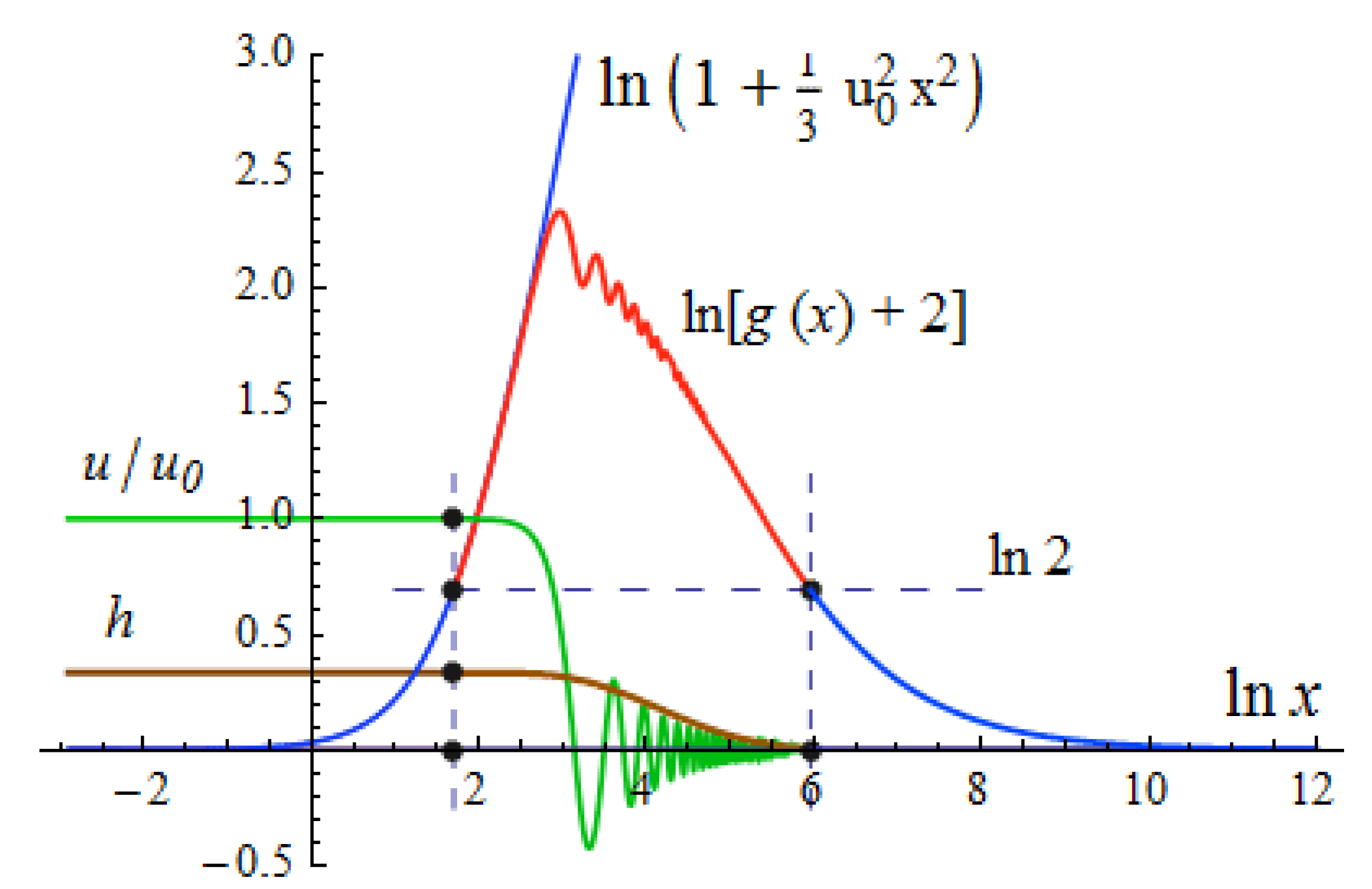
Under the restriction , the metric component starting from at the center, grows with increasing achieves its maximum value, and decreases back to as The function remains negative within the whole interval There is no gravitational radius where . Schwarzschild’s is simply an asymptote applicable at This property is inherent in equilibrium gravitating clusters of both bosons and fermions. The existence of a finite critical mass is a direct consequence of the restriction .
On the other hand, there are no visible restrictions on the total mass of a point-like gravitating object in the Schwarzschild solution. However, is positive at , so that the regularity condition in the center is not satisfied. Schwarzschild’s solution could be regarded as an approximation of the field produced by a body whose size is small compared to the distance from the observer. To satisfy the requirement of regularity in the center, i.e., there should be another gravitational radius inside the gravitating body, where changes sign also. I am not aware of such a regular static solution, compatible with Einstein’s hypothesis ( everywhere).
1.3. Regularity Instead of det
The determinant
is not an invariant. I allowed myself to analyze what would happen if,
instead of the requirement , a weaker condition of regularity is applied. Allowing
to change sign, I reconsidered the equilibrium structure of a spherically symmetric gravitating Bose–Einstein condensate [
16]. By not using the representation
that fixes the sign, I avoid the trouble of the incompleteness of Schwarzschild’s coordinate system [
17,
18,
19]; see also [
20] §103 and [
21] §14.
From the point of view of equilibrium in its own gravitational field, it is implied that the number of particles is large, and all interactions, except the gravitational one, are not significant. At the same time, it is assumed that gravitation does not violate the exchange interaction of elementary particles of the Standard Model.
My detailed analysis [
16] confirmed the existence of static solutions where
changes its sign twice:
at
and at
; wherein
The signature of the metric tensor is changed to
within the spherical layer
Outside this layer, at
and
the signature is
as usual.
Nature gave a wonderful gift for us: at absolute zero, the wave function of the ultra quantum condensate of neutral bosons is a classical scalar field (see [
22] §30). The wave function, as a scalar field, satisfies the Klein–Gordon equation with
being the coefficient at the highest derivative. The Klein–Gordon equation is not determined at
Gravitational radii are the boundaries of the intervals where the Klein–Gordon equation satisfies the theorem of existence and uniqueness. The boundary conditions at
and
can be chosen so that the gravitational radius
inside the gravitating object is a regular point. In this case, the second gravitational radius
has to be the termination point. The sphere
is the border of the volume, occupied by the gravitating matter. For a remote observer,
is the event horizon.
If
on the surface of a gravitating body, then it follows directly from the Einstein equations that the energy density vanishes at
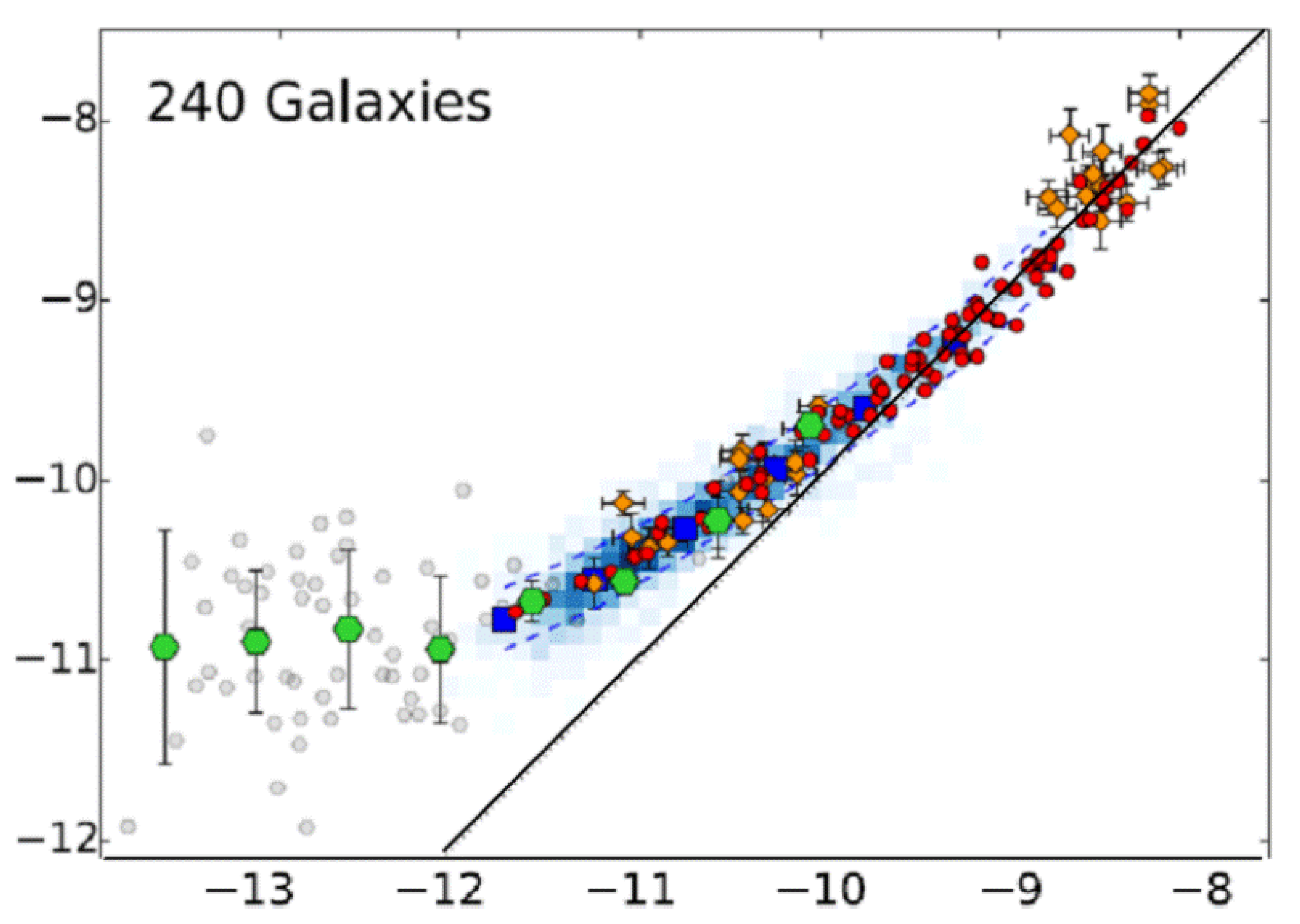
and the pressure does not. Definitely, a static state of matter with a high pressure on the interface with a vacuum cannot exist. However, a pressure balance is possible at the interface with the surrounding dark matter. The amount of dark matter in the Universe, according to existing estimates, is several times larger than the amount of ordinary baryonic matter. Using a longitudinal vector field, it is possible to describe adequately the observed manifestations of dark matter, including the galaxy rotation curves [
23] and the bending of light by dark matter on the periphery of a galaxy [
24]. The balance of pressure on the interface allows connecting the parameters of a black hole with the parameters of dark matter. In particular, the speed on the plateau of a galaxy rotation curve as a function of the black hole’s mass is determined; see [
16], Formula (68).
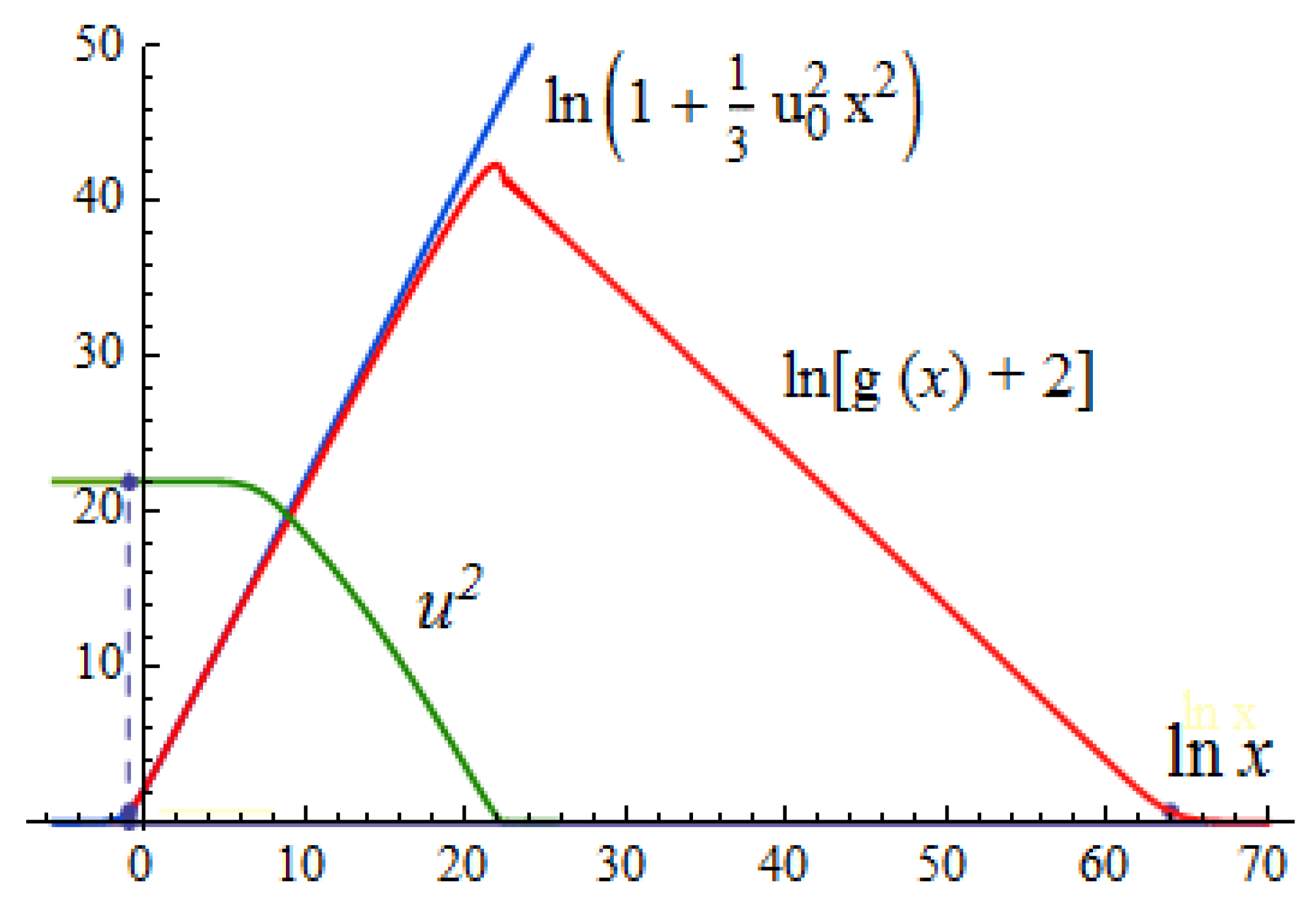
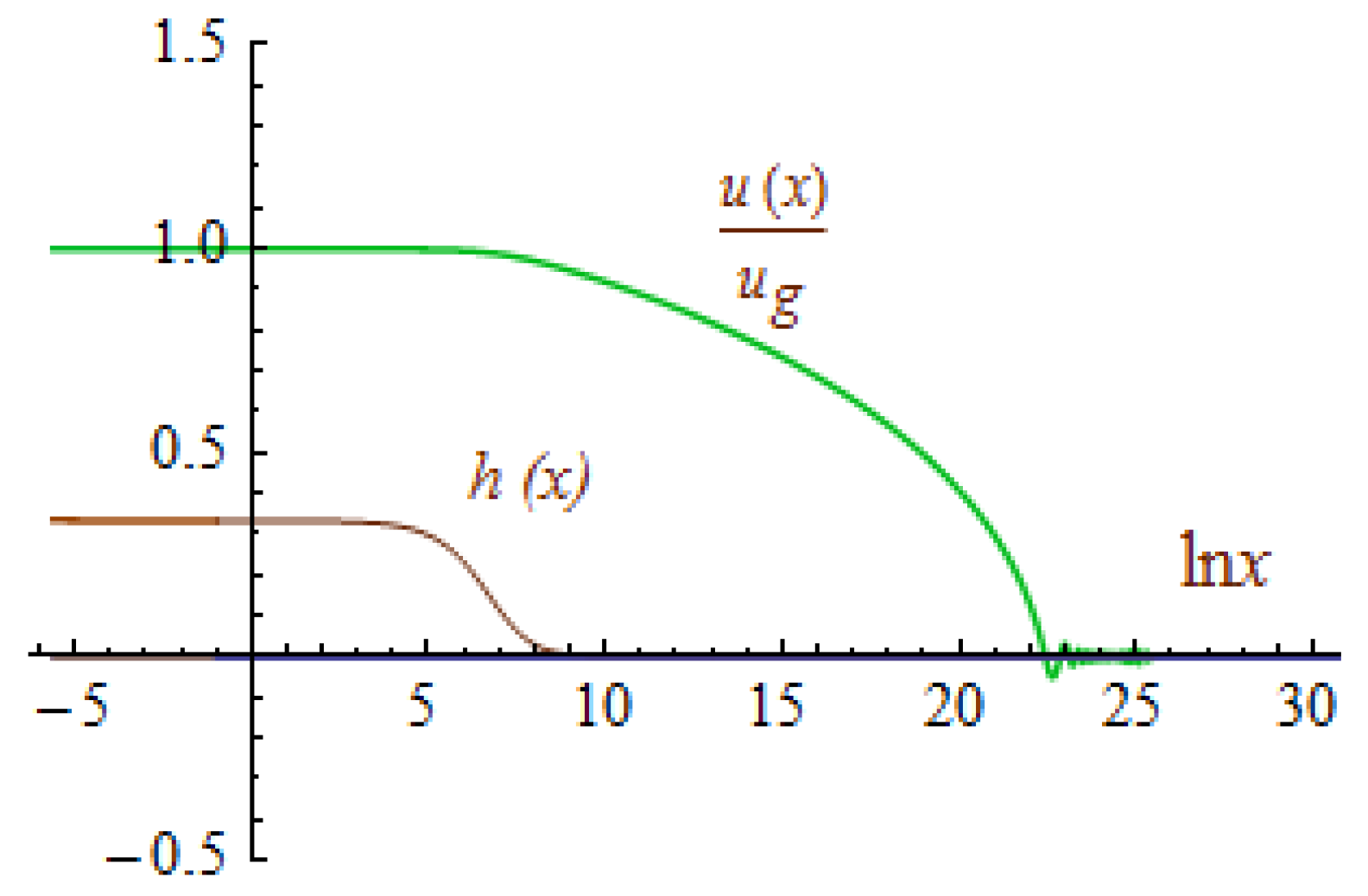
Considering only the dominant gravitational interaction, we are not taking into account the non-ideality of the Bose gas, as well as the possible transformation of the bosons into some other particles. As a result, with no account of elasticity, the amplitude of the scalar field diverges logarithmically at
[
16]. This divergence does not affect the mass appearing in the Schwarzschild asymptote, which is visible to a remote observer. At present, we do not know what the bosons of the Standard Model could be turned into with a further increase in pressure. What we can do is to take into account the non-ideality of boson gas using the so-called “model
”. The equilibrium state of a gravitating Bose–Einstein condensate with the account of its elasticity is considered in this article.
2. Behind the Horizon
Getting away from Einstein’s hypothesis, I do not use the sign-fixing representation
in the spherically symmetric metric:
Generally speaking, the derivation of the Einstein equations inside the interval
where
and outside, where
should have been carried out separately. In both cases, the static gravitational field, created by a spherically symmetric distribution of matter, satisfies the same Einstein equations (see (100.4) and (100.6) in [
20]). We write them down in the form:
Gravitational constant
s
2/g × cm,
cm
3/g × s
2. Relation:
follows directly from the Einstein Equations (
2) and (
3).
The general solution to Equation (
2) is:
is a constant of integration.
is a regular function, provided that the integral in (
5) converges. The convergence of the integral in Equation (
5) means that the mass within the layer
:
is finite. If the total mass
is finite, the metric component
is a smooth continuous function within the whole space
. The regularity of
follows from the finiteness of the total mass of matter, regardless of its physical nature. From the convergence of the integral (
6) as
, it follows that:
When (
7) is fulfilled, the ratio of the circumference to the diameter tends to
at
(a necessary condition for a regular center).
In the Schwarzschild solution [
1]:
At
, Newton’s law is applicable, and the Schwarzschild radius
is proportional to the visible mass
M of a gravitating point-like object:
However, it does not satisfy the regularity condition (
7) in the center. Actually, (
8) is applicable outside a spherically symmetric gravitating body, including its boundary, provided that above the surface
at
. From Schwarzschild’s solution (
8), we get the derivative:
Substituting it into Equation (
2), we confirm that the energy density vanishes on the surface
On the contrary, as follows from Equation (
3), the pressure remains finite on the surface:
It is not clear how a medium can exist in a static equilibrium state with uncompensated pressure on the interface with a vacuum. Apparently, this is the most likely reason why no static solutions without limitation on mass had yet been found. Nevertheless, an equilibrium state of a black hole becomes possible due to the presence of dark matter. The balance of pressures at the interface of a black hole and dark matter is able to support a static equilibrium of these two phases [
16].
3. Gravitating Scalar Field
The Lagrangian of a complex scalar field
in a curved space-time with the metric tensor
(
1) has the form:
In accordance with the least action principle,
and
satisfy the Klein–Gordon equation:
Klein–Gordon Equation (
14) is invariant against changing the sign of the determinant of the metric tensor, because
in the numerator and denominator cancel each other.
Considering the equilibrium state of matter in its own gravitational field, people take into account dominating gravitational forces, and ignore all other interactions. In the application to an ultra quantum Bose–Einstein condensate, I believe that a strong gravitational field does not violate the exchange interaction of bosons.
The main characteristic determining the gravitational properties of a scalar field is the mass of a quantum
m. In power series of the potential:
is a constant having the dimension
and related to the mass of the quantum
m:
The terms
and higher degrees are corrections for collisions of particles and/or other interactions of a non-gravitational nature. Without these terms, the wave function diverges logarithmically as
The logarithmic divergence of the wave function in the center takes place because, in view of dominating gravity, the interactions of another physical nature are not taken into account.
In the paper [
11], within the framework of Einstein’s hypothesis, the term
was added to the Lagrangian in order to take into account the non-gravitational pair interaction of bosons. It was shown that the equilibrium configuration in this model differs noticeably from the case of non-interacting bosons even when
In the Gross–Pitaevski equation [
25,
26] for the wave function of the laboratory Bose–Einstein condensate in rubidium vapor [
27] and in sodium vapor [
28], the corresponding nonlinear term is associated with pair collisions of bosons. As applied to the rarefied gas of atoms of the laboratory Bose–Einstein condensate,
is the coupling constant, expressed in terms of the s-scattering amplitude (length)
a of bosons by one another:
[
29]. Since there is no reason to consider the gravitating Bose–Einstein condensate as a rarefied boson gas,
is not reduced to pair collisions only.
is a model parameter characterizing the physical properties of the medium, including its elasticity. With the account of elasticity, the potential (
15) is:
Time is a cyclic coordinate in a static field. The energy of a single quantum
is the integral of motion. For a weak field in a flat space-time, Klein–Gordon Equation (
14) is a linear one. Its solution is a plane wave
, describing the motion of a particle with the relativistic spectrum
. In a curved space-time,
E is the conserved energy of the field per one quantum. A scalar field in the state of definite energy
E has the form:
Radial wave function
obeys the equation:
Note that
is the coefficient at the highest derivative in Equation (
17). The Klein–Gordon equation is not defined on hyperspheres
where
.
The Lagrangian (
13) of a scalar field does not depend on the derivatives of the metric tensor. The energy-momentum tensor is derived by the formula:
The components of the mixed energy-momentum tensor, acting in Einstein Equations (
2) and (
3), are:
The relation:
follows from (
18)
Enthalpy
does not depend on
In the model
, only elastic collisions of particles are taken into account. Dissipative processes are ignored, and as a result, the gravity and collisions of particles do not change the heat function of the system as a whole.
It is convenient to reduce the set of Klein–Gordon and Einstein Equations (
17), (
2) and (
3) to the normal form, using the relations (
4) and (
19). In the dimensionless variables:
we have a system of four first-order equations, resolved with respect to derivatives:
This set of equations contains one dimensionless parameter:
characterizing the elasticity of the condensate. In terms of dimensionless functions, the active components of the energy-momentum tensor (
18) are:
The rest energy of massive bosons of the Standard Model is of the order of 100 GeV. Based on the bosons of the Standard Model, for quantitative estimates, I am going to assume the boson rest mass to be:
The corresponding de Broglie wavelength
ƛ is:
The scales of the energy density
and particle density
are of the order:
4. In the Vicinity of a Gravitational Radius
Denote the dimensionless gravitational radii:
Equations (
21)–(
24) are defined separately in three intervals:
and
They are not defined at
and at
because, on these hyperspheres, the coefficient at the highest derivative in the scalar field Equation (
17) is zero. Hyperspheres
and
are the outer boundaries of intervals where Equations (
21)–(
24) satisfy the theorem of existence and uniqueness.
It follows from Equation (
24) that at
(
means from above and
from below):
Here,
are one-sided limits either from above or from below. The energy-momentum tensor (
18) is regular at
where
For this reason, the dimensionless wave function
should be continuous at
Substituting (
31) into Equation (
23), we obtain:
Without elasticity
, the derivative (
33) reduces to Equation (29) in [
16]. With the account of elasticity, or without,
is a linear regular function at the gravitational radius
The derivative
does not depend on the behavior of
and
at
. The assumption of linearity for
at
is not required in advance.
It follows from Equations (
31) and (
33) that:
On the left-hand side,
; thus, the right-hand side of (
34) is also a positive quantity. The derivative
in (
33) is a non-zero constant. The factor
in (
34) changes sign at
. Therefore, the combination
in square brackets has different signs at
and
As far as
the expression (
34) makes sense if
at
and
at
Therefore, the combination
either vanishes at
or its sign is different at
and at
In the latter case
and
has a gap. As applied to our two gravitational radii (
30),
is a regular gravitational radius and
is the termination point.
4.1. Regular Gravitational Radius
Since the components
and
(
32) of the energy-momentum tensor have no singularity at
, it is natural to assume that the component
of the metric tensor is a continuous function:
Moreover, the functions
,
are continuous at
also. In accordance with (
31),
at
In addition to
(
33), we find the derivatives
and
at
from Equations (
22) and (
24):
The connection (
35) separates a regular solution to Equations (
21)–(
24), continuous at the interface
between the regions of different signatures of the metric tensor:
It is convenient to use these relations as boundary conditions in the close vicinity of the interface The numerical integration has to be carried out separately for both sides.
There are three free dimensionless parameters
,
and
Parameter
characterizes the elasticity of the condensate. In the model “
”, dimensionless
is a constant, independent of the density. One of the two remaining degrees of parametric freedom has to be used to ensure regularity in the center:
. The last degree of freedom allows determining the equilibrium structure of the gravitating Bose–Einstein condensate as a function of its total mass. The search for a regular static solution to the system of Equations (
21)–(
24) for a gravitating condensate of finite total mass is a nonlinear eigenvalue problem.
4.2. Event Horizon
Since the roles of all three degrees of parametric freedom have already been distributed, the second dimensionless gravitational radius
has to be the termination point: in accordance with (
11),
is the dimensionless radius of the sphere bounding the volume occupied by the condensate. For a remote observer,
is the event horizon.
The area
is a layer with the violated signature
of the metric tensor.
in this zone. In this interval, the functions
, and
satisfy Equations (
21)–(
24) with boundary conditions (
37). At
, the energy density vanishes (
11). Comparing
(
10) with (
33), valid for both cases
and
, we find that at the termination point
(on the event horizon), the scalar field
is nonzero:
Since the radius
of the horizon is proportional to the total mass
M of the condensate (
9), the density of a condensate at the termination point is inversely proportional to the square of total mass,
On the surface of a supermassive black hole, the term
in the potential (
16) is a negligible correction in view of (
38).
According to (
12), the pressure on the surface is also inversely proportional to the square of total mass. However, the pressure does not vanish at
A static state of a Bose–Einstein condensate with an uncompensated sharp surge of pressure at the interface with a vacuum cannot exist. However, this is without dark matter. The presence of dark matter outside the condensate can make it possible to ensure the pressure balance at the interface of these two media [
16]. The pressure balance allows establishing a connection between the parameters of a black hole and dark matter. In particular, the dependence of the plateau velocity of a galaxy rotation curve on the mass of a black hole is determined; see (68) in [
16].
At
in the close vicinity of the event horizon
its derivative
(
10), the metric component
and
In the close vicinity of the event horizon
, Equations (
21), (
22), and (
24) are simplified. The density
terminates with a nonzero value in a square root manner:
At
, the logarithmic derivative of the metric component
grows as the inverse square root:
Gravitational force, acting on a test body, is proportional to
([
20], Problem 1 at the end of §88). It is directed toward the center. The sphere
is impenetrable from the inside.
The density and pressure of the condensate decrease with distance from the center. The lifetime of the Standard Model bosons drops down with decreasing pressure. Therefore, the concentration of dominant bosons decreases with the distance from the center. The composition of matter within a black hole is a continuous quark-to-neutron transition from the center toward the surface. Changes in the composition of matter are not taken into account by the “
” model. If the composition in the near-surface zone differs from the central one, then the sharp root-like growth of
at
(
39) can become smoothed out. Some more features of the composition of a black hole depending on its mass are discussed below in
Section 5. The structure of the shell of a black hole is a worthy topic for further consideration.
6. Conclusions
After I replaced the constraint by a weaker requirement of regularity (all invariants of are finite), it became possible to find a regular static spherically symmetric solution to the Einstein equations with no restriction on mass. Regular static solutions to the Einstein equations, with no limitation on mass, describe the state of a black hole to which the gravitational collapse leads. By not using the representation that fixes the sign, I avoided long-standing problems, such as: a singularity in the center and the incompleteness of the reference frame in the Schwarzschild solution; how the process of unlimited compression of a black hole can continue throughout the entire lifetime of the Universe. Previously unknown static solutions, describing the states of ultimately compressed black holes, confirm that a static state of matter with the ultra relativistic equation of state does not contradict Einstein’s general theory of relativity.
The price for the static solution is the existence of a spherical layer with a broken metric signature . This layer is located beyond the event horizon. Though it does not lead to logical contradictions, the physical meaning of a layer with the metric signature still has to be understood.