1. Introduction
Do we live inside a computer simulation? Skepticism about our perceptions of reality have existed for centuries, such as the “Buttlerfly Dream” in
Zhuangzi or Plato’s Cave. However, the development of ever more sophisticated computers in the modern era has led to a resurgence of interest in the possibility that what we perceive as reality may in fact be an illusion, simulated in some inaccessible reality above us. Bostrom [
1] formalized this possibility in his simulation argument, suggesting that one of three distinct propositions must be true.
“The fraction of human-level civilizations that reach a posthuman stage (that is, one capable of running high-fidelity ancestor simulations) is very close to zero”;
“The fraction of posthuman civilizations that are interested in running simulations of their evolutionary history, or variations thereof, is very close to zero”;
“The fraction of all people with our kind of experiences that are living in a simulation is very close to one”.
The simulation argument has grown in public attention in recent years, in part due to well-known figures such as Elon Musk expressing support for the idea, with statements such as “there’s a billion to one chance we’re living in base reality” [
2]. Perhaps as a product of this, the media has often described the idea as not just a possibility but in fact a high probability (e.g., [
3,
4]), which would correspond to proposition 3 of Bostrom [
1], and thus the rejection of proposition 1 and 2. However, this conditional remains unproven and thus propositions 1 and 2 remain viable and consistent with our knowledge and experience.
The simulation argument is not without counter-argument. One approach to countering the idea is to ask whether a Universe-level simulation is even possible given our understanding of the laws of nature, in other words advocating for proposition 1 [
5,
6,
7]. For example, Ringel and Kovrizhin [
7] argue that simulating quantum systems is outside the scope of physical plausibility. This physical argument quickly runs into a more metaphysical obstacle though if we concede that the possibility that our observations and understanding of physics may in fact be simulated. In such a case, our knowledge of physics is wholly local to the simulation and may have no real bearing on the constraints that affect a parent reality, whose rules and limitations may be entirely different. Moreover, such a detailed quantum-level simulation may not even be necessary to convincingly emulate reality. Reality could be rendered in real-time locally to deceive
1 the inhabitants, rather than attempting to generate the entire system at once. Indeed, quantum systems need not truly be emulated, only our perceived observations of those systems, which may be far easier.
On this basis, it is suggested that physical arguments cannot convincingly reject the simulation argument. Nevertheless, they clearly highlight how it cannot be trivially assumed that proposition 1 is unquestionably true. What other lines of reasoning might offer insight here?
At its core, the simulation hypothesis concerns a statistical argument, so let us consider using statistical theory to address the question. Statements such as Elon Musk’s “billion to one chance” have popularized the position of high statistical confidence associated with this argument. That position stems from a frequentist perspective: count-up how many simulated realities there are versus non-simulated ones and use that ratio to make deduction. However, it is flawed because it tacitly discounts propositions 1 and 2. It is useful to combine these two propositions into a single hypothesis since their outcome is the same, whether by capability or choice, we will not simulate realities in which conscious self-aware beings one day reside. For notational convenience, let us dub this the “physical hypothesis”, . As the last of three mutually exclusive propositions, proposition 3 necessarily requires that propositions 1 and 2 are false, making false. We dub this alternative hypothesis as ), the hypothesis that Bostrom-like simulations are run by posthuman civilizations.
Certainly, if we reject outright, then would be true by deduction and thus the probability that we are the base civilization is small via proposition 3. However, this is a clearly presumptive approach, unless one had some unambiguous evidence that could fully exclude . A rigorous statistical treatment should weigh the hypotheses appropriately and assign probabilities which concede this possibility. This is accomplished through a Bayesian framework of probability, which is presented in what follows.
2. A Statistical Analysis of the Simulation Argument
As argued in the introduction, an evaluation of the probability that we live in a simulated reality is best tackled from a Bayesian perspective. The key to Bayesian statistics is Bayes’ theorem, which relates conditional probabilities to one another. We note that arguments based on conditional probability theory have been made previously, such as Weatherson [
8]. In this work, a deeper Bayesian approach is sought using the methods of model selection and model averaging, in order to more directly evaluate a quantitive measure of the probability that we live in a simulation.
To accomplish this, it is necessary to first establish results pertaining to the likelihood of observing reality as we perceive it (our data) under each hypothesis under consideration (in our case and ).
2.1. Dreams within Dreams
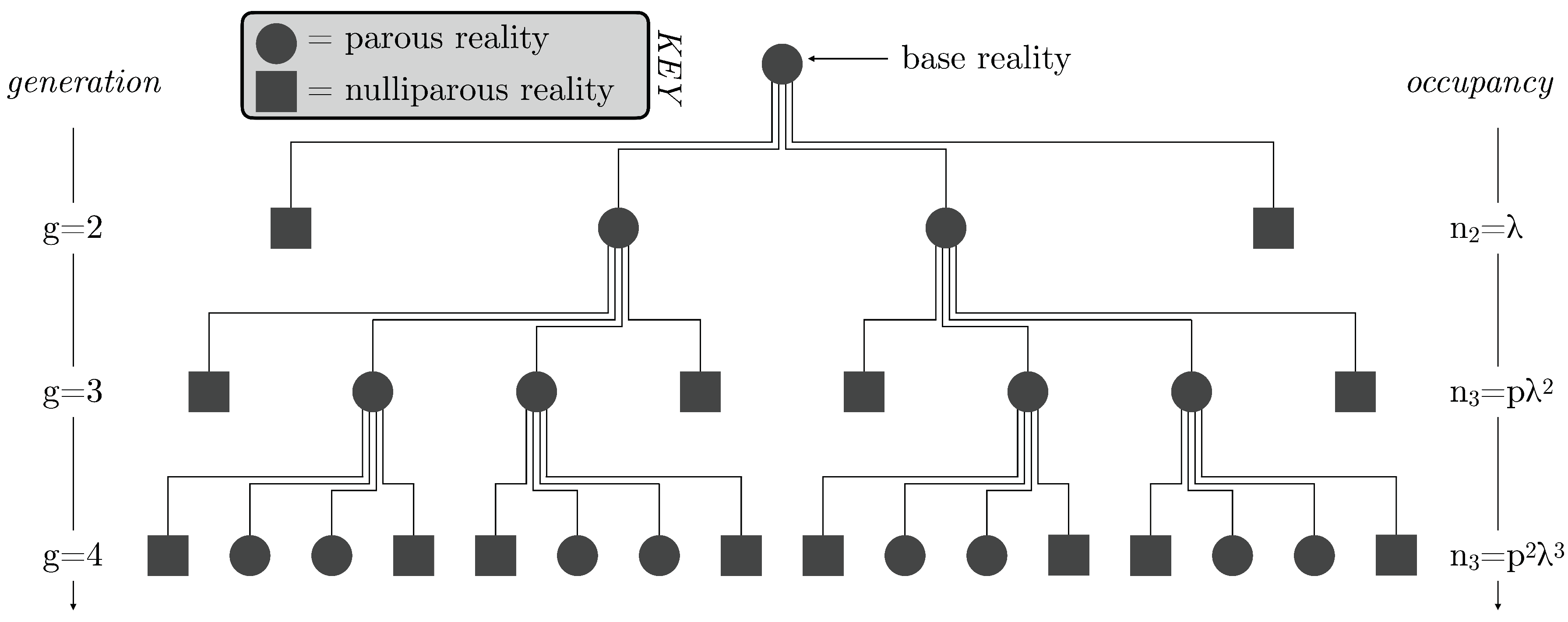
We begin with the hypothesis , which describes proposition 3. Let us consider that there exists a base civilization, which is responsible for creating a suite of simulated realities. This base civilization is referred to as representing generation and its “daughter” simulations as .
Each of these daughter simulations has a probability
p of itself going on to create a suite simulations within its simulated reality, dreams within dreams. These parous realities produce a
generation, which can itself then create more simulations, and so on. This creates a hierarchy of simulations, with the base civilization—representing the only non-simulated reality—sat at the top, as depicted in
Figure 1.
This work treats this hierarchy as representing the ensemble of simulated realities that will ever exist, over all times. It is suggested that it is more constructive to pose the problem in this way, because within the simulated realities, time itself is a construct. It does not really make much sense to talk about the “passage of time” within these realities, since they may not align to any real world chronological definitions. They may occur almost instantaneously, played out at some scaled version of time, or something in-between with the simulation paused, sped-up, slowed-down at arbitrary points.
Given that our hierarchy represents the ensemble of all realities that will ever exist, one might wonder how deep the rabbit hole goes. We suggest that there should exist some limit to how deep the generations can indeed go, some maximum value for g, denoted by G. This is motivated by the fact the base civilization is truly responsible for simulating all of the daughters beneath it, and it presumably has some finite computational limit at its disposal. By spreading this computational power amongst second-generation daughters, each of those simulations necessarily has less computational resources than the base civilization devoted to creating simulations. In fact, a second-generation civilization has even less capacity than this since some finite fraction of this resource is being used to generate the reality around it, besides from computers within that reality. More generally, generation g has a computational resource of less than that which the base civilization devotes to simulation work.
Given that each generation has less computational power than the last, one might suggest that this implies that and p should decrease as g increases. This is certainly possible, but it is not strictly necessary—p and could remain approximately constant with respect to g with the simulations just becoming coarser in fidelity at each level, smaller in volume, poorer in detail. This might be expected is the sims are modeled upon the parent, with similar motivations and judgement. Despite this, even at some very deep level, the volume and fidelity may be perfectly sufficient to emulate what we recognize as reality. For this reason, it is argued here that there is not a good justification for invoking a variable model for and p, which would only serve to add more complexity than warranted given our state of knowledge of the system.
Nevertheless, the finite computational power will impose some limit on g, denoted by G. Accordingly, from the perspective of the last generation, it is technically impossible to ever build a computer capable of simulating any kind reality where conscious beings reside. Their simulations would instead be limited to more simplified programs, surely impressive still, but not sufficient to create beings of the same conscious, self-aware experience of reality that we enjoy.
Before proceeding, we briefly mention that although what follows is a statistical calculation, the model is itself deterministic rather than probabilistic. For example each parent simulation spawns the same number of simulations. More realistically, we should expect the number to be a random variate drawn from some underlying distribution. Whilst it may be interesting to calculate that more mathematically challenging case, we argue here that it is somewhat unnecessary as even this single argument will be sufficient given the extremely limited knowledge about the details of the simulated realities, and again we favour invoking as simple a model as tenable given our great lack of knowledge about simulated realities.
2.2. Simulation Counting
It is straight-forward to work through the first few generations and evaluate the number of simulations in play. The second generation () will contain simulations, of which will themselves be parous. If each of these simulations yield simulations themselves, then one arrives at simulations in the third generation. Following this, one may show that in the generation there are simulations.
We can now calculate the total number of simulated realities using the formula
where
G is the total number of generations. Before proceeding, it is useful to calculate a couple of useful results using this formula. First, within the scenario described, the vast majority of realities are of course simulated. This really forms the basis of the oft-quoted statement that we most likely live in a simulation. Let us write that the probability that we live in a simulation, given a conditional denoted by CES, and also given that hypothesis
holds, is
What is this CES conditional? In Bayesian statistics, our inferences are always conditioned upon some data/experience, otherwise one is simply left with the prior beliefs. Since the simulation argument is one of skepticism, it plausibly opens a slippery slope where essentially any conditional information could be treated skeptically. For example, if our data is that X humans have lived thus far prior in the pre-simulation era, that could be challenged on the basis that our memories and records of how many humans have lived is also simulated, and indeed our existence could be as nascent as a few minutes ago [
9]. In the face of such skepticism, the only conditional upon which we can affirm any confidence is characterized by René Descartes’ famous “cogito, ergo sum”—CES. In this work, the conditional here really just describes the fact that we are self-aware thinking beings that live in some kind of reality, whether it be real or not.
We note that the number of simulations grows exponentially with each generation, such that the last generation,
, contains a substantial fraction of the total number, given by
In the limit of large
G, or really that
, this becomes
Thus, for all , most realities reside in the lowest level of the hierarchy.
2.3. Counting Nulliparous Simulations
Let us now consider that we have access to an additional piece of information: we do not live in a reality that has spawned simulated realities, we are in a nulliparous reality. This new conditional information supplants “cogito, ergo sum” when available, since it implicitly includes that statement.
It is noted that Poundstone [
10] qualitatively describes an ostensibly similar conditional by distinguishing between people/sims that live before and after the invention of simulation technology. Critically though, Poundstone [
10] consider the problem in terms of the number of individuals that live before and after this time, which introduces analogous issues of reference class choices and self-sampling measures [
11] that have often been central in debates concerning the related Doomsday argument [
12,
13,
14,
15,
16,
17]. It also depends on the assumption that civilizations capable of running simulations will persist far beyond the dawn of simulation technology, so much so that most ancestor simulations are of epochs after it is invention. No such assumptions will be made in what follows, in an effort to cast the problem in a more agnostic light.
As before, we continue to work under the conditional hypothesis of . Under this hypothesis, the base civilization must be parous, for if it were nulliparous then there would no simulated realities and propositions 1 or 2 would be in effect, which are mutually exclusive with proposition 3 (which in turn defines ). Since the base civilization is parous, then the conditional information that our existence is nulliparous would immediately establish that we are not the base civilization (under the conditional of hypothesis ).
One can distinguish between two forms of nulliparity. The first is simply that we live at the bottom of the hierarchy, the sewer of reality. After all, Equation (
4) establishes that these base simulations make up the majority of all realities
2. In such a case, the computational power available to the sentient beings within those realities would simply be insufficient to feasibly ever generate daughter simulations capable of sentient thought themselves. Here, then, proposition 2 is in effect.
As pointed out by Sean Carroll, this poses somewhat of a contradiction [
18]. If proposition 3 is true then, then it is possible to simulate realities, and via Equation (
2) we most likely live in a simulation, and yet more via Equation (
4) it is most likely a lowest level simulation, who are incapable of simulating reality. The conclusion that we most likely live in a reality incapable of simulating reality, yet have assumed simulating reality is possible, forms Carroll’s contradiction. We suggest here that this contradiction can somewhat dissolved by the considering that the lowest level may indeed not be capable of generating their own reality simulations, but are plausibly capable of still making very detailed simulations that fall short of generating sentience. Accordingly, they would still suggest that it might be at least possible to simulate realities and arrive at Bostom’s trilemma all the same.
The less likely possibility is that we live in some higher level, but one of the realities that has not produced a daughter—which could be because of either proposition 1 or 2.
The total number of simulated realities between level
and
multiplied by
will yield the number of nulliparous simulations which do not reside in the lowest level, given by
Adding this to the full membership of the lowest generation of the hierarchy yields the total number of nulliparous simulated realities:
Accordingly, nulliparous simulations represent the following fraction of all realities
where one can see that in the limit of large
G this just becomes
2.4. The Physical Hypothesis
We have now derived the necessary results to evaluate hypothesis
, but when evaluating models in Bayesian statistics it is always necessary to compare it to some alternative(s)—in our case
. In this hypothesis,
, the probability that we are nulliparous is unity by construction of the hypothesis’ definition:
Similarly, it is trivial to also write that
2.5. Bayes Factors Conditioned Upon Nulliparity
Let us finally turn to evaluating a Bayes factor, the metric of Bayesian model comparison, between the two models. In what follows, we use the nulliparous observation as a piece of information to condition our inference upon, but will relax this after to explore its impact.
In general, we can write the odds ratio between hypotheses
and
, conditioned upon some data
:
The prior ratio is generally set as unity for models with no a-priori preference between them, such that the odds ratio equals the Bayes factor. This is often dubbed the “Principle of Indifference”, argued for by Pierre-Simon Laplace, and can be thought of as a vague prior. In our case, the “data” we leverage is that we are nulliparous when it comes to simulating realities. We may thus write out the Bayes factor in the above using Equations (
8) and (
9) to give
Since can be an arbitrarily large number, then this implies the Bayes factor is close to unity. In other words, it is approximately just as likely that hypothesis is true as the physical hypothesis, given the fact we live in a nulliparous reality. However, since is always a finite number, then in fact the Bayes factor is , which means that there is a slight preference for the physical hypothesis.
2.6. Understanding the Transition from Near-Certainty to Ambiguity
When we condition our inference on the fact that we are a nulliparous reality, and employ a simple but instructive model describing a hierarchical simulated reality, we find that the Bayes factor is close to unity. In other words, there is no statistical preference for the simulation hypothesis over the null hypothesis of a physical reality.
So what changed in the statistical reasoning presented here versus the more commonly quoted conclusion that we are statistically very likely to live in a simulated reality? After all, this is a rather dramatic turn around in conclusion given that the simulation hypothesis has conventionally been framed as a statistical argument and that is the line of reasoning used in this work.
There are two modifications to our thinking here than are not usually described in arguments regarding the simulation hypothesis. The first is that we have included this extra conditional information of nulliparity. The second is that we have used Bayesian statistics. So we briefly consider these in turn to evaluate where the argument changed.
2.6.1. Neglecting our Nulliparity
Our existence as a nulliparous reality has been used as the data upon which our Bayesian inference is conditioned, but let us now ignore that data and repeat the Bayes factor calculation without it, to see how the conclusions change. In the absence of this information, what other information are we going to condition our inference upon? The only real “data” left is CES.
Before we can write down the revised Bayes factor, we first need to ask, what is the probability of finding ourselves in a reality under the simulation hypothesis, i.e., ? Of course the answer is one, all simulations in the hierarchy are realities from the perspective of the inhabitants. This conditional was implicitly present in the previous inference too but now we explicitly write it out since there is an absence of any other information. Similarly, for the physical hypothesis, we have .
This means that the Bayes factor is straight-forwardly:
If we compare this to Equation (
12), it is almost identical—there too we obtained nearly even odds between the two hypotheses. Therefore, this reveals that our modification of including the nulliparous information is not responsible for the revised conclusion of ∼50:50 odds for the simulation hypothesis. By deduction, that indicates that it is the Bayesian treatment of probabilities that must be responsible.
2.6.2. Negating Bayesian Model Comparison
To demonstrate this, let us see if we can recover the often claimed conclusion that statistically we are more likely to live a simulation than reality by sheer numbers. This is straight-forward to see when one operates under the tacit assumption that the is true. If we assert that is true, then the vast majority of realities are indeed simulated. However, the fallacy of this argument is that we have already assumed it is correct, whereas the Bayes factors derived earlier compare the hypothesis that it is/it is not true. This is the key difference driving the radically different conclusions.
To show this, let us now treat
as a fixed conditional. We can no longer ask if the simulation hypothesis, as defined by
is true, since it is asserted as so. Instead, we ask what is the probability that
(we are the first generation in the hierarchy) given that we exist?
Since the number of simulations can be very large, this recovers the conventional conclusion that we are almost certainly living in a simulation. This is really just a frequentist argument and is clearly conditional upon the simulation hypothesis itself already being true.
We can also modify the above to include the conditional that we exist in a nulliparous reality, as before. Given that only simulated realities exist in such a state in the hypothesis , then this simply yields .
2.7. Bayesian Model Averaging with the “Cogito, Ergo Sum” Conditional
Thus far we have evaluated (i) the probability that we are the base reality when proposition 3/hypothesis is true (a very small number); (ii) the probability that we are in the base reality when is true (which is trivially 1); and (iii) the Bayes factor between hypotheses and ,
The latter does not quite provide a direct answer to the question as to whether we live inside a simulation though, since one of the realities embedded within is real—namely the base reality. However, ideally we would combine these three results to evaluate the probability that marginalized over our uncertainty about which hypothesis is correct.
This can actually be formalized through the use of Bayesian model averaging. Let us say we wish to evaluate the probability that
(i.e., we are the first generation) as we did in Equation (
14), but now we wish to relax the conditional assumption made earlier that
is assumed to be true. Instead, we can calculate the probability that
for both hypotheses weighted by their model evidence in their favour, known as Bayesian model averaging. By doing so, we incorporate our ignorance about which model is correct. This essentially looks like a discrete marginalization over hypothesis-space:
We may now use results from earlier, including Equation (
14), to re-write this as
From Equation (
13), we have
and so using Bayes’ theorem this becomes
To make progress, we must assign the prior hypothesis probabilities, which is typically simply set to unity as an uninformative choice, giving
We also exploit the fact that the sum of all probabilities must equal one, such that
Simultaneously solving the last two equations gives
Finally, plugging this back into Equation (
16) gives
From the above, we have that the probability that we live in the base reality, , is one-half plus some additional term which depends on the number of simulations in the simulation hypothesis, . Since , then as expected. This means that for all , asymptotically tending towards one half in the limit of large . On this basis, it is in fact more likely that we live in the base reality than a simulation, although it may be only very slightly more preferable depending on one’s assumptions for .
2.8. Bayesian Model Averaging with the Nulliparous Conditional
For completion, we will now repeat the previous subsection but replace the conditional “in a reality” with the nulliparous case.
In this case the likelihoods are binary, giving
The Bayes factor between the two models, from Equation (
12), can be written (in the limit of large
G) as
which again we simplify by invoking even a-priori odds between the models
We combine this with the fact that sum of the probabilities equals one, as before, to write that
Note that in the simulation hypothesis, within which finds its definition, that the term is . Examination of our formula indeed reveals, as before that, , with the formula asymptotically tending towards a half (but always remaining greater than it) for large . As also with before then, the conclusion is that we are more likely to be living in the reality, although perhaps only with slight preference.
2.9. What If We Were Parous?
Although we are presently not a parous reality, it is interesting to consider how the results derived thus far would change if tomorrow we began producing Bostrom-like simulations. For hypothesis
, it is simple to write that
Through Bayesian model averaging, we have that the probability of
, with the condition of being parous, is given by
The second row goes to zero since
via Equation (
28).
Since
, then
by requirement that the probabilities sum to one.
Under hypothesis
, we have already calculated that a fraction
are nulliparous via Equation (
8). Accordingly, one minus this are parous, which equals
. The total number of parous realities is therefore
. Only one of these is the base reality, and so we have
For large G, and thus this probability approaches zero. Accordingly, if we become a parous reality, in other we start producing Bostrom-like simulations, the probability that we live in a simulated reality radically shifts from just below one-half to just approaching zero.
3. Discussion
In this work, we have divided the three propositions of Bostrom [
1] into two hypotheses: one where simulated realities are produced (
) and one where they are not (
). Comparing the models with Bayesian statistical methods, it is found that that the Bayes factor is approximately unity, with a slight preference towards
. Whilst the Bayes factor can be objectively stated without the need to assign any priors, the odds ratio between the two models depends on the prior model probabilities (
). A standard choice is to assume all models are a-priori as likely as each other, but this could be challenged as being too generous to model
, on the basis that it is an intrinsically far more complex model.
If one goes further and assigns a value to the ratio of the prior model probabilities, then one can use Bayesian model averaging to marginalize over the models, weighted by their posterior probabilities. If one does not penalize the model for its complexity and simply assigns even a-priori odds, then it is still found that the probability we live in base reality—after marginalizing over the model uncertainties—is still not the favored outcome, with a probability less than 50%. As the number of simulations grows very large, this probability tends towards 50%, and thus it is argued here that the most generous probability that can be assigned to the idea that we live inside a simulation is one half.
It is argued that the results presented are robust against the choice of self sampling. For example, if one replaced the conditionals used here, which describe the reality in which one finds oneself, with the number of sims in each state/reality, this would not noticeably affect the results under the assumption that the number of sims per reality is evenly distributed. This is because our results asymptotically tend towards 50% in the case of a large number of realities, but that would be equally so if one replaced realities with sims instead, which would display the same asymptotic behaviour.