Radiation Problems Accompanying Carrier Production by an Electric Field in the Graphene
Abstract
1. Introduction
2. Kinetic Equations Describing Quantum Excitations in Graphene Placed in an Electric Field
2.1. Kinetic Equations Describing Zero Order Processes
2.2. Inclusion an Interaction with Quantized Electromagnetic Field
3. Setting of the Problem
4. Studying Processes in Specific External Fields
4.1. Models of External Fields
4.2. Low-Density Approximation
4.3. Calculating Kernels
5. Spectral Composition of Quantum Radiation
5.1. Annihilation Channel
5.2. Channel of the Momentum Redistribution
5.3. Comments on the Results Obtained
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| KE | kinetic equation |
| CI | collision integral |
| eh | electron-hole |
| BBGKY | Bogoliubov–Born–Green–Kirkwood–Yvon |
References
- Klein, O. Die Reflexion von Elektronen an einem Potentialsprung nach der relativistischen Dynamik von Dirac. Z. Physik 1929, 53, 157–165. [Google Scholar] [CrossRef]
- Klein, O. Elektrodynamik und Wellenmechanik vom Standpunkt des Korrespondenzprinzips. Z. Physik 1927, 41, 407–442. [Google Scholar] [CrossRef]
- Sauter, F. Über das Verhalten eines Elektrons im homogenen elektrischen Feld nach der relativistischen Theorie Diracs. Z. Physik 1931, 69, 742–764. [Google Scholar] [CrossRef]
- Sauter, F. Zum “Kleinschen Paradoxon”. Z. Physik 1932, 73, 547–552. [Google Scholar] [CrossRef]
- Schwinger, J. On Gauge Invariance and Vacuum Polarization. Phys. Rev. 1951, 82, 664–679. [Google Scholar] [CrossRef]
- Nikishov, A.I. Pair Production by a Constant Electric Field. Sov. Phys. JETP 1970, 30, 660–663. [Google Scholar]
- Nikishov, A.I. Barrier scattering in field theory removal of Klein paradox. Nucl. Phys. B 1970, 21, 346–358. [Google Scholar] [CrossRef]
- Nikishov, A.I. Problems of intense external-field intensity in quantum electrodynamics. J. Russ. Laser Res. 1985, 6, 619–717. [Google Scholar] [CrossRef]
- Narozhnyi, N.B.; Nikishov, A.I. The Simplist processes in the pair creating electric field. Sov. J. Nucl. Phys. 1970, 11, 596. [Google Scholar]
- Narozhnyi, N.B.; Nikishov, A.I. Pair production by a periodic electric field. Sov. Phys. JETP 1974, 38, 427. [Google Scholar]
- Ruffini, R.; Vereshchagin, G.; Xue, S. Electron-Positron Pairs in Physics and Astrophysics: From Heavy Nuclei to Black Holes. Phys. Rep. 2010, 487, 1–140. [Google Scholar] [CrossRef]
- Gelis, F.; Tanji, N. Schwinger mechanism revisited. Prog. Part. Nucl. Phys. 2016, 87, 1–49. [Google Scholar] [CrossRef]
- Gitman, D.M. Processes of arbitrary order in quantum electrodynamics with a pair-creating external field. J. Phys. A 1977, 10, 2007. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Gitman, D.M. Furry Picture for Quantum Electrodynamics with Pair-Creating External Field. Fortschr. Phys. 1981, 29, 381–412. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Gitman, D.M.; Shvartsman, S.M. Quantum Electrodynamics with Unstable Vacuum; Springer: Berlin/Heidelberg, Germany, 1991; ISBN 978-3-642-84260-3. [Google Scholar]
- Hansen, A.; Ravndal, F. Klein’s Paradox and Its Resolution. Phys. Scr. 1981, 23, 1036. [Google Scholar] [CrossRef]
- Gavrilov, S.P.; Gitman, D.M. Quantization of charged fields in the presence of critical potential steps. Phys. Rev. D 2016, 93, 045002. [Google Scholar] [CrossRef]
- Bagrov, V.G.; Gitman, D.M.; Shvartsman, S.M. Concerning the production of electron-positron pairs from vacuum. Sov. Phys. JETP 1975, 41, 191–194. [Google Scholar]
- Gavrilov, S.P.; Gitman, D.M. Vacuum Instability in External Fields. Phys. Rev. D 1996, 53, 7162. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Frolov, V.M. Production of particles from vacuum by a uniform electric-field with periodic time-dependence. Sov. J. Nucl. Phys. 1974, 19, 451–456. [Google Scholar]
- Adorno, T.C.; Gavrilov, S.P.; Gitman, D.M. Particle creation from the vacuum by an exponentially decreasing electric field. Phys. Scr. 2015, 90, 074005. [Google Scholar] [CrossRef]
- Adorno, T.C.; Gavrilov, S.P.; Gitman, D.M. Particle creation by peak electric field. Eur. Phys. J. C 2016, 76, 447. [Google Scholar] [CrossRef]
- Adorno, T.C.; Ferreira, R.; Gavrilov, S.P.; Gitman, D.M. Peculiarities of Pair Creation by a Peak Electric Field. Russ. Phys. J. 2017, 60, 417. [Google Scholar] [CrossRef]
- Adorno, T.C.; Gavrilov, S.P.; Gitman, D.M. Exactly solvable cases in QED with t-electric potential steps. Int. J. Mod. Phys. A 2017, 32, 1750105. [Google Scholar] [CrossRef]
- Adorno, T.C.; Ferreira, R.; Gavrilov, S.P.; Gitman, D.M. Role of switching-on and -off effects in the vacuum instability. Int. J. Mod. Phys. A 2018, 33, 1850060. [Google Scholar] [CrossRef]
- Adorno, T.C.; Gavrilov, S.P.; Gitman, D.M. Violation of vacuum stability by inverse square electric fields. Eur. Phys. J. C 2018, 78, 1021. [Google Scholar] [CrossRef]
- Gavrilov, S.P.; Gitman, D.M. Scattering and pair creation by a constant electric field between two capacitor plates. Phys. Rev. D 2016, 93, 045033. [Google Scholar] [CrossRef]
- Gavrilov, S.P.; Gitman, D.M.; Shishmarev, A.A. Particle scattering and vacuum instability by exponential steps. Phys. Rev. D 2017, 96, 096020. [Google Scholar] [CrossRef]
- Adorno, T.C.; Gavrilov, S.P.; Gitman, D.M. Vacuum instability in a constant inhomogeneous electric field: A new example of exact nonperturbative calculations. Eur. Phys. J. C 2020, 80, 88. [Google Scholar] [CrossRef]
- Dunne, G.V. New strong-field QED effects at extreme light infrastructure. Eur. Phys. J. D 2009, 55, 327–340. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Peres, N.M.R. Colloquium: The transport properties of graphene: An introduction. Rev. Mod. Phys. 2010, 82, 2673. [Google Scholar] [CrossRef]
- Vozmediano, M.A.H.; Katsnelson, M.I.; Guinea, F. Gauge fields in graphene. Phys. Rep. 2010, 496, 109–148. [Google Scholar] [CrossRef]
- Das Sarma, D.; Adam, S.; Hwang, E.H.; Rossi, E. Electronic transport in two-dimensional graphen. Rev. Mod. Phys. 2011, 83, 407. [Google Scholar] [CrossRef]
- Semenoff, G.W. Condensed-Matter Simulation of a Three-Dimensional Anomaly. Phys. Rev. Lett. 1984, 53, 2449. [Google Scholar] [CrossRef]
- Allor, D.; Cohen, T.D.; McGady, D.A. The Schwinger mechanism and graphene. Phys. Rev. D 2008, 78, 096009. [Google Scholar] [CrossRef]
- Dóra, B.; Moessner, R. Nonlinear electric transport in graphene: Quantum quench dynamics and the Schwinger mechanism. Phys. Rev. B 2010, 81, 165431. [Google Scholar] [CrossRef]
- Lewkowicz, M.; Rosenstein, B. Dynamics of Particle-Hole Pair Creation in Graphene. Phys. Rev. Lett. 2009, 102, 106802. [Google Scholar] [CrossRef]
- Rosenstein, B.; Lewkowicz, M.; Kao, H.C.; Korniyenko, Y. Ballistic transport in graphene beyond linear response. Phys. Rev. B 2010, 81, 041416(R). [Google Scholar] [CrossRef]
- Kao, H.C.; Lewkowicz, M.; Rosenstein, B. Ballistic transport, chiral anomaly, and emergence of the neutral electron-hole plasma in graphene. Phys. Rev. B 2010, 82, 035406. [Google Scholar] [CrossRef]
- Lewkowicz, M.; Kao, H.C.; Rosenstein, B. Signature of the Schwinger pair creation rate via radiation generated in graphene by a strong electric current. Phys. Rev. B 2011, 84, 035414. [Google Scholar] [CrossRef]
- Vandecasteele, N.; Barreiro, A.; Lazzeri, M.; Bachtold, A.; Mauri, F. Current-voltage characteristics of graphene devices: Interplay between Zener-Klein tunneling and defects. Phys. Rev. B 2010, 82, 045416. [Google Scholar] [CrossRef]
- Gavrilov, S.P.; Gitman, D.M.; Yokomizo, N. Dirac fermions in strong electric field and quantum transport in graphene. Phys. Rev. D 2012, 86, 125022. [Google Scholar] [CrossRef]
- Gavrilov, S.P.; Gitman, D.M. Radiative Processes in Graphene and Similar Nanostructures at Strong Electric Fields. Russ. Phys. J. 2017, 59, 1870–1874. [Google Scholar] [CrossRef][Green Version]
- Popov, V.S.; Marinov, M.S. e+e--Pair production in variable electric field. Sov. J. Nucl. Phys. 1973, 16, 449. [Google Scholar]
- Grib, A.A.; Mamaev, S.G.; Mostepanenko, V.M. Vacuum Quantum Effects in Strong Fields; Friedmann Laboratory Publishing: St. Petersburg, Russia, 1994. [Google Scholar]
- Bialynicky-Birula, I.; Gornicki, P.; Rafelski, J. Phase space structure of the Dirac vacuum. Phys. Rev. D 1991, 44, 1825. [Google Scholar] [CrossRef]
- Schmidt, S.M.; Blaschke, D.; Röpke, G.; Smolyansky, S.A.; Prozorkevich, A.V.; Toneev, V.D. A Quantum kinetic equation for particle production in the Schwinger mechanism. Int. J. Mod. Phys. E 1998, 7, 709–718. [Google Scholar] [CrossRef]
- Kluger, Y.; Mottola, E.; Eisenberg, J. Quantum Vlasov equation and its Markov limit. Phys. Rev. D 1998, 58, 125015. [Google Scholar] [CrossRef]
- Mamaev, S.G.; Trunov, N.N. Vacuum polarization and particle production in a non-stationary homogeneous electromagnetic field. Sov. J. Nucl. Phys. 1979, 30, 677. [Google Scholar]
- Dumlu, C.K. Quantum kinetic approach and the scattering approach to vacuum pair production. Phys. Rev. D 2009, 79, 065027. [Google Scholar] [CrossRef]
- Fedotov, A.M.; Gelfer, E.G.; Korolev, K.Y.; Smolyansky, S.A. Kinetic equation approach to pair production by a time-dependent electric field. Phys. Rev. D 2011, 83, 025011. [Google Scholar] [CrossRef]
- Blaschke, D.B.; Smolyansky, S.A.; Panferov, A.D.; Juchnowski, L. Particle Production in Strong Time-dependent Fields. arXiv 2017, arXiv:1704.04147. [Google Scholar]
- Smolyansky, S.A.; Panferov, A.; Blaschke, D.; Gevorgayn, N. Nonperturbative Kinetic Description of Electron-Hole Excitations in Graphene in a Time Dependent Electric Field of Arbitrary Polarization. Particles 2019, 2, 208–230. [Google Scholar] [CrossRef]
- Panferov, A.D.; Churochkin, D.V.; Fedotov, A.M.; Smolyansky, S.A.; Blaschke, D.B.; Gevorgyan, N.T. Nonperturbative kinetic description of e-h excitations in graphene due to a strong, time-dependent electric field. In Proceedings of the Ginzburg Centennial Conference on Physics, Moscow, Russia, 29 May–3 June 2017; Available online: http://gc2.lpi.ru/proceedings/panferov.pdf (accessed on 16 March 2020).
- Smolyansky, S.A.; Blaschke, D.B.; Dmitriev, V.V.; Panferov, A.D.; Gevorgyan, N.T. Back reaction in graphene excited by a strong laser field. In Proceedings of the Helmholtz International Summer School, Dubna, Russia, 22 July–2 August 2019; Available online: https://indico.jinr.ru/event/797/material/slides/9.pdf (accessed on 16 March 2020).
- Blaschke, D.B.; Dmitriev, V.V.; Röpke, G.; Smolyansky, S.A. BBGKY kinetic approach for an e-e+γ plasma created from the vacuum in a strong laser-generated electric field: The one-photon annihilation channel. Phys. Rev. D 2011, 84, 085028. [Google Scholar] [CrossRef]
- Smolyansky, S.A.; Panferov, A.D.; Pirogov, S.O.; Fedotov, A.M. Self-consistent kinetic equations for e-e+γ -plasma generated from vacuum by strong electric field. arXiv 2019, arXiv:1901.02305. [Google Scholar]
- Bloch, J.C.R.; Mizerny, V.A.; Prozorkevich, A.V.; Roberts, C.D.; Schmidt, S.M.; Smolyansky, S.A.; Vinnik, D.V. Pair creation: Back reactions and damping. Phys. Rev. D 1999, 60, 116011. [Google Scholar] [CrossRef]
- Abbott, T.A.; Griffiths, D.J. Acceleration without radiation. Am. J. Phys. 1985, 53, 1203–1211. [Google Scholar] [CrossRef]
- Baudisch, M.; Marini, A.; Cox, J.D.; Zhu, T.; Silva, F.; Teichmann, S.; Massicotte, M.; Koppens, F.; Levitov, L.S.; García de Abajo, F.J.; et al. Ultrafast nonlinear optical response of Dirac fermions in graphene. Nat. Commun. 2018, 9, 1–6. [Google Scholar] [CrossRef]
- Bowlan, P.; Martinez-Moreno, E.; Reimann, K.; Elsaesser, T.; Woerner, M. Ultrafast terahertz response of multilayer graphene in the nonperturbative regime. Phys. Rev. B 2014, 89, 041408. [Google Scholar] [CrossRef]
- Ishikava, K.L. Nonlinear optical response of graphene in time domain. Phys. Rev. B 2010, 82, 201402(R). [Google Scholar] [CrossRef]
- Ishikava, K.L. Electronic response of graphene to an ultrashort intense terahertz radiation pulse. New J. Phys. 2013, 15, 055021. [Google Scholar] [CrossRef]
- Smolyansky, S.A.; Panferov, A.D.; Blaschke, D.B.; Gevorgyan, N.T. Kinetic Equation Approach to Graphene in Strong External Fields. Particles 2020, 3, 456–476. [Google Scholar] [CrossRef]
- Smolyansky, S.A.; Fedotov, A.M.; Dmitriev, V.V. Kinetics of the vacuum plasma in e+e− a strong electric field and problem of radiation. Mod. Phys. Lett. A 2020, 35, 2040028. [Google Scholar] [CrossRef]
- Otto, A.; Kämpfer, B. Afterglow of the dynamical Schwinger process: Soft photons amass. Phys. Rev. D 2017, 95, 125007. [Google Scholar] [CrossRef]
- de Groot, S.R.; van Leeuwen, W.A.; van Weert, C.G. Kinetic Theory: Principles and Application; North-Hollan Comp.: Amsterdam, The Netherlands; New York, NY, USA; Oxford, UK, 1980. [Google Scholar]
- Kadanoff, L.P.; Baym, G. Quantum Statistical Mechanics; Pines, D., Ed.; W.A. Benjamin, Inc.: New York, NY, USA, 1962; ISBN 978-0367320102. [Google Scholar]
- Zubarev, D.; Morozov, V.; Röpke, G. Statistical Mechanics of Nonequilibrium Processes; Akademie Verlag: Berlin, Germany, 1996; Volume 1, ISBN 3-05-501708-0. [Google Scholar]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. AC Conductivity of Graphene from Tight-Binding Model to 2+1 Dimensional Quantum Electrodynamics. Int. J. Mod. Phys. B 2007, 21, 4611. [Google Scholar] [CrossRef]
- Dabrowski, R.; Dunne, G.V. Super-adiabatic Particle Number in Schwinger and de Sitter Particle Production. Phys. Rev. D 2014, 90, 025021. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Creation of quasiparticles in graphene by a time-dependent electric field. Phys. Rev. D 2013, 87, 125011. [Google Scholar] [CrossRef]
- Blaschke, D.B.; Prozorkevich, A.V.; Röpke, G.; Roberts, C.D.; Schmidt, S.M.; Shkirmanov, D.S.; Smolyansky, S.A. Dynamical Schwinger effect and high-intensity lasers. realising nonperturbative QED. Eur. Phys. J. D 2009, 55, 341. [Google Scholar] [CrossRef]
- Hebenstreit, F.; Alkofer, R.; Dunne, G.V.; Gies, H. Momentum Signatures for Schwinger Pair Production in Short Laser Pulses with a Subcycle Structure. Phys. Rev. Lett. 2009, 102, 150404. [Google Scholar] [CrossRef] [PubMed]
- Amirov, R.K.; Smolyanskii, S.A.; Shechter, L.S. On the theory of quantum kinetic processes in strong alternating fields. Theor. Math. Phys. 1974, 21, 1116–1124. [Google Scholar] [CrossRef]
- Seminozhenko, V.P. Kinetics of interacting quasiparticles in strong external fields. Phys. Rep. 1982, 91, 105. [Google Scholar] [CrossRef]
- Smolyansky, S.A.; Fedotov, A.M.; Dmitriev, V.V. BBGKY Method in Strong Field QED. PEPAN 2020, 51, 595–598. [Google Scholar] [CrossRef]
- Blaschke, D.B.; Kämpfer, B.; Schmidt, S.M.; Panferov, A.D.; Prozorkevich, A.V.; Smolyansky, S.A. Properties of the electron-positron plasma created from a vacuum in a strong laser field: Quasiparticle excitations. Phys. Rev. D 2013, 88, 045017. [Google Scholar] [CrossRef]
- Titov, A.I.; Kämpfer, B.; Hosaka, A.; Takabe, H. Quantum Processes in Short and Intensive Electromagnetic Fields. PEPAN 2016, 47, 835–899. [Google Scholar] [CrossRef]
| 1. | Here, and what follows, are Pauli matrices,
|
| 2. | We note that the back reaction classical radiation accompanying the particle production by a slowly varying strong external electric field was evaluated in Ref. [43]. In this case, the backreaction field is also strong and slowly varying. |
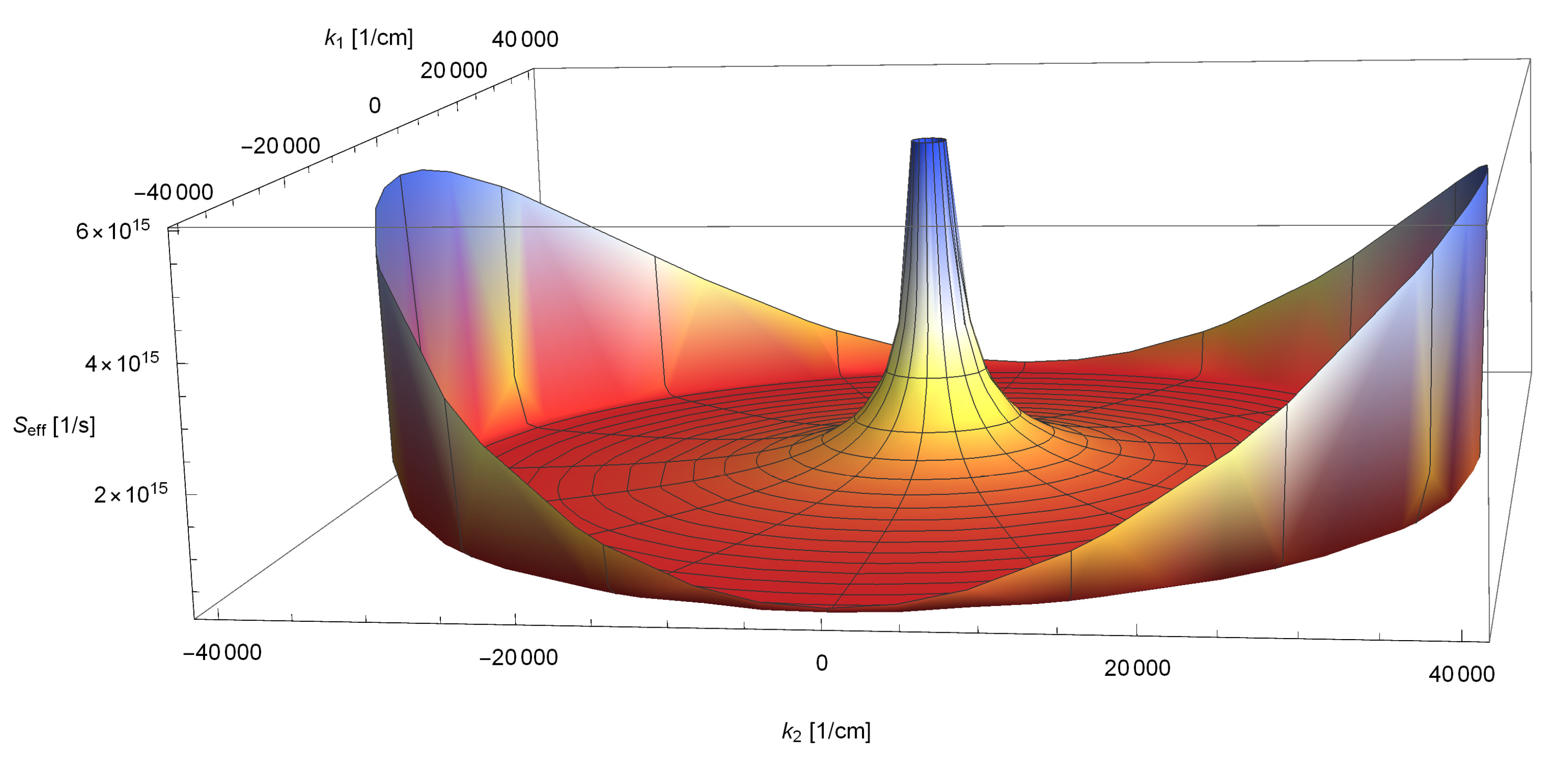

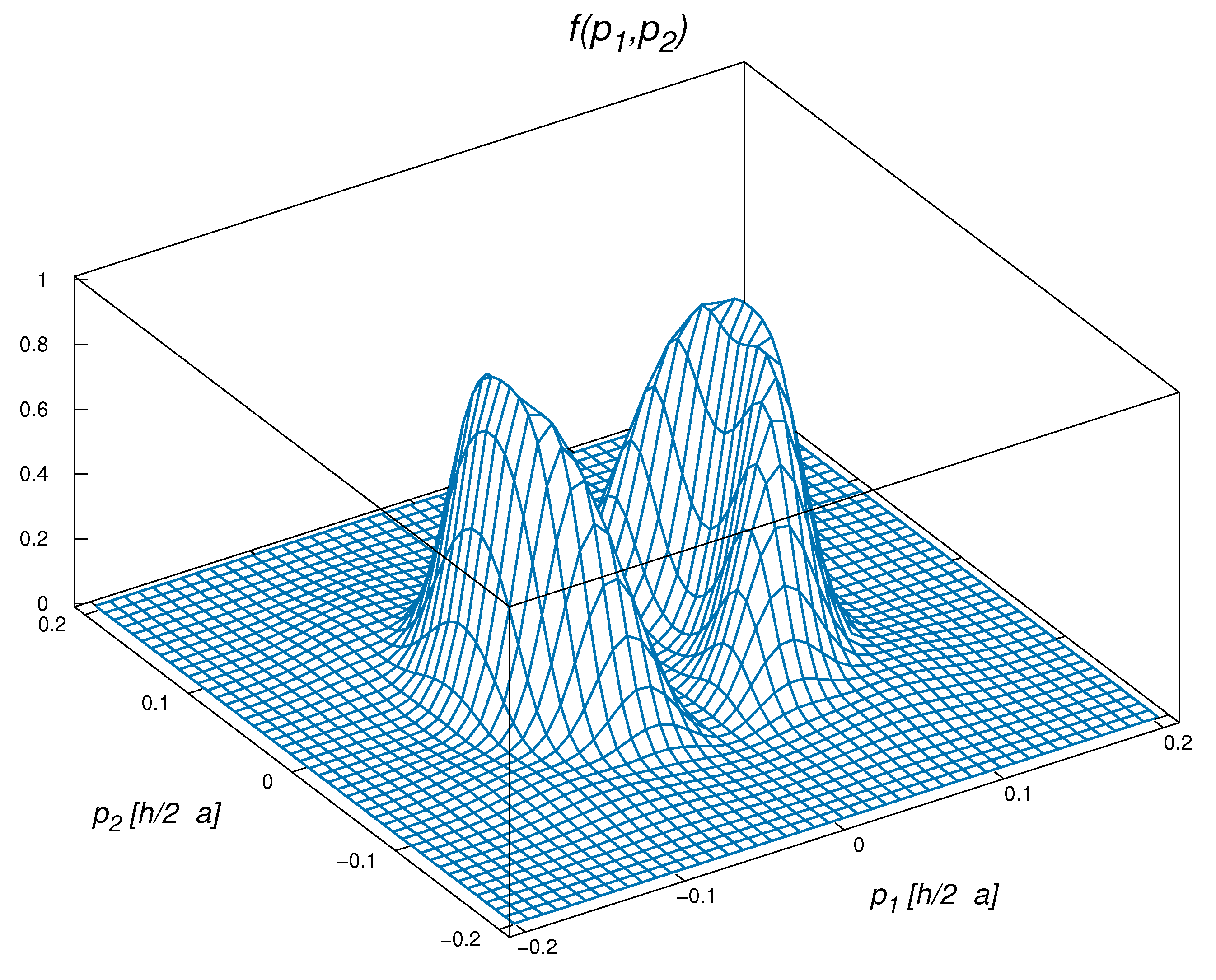

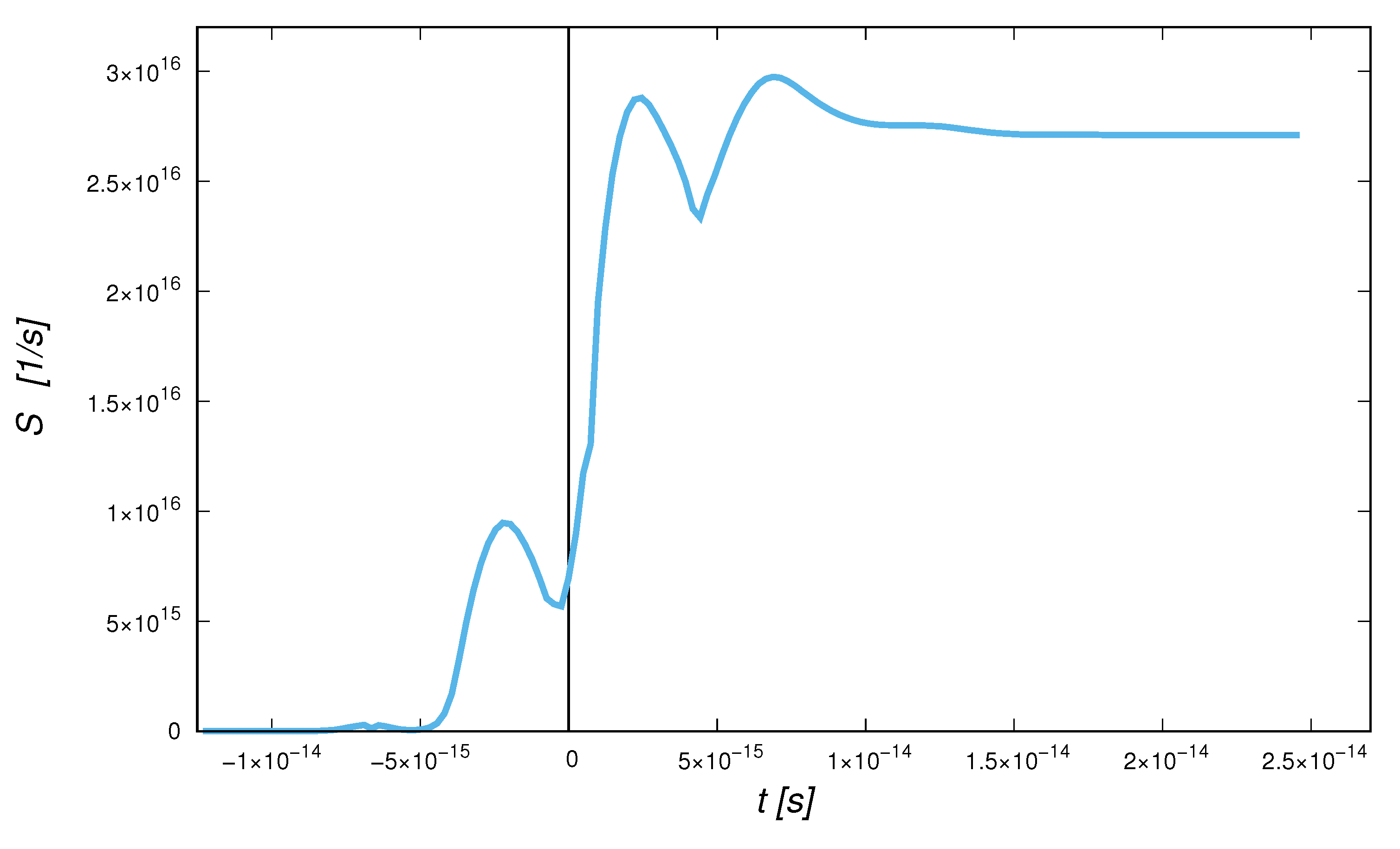
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavrilov, S.P.; Gitman, D.M.; Dmitriev, V.V.; Panferov, A.D.; Smolyansky, S.A. Radiation Problems Accompanying Carrier Production by an Electric Field in the Graphene. Universe 2020, 6, 205. https://doi.org/10.3390/universe6110205
Gavrilov SP, Gitman DM, Dmitriev VV, Panferov AD, Smolyansky SA. Radiation Problems Accompanying Carrier Production by an Electric Field in the Graphene. Universe. 2020; 6(11):205. https://doi.org/10.3390/universe6110205
Chicago/Turabian StyleGavrilov, Sergei P., Dmitry M. Gitman, Vadim V. Dmitriev, Anatolii D. Panferov, and Stanislav A. Smolyansky. 2020. "Radiation Problems Accompanying Carrier Production by an Electric Field in the Graphene" Universe 6, no. 11: 205. https://doi.org/10.3390/universe6110205
APA StyleGavrilov, S. P., Gitman, D. M., Dmitriev, V. V., Panferov, A. D., & Smolyansky, S. A. (2020). Radiation Problems Accompanying Carrier Production by an Electric Field in the Graphene. Universe, 6(11), 205. https://doi.org/10.3390/universe6110205





