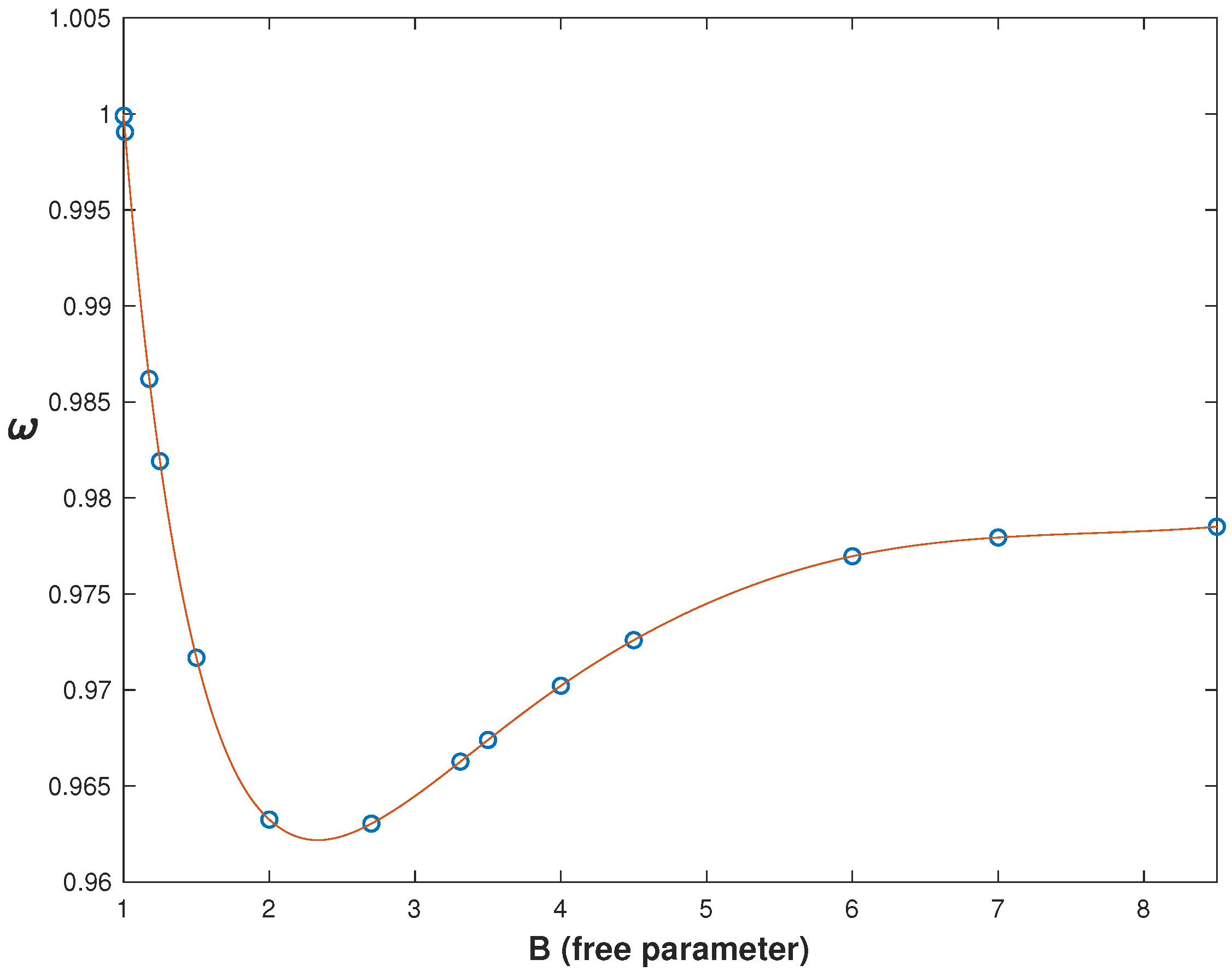1. Introduction: Gravity in Particle Physics
It is generally accepted that gravity’s role in the process of the formation and structure of elementary particles is negligible, due to the very small intensity of gravitation interaction. Quantitively, the ratio
of Newton’s attraction and Coulomb’s repulsion forces between two identical charged massive particles (separated by arbitrary distance) is
where
represents the effective gravitational charge, while
m and
e are the mass and the (elementary) electric charge of the particles, respectively. For a typical elementary particle,
is very small:
. Forces become compatible only at the Planck’s scale
gr.
However, there are a number of indications of the potentially essential role that gravity can play in the microworld. Some indications come from the structure of the celebrated Kerr–Newman solution to the Einstein–Maxwell electrovacuum system. Indeed, for the value of the Kerr parameter
, which corresponds to the proper value of the electron’s spin, the solution is free of horizon, has a ring-like singularity and can reproduce almost all quantum numbers of the electron [
1,
2]. Specifically, the gyromagnetic ratio is equal to that of Dirac’s fermion [
3,
4], while “self-quantization” of the electric charge can be naturally achieved in the framework of the so-called algebrodynamic [
5].
With that said, we are not aware of any serious attempt to theoretically obtain such an extremely small value of this “magic” dimensionless number. In this paper, we present a simple field model in which it seems possible to naturally fix a particular value of .
In other approaches (see, e.g., [
6,
7,
8]) one also claims to construct a realistic model of an
extended elementary particle in which gravitational self-interaction plays an essential role. Usually, these models are based on regular solutions (soliton-like, particle-like, etc.) for a coupled system of the gravitational and other fields’ equations.
Even in a model without additionally inserted nonlinearity of the involved fields, corresponding systems of equations are effectively nonlinear. As an example, consider the simple non-relativistic Schrödinger–Poisson system of equations (also known as Schrödinger–Newton equation) proposed in [
9,
10]
1, as a model for describing the process of the wavefunction reduction induced by self-gravitation of distributed parts of a massive quantum-like particle
in which the gravitational self-energy
U which defines the particle’s
-function is itself determined by the probability distribution
. Despite the fact that both equations are linear by themselves, after resolving the second equation w.r.t
U and substituting
U into the first equation, we obtain a highly nonlinear equation of the form
which is in the fourth order in the derivative.
In [
14], a discrete energy spectrum of regular solutions to (
2) has been obtained in the stationary spherical symmetric case. Note also that relativistic generalization of this model [
15] is based on a coupled system of Dirac and Maxwell-like equations, in which the latter effectively substitute the Einstein gravity.
As a rule, corresponding objects must be treated as macroscopic since their masses is in the Planck’s range or even greater [
16]. On the other hand, they differ from the so-called regular black holes (see, e.g., [
17]), being not only free of the central singularity, but free of any horizon as well. In [
18], these were called gravitational lumps (G-lumps), in [
19] (mini-) soliton stars. In the case when the scalar field is an essential constituent of the model, such field distributions are called (mini-) boson stars [
20,
21].
According to one of the classifications presented—in [
16]—in the case of scalar field coupled to gravity, one distinguishes between mini-boson stars, boson stars and (mini)-soliton stars in the following way:
It is a mini-boson star if the only non-kinetic term present in the scalar field Lagrangian is the mass term;
It is a boson star if additional nonlinearity is inserted into the Klein–Gordon equation;
(Mini)-soliton stars correspond to solutions which have a flat limit, i.e., to the soliton-like solutions that exist in the Minkowski space-time.
As to the range of dimensions and masses corresponding to these objects, they depend not only on the type of solution considered, but on the range of parameters selected, namely, on the value of the bare mass m and on the scalar self-interaction constant. That is why various solutions can be identified with quite different (astro-)physical objects.
Such models are semi-classical in origin, since what we seek are regular (soliton-like) solutions to the field equations which possess finite and, sometimes, the discrete spectrum of Noether’s integrals defining the values of corresponding quantum numbers (mass, spin, charge, etc.). Thereby, one usually disregards gravity and deals with nonlinear fundamental fields in Minkowski space-time. Gravity can be then taken into account as an extremely small correction.
A major difficulty in such models is the form of the chosen nonlinearity, which remains almost arbitrary. A proposed alternative is to compose a system where the well-known set of linear fundamental fields (corresponding to Maxwell, Dirac or Klein–Gordon equations) are coupled, and thus form an effectively nonlinear system of equations. By that, the form of effective nonlinearity becomes rigidly fixed by the requirement of gauge invariance.
2. Rosen’s Model and Its Counterpart on a Curved Manifold
From various models for extended particles, the Dirac–Maxwell system of equations for the spinor and electromagnetic fields coupled via the minimal electromagnetic interaction is, certainly, one of the most attractive. Remarkably, it is a direct semi-classical analogue of the operator equations of quantum electrodynamics. As it was discovered in [
22,
23,
24], the model possesses a class of regular stationary axisymmetric solutions which correspond to fermions of any half-integer spin [
23] with an elementary electric charge and proper value of the magnetic moment. Unfortunately, for all the solutions, the masses turns out to be negative.
A much simpler model of minimally coupled complex Klein–Gordon (
) and Maxwell (
) fields was first proposed by N. Rosen as early as in 1939 [
25]. The Lagrangian reads
where
and
. For the field equations corresponding to (
4), there exists a class of regular stationary spherically symmetrical solutions which can possess any integer spin [
26]. Rosen even made an attempt [
27] to extract the value of the fine structure constant
, making use of the solution corresponding to the minimum of the self-energy. However, the attempt failed and the masses of all the solutions, again, turned out negative.
As an attempt to solve the problem of negative mass, one can try to change the signs of the kinetic and mass terms in the Lagrangian. In the flat case, this leads to the canonical Lagrangian of the Klein–Gordon field and the solutions with a positive definite energy density. However, it is easy to demonstrate that regular solutions do not exist in this case even if minimal interaction with Maxwell’s field was taken into account, as in (
4).
At this point, it seems quite natural to include gravity. Indeed, even with such a small interaction constant, the behavior of field functions can change drastically and allow for the existence of regular solutions with positive proper energy (mass). This means that, according to the above-described classification [
16,
19], the solutions will not belong to the so-called soliton-like class, but will describe an (electrically charged) “mini-boson” distribution. However, as we have already mentioned, this and other classifications are rather “voluntaristical”.
Thus, we are led to consider the following three-field Lagrangian
where
,
and
R is the Riemannian curvature scalar. The dimensional constants
and
k (or, equivalently,
) should be fixed
a posteriori. However, in order to establish the right “charge-spin” ratio [
26] and in correspondence with quantum theory, we set
, and it would also be natural to consider the priming mass
m in the range typical for elementary particles.
3. General Characteristics of the Three-Field Model
After scale transformations of coordinates (reduction to the Compton scale) and field functions of the form
the Lagrangian (
5) transforms in the following way
where
is the fine structure constant, and the dimensionless Lagrangian
L has the following form (
)
L contains only a sole dimensionless parameter,
being—as discussed earlier—of the order
for a typical elementary particle. However,
we cannot set it to zero, since regular solutions disappear in this case.
Exploiting regular solutions of the three-field model to describe the structure of (charged massive) elementary particles seems quite natural. Indeed, any of these particles produce an electromagnetic, a gravitational and a wave-like field. On the other hand, the choice of the Klein–Gordon field can be considered only as a first step to the study of the more attractive but complicated Dirac–Maxwell–Einstein model.
Even in the case of scalar field, when the field equations allow for spherically symmetric ansatz, the search for regular solutions is an extremely complicated problem. We are aware of only one work [
28] where this problem had been posed and preliminary results obtained. However, the paper is not complete and contains some imprecise results in numerical calculations. Therefore, we have made an attempt here to further elaborate the above three-field model.
Varying the action functional
corresponding to Lagrangian (
6) w.r.t
and the metric
, we obtain the field equations in the form
where
and
is the (renormed) energy-momentum tensor,
being the invariant
.
Finally, from the corresponding Equation (
7), one can obtain the dimensionless electric charge
q and energy
w of the regular solution, which are related to the corresponding dimensional electric charge
Q and energy
W as
so that one can ensure that their values are typical for elementary particles if, for
, one would have, for dimensionless charge and energy (mass)
.
4. Stationary Spherically Symmetric Ansatz
Equation (
7) allow for the following canonical ansatz
where the two metric functions
2 depend on the radial coordinate
r.
The corresponding action potential takes the form
where
denotes derivation w.r.t. the coordinate
r. Varying (
11) w.r.t.
, one obtains the field equations in the form
where the shifted electric potential is
. The last two equations in (
12) correspond to two independent Einstein equations corresponding to the (
) and (
) components, respectively. From the third equation of (
12), the energy density is seen to be a positive definite.
As for the other two Einstein equations, which are not contained in the system (
7) and correspond to (
) and (
) components, they both have the same form
and are known to identically hold on the solutions to (
12). It is worthy to note that, according to the stress–energy tensor (SET) components in the r.h.s. of (
12) and (
13), the corresponding radial and tangential pressure are generally different. However, as we shall see below, for regular solutions near the center
, the derivative terms therein turn to zero, so that, asymptotically, one has a fully isotropic SET and corresponding de Sitter core.
We now start to seek regular asymptotically flat solutions to the system (
12). Specifically, at great distances we should achieve (by proper fitting of the initial values)
and for metric functions, the Reissner–Nordström asymptotics
with
M being (twice the) gravitational charge of the distribution.
Near the center
, the regular behavior of field functions has the form:
in which a very important parameter
enters.
B is the ratio of initial values
and
. Indeed, the system (
12) is invariant under the transformation
under which the parameter
B preserves its value, and thus can be accepted as the principal parameter defining the form and characteristics of regular solutions to (
12). Note that the symmetry (
17) is related to the possibility of redefining the time coordinate and, consequently, the frequency parameter
which enters the expression for the shifted electric potential
.
5. Regular Solutions: Procedure of Numerical Integration
Let us now consider the procedure of integrating the system (
12), seeking the solutions with the above-described regular behavior in the center and at infinity. For a given
and for any selected value of the sole free parameter
B, one takes arbitrary
(and thus, the corresponding
) and starts to fit
to ensure
3 exponential decrease in
at sufficiently large
r, up to the value
at which the solution either blows up,
, or changes its sign,
.
From the last Equation (
12), it follows that in the range
, the asymptotic behavior of metric function
will be more general than that given in (
15), and it will be non-Halileian, namely,
with
C being an arbitrary constant. However, using the symmetry (
17), we can renorm the obtained solution by shifting its asymptotic value to the Halileian one represented in (
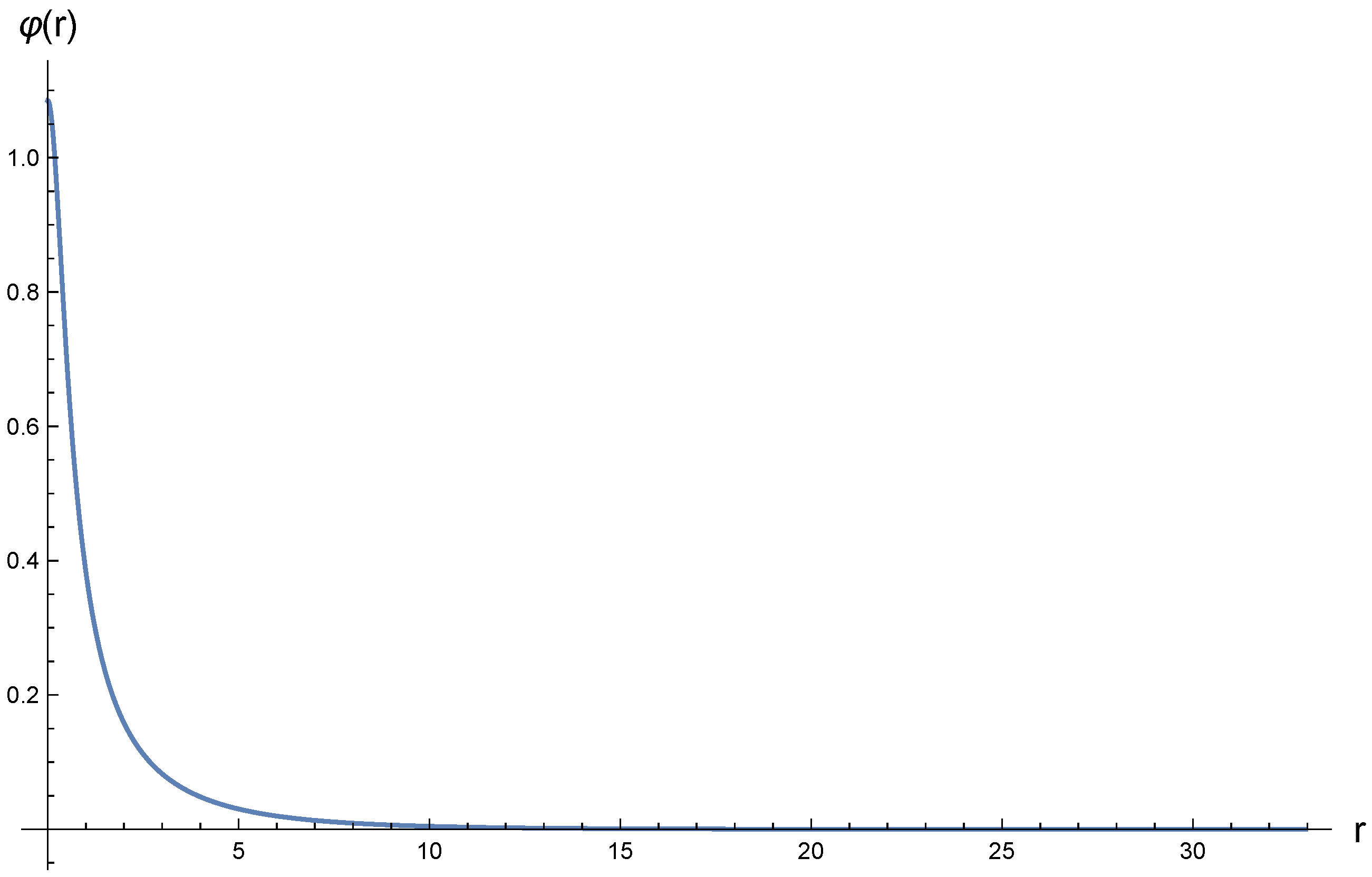
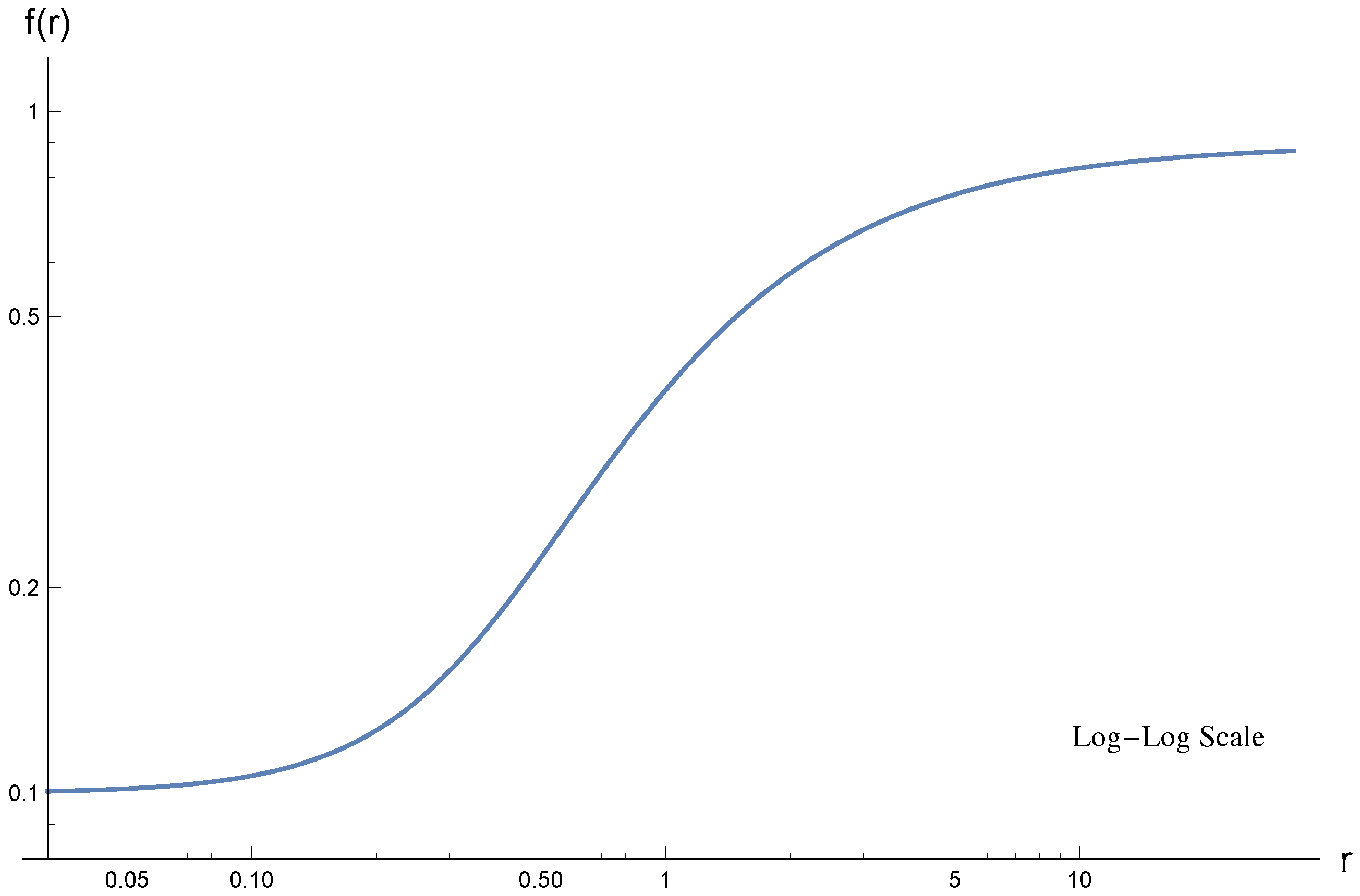
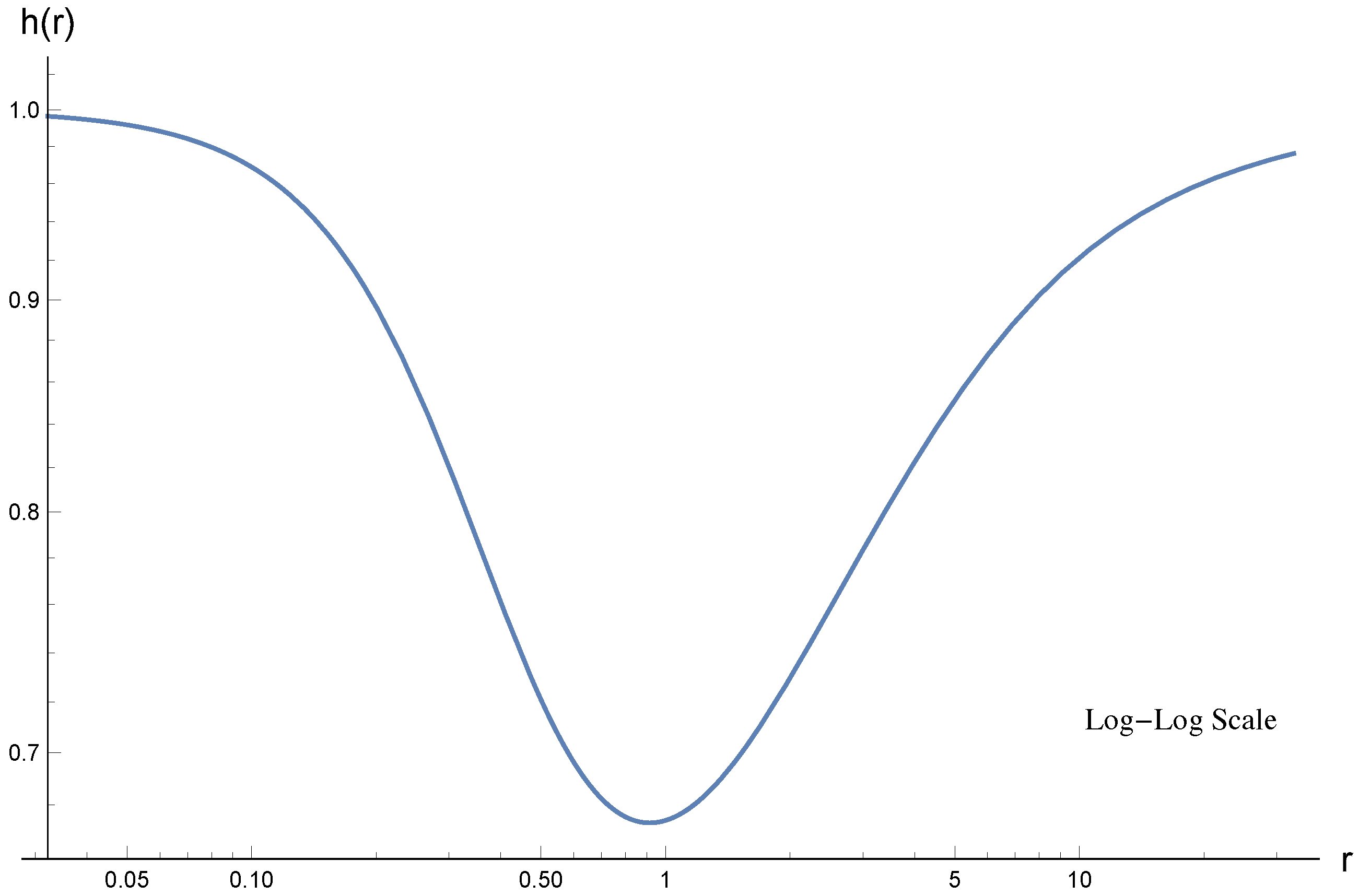
14). Typical forms of the scalar and shifted electric potential fields, together with the two metric functions for the values of parameters
, which correspond to the local minimum of energy, see below, are plotted in
Figure 1,
Figure 2,
Figure 3 and
Figure 4 respectively. We see that the metrics do not change their signature, so that all the obtained solutions are free of horizon. We note that in the neutral case, when the electromagnetic field is absent, such a property was first discovered in [
30] and analytically proved later in [
31] (called the “no-go theorem” therein).
Now, using values of the functions at the breaking point
and asymptotics (
14) and (
15), we can compute the characteristics of the obtained regular solution, namely the electric charge
, frequency
and gravitational charge
.
Finally, using the first and third equations in (
12), we integrate (in the range
) the charge and energy density with the already-found initial values of field functions and obtain the total electric charge
and the inertial mass
If the precision of integration is sufficient, one should satisfy the integral identities
where the mass equality has the meaning of the equivalence principle.
6. Regular Solution: Characteristics and Dependence on Parameters
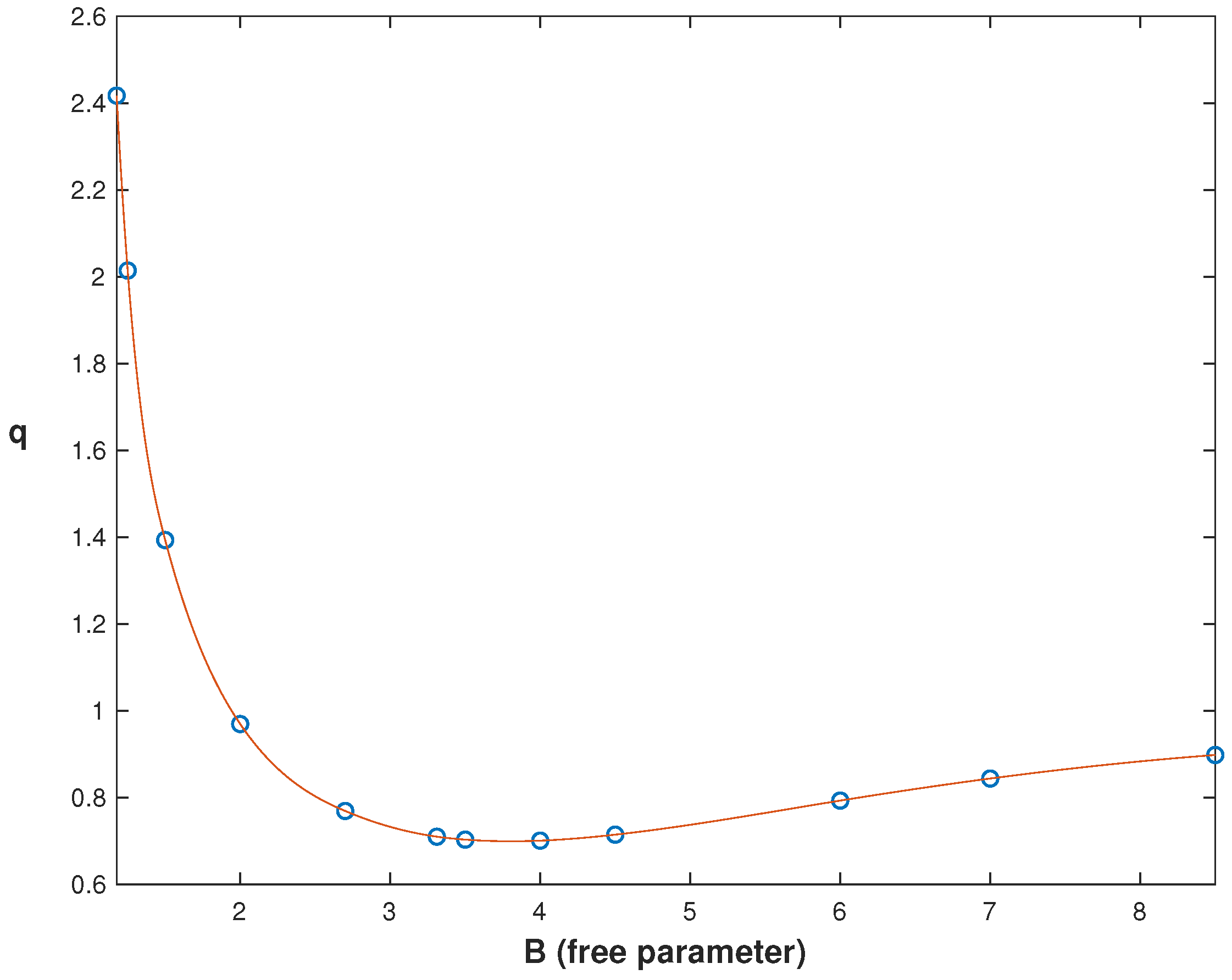
We now present the results of the numerical study of the regular solutions to (
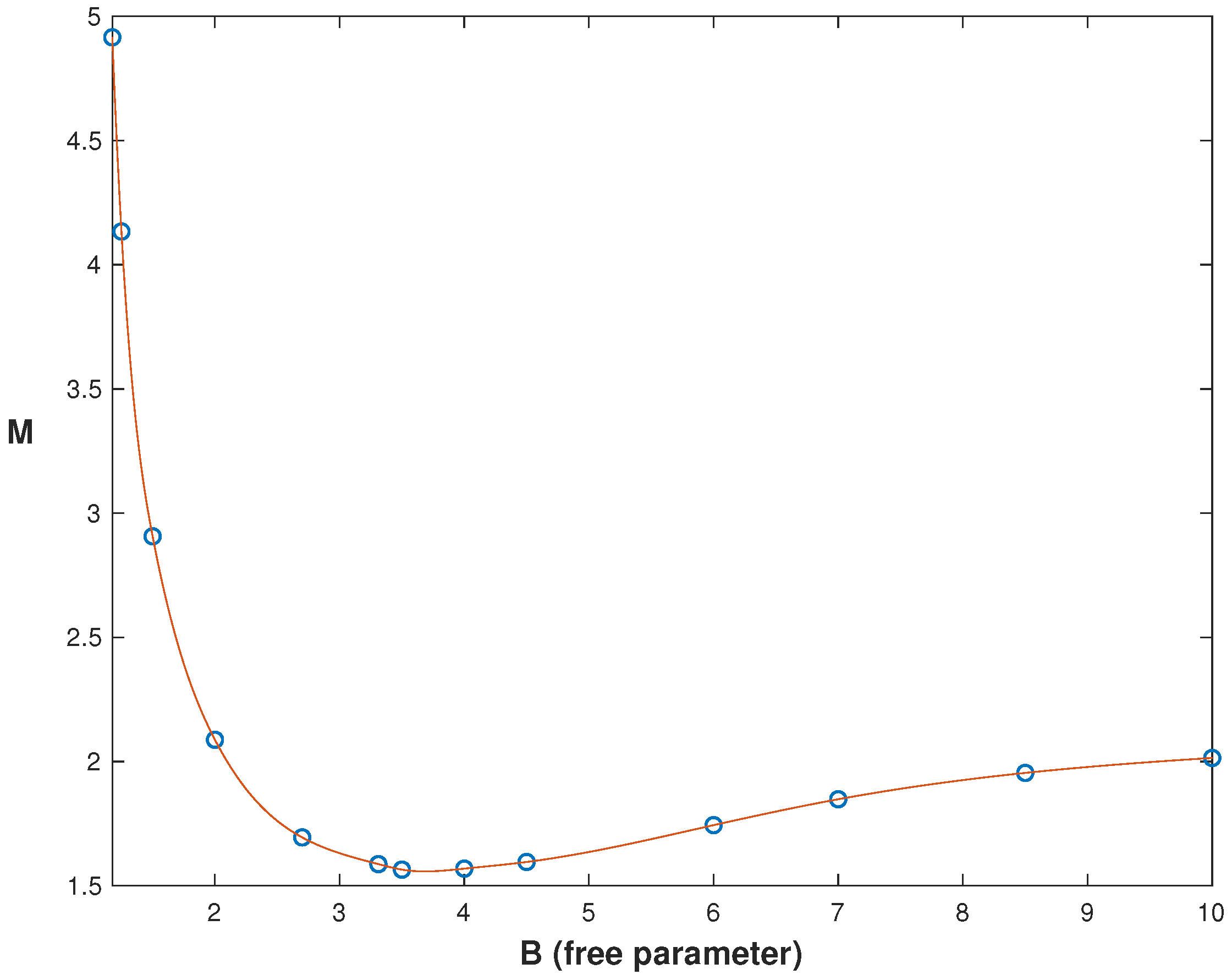
12). For the value of parameter
4 , the plots of electric charge
q, mass
M and frequency
associated with the solutions are plotted in
Figure 5,
Figure 6 and
Figure 7 as functions of the principal free parameter
B.
From these data, we conclude that:
The solutions exist only in a narrow range of the frequency parameter
near the boundary value
. For
, the asymptotic of the scalar field differs from the Yukawa’s form and corresponds
5 to
;
All three characteristics have a minimum of almost equal values of the free parameter B;
There are some additional local minima for the values of electric charge and energy (in other range of the parameter B, not represented in the figures).
Let us now take into account that a fixed value of
corresponds, in view of (
1), to the bare mass
, where
is the Planck’s mass,
gr, and
is the fine structure constant. For the dimensional mass
, according to (
9), one then has [
28]
while for the electric charge,
We assume now that the stable solution corresponds to the local minimum of the proper energy (mass), which occurs at
and corresponds to the following characteristics:
, and the effective radius of the scalar field distribution is about
. Dimensional physical characteristics (
19) and (
20) are then equal to
with
cm being the Planck’s length.
Thus, we deal here with an extremely compact electrically charged object of a Planck’s range mass (hypothetical “maximon”). However, this object possesses a discrete energy spectrum and is, therefore, “semi-quantum” in origin, proving the old idea of M.A. Markov on its nature as an elementary particle of a maximal possible mass [
32].
We can further seek regular solutions which correspond to a number of nodes for the scalar field function . For such solutions, there again exists a range of the parameter B, corresponding to the local minima of the energy. We evaluate the values of minimal energy (mass) of the one-node and two-node “excited” states as (compared with for the “ground state”, see above).
Let us now follow the dependence of solutions on the parameter . For , say, the dependence of the characteristics on the parameter B preserves all the properties represented above for . In particular, the minimal energy is now equal to and corresponds to .
Unfortunately, the procedure of numerical integration becomes unstable for , so that the most interesting range of parameters corresponding to the characteristics of particles remains unattainable. Our attempt to evaluate probable characteristics at such values of was unsuccessful, even after applying the variational methods.
On the other hand, this means that there still remains a possibility of such particle-like solutions existing in the model. It can be conjectured that, in this case, one could fix the values of the two free parameters and B through the requirement of minimum for the values of both the electric charge and energy (mass). At the moment, however, realization of this program (which claims, in particular, to obtain the magic number at the range of ) looks hardly probable.
7. Electrically Neutral Solutions
Consider now the “macroscopic” sector of regular solutions, which corresponds to the range
. We then obtain, from solutions in this range, that the dimensionless electric charge
q and mass
M weakly depend on
. According to (
19), that means that physical mass grow as
. For
, corresponding solutions can thus be identified as weakly charged, see (
20), star-like, or even supermassive objects.
Finally, in the limit
which corresponds to
, the model reduces to the system of the minimally coupled Einstein and Klein–Gordon equations derived from the Lagrangian (compare with (
5))
which, in the dimensionless form, contains no free parameters at all. Physical mass can be then evaluated as follows [
30]
with
M being the dimensionless mass of the solutions. Thus, for the quantum mechanical range of the bare mass
m, one deals here with electrically neutral objects with mass
gr
, that is, with the hypothetical mini-boson stars (see, e.g., [
19,
21]).
In fact, regular solutions to the equations resulting from (
22) were considered in several works. Particularly, in [
30], the absence of a horizon for these solutions was discovered. However, the dependence of the characteristics on the sole free parameter
which can fix the discrete energy spectrum, to our knowledge, has not yet been retraced.
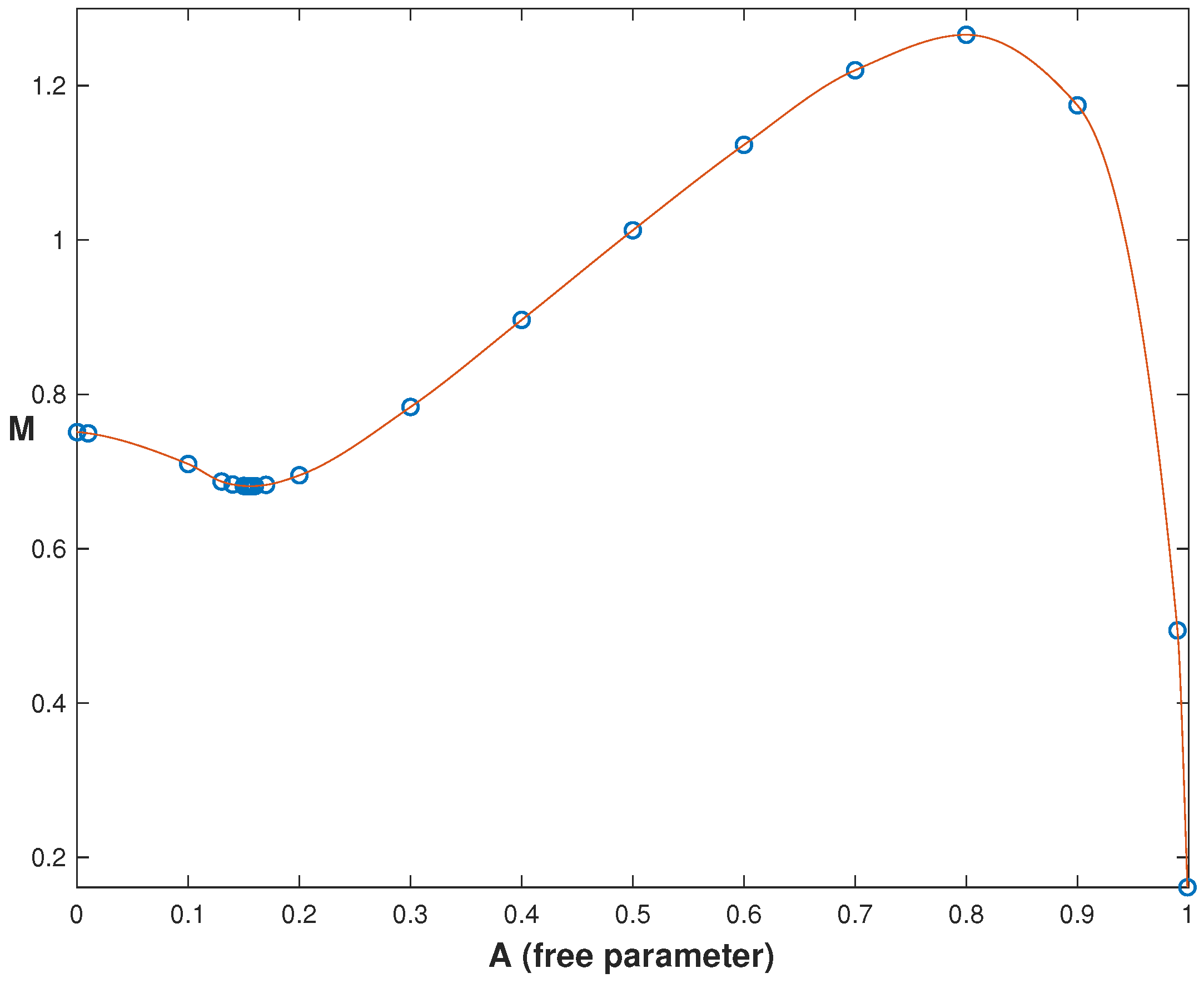
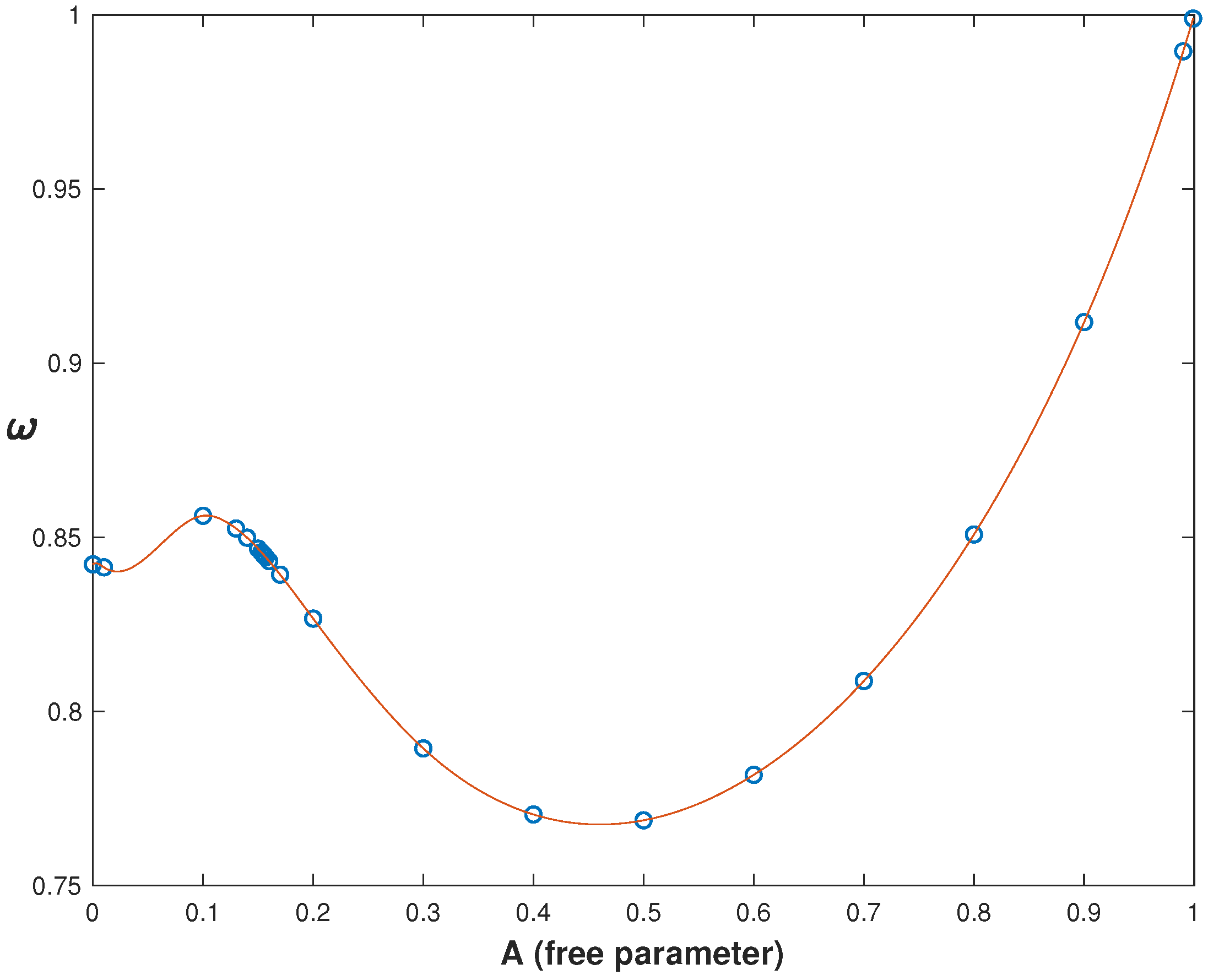
In our model, the dependence of the mass
M and the frequency
on the parameter
A are represented in
Figure 8 and
Figure 9, respectively. One of the two local minima of energy corresponds to
and, in the minimum
M, is equal to
; the other, deeper minimum is achieved when
A, together with
, approach the extreme allowed value equal to unity; the minimal value of energy is then about
. Note also that the frequency values are located again in a narrow interval
near the cut-off value
.
8. Conclusions
We considered a model of three minimally coupled canonical fields: electromagnetic, gravitational and massive scalar fields. In the stationary spherically symmetric case, we looked for regular, “soliton-like” solutions to the system of field equations. All solutions are electrically charged, free of horizon, and possess finite positive proper energy associated with inertial (and equal gravitational) mass.
Our main goal was to find the solutions whose characteristics reproduce those of a typical elementary particle. Such solutions should correspond to the value of the sole parameter , which enters the dimensionless Lagrangian and relates the gravitational/electromagnetic interaction ratio of two charged massive particles.
We expected to obtain a proper discrete set of (ground and excited) states, making use of the requirement of electric charge and mass to achieve minimal values; in this case, one could naturally explain the “magic” number within the framework of a rather simple and natural three-field model free of any additionally inserted nonlinearity.
Unfortunately, the procedure of numerical integration breaks in the range of parameters , and we were unable to find some analytical explanation for this fact. Thus, it remains an open question whether true particle-like solutions could exist in the model.
Meanwhile, for the range we followed the dependence of the solutions’ characteristics (charge, mass and frequency) on the other free parameter of the model B and found that energy has a local minimum at some values of B (both for the ground state and first two excited states, related to the scalar field distributions with nodes). Thus, our model describes a “semi-quantum” charged object with a discrete energy/mass spectrum whose dimensions and mass lie in the Planckian range, cm and gr, respectively. Appropriate interpretation of such objects is obscure; in the literature, these are called (regular) “maximons”, “planckeons”, etc.
Further, we considered the limit
in which the electric field is eliminated and one effectively deals with the system of minimally coupled gravitational and massive scalar fields. Regular solutions in this model (with and without non-linear terms in the Klein–Gordon equation) have been repeatedly examined, starting perhaps from [
30]. It is well-known that the metric in such models does not contain a horizon, while corresponding mass lies in the solar range. To our knowledge, we are the first to obtain the discrete energy spectrum of such macroscopic objects, from the condition of minimal proper energy (mass). Nonetheless, the identification of such objects with real astrophysical entities looks problematic. At the end, “(mini-) boson stars” might be a purely mathematical construction.
In future work we will further elucidate the physically promising but mathematically very complicated problem of the existence of true “particlelike” solutions (in the range ) in the above-studied three-field model. It would also be intriguing to consider the “” problem in the framework of the more realistic system of equations for Maxwell–Dirac–Einstein-coupled fields.