Mapping the Narrow-Line Seyfert 1 Galaxy 1H 0323+342
Abstract
1. Introduction
2. Mass of the Central Black Hole
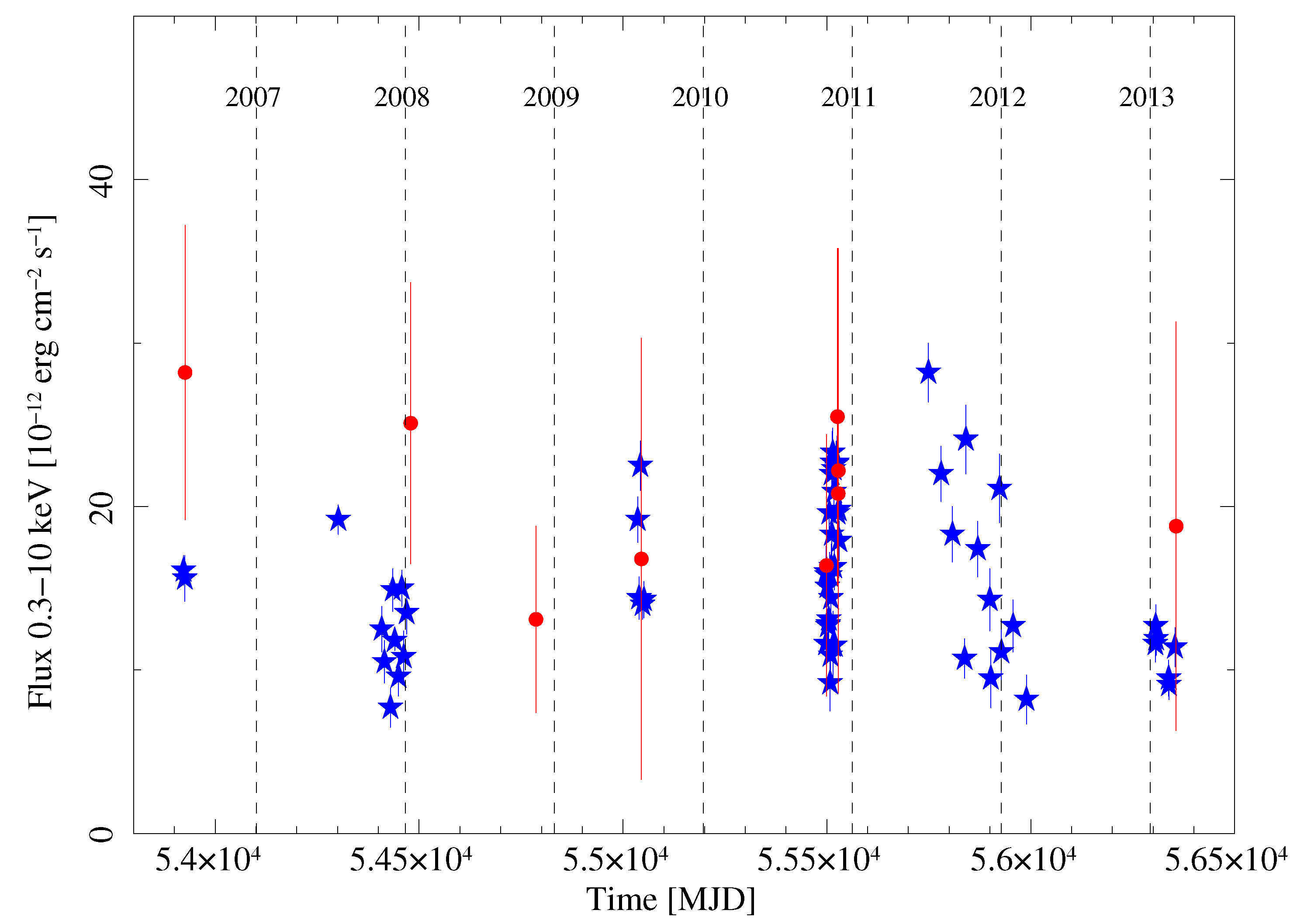
3. The Jet Structure
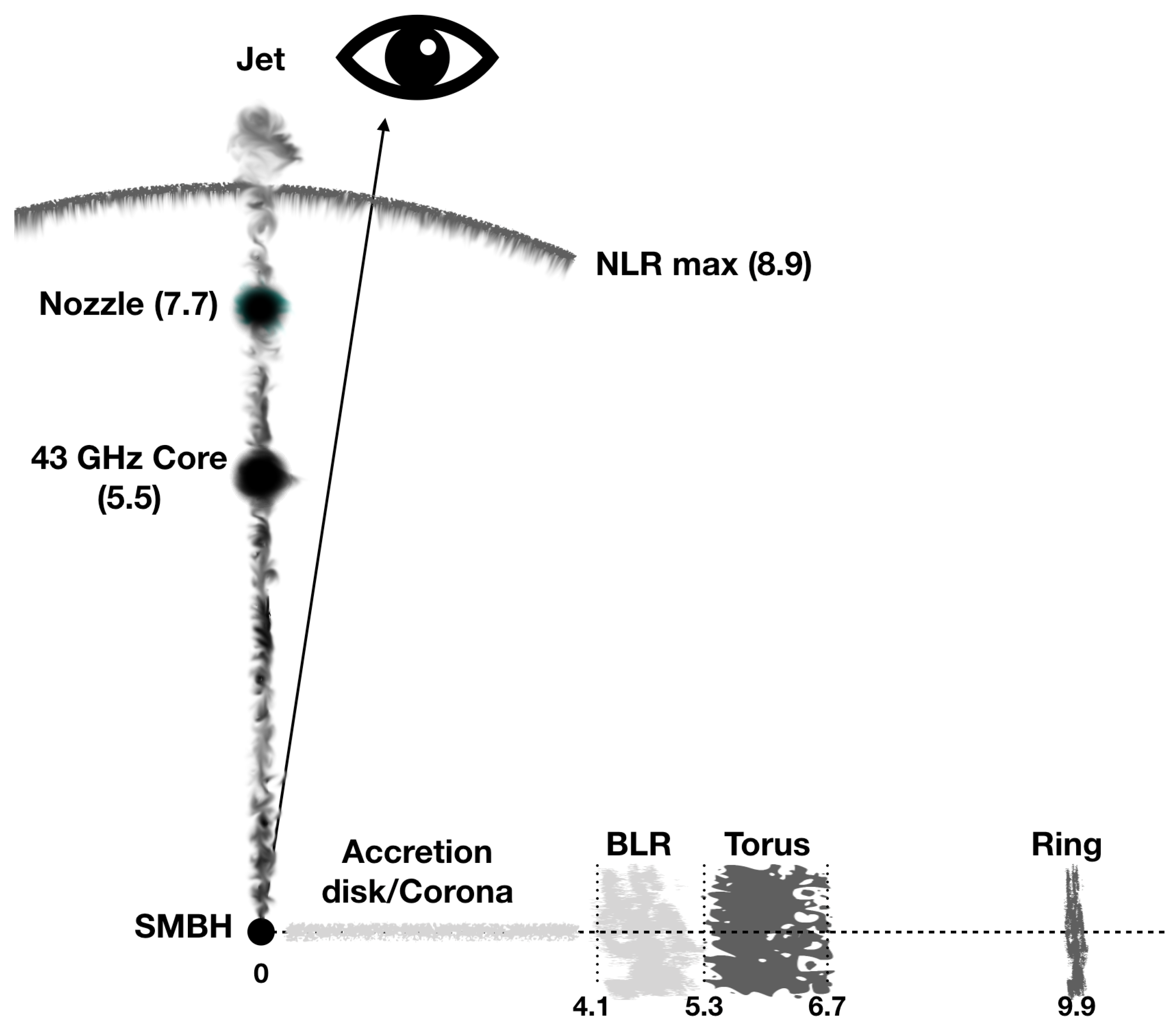
4. The Map
Author Contributions
Funding
Conflicts of Interest
References
- Zhou, H.; Wang, T.; Yuan, W.; Shan, H.; Komossa, S.; Lu, H.; Liu, Y.; Xu, D.; Bai, J.M.; Jiang, D.R. A narrow-line Seyfert 1-blazar composite nucleus in 2MASX J0324+3410. Astrophys. J. Lett. 2007, 658, L13–L16. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Berenji, B.; et al. Radio-loud narrow-nine Seyfert 1 galaxies as a new class of gamma-ray active galactic nuclei. Astrophys. J. 2009, 707, L142–L147. [Google Scholar] [CrossRef]
- Wajima, K.; Fujisawa, K.; Hayashida, M.; Isobe, N.; Ishida, T.; Yonekura, Y. Short-term radio variability and parsec-scale structure in a gamma-ray narrow-line Seyfert 1 galaxy 1H 0323+342. Astrophys. J. 2014, 781, 75. [Google Scholar] [CrossRef]
- Fuhrmann, L.; Karamanavis, V.; Komossa, S.; Angelakis, E.; Krichbaum, T.P.; Schulz, R.; Kreikenbohm, A.; Kadler, M.; Myserlis, I.; Ros, E.; et al. Inner jet kinematics and the viewing angle towards the γ-ray narrow-line Seyfert 1 galaxy 1H 0323+342. Res. Astron. Astrophys. 2016, 16, 176. [Google Scholar] [CrossRef]
- Doi, A.; Hada, K.; Kino, M.; Wajima, K.; Nakahara, S. A recollimation shock in a stationary jet feature with limb-brightening in the gamma-ray-emitting narrow-line Seyfert 1 galaxy 1H 0323+342. Astrophys. J. Lett. 2018, 857, L6. [Google Scholar] [CrossRef]
- Hada, K.; Doi, A.; Wajima, K.; D’Ammando, F.; Orienti, M.; Giroletti, M.; Giovannini, G.; Nakamura, M.; Asada, K. Collimation, acceleration, and recollimation shock in the jet of gamma-ray emitting radio-loud narrow-line Seyfert 1 galaxy 1H 0323+342. Astrophys. J. 2018, 860, 141. [Google Scholar] [CrossRef]
- Kovalev, Y.Y.; Pushkarev, A.B.; Nokhrina, E.E.; Plavin, A.V.; Beskin, V.S.; Chernoglazov, A.; Lister, M.L.; Savolainen, T. Discovery of geometry transition in nearby AGN jets. arXiv 2019, arXiv:1907.01485. in press. [Google Scholar]
- Lister, M.L.; Homan, D.C.; Hovatta, T.; Kellermann, K.I.; Kiehlmann, S.; Kovalev, Y.Y.; Max-Moerbeck, W.; Pushkarev, A.B.; Readhead, A.C.S.; Ros, E.; et al. MOJAVE XVII. Jet kinematics and parent population properties of relativistically beamed radio-loud blazars. Astrophys. J. 2019, 874, 43. [Google Scholar] [CrossRef]
- León Tavares, J.; Kotilainen, J.; Chavushyan, V.; Añorve, C.; Puerari, I.; Cruz-González, I.; Patiño-Alvarez, V.; Antón, S.; Carramiñana, A.; Carrasco, L.; et al. The host galaxy of the gamma-ray narrow-line Seyfert 1 galaxy 1H 0323+342. Astrophys. J. 2014, 795, 58. [Google Scholar] [CrossRef]
- Peterson, B.M.; Dalla Bontá, E. Reverberation mapping and implications for narrow-line Seyfert 1 galaxies. Proc. Sci. 2018, NLS1-2018, 008. [Google Scholar]
- Foschini, L.; Berton, M.; Caccianiga, A.; Ciroi, S.; Cracco, V.; Peterson, B.M.; Angelakis, E.; Braito, V.; Fuhrmann, L.; Gallo, L.; et al. Properties of flat-spectrum radio-loud narrow-line Seyfert 1 galaxies. A&A 2015, 575, A13. [Google Scholar]
- Landt, H.; Ward, M.J.; Baloković, M.; Kynoch, D.; Storchi-Bergmann, T.; Boisson, C.; Done, C.; Schimoia, J.; Stern, D. On the black hole mass of the γ-ray emitting narrow-line Seyfert 1 galaxy 1H 0323+342. MNRAS 2017, 464, 2565–2576. [Google Scholar] [CrossRef]
- Wang, F.; Du, P.; Hu, C.; Bai, J.M.; Wang, C.J.; Yi, W.M.; Wang, J.-G.; Zhang, J.-J.; Xin, Y.-X.; Lun, B.-L.; et al. Reverberation mapping of the gamma-ray loud narrow-line Seyfert 1 galaxy 1H 0323+342. Astrophys. J. 2016, 824, 149. [Google Scholar] [CrossRef]
- Pan, H.-W.; Yuan, W.; Yao, S.; Komossa, S.; Jin, C. Independent estimation of black hole mass for the γ-ray detected archetypal narrow-line Seyfert 1 galaxy 1H 0323+342 from X-ray variability. Astrophys. J. 2018, 866, 69. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F. Fermi/LAT broad emission line blazars. MNRAS 2015, 448, 1060–1077. [Google Scholar] [CrossRef]
- Ikejiri, Y.; Uemura, M.; Sasada, M.; Ito, R.; Yamanaka, M.; Sakimoto, K.; Arai, A.; Fukazawa, Y.; Ohsugi, T.; Kawabata, K.S.; et al. Photopolarimetric Monitoring of Blazars in the Optical and Near-Infrared Bands with the Kanata Telescope. I. Correlations between Flux, Color, and Polarization. PASJ 2011, 63, 639–675. [Google Scholar] [CrossRef]
- Foschini, L. Powerful relativistic jets in narrow-line Seyfert 1 galaxies (review). Proc. Sci. 2012, Seyfert 2012, 10. [Google Scholar]
- Foschini, L.; Maraschi, L.; Tavecchio, F.; Ghisellini, G.; Gliozzi, M.; Sambruna, R.M. Blazar nuclei in radio-loud narrow-line Seyfert 1? Adv. Space Res. 2009, 43, 889–894. [Google Scholar] [CrossRef][Green Version]
- Antòn, S.; Browne, I.W.A.; Marchã, M.J. The colour of the narrow-line Sy1-blazar 0324+3410. A&A 2008, 490, 583–587. [Google Scholar]
- Kawaguchi, T. Comptonization in super-Eddington accretion flow and growth timescale of supermassive black holes. Astrophys. J. Lett. 2003, 593, 69–84. [Google Scholar] [CrossRef][Green Version]
- Bentz, M.; Denney, K.D.; Grier, C.J.; Barth, A.J.; Peterson, B.M.; Vestergaard, M.; Bennert, V.N.; Canalizo, G.; De Rosa, G.; Filippenko, A.V.; et al. The low-luminosity end of the radius-luminosity relationship for active galactic nuclei. Astrophys. J. 2013, 767, 149. [Google Scholar] [CrossRef]
- Castelló-Mor, N.; Netzer, H.; Kaspi, S. Super- and sub-Eddington accreting massive black holes: A comparison of slim and thin accretion discs through study of the spectral energy distribution. MNRAS 2016, 458, 1839–1858. [Google Scholar] [CrossRef][Green Version]
- Netzer, H. Bolometric correction factors for Active Galactic Nuclei. MNRAS 2019, 488, 5185–5191. [Google Scholar] [CrossRef]
- Elitzur, M. The toroidal obscuration of active galactic nuclei. New Astron. Rev. 2008, 52, 274–288. [Google Scholar] [CrossRef]
- Fischer, T.C.; Kraemer, S.B.; Schmitt, H.R.; Micchi, L.L.; Crenshaw, D.M.; Revalski, M.; Vestergaard, M.; Elvis, M.; Gaskell, C.M.; Hamann, F.; et al. Hubble Space Telescope observations of extended [O III]λ5007 emission in nearby QSO2s: new constraints on AGN host galaxy interaction. Astrophys. J. 2018, 865, 102. [Google Scholar] [CrossRef]
- Berton, M.; Foschini, L.; Ciroi, S.; Cracco, V.; La Mura, G.; Di Mille, F.; Rafanelli, P. [O III] line properties in two samples of radio-emitting narrow-line Seyfert 1 galaxies. A&A 2016, 591, A88. [Google Scholar]
- Lister, M.L.; Aller, M.F.; Aller, H.D.; Homan, D.C.; Kellermann, K.I.; Kovalev, Y.Y.; Pushkarev, A.B.; Richards, J.L.; Ros, E.; Savolainen, T. MOJAVE XIII. Parsec-scale AGN jet kinematics analysis based on 19 years of VLBA observations at 15 GHz. Astrophys. J 2016, 152, 12. [Google Scholar] [CrossRef]
- Liodakis, I.; Hovatta, T.; Huppenkothen, D.; Kiehlmann, S.; Max-Moerbeck, W.; Readhead, A.C. Constraining the limiting brightness temperature and Doppler factors for the largest sample of radio-bright blazars. Astrophys. J. 2018, 866, 137. [Google Scholar] [CrossRef]
- Asada, K.; Nakamura, M. The structure of the M87 jet: A transition from parabolic to conical streamlines. Astrophys. J. 2012, 745, L28. [Google Scholar] [CrossRef]
- Allen, S.W.; Allen, S.W.; Dunn, R.J.H.; Fabian, A.C.; Taylor, G.B.; Reynolds, C.S. The relation between accretion rate and jet power in X-ray luminous elliptical galaxies. MNRAS 2006, 372, 21–30. [Google Scholar] [CrossRef]
- Heinz, S.; Sunyaev, R.A. The non-linear dependence of flux on black hole mass and accretion rate in core-dominated jets. MNRAS 2003, 343, L59–L64. [Google Scholar] [CrossRef]
- Paliya, V.; Stalin, C.S.; Ravikumar, C.D. Fermi monitoring of radio-loud narrow-line Seyfert 1 galaxies. Astrophys. J. 2015, 149, 41. [Google Scholar]
- Ghisellini, G.; Tavecchio, F.; Maraschi, L.; Celotti, A.; Sbarrato, T. The power of relativistic jets is larger than the luminosity of their accretion disks. Nature 2014, 515, 376–378. [Google Scholar] [CrossRef] [PubMed]
- Marscher, A.P.; Jorstad, S.G.; D’Arcangelo, F.D.; Smith, P.S.; Williams, G.G.; Larionov, V.M.; Oh, H.; Olmstead, A.R.; Aller, M.F.; Aller, H.D.; et al. The inner jet of an active galactic nucleus as revealed by a radio-to-γ-ray outburst. Nature 2008, 452, 966–969. [Google Scholar] [CrossRef] [PubMed]
- Sikora, M.; Moderski, R.; Madejski, G.M. 3C 454.3 Reveals the Structure and Physics of Its “Blazar Zone”. Astrophys. J. 2008, 675, 71–78. [Google Scholar] [CrossRef][Green Version]
- Foschini, L.; Ghisellini, G.; Tavecchio, F.; Bonnoli, G.; Stamerra, A. Short time scale variability at gamma rays in FSRQs and implications on the current models. In Proceedings of the III Fermi Symposium, Roma, Italy, 9–12 May 2011. eConf C110509. [Google Scholar]
| 1 | This measurement was done by Zhou [1], but an older value of was often used (e.g., NASA/IPAC Extragalactic Database). The differences are minimal: % for the luminosity, pc/mas vs. pc/mas for the conversion of angle to linear size. In this work, we used all the quantities for . When we used values from literature with , we corrected for the different z. |
| 2 | Monitoring Of Jets in Active galactic nuclei with VLBA Experiments: https://www.physics.purdue.edu/MOJAVE/. |
| 3 | Obviously, it is not on the torus, as the two structures are perpendicular each other. |
| Mass | Method | Reference |
|---|---|---|
| () | ||
| H luminosity and FWHM, single epoch spectrum | [1] | |
| fit of the accretion disk, Shakura–Sunyaev model | [2] | |
| H luminosity and , single epoch spectrum | [11] | |
| Reverberation mapping H | [13] | |
| single epoch spectrum, Pa, H, H, excess variance at X-rays | [12] | |
| excess variance, PSD bend frequency at X-rays | [14] | |
| Black hole-bulge relationship, R and filters | [9] |
| Feature | Angular | Linear | Deprojected | Reference |
|---|---|---|---|---|
| (mas) | (pc) | (pc) | ||
| 43 GHz Core | 0.32 | [6] | ||
| Convergence | 54 | [5] | ||
| Intensity Peak | 57 | [5] | ||
| Jet length GHz | [19] |
| Feature | Size | Size |
|---|---|---|
| () | (pc) | |
| Gravitational Radius | 1 | |
| Broad-line region | ||
| Bondi radius | ||
| Torus (inner radius) | ||
| Jet 43 GHz Core | ||
| Torus (outer radius) | ||
| Jet Convergence (nozzle) | 54 | |
| Jet Intensity Peak | 57 | |
| Narrow-line region (outer radius) | 794 | |
| Ring/Spiral Arm | ||
| Jet length |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foschini, L.; Ciroi, S.; Berton, M.; Vercellone, S.; Romano, P.; Braito, V. Mapping the Narrow-Line Seyfert 1 Galaxy 1H 0323+342. Universe 2019, 5, 199. https://doi.org/10.3390/universe5090199
Foschini L, Ciroi S, Berton M, Vercellone S, Romano P, Braito V. Mapping the Narrow-Line Seyfert 1 Galaxy 1H 0323+342. Universe. 2019; 5(9):199. https://doi.org/10.3390/universe5090199
Chicago/Turabian StyleFoschini, Luigi, Stefano Ciroi, Marco Berton, Stefano Vercellone, Patrizia Romano, and Valentina Braito. 2019. "Mapping the Narrow-Line Seyfert 1 Galaxy 1H 0323+342" Universe 5, no. 9: 199. https://doi.org/10.3390/universe5090199
APA StyleFoschini, L., Ciroi, S., Berton, M., Vercellone, S., Romano, P., & Braito, V. (2019). Mapping the Narrow-Line Seyfert 1 Galaxy 1H 0323+342. Universe, 5(9), 199. https://doi.org/10.3390/universe5090199








