Hot Accretion Flow in Two-Dimensional Spherical Coordinates: Considering Pressure Anisotropy and Magnetic Field
Abstract
1. Introduction
2. Basic MHD Equations
2.1. Self-Similar Solutions
2.2. System of Differential Equations
2.3. Boundary Conditions
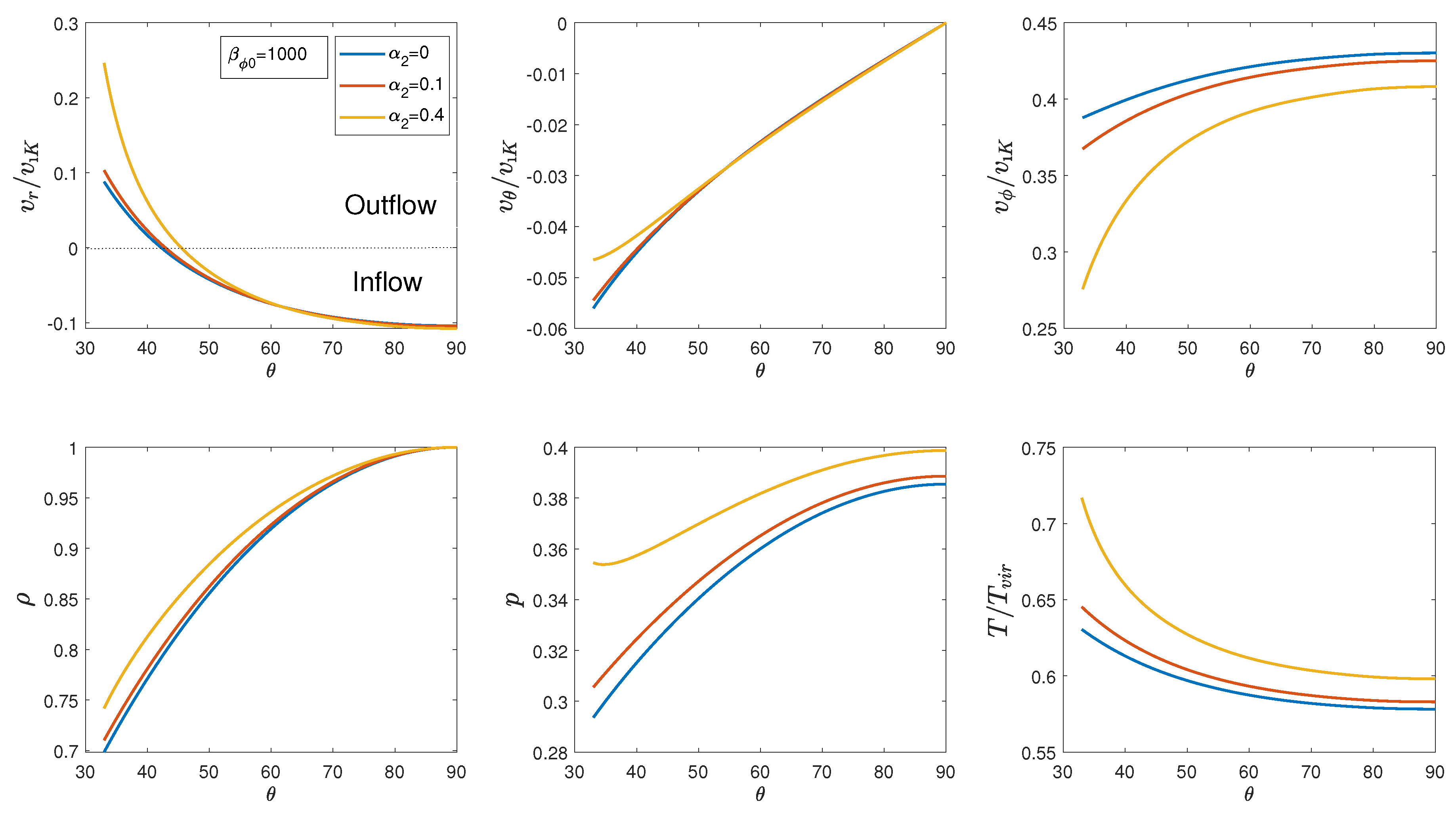
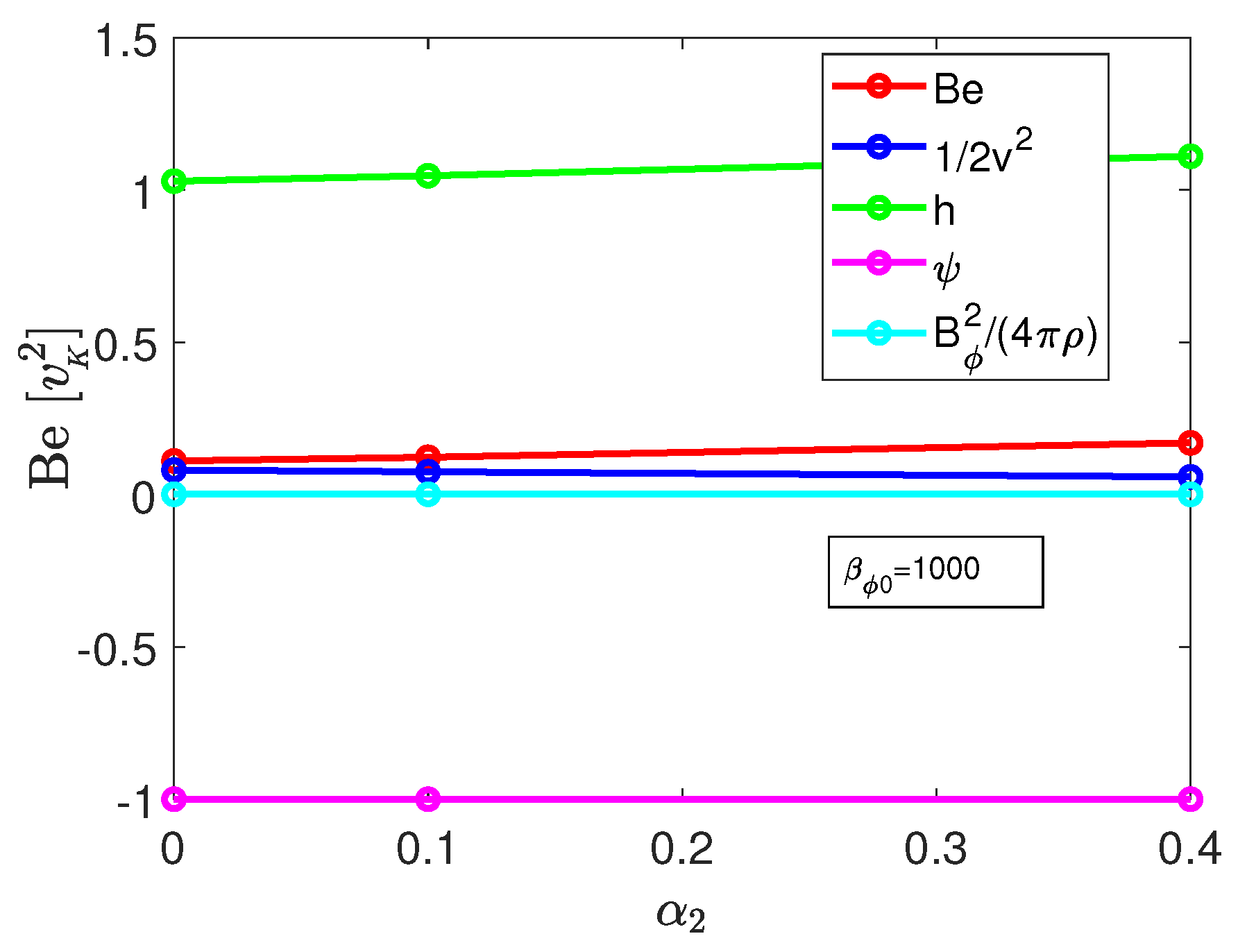
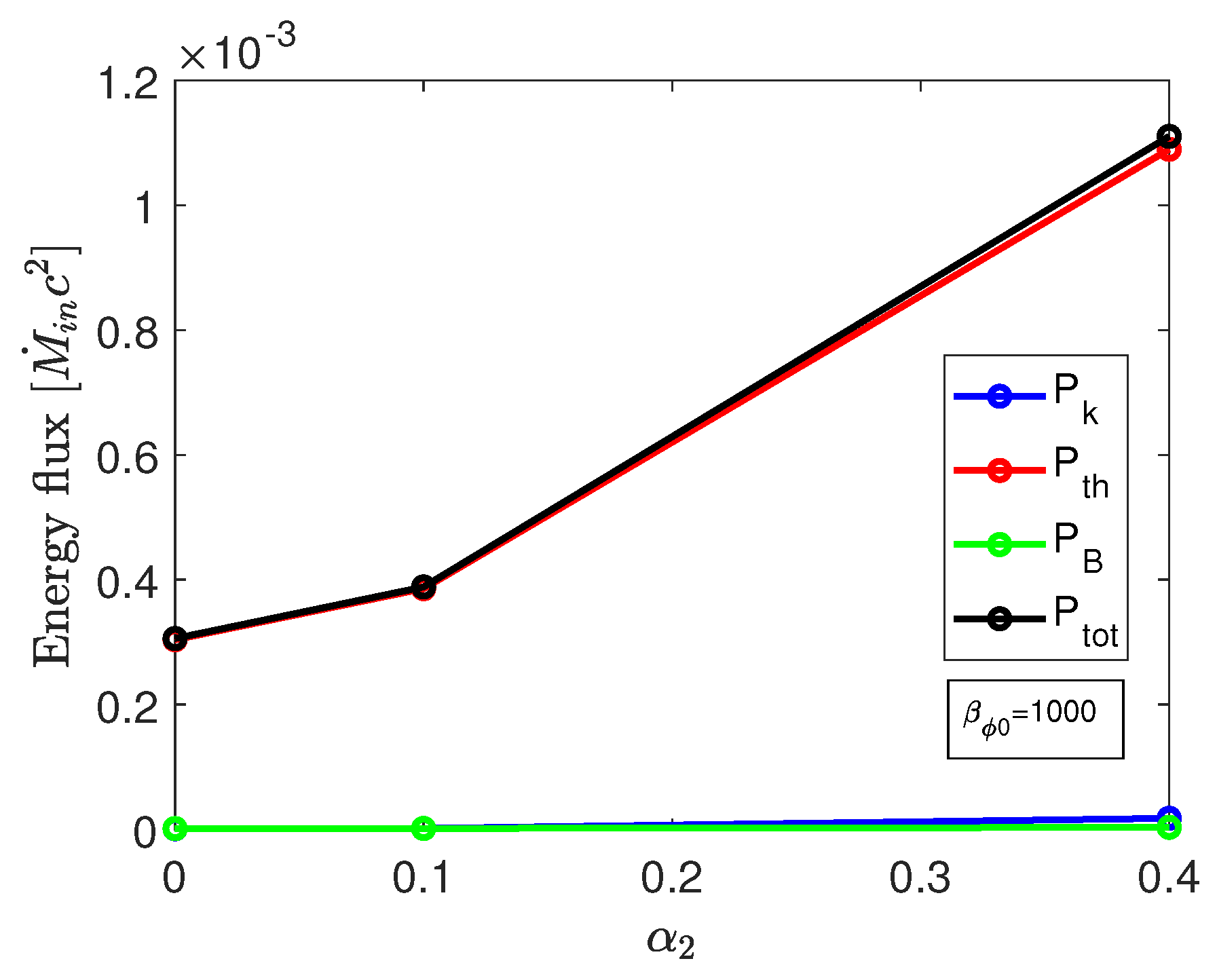
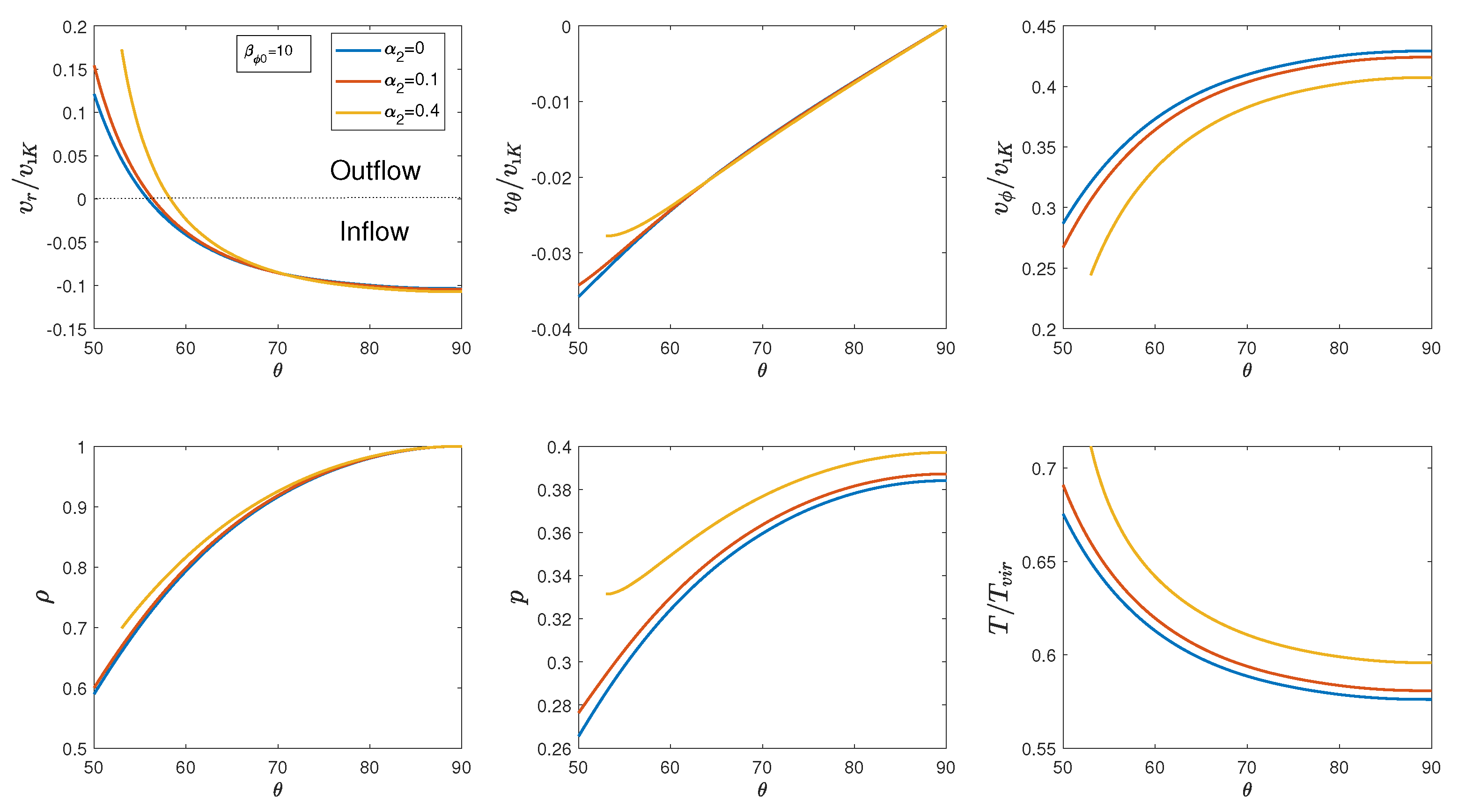
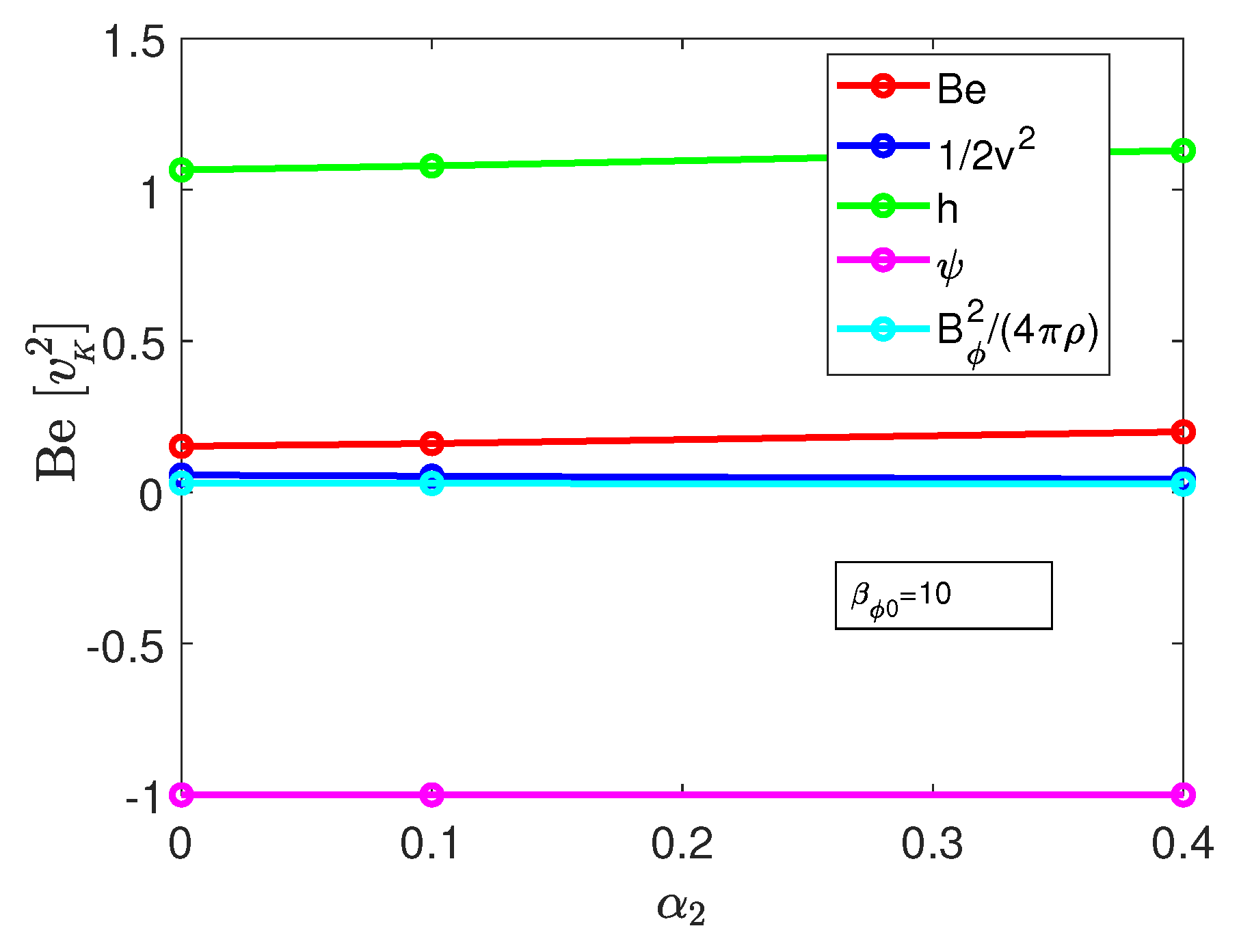
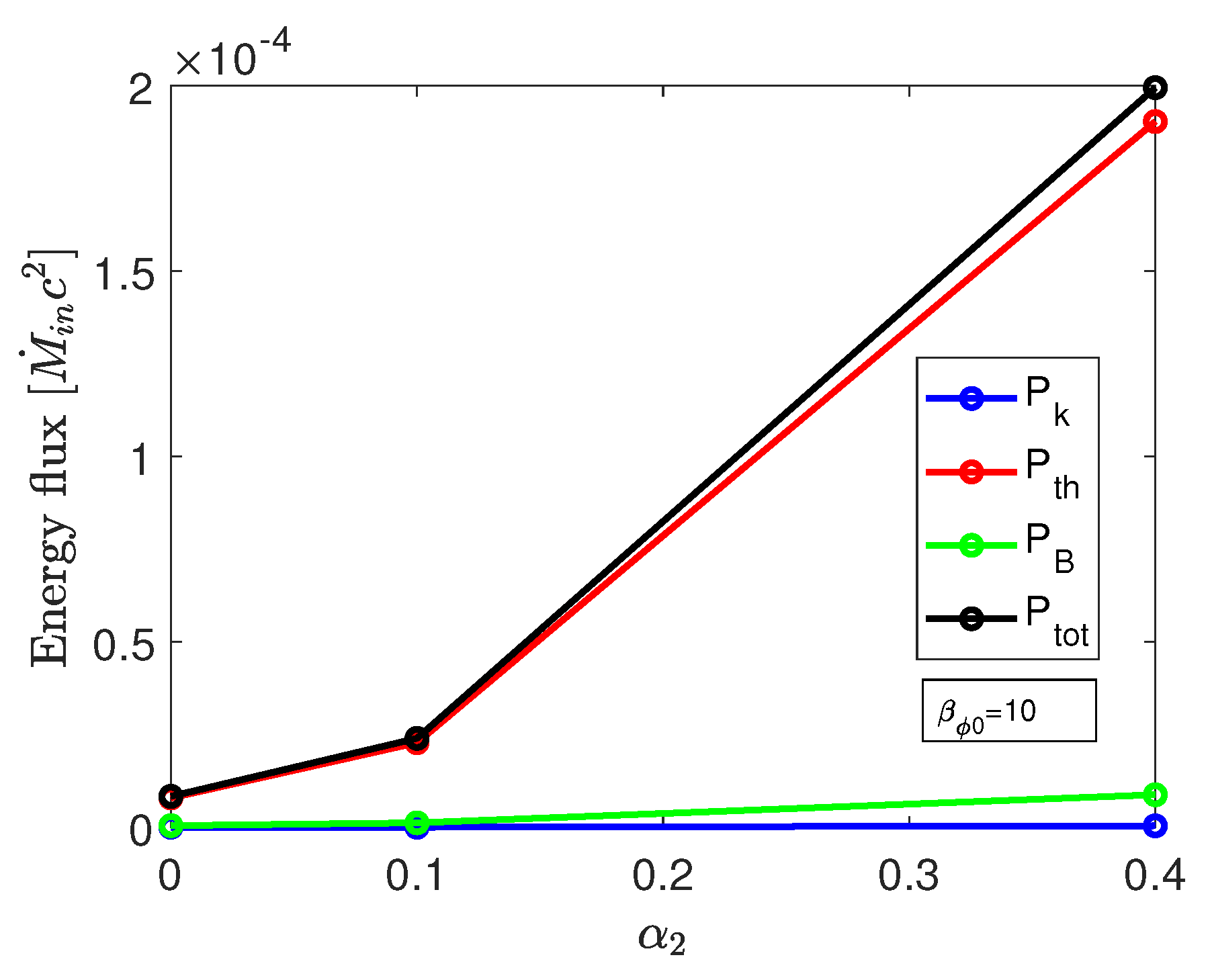
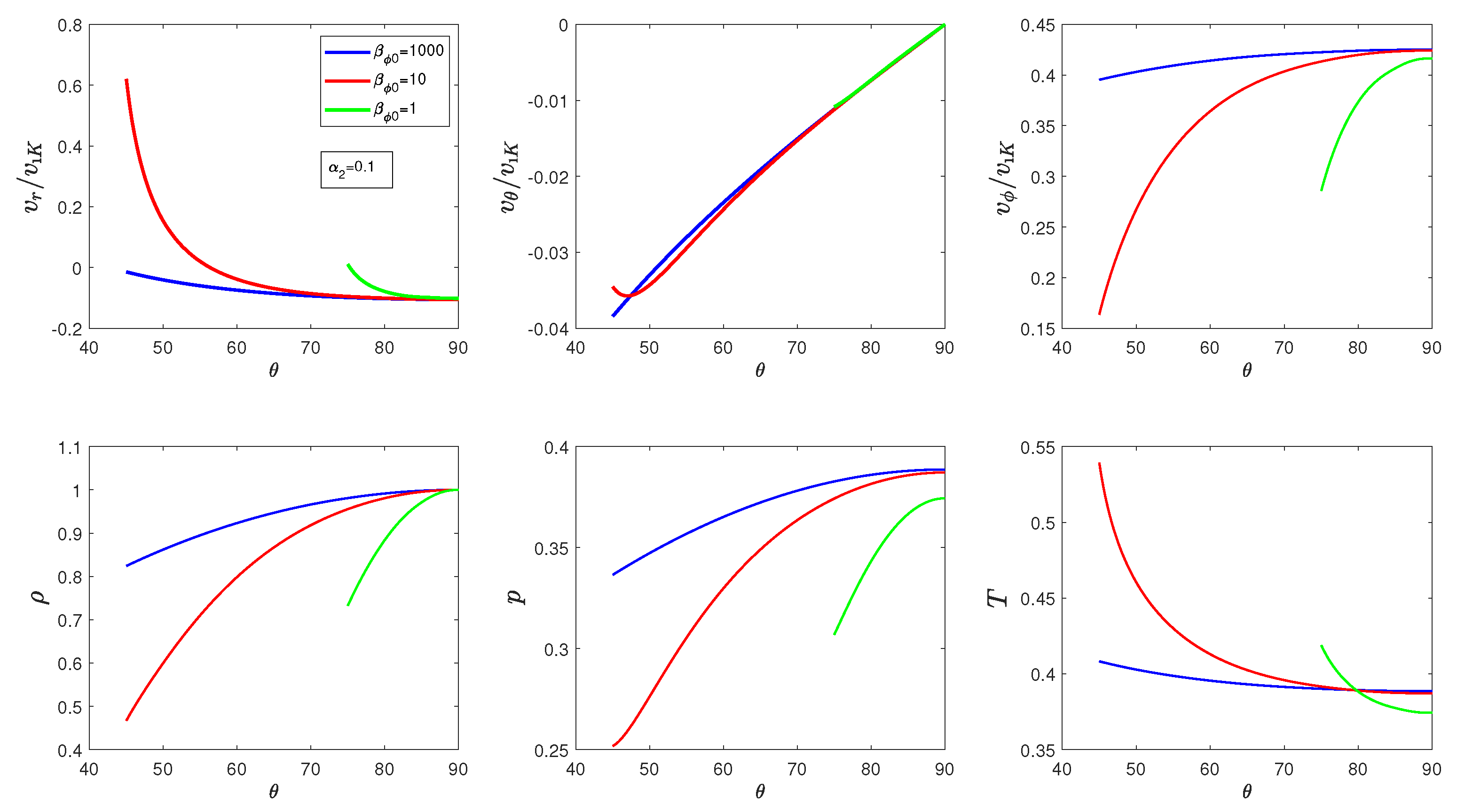
3. Results
3.1. Model with Weak Magnetic Field
3.2. Model with Stronger Magnetic Fields
4. Summary and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Blandford, R.; Payne, D.G. Hydromagnetic flows from accretion discs and the production of radio jets. Mon. Not. R. Astron. Soc. 1982, 199, 883–903. [Google Scholar] [CrossRef]
- Ferreira, J.; Pelletier, G. Low Mass Star Formation—From Infall to Outflow, Poster Proceedings of IAU Symp. No. 182; Malbet, F., Castets, A., Eds.; Observatoire de Grenoble: Chamonix, France, 1997; p. 112. [Google Scholar]
- Stepanovs, S.; Fendt, C. An extensive numerical survey of the correlation between outflow dynamics and accretion disk magnetization. Astrophys. J. 2016, 825, 14. [Google Scholar] [CrossRef]
- Murphy, G.C.; Ferreira, J.; Zanni, C. Large scale magnetic fields in viscous resistive accretion disks-I. Ejection from weakly magnetized disks. Astron. Astrophys. 2010, 512, A82. [Google Scholar] [CrossRef]
- Sheikhnezami, S.; Fendt, C.; Porth, O.; Vaidya, B.; Ghanbari, J. Bipolar jets launched from magnetically diffusive accretion disks. I. ejection efficiency versus field strength and diffusivity. Astrophys. J. 2012, 757, 65. [Google Scholar] [CrossRef]
- Stepanovs, D.; Fendt, C.; Sheikhnezami, S. Modeling MHD accretion-ejection: Episodic ejections of jets triggered by a mean-field disk dynamo. Astrophys. J. 2014, 796, 29. [Google Scholar] [CrossRef]
- Ichimaru, S. Bimodal behavior of accretion disks-Theory and application to Cygnus X-1 transitions. Astrophys. J. 1977, 214, 840–855. [Google Scholar] [CrossRef]
- Rees, M.J.; Begelman, M.C.; Blandford, R.D.; Phinney, E.S. Ion-supported tori and the origion of radio jets. Nature 1982, 295, 17. [Google Scholar] [CrossRef]
- Narayan, R.; Yi, I. Advection-dominated accretion: A self-similar solution. Astrophys. J. 1994, 428, L13–L16. [Google Scholar] [CrossRef]
- Stone, J.M.; Pringle, J.E.; Begelman, M.C. Hydrodynamical non-radiative accretion flows in two dimensions. Mon. Not. R. Astron. Soc. 1999, 310, 1002–1016. [Google Scholar] [CrossRef]
- Igumenshchev, I.V.; Abramowicz, M.A. Rotating accretion flows around black holes: Convection and variability. Mon. Not. R. Astron. Soc. 1999, 303, 309–320. [Google Scholar] [CrossRef]
- Igumenshchev, I.V.; Abramowicz, M.A. Two-dimensional models of hydrodynamical accretion flows into black holes. Astrophys. J. 2000, 130, 463. [Google Scholar] [CrossRef]
- Hawley, J.F.; Balbus, S.A.; Stone, J.M. A magnetohydrodynamic nonradiative accretion flow in three dimensions. Astrophys. J. 2011, 554, L49. [Google Scholar] [CrossRef]
- Machida, M.; Matsumoto, R.; Mineshige, S. Convection-dominated, magnetized accretion flows into black holes. Publ. Astron. Soc. Jpn. 2001, 53, L1–L4. [Google Scholar] [CrossRef]
- Stone, J.M.; Pringle, J.E. Magnetohydrodynamical non-radiative accretion flows in two dimensions. Mon. Not. R. Astron. Soc. 2011, 322, 461–472. [Google Scholar] [CrossRef]
- Hawley, J.F.; Balbus, S.A. The dynamical structure of nonradiative black hole accretion flows. Astrophys. J. 2002, 573, 738. [Google Scholar] [CrossRef]
- De Villiers, J.P.; Hawley, J.F.; Krolik, J.H. Magnetically driven accretion flows in the Kerr metric. I. Models and overall structure. Astrophys. J. 2003, 599, 1238. [Google Scholar] [CrossRef]
- Pen, U.L.; Matzener, C.D.; Wong, S. The Fate of Nonradiative Magnetized Accretion Flows: Magnetically Frustrated Convection. Astrophys. J. 2003, 596, L207. [Google Scholar] [CrossRef]
- Beckwith, K.; Hawley, J.F.; Krolik, J.H. The influence of magnetic field geometry on the evolution of black hole accretion flows: Similar disks, drastically different jets. Astrophys. J. 2008, 678, 1180. [Google Scholar] [CrossRef]
- Pang, B.; Pen, U.-L.; Matzner, C.D.; Green, S.R.; Liebendorfer, M. Numerical parameter survey of non-radiative black hole accretion: Flow structure and variability of the rotation measure. Mon. Not. R. Astron. Soc. 2011, 415, 1228–1239. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Narayan, R.; McKinney, J.C. Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole. Mon. Not. R. Astron. Soc. 2011, 418, L79–L83. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; McKinney, J.C. Prograde and retrograde black holes: Whose jet is more powerful? Mon. Not. R. Astron. Soc. 2012, 423, L55–L59. [Google Scholar] [CrossRef]
- Yuan, F.; Wu, M.; Bu, D. Numerical simulation of hot accretion flows. I. A large radial dynamical range and the density profile of accretion flow. Astrophys. J. 2012, 761, 129. [Google Scholar] [CrossRef]
- Yuan, F.; Bu, D.; Wu, M. Numerical simulation of hot accretion flows. II. Nature, origin, and properties of outflows and their possible observational applications. Astrophys. J. 2012, 761, 130. [Google Scholar] [CrossRef]
- McKinney, J.; Tchekhovskoy, A.; Blandford, R. General relativistic magnetohydrodynamic simulations of magnetically choked accretion flows around black holes. Mon. Not. R. Astron. Soc. 2012, 423, 3083–3117. [Google Scholar] [CrossRef]
- Narayan, R.; Sadowski, A.; Penna, R.F.; Kulkarni, A.K. GRMHD simulations of magnetized advection-dominated accretion on a non-spinning black hole: Role of outflows. Mon. Not. R. Astron. Soc. 2010, 426, 3241–3259. [Google Scholar] [CrossRef]
- Li, J.; Ostriker, J.; Sunyaev, R. Rotating accretion flows: From infinity to the black hole. Astrophys. J. 2013, 767, 105. [Google Scholar] [CrossRef]
- Sadowski, A.; Narayan, R.; Penna, R.; Zhu, Y. Energy, momentum and mass outflows and feedback from thick accretion discs around rotating black holes. Mon. Not. R. Astron. Soc. 2013, 436, 3856–3874. [Google Scholar] [CrossRef]
- Ho, L.C. Nuclear activity in nearby galaxies. Annu. Rev. Astron. Astrophys. 2008, 46, 475–539. [Google Scholar] [CrossRef]
- Antonucci, R. A panchromatic review of thermal and nonthermal active galactic nuclei. Astron. Astrophys. Trans. 2012, 27, 557–602. [Google Scholar]
- Done, C. Accretion flows in Binaries and AGN. In Proceedings of the Suzaku-MAXI 2014: Expanding the Frontiers of the X-ray Universe, Matsuyama, Japan, 19–22 February 2014; p. 300. [Google Scholar]
- Esin, A.A.; McClintock, J.E.; Narayan, R. Advection-Dominated Accretion and the Spectral States of Black Hole X-ray Binaries: Application to Nova Muscae 1991. Astrophys. J. 1997, 489, 865–889. [Google Scholar] [CrossRef]
- Fender, R.P.; Belloni, T.M.; Gallo, E. Towards a unified model for black hole X-ray binary jets. Mon. Not. R. Astron. Soc. 2004, 355, 1105–1118. [Google Scholar] [CrossRef]
- Zdziarski, A.A.; Gierliński, M. Radiative processes, spectral states and variability of black-hole binaries. Prog. Theor. Phys. Suppl. 2004, 155, 99–119. [Google Scholar] [CrossRef]
- Narayan, R. Low-luminosity accretion in black hole X-ray binaries and active galactic nuclei. Astrophys. Space Sci. 2005, 300, 177–188. [Google Scholar] [CrossRef]
- Remillard, R.A.; McClintock, J.E. X-ray properties of black-hole binaries. Annu. Rev. Astron. Astrophys. 2006, 44, 49–92. [Google Scholar] [CrossRef]
- Narayan, R.; McClintock, J.E. Advection-dominated accretion and the black hole event horizon. New Astron. Rev. 2008, 51, 733–751. [Google Scholar] [CrossRef]
- Belloni, T.M. States and transitions in black hole binaries. In The Jet Paradigm—From Microquasars to Quasars; Springer: Berlin/Heidelberg, Germany, 2010; pp. 53–84. [Google Scholar]
- Wu, Q.; Cao, X.; Ho, L.C.; Wang, D. A physical link between jet formation and hot plasma in active galactic nuclei. Astrophys. J. 2013, 700, 31. [Google Scholar] [CrossRef]
- Yuan, F.; Narayan, R. Hot accretion flows around black holes. Annu. Rev. Astron. Astrophys. 2014, 52, 529–588. [Google Scholar] [CrossRef]
- Crenshaw, D.M.; Kraemer, S.B. Feedback from mass outflows in nearby active galactic nuclei. I. Ultraviolet and X-ray absorbers. Astrophys. J. 2012, 753, 75. [Google Scholar] [CrossRef]
- Tombesi, F.; Sambruna, J.N.; Reeves, J.N.; Braito, V.; Ballo, L.; Gofford, J.; Cappi, M.; Mushotzky, R.F. Discovery of ultra-fast outflows in a sample of broad-line radio galaxies observed with suzaku. Astrophys. J. 2010, 719, 700. [Google Scholar] [CrossRef]
- Tombesi, F.; Tazaki, F.; Mushotzky, R.F.; Ueda, Y.; Cappi, M.; Gofford, J.; Reeves, J.N.; Guainazzi, M. Ultrafast outflows in radio-loud active galactic nuclei. Mon. Not. R. Astron. Soc. 2014, 443, 2154–2182. [Google Scholar] [CrossRef]
- Wang, Q.D.; Nowak, M.A.; Markoff, S.B.; Baganoff, F.K.; Nayakshin, S.; Yuan, F.; Cuadra, J.; Davis, J.; Dexter, J.; Fabian, A.C.; et al. Dissecting X-ray–emitting gas around the center of our galaxy. Science 2013, 341, 981–983. [Google Scholar] [CrossRef] [PubMed]
- Cheung, E.; Bundy, K.; Cappellari, M.; Peirani, S.; Rujopakarn, W.; Westfall, K.; Yan, R.; Bershady, M.; Greene, J.E.; Heckman, T.M.; et al. Suppressing star formation in quiescent galaxies with supermassive black hole winds. Nature 2016, 533, 504. [Google Scholar] [CrossRef] [PubMed]
- Ma, M.; Roberts, S.R.; Li, Y.; Wang, Q.D. Spectral energy distribution of the inner accretion flow around Sgr A* - clue for a weak outflow in the innermost region. Mon. Not. R. Astron. Soc. 2019, 483, M5614. [Google Scholar] [CrossRef]
- Homan, J.; Neilson, J.; Allen, J.L.; Chakrabarty, D.; Fender, R.; Fridriksson, J.K.; Remillard, R.A.; Schulz, N. Evidence for simultaneous jets and disk winds in luminous low-mass X-ray binaries. Astrophys. J. 2016, 830, L5. [Google Scholar] [CrossRef]
- Yuan, F.; Gan, Z.; Narayan, R.; Sadowski, A.; Bu, D.; Bai, X. Numerical simulation of hot accretion flows. III. revisiting wind properties using the trajectory approach. Astrophys. J. 2015, 804, 101. [Google Scholar] [CrossRef]
- Bu, D.; Yuan, F.; Wu, M.; Cuadra, J. On the role of initial and boundary conditions in numerical simulations of accretion flows. Mon. Not. R. Astron. Soc. 2013, 434, 1692–1701. [Google Scholar] [CrossRef]
- Bu, D.; Yuan, F.; Gan, Z.; Yang, X. Hydrodynamical numerical simulation of wind production from black hole hot accretion flows at very large radii. Astrophys. J. 2016, 818, 83. [Google Scholar] [CrossRef]
- Bu, D.; Yuan, F.; Gan, Z.; Yang, X. Magnetohydrodynamic numerical simulation of wind production from hot accretion flows around black holes at very large radii. Astrophys. J. 2016, 823, 90. [Google Scholar] [CrossRef]
- Xie, F.; Yuan, F. The influences of outflow on the dynamics of inflow. Astrophys. J. 2008, 681, 499. [Google Scholar] [CrossRef]
- Li, S.L.; Cao, X.W. Global dynamics of advection-dominated accretion flows with magnetically driven outflow. Mon. Not. R. Astron. Soc. 2009, 400, L1734. [Google Scholar] [CrossRef]
- Li, S.L.; Cao, X.W. The kinetic power of jets magnetically accelerated from advection-dominated accretion flows in radio galaxies. Mon. Not. R. Astron. Soc. 2010, 405, L61. [Google Scholar] [CrossRef]
- Gu, W.M. Mechanism of Outflows in Accretion System: Advective Cooling Cannot Balance Viscous Heating? Astrophys. J. 2015, 799, 71. [Google Scholar] [CrossRef]
- Ghasemnezhad, M.; Abbassi, S. The influence of outflow and global magnetic field on the structure and spectrum of resistive CDAFs. Astrophys. Space Sci. 2016, 361, 372. [Google Scholar] [CrossRef]
- Ghasemnezhad, M.; Abbassi, S. The influence of large-scale magnetic field in the structure of supercritical accretion flow with outflow. Mon. Not. R. Astron. Soc. 2017, 469, 3307. [Google Scholar] [CrossRef]
- Bu, D.; Mosallanezhad, A. The effects of magnetic field strength on the properties of wind generated from hot accretion flow. Astron. Astrophys. 2018, 615, A35. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Choi, E.; Ciotti, L.; Novak, G.S.; Proga, D. Momentum driving: Which physical processes dominate active galactic nucleus feedback? Astrophys. J. 2010, 722, 642. [Google Scholar] [CrossRef]
- Ciotti, L.; Ostriker, J.P.; Proga, D. Feedback from central black holes in elliptical galaxies. III. Models with both radiative and mechanical feedback. Astrophys. J. 2010, 717, 708. [Google Scholar] [CrossRef]
- Ciotti, L.; Pellegrini, S.; Negri, A.; Ostriker, J.P. The Effect of Agn Feedback on the Interstellar Medium of Early-Type Galaxies: 2D Hydrodynamical Simulations of the Low-Rotation Case. Astrophys. J. 2017, 835, 15. [Google Scholar] [CrossRef]
- Weinberger, R.; Springel, V.; Hernquist, L.; Pillepich, A.; Marinacci, F.; Pakmor, R.; Nelson, D.; Genel, S.; Vogelsberger, M.; Naiman, J.; et al. Simulating galaxy formation with black hole driven thermal and kinetic feedback. Mon. Not. R. Astron. Soc. 2017, 465, 3291–3308. [Google Scholar] [CrossRef]
- Weinberger, R.; Springel, V.; Pakmor, R.; Nelson, D.; Genel, S.; Pillepich, A.; Vogelsberger, M.; Marinacci, F.; Naiman, J.; Torrey, P.; et al. Supermassive black holes and their feedback effects in the IllustrisTNG simulation. Mon. Not. R. Astron. Soc. 2018, 479, 4056–4072. [Google Scholar] [CrossRef]
- Yuan, F.; Yoon, D.; Li, Y.; Gan, Z.M.; Ho, L.C.; Guo, F. Active galactic nucleus feedback in an elliptical galaxy with the most updated AGN physics. I. low angular momentum case. Astrophys. J. 2018, 857, 121. [Google Scholar] [CrossRef]
- Yoon, D.; Yuan, F.; Gan, Z.; Ostriker, J.P.; Li, Y.; Ciotti, L. Active galactic nucleus feedback in an elliptical galaxy with the most updated AGN physics. II. high angular momentum case. Astrophys. J. 2018, 864, 6. [Google Scholar] [CrossRef]
- Bu, D.; Yang, X. Quenching Black Hole Accretion by Active Galactic Nuclei Feedback. Astrophys. J. 2019, 871, 138B. [Google Scholar] [CrossRef]
- Tanaka, T.; Menou, K. Hot accretion with conduction: Spontaneous thermal outflows. Astrophys. J. 2006, 649, 345. [Google Scholar] [CrossRef]
- Johnson, B.M.; Quataert, E. The effects of thermal conduction on radiatively inefficient accretion flows. Astrophys. J. 2007, 660, 1273. [Google Scholar] [CrossRef][Green Version]
- Chandra, M.; Gammie, C.F.; Foucart, F.; Quataert, E. An extended magnetohydrodynamics model for relativistic weakly collisional plasmas. Astrophys. J. 2015, 810, 162. [Google Scholar] [CrossRef]
- Foucart, F.; Chandra, M.; Gammie, C.F.; Quataert, E. Evolution of accretion discs around a kerr black hole using extended magnetohydrodynamics. Mon. Not. R. Astron. Soc. 2016, 456, 1332. [Google Scholar] [CrossRef]
- Kunz, M.W.; Schekochihin, A.A.; Stone, J.M. Firehose and mirror instabilities in a collisionless shearing plasma. Phys. Rev. Lett. 2014, 112, 205003. [Google Scholar] [CrossRef]
- Hellinger, P.; Trávníček, P.M. Proton temperature-anisotropy-driven instabilities in weakly collisional plasmas: Hybrid simulations. J. Plasma Phys. 2015, 81, 305810103. [Google Scholar] [CrossRef]
- Riquelme, M.A.; Mario, A.; Quataert, E.; Verscharen, D. Particle-in-cell simulations of continuously driven mirror and ion cyclotron instabilities in high beta astrophysical and heliospheric plasmas. Astrophys. J. 2015, 800, 27. [Google Scholar] [CrossRef]
- Sironi, L.; Narayan, R. Electron heating by the ion cyclotron instability in collisionless accretion flows. I. Compression-driven instabilities and the electron heating mechanism. Astrophys. J. 2015, 800, 88. [Google Scholar] [CrossRef]
- Parrish, I.J.; Stone, J.M. Saturation of the magnetothermal instability in three dimensions. Astrophys. J. 2007, 664, 135. [Google Scholar] [CrossRef]
- Sharma, P.; Quataert, E.; Stone, J.M. Spherical accretion with anisotropic thermal conduction. Mon. Not. R. Astron. Soc. 2008, 389, 1815–1827. [Google Scholar] [CrossRef]
- Bu, D.; Yuan, F.; Stone, J.M. Magnetothermal and magnetorotational instabilities in hot accretion flows. Mon. Not. R. Astron. Soc. 2011, 413, 2808. [Google Scholar] [CrossRef][Green Version]
- Quataert, E. A dynamical model for hot gas in the Galactic center. Astrophys. J. 2004, 613, 322. [Google Scholar] [CrossRef]
- Bu, D.; Wu, M.; Yuan, Y. Effects of anisotropic thermal conduction on wind properties in hot accretion flow. Mon. Not. R. Astron. Soc. 2016, 459, 746. [Google Scholar] [CrossRef][Green Version]
- Quataert, E.; Dorl, W.; Hammett, G.W. The Magnetorotational Instability in a Collisionless Plasma. Astrophys. J. 2002, 577, 524. [Google Scholar] [CrossRef]
- Sharma, P.; Hammett, G.W.; Quataert, E. Transition from collisionless to collisional magnetorotational instability. Astrophys. J. 2003, 596, 1121. [Google Scholar] [CrossRef]
- Wu, M.; Bu, D.; Gan, Z.; Yuan, Y. Hot accretion flow with anisotropic viscosity. Astrophys. J. 2017, 608, A114. [Google Scholar] [CrossRef]
- King, A.R.; Pringle, J.E.; Livio, M. Accretion disc viscosity: How big is alpha? Mon. Not. R. Astron. Soc. 2007, 376, 1740. [Google Scholar] [CrossRef]
- Bu, D.; Xu, P.; Zhu, B. Self-Similar Solution of Hot Accretion Flow with Anisotropic Pressure. Universe 2019, 5, 89. [Google Scholar] [CrossRef]
- Machida, M.; Hayashi, M.R.; Matsumoto, R. Global simulations of differentially rotating magnetized disks: Formation of low-ßfilaments and structured coronae. Astrophys. J. 2000, 532, L67. [Google Scholar] [CrossRef] [PubMed]
- Hirose, S.; Krolik, J.H.; De Villiers, J.P.; Hawley, J.H. Magnetically driven accretion flows in the Kerr metric. II. Structure of the magnetic field. Astrophys. J. 2004, 606, 1083. [Google Scholar] [CrossRef]
- Bai, X.N.; Stone, J.M. Local study of accretion disks with a strong vertical magnetic field: Magnetorotational instability and disk outflow. Astrophys. J. 2013, 767, 30. [Google Scholar] [CrossRef]
- Mosallanezhad, A.; Bu, D.; Yuan, F. Two-dimensional inflow-wind solution of black hole accretion with an evenly symmetric magnetic field. Mon. Not. R. Astron. Soc. 2016, 456, 2877–2884. [Google Scholar] [CrossRef][Green Version]
- Braginskii, S.I. Transport processes in a plasma. Reviews of plasma physics. Rev. Plasma Phys. 1965, 1, 205. [Google Scholar]
- Balbus, S.A. Viscous shear instability in weakly magnetized, dilute plasmas. Astrophys. J. 2004, 616, 857. [Google Scholar] [CrossRef][Green Version]
- Salvesen, G.; Simon, J.B.; Armitage, P.J.; Begelman, M.C. Accretion disc dynamo activity in local simulations spanning weak-to-strong net vertical magnetic flux regimes. Mon. Not. R. Astron. Soc. 2016, 457, 857–874. [Google Scholar] [CrossRef]
- Narayan, R.; Yi, I. Advection-dominated accretion: Self-similarity and bipolar outflows. Astrophys. J. 1995, 444, 231–243. [Google Scholar] [CrossRef]
- Xue, L.; Wang, J.-C. The Effect of Outflow on Advection-dominated Accretion. Astrophys. J. 2005, 623, 372. [Google Scholar] [CrossRef][Green Version]
- Jiao, C.L.; Wu, X.B. On the structure of accretion disks with outflows. Astrophys. J. 2011, 733, 112. [Google Scholar] [CrossRef]
- Das, U.; Begelman, M.C.; Lesur, G. Instability in strongly magnetized accretion discs: A global perspective. Mon. Not. R. Astron. Soc. 2018, 473, 2791–2812. [Google Scholar] [CrossRef]
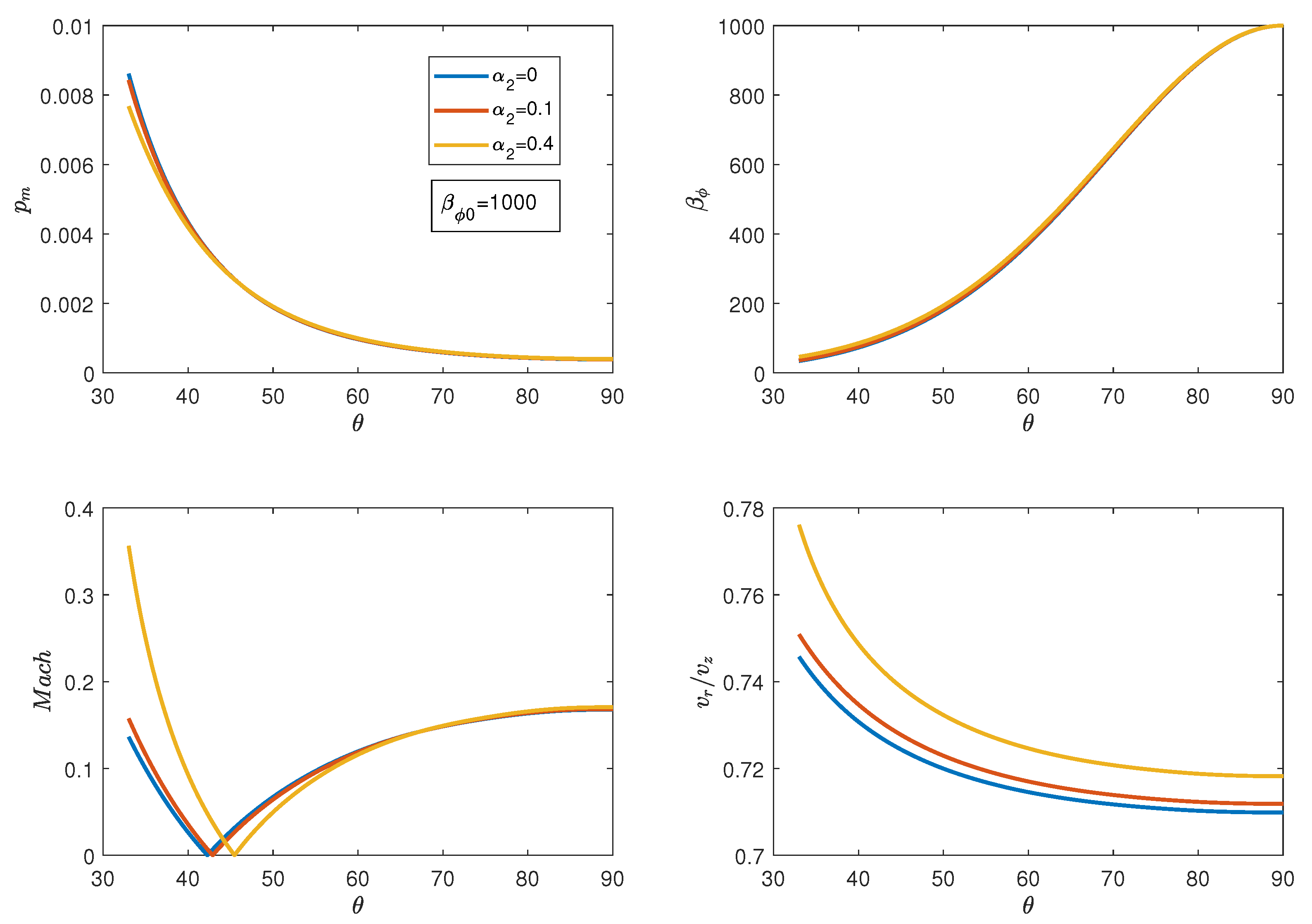
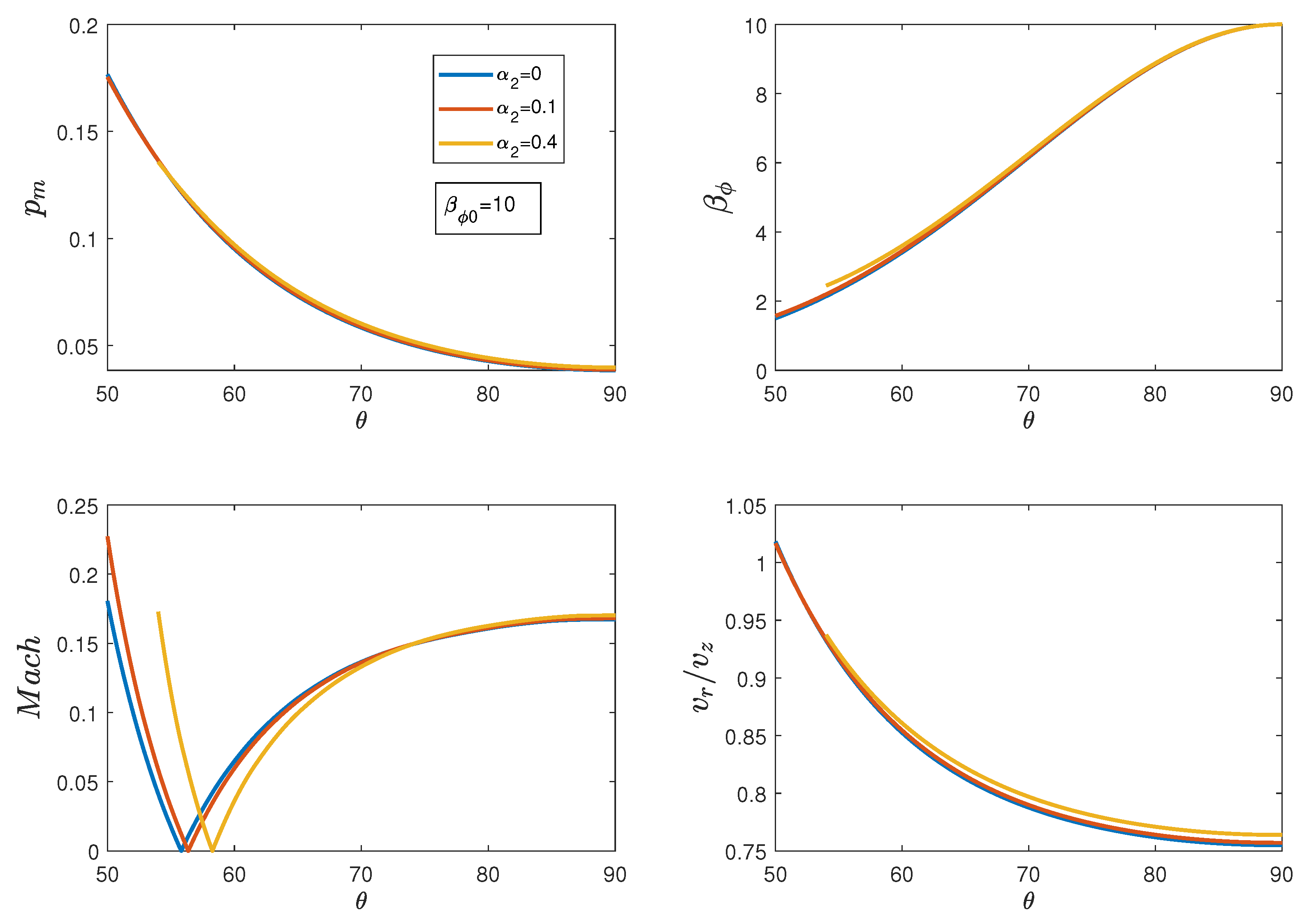
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, H.-H.; Bu, D.-F. Hot Accretion Flow in Two-Dimensional Spherical Coordinates: Considering Pressure Anisotropy and Magnetic Field. Universe 2019, 5, 197. https://doi.org/10.3390/universe5090197
Deng H-H, Bu D-F. Hot Accretion Flow in Two-Dimensional Spherical Coordinates: Considering Pressure Anisotropy and Magnetic Field. Universe. 2019; 5(9):197. https://doi.org/10.3390/universe5090197
Chicago/Turabian StyleDeng, Hui-Hong, and De-Fu Bu. 2019. "Hot Accretion Flow in Two-Dimensional Spherical Coordinates: Considering Pressure Anisotropy and Magnetic Field" Universe 5, no. 9: 197. https://doi.org/10.3390/universe5090197
APA StyleDeng, H.-H., & Bu, D.-F. (2019). Hot Accretion Flow in Two-Dimensional Spherical Coordinates: Considering Pressure Anisotropy and Magnetic Field. Universe, 5(9), 197. https://doi.org/10.3390/universe5090197



