Abstract
This manuscript aims at giving new advances on the functional renormalization group applied to the tensorial group field theory. It is based on the series of our three papers (Lahoche, et al., Class. Quantum Gravity 2018, 35, 19), (Lahoche, et al., Phys. Rev. D 2018, 98, 126010) and (Lahoche, et al., Nucl. Phys. B, 2019, 940, 190–213). We consider the polynomial Abelian models without the closure constraint. More specifically, we discuss the case of the quartic melonic interaction. We present a new approach, namely the effective vertex expansion method, to solve the exact Wetterich flow equation and investigate the resulting flow equations, especially regarding the existence of non-Gaussian fixed points for their connection with phase transitions. To complete this method, we consider a non-trivial constraint arising from the Ward–Takahashi identities and discuss the disappearance of the global non-trivial fixed points taking into account this constraint. Finally, we argue in favor of an alternative scenario involving a first order phase transition into the reduced phase space given by the Ward constraint.
1. Introduction
In seeking a theory to unify modern physics, i.e., a well-defined theory of quantum gravity, numerous contributions have been made. Despite the fact that none of them has given a complete resolution to the problem, several major advances have been observed. Of these advances, we count the very recent propositions such as loop quantum gravity [1,2], dynamical triangulation [3,4,5], noncommutative geometry [6,7], group field theories (GFTs) [8,9,10,11,12], and tensors models (TMs) [13,14,15,16,17,18,19,20,21,22]. These approaches are considered as new background independent approaches according to several theoreticians. GFTs are quantum field theories over the group manifolds and are considered as the second quantization version of loop quantum gravity [12]. These theories are characterized by the specific form of non-locality in their interactions. TMs, especially colored ones, allow one to define probability measures on simplicial pseudo-manifolds such that the tensor of rank d represents a -simplex. TMs admit the large N-limit (N is the size of the tensor) dominated by the graphs called melons, thanks to the Gurau breakthrough [20,21,22]. The large N-limit or the leading order encodes a sum over a class of colored triangulations of the D-sphere, and its behavior is a powerful tool that allows us to understand the continuous limit of these models through, for instance, the study of critical exponents and phase transitions. TM and GFT are combined to give birth to a new class of field theories called tensorial group field theory. These class of field models enjoy renormalization and asymptotic freedom [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38].
Using the functional renormalization group (FRG) method, it is also possible to identify the equivalent of the Wilson–Fisher fixed point for some particular cases of models.
There are several ways to introduce the FRG in field theories. The first approach is the one pioneered by Wilson, simple and intuitive and therefore yielding a powerful way to think about quantum field theories [39,40]. This method allows a smooth interpolation between the known microscopic laws IR-regime and the complicated macroscopic phenomena in physical systems’ UV-regime and is constructed with the incomplete integration as the cutoff procedure. Well after, Polchinski provided a new approach called the Wilson–Polchinski FRG equation [41] to address the same question inspired by the Wilson method. This very practicable method may be integrated with an arbitrary cutoff function and expanded up to the next leading order of the derivative expansion. Despite the fact that all these approaches seem to be nonperturbative, in practice, the perturbative solution has appeared more attractive. More recently, the so-called Wetterich flow equation [42] was proposed to study the nonperturbative FRG, and this study requires approximations or truncations and numerical analysis, which is not very well controlled. The FRG equation allows determining the fixed points and probably the phase transition. These phase transitions in the case of TGFTmodels may help to identify the emergence of general relativity and quantum mechanics through the pre-geometrogenesis scenario [43,44,45,46]. Indeed, the way the quantum degrees of freedom are organized to shape a geometric structure that can be identified with a semi-classical space-time is one of the challenges for the GFT approach. In the geometrogenesis point of view, the standard space-time geometry is understood as an emergent property, the scenario leading to this geometric limit being assumed quite close to Bose–Einstein condensation in condensed matter physics. Evidences for this scenario were provided by FRG analysis [47,48,49,50,51,52,53,54,55]. In the recent works [56,57,58], the effective vertex expansion (EVE) method was used in the context of the FRG. This leads to the definition of a new class of equations called structure equations that help to solve the Wetterich flow equations. Taking into account the leading order contribution in the symmetric phase, the non-perturbative regime without truncation can be studied. The Ward–Takahashi (WT) identities are also derived [59,60,61] and become a constraint along the flow. Note that the WT-identities are universal for all field theories having a symmetry, and are not specific to TGFT. Therefore, all the fixed points must belong inside the domain of this constraint line, before being considered as an acceptable fixed point. In the case of quartic melonic TGFT models, it has been shown that the fixed point occurring from the solution of the Wetterich equation violates this constraint for any choice of the regulator function. This violation is also independent of the method used to find this fixed point, whether it is the truncation or the EVE method. This point will be discussed carefully in this note. Let us remark that most of the TGFT models previously studied in the literature were shown to admit at least a nontrivial fixed point and therefore a phase transition. The phase transitions are very useful in the likely emergence of the metric and are linked to the existence of fixed points, which becomes unavoidable in the search for models that may probably describe our universe after the geometrogenesis scenario. However, in this paper, we study the quartic -TGFT models and prove that no fixed points can be found. First of all, we consider the Wilson–Polchinski renormalization group method and show the weakness of this method in the nonperturbative regime. Then, we consider the nonperturbative Wetterich flow equation from which the nonperturbative analysis can be made by an approximation on the average effective action, called truncation. The EVEmethod is used to get around the approximation and therefore solves the flow without truncation. The set of Ward–Takahashi identities and structure equations are derived to provide a nontrivial constraint on the reliability of the approximation schemes, i.e., the truncation and the choice of the regulator.
The paper is organized as follows: In Section 2, we recall the FGR method by Wilson–Polchinski and apply it in the context of TGFT. Despite the efficiencies of this method, we will present some questions that arise, in the search for a nonperturbative solution, and then, we will go further into the Wetterich flow equation. Section 3 is dedicated to the description of the Wetterich flow equation and the corresponding solution when the truncation method is applied. We also show that the only nontrivial fixed point, which comes from the solution of the flows, violates the Ward identities. In Section 4, we perform new nonperturbative analysis using the so-called structure equations given, and the solutions of the flow equations are also derived. In the last Section 5, we provide a discussion and conclusion to our work.
2. Introduction to the Nonperturbative Renormalization for TGFT
FRG is a powerful ingredient to think about when it comes to quantum field theories. Generally, in every situation where the scale belongs to a range of correlated variables, the theory may be treated by the renormalization group (RG). The first conceptual framework is Wilson’s version of the RG, which by Polchinski, may be applied in the case of quantum field theory. In this section, we discuss the nonperturbative renormalization group using not only the Wilson–Polchinski equation, but also the Wetterich flow equation. We discuss each method and consider the Wetterich flow equation as more suitable for the treatment of FRG applied to TGFT. Thanks to the Wilson method, the renormalization and renormalization group are understood as a coarse-graining process from a microscopic theory toward an effective long-distance theory. There are in fact different implementations of this idea, depending on the context. In the context of TGFT, we consider the pair of complex fields and , which take values of d-copies of arbitrary group G:
In a particular case, we assume that is an Abelian compact Lie group. For the rest, we only consider the Fourier transform of the fields and denoted by and , respectively, , written as (for , ):
The description of the statistical field theory is given by the partition function :
where is the interaction functional action assumed to be tensor invariant, J, the external currents, and a shorthand notation for:
The Gaussian measure is then fixed with the choice of the covariance C. In this paper, we adopt a Laplacian-type propagator of the form:
In order to prevent the UV divergences and suppress the high momenta contributions, the propagator (5) has to be regularized. In the usual case, the Schwinger regularization is used:
In the general case, by defining the function such that the condition is satisfied for and , we can write the propagator as a Laplace transform:
Then, we shall make the simplest choice , where is the Heaviside function, in order to recover the Schwinger regularization (6). For the rest, we keep in mind that the propagator is regularized, and the infinite limit will be given in an appropriate way. In this case, the following result in well satisfied:
Proposition 1.
Let us consider two non-normalized Gaussian measures and whose covariances C and are related by and such that C, , and Δ are assumed to be positive. Then, we get the following relation:
where and .
Proof.
The proof of this formula can simply be given using the definition of the Gaussian measure with mean zero and covariance matrix C as:
and the fact that:
□
We introduce tensorial unitary invariants, or simply tensorial invariants. An invariant is a polynomial in the tensor entries and that is invariant under the following action of (N being the size of the tensors):
The algebra of invariant polynomials is generated by a set of polynomials labeled as bubbles. A bubble is a connected, bipartite graph, regular of degree d, whose edges must be colored with a color belonging to the set and such that all d colors are incident at each vertex (and incident to exactly once). Examples of bubbles are displayed in Figure 1.
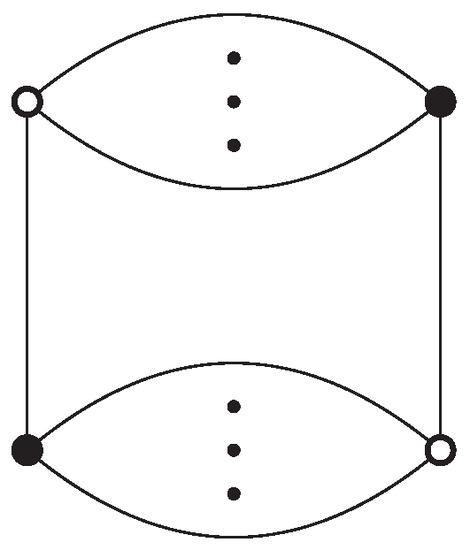
Figure 1.
The four-vertex bubble for which the dots indicate multiple edges.
In this paper, we consider the quartic melonic model, which is proven to be renormalizable in all orders in the perturbative theory. The interaction of this model taking into account the leading order contributions (melon) is written graphically as:
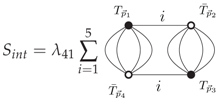 Note that the interaction (12) is invariant under the unitary transformations . In contrast, this is not the case for the kinetic terms and source terms due to the non-trivial propagator and sources J and . This implies the existence of a non-trivial Ward-identity, which becomes a strong constraint and will be taking into account from the FRG point of view.
Note that the interaction (12) is invariant under the unitary transformations . In contrast, this is not the case for the kinetic terms and source terms due to the non-trivial propagator and sources J and . This implies the existence of a non-trivial Ward-identity, which becomes a strong constraint and will be taking into account from the FRG point of view.

2.1. Wilson–Polchinski Equation
In this subsection, we discuss the Wilson–Polchinski RG equation and provide the corresponding solutions of the quartic melonic TGFT. For this, let us introduce a dilatation parameter . This parameter will be used as an evolution parameter in the integration around the UV modes. The RG idea is that if we want to describe the phenomena at scales down to s, then we should be able to use the set of variables defined at the scale s. Indeed, define the variation:
In the case where s is close to one, denoting by the infinitesimal version of the above variation, we get:
such that the partition function can be written as an integral over two fields, respectively associated with the “slow” and “rapid” modes. Starting with the partition function at scale , we get:
Proposition 1 allows us to decompose into two Gaussian integrals over two fields, and , corresponding respectively to the “rapid” and “slow” modes, with covariances and :
Then, identify the effective action at scale as:
and the decomposition (16) becomes:
Now, for an infinitesimal step, keeping only the leading order terms in when s is very close to one, we find:
with . At the same time, expanding the left-hand side of (18) in powers of and identifying the power of leads to:
Graphically, this equation is given by (and is considered as the Wilson–Polchinski RG equation):
 Note that we may consider not only as a fundamental scale, but also as an arbitrary step in the flow, meaning that Equation (20) holds at each step of the flow. Physically, Equation (20) explains how the couplings are affected when the fundamental scale changes and is therefore the one pioneering ideas of the renormalization group flow firstly given by Wilson. This approach follows from a remarkably simple and intuitive idea and yields a very powerful way to think about quantum field theories. The relation (21) can be also expanded in the following result:
Note that we may consider not only as a fundamental scale, but also as an arbitrary step in the flow, meaning that Equation (20) holds at each step of the flow. Physically, Equation (20) explains how the couplings are affected when the fundamental scale changes and is therefore the one pioneering ideas of the renormalization group flow firstly given by Wilson. This approach follows from a remarkably simple and intuitive idea and yields a very powerful way to think about quantum field theories. The relation (21) can be also expanded in the following result:

Proposition 2.
The set of Wilson–Polchinski renormalization group equations is given by:
where , . In this formula, we denote by the number of black and white nodes in each interactions, and we consider the following expansion for :
Proof.
A pragmatic way to introduce field strength renormalization is the following. We consider a wave function and the regularized field at the scale . A new functional is associated to this field such as . Equation (20) is then modified into (we deleted the tildes notation):
Then, by considering the following expansion for :
we get the relation (22). □
The Wilson–Polchinski equation is a leading order equation in the perturbation rather than the loop expansion. Note that we can show that this equation can be turned into a Fokker–Planck equation, and therefore, it may be formally solved by a standard method. The rest of this section is devoted to a perturbative analysis of the flow equations. Before starting this computation, we have to make the approximation regime precise. We shall consider only the UV limit, which corresponds to the higher values of the scale parameter s, or to the higher momenta variables , or also for the smaller distances, and we assume that and are large. However, the analysis in the UV regime can be extended to the IR limit, which corresponds to the smaller values of the scale parameter s. More precisely, our approximation can be characterized by both and in the UV and by in the IR. At scale and up to contributions of order , keeping only the melonic contribution, the action provided from (12) is assumed to be of the form:
where the first two terms take into account the fact that the parameter of the Gaussian measure, the mass, and the Laplacian term can be affected by the integration of the UV modes, and these counter-terms, assumed to be of order , take into account these modifications. The vertex is a product of the delta function and is given by:
Moreover, note that in this approach, the corrections to the Laplacian term are not suppressed by an effective counter-term in the action, but absorbed in the wave function renormalization. It is fixed such that all the Laplacian corrections are canceled by the term in the RG equation for . We adopt the standard ansatz, namely that the generic interaction of valence n is of order . This allows us to organize systematically the perturbative solution, for which we shall construct the order.
2.1.1. at Order
The first corrections occur at order for , whose flow equation is written as:
where:
and and . The r.h.s involves two typical contributions, which are pictured graphically in Figure 2, where the contraction with is represented by a dotted line with a gray box.
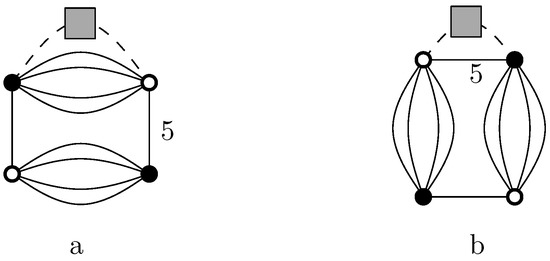
Figure 2.
The two graphs contributing to the interaction of degree two. Melonic (a) and non-melonic (b).
In the UV limit that we consider, the non-melonic contractions of the type on Figure 2b, creating only one internal face (of the color five on this figure), can be neglected in comparison to the melonic contributions of the form of Figure 2a. Retaining only the melonic contractions, Equation (28) becomes:
with . Expanding this relation in powers of , we generate mass and wave function corrections, and also the sub-dominant corrections, involving powers of greater than two. They correspond to the first deviation to the original form (26). Neglecting these sub-dominant contributions, we get the expansion:
for which we only keep the leading order terms in s, and we can extract the dominant contributions to the mass and wave-function renormalization. The term in generates a non-local two-point interaction of the form , where is the Laplacian on , and the first term generates a mass correction. Summing over the five colors, we find, at first order in :
2.1.2. and at Order
Let us focus on the second order perturbative solution, i.e., at , in which we have to take into account the contributions of interactions of valence six, , verifying the flow equation:
which can be easily integrated with the initial condition as:
As for the interaction of degree one, the structure of this effective interaction can be understood as a contraction between two bubbles, as pictured in Figure 3, where the dotted line with a gray box represents the contraction with .
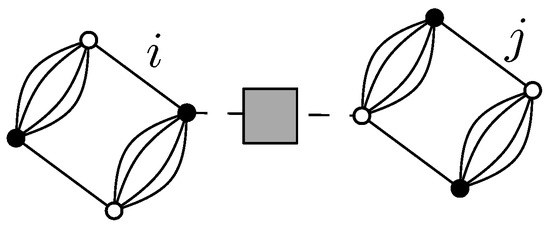
Figure 3.
Typical graph contributing to the interaction of of degree six.
Let us now build the effective coupling for the quartic melonic interaction at order , for which we shall extract only the leading behavior. From the Wilson–Polchinski flow Equation (22), it seems that the coupling evolution receives many contributions in which the first one comes from . Now, deriving two times this interaction with respect to the fields, we obtain an interaction of degree two, which can be either 1PI, when the contraction with links two black and white nodes of two different bubbles, or one-particle reducible (1PR) if the two nodes stand on the same interaction bubble. Explicitly, we get:
where:
and:
Equation (35) gives the exact behavior for the beta function at order , but we can easily see that it reduces to the expression of the beta function already obtained for the one-loop computation in the deep UV sector. Indeed, retaining only the melonic contributions and noting that 1PR contributions of the r.h.s are exactly canceled by the term involving the mass correction in the l.h.s, we get:
The computation of the loop appearing on the r.h.s leads to:
from which we finally deduce that:
which, as claimed before, is exactly the value of the one-loop beta function already obtained in the one-loop computation of the beta function.
We conclude that the main advantage of the Wilson–Polchinski equation is that it provides a very well-defined interpretation of the renormalization group flow in the space of couplings. However, except for perturbative computations, the Wilson–Polchinski equation is more adapted to mathematical and formal proofs than to non-perturbative analysis. The analysis beyond the perturbative level requires another formulation of the coarse-graining renormalization group, called Wetterich equation, which allows one usually to better capture the non-perturbative effects. The price to pay is an approximation scheme that is a bit more difficult to use. This non-perturbative approach to the renormalization group flow will be the subject of the next sections.
3. Wetterich Flow Equation
The Wetterich method and its incarnation into the FRG approach are a set of techniques allowing one to go beyond the difficulties coming from the Wilson–Polchinski equation, in particular in regards to tracking non-perturbative aspects. The Wetterich equation is a first order functional integro-differential equation for the effective action. The central object of the method is a continuous set of models labeled with a real parameter s running from UV scales () to the IR scales (). The physical running scale defined for each models what is UV and what is IR, the fluctuation with a large size with respect to the referent scale (the UV fluctuations) being integrated out. The renormalization group equation then describes how the coupling constant changes when the referent scale changes. Each model is characterized by a specific partition function , labeled by s and defined as:
As a result, the original model corresponds to , and because physically, this limit has to match with the IR limit , we require that vanish in the same limit. The term , called the IR regulator, plays the same role as a momentum-dependent mass term, becoming very large in the UV and vanishing in the IR. It is chosen ultra-local in the usual sense:
the regulating function being chosen to satisfy the boundary conditions in the UV/IR limit. Moreover, for s fixed, aims at freezing the long-distance fluctuations, which are discarded from the functional integration. In formula: for , and in the opposite limit.
The object for which we track the evolution is called effective averaged action , defined as (a slightly modified version of) the Legendre transform of the standard free energy :
This definition ensures that satisfies the physical boundary conditions where denotes some fundamental UV cutoff. The fields M and are the mean values of T and respectively and are given by:
where . In general, the regulator is chosen to be and such that the boundary conditions in the UV/IR limit are well satisfied.Taking the first derivative with respect to the flow parameter s, one can deduce the Wetterich equation, describing the behavior of the effective action when s changes [62,63,64,65,66]:
where denotes the second order partial derivative of with respect to the mean fields M and . This equation is exact, but generally impossible to solve exactly. A large part of the FRG approach is then devoted to approximate the exact trajectory of the RG flow. In this review, we will discuss two methods, the truncation method and the effective vertex expansion method.
This section is especially devoted to the truncations. The general strategy is to cut crudely into the full theory space, projecting the flow systematically into the interior of a finite dimensional subspace. The average effective action is chosen to be of the form:
where N is finite, stands for the interaction function of order n, and and are the mass and coupling constants. With this truncation and with an appropriate regulator, it is possible to solve the Wetterich flow Equation (45). In the case of quartic melonic interaction and by taking the standard modified Litim regulator [65,67,68]
the Wetterich equation can be solved analytically and the phase diagram may be given [56,57,58]. The corresponding nontrivial fixed points can be studied taking into account the behavior of the flow around these points. Note that the validity of the fixed point requires some analysis taking into account the Ward–Takahashi identities as a new constraint along the flow line. The full violation of this constraint for quartic melonic interaction makes this class of fixed points unphysical. We discuss this point in detail in this section (for more detail, see Section 3.1). Taking into account only the relevant contributions for large k (in the deep UV), the flow equations are written as:
with the renormalization condition:
where:
Explicitly using the integral representation of the above sum and with , , we get:
In order to get an autonomous system, the standard strategy consist at extracting from the couplings the part coming from their own scaling, defining their canonical dimension. Strictly speaking, fields, couplings, and all the parameters involved in the theory are dimensionless, because there is no referent space-time, and then no referent scale. The canonical dimension emerges taking into account quantum corrections and is usually defined as the optimal scaling, with respect to the UV cut-off of the quantum corrections. Conversely, it can be defined as the scaling transformation allowing one to get an autonomous system. Note that these two points of view are note strictly equivalent, especially with respect to the choice of the initial content of the theory. For our purpose however, the two strategies provide exactly the same rescaling, and in terms of dimensionless parameter , , the system (48) becomes:
where , and:
The solutions of the system (52) are given analytically:
Numerically:
Apart from the fact that we have a singularity line around the point in the flow Equation (48), another second singularity arises from the anomalous dimension denominator and corresponds to a line of singularity, with equation:
This line of singularity splits the two-dimensional phase space of the truncated theory into two connected regions characterized by the sign of the function : the region I, connected to the Gaussian fixed point for and the region for . For , the flow becomes ill defined. The existence of this singularity is a common feature for expansions around the vanishing mean field, and the region I may be viewed as the domain of validity of the expansion in the symmetric phase. Note that to ensure the positivity of the effective action, the melonic coupling must be positive, as well. Therefore, we expect that the physical region of the reduced phase space corresponds to the region . From the definition of the connected region I and because of the explicit expression (53), we deduce that:
Then, only the fixed point is taken into account. In the next subsection, we will discuss the violation of the Ward identity around this fixed point and then clarify our analysis given in [56]. The phase diagram is given in Figure 4.
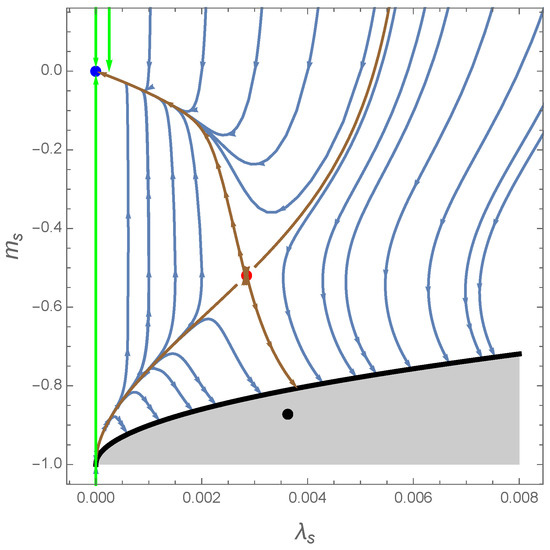
Figure 4.
Renormalization group flow trajectories around the relevant fixed points obtained from a numerical integration. The Gaussian fixed point and the first non-Gaussian fixed point are respectively in blue and in red, and the last fixed point is in black. This fixed point is in the grey region bounded by the singularity line corresponding to the denominator of . Finally, in green and brown, we draw the eigendirections around Gaussian and non-Gaussian fixed points, respectively. Note that that arrows of these fixed points are the flow oriented from IR to UV.
Convenient Search of the Ward Identities
Let , where the are infinite size unitary matrices in momentum representation. We define the transformation:
such that the interaction term is invariant, i.e., Then, consider an infinitesimal transformation:
where is the identity on , the identity on , and denotes the skew-symmetric Hermitian matrix such that and . The invariance of the path integral (3) means , i.e.:
Computing each term separately, we get, successively using the linearity of the operator :
where , , , and . is the renormalized wave function usually denoted by Z. We get the following result:
Proposition 3.
The Ward identity gives the relation between two- and four-point functions as:
where, defined by , the 1PI four-point function, we get:
Proof.
The formal invariance of the path integral implies that the variations of these terms have to be compensated by a nontrivial variation of the source terms. Combining the expressions (60)–(63), we come to:
where we have used the fact that, for all polynomial , the following identity holds:
Equation (66) is satisfied for all i. Now, expanding each derivative, the partition function of the theory defined by the action (12) verifies the following (WT identity),
The WI-identity contains some information on the relations between the Green functions. In particular, they provide a relation between four- and two-points functions, which may be translated as a relation between wave function renormalization Z and vertex renormalization . Applying on the left-hand side of (68) and taking into account the relations:
as well as the definition , we find that:
and therefore, Proposition 3 is well given. □
In the deep UV, for a large-scale s, a continuous approximation for variables is suitable. Then, setting , , , we get finally, in the deep UV, that the four- and two-point functions are related as (on both sides, ):
To give further comment on the structure of this equation, we have to specify the structure of the vertex function. To this end, we use this loop to discard the irrelevant contributions, and we keep only the melonic componentof the function , denoted by . In the symmetric phase, the melonic contribution may be defined as the part of the function that decomposes as a sum of melonic diagrams in the perturbative expansion. The structure of the melonic diagrams has been extensively discussed in the literature and specifically for the approach that we propose here in [57,58]. Formally, they are defined as the graphs optimizing the power counting; and the family can be built from the recursive definition of the vacuum melonic diagrams, from the cutting of some internal edges. Among there interesting properties, these constructions imply the following statement:
Proposition 4.
Let be a -point 1PI melonic diagram built with more than one vertex for a purely-quartic melonic model. We call external vertices the vertices hooked to at least one external edge of having:
- two external edges per external vertices, sharing external faces of length one.
- N external faces of the same color running through the interior of the diagram.
As a direct consequence of Proposition 4, we expect that the melonic four-point function is decomposed as:
the index i running from one to d corresponding to the color of the two internal faces running through the interiors of the diagrams building . Moreover, the mono-colored components have the following structure:
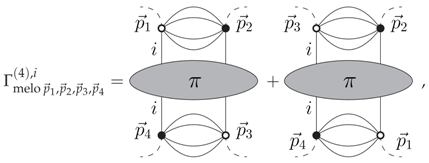 the permutation of the external momenta and coming from Wick’s theorem: there are four ways to hook the external fields on the external vertices (two per type of field). Moreover, the simultaneous permutation of the black and white fields provides exactly the same diagram, and we count twice each configuration pictured on the previous equation. This additional factor of two is included in the definition of the matrix , whose entries depend on the components i of the external momenta running on the boundaries of the external faces of colors i, connecting together the end vertices of the diagrams building .
the permutation of the external momenta and coming from Wick’s theorem: there are four ways to hook the external fields on the external vertices (two per type of field). Moreover, the simultaneous permutation of the black and white fields provides exactly the same diagram, and we count twice each configuration pictured on the previous equation. This additional factor of two is included in the definition of the matrix , whose entries depend on the components i of the external momenta running on the boundaries of the external faces of colors i, connecting together the end vertices of the diagrams building .

Inserting (73) into the Ward identity given from Equation (71), we get some contributions on the left-hand side, the only one relevant among them in the deep UV being, graphically:
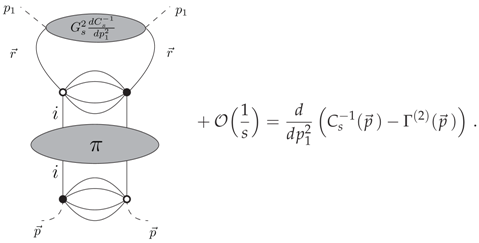 Setting and using the definition of , as well as the definition of , the right-hand side is reduced to . Moreover, the diagram on the left-hand side can be written with the following equation such that the following equality holds:
where we have defined as:
Finally, from Definition (73) we expect that , and because of the renormalization conditions (49), we must have the relation: . Therefore, in the deep UV regime, the Ward identity between four- and two-point functions provides a nontrivial relation between effective coupling and wave function renormalization:
Setting and using the definition of , as well as the definition of , the right-hand side is reduced to . Moreover, the diagram on the left-hand side can be written with the following equation such that the following equality holds:
where we have defined as:
Finally, from Definition (73) we expect that , and because of the renormalization conditions (49), we must have the relation: . Therefore, in the deep UV regime, the Ward identity between four- and two-point functions provides a nontrivial relation between effective coupling and wave function renormalization:

Remark 1.
Let us give some important remarks regarding the derivation of the Ward identity (77). First of all, the WI is totally disconnected from the approximation used to solve the non-perturbative Wetterich Equation (45). The Wetterich equation and Ward identity are both functional results, deduced from the definition of the partition function, and have to be treated on the same footing. Their origins, moreover, are completely disconnected. One of them comes from the scale dependence of the model due to the regulator term; the second one comes from the symmetry violation of the action (including source terms) under the group and the formal translation-invariance of the Lebesgue measure. Viewing the set having a continuous family of models, one can say that the Wetterich equation dictates how to move from to , whereas the WI are constraints between the observables at fixed s.
From now on, in the hope to provide the proof that does not live in the constraint line coming from the Ward identity (77), let us give the following result, which will be proven in the next section.
Proposition 5.
Structure equation for effective coupling:In the deep UV, the effective melonic coupling is given in terms of the renormalized coupling and the renormalized effective loop as:
where we defined the quantity as:
The constraint provided from the Ward identity, which relies on the -functions and the anomalous dimension, is given by:
This relation needs to be taken into account in the Wetterich flow equation and therefore in the search of fixed points. To prove this relation, let us consider the derivative of Z with respect to s using Expressions (77) and (78):
In the above relation, we have used the decomposition of . We remark that the Ward identity (77) can be written as where . Then, (80) becomes:
We now use the dimensionless quantities , , such that and reexpressing (81) as:
where and can be simply computed using the integral representation of the sum. We come to:
and therefore, (79) is well given. It is time to prove that this constraint violates the existence of the fixed point . Let p be a arbitrary fixed point of the theory. We get Then, the constraint (79) implies that at the point p, we get:
The particular solution corresponds to the Gaussian fixed point. For , we have only:
It is clear that the fixed point , violates these constraints, i.e., does not satisfy the constraint Equation (85). The same conclusion can be made for all choices of the regulator; see [56]. Finally, it is possible to improve the truncation by using the so-called effective vertex expansion. In this case, the fixed point obtained by solving the flow equation also violates the Ward constraint (85). We will study this point in the next section.
4. Effective Vertex Expansion Method for the Melonic Sector
The effective vertex-expansion described in [56,57,58] allows establishing the structure of the Feynman graphs of our models and leads to the structure equations in the leading order sector. It can help to establish the flow equations without truncation. The Feynman graphs of the colored tensor model are -colored graphs [20,21,22]. For the sake of completeness, we remind here about a few facts about these graphs, their representation as stranded graphs, and their uncolored version. The graphs that we consider possibly bear external edges, that is to say half-edges hooked to a unique vertex. We denote a a colored graph and the set of its internal edges (). A colored graph is said closed if it has no external edges and open otherwise. Let be a -colored graph and S a subset of . We denote as the spanning subgraph of induced by the edges of colors in S. Then, for all , , a face of colors is a connected component of . A face is open (or external) if it contains an external edge and closed (or internal) otherwise. The set of closed faces of a graph is written (). The structure of the boundary graph of denoted by will be useful in the construction of the leading order contribution, which may be considered in the derivative expansion to compute the structure equations and therefore the flow equations.
Definition 1.
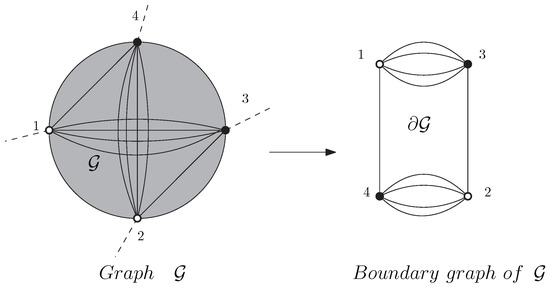
Consider as a connected Feynman graph with external edges. The boundary graph is obtained from keeping only the external blacks and whites nodes hooked to the external edges, connected together with colored edges following the path drawn from the boundaries of the external faces in the interior of the graph . is then a tensorial invariant itself with N black (resp. whites) nodes. An illustration is given in Figure 5.

Figure 5.
An opening Feynman graph with four external edges and its boundary graph. The strand in the interior of represents the path following the external faces.
The power counting theorem of these models shows that the divergence degree of arbitrary Feynman graph is:
The topological operation on the edge of the graph such as contraction is studied extensively in much of the literature. We let the reader consult [20,21,22] and the references therein. This operation plays an important role in the power counting theorem and allows identifying the structure of the graph. It makes the connection between the divergence degree of and the spanning tree denoted by . Let “∖” be the operation of contraction, and we get the following proposition:
Proposition 6.
Under the contraction of the spanning tree edge, the number of internal faces is invariant, i.e., The graph is called the rosette.
Note that the contraction of the edge , which leads to the corresponding graph , is such that and the divergent degree of the rosette can be easily computed, using the following formula corresponding to the contraction of the k-dipole: Then, the arbitrary Feynman graph is melonic if its boundary graph has the elementary melon structure, i.e., the number of faces is maximal:
The existence of the -expansion of tensors models (N denoting the size of the tensor), which provides in return a topological expansion of the partition function in terms of the generalization of the genus called the Gurau number , does not yield a topological expansion, but rather a combinatorial expansion in terms of the degree of the graph. For a colored closed graph , the degree is such that for the melon, .
4.1. Structure Equations and Compactability with Ward Identities
The structure equations are the relations between the correlation function and allow establishing a constraint between -functions for mass, interaction couplings, and wave function renormalization. These relations are obtained in the deep UV limit (i.e., in the domain ) without any assumption about the -functions and without any truncation of the effective action . The only assumption concern the choice of the initial conditions, ensuring the perturbative consistency of the full partition function. The first structure equation concerns the self energy (or 1PI two-point functions). It takes place as the closed equation for self energy.1 Let us summarize this in the following proposition:
Proposition 7.
In the melonic sector, the self energy is given by the closed equation, which takes into account the effective coupling as:
In the same way, in the melonic sector, the perturbative zero-momenta 1PI four-point contribution is given by:
where is defined as:
being the effective propagator: Let us recall that and are the counter-terms discarding the UV divergences of the original partition function, and the initial conditions in the UV are given such that the classical action contains only renormalizable interactions.
Proof.
Concerning the proof of Relation (88), we let the reader consult [60]. Let us define as the zero momenta melonic four-point functions made into the graphs for which two vertices may be singularized (i.e., by graphs that are at least of order two in the perturbative expansion). We have2:
Because of the face connectivity of the melonic diagrams, the boundary vertices may be such that the two internal faces of the same color running on the interior of the diagrams building pass through of them. Then, we have the following structure:
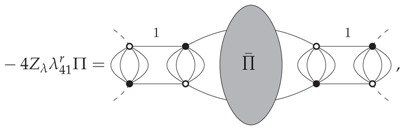 where the grey disk is a sum of Feynman graphs. Note that it is the only configuration of the external vertices in agreement with the assumption that is built with the melonic diagrams. Any other configurations of the external vertices are not melonics. At the lowest order, the grey disk corresponds to propagator lines,
where the grey disk is a sum of Feynman graphs. Note that it is the only configuration of the external vertices in agreement with the assumption that is built with the melonic diagrams. Any other configurations of the external vertices are not melonics. At the lowest order, the grey disk corresponds to propagator lines,
 Note that the external faces have the same color. Now, we can extract the amputated component of , say (which contains at least one vertex and is irreducible by hypothesis), extracting the effective melonic propagators connected to the dotted lines linked to . We get:
Note that the external faces have the same color. Now, we can extract the amputated component of , say (which contains at least one vertex and is irreducible by hypothesis), extracting the effective melonic propagators connected to the dotted lines linked to . We get:
 At first order, is built with a single vertex, and there is only one configuration in agreement with the melonic structure, i.e., maximizing the number of internal faces. The higher order contributions contain at least two vertices, and the argument may be repeated so that the function appears. Finally, we deduce the closed relation:
At first order, is built with a single vertex, and there is only one configuration in agreement with the melonic structure, i.e., maximizing the number of internal faces. The higher order contributions contain at least two vertices, and the argument may be repeated so that the function appears. Finally, we deduce the closed relation:
 This equation can be solved recursively as an infinite sum:
This equation can be solved recursively as an infinite sum:
 which can be formally solved as:
which can be formally solved as:
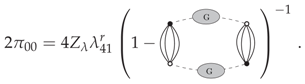 The loop diagram
The loop diagram 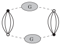 may be easily computed recursively from the definition of melonic
diagrams or directly using Wick theorem for a one-loop computation with the effective propagator G. The result is:
may be easily computed recursively from the definition of melonic
diagrams or directly using Wick theorem for a one-loop computation with the effective propagator G. The result is:
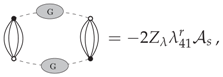 and the proposition is proven. □
and the proposition is proven. □





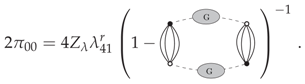
 may be easily computed recursively from the definition of melonic
diagrams or directly using Wick theorem for a one-loop computation with the effective propagator G. The result is:
may be easily computed recursively from the definition of melonic
diagrams or directly using Wick theorem for a one-loop computation with the effective propagator G. The result is:
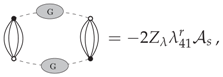
Note that this construction can be easily checked to be compatible with the Ward identity, especially in the form of (74). Conversely, the last result may be derived directly from Equation (74) and from the closed equation for the two-point function (88) (see [58]). To prove these two results, we only assume that the classical mean field vanishes, and we deduce from our previous proof, essentially based on the assumption that the effective vertices are analytic with respect to the renormalized coupling, that the analytic domain covers what we called the symmetric phase. In the hope to extract the expression of the counter-terms at all orders and to show that the wave function renormalization and the four-point vertex renormalization are the same, we have the following result:
Proposition 8.
Choosing the following renormalization prescription:
where and are the renormalized mass and coupling constant, the counter-terms are given by:
where denotes the melonic self-energy.
Proof.
From Proposition 1, we can get:
Then, setting , we deduce that:
We now concentrate our self on and . Without loss of generality, the inverse of the effective propagator has the following structure:
with the notation: . Then, from the renormalization conditions, we have:
Setting in the closed equation for the two-point correlation function and by deriving with respect to for , we get:
Using the explicit expression for in (102), we get finally:
□
Now, consider the mono-color four-point function . If we replace by its expression from Proposition 8, we deduce that:
with the definition: . In other words, we have an explicit expression for the effective coupling ,
from which we get:
In the above relation, we introduce the dot notation :
In Proposition 8, we have investigated the relations between counter-terms, i.e., we have considered the melonic equations as Ward identities for . Far from the initial conditions, the Taylor expansion of the two-point function is written as:
We call the “physical” or effective mass parameter the first term in the above relation:
while the coefficient is the effective wave function renormalization and is denoted by , i.e.,
Now, let us consider the closed equation given in Proposition (88). By deriving with respect to and by taking , we get:
Using Equation (110), we can express in terms of the effective coupling , and we get:
Then, we come to the following relation
At this stage, without any confusion, let us clarify that: is the wave function counter-term, i.e., whose divergent part cancels the loop divergences and whose finite part depends on the renormalization prescription. however is fixed to one for from our renormalization conditions.
4.2. Flow Equation from the EVE Method
There are different methods to improve the crude truncations in the FRG literature. However, their applications for TGFTs remain difficult due to the non-locality of the interactions over the group manifold on which the fields are defined. A step to go out of the truncation method was done recently in [57,58] with the effective vertex expansion (EVE) method. Basically, the strategy is to close the infinite tower of equations coming from the exact flow equation, instead of crudely truncating them. The strategy is to complete the structure Equation (78) with a structure equation for , expressing it in terms of the marginal coupling and the effective propagator only. In this way, the flow equations around marginal couplings are completely closed. Note that this approach crosses the first hypothesis motivating the truncation: we expect that so far from the deep UV, only the marginal interactions survive and drag the complete RG flow. Moreover, any fixed point of the autonomous set of resulting equations is automatically a fixed point for any higher effective melonic vertices built from effective quartic interactions. Finally, a strong improvement of this method with respect to the truncation method, already pointed out in [57,58], is that it allows keeping the complete momenta dependence of the effective vertex. This dependence generates a new term on the right-hand side of the equation for , moving the critical line from its truncation’s position.
Let us consider the flow equation for , obtained from (45), derived with respect to M and :
where we discard all the odd contributions, vanishing in the symmetric phase. Deriving on both sides with respect to and setting , we get:
where the “prime” designates the partial derivative with respect to . In the deep UV (), the argument used in the -truncation to discard non-melonic contributions holds, and we keep only the melonic diagrams. Moreover, to capture the momentum dependence of the effective melonic vertex and compute the derivative , knowledge of is required. It can be deduced from the same strategy as for the derivation of the structure Equation (78), up to the replacement:
from which we get:
The derivative with respect to may be easily performed, and from the renormalization condition (49), we obtain:
while the leading order flow equation for becomes:
As announced, a new term appears with respect to the truncated version (48), which contains a dependence on and then moves the critical line. The flow equation for mass may be obtained from (119) setting on both sides. Finally, the flow equation for the marginal coupling may be obtained from Equation (45) deriving it twice with respect to each mean field M and . As explained before, it involves at leading order, and to close the hierarchy, we use the marginal coupling as a driving parameter and express it in terms of and only. Once again, from Proposition 4, have to be split into d mono-colored components :
The structure equation for may be deduced following the same strategy as for , from Proposition 4. Starting from a vacuum diagram, a leading order four-point graph may be obtained opening successively two internal tadpole edges, both on the boundary of a common internal face. This internal face corresponds for the resulting four-point diagram to the two external faces of the same colors running through the interior of the diagram. In the same way, a leading order six-point graph may be obtained cutting another tadpole edge on this resulting graph, once again on the boundary of one of these two external faces. The reason this works is that, in this way, the number of discarded internal faces is optimal, as well as the power counting. From this construction, it is not hard to see that the zero-momenta vertex function must have the following structure (see [57,58] for more details):
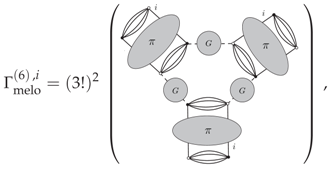 the combinatorial factor coming from the permutation of external edges. Translating the diagram into equation and taking into account symmetry factors, we get:
with:
Note that this structure equation may be deduced directly from Ward identities, as pointed-out in [58,60]. The equation closing the hierarchy is then compatible with the constraint coming from unitary invariance. The flow equations involve now some new contributions depending on two sums, and , defined without regulation function . However, they are both power-counting convergent in the UV, and the renormalizability theorem ensures their finiteness for all orders in the perturbation theory. For this reason, they become independent of the initial conditions at scale for ; and as pointed out in [58], we get, using Litim’s regulator:
and:
The complete flow equation for zero-momenta four-point coupling is written explicitly as:
Keeping only the melonic contributions, we get finally the following autonomous system by using Litim’s regulation:
where the anomalous dimension is then given by:
the combinatorial factor coming from the permutation of external edges. Translating the diagram into equation and taking into account symmetry factors, we get:
with:
Note that this structure equation may be deduced directly from Ward identities, as pointed-out in [58,60]. The equation closing the hierarchy is then compatible with the constraint coming from unitary invariance. The flow equations involve now some new contributions depending on two sums, and , defined without regulation function . However, they are both power-counting convergent in the UV, and the renormalizability theorem ensures their finiteness for all orders in the perturbation theory. For this reason, they become independent of the initial conditions at scale for ; and as pointed out in [58], we get, using Litim’s regulator:
and:
The complete flow equation for zero-momenta four-point coupling is written explicitly as:
Keeping only the melonic contributions, we get finally the following autonomous system by using Litim’s regulation:
where the anomalous dimension is then given by:

The new anomalous dimension has two properties that distinguish it from its truncation version. First of all, as announced, the singularity line moves toward the axis, extending the symmetric phase domain. In fact, the improvement is optimal, the critical line being deported under the singularity line . In standard interpretations [57], the presence of the region is generally assumed to come from a bad expansion of the effective average action around the vanishing mean field, becoming a spurious vacuum in this region.
However, the EVE method shows that the singularity line obtained using truncation is completely discarded taking into account the momentum dependence of the effective vertex. The second improvement comes from the fact that the anomalous dimension may be negative and vanishes on the line of equation , with:
Interestingly, there are now two lines in the maximally-extended region where physical fixed points are expected. However, numerical integrations show that the improved flow equations admit a non-Gaussian fixed point , which is numerically very close to the fixed point obtained in the truncation method, i.e., , and then unphysical as well. Figure 6 summarize all these results.
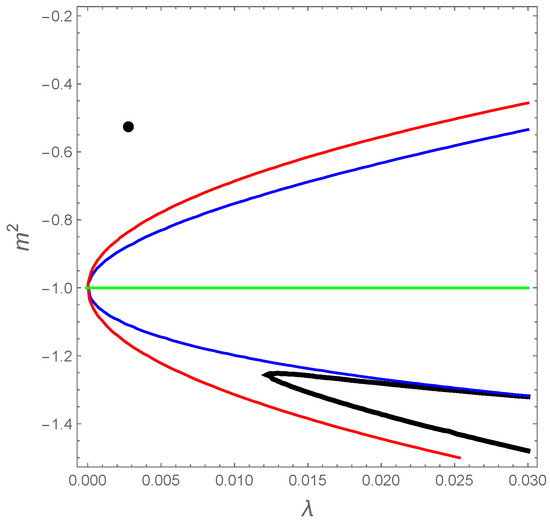
Figure 6.
The relevant lines over the maximally-extended region I′, bounded at the bottom with the singularity line m2 = −1 (in green). The blue and red curves correspond respectively to the equations L = 0 and Ω = 0. Moreover, the black point corresponds to the numerical non-Gaussian fixed point, so far from the two previous physical curves.
4.3. Exploration of the Physical Phase Space
In this section, we will show that the EVE method leads to an alternative first order phase transition scenario, despite the fact that the fixed point is discarded. Secondly, we also prove that this new behavior is only observed using the EVE method and cannot be obtained by implementing the usual truncation as the approximation.
(1) Despite the fact that the constraint Equation (79) is not compatible with the fixed point , this is not the end of the world. The constraint given by Equation (79) defines a one-dimensional subspace, say , into the whole bi-dimensional phase space . Obviously, the Ward identity will be violated everywhere except along this one-dimensional subspace ; for this reason, we call the physical phase spacethis subspace.
Solving with respect to , we can extract the coupling constant as a function of the renormalized mass parameter . After a few hand computations, we get:
These solutions provide only one non-trivial parametrized equation for the physical subspace : . Interestingly, it is not hard to check that the presence of the factor in the numerator cancels all the formal divergences occurring for , such that the flow becomes regular at this point. However, other divergences occur, one of them being common to each beta functions. To understand the structure of the effective flow into the physical subspace, we have to insert the solutions (135) into the flow Equation (132). However, even to do this, let us discuss the solution (135) in a few words. Because the theory is asymptotically free, we may expect that and have to vanish simultaneously. What we know is that, in the vicinity of the Gaussian fixed point , the constraint is approximately satisfied. For instance, up to contributions, the Equation (79) reduces as:
which is identically satisfied by the one-loop beta equation ; see (132). As a result, in a small domain around , the flow behaves approximately according to the Ward constraint, but as soon as the flow leaves this region, the Ward constraint is violated, except along , where it holds strictly. Note that, for , the value of is very large () and far away from the vicinity of the Gaussian fixed point.
Now, let us move on to the solutions (135). The solution corresponds to trivial flow, and:
On the other hand, inserting the non-trivial solution , we get:
and:
As announced, the divergences at the value has been discarded. However, some new divergences occur. First of all, the equation for becomes singular for the positive value . A second singularity occurs for the value , which is common for , , and ; and a third singularity occurs for in the expression of , which is the same as the singularity of . We now discuss this picture. To this end, let us examine the points at which the beta function vanishes. We get:
Because , we recover our previous conclusion, in the whole theory space ; no fixed point can be found using the exact FRG with the EVE method taking into account the Ward constraint. The -function of the mass vanishes at the point on the projected phase space . Furthermore, and , being a small positive value, and the flow into the physical phase space changes direction at this point, pointing toward the positive mass direction for and toward the negative mass direction for . In the last case, the flow continues on this way and reaches the singularity, where the flow becomes undefined. Both of these features are reminiscent of a first order phase transition on the physical phase space—the singularity may indicate a point at which the effective action becomes undefined, or where the expansion around the null vacuum fails to exist—the last statement having to be rigorously investigated.
The same analysis may be performed when we consider the following prescription: by extracting the mass parameter as a function of the constant : in the constraint equation and solving the -function of the coupling. In this case, the coupling becomes the parameter, and for the point , we get a singularity corresponding to the value (see Figure 7b). Note that around , the coupling becomes very small:
and we reach a new perturbative regime for small and small .
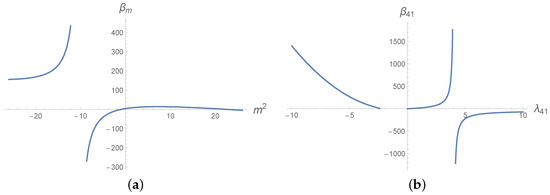
Figure 7.
Plot of as a function of using the constraint equation. We get the singularity at the point , corresponding to the coupling value (a). Plot of as function of in the parametrization of the physical phase space. The singularity occurs at the point (b).
(2) When we investigated the truncation method, we did not provide such a discussion. To compare the methods, let us consider the same strategy for the phase space described with the truncation method. Solving the constraint , we get:
By replacing this solution in the flow equations of mass and coupling (48), we get:
Now, setting , only the Gaussian fixed point survives. Furthermore, the last solution leads to:
One more time, we recover that no solutions such that exist. Moreover, we recover that vanishes for a negative mass value, not so far from ; and that the singularity at this value has been completely discarded from the solution of the Ward constraint. However, the common singularity of the beta functions as some other aspects of the previous flow equations are not reproduced in the truncation framework. The nature of the singularities, for and , remains mysterious in our formalism. Obviously, they are a consequence of the improvement coming from the EVE method, and their understanding may increase our knowledge about the behavior of the TGFT renormalization group flow.
5. Conclusions
In this manuscript, we have studied with different methods the FRG applied to TGFT. First, we have derived the Wilson–Polchinski equation and given the perturbative solution. Secondly, we derived the Wetterich flow equation using the usual approximation, called truncation. The analytic solution of this equation was given. We obtained a fixed point denoted by . Then, we investigated the Ward identities as a new constraint along the flow and showed that the fixed point violates this constraint. Finally, we improved the study of FRG by replacing the truncation method by the so-called EVE. The flow equation was improved, and the corresponding solution was not so far from , i.e., . However, the Ward identities are strongly violated at this fixed point, and therefore this unique fixed point seems to be unphysical. We have also showed the importance of the EVE method in the sense that, despite the fact that the fixed point needs to be discarded, a first order phase transition exists very far from this point in the subspace of the theory space. We have showed that this new behavior cannot be observed using the truncation as the approximation.
In this review, we focused on the EVE method for the melonic approximation, and especially on the quartic melonic just-renormalizable sector. The complete quartic sector, including all the connected quartic bubbles, has already been considered in a complementary work [57], and the conclusion about the incompatibility with nonperturbative fixed points and Ward identities holds. The graphs added to the quartic melonic ones to complete the quartic sector have been called pseudo-melons due to the similarities of their respective leading order Feynman graphs. Finally, even if we expect that some aspects of the EVE method improve the standard truncation method, some limitations have to be addressed for future works. In particular, our investigations were limited to the symmetric phase, ensuring convergence of any expansion around the vanishing classical mean field. Moreover, we have retained only the first terms in the derivative expansion of the two-point function and only considered the local potential approximation, i.e., potentials that can be expanded as an infinite sum of connected melonic (and pseudo-melonic) interactions. Finally, a rigorous investigation of the behavior of the renormalization group flow into the physical phase space has to be addressed in the continuation of current works on this topic.
Author Contributions
Conceptualization, V.L. and D.O.-S.; methodology, V.L. and D.O.-S.; software, V.L. and D.O.-S.; validation, V.L. and D.O.-S.; formal analysis, V.L. and D.O.-S.; investigation, V.L. and D.O.-S.; resources, V.L. and D.O.-S.; data curation, V.L. and D.O.-S.; writing–original draft preparation, V.L. and D.O.-S.; writing–review and editing, V.L. and D.O.-S.; visualization, V.L. and D.O.-S.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rovelli, C. Loop quantum gravity. Living Rev. Relat. 1998, 1, 5. [Google Scholar] [CrossRef] [PubMed]
- Rovelli, C.; Upadhya, P. Loop quantum gravity and quanta of space: A Primer. arXiv, 1998; arXiv:gr-qc/9806079. [Google Scholar]
- Ambjorn, J.; Burda, Z.; Jurkiewicz, J.; Kristjansen, C.F. Quantum gravity represented as dynamical triangulations. Acta Phys. Pol. B 1992, 23, 991–1030. [Google Scholar] [CrossRef]
- Ambjorn, J. Quantum gravity represented as dynamical triangulations. Class. Quantum Gravity 1995, 12, 2079–2134. [Google Scholar] [CrossRef]
- Ambjørn, J.; Görlich, A.; Jurkiewicz, J.; Loll, R. Quantum Gravity via Causal Dynamical Triangulations. In Springer Handbook of Spacetime; Springer: Berlin/Heidelberg, Germany, 2014; pp. 723–741. [Google Scholar]
- Connes, A.; Lott, J. Particle Models and Noncommutative Geometry (Expanded Version). Nucl. Phys. B Proc. Suppl. 1991, 18, 29–47. [Google Scholar] [CrossRef]
- Aastrup, J.; Grimstrup, J.M. Intersecting connes noncommutative geometry with quantum gravity. Int. J. Mod. Phys. A 2007, 22, 1589–1603. [Google Scholar] [CrossRef]
- Oriti, D. A Quantum field theory of simplicial geometry and the emergence of spacetime. J. Phys. Conf. Ser. 2007, 67, 012052. [Google Scholar] [CrossRef]
- De Cesare, M.; Pithis, A.G.A.; Sakellariadou, M. Cosmological implications of interacting Group Field Theory models: Cyclic Universe and accelerated expansion. Phys. Rev. D 2016, 94, 064051. [Google Scholar] [CrossRef]
- Gielen, S.; Sindoni, L. Quantum Cosmology from Group Field Theory Condensates: A Review. arXiv, 2016; arXiv:1602.08104. [Google Scholar] [CrossRef]
- Gielen, S.; Oriti, D. Cosmological perturbations from full quantum gravity. arXiv, 2017; arXiv:1709.01095. [Google Scholar] [CrossRef]
- Oriti, D.; Ryan, J.P.; Thurigen, J. Group field theories for all loop quantum gravity. New J. Phys. 2015, 17, 023042. [Google Scholar] [CrossRef]
- Gurau, R. Colored Group Field Theory. Commun. Math. Phys. 2011, 304, 69–93. [Google Scholar] [CrossRef]
- Rivasseau, V. Constructive Tensor Field Theory. arXiv, 2016; arXiv:1603.07312. [Google Scholar] [CrossRef]
- Rivasseau, V. Random Tensors and Quantum Gravity. arXiv, 2016; arXiv:1603.07278. [Google Scholar] [CrossRef]
- Rivasseau, V. The Tensor Theory Space. Fortschr. Phys. 2014, 62, 835–840. [Google Scholar] [CrossRef]
- Rivasseau, V. The Tensor Track, III. Fortschr. Phys. 2014, 62, 81–107. [Google Scholar] [CrossRef]
- Rivasseau, V. The Tensor Track, IV. arXiv, 2016; arXiv:1604.07860. [Google Scholar]
- Rivasseau, V. The Tensor Track: An Update. arXiv, 2012; arXiv:1209.5284. [Google Scholar]
- Gurau, R. The complete 1/N expansion of colored tensor models in arbitrary dimension. Ann. Henri Poincare 2012, 13, 399–423. [Google Scholar] [CrossRef]
- Gurau, R. The 1/N expansion of colored tensor models. Ann. Henri Poincare 2011, 12, 829. [Google Scholar] [CrossRef]
- Gurau, R. The 1/N Expansion of Tensor Models Beyond Perturbation Theory. Commun. Math. Phys. 2014, 330, 973–1019. [Google Scholar] [CrossRef]
- Carrozza, S.; Oriti, D.; Rivasseau, V. Renormalization of Tensorial Group Field Theories: Abelian U(1) Models in Four Dimensions. Commun. Math. Phys. 2014, 327, 603–641. [Google Scholar] [CrossRef]
- Carrozza, S. Tensorial methods and renormalization in Group Field Theories. arXiv, 2013; arXiv:1310.3736. [Google Scholar]
- Carrozza, S.; Oriti, D.; Rivasseau, V. Renormalization of a SU(2) Tensorial Group Field Theory in Three Dimensions. Commun. Math. Phys. 2014, 330, 581–637. [Google Scholar] [CrossRef]
- Ben Geloun, J. Renormalizable Models in Rank d ≥ 2 Tensorial Group Field Theory. Commun. Math. Phys. 2014, 332, 117–188. [Google Scholar] [CrossRef]
- Lahoche, V.; Oriti, D. Renormalization of a tensorial field theory on the homogeneous space SU(2)/U(1). arXiv, 2015; arXiv:1506.08393. [Google Scholar]
- Lahoche, V.; Oriti, D.; Rivasseau, V. Renormalization of an Abelian Tensor Group Field Theory: Solution at Leading Order. J. High Energy Phys. 2015, 2015, 95. [Google Scholar] [CrossRef]
- Ben Geloun, J.; Livine, E.R. Some classes of renormalizable tensor models. J. Math. Phys. 2013, 54, 082303. [Google Scholar] [CrossRef]
- Ousmane Samary, D.; Vignes-Tourneret, F. Just Renormalizable TGFT’s on U(1)d with Gauge Invariance. Commun. Math. Phys. 2014, 329, 545–578. [Google Scholar] [CrossRef]
- Ben Geloun, J.; Ousmane Samary, D. 3D Tensor Field Theory: Renormalization and One-loop β-functions. Ann. Henri Poincare 2013, 14, 1599–1642. [Google Scholar] [CrossRef]
- Ben Geloun, J.; Rivasseau, V. A Renormalizable 4-Dimensional Tensor Field Theory. Commun. Math. Phys. 2013, 318, 69–109. [Google Scholar] [CrossRef]
- Ben Geloun, J.; Toriumi, R. Renormalizable Enhanced Tensor Field Theory: The quartic melonic case. arXiv, 2017; arXiv:1709.05141. [Google Scholar] [CrossRef]
- Ben Geloun, J.; Bonzom, V. Radiative corrections in the Boulatov-Ooguri tensor model: The 2-point function. Int. J. Theor. Phys. 2011, 50, 2819–2841. [Google Scholar] [CrossRef]
- Ben Geloun, J. Two and four-loop β-functions of rank 4 renormalizable tensor field theories. Class. Quantum Gravity 2012, 29, 235011. [Google Scholar] [CrossRef]
- Ousmane Samary, D. Beta functions of U(1)d gauge invariant just renormalizable tensor models. Phys. Rev. D 2013, 88, 105003. [Google Scholar] [CrossRef]
- Rivasseau, V. Why are tensor field theories asymptotically free? EPL Europhys. Lett. 2015, 111, 60011. [Google Scholar] [CrossRef]
- Carrozza, S. Discrete Renormalization Group for SU(2) Tensorial Group Field Theory. Ann. Inst. Henri Poincaré Comb. Phys. Interact. 2015, 2, 49–112. [Google Scholar] [CrossRef]
- Wilson, K.G. Renormalization Group and Critical Phenomena. I. Phys. Rev. B 1971, 4, 3174–3183. [Google Scholar] [CrossRef]
- Wilson, K.G. Renormalization Group and Critical Phenomena. II. Phys. Rev. B 1971, 4, 3184–3205. [Google Scholar] [CrossRef]
- Polchinski, J. Renormalization and Effective Lagrangians. Nucl. Phys. B 1984, 231, 269–295. [Google Scholar] [CrossRef]
- Wetterich, C. Exact evolution equation for the effective potential. Phys. Lett. B 1993, 301, 90–94. [Google Scholar] [CrossRef]
- Oriti, D. Levels of spacetime emergence in quantum gravity. arXiv, 2018; arXiv:1807.04875. [Google Scholar]
- Oriti, D. Disappearance and emergence of space and time in quantum gravity. Stud. Hist. Philos. Sci. B 2014, 46, 186–199. [Google Scholar] [CrossRef]
- Markopoulou, F. Conserved quantities in background independent theories. J. Phys. Conf. Ser. 2007, 67, 012019. [Google Scholar] [CrossRef]
- Wilkinson, S.A.; Greentree, A.D. Geometrogenesis under Quantum Graphity: Problems with the ripening Universe. Phys. Rev. D 2015, 92, 084007. [Google Scholar] [CrossRef]
- Geloun, J.B.; Martini, R.; Oriti, D. Functional Renormalisation Group analysis of Tensorial Group Field Theories on . arXiv, 2016; arXiv:1601.08211. [Google Scholar]
- Geloun, J.B.; Martini, R.; Oriti, D. Functional Renormalization Group analysis of a Tensorial Group Field Theory on . Europhys. Lett. 2015, 112, 31001. [Google Scholar] [CrossRef]
- Benedetti, D.; Lahoche, V. Functional Renormalization Group Approach for Tensorial Group Field Theory: A Rank-6 Model with Closure Constraint. arXiv, 2015; arXiv:1508.06384. [Google Scholar] [CrossRef]
- Benedetti, D.; Ben Geloun, J.; Oriti, D. Functional Renormalisation Group Approach for Tensorial Group Field Theory: A Rank-3 Model. J. High Energy Phys. 2015, 2015, 84. [Google Scholar] [CrossRef]
- Ben Geloun, J.; Koslowski, T.A.; Oriti, D.; Pereira, A.D. Functional Renormalization Group analysis of rank 3 tensorial group field theory: The full quartic invariant truncation. Phys. Rev. D 2018, 97, 126018. [Google Scholar] [CrossRef]
- Carrozza, S.; Lahoche, V. Asymptotic safety in three-dimensional SU(2) Group Field Theory: Evidence in the local potential approximation. Class. Quantum Gravity 2017, 34, 115004. [Google Scholar] [CrossRef]
- Lahoche, V.; Ousmane Samary, D. Functional renormalization group for the U(1)- tensorial group field theory with closure constraint. Phys. Rev. D 2017, 95, 045013. [Google Scholar] [CrossRef]
- Carrozza, S.; Lahoche, V.; Oriti, D. Renormalizable Group Field Theory beyond melonic diagrams: An example in rank four. Phys. Rev. D 2017, 96, 066007. [Google Scholar] [CrossRef]
- Ben Geloun, J. Ward–Takahashi identities for the colored Boulatov model. J. Phys. A 2011, 44, 415402. [Google Scholar] [CrossRef]
- Lahoche, V.; Ousmane Samary, D. Ward identity violation for melonic T4-truncation. arXiv, 2018; arXiv:1809.06081. [Google Scholar] [CrossRef]
- Lahoche, V.; Ousmane Samary, D. Nonperturbative renormalization group beyond melonic sector: The Effective Vertex Expansion method for group fields theories. arXiv, 2018; arXiv:1809.00247. [Google Scholar] [CrossRef]
- Lahoche, V.; Ousmane Samary, D. Unitary symmetry constraints on tensorial group field theory renormalization group flow. Class. Quantum Gravity 2018, 35, 195006. [Google Scholar] [CrossRef]
- Pérez-Sánchez, C.I. The full Ward–Takahashi Identity for colored tensor models. arXiv, 2016; arXiv:1608.08134. [Google Scholar] [CrossRef]
- Ousmane Samary, D. Closed equations of the two-point functions for tensorial group field theory. Class. Quantum Gravity 2014, 31, 185005. [Google Scholar] [CrossRef]
- Ousmane Samary, D.; Pérez-Sánchez, C.I.; Vignes-Tourneret, F.; Wulkenhaar, R. Correlation functions of a just renormalizable tensorial group field theory: The melonic approximation. Class. Quantum Gravity 2015, 32, 175012. [Google Scholar] [CrossRef]
- Wetterich, C. Average Action and the Renormalization Group Equations. Nucl. Phys. B 1991, 352, 529–584. [Google Scholar] [CrossRef]
- Wetterich, C. Effective average action in statistical physics and quantum field theory. Int. J. Mod. Phys. A 2001, 16, 1951–1982. [Google Scholar] [CrossRef]
- Berges, J.; Tetradis, N.; Wetterich, C. Nonperturbative renormalization flow in quantum field theory and statistical physics. Phys. Rep. 2002, 363, 223–386. [Google Scholar] [CrossRef]
- Delamotte, B. An Introduction to the nonperturbative renormalization group. Lect. Notes Phys. 2012, 852, 49–132. [Google Scholar]
- Nagy, S. Lectures on renormalization and asymptotic safety. Ann. Phys. 2014, 350, 310–346. [Google Scholar] [CrossRef]
- Litim, D.F. Optimization of the exact renormalization group. Phys. Lett. B 2000, 486, 92–99. [Google Scholar] [CrossRef]
- Litim, D.F. Derivative expansion and renormalization group flows. J. High Energy Phys. 2001, 2001, 59. [Google Scholar] [CrossRef]
| 1 | The rank of the tensors is fixed to five, and we denote it by d to clarify the proof(s). |
| 2 | The notations are similar to the ones used for the previous proof. The context however allows excluding any confusion. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).