Primordial Gravitational Waves and Reheating in a New Class of Plateau-Like Inflationary Potentials
Abstract
1. Introduction
2. The Parametrization
3. Reheating and -Folding
4. The Generalised Gaussian Model
4.1. The Potential for
4.2. The Potential for
5. Results
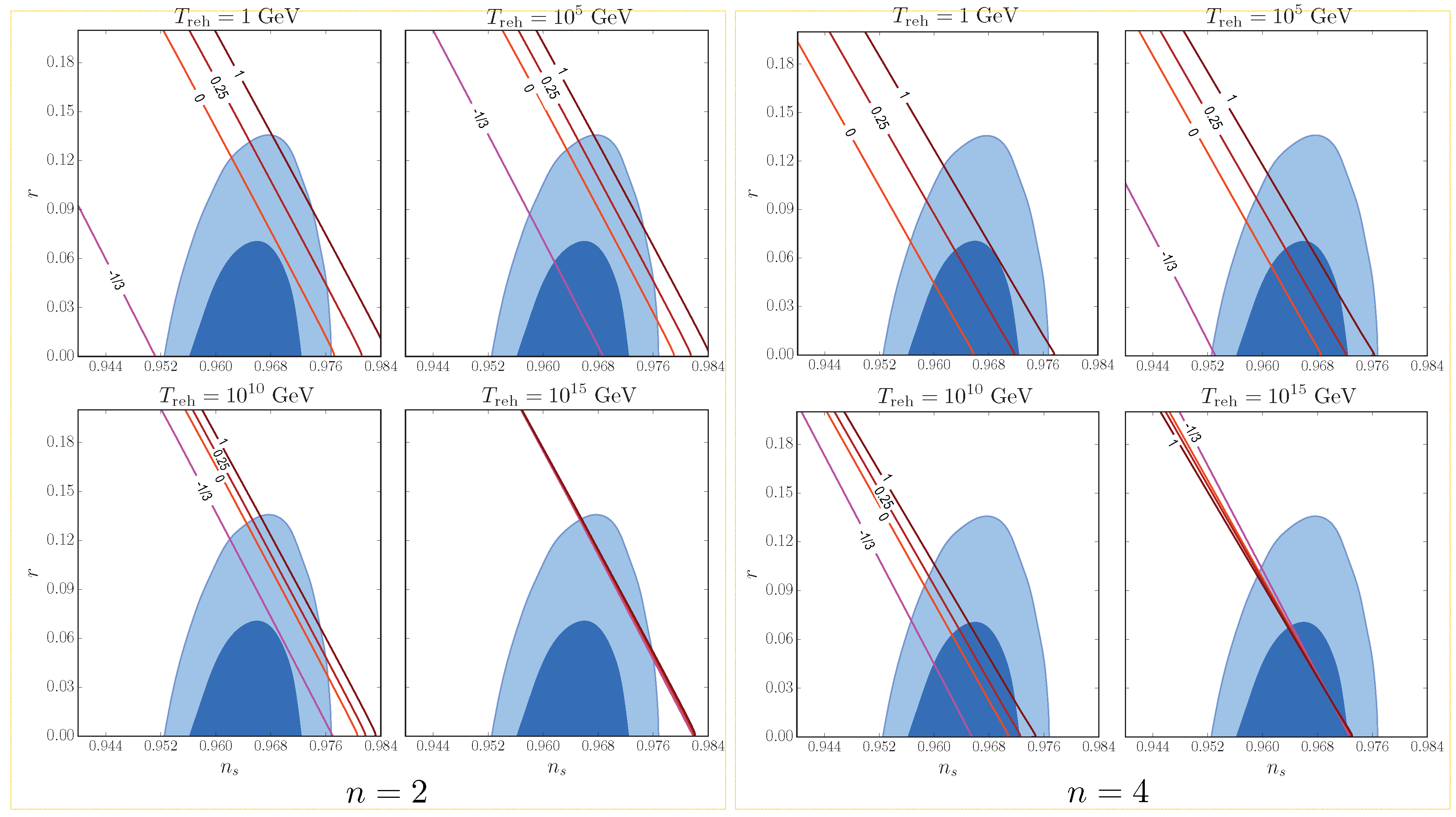
5.1. and r
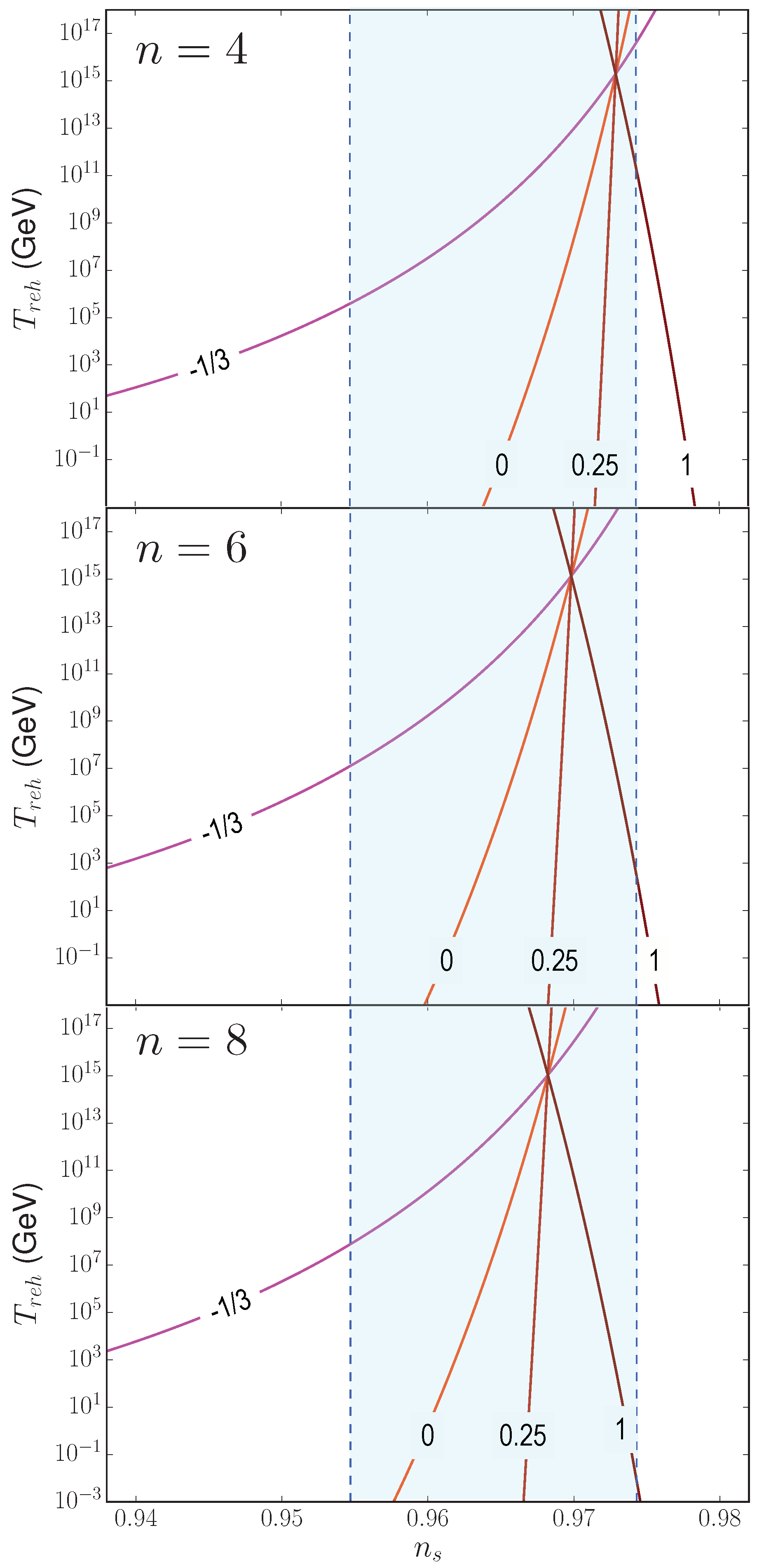
5.2. Reheating Temperature
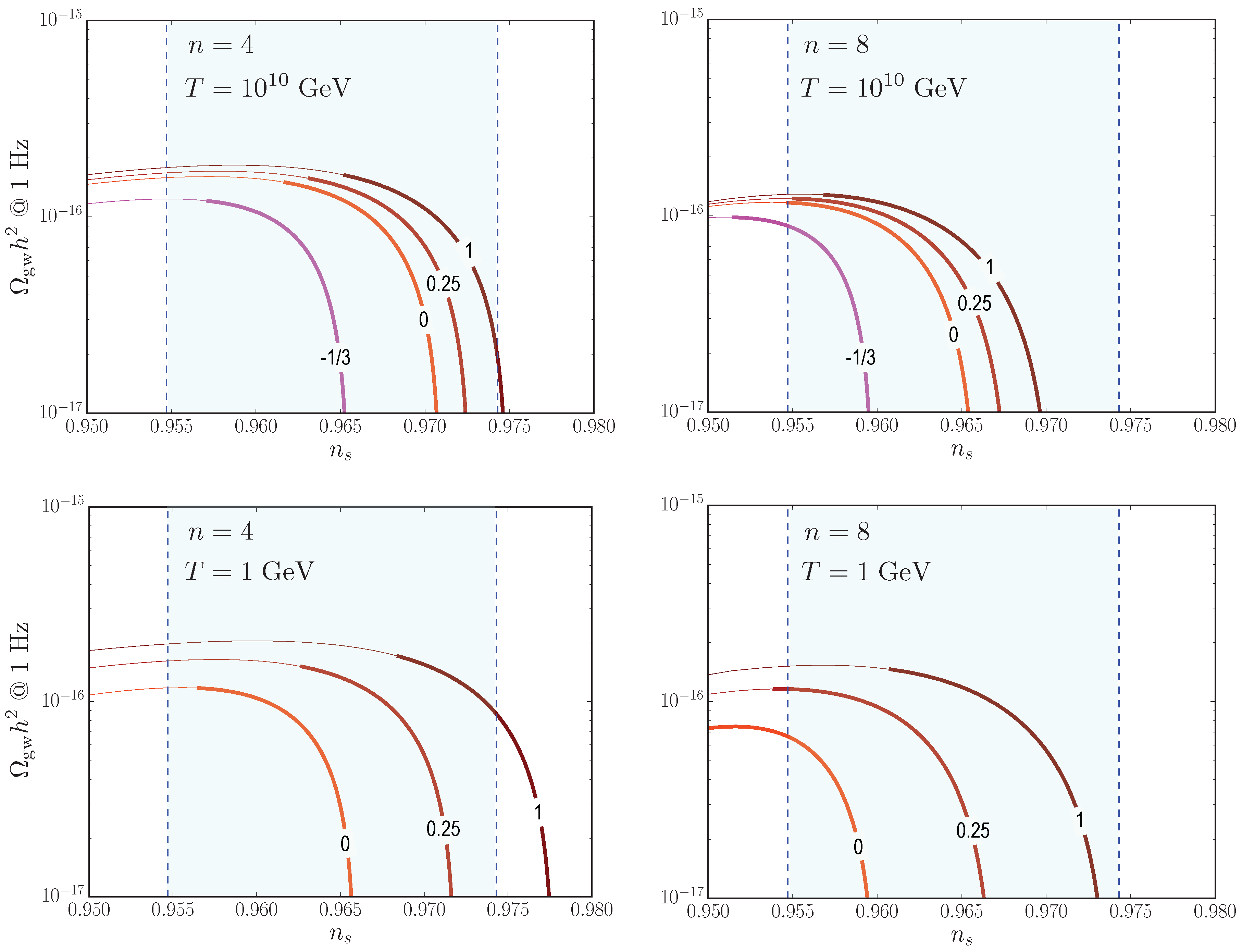
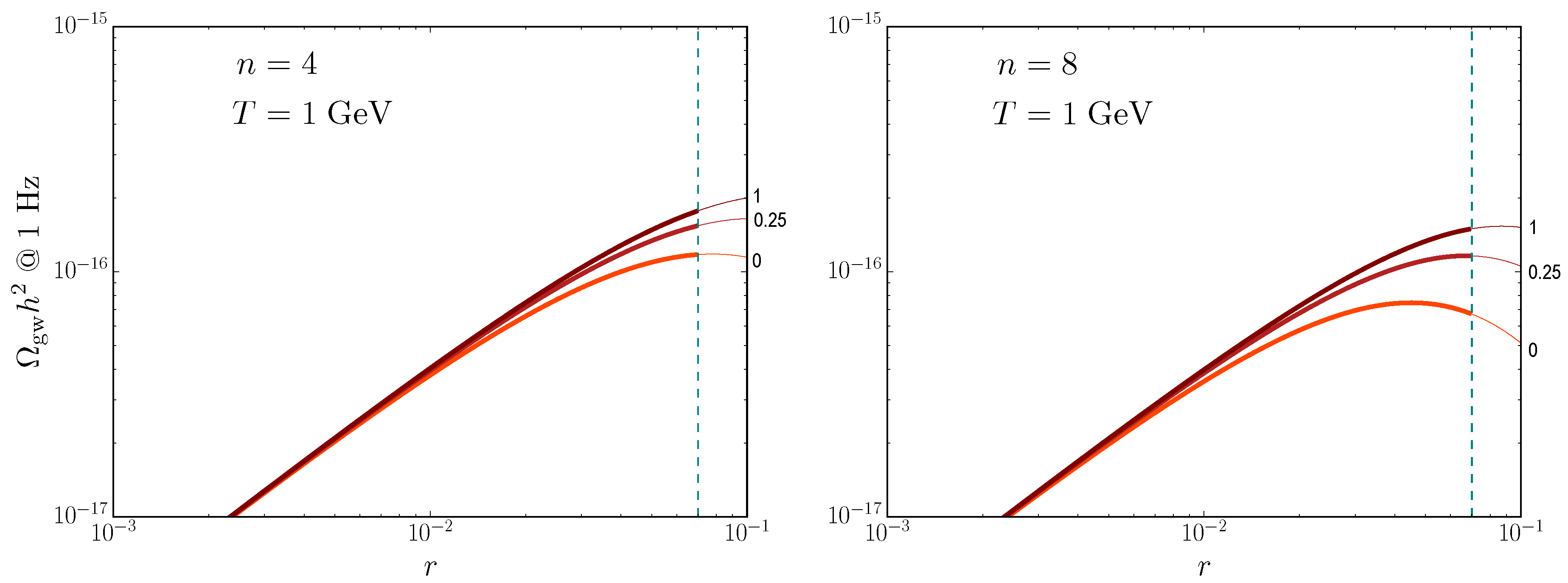
5.3. Primordial Gravitational Waves at 1 Hz
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Available online: https://www.elisascience.org (accessed on 29 June 2018).
- Corbin, V.; Cornish, N.J. Detecting the cosmic gravitational wave background with the Big Bang Observer. Class. Quantum Gravity 2006, 23, 2435–2446. [Google Scholar] [CrossRef]
- Available online: http://tamago.mtk.nao.ac.jp/decigo/index_E.html (accessed on 29 June 2018).
- COrE Collaboration. COrE (Cosmic Origins Explorer) a White Paper. arXiv, 2011; arXiv:1102.2181. [Google Scholar]
- CORE Collaboration. Exploring Cosmic Origins with CORE: Inflation. arXiv, 2016; arXiv:1612.08270. [Google Scholar]
- Available online: http://litebird.jp/eng (accessed on 29 June 2018).
- Leach, S.M.; Liddle, A.R. Inflationary perturbations near horizon crossing. Phys. Rev. D 2001, 63, 043508. [Google Scholar] [CrossRef]
- Kofman, L.; Linde, A.; Starobinsky, A.A. Reheating after inflation. Phys. Rev. Lett. 1994, 73, 3195–3198. [Google Scholar] [CrossRef] [PubMed]
- Allahverdi, R.; Brandenberger, R.; Cyr-Racine, F.Y.; Mazumdar, A. Reheating in Inflationary Cosmology: Theory and Applications. Annu. Rev. Nucl. Part. Sci. 2010, 60, 27–51. [Google Scholar] [CrossRef]
- Bassett, B.A.; Tsujikawa, S.; Wands, D. Inflation dynamics and reheating. Rev. Mod. Phys. 2006, 78, 537–589. [Google Scholar] [CrossRef]
- Chongchitnan, S. Inflation model building with an accurate measure of e-folding. Phys. Rev. D 2016, 94, 043526. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Liddle, A.R.; Parsons, P.; Barrow, J.D. Formalising the Slow-Roll Approximation in Inflation. Phys. Rev. D 1994, 50, 7222–7232. [Google Scholar] [CrossRef]
- Lidsey, J.E.; Liddle, A.R.; Kolb, E.W.; Copeland, E.J.; Barreiro, T.; Abney, M. Reconstructing the Inflaton Potential—An Overview. Rev. Mod. Phys. 1997, 69, 373–410. [Google Scholar] [CrossRef]
- Chongchitnan, S.; Efstathiou, G. Dynamics of the Inflationary Flow Equations. Phys. Rev. D 2005, 72, 083520. [Google Scholar] [CrossRef]
- Coone, D.; Roest, D.; Vennin, V. The Hubble flow of plateau inflation. J. Cosmol. Astropart. Phys. 2015, 2015, 010. [Google Scholar] [CrossRef]
- Chongchitnan, S. Inflationary e-folding and the implications for gravitational-wave detection. arXiv, 2017; arXiv:1705.02712. [Google Scholar]
- Chongchitnan, S.; Efstathiou, G. Accuracy of slow-roll formulae for inflationary perturbations: implications for primordial black hole formation. J. Cosmol. Astropart. Phys. 2007, 2007, 011. [Google Scholar] [CrossRef]
- Adams, J.; Cresswell, B.; Easther, R. Inflationary perturbations from a potential with a step. Phys. Rev. D 2001, 64, 123514. [Google Scholar] [CrossRef]
- Ashoorioon, A.; van de Bruck, C.; Millington, P.; Vu, S. Effect of transitions in the Planck mass during inflation on primordial power spectra. Phys. Rev. D 2014, 90, 103515. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C. First CMB constraints on the inflationary reheating temperature. Phys. Rev. D 2010, 82, 023511. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Vennin, V. Encyclopædia Inflationaris. Phys. Dark Universe 2014, 5, 75–235. [Google Scholar] [CrossRef]
- Muñoz, J.B.; Kamionkowski, M. Equation-of-state parameter for reheating. Phys. Rev. D 2015, 91, 043521. [Google Scholar] [CrossRef]
- Rehagen, T.; Gelmini, G.B. Low reheating temperatures in monomial and binomial inflationary models. J. Cosmol. Astropart. Phys. 2015, 2015, 039. [Google Scholar] [CrossRef]
- Ringeval, C.; Suyama, T.; Yokoyama, J. Magneto-reheating constraints from curvature perturbations. J. Cosmol. Astropart. Phys. 2013, 2013, 020. [Google Scholar] [CrossRef]
- Kolb, E.W.; Turner, M.S. The Early Universe. Front. Phys. 1990, 69, 1–547. [Google Scholar]
- De Salas, P.F.; Lattanzi, M.; Mangano, G.; Miele, G.; Pastor, S.; Pisanti, O. Bounds on very low reheating scenarios after Planck. Phys. Rev. D 2015, 92, 123534. [Google Scholar] [CrossRef]
- Choi, K.Y.; Takahashi, T. A new bound on the low reheating temperature with dark matter. arXiv, 2017; arXiv:1705.01200. [Google Scholar]
- Podolsky, D.; Felder, G.N.; Kofman, L.; Peloso, M. Equation of state and beginning of thermalization after preheating. Phys. Rev. D 2006, 73, 023501. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2015 results. XX. Constraints on inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar]
- Ijjas, A.; Steinhardt, P.J.; Loeb, A. Inflationary paradigm in trouble after Planck2013. Phys. Lett. B 2013, 723, 261–266. [Google Scholar] [CrossRef]
- Guth, A.H.; Kaiser, D.I.; Nomura, Y. Inflationary paradigm after Planck 2013. Phys. Lett. B 2014, 733, 112–119. [Google Scholar] [CrossRef]
- Carrasco, J.J.M.; Kallosh, R.; Linde, A. α-attractors: Planck, LHC and dark energy. J. High Energy Phys. 2015, 2015, 147. [Google Scholar] [CrossRef]
- Kallosh, R.; Linde, A.; Roest, D. Superconformal inflationary α-attractors. J. High Energy Phys. 2013, 2013, 198. [Google Scholar] [CrossRef]
- Gelmini, G.; Palomares-Ruiz, S.; Pascoli, S. Low Reheating Temperature and the Visible Sterile Neutrino. Phys. Rev. Lett. 2004, 93, 081302. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.ligo.caltech.edu (accessed on 29 June 2018).
- Brandenberger, R.; Peter, P. Bouncing Cosmologies: Progress and Problems. Found. Phys. 2017, 47, 797–850. [Google Scholar] [CrossRef]
- Chongchitnan, S.; Efstathiou, G. Prospects for direct detection of primordial gravitational waves. Phys. Rev. D 2006, 73, 083511. [Google Scholar] [CrossRef]
- Buonanno, A.; Sathyaprakash, B.S. Sources of Gravitational Waves: Theory and Observations. arXiv, 2014; arXiv:1410.7832. [Google Scholar]
- Chiara Guzzetti, M.; Bartolo, N.; Liguori, M.; Matarrese, S. Gravitational waves from inflation. arXiv, 2016; arXiv:1605.01615. [Google Scholar]
- BICEP2 Collaboration; Keck Array Collaboration. Improved Constraints on Cosmology and Foregrounds from BICEP2 and Keck Array Cosmic Microwave Background Data with Inclusion of 95 GHz Band. Phys. Rev. Lett. 2016, 116, 031302. [Google Scholar]
| 1. | As long as , which is a consequence of the Null-Energy Condition. |
| 2. | In particular, Reference [16] used the Hamilton-Jacobi approach to construct a family of plateau-like potentials using truncated series with stochastic coefficients drawn from special distributions, whereas we construct similar models using a simple Gaussian function. |

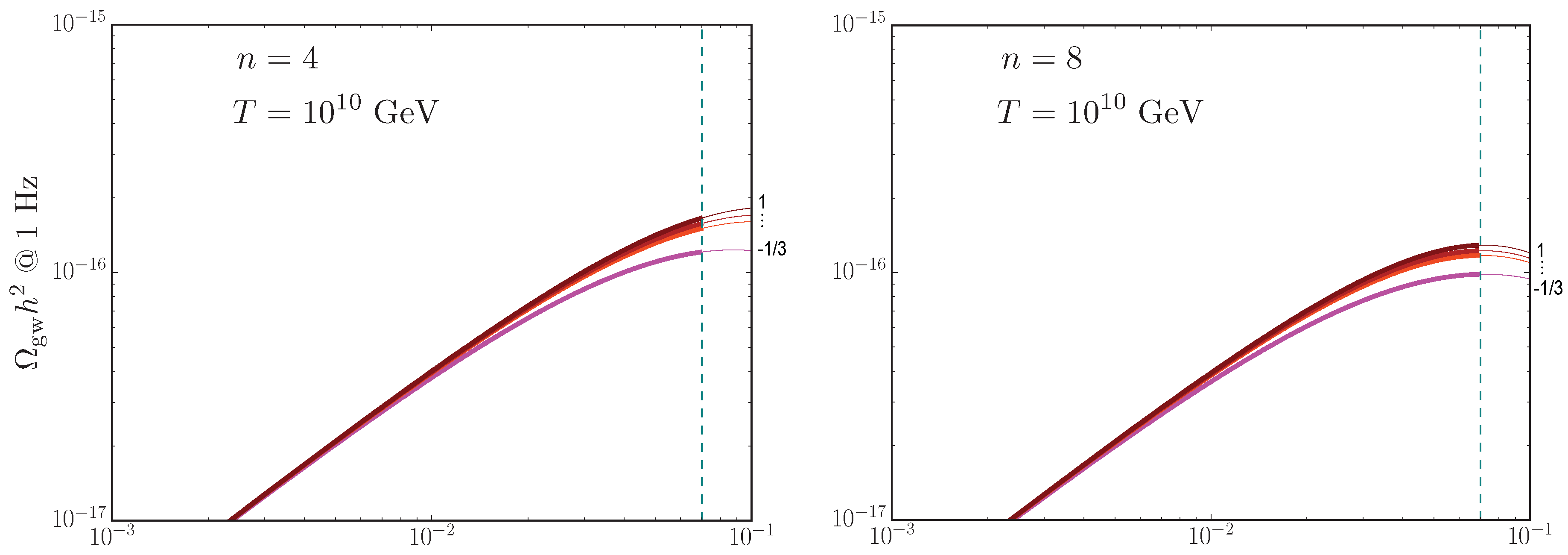
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chongchitnan, S. Primordial Gravitational Waves and Reheating in a New Class of Plateau-Like Inflationary Potentials. Universe 2018, 4, 77. https://doi.org/10.3390/universe4070077
Chongchitnan S. Primordial Gravitational Waves and Reheating in a New Class of Plateau-Like Inflationary Potentials. Universe. 2018; 4(7):77. https://doi.org/10.3390/universe4070077
Chicago/Turabian StyleChongchitnan, Siri. 2018. "Primordial Gravitational Waves and Reheating in a New Class of Plateau-Like Inflationary Potentials" Universe 4, no. 7: 77. https://doi.org/10.3390/universe4070077
APA StyleChongchitnan, S. (2018). Primordial Gravitational Waves and Reheating in a New Class of Plateau-Like Inflationary Potentials. Universe, 4(7), 77. https://doi.org/10.3390/universe4070077



