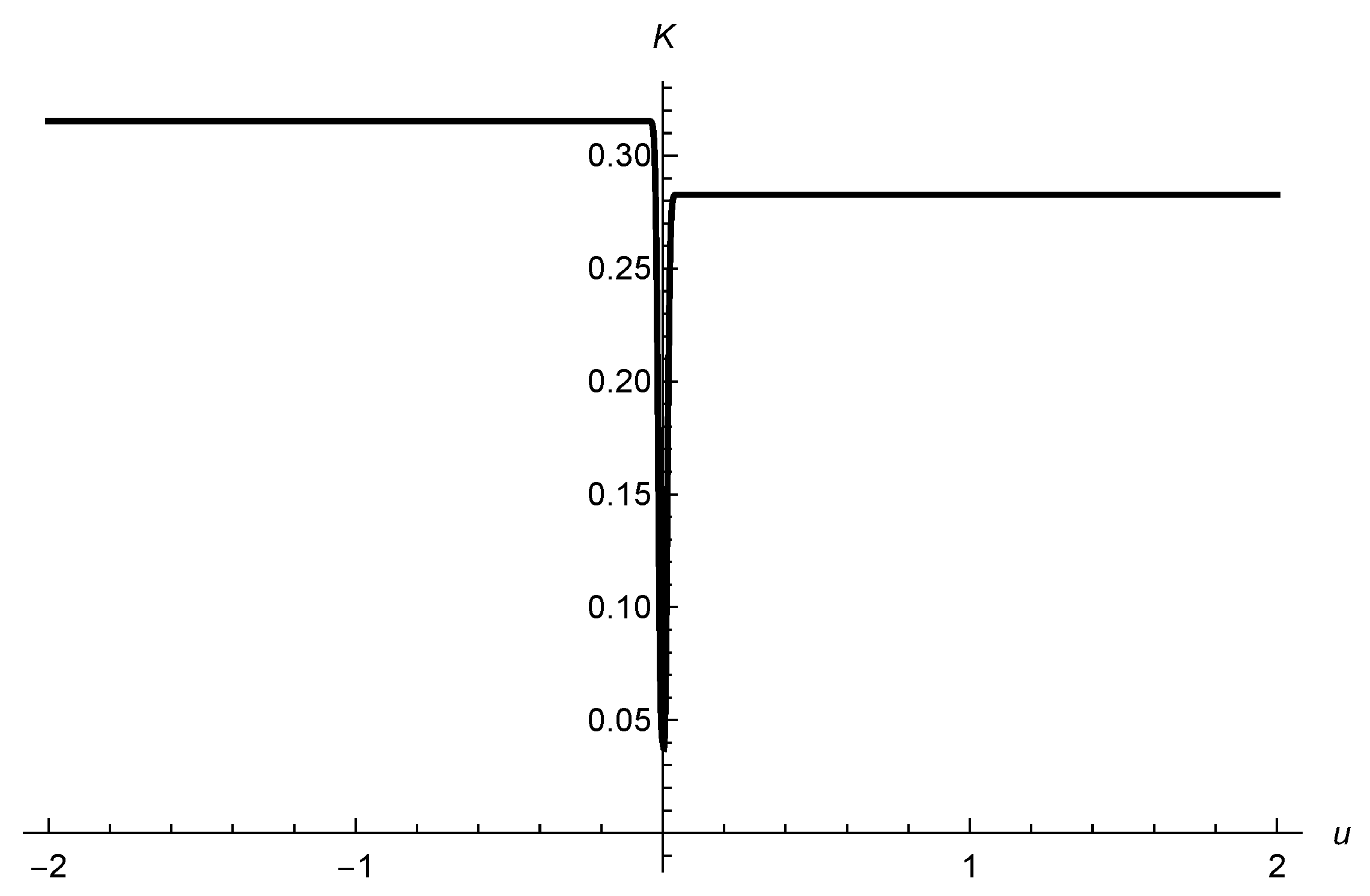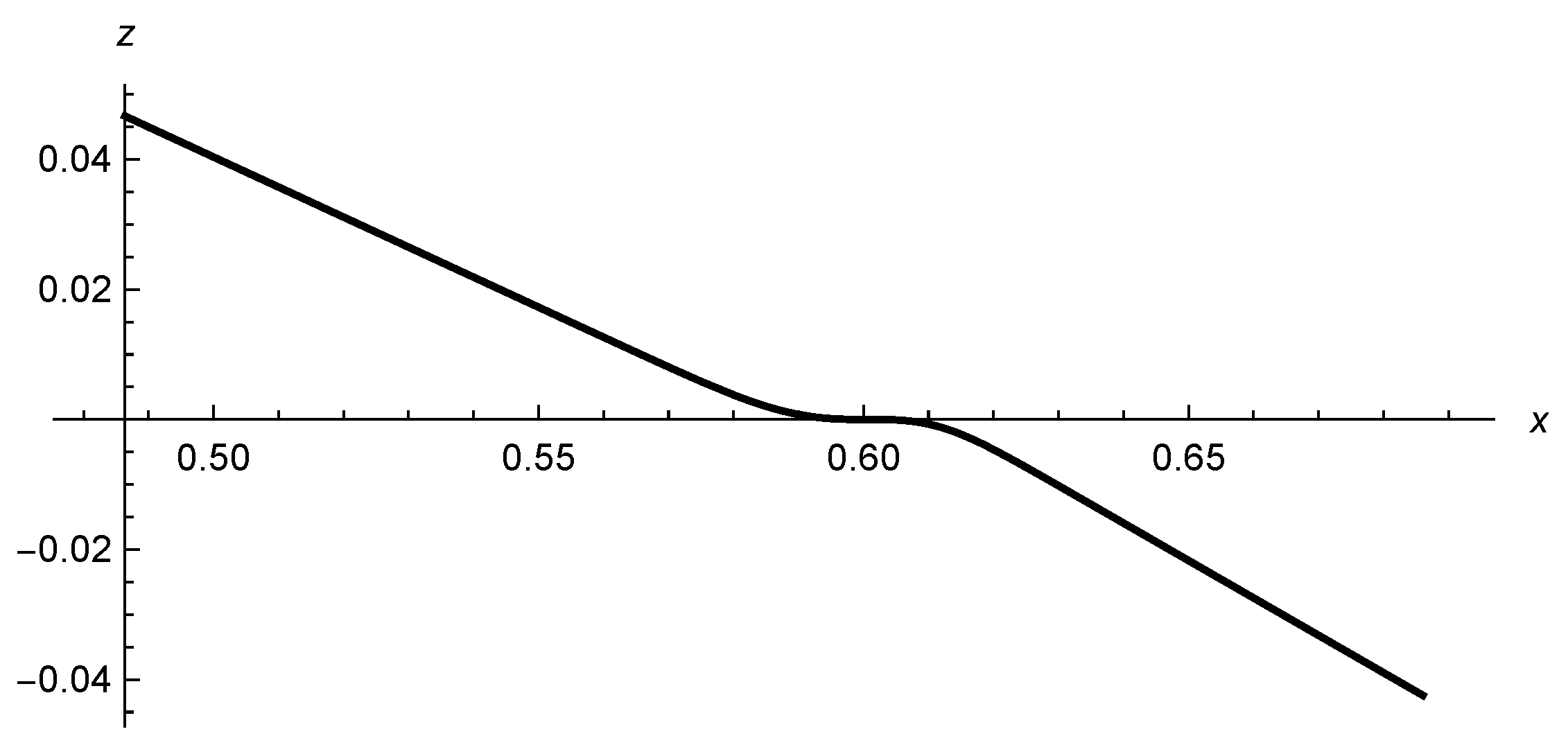Variations of the Energy of Free Particles in the pp-Wave Spacetimes

Abstract

We consider the action of exact plane gravitational waves, or pp-waves, on free particles. The analysis is carried out by investigating the variations of the geodesic trajectories of the particles, before and after the passage of the wave. The initial velocities of the particles are non-vanishing. We evaluate numerically the kinetic energy per unit mass of the free particles and obtain interesting, quasi-periodic behavior of the variations of the kinetic energy with respect to the width $\lambda$ of the Gaussian that represents the wave. The variation of the energy of the free particle is expected to be exactly minus the variation of the energy of the gravitational field, and therefore provides an estimation of the local variation of the gravitational energy. The investigation is carried out in the context of short bursts of gravitational waves, and of waves described by normalized Gaussians, that yield impulsive waves in a certain limit.

1. Introduction

Non-linear plane gravitational waves, or parallelly-propagated plane-fronted gravitational waves, are exact vacuum solutions of the Einstein equations. They are also denoted simply as pp-waves. The space-time before and after the passage of the wave is normally taken to be flat or nearly flat, for suitable amplitudes of the waves. The metric tensor that describes the plane wave space-time has a very simple structure. Assuming that the wave propagates along the z direction, the line element reads:

$$d{s}^2=d{x}^2+d{y}^2+2dudv+H(x,y,u)d{u}^2,$$

(1)

in $(u,v,x,y)$ coordinates. In the flat space-time region, we may identify:

$$u=\frac{1}{\sqrt{2}}(z-t),$$

(2)

$$u=\frac{1}{\sqrt{2}}(z+t),$$

(3)

The coordinates $(x,y)$ parametrize the planes parallel to the wave front. The line element depends essentially on a function $H(x,y,u)$.

The class of exact solutions that describe these waves is known as the Kundt family of space-times, and they were studied in great detail by Ehlers and Kundt [1,2] (see also [3,4]). The dependence of the function H on the variable u is, to a large extent, arbitrary, a feature that is typical of solutions of wave equations. In view of this arbitrariness, the function H may be modeled so that it represents a short burst of gravitational wave, in which case the u dependence of H may be given by smooth Gaussians or derivatives of Gaussians. The function H must only satisfy [1]:

$${\nabla }^{2}H=\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\right)H=0.$$

(4)

We assume that, far from the source, we may approximate a realistic gravitational wave by an exact plane wave, exactly as we do in the study of electromagnetic waves. The non-linear gravitational wave space-time is geodesically complete. The form above of the line element (1), in the coordinates $(u,v,x,y)$, was first presented by Brinkmann [5].

The physical viability of these exact wave solutions has been supported by Penrose [6], who argued that the waves are physically acceptable, in similarity to the classical, source free, monochromatic plane electromagnetic waves. Penrose also addressed technical issues regarding the establishment of a global Cauchy hypersurface in these space-times. According to him, a light cone in an event Q in the past (after the passage) of the wave can never meet an event R ahead (before the passage) of the wave. Thus, the Cauchy data on a hypersurface that contains the event Q cannot give information for specifying the wave amplitude on R. However, as we discussed above, the wave amplitude (contained in the function H) is necessarily an arbitrary function of u. Electromagnetic and gravitational waves are both assumed to travel at the same speed, the speed of light. The pp-waves do not violate any physical principle or property, such as causality, for instance.

Non-linear gravitational waves have been recently studied in the analysis of the memory effect [7,8,9,10,11]. The latter effect is established by the permanent displacement of free particles, after the passage of a wave. The displacement in the three-dimensional space may also be followed by a variation of the velocities of the particles. The effect has been formulated by Zel’dovich and Polnarev [12] and by Braginsky and Grishchuk [13], even though Ehlers and Kundt [1] evaluated the variation of the velocities of free particles after the passage of a pp-wave earlier. The memory effect is relevant and conceptually important to future observations of gravitational waves in space, and to a better understanding of gravitational waves in general.

The u dependence of H may be given by Gaussians, as mentioned above, or derivatives of Gaussians. Normalized Gaussians, such as:

$$\frac{1}{\lambda \sqrt{2\pi }}{\int }_{-\infty }^{+\infty }du{e}^{-(u^2/2{\lambda }^2)}=1,$$

(5)

lead to impulsive gravitational waves in the limit $\lambda \to 0$. The Gaussian becomes a delta function, and the analysis of the geodesics may be carried out analytically. By working with the limit $\lambda \to 0$ of the Gaussian function, and not strictly with the delta functions themselves, one may overcome difficulties that arise from the ill-defined products of delta functions. This is the procedure adopted in [14,15] and which allows solving analytically the geodesic equations (see also [9]). We mention that the completeness of general pp-wave space-times has recently been considered in [16], and pp-waves with gyratons were investigated in [17]. Gyratonic pp-waves are not vacuum solutions of the field equations. They are generated by a source that travels at the speed of light, and that is described by the radiation density and by a quantity that represents the spinning character of the source. These waves yield the source-free pp-waves in a certain limit.

The u dependence of H in terms of derivatives of Gaussians has been considered in the context of the memory effect, as for instance in [7,8]. The advantage of working specifically with the second derivative of the Gaussian is that one does not need a multiplicative dimensional constant in H. Recall that in Equation (3), H must have dimension (length)${}^{-2}$, and therefore, the second derivative of the Gaussian, $(d^2/d{u}^2)$, eliminates the necessity of a dimensional amplitude.

An interesting feature of non-linear plane gravitational waves is that their action on free particles may reduce the kinetic energy [18], as well as the angular momentum of the particles [19]. One would expect, a priori, that the energy of a particle would always increase after the passage of the wave. This is obviously the case if the particles are initially at rest. The increasing or decreasing of kinetic energy of the free particles depends essentially on the initial conditions of the latter. Therefore, a pp-wave may remove energy from a medium, and this feature may explain why a gravitational wave travels in space for periods of time such as billions of years. If the gravitational wave were to only transfer energy to the medium, which may be characterized as a cloud of particles (an idea first proposed by Bondi [20]), then it would be difficult to understand how a gravitational wave can travel in space without dissipating for such long periods of time.

The feature mentioned above has implications for the concept of gravitational energy-momentum. The exchange of gravitational energy-momentum and angular momentum between the particle and the field takes place locally, i.e., where the free particles are located. Therefore, it seems reasonable to assume that the increasing or decreasing of gravitational energy also takes place locally. Since the kinetic energy of the particles (before, during or after the passage of the wave, in a flat space-time region) cannot be removed by a coordinate transformation, the gravitational energy also cannot be removed by such a transformation (the removal of the gravitational field and, consequently, of the gravitational energy, by a coordinate transformation is a standard assumption against the localization of the gravitational energy).

In this article, we continue our analysis developed in [18,19] and search for discrete or periodic structures in the behavior of a free particle, in the pp-wave space-times. The particles in consideration are free, except that they are subject only to the gravitational field of the wave, and the space-time is essentially flat outside the wave front (before and after the passage of the wave), in view of the fall off of the Gaussians. Our idea is that instead of looking for particular features of the gravitational field or gravitational energy, we investigate the properties of the free particles and infer the corresponding behavior (variation) of the gravitational field properties. We find that the quantity $\Delta K$ = (final kinetic energy per unit mass) − (initial kinetic energy per unit mass) oscillates when varied with respect to $\lambda$, which is a quantity that is proportional to the width of the Gaussian, as in Equation (5). The zeros of $\Delta K$ arise in discrete values. In addition, we find that although the energy of a single particle changes continuously during the passage of the wave, there arise certain jumps and peaks in the expression of the kinetic energy as a function of u. The increasing or decreasing of the kinetic energy takes place by means of a sequence of peaks, which suggests the exchange of small packages of energy in a hypothetical quantum formulation of the problem. We comment on and speculate about these peaks in the last sections of this article.

In Section 2, we present the underlying mathematical formulation and the basic geodesic equations for a particle in the pp-wave space-time. In Section 3, we present several relevant figures that we obtain by using the program MATHEMATICA. It seems that there does not exist exact, general solutions of the geodesic equations if the amplitude of the wave is given by Gaussians or derivatives of Gaussians. For this reason, we resort to computer programs to obtain graphic results. Finally, in Section 4, we discuss the results obtained in Section 3 and speculate about a possible way to evaluate the quantum of gravitational energy.

2. The Geodesic Equations

A non-linear plane gravitational wave may be written in several different forms [3]. One possible form is the plane-fronted gravitational wave that we assume to propagate in the z direction and which is given by Equation (1). This form for the line element was first proposed by Brinkmann [5]. With the help of Equations (2) and (3), we rewrite the line element (1) in $(t,x,y,z)$ coordinates. It reads:

$$d{s}^2=\left(\frac{H}{2}-1\right)d{t}^2+d{x}^2+d{y}^2+\left(\frac{H}{2}+1\right)d{z}^2-Hdtdz.$$

(6)

We are assuming $c=1$. The function H must satisfy only Equation (4). As we mentioned earlier, the dependence of H on the retarded time $(-u)$ is arbitrary. The geodesic equations in terms of the $t,x,y,z$ coordinates are [21]:

$$2\ddot{t}+\sqrt{2}H\ddot{u}+\sqrt{2}\dot{H}\dot{u}-\frac{1}{\sqrt{2}}\frac{\partial H}{\partial u}{\dot{u}}^2=0,$$

(7)

$$2\ddot{x}-\frac{\partial H}{\partial x}{\dot{u}}^2=0,$$

(8)

$$2\ddot{y}-\frac{\partial H}{\partial y}{\dot{u}}^2=0,$$

(9)

$$2\ddot{z}+\sqrt{2}H\ddot{u}+\sqrt{2}\dot{H}\dot{u}-\frac{1}{\sqrt{2}}\frac{\partial H}{\partial u}{\dot{u}}^2=0,$$

(10)

where the dot represents the derivative with respect to s. From the first and fourth equations above, we get:

$$\ddot{z}-\ddot{t}=0\to \ddot{u}=0\to \dot{u}=\frac{1}{\sqrt{2}}(\dot{z}-\dot{t})=constant.$$

(11)

We assume the constant on the right-hand side of the equation above to be one and, thus, consider u to parametrize the geodesic curves.

Except for constant multiplicative factors, the function H may be given by the + or × polarizations, according to:

$$H=A_{+}\left(u\right)(x^2-y^2),$$

(12)

$$H=A_{\times }\left(u\right)xy,$$

(13)

or by a linear combination of these quantities.

The two expressions above of H satisfy Equation (4). Both expressions lead to the same qualitative behavior for the geodesics and kinetic energy of the particles. In the present analysis, we will consider the amplitudes $A_{+}\left(u\right)$ and $A_{\times }\left(u\right)$ to be given by regular Gaussians, which represent short bursts of gravitational waves, and by normalized Gaussians (Normalized not necessarily to one. We will choose multiplicative constants that yield satisfactory figures). The latter is typically given by:

$$A_{(+,\times )}\simeq \frac{1}{\lambda }{e}^{-(u^2/2{\lambda }^2)}.$$

(14)

The effect of a gravitational wave on a free particle is assumed to be very weak. The kinetic energy per unit mass K of the free particles is considered as:

$$2K=\frac{1}{2}(V_x^2+V_y^2+V_z^2),$$

(15)

where the velocities are $V_x=dx/du$, $V_y=dy/du$ and $V_z=dz/du$. Thus, in view of Equation (2), we have:

$$K=\frac{1}{2}\left[{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2+{\left(\frac{dz}{dt}\right)}^2\right],$$

(16)

which is, certainly, a valid expression before and after the passage of the wave, in which case the space-time is flat, or nearly flat.

3. Kinetic Energy and Geodesics of Free Particles

The particles that we consider in the present analysis are idealized entities that do not affect the gravitational field of the wave. Ehlers and Kundt [1] already pointed out that, in principle, a more realistic approach would require taking into account the interaction between an ordinary massive particle and the wave. For the time being, this is a very complicated issue to be addressed analytically, and even numerically. However, in view of the arbitrariness in the u dependence of H, the actual interaction between a massive particle and the wave will not change the qualitative results obtained by just investigating ordinary geodesics in space-time. We can formally make the gravitational field of the wave more intense than the field of a massive test particle, even though the gravitational wave is taken to be weak.

In our previous investigations on this issue [18,19], we found that the initial conditions are of extreme importance for obtaining certain variations, such as the increasing or decreasing of the kinetic energy of the particles. So far, it is not clear what is the relation between the variations of the geodesics, energy, momentum and angular momentum of the particles, on the one hand, and the initial conditions, on the other hand. We will assume that the initial conditions for an astrophysical system like a star, for instance, especially regarding the initial velocities, are roughly the same for all material components of the system (considering, of course, that the translational velocity of the star is much greater than the relative velocities between its molecules).

According to Equation (2), a positive variation of t corresponds to a negative variation of u. Thus, the increase of the time parameter t, for an observer in the flat space-time before or after the passage of the wave, corresponds to the decreasing values of u. We will define the variation $\Delta K$ of the kinetic energy per unit mass of the free particles by:

$$\Delta K=K_f-K_i,$$

(17)

where $K_f$ and $K_i$ are evaluated at $u=-200$ and $u=+200$, respectively, in natural units. We also define the normalized variation $\Delta K_N$ according to:

$$\Delta K_N=\frac{K_f-K_i}{K_f+K_i}.$$

(18)

where again, $K_f$ and $K_i$ are evaluated at $u=-200$ and $u=+200$, respectively. In the analysis below, we will obtain the kinetic energy of the free particles, and certain geodesics, by means of the program MATHEMATICA. As to our knowledge, the general, exact solutions of the geodesic equations are not known, if the amplitude of the wave is given by Gaussians. As we mentioned above, the geodesic equations and the kinetic energy of the free particles are highly dependent on the initial conditions. We will consider three sets of initial conditions, all at $u=0$. These conditions yield suitable graphic results. In natural units, they read:

$$I:{\rho }_0=0.6,{\varphi }_0=0,z_0=0,{\dot{\rho }}_0=0.2,{\dot{\varphi }}_0=0,{\dot{z}}_0=0,$$

(19)

$$II:{\rho }_0=0.6,{\varphi }_0=0,z_0=0,{\dot{\rho }}_0=-0.2,{\dot{\varphi }}_0=0,{\dot{z}}_0=0,$$

(20)

$$III:{\rho }_0={10}^{-5},{\varphi }_0=0,z_0=0,{\dot{\rho }}_0={10}^{-5},{\dot{\varphi }}_0=0,{\dot{z}}_0=0.$$

(21)

The $(\rho ,\varphi )$ variables are related to the $(x,y)$ variables by means of the standard relations $x=\rho \cos \varphi$, $y=\rho \sin \varphi$. Thus,

$$x^2-y^2={\rho }^2(2{\cos }^2\varphi -1),xy=\frac{1}{2}{\rho }^2\sin \left(2\varphi \right).$$

3.1. Non-Normalized Gaussians

We will first address non-normalized Gaussians and choose two expressions for the function H. The expressions are:

$$\begin{array}{ccc}\hfill H_1& =& -{\rho }^2\left(u\right)[2{\cos }^2\left(\varphi \left(u\right)\right)-1]e^{-u^2/{\lambda }^2},\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill H_2& =& \frac{1}{2}{\rho }^2\left(u\right)\sin \left(2\varphi \left(u\right)\right)e^{-u^2/{\lambda }^2}.\hfill \end{array}$$

(23)

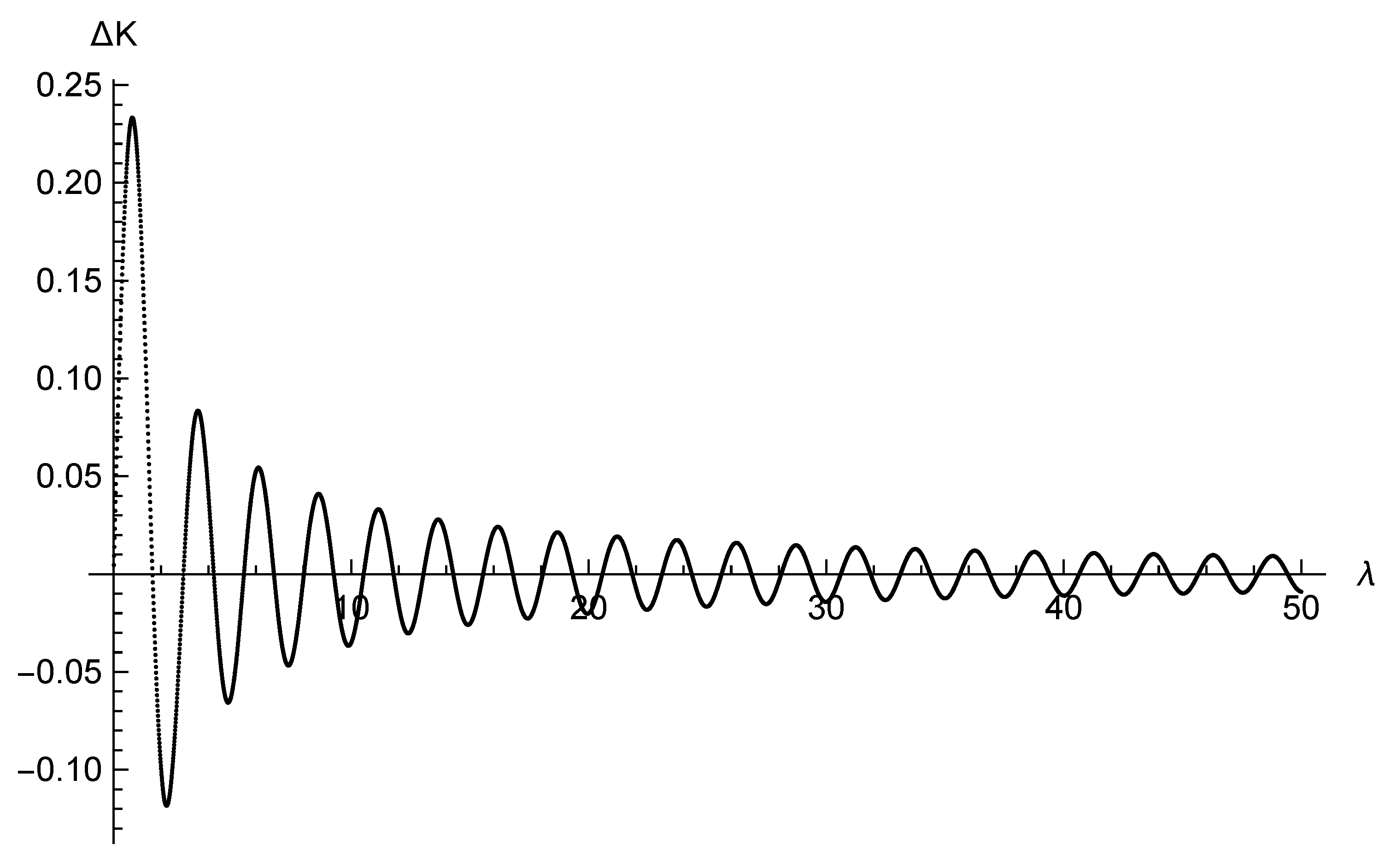
The quantity $\lambda$ is related to the width of the wave. Differently from our previous analyses [18], we are now choosing a minus sign in Equation (22), which just amounts to choosing $y^2-x^2$ instead of $x^2-y^2$. We will plot the variation $\Delta K$ with respect to $\lambda$. The result is presented in Figure 1.

In natural units, $\lambda$ has dimension of length, and $\Delta K$ is dimensionless, since it is per unit mass. Not only the initial conditions, but also the value of the quantity $\lambda$ are relevant to obtain a decrease or increase of the kinetic energy of the particle. However, in this case, we see that certain discrete values of $\lambda$ yield $\Delta K=0$. The quasi-periodic behavior of the variation of the kinetic energy is more strengthened if we consider $\Delta K_N$ with respect to $\lambda$. The result is very much similar and is displayed in Figure 2.

We see that a quasi-periodic structure is hidden in the field quantities and geodesic equations. Note that there are no periodic functions in Equations (7)–(10). We also see that for certain small values of $\lambda$, the impact on the particle is higher than for large values of $\lambda$. This is the case when the “sandwich” wave is concentrated in a small interval $\delta u$ around $u=0$. The figure above for $\Delta K_N$ may be given analytically, to a very good approximation, by the expression:

$$\Delta K_N=f{e}^{-\left(a\lambda \right)/100}\sin \left(\frac{b\lambda }{100}+c\right),$$

(24)

where $f=0.55108$, $a=0.0201072$, $b=2.50067$ and $c=1.32005$, in natural units. The maximal energy transfer between the particle and the field occur at the maxima and minima of $\Delta K_N$, and the corresponding values of $\lambda$ are given by:

$$\frac{b\lambda }{100}+c=\frac{\pi }{2}+n\pi ,$$

where n is an integer.

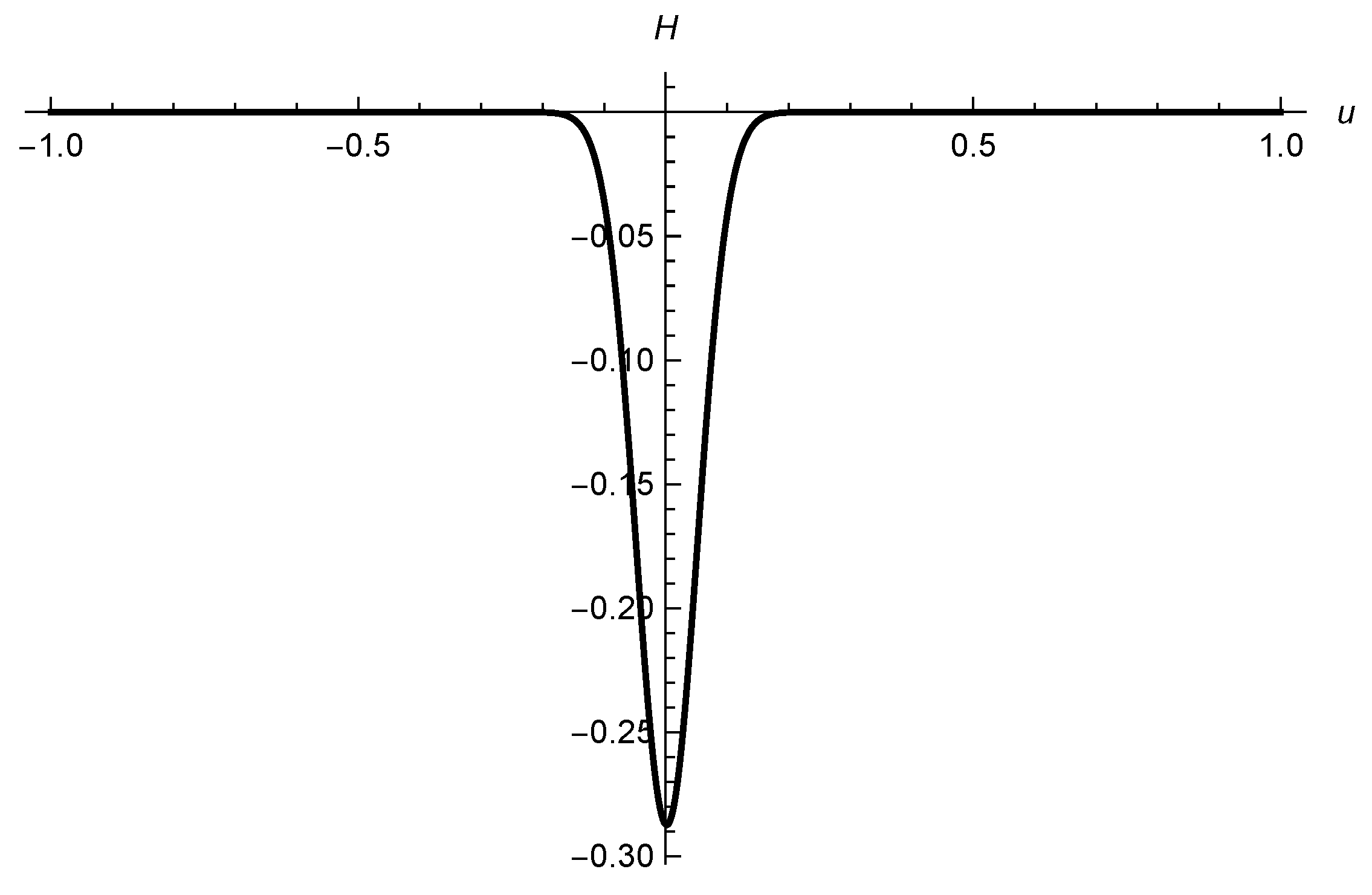
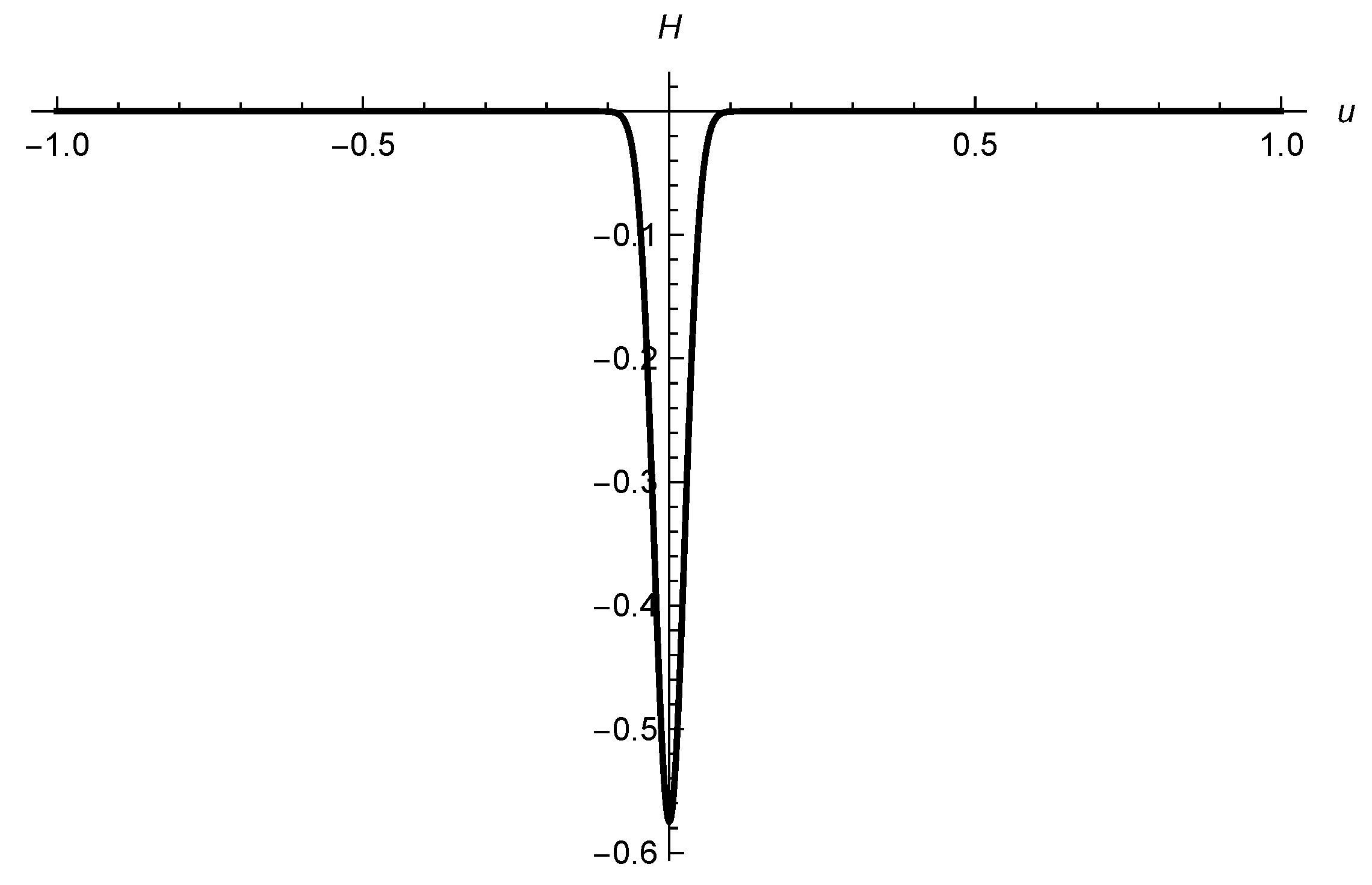
The behavior above of $\Delta K_N$ is not always oscillating. In order to verify this feature, let us now consider $H_2$, with the initial conditions I and II. The result is displayed in Figure 3 and Figure 4.

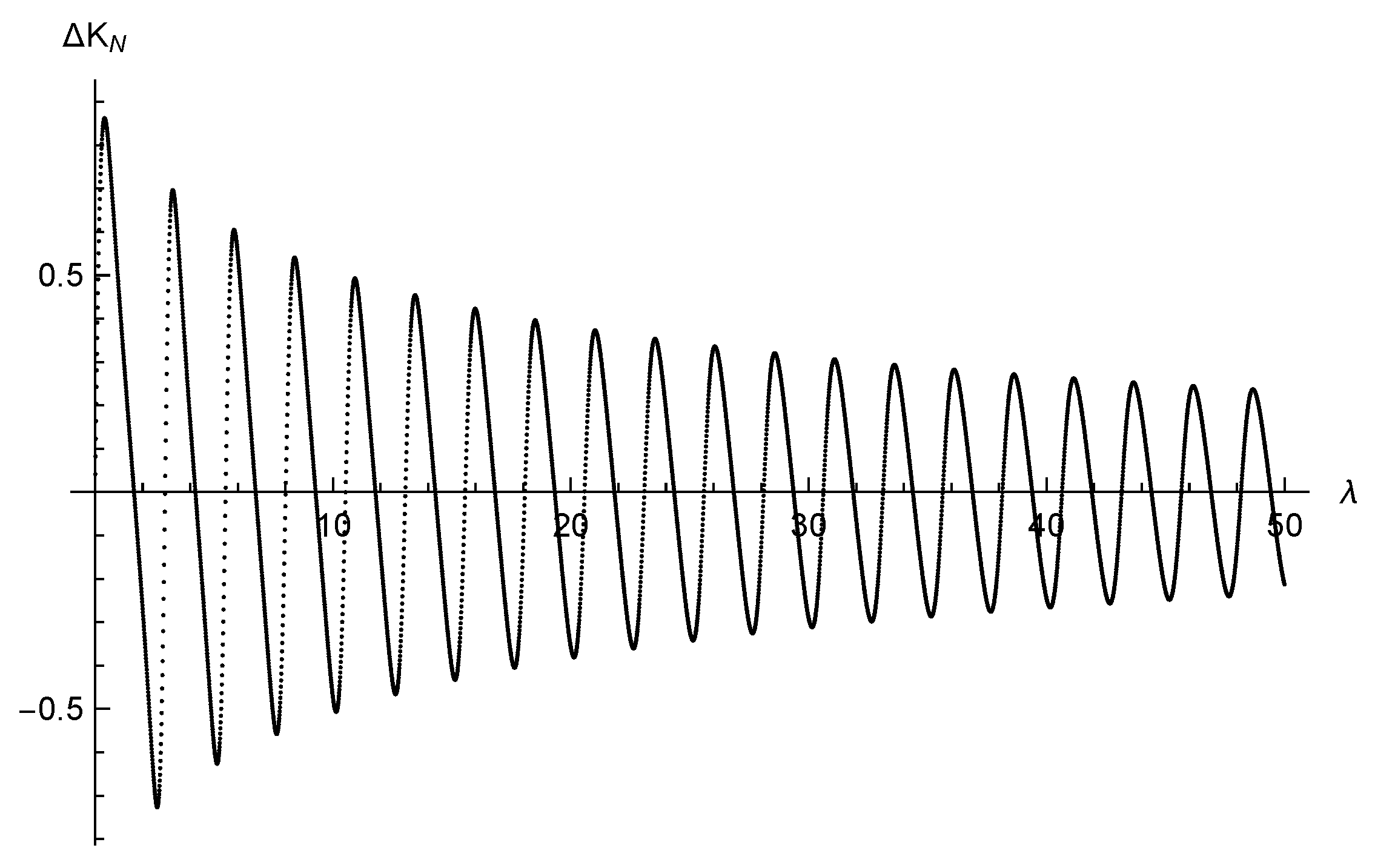
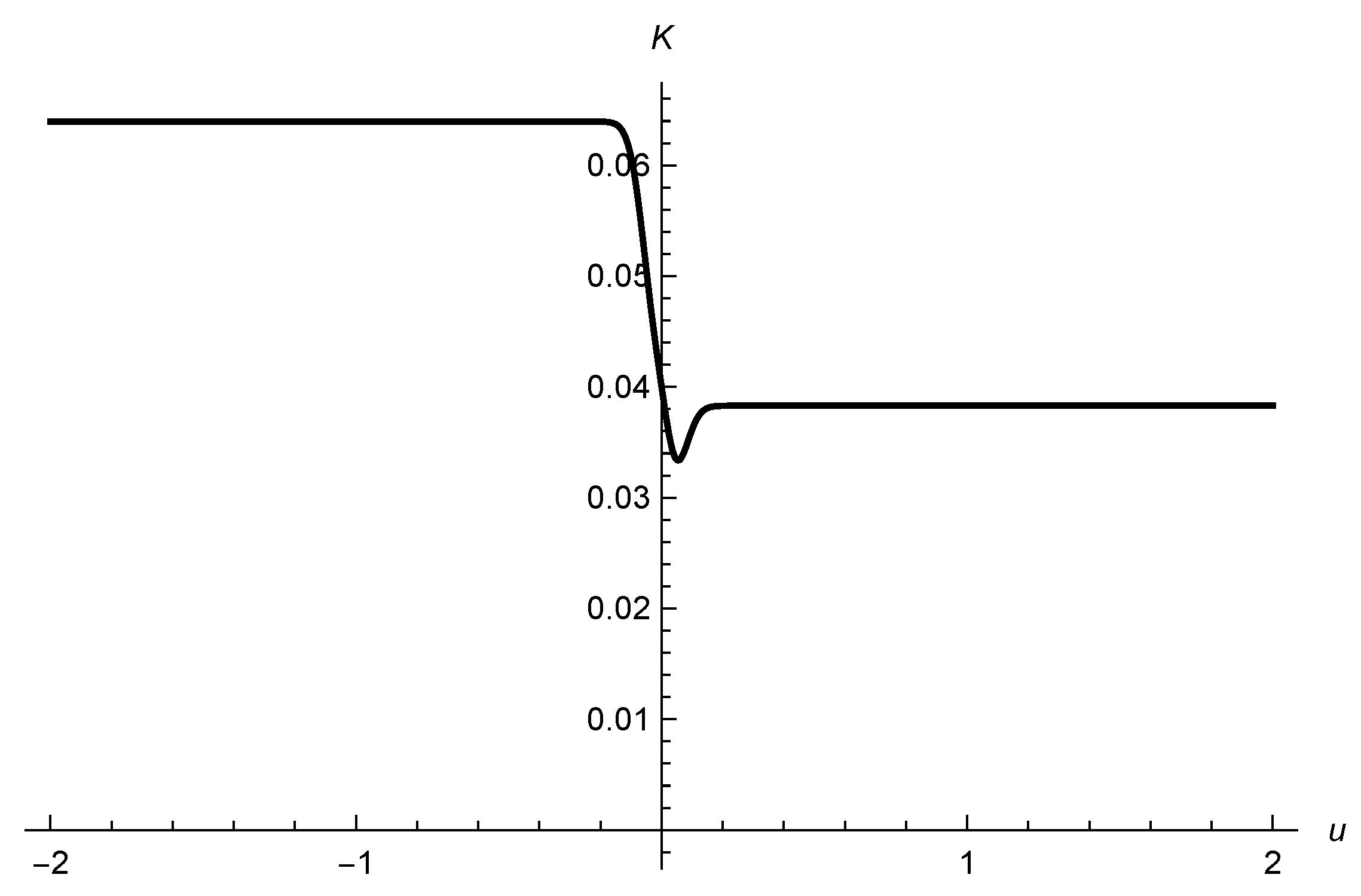
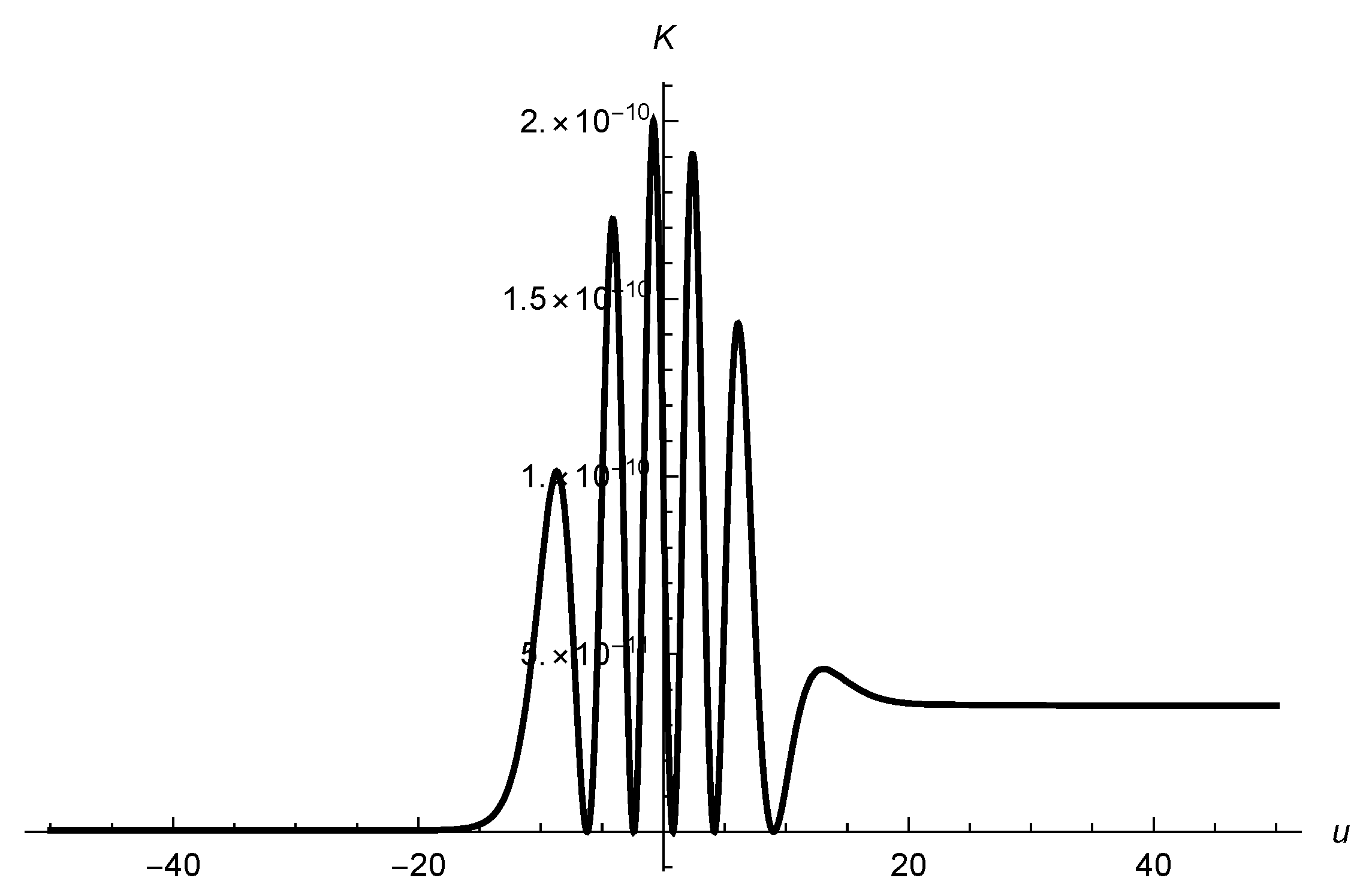
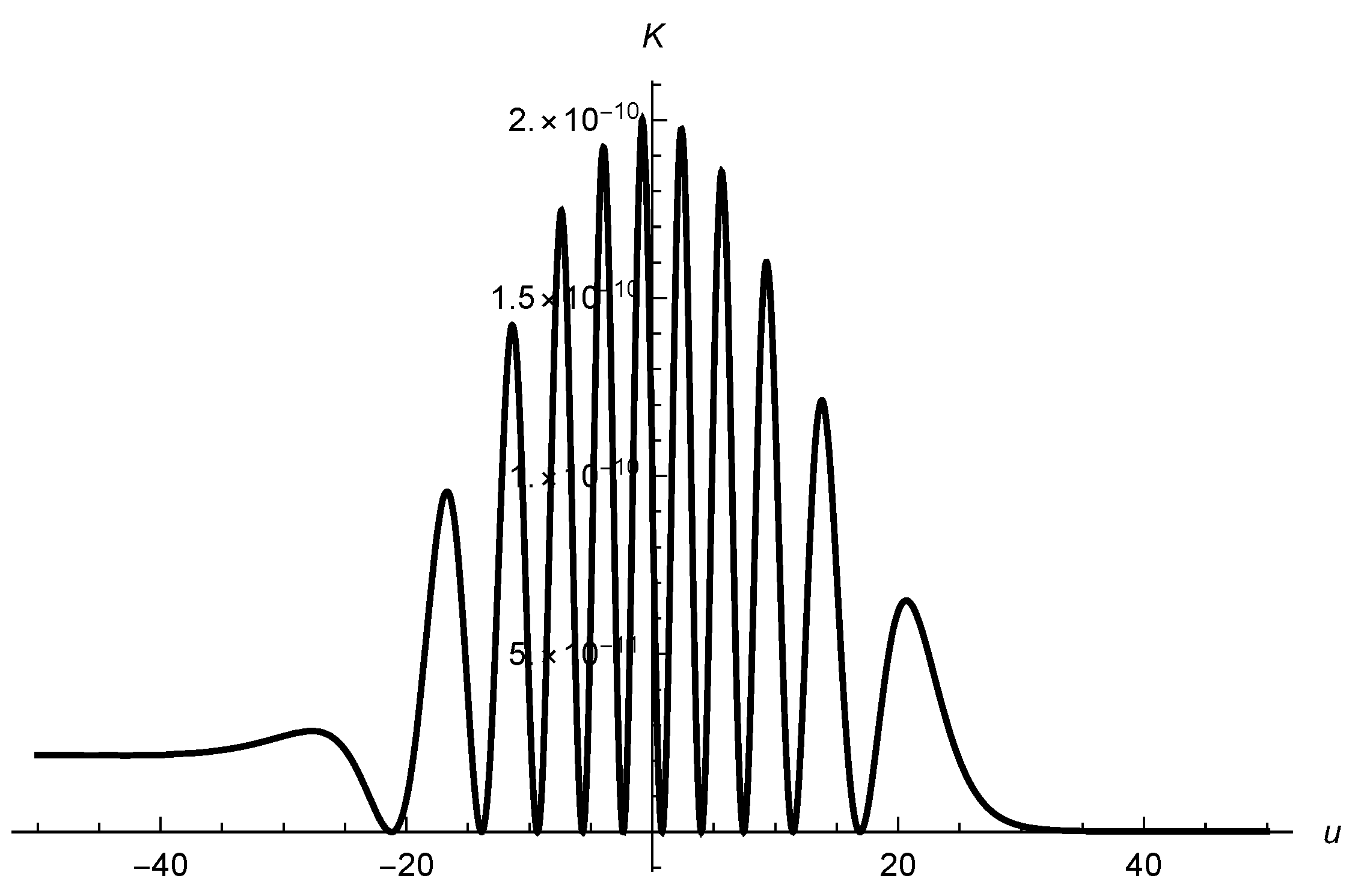
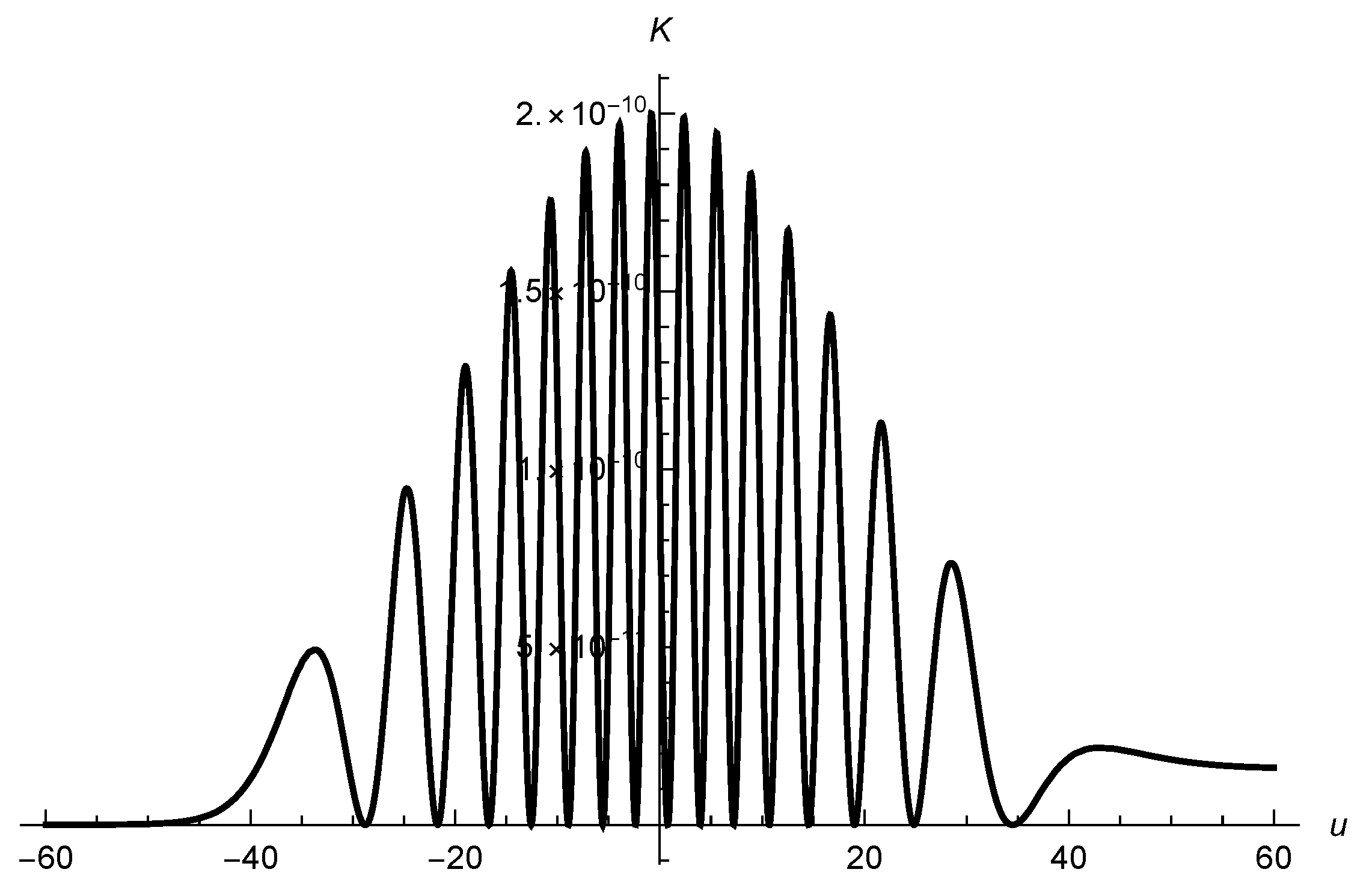
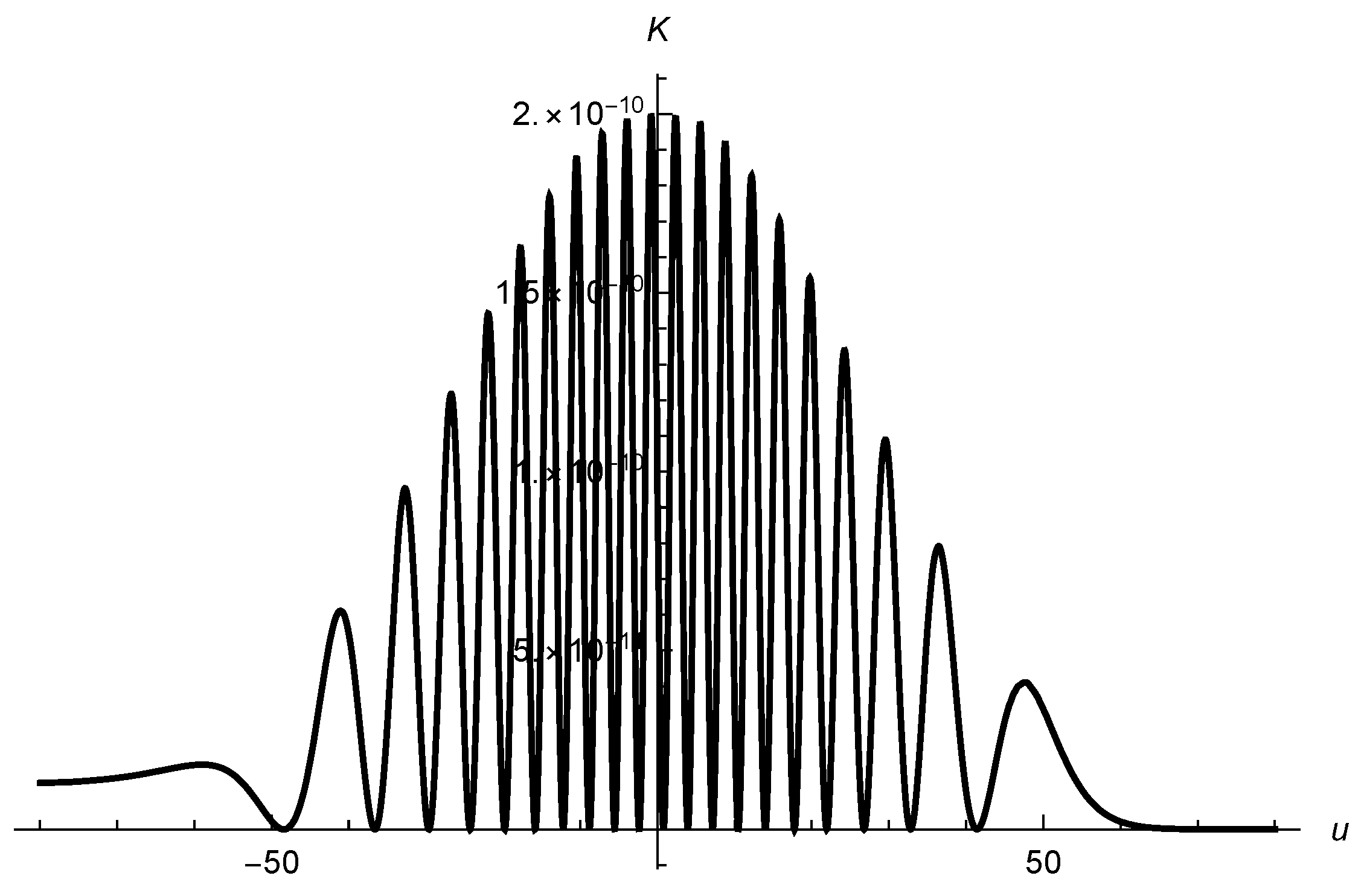
Next, we examine the behavior of the kinetic energy K as a function of u, in order to probe its variation during the passage of the wave. For this purpose, we choose the function $H_1$ and the initial conditions III, considering four values of the width $\lambda$. The results are displayed in Figure 5, Figure 6, Figure 7 and Figure 8,

We see that the energy of the particle varies by a sequence of jumps and peaks, as if absorbing and releasing certain amounts of energy. One first attempt of an explanation of these figures consists of assuming that the particle exchanges small packages of energy with the gravitational field. In a hypothetical quantum formulation of the problem, this would indeed be a natural assumption. The difference between any two peaks of energy would be a multiple of the quantum of gravitational energy. Considering together Figure 1, Figure 2 and Figure 5, Figure 6, Figure 7 and Figure 8, we may conclude that the particle is excited during the passage of the wave, around $u=0$, in a certain interval $\delta u$, and depending on the width $\lambda$ of the wave, the final state of the particle may be less energetic than the initial state for reasons that are not yet clear, but we may consider the following possibility: when the particle gains kinetic energy, the energy is extracted from the wave; when it loses kinetic energy, the particle produces gravitational radiation and increases the energy and intensity (although to a very small extent) of the incoming gravitational wave. In any case, we can certainly conclude that there is an actual exchange of energy between the particle and the gravitational field. In the last section of the article, we comment on the possible energy exchange between the gravitational and electromagnetic fields, according to investigations in the literature.

3.2. Normalized Gaussians

Our main interest in this subsection is to verify the dependence of the physical properties of the particle as we vary $\lambda$, when the particle is hit by a normalized gravitational wave, and infer the results when $\lambda \to 0$ and the Gaussian tends to a delta function. For this purpose, we will consider a normalized wave determined by the function $H_3$,

$$H_3=-\frac{1}{10\lambda \sqrt{2\pi }}{\rho }^2\left(u\right)[2{\cos }^2\left(\varphi \left(u\right)\right)-1]e^{-u^2/\left(2{\lambda }^2\right)}.$$

(25)

All initial conditions in this subsection will be given by Equation (19), the initial conditions I. We plot below, side by side, the kinetic energy of the particle and the function $H_3$, both as a function of u, for $\lambda =0.05$, $\lambda =0.025$ and $\lambda =0.01$. In the figure of the function $H_3$, we make $\rho ={\rho }_0$ and $\varphi ={\varphi }_0$, given by the initial conditions I.

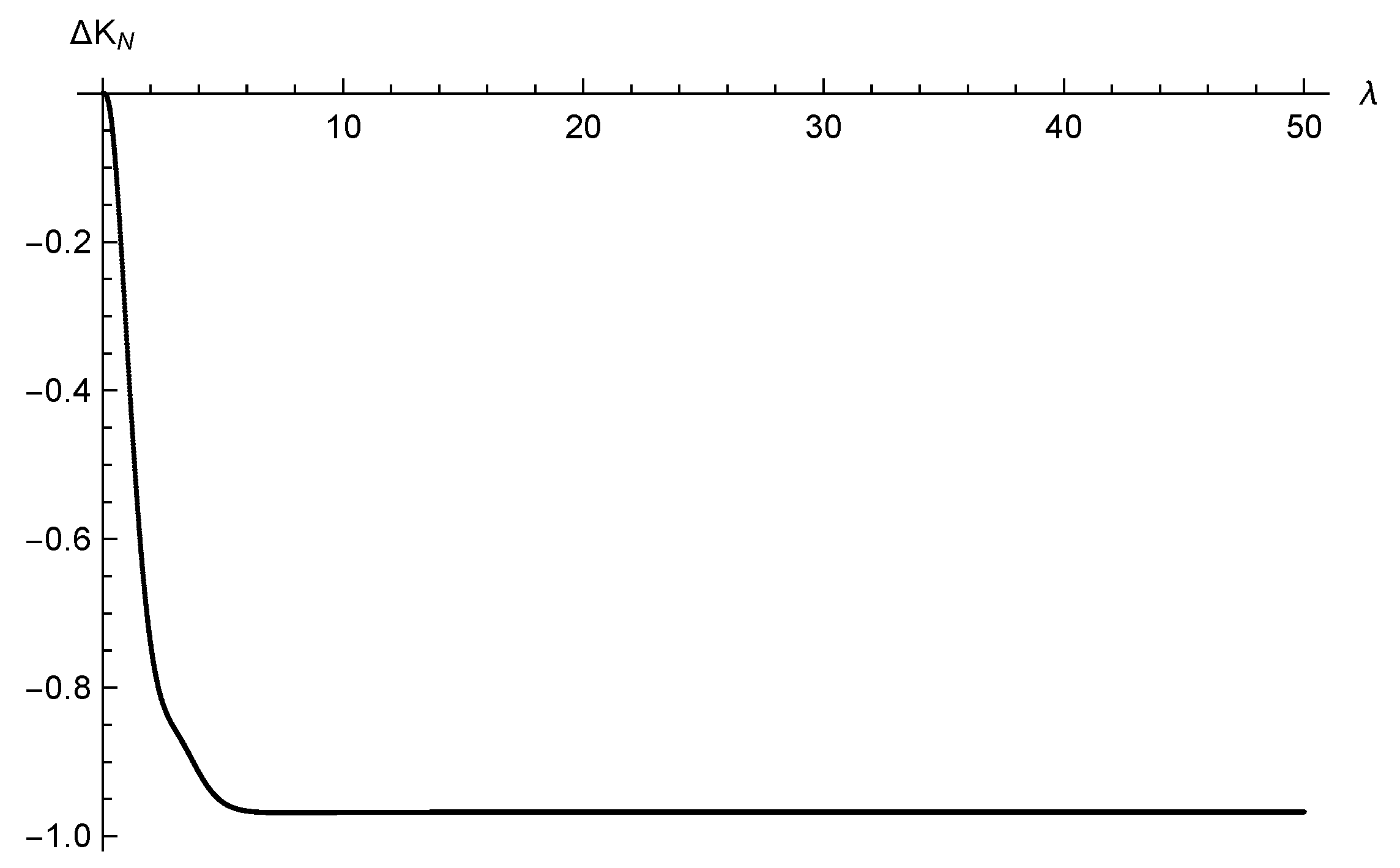
The sequence of Figure 10, Figure 12 and Figure 14 clearly indicate that the functions $H_3\left(u\right)$ approaches a (negative) delta function. By carefully observing the values of K on the vertical axis of Figure 9, Figure 11 and Figure 13, we see that the gap $\Delta K$ between the final and initial energy of the particle increases as we consider smaller and smaller values of $\lambda$. For the initial conditions considered, the absolute values of both $K_f$ and $K_i$ are increasing as we decrease $\lambda$. 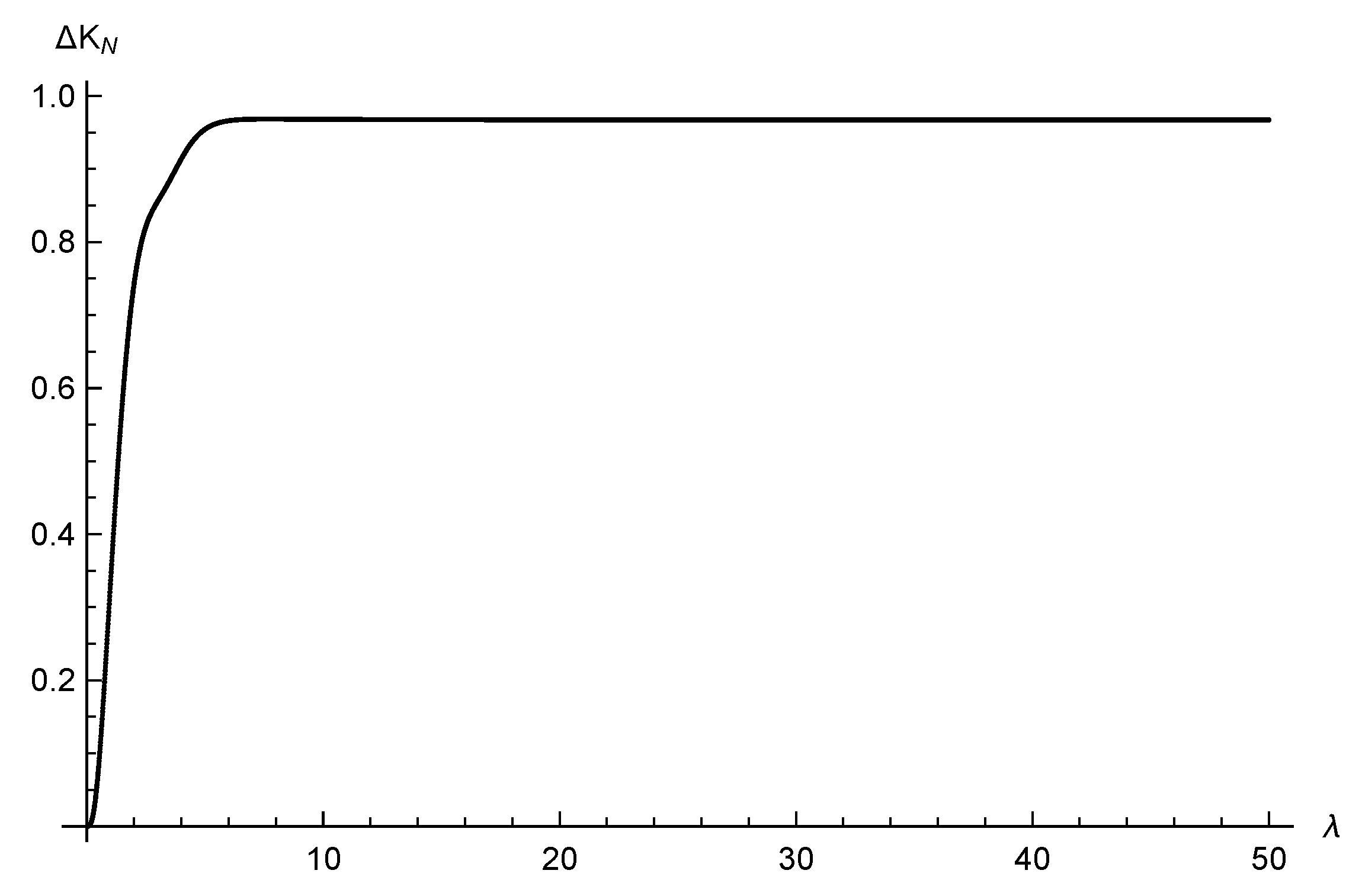However, the normalized variation of the kinetic energy of the particle $\Delta K_N$ tends to zero when $\lambda \to 0$, according to Figure 15, and tends to a constant value for large values of $\lambda$.

The feature discussed above, regarding the effect of the variation of $\lambda$ on $\Delta K_N$, also takes place in the geodesics of the particles. The particle seems to be less sensitive to very small values of $\lambda$ (in fact, values of $\lambda$ close to zero), as we can see in Figure 16, Figure 17 and Figure 18.

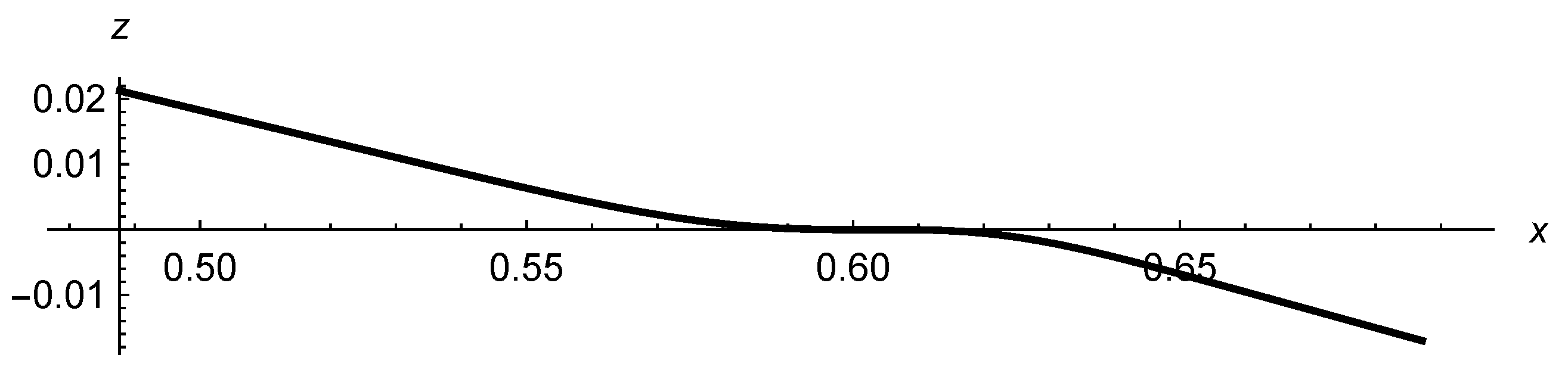
For the simplicity of presentation, we have chosen to plot the trajectory of the particle only in the x-z plane. We see that the smaller the value of $\lambda$, the weaker is the effect of the gravitational wave on the trajectory of the particle. Considering together Figure 2, Figure 3 and Figure 4 and Figure 15, we may conclude that $\Delta K_N\to 0$ when $\lambda \to 0$. This conclusion is likely to hold for normalized and non-normalized Gaussians profiles.

4. Conclusions

In this article, we investigated particular features of free particles under the action of pp-waves. We have paid special attention to the kinetic energy per unit mass of the particles. The first conclusion is that there is an actual exchange of energy (and momentum and angular momentum) between the particles and the gravitational field of the wave. The second conclusion (that in fact was achieved in our previous investigations [18,19]) is that the final energy of the particle may be smaller or higher than the initial energy, and that this feature depends on the initial conditions of the free particles, which are not initially at rest. The third conclusion is that the variation $\Delta K$ of the kinetic energy of the particles depends also on the width $\lambda$ of the wave, and this dependence exhibits (not for all initial conditions) a surprising quasi-periodic behavior. Finally, we have seen that $\Delta K_N\to 0$ when $\lambda \to 0$, in all cases investigated. This property should hold for all normalized Gaussians. We assume that the variation of the kinetic energy of the free particle is exactly minus the variation of the gravitational energy of the wave. Therefore, the analysis of energy of free particles yields an indirect evaluation of the variation of the gravitational energy.

We note that periodic motion of free particles under the action of an exact, non-linear plane wave was obtained in [10], for suitable initial conditions of the particle. Such periodic motion is obtained by directly introducing harmonic functions in the wave amplitude, and for this reason, the resulting periodic trajectories in space-time bear no physical or mathematical relationship with the one described in Section 3.1. We also note that recently, an analytic investigation of $\Delta K=K_f-K_i$ was carried out in [22]. The authors of the latter adopt a different function for the amplitude of the wave (which is not a Gaussian), so that the geodesic equations may be solved analytically. They arrive at the same conclusion of [18], namely that the final kinetic energy of the free particle may be smaller or larger than the initial energy, after the passage of the pp-wave.

The higher is the value of $\lambda$, the longer (in time) is the interaction of the particle with the wave, a feature that is suggested by Figure 5, Figure 6, Figure 7 and Figure 8. We establish the hypothesis that during the passage of the wave, the particle and the gravitational field exchange small packages of energy and that the difference between any two peaks of energy in Figure 5, Figure 6, Figure 7 and Figure 8 may be a multiple of the quantum of gravitational energy, in a hypothetical quantum formulation. Likewise, the energy gaps in Figure 9, Figure 11 and Figure 13 should also be a multiple of a minimum gravitational energy. The quantum of gravitational energy could be found, on speculative grounds, by means of a Millikan-type procedure (i.e., the procedure that allowed Millikan to determine the charge of the electron), after the analysis of a huge number of figures. However, maybe one would need to consider a quantized particle, instead of a classical one. This issue will be investigated in the future, together with the nature of the oscillations in Figure 1 and Figure 2.

Throughout the article, we have analyzed the energy exchange between gravitational waves and free particles (i.e., particles that are subject only to the gravitational wave, but which are otherwise free). However, the exchange of energy between gravitational waves and electromagnetic fields has already been investigated in the literature, in the context of the linearized gravitational field. (I) Gertsenshtein [23] showed that in the interaction of a gravitational wave with a static magnetic field, electromagnetic radiation may be created. The energy of electromagnetic radiation is likely to come from the energy of the gravitational waves. (II) The graviton-photon interaction analyzed by Skobelev [24] (graviton + graviton → photon + photon, photon + photon → graviton + graviton and photon + graviton → photon + graviton) also points to an energy exchange between the gravitational and electromagnetic fields. (III) Similar investigations have been carried out by Jones et al. [25,26], who studied particle production in a gravitational wave background and analyzed the generation of electromagnetic radiation (photons) in the interaction of the gravitational wave with the quantum vacuum field fluctuations. The analyses in the four references above share similarities with the present investigation, in the sense that energy can be transferred between the gravitational waves (the quantum of gravitational energy) and the quantized electromagnetic field. The gravitational waves can gain or lose energy in these processes. The localizability of the gravitational energy is a mandatory feature in all these investigations.