Inflationary f (R) Cosmologies
Abstract
1. Introduction
2. Matter Description
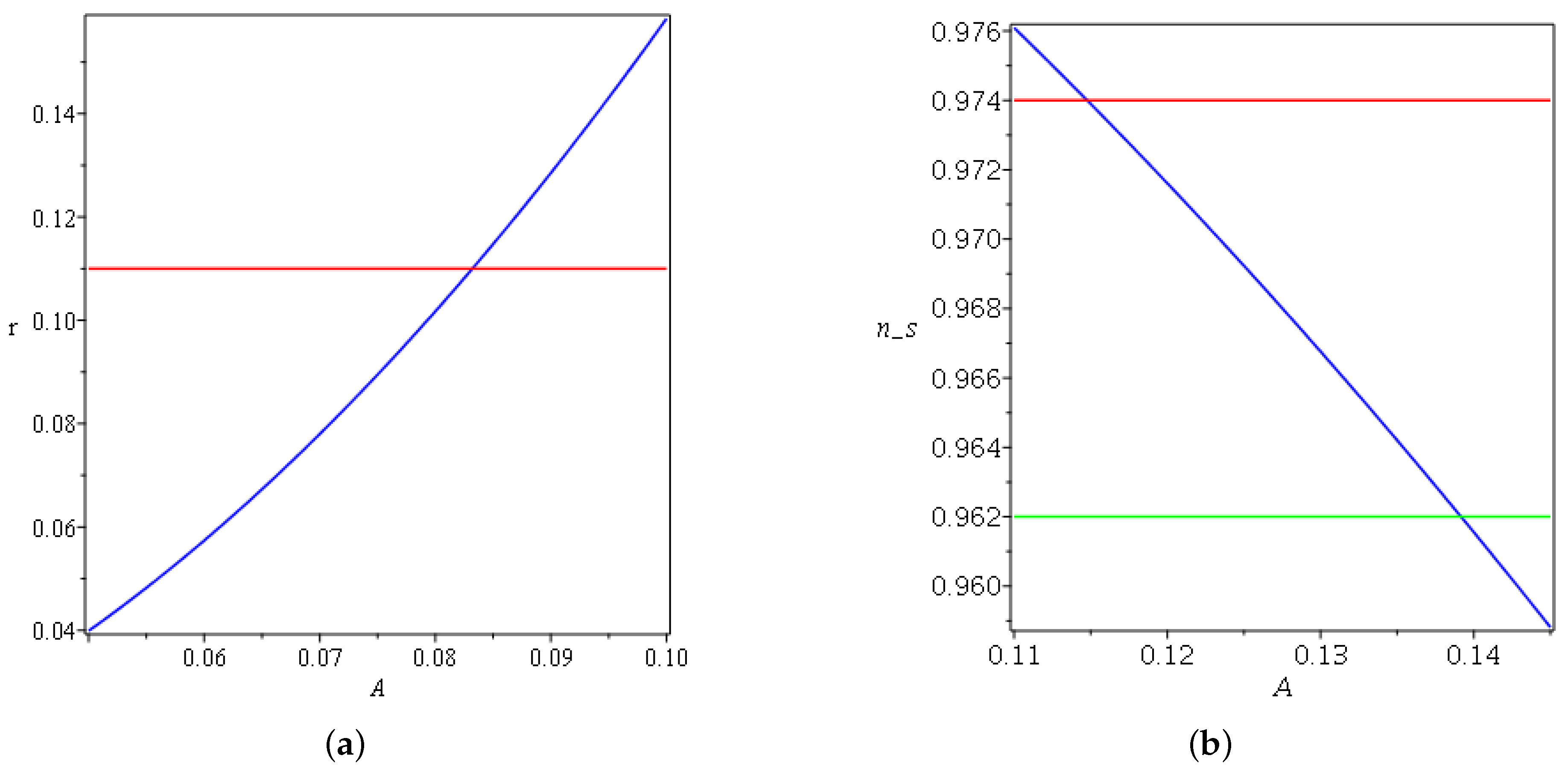
3. Exponential Expansion
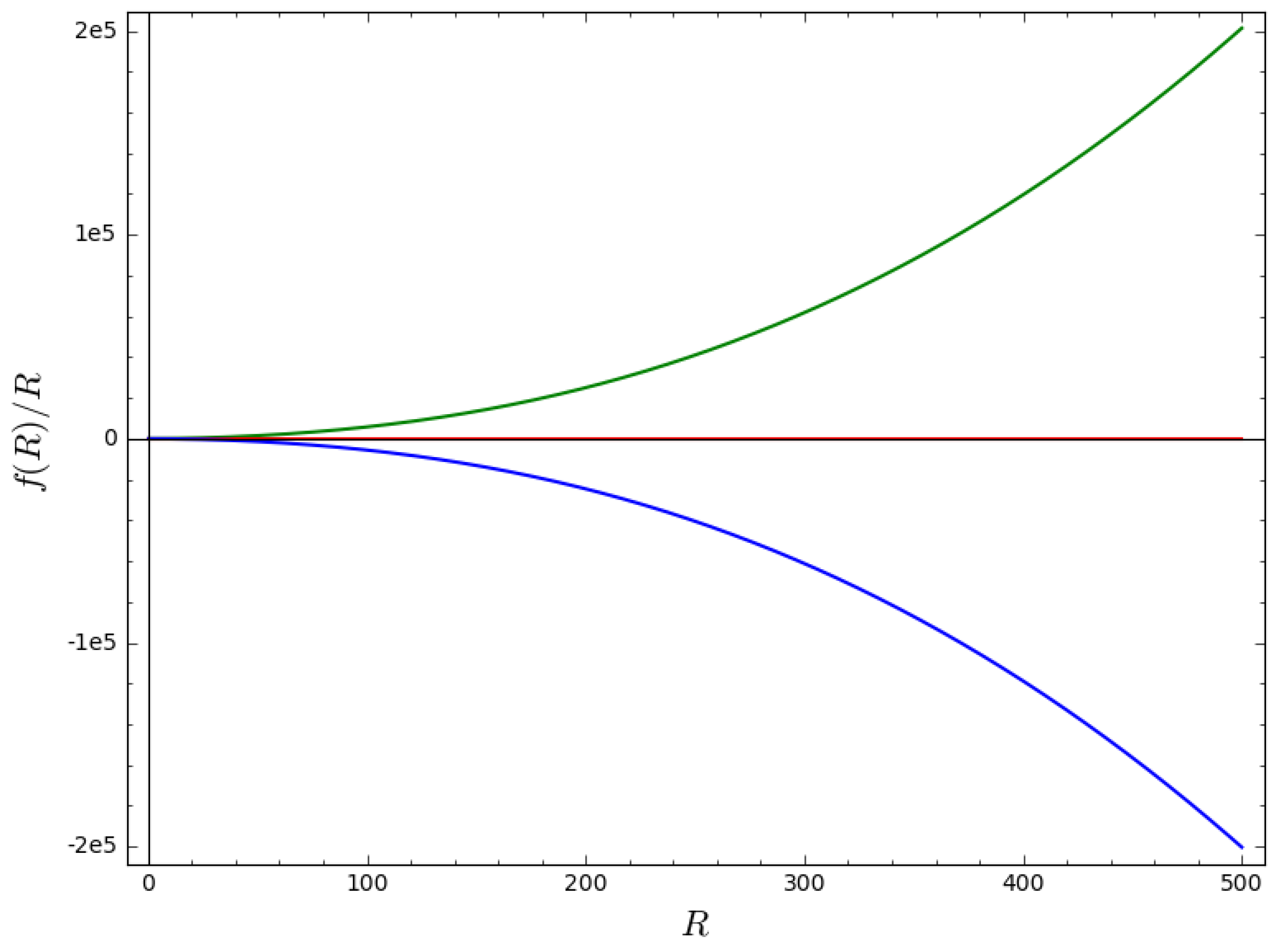
3.1. Reconstruction of for Exponential Expansion Models
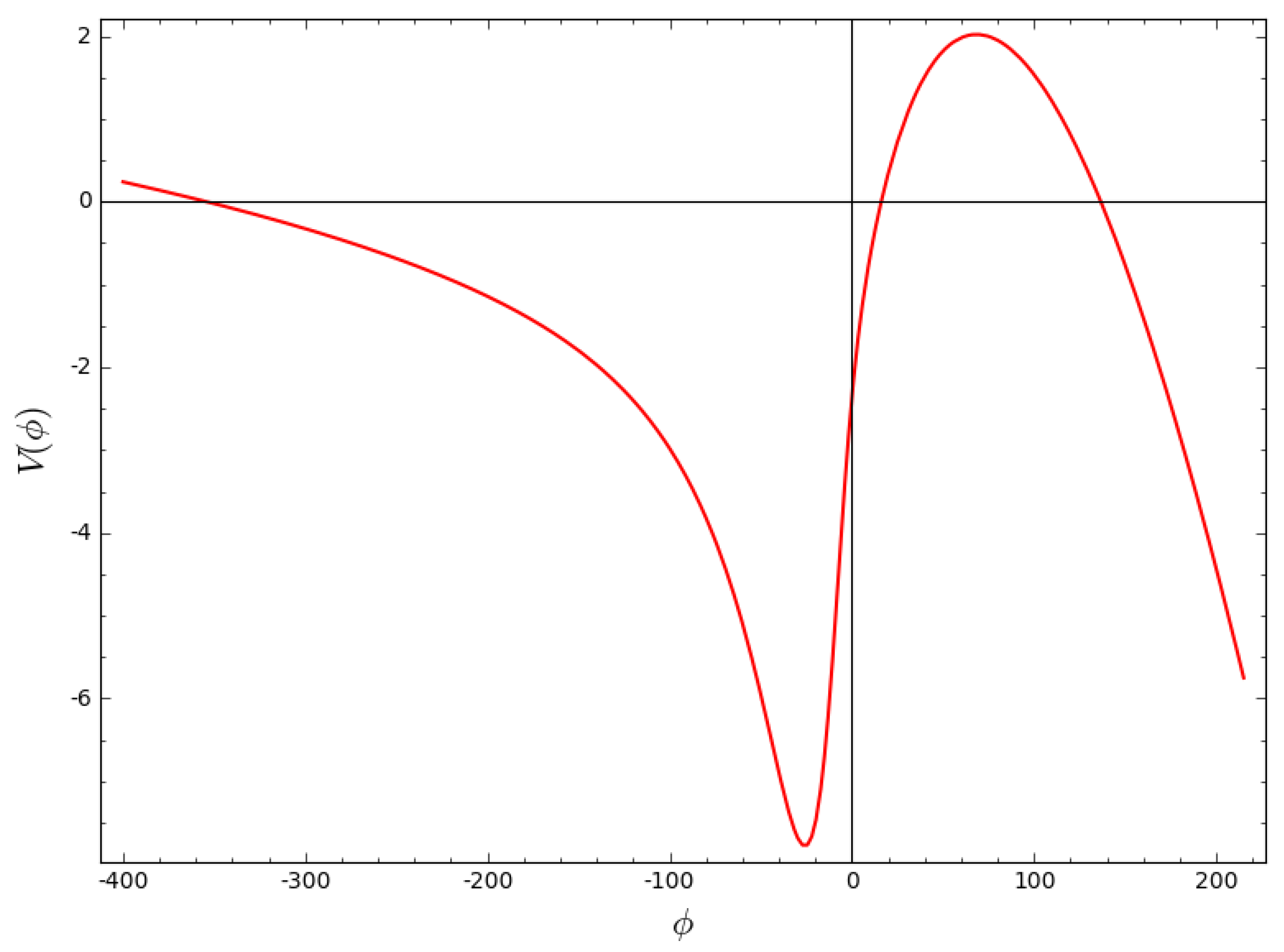
3.2. Potential for Exponential Expansion Models
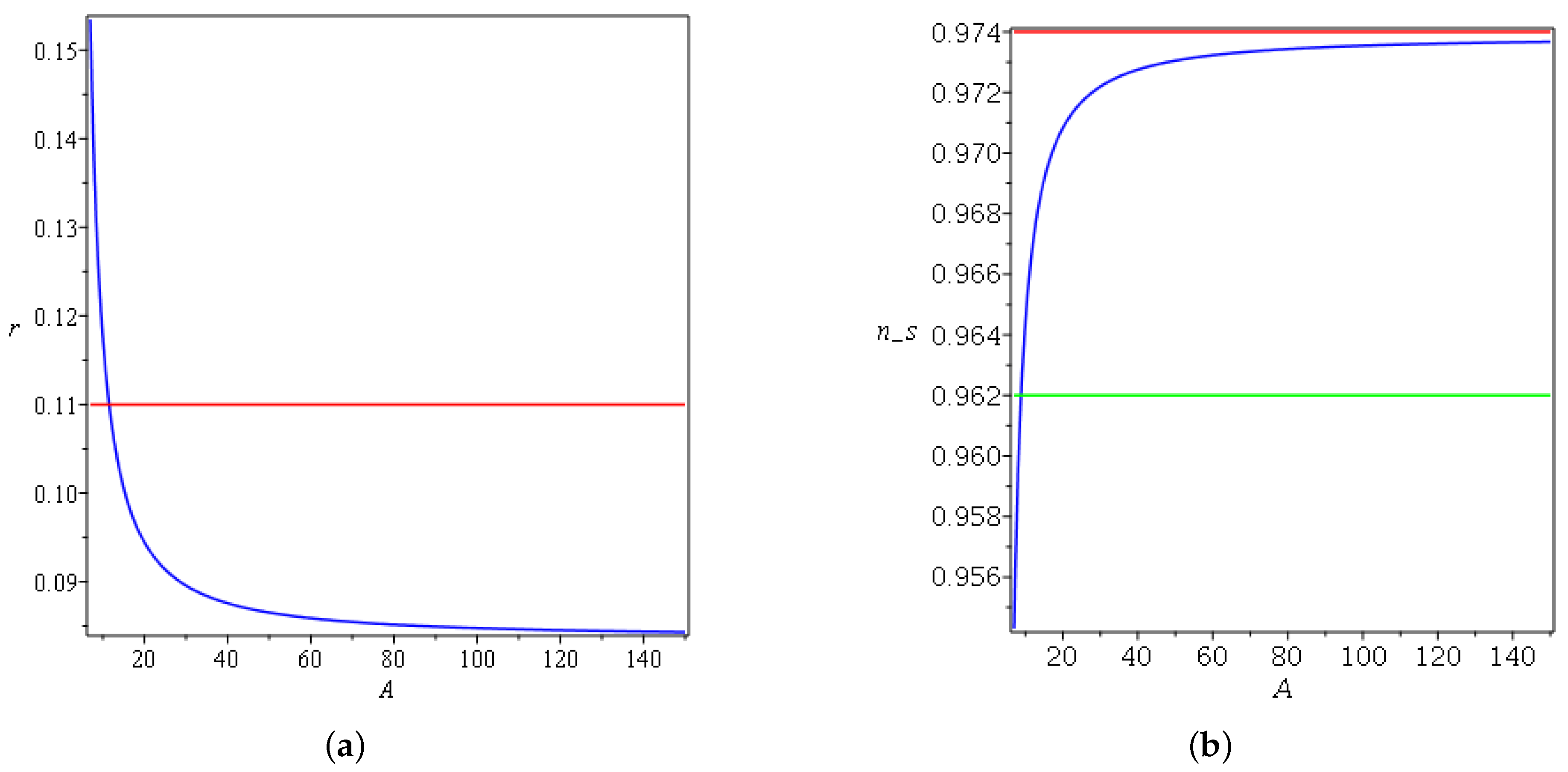
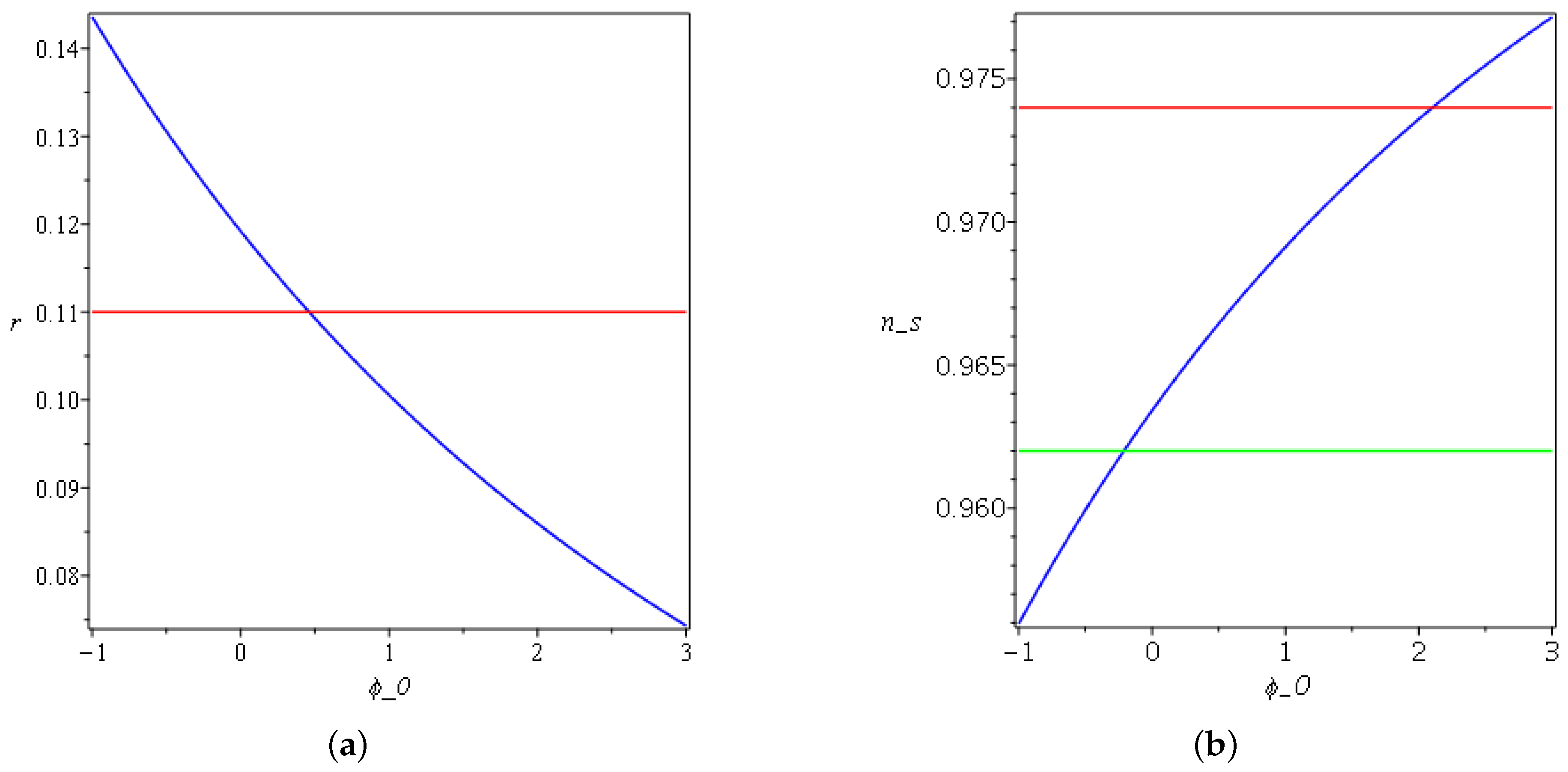
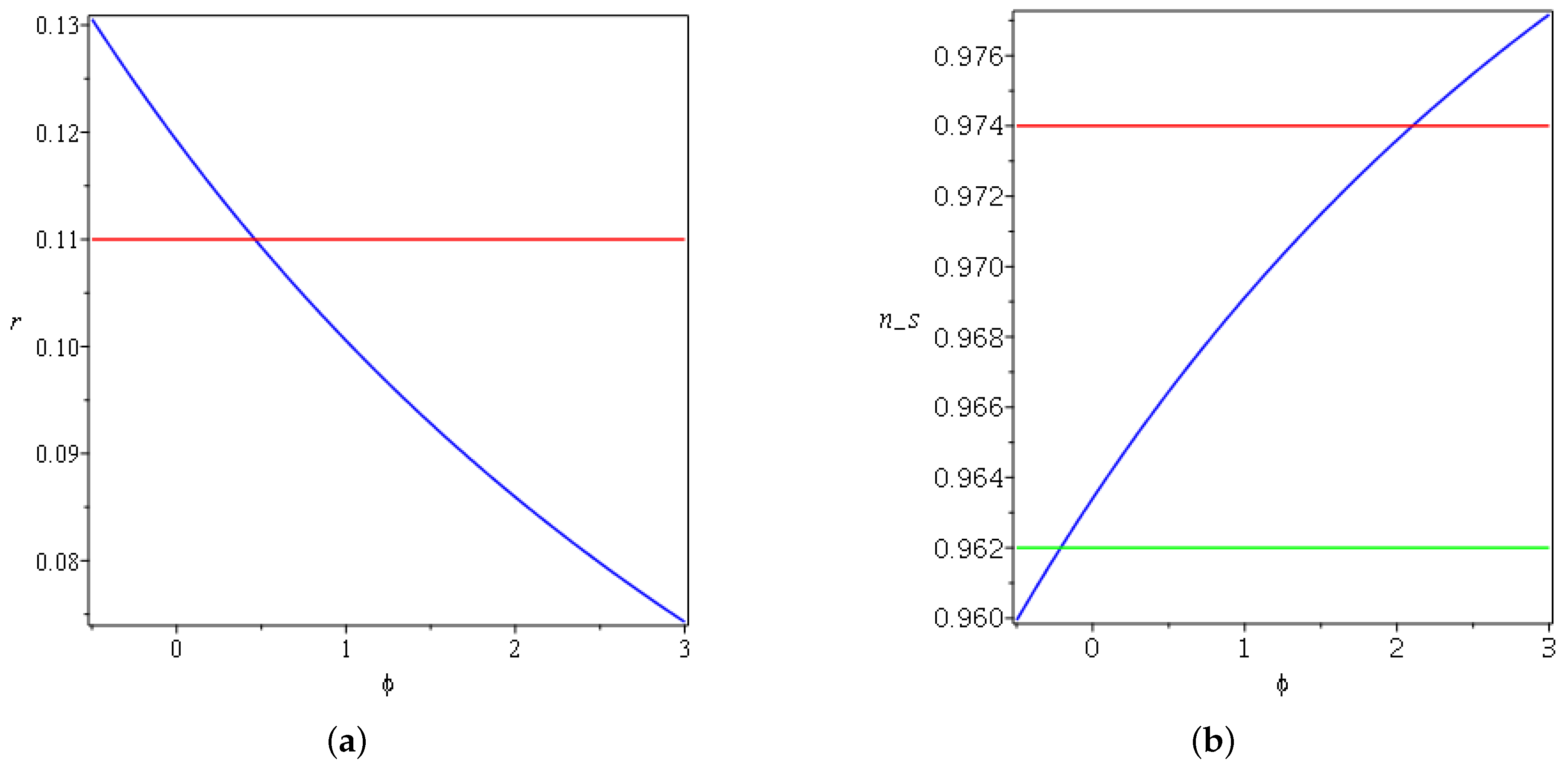
4. Linear Expansion
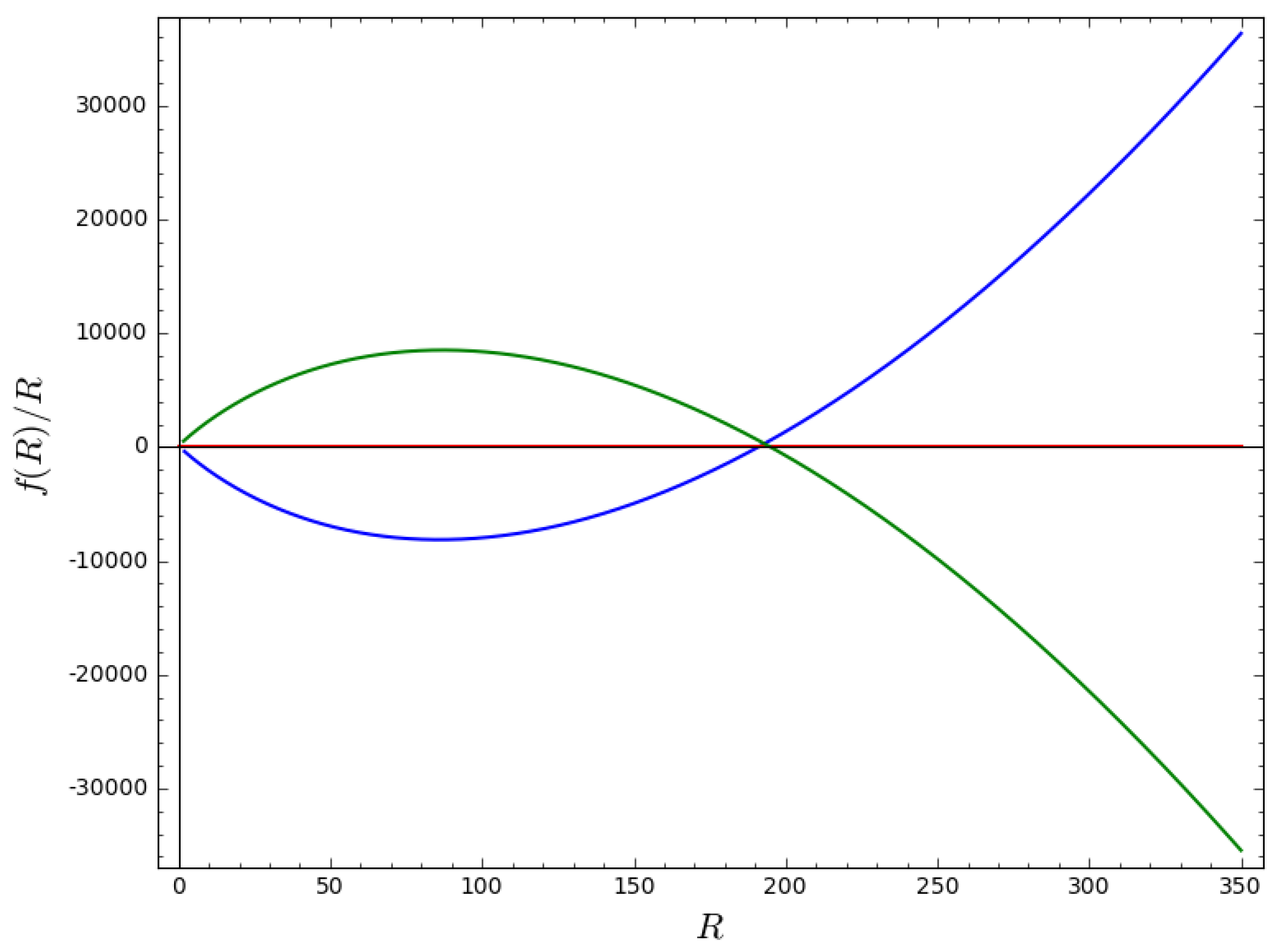
4.1. Reconstruction of for Linear Inflation Models
4.2. Potential for Linear Inflation Models
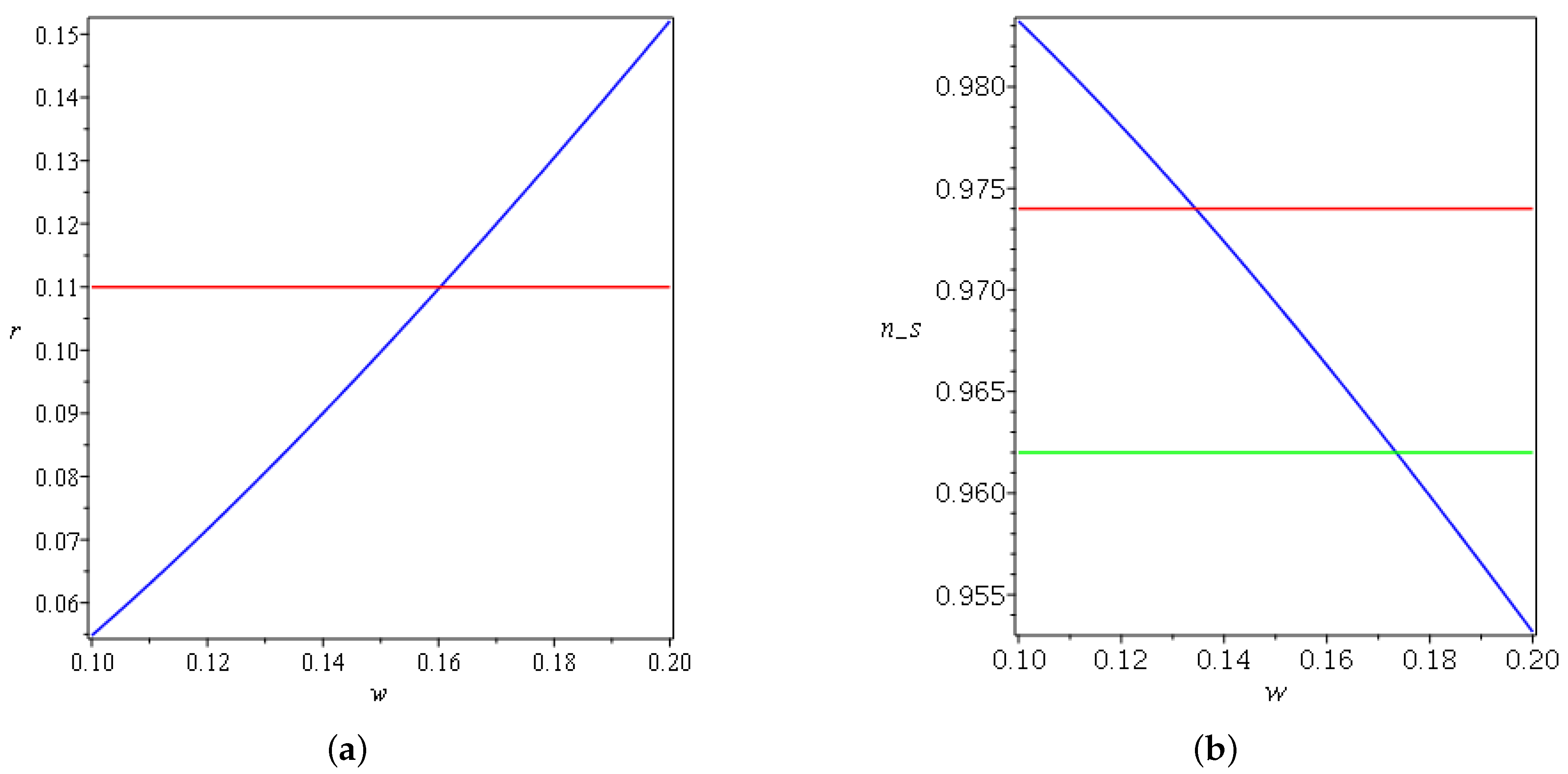
5. Application to Inflation Epoch
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar]
- Barrow, J.D.; Paliathanasis, A. Reconstructions of the dark-energy equation of state and the inflationary potential. arXiv, 2016; arXiv:1611.06680. [Google Scholar]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1–104. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of curvature: Unification of inflation and cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Unifying inflation with ΛCDM epoch in modified f (R) gravity consistent with Solar System tests. Phys. Lett. B 2007, 657, 238–245. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Future evolution and finite-time singularities in f (R) gravity unifying inflation and cosmic acceleration. Phys. Rev. D 2008, 78, 046006. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From f (R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar]
- Bamba, K.; Nojiri, S.; Odintsov, S.D.; Sáez-Gómez, D. Inflationary universe from perfect fluid and f (R) gravity and its comparison with observational data. Phys. Rev. D 2014, 90, 124061. [Google Scholar]
- Amin, M.; Khalil, S.; Salah, M. A viable logarithmic f (R) model for inflation. J. Cosmol. Astropart. Phys. 2016, 2016, 043. [Google Scholar]
- Li, B.; Barrow, J.D. Cosmology of f (R) gravity in the metric variational approach. Phys. Rev. D 2007, 75, 084010. [Google Scholar] [CrossRef]
- Chakraborty, S.; SenGupta, S. Solving higher curvature gravity theories. Eur. Phys. J. C 2016, 76, 552. [Google Scholar] [CrossRef]
- Sáez-Gómez, D. Modified f (R) gravity from scalar-tensor theory and inhomogeneous EoS dark energy. Gen. Relativ. Gravit. 2009, 41, 1527–1538. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Sáez-Gómez, D. Cosmological reconstruction of realistic modified f (R) gravities. Phys. Lett. B 2009, 681, 74–80. [Google Scholar] [CrossRef]
- Ntahompagaze, J.; Abebe, A.; Mbonye, M. On f (R) gravity in scalar-tensor theories. Int. J. Geom. Methods Mod. Phys. 2017, 14, 1750107. [Google Scholar] [CrossRef]
- Sami, H.; Namane, N.; Ntahompagaze, J.; Elmardi, M.; Abebe, A. Reconstructing f (R) Gravity from a Chaplygin Scalar Field in de Sitter Spacetimes. arXiv, 2017; arXiv:1706.07790. [Google Scholar]
- Faraoni, V. De Sitter space and the equivalence between f (R) and scalar-tensor gravity. Phys. Rev. D 2007, 75, 067302. [Google Scholar] [CrossRef]
- Paliathanasis, A. f (R)-gravity from Killing tensors. Class. Quantum Gravity 2016, 33, 075012. [Google Scholar] [CrossRef]
- Paliathanasis, A.; Tsamparlis, M.; Basilakos, S. Constraints and analytical solutions of f (R) theories of gravity using Noether symmetries. Phys. Rev. D 2011, 84, 123514. [Google Scholar] [CrossRef]
- Guth, A.H. Inflation. Proc. Natl. Acad. Sci. USA 1993, 90, 4871–4877. [Google Scholar] [CrossRef] [PubMed]
- Linde, A. Inflationary cosmology after Planck. In Post-Planck Cosmology: Lecture Notes of the Les Houches Summer School: Volume 100, July 2013; Oxford University Press: Oxford, UK, 2015; Volume 100, pp. 231–303. [Google Scholar]
- Bassett, B.A.; Tsujikawa, S.; Wands, D. Inflation dynamics and reheating. Rev. Mod. Phys. 2006, 78, 537–589. [Google Scholar] [CrossRef]
- Huang, Q.G. A polynomial f (R) inflation model. J. Cosmol. Astropart. Phys. 2014, 2014, 035. [Google Scholar] [CrossRef]
- Ellis, G.; Madsen, M. Exact scalar field cosmologies. Class. Quantum Gravity 1991, 8, 667–676. [Google Scholar] [CrossRef]
- Gorini, V.; Kamenshchik, A.; Moschella, U.; Pasquier, V. The Chaplygin Gas as a Model for Dark Energy. In Proceedings of the Tenth Marcel Grossmann Meeting, Rio de Janeiro, Brazil, 16–18 July 2003; pp. 840–859. [Google Scholar]
- Frolov, A.V. Singularity problem with f (R) models for dark energy. Phys. Rev. Lett. 2008, 101, 061103. [Google Scholar] [CrossRef] [PubMed]
- Liddle, A.R.; Parsons, P.; Barrow, J.D. Formalizing the slow-roll approximation in inflation. Phys. Rev. D 1994, 50, 7222–7232. [Google Scholar] [CrossRef]
- Liddle, A.R.; Lyth, D.H. COBE, gravitational waves, inflation and extended inflation. Phys. Lett. B 1992, 291, 391–398. [Google Scholar] [CrossRef]
- Ade, P.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.; Barreiro, R.; et al. Planck 2015 results-XX. Constraints on inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sami, H.; Ntahompagaze, J.; Abebe, A. Inflationary f (R) Cosmologies. Universe 2017, 3, 73. https://doi.org/10.3390/universe3040073
Sami H, Ntahompagaze J, Abebe A. Inflationary f (R) Cosmologies. Universe. 2017; 3(4):73. https://doi.org/10.3390/universe3040073
Chicago/Turabian StyleSami, Heba, Joseph Ntahompagaze, and Amare Abebe. 2017. "Inflationary f (R) Cosmologies" Universe 3, no. 4: 73. https://doi.org/10.3390/universe3040073
APA StyleSami, H., Ntahompagaze, J., & Abebe, A. (2017). Inflationary f (R) Cosmologies. Universe, 3(4), 73. https://doi.org/10.3390/universe3040073




