Dark Energy, QCD Axion, and Trans-Planckian-Inflaton Decay Constant
Abstract
1. Introduction
2. On Global Symmetries
2.1. The ’t Hooft Mechanism
2.2. Breaking Scales
3. The “Invisible” Axion
3.1. Axion Inhomogeneities in Galaxies and Mini-Clusters
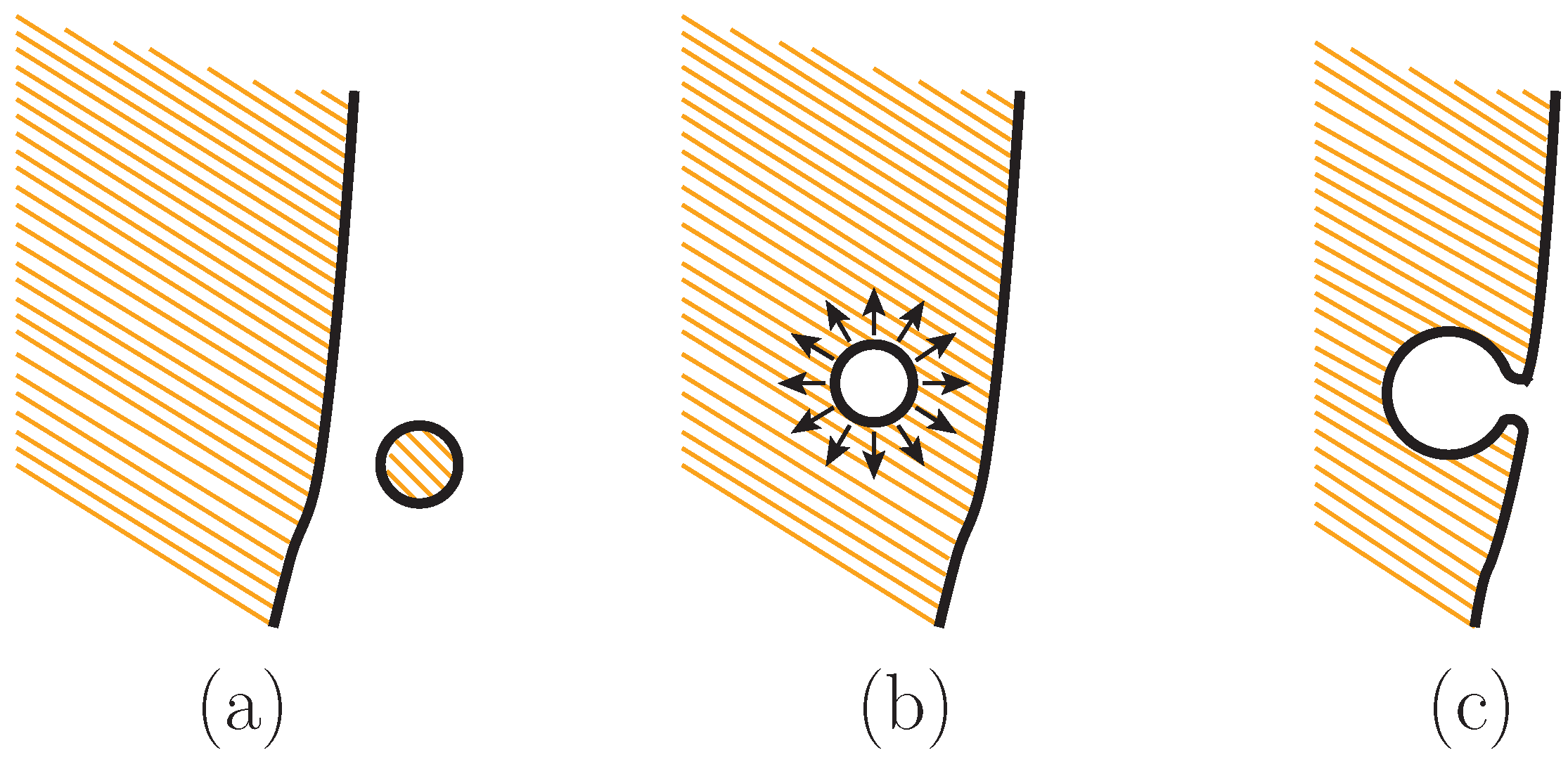
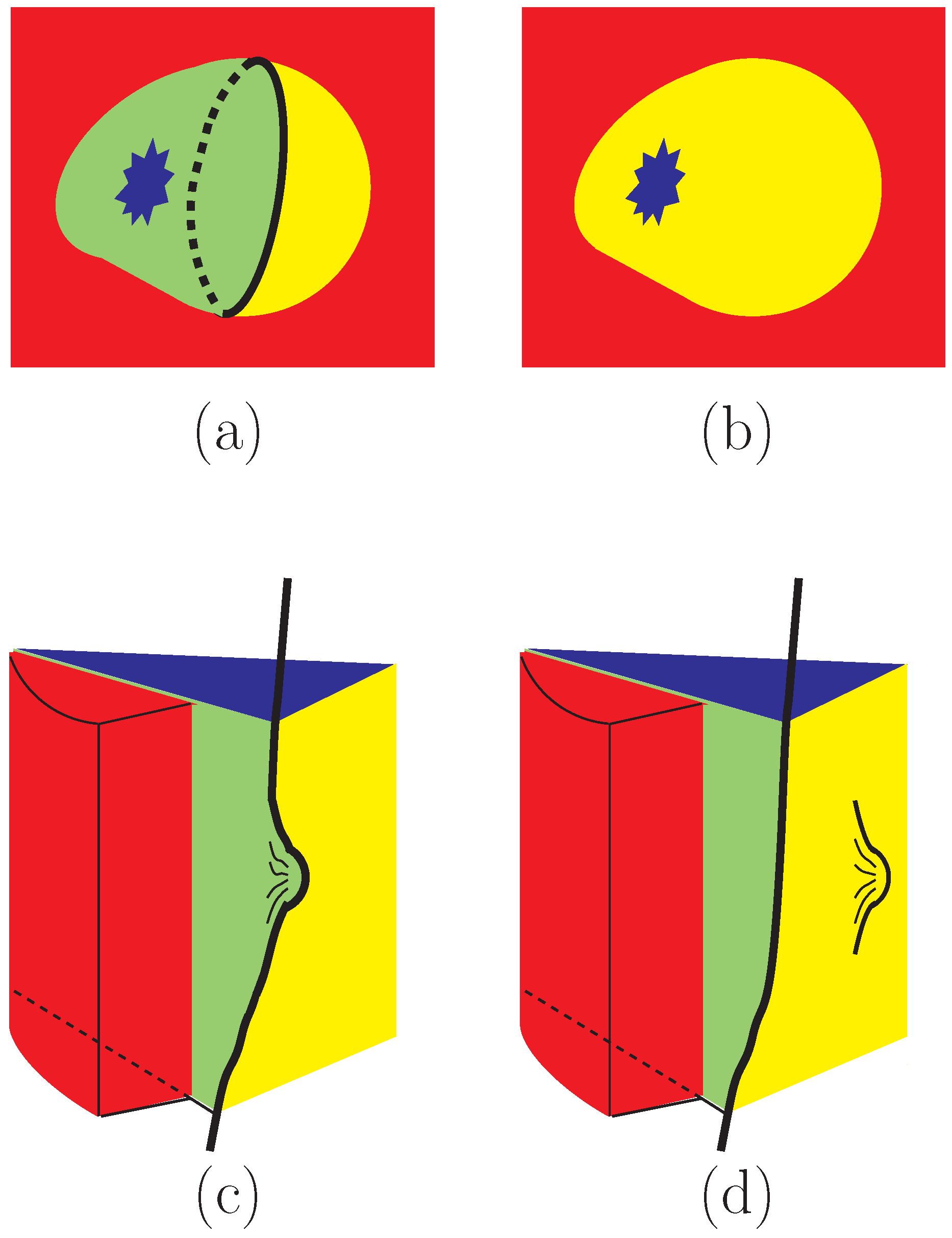
3.2. The Domain Wall Problem in “Invisible” Axion Models
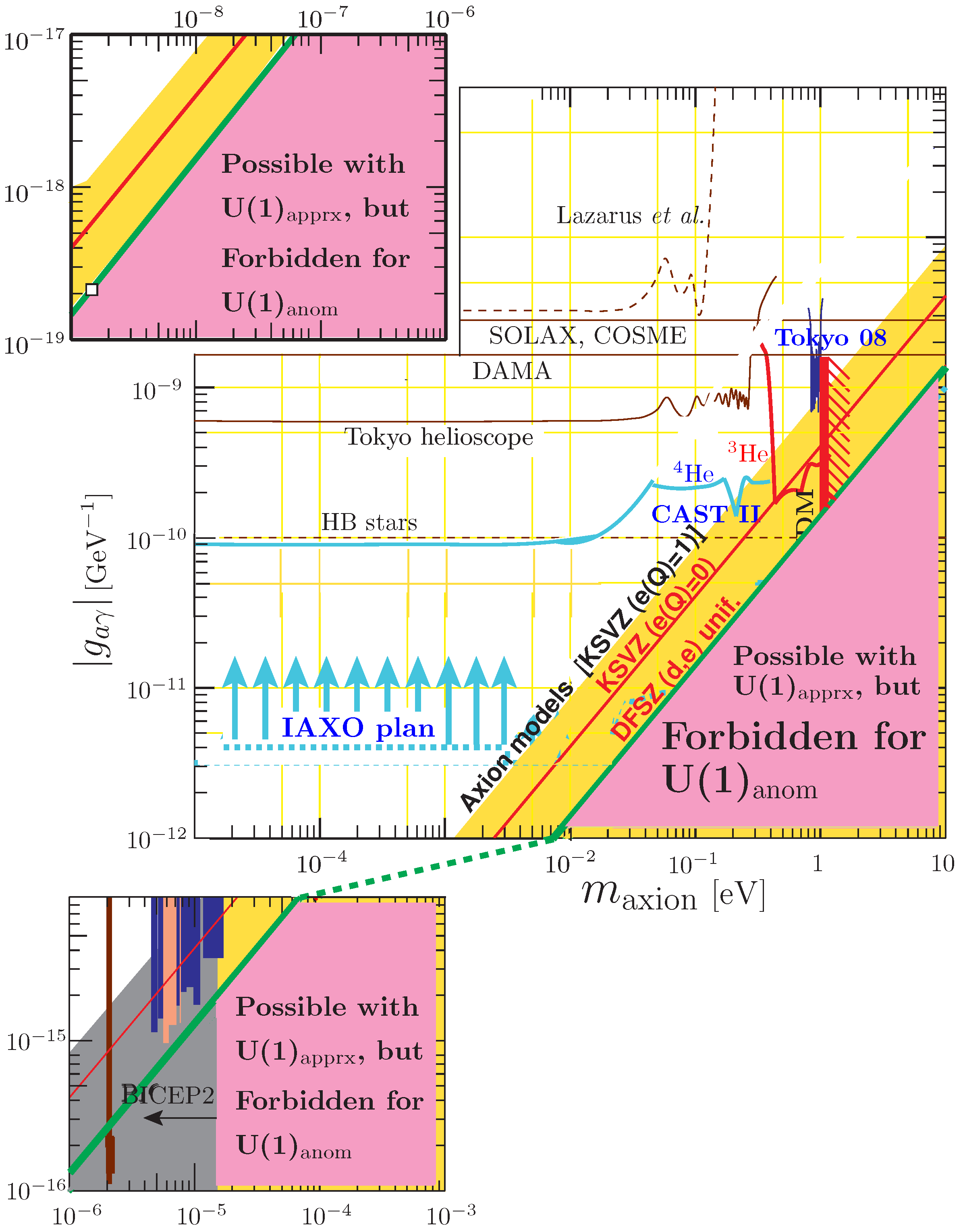
3.3. Searches of “Invisible” Axions
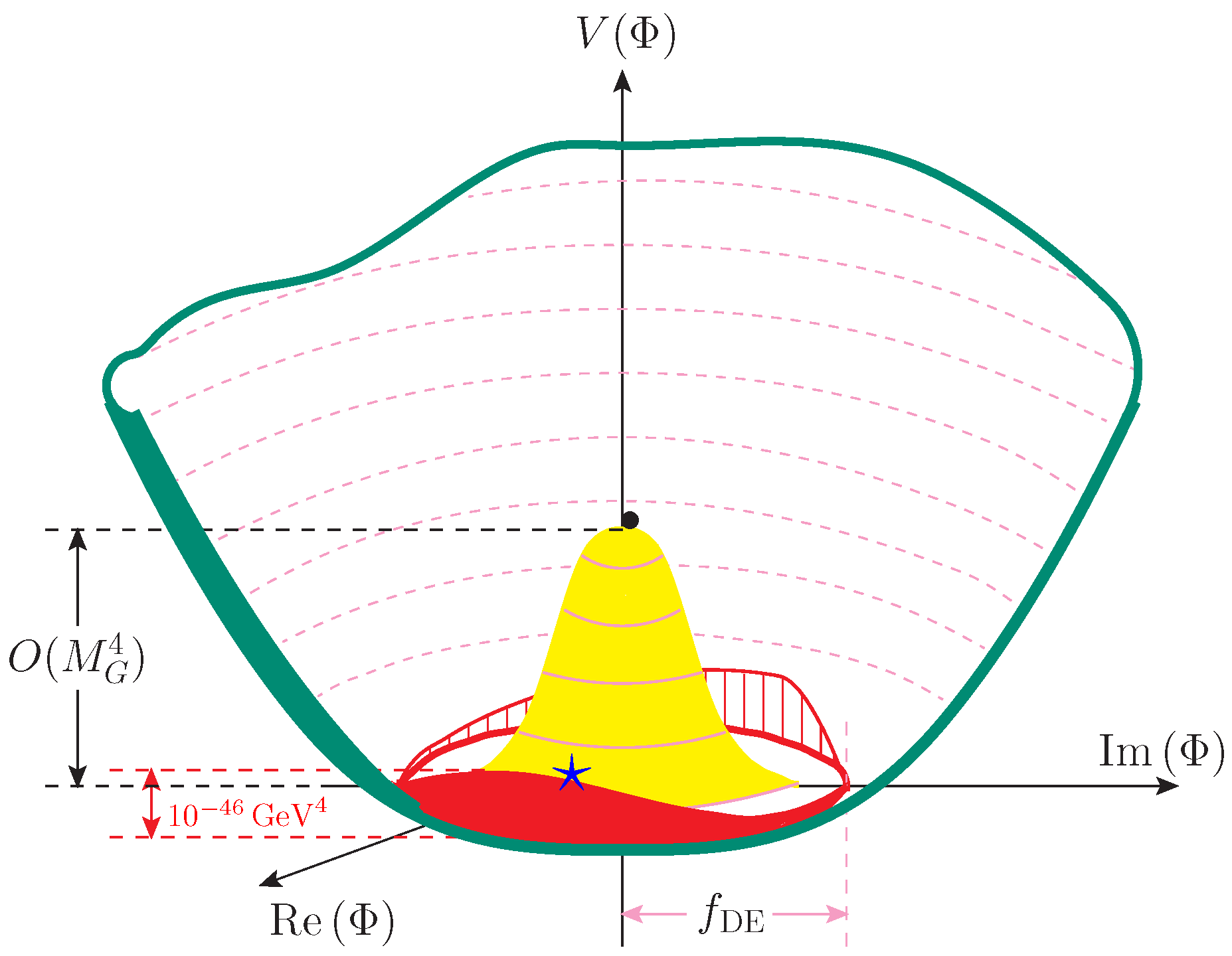
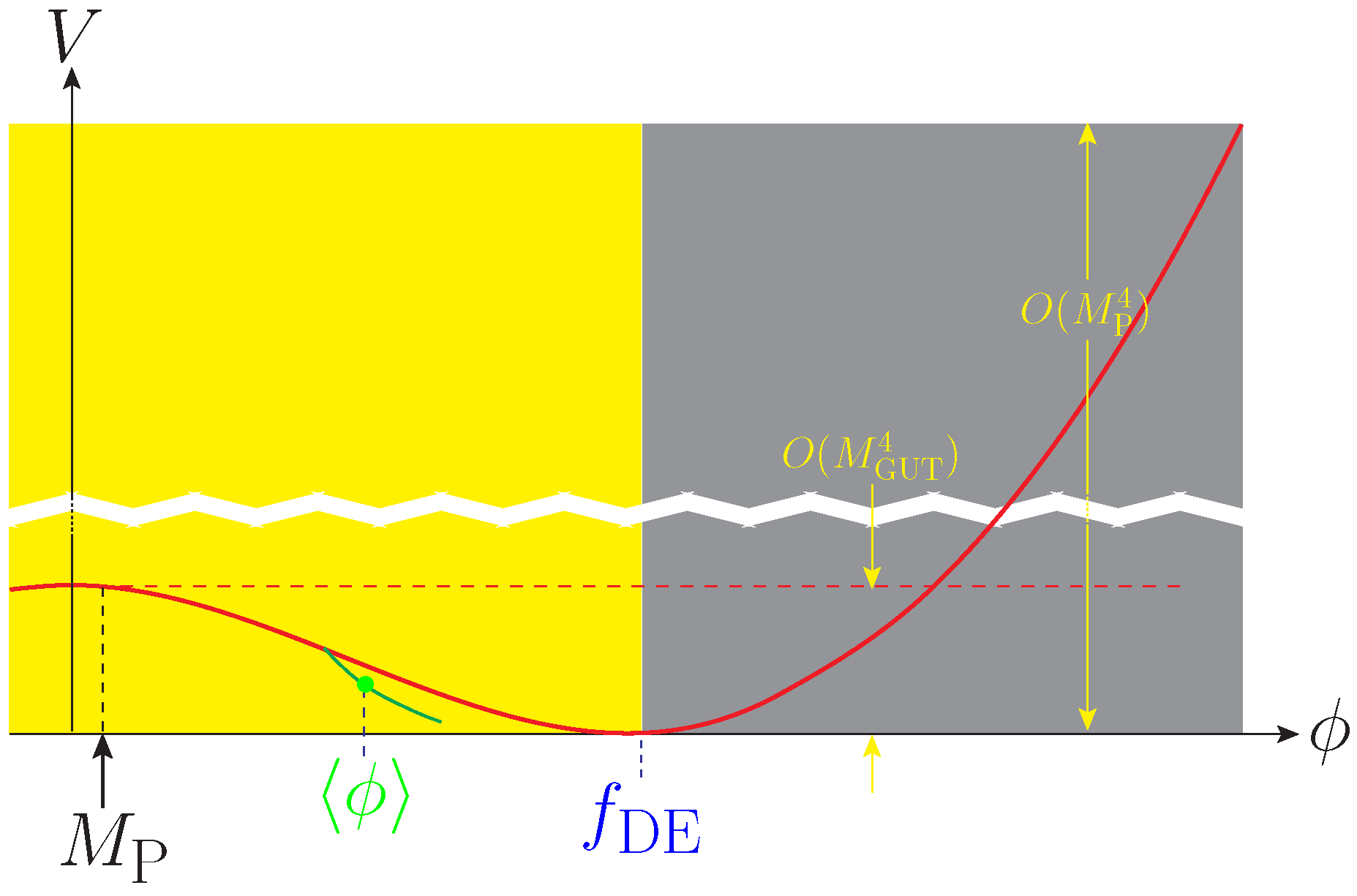
4. A BCM as Dark Energy
5. Inflation and Gravity Waves in the Beginning
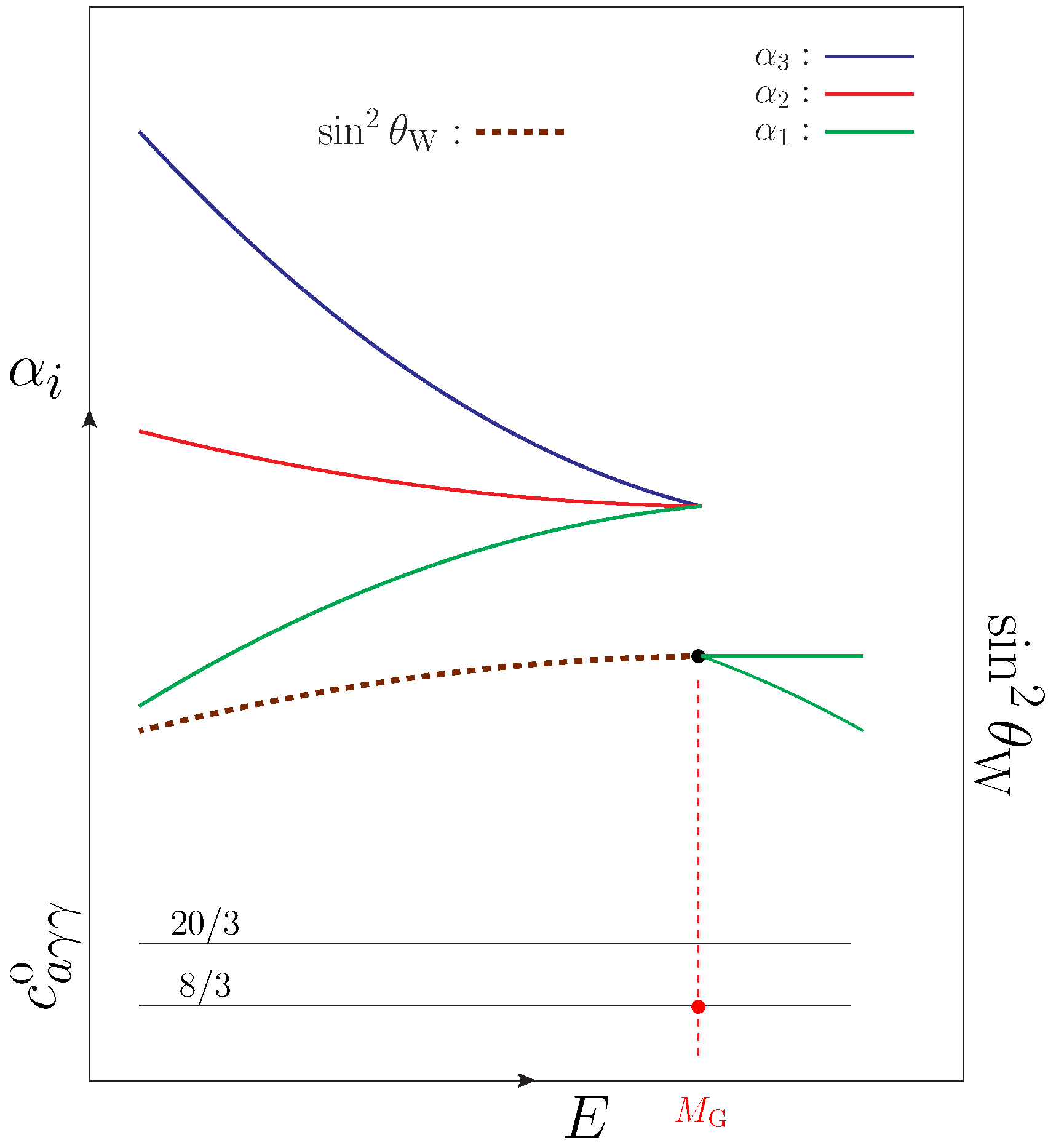
6. Global Symmetries and Non-Abelian Gauge Groups
7. Discussion and Conclusions
Acknowledgments
Conflicts of Interest
References
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Kim, J.E.; Semertzidis, Y.; Tsujikawa, S. Bosonic coherent motions in the Universe. Front. Phys. 2014, 2, 60. [Google Scholar] [CrossRef]
- Del Popolo, A. Non-baryonic dark matter in cosmology. Int. J. Mod. Phys. D 2014, 23, 1430005. [Google Scholar] [CrossRef]
- Blumenthal, G.R.; Faber, S.M.; Primack, J.R.; Rees, M.J. Formation of galaxies and large scale structure with cold dark matter. Nature 1984, 311, 517–525. [Google Scholar] [CrossRef]
- Zwicky, F. Die Rotverschiebung von extragalaktischen Nebeln. Helv. Phys. Acta 1933, 6, 110–127. [Google Scholar] [CrossRef]
- Trimble, V. Existence and nature of dark matter in the Universe. Ann. Rev. Astron. Astrophys. 1987, 25, 425–472. [Google Scholar] [CrossRef]
- Hut, P. Limits on masses and number of neutral weakly interacting particles. Phys. Lett. B 1977, 69, 85–88. [Google Scholar] [CrossRef]
- Lee, B.W.; Weinberg, S. Cosmological lower bound on heavy neutrino masses. Phys. Rev. Lett. 1977, 39, 165–168. [Google Scholar] [CrossRef]
- Goldberg, H. Constraint on the photino mass from cosmology. Phys. Rev. Lett. 1983, 50, 1419–1422. [Google Scholar] [CrossRef]
- Preskill, J.; Wise, M.B.; Wilczek, F. Cosmology of the invisible axion. Phys. Lett. B 1983, 120, 127–132. [Google Scholar] [CrossRef]
- Abbott, L.F.; Sikivie, P. A cosmological bound on the invisible axion. Phys. Lett. B 1983, 120, 133–136. [Google Scholar] [CrossRef]
- Dine, M.; Fischler, W. The not so harmless axion. Phys. Lett. B 1983, 120, 137–141. [Google Scholar] [CrossRef]
- Kim, J.E. Weak interaction singlet and strong CP invariance. Phys. Rev. Lett. 1979, 43, 103–107. [Google Scholar] [CrossRef]
- Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. Can confinement ensure natural CP invariance of strong interactions? Nucl. Phys. B 1980, 166, 493–506. [Google Scholar] [CrossRef]
- Zhitnitskij, A.R. On possible suppression of the axion hadron interactions. Yad. Fiz. 1980, 31, 497–504. (In Russian) [Google Scholar]
- Dine, M.; Fischler, W.; Srednicki, M. A simple solution to the strong CP problem with a harmless axion. Phys. Lett. B 1981, 104, 199–202. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating Universe and a cosmological constant. Astrophys. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Hook, I.M. Measurements of Omega and Lambda from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Einstein, A. Cosmological considerations in the general theory of relativity. Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.) 1917, 1917, 142–152. [Google Scholar]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1. [Google Scholar] [CrossRef]
- Veltman, M. Cosmology and the Higgs mechanism. Phys. Rev. Lett. 1975, 34, 777. [Google Scholar] [CrossRef]
- Lemaître, G. Contributions to a British Association Discussion on the Evolution of the Universe. Nature 1931, 128, 704–706. [Google Scholar] [CrossRef]
- Guth, A.H. The inflationary Universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Kim, J.E.; Nilles, H.P. Dark energy from approximate U(1)de symmetry. Phys. Lett. B 2014, 730, 53–58. [Google Scholar] [CrossRef]
- Kim, J.E. Modeling the small dark energy scale with a quintessential pseudoscalar boson. J. Korean Phys. Soc. 2014, 64, 795–805. [Google Scholar] [CrossRef]
- Freese, K.; Frieman, J.A.; Olinto, A.V. Natural inflation with pseudo Nambu–Goldstone bosons. Phys. Rev. Lett. 1990, 65, 3233–3236. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.E.; Nilles, H.P.; Peloso, M. Completing natural inflation. J. Cosmol. Astropart. Phys. 2005, 1, 61–70. [Google Scholar] [CrossRef]
- Silveira, V.; Zee, A. Scalar phantoms. Phys. Lett. B 1985, 161, 136–140. [Google Scholar] [CrossRef]
- Patt, B.; Wilczek, F. Higgs-field portal into hidden sectors. arXiv, 2006; arXiv:hep-ph/0605188. [Google Scholar]
- Schabinger, R.; Wells, J.D. Minimal spontaneously broken hidden sector and its impact on Higgs boson physics at the large hadron collider. Phys. Rev. D 2005, 72, 093007. [Google Scholar] [CrossRef]
- Giddings, S.B.; Strominger, A. Axion induced topology change in quantum gravity and string theory. Nucl. Phys. B 1988, 306, 890–907. [Google Scholar] [CrossRef]
- Gilbert, G. Wormhole induced proton decay. Nucl. Phys. B 1989, 328, 159–170. [Google Scholar] [CrossRef]
- Krauss, L.M.; Wilczek, F. Discrete gauge symmetry in continuum theories. Phys. Rev. Lett. 1989, 62, 1221–1223. [Google Scholar] [CrossRef] [PubMed]
- Ibanez, L.E.; Ross, G.G. Discrete gauge symmetries and the origin of baryon and lepton number conservation in supersymmetric versions of the standard model. Nucl. Phys. B 1992, 368, 3–37. [Google Scholar] [CrossRef]
- Banks, T.; Dine, M. Note on discrete gauge anomalies. Phys. Rev. D 1992, 45, 1424–1427. [Google Scholar] [CrossRef]
- Preskill, J.; Trivedi, S.P.; Wilczek, F.; Wise, M.B. Cosmology and broken discrete symmetry. Nucl. Phys. B 1991, 363, 207–220. [Google Scholar] [CrossRef]
- Kim, J.E. Abelian discrete symmetries ZN and ZnR from string orbifolds. Phys. Lett. B 2013, 726, 450–455. [Google Scholar] [CrossRef]
- Choi, K.S.; Kim, J.E.; Kyae, B.; Nam, S. Hairs of discrete symmetries and gravity. Phys. Lett. B 2017, 769, 430–435. [Google Scholar] [CrossRef]
- ’t Hooft, G. Renormalizable Lagrangians for massive Yang-Mills fields. Nucl. Phys. B 1971, 35, 167–188. [Google Scholar] [CrossRef]
- Kim, J.E. The strong CP problem in orbifold compactifications and an SU(3)×SU(2)×U(1)n model. Phys. Lett. B 1988, 207, 434–440. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP conservation in the presence of pseudoparticles. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Bethke, S.; Dissertori, G.; Salam, G.P. Quantum Chromodynamics. In Review of Particle Physics; IOP Publishing: Beijing, China, 2016; Volume 40, pp. 132–150. [Google Scholar]
- di Cortona, G.G.; Hardy, E.; Vega, J.P.; Villadoro, G. The QCD axion, precisely. J. High Energy Phys. 2016, 2016, 34. [Google Scholar] [CrossRef]
- Gondolo, P.; Visinelli, L. Axion cold dark matter in view of BICEP2 results. Phys. Rev. Lett. 2014, 113, 011802. [Google Scholar] [CrossRef] [PubMed]
- Dimopoulos, S.; Kachru, S.; McGreevy, J.; Wacker, J.G. N-flation. J. Cosmol. Astropart. Phys. 2008, 2008, 003. [Google Scholar] [CrossRef]
- Ringwald, A.; Rosenberg, L.J.; Rybka, G. Axions and other similar particles. In Review of Particle Physics; IOP Publishing: Beijing, China, 2016; Volume 40, pp. 686–714. [Google Scholar]
- Carroll, S.M. Quintessence and the rest of the world. Phys. Rev. Lett. 1998, 81, 3067–3070. [Google Scholar] [CrossRef]
- Kim, J.E.; Marsh, D.J. An ultralight pseudoscalar boson. Phys. Rev. D 2016, 93, 025027. [Google Scholar] [CrossRef]
- Marsh, D.J. Axion cosmology. Phys. Rep. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Hui, L.; Ostriker, J.P.; Tremaine, S.; Witten, E. Ultralight scalars as cosmological dark matter. Phys. Rev. D 2017, 95, 043541. [Google Scholar] [CrossRef]
- Wilczek, F. Axions and family symmetry breaking. Phys. Rev. Lett. 1982, 49, 1549–1552. [Google Scholar] [CrossRef]
- Reiss, D.B. Can the family group be a global symmetry? Phys. Lett. B 1982, 115, 217–220. [Google Scholar] [CrossRef]
- Gelmini, G.B.; Nussinov, S.; Yanagida, T. Does nature like Nambu-Goldstone bosons? Nucl. Phys. B 1983, 219, 31–40. [Google Scholar] [CrossRef]
- Berezhiani, Z.G.; Khlopov, M.Y. Cosmology of spontaneously broken gauge family symmetry with axion solution of the strong CP problem. Z. Phys. C Part. Fields 1991, 49, 73–78. [Google Scholar] [CrossRef]
- Baker, C.A.; Doyle, D.D.; Geltenbort, P.; Green, K.; Van der Grinten, M.G.D.; Harris, P.G.; Richardson, J.D. Improved experimental limit on the electric dipole moment of the neutron. Phys. Rev. Lett. 2006, 97, 131801. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, M.; Maskawa, T. CP violation in the renormalizable theory of weak interaction. Prog. Theor. Phys. 1973, 49, 652–657. [Google Scholar] [CrossRef]
- Weinberg, S. Gauge theory of CP violation. Phys. Rev. Lett. 1976, 37, 657–661. [Google Scholar] [CrossRef]
- Mohapatra, R.N. Renormalizable model of weak and electromagnetic interactions with CP violation. Phys. Rev. D 1972, 6, 2023. [Google Scholar] [CrossRef]
- Glashow, S.L.; Weinberg, S. Natural conservation laws for neutral currents. Phys. Rev. D 1977, 15, 1958. [Google Scholar] [CrossRef]
- Weinberg, S. A new light boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of strong P and T invariance in the presence of instantons. Phys. Rev. Lett. 1978, 40, 279–282. [Google Scholar] [CrossRef]
- Kim, J.E. Light pseudoscalars, particle physics and cosmology. Phys. Rep. 1987, 150, 1–177. [Google Scholar] [CrossRef]
- Peccei, R.D. A Short Review of Axions. In Proceedings of the 19th International Conference on High Energy Physics, Tokyo, Japan, 23–30 August 1978. [Google Scholar]
- Bég, M.A.B.; Tsao, H.S. Strong P and T noninvariances in a superweak theory. Phys. Rev. Lett. 1978, 41, 278–281. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Senjanović, G. Natural suppression of strong P and T noninvariance. Phys. Lett. B 1978, 79, 283–286. [Google Scholar] [CrossRef]
- Segrè, G.; Weldon, H.A. Natural suppression of strong P and T violations and calculable mixing angles in SU(2)×U(1). Phys. Rev. Lett. 1979, 42, 1191. [Google Scholar] [CrossRef]
- Barr, S.; Langacker, P. A superweak gauge theory of CP-invariance violation. Phys. Rev. Lett. 1979, 42, 1654–1658. [Google Scholar] [CrossRef]
- Georgi, H. A model of soft CP violation. Hadronic J. 1978, 1, 155. [Google Scholar]
- Nelson, A. Naturally weak CP violation. Phys. Lett. B 1984, 136, 387–391. [Google Scholar] [CrossRef]
- Barr, S.M. Solving the strong CP problem without the Peccei-Quinn symmetry. Phys. Rev. Lett. 1984, 53, 329–332. [Google Scholar] [CrossRef]
- Lee, T.D. A theory of spontaneous T violation. Phys. Rev. D 1973, 8, 1226–1239. [Google Scholar] [CrossRef]
- Gershon, T.; Nir, Y. CP violation in the quark sector. In Review of Particle Physics; IOP Publishing: Beijing, China, 2016; Volume 40, pp. 233–245. [Google Scholar]
- Vafa, C.; Witten, E. Parity conservation in QCD. Phys. Rev. Lett. 1984, 53, 535–536. [Google Scholar] [CrossRef]
- Georgi, H.; Randall, L. Flavor conserving CP violation in invisible axion models. Nucl. Phys. B 1986, 276, 241–252. [Google Scholar] [CrossRef]
- Hiramatsu, T.; Kawasaki, M.; Saikawa, K.I.; Sekiguchi, T. Axion cosmology with long-lived domain walls. J. Cosmol. Astropart. Phys. 2013, 2013, 001. [Google Scholar] [CrossRef]
- Bae, K.J.; Huh, J.H.; Kim, J.E. Update of axion CDM energy. arXiv, 2008; arXiv:1704.07542[hep-ph]. [Google Scholar]
- Raffelt, G.G. Astrophysical axion bounds. In Axions; Springer: Berlin/Heidelberg, Germany, 2008; pp. 51–71. [Google Scholar] [CrossRef]
- Berezhiani, Z.G.; Sakharov, A.S.; Khlopov, M.Y. Primordial background of cosmological axions. Sov. J. Nucl. Phys. 1992, 55, 1063–1071. [Google Scholar]
- Kim, J.E.; Carosi, G. Axions and the strong CP problem. Rev. Mod. Phys. 2010, 82, 557–602. [Google Scholar] [CrossRef]
- Kim, J.E. Constraints on very light axions from cavity experiments. Phys. Rev. D 1998, 58, 055006. [Google Scholar] [CrossRef]
- Adler, S.L.; Bardeen, W.A. Absence of higher order corrections in the anomalous axial vector divergence equation. Phys. Rev. 1969, 182, 1517–1536. [Google Scholar] [CrossRef]
- Primakoff, H. Photo-production of neutral mesons in nuclear electric fields and the mean life of the neutral meson. Phys. Rev. 1951, 81, 899. [Google Scholar] [CrossRef]
- Sikivie, P. Experimental tests of the ‘invisible’ axion. Phys. Rev. Lett. 1984, 52, 695. [Google Scholar] [CrossRef]
- Hong, J.; Kim, J.E.; Nam, S.; Semertzidis, Y. Calculations of resonance enhancement factor in axion-search tube-experiments. arXiv, 2017; arXiv:1403.1576[hep-ph]. [Google Scholar]
- Sikivie, P. Detection rates for ‘invisible’ axion searches. Phys. Lett. D 1985, 32, 2988–2991. [Google Scholar] [CrossRef]
- Krauss, L.; Moody, J.; Wilczek, F.; Morris, D.E. Calculations for cosmic axion detection. Phys. Rev. Lett. 1985, 55, 1797–1880. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.E. A model of flavor unity. Phys. Rev. Lett. 1980, 45, 1916–1919. [Google Scholar] [CrossRef]
- Kim, J.E. Calculation of axion-photon-photon coupling in string theory. Phys. Lett. B 2014, 735, 95–100. [Google Scholar] [CrossRef]
- Kim, J.E.; Kyae, B.; Nam, S. The anomalous U(1) global symmetry and flavors from an SU(5)×SU(5)’ GUT in Z12-I orbifold compactification. arXiv, 2017; arXiv:1703.05345[hep-ph]. [Google Scholar]
- Choi, K.S.; Kim, I.W.; Kim, J.E. String compactification, QCD axion and axion-photon-photon coupling. J. High Energy Phys. 2007, 2007, 116. [Google Scholar] [CrossRef]
- Kim, J.E.; Nam, S. Couplings between QCD axion and photon from string compactification. Phys. Lett. B 2016, 759, 149–153. [Google Scholar] [CrossRef]
- Huh, J.H.; Kim, J.E.; Kyae, B. SU(5)×SU(5)’ from Z12-I. Phys. Lett. D 2009, 80, 115012. [Google Scholar]
- Sakharov, A.S.; Khlopov, M.Y. The nonhomogeneity problem for the primordial axion field. Phys. Atom. Nucl. 1994, 57, 485–487. [Google Scholar]
- Kolb, E.W.; Tkachev, I.I. Axion miniclusters and Bose stars. Phys. Rev. Lett. 1993, 71, 3051–3054. [Google Scholar] [CrossRef] [PubMed]
- Khlopov, M.Y.; Rubin, S.G. Primordial structure of massive black hole clusters. Astropart. Phys. 2005, 23, 265–277. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Kobzarev, I.Y.; Okun, L.B. Cosmological consequences of the spontaneous breakdown of discrete symmetry. Zh. Eksp. Teor. Fiz. 1974, 67, 3–11. [Google Scholar]
- Sikivie, P. Axions, domain walls, and the early Universe. Phys. Rev. Lett. 1982, 48, 1156–1159. [Google Scholar] [CrossRef]
- Vilenkin, A.; Everett, A.E. Cosmic strings and domain walls in models with Goldstone and pseudo-Goldstone bosons. Phys. Rev. Lett. 1982, 48, 1867–1870. [Google Scholar] [CrossRef]
- Barr, S.M.; Choi, K.; Kim, J.E. Axion cosmology in superstring models. Nucl. Phys. B 1987, 283, 591–604. [Google Scholar] [CrossRef]
- Lazarides, G.; Shafi, Q. Axion models with no domain wall problem. Phys. Lett. B 1982, 115, 21–25. [Google Scholar] [CrossRef]
- Choi, K.; Kim, J.E. Domain walls in superstring models. Phys. Rev. Lett. 1985, 55, 2637–3640. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.E. High scale inflation, model-independent string axion, and QCD axion with domain wall number one. Phys. Lett. B 2014, 734, 68–71. [Google Scholar] [CrossRef]
- Barr, S.M.; Kim, J.E. New confining force solution of the QCD axion domain-wall problem. Phys. Rev. Lett. 2014, 113, 241301. [Google Scholar] [CrossRef] [PubMed]
- Witten, E. Cosmic superstrings. Phys. Lett. B 1985, 153, 243–246. [Google Scholar] [CrossRef]
- Kim, J.E. Axionic domain wall number related to U(1)anom global symmetry. Phys. Lett. B 2016, 759, 58–63. [Google Scholar] [CrossRef]
- CAPP Site. Available online: http://capp.ibs.re.kr/html/capp_en (accessed on 8 September 2017).
- Ade, P.A.; Aikin, R.W.; Barkats, D.; Benton, S.J.; Bischoff, C.A.; Bock, J.J.; Brevik, J.A.; Buder, I.; Bullock, E.; Dowell, C.D.; et al. Detection of B-mode polarization at degree angular scales by BICEP2. Phys. Rev. Lett. 2014, 112, 241101. [Google Scholar] [CrossRef] [PubMed]
- Marsh, D.J.; Grin, D.; Hlozek, R.; Ferreira, P.G. Tensor interpretation of BICEP2 results severely constrains axion dark matter. Phys. Rev. Lett. 2014, 113, 011801. [Google Scholar] [CrossRef] [PubMed]
- Ade, P.A.; Ahmed, Z.; Aikin, R.W.; Alexander, K.D.; Barkats, D.; Benton, S.J.; Bischoff, C.A.; Bock, J.J.; Bowens-Rubin, R.; Brevik, J.A.; et al. Improved constraints on cosmology and foregrounds from BICEP2 and Keck Array cosmic microwave background data with Inclusion of 95 GHz band. Phys. Rev. Lett. 2016, 116, 031302. [Google Scholar] [CrossRef] [PubMed]
- Choi, K.; Kim, J.E. Harmful axions in superstring models. Phys. Lett. B 1985, 154, 393–396. [Google Scholar] [CrossRef]
- Svrcek, P.; Witten, E. Axions in string theory. J. High Energy Phys. 2006, 2006, 051. [Google Scholar] [CrossRef]
- Kim, J.E. Natural Higgs-flavor-democracy solution of the μ problem of supersymmetry and the QCD axion. Phys. Rev. Lett. 2013, 111, 031801. [Google Scholar] [CrossRef] [PubMed]
- Linde, A.D. A new inflationary Universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for grand unified theories with radiatively induced symmetry breaking. Phys. Rev. Lett. 1982, 48, 1220–1223. [Google Scholar] [CrossRef]
- Linde, A.D. Chaotic inflation. Phys. Lett. B 1983, 129, 177–181. [Google Scholar] [CrossRef]
- Hawking, S.W. The development of irregularities in a single bubble inflationary Universe. Phys. Lett. B 1982, 115, 295–297. [Google Scholar] [CrossRef]
- Guth, A.H.; Pi, S.Y. Fluctuations in the new inflationary Universe. Phys. Rev. Lett. 1982, 49, 1110–1113. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Chibisov, G.V. Quantum fluctuations and a nonsingular Universe. J. Exp. Theor. Phys. Lett. 1981, 33, 532–535. [Google Scholar]
- Liddle, A.R.; Lyth, D.H. The cold dark matter density perturbation. Phys. Rep. 1993, 231, 1–105. [Google Scholar] [CrossRef]
- Smoot, G.F.; Bennett, C.L.; Kogut, A.; Wright, E.L.; Aymon, J.; Boggess, N.W.; Cheng, E.S.; De Amici, G.; Gulkis, S.; Hauser, M.G.; et al. Structure in the COBE differential microwave radiometer first year maps. Astrophys. J. 1992, 396, 1–5. [Google Scholar] [CrossRef]
- Lyth, D.H. What would we learn by detecting a gravitational wave signal in the cosmic microwave background anisotropy? Phys. Rev. Lett. 1997, 78, 1861–1863. [Google Scholar] [CrossRef]
- Choi, K.Y.; Kim, J.E.; Kyae, B. Perspective on completing natural inflation. arXiv, 2015; arXiv:1410.1762[hep-th]. [Google Scholar]
- McAllister, L.; Silverstein, E.; Westphal, A.; Wrase, T. The powers of monodromy. arXiv, 2014; arXiv:1405.3652[hep-th]. [Google Scholar]
- Mirbabayi, M.; Senatore, L.; Silverstein, E.; Zaldarriaga, M. Gravitational waves and the scale of inflation. Phys. Rev. D 2015, 91, 063518. [Google Scholar] [CrossRef]
- Graham, P.W.; Kaplan, D.E.; Rajendran, S. Cosmological relaxation of the electroweak scale. Phys. Rev. Lett. 2015, 115, 221801. [Google Scholar] [CrossRef] [PubMed]
- Choi, K.; Kim, H.; Yun, S. Natural inflation with multiple sub-Planckian axions. Phys. Rev. D 2014, 90, 023545. [Google Scholar] [CrossRef]
- Kaplan, D.E.; Rattazzi, R.A. clockwork axion. Phys. Rev. D 2016, 93, 085007. [Google Scholar] [CrossRef]
- Choi, K.; Im, S.H. Constraints on relaxion windows. J. High Energy Phys. 2016, 2016, 93. [Google Scholar] [CrossRef]
- Flacke, T.; Frugiuele, C.; Fuchs, E.; Gupta, R.S.; Perez, G. Phenomenology of relaxion-Higgs mixing. J. High Energy Phys. 2017, 2017, 1–48. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW150914: Implications for the stochastic gravitational wave background from binary black holes. Phys. Rev. Lett. 2016, 116, 131102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW151226: Observation of gravitational waves from a 22-Solar-mass binary black hole coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW170104: Observation of a 50-Solar-mass binary black hole coalescence at redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.E. Gravity wave and model-independent axion. J. Korean Phys. Soc. 2017, 71, 127–129. [Google Scholar] [CrossRef]
- Belavin, A.A.; Polyakov, A.M.; Schwartz, A.S.; Tyupkin, Y.S. Pseudoparticle solutions of the Yang-Mills equations. Phys. Lett. B 1975, 59, 85–87. [Google Scholar] [CrossRef]
- Fukugita, M.; Yanagida, T. Baryogenesis without grand unification. Phys. Lett. B 1986, 174, 45–47. [Google Scholar] [CrossRef]
- Covi, L.; Kim, J.E.; Kyae, B.; Nam, S. Leptogenesis with high-scale electroweak symmetry breaking and an extended Higgs sector. Phys. Rev. D 2016, 94, 065004. [Google Scholar] [CrossRef]
- Kim, J.E.; Seo, M. Parametrization of the CKM matrix. Phys. Rev. D 2011, 84, 037303. [Google Scholar] [CrossRef]
- Kim, J.E. The CKM matrix with maximal CP violation from Z12 symmetry. Phys. Lett. B 2011, 704, 360–366. [Google Scholar] [CrossRef]
- Kim, J.E.; Nam, S. Unifying CP violations of quark and lepton sectors. The Eur. Phys. J. C 2015, 75, 619. [Google Scholar] [CrossRef]
| 1. | With two light quarks, is larger than . |
| 2. | If is much lower than the above bound at the level of GeV, the axion condensation can convert to thermal axions [78]. |
| 3. | For the , the symmetry is better to be exact at tree level or almost exact toward the solution of the strong CP problem with as discussed in Section 3. |
| 4. | If the symmetry breaking is soly by the non-Abelian anomaly, then we obtain . |



| KSVZ: | DFSZ: pair | Higgs | ||
|---|---|---|---|---|
| 0 | non-SUSY | |||
| non-SUSY | ||||
| GUTs | ||||
| SUSY | ||||
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.E. Dark Energy, QCD Axion, and Trans-Planckian-Inflaton Decay Constant. Universe 2017, 3, 68. https://doi.org/10.3390/universe3040068
Kim JE. Dark Energy, QCD Axion, and Trans-Planckian-Inflaton Decay Constant. Universe. 2017; 3(4):68. https://doi.org/10.3390/universe3040068
Chicago/Turabian StyleKim, Jihn E. 2017. "Dark Energy, QCD Axion, and Trans-Planckian-Inflaton Decay Constant" Universe 3, no. 4: 68. https://doi.org/10.3390/universe3040068
APA StyleKim, J. E. (2017). Dark Energy, QCD Axion, and Trans-Planckian-Inflaton Decay Constant. Universe, 3(4), 68. https://doi.org/10.3390/universe3040068