Observational Consequences of an Interacting Multiverse
Abstract
:1. Introduction
2. Interacting Multiverse
2.1. Quantum Multiverse
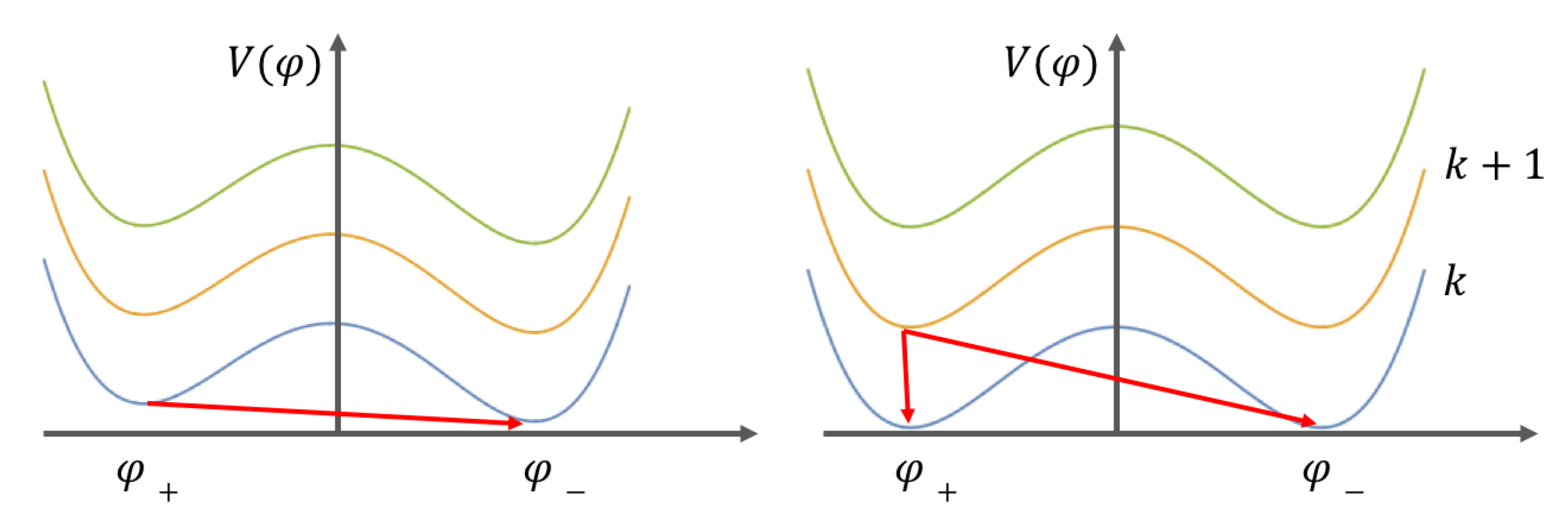
2.2. Interacting Scheme
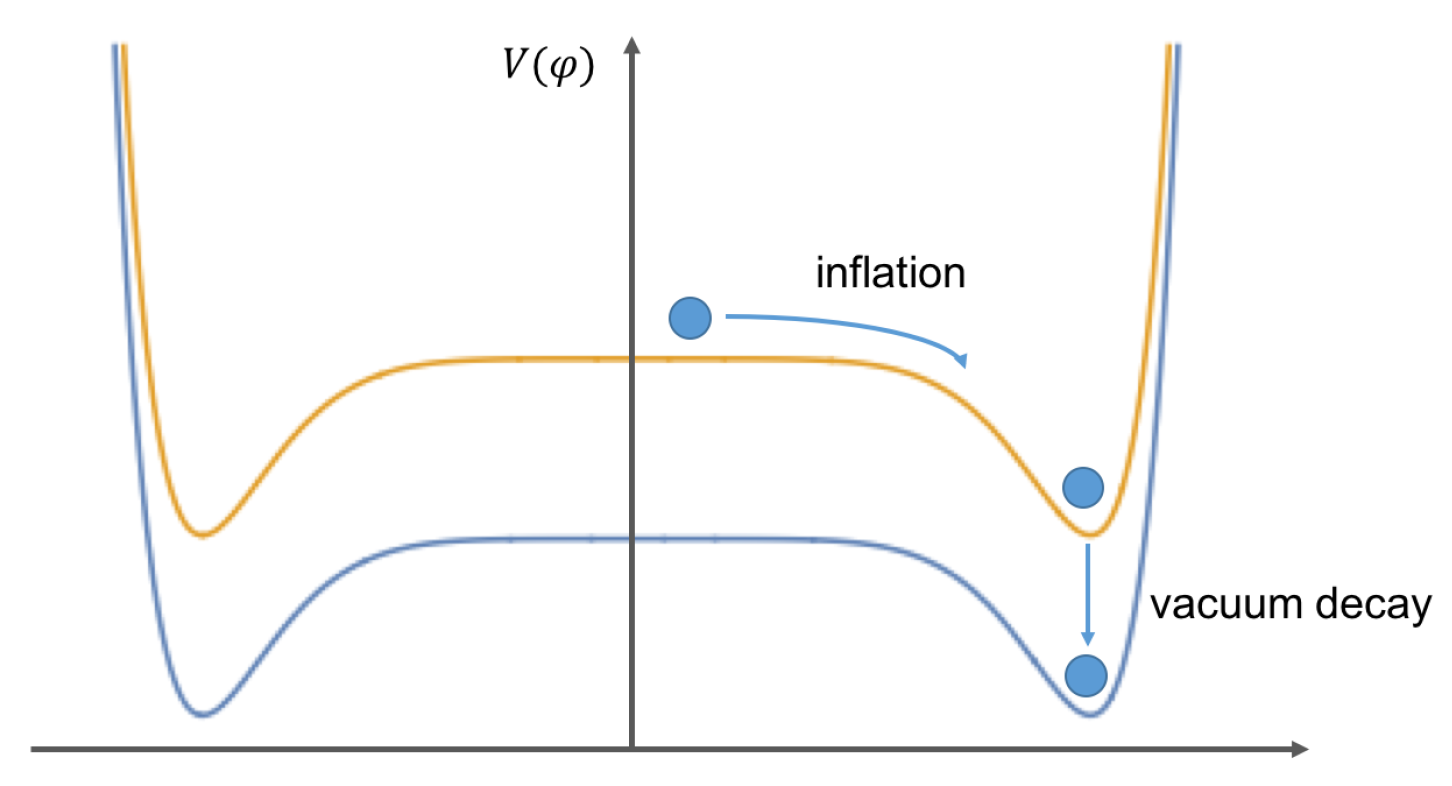
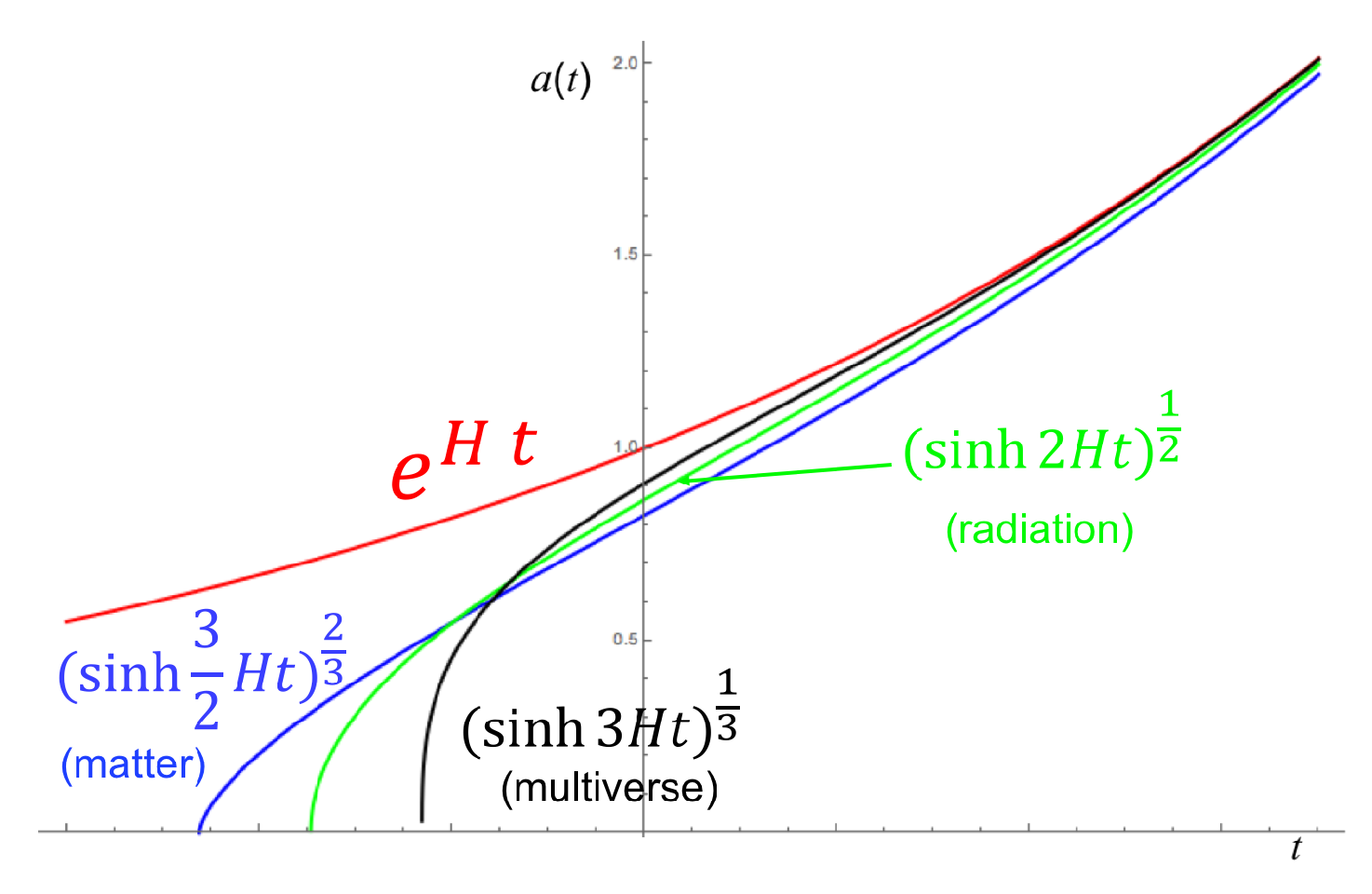
2.3. Modified Properties
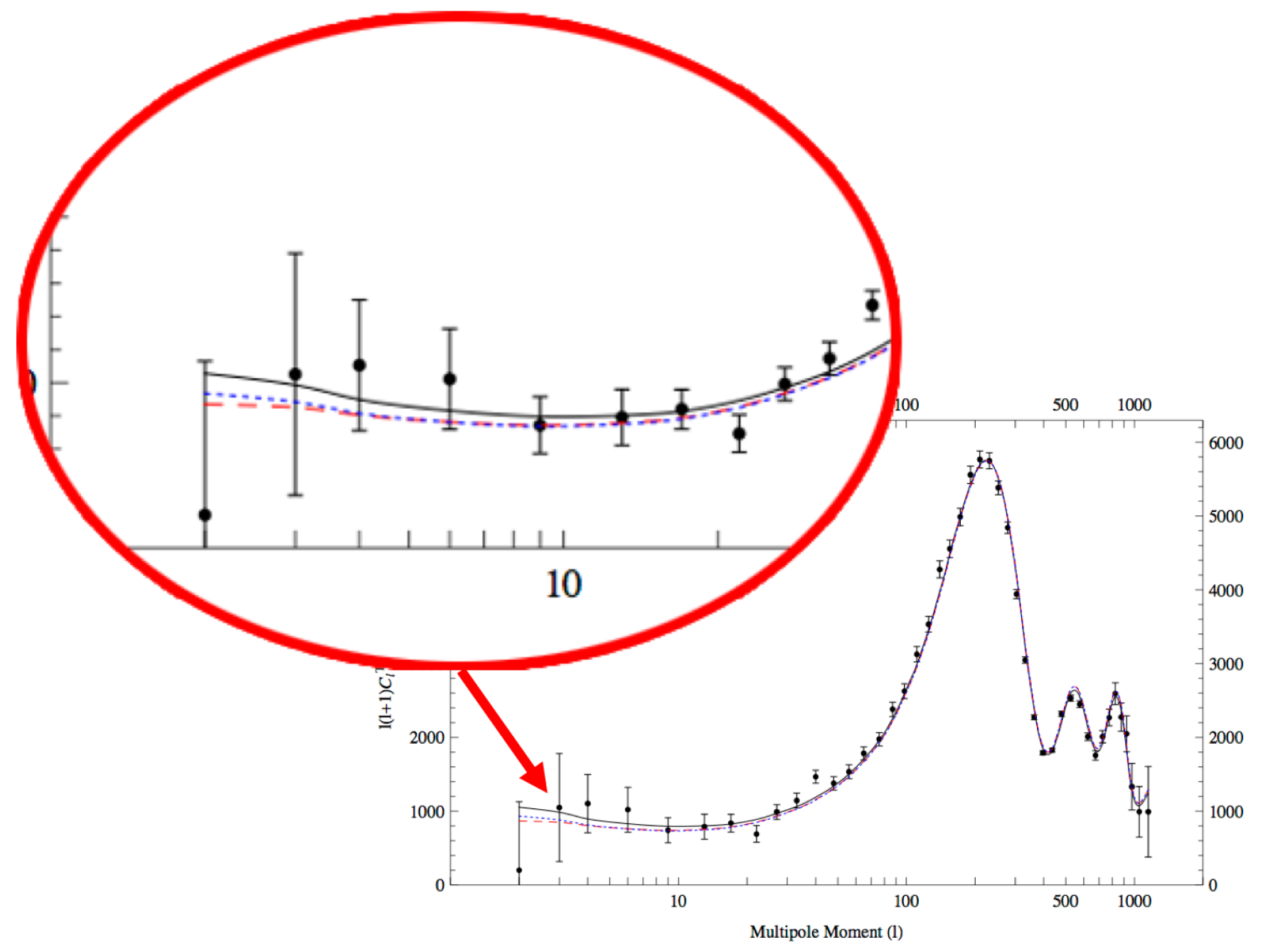
3. Observational Imprints
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Carr, B. (Ed.) Universe or Multiverse; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Holman, R.; Mersini-Houghton, L.; Takahashi, T. Cosmological avatars of the Landscape I, II. Phys. Rev. D 2008, 77, 063511. [Google Scholar] [CrossRef]
- Kanno, S. Impact of quantum entanglement on spectrum of cosmological fluctuations. J. Cosmol. Astropart. Phys. 2014, 2014, 029. [Google Scholar] [CrossRef]
- Strominger, A. Baby Universes. In Quantum Cosmology and Baby Universes; Coleman, S., Hartle, J.B., Piran, T., Weinberg, S., Eds.; World Scientific: London, UK, 1990; Volume 7. [Google Scholar]
- Robles-Pérez, S.; González-Díaz, P.F. Quantum state of the multiverse. Phys. Rev. D 2010, 81, 083529. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Garay, I.; Robles-Pérez, S. Effects of a scalar field on the thermodynamics of interuniversal entanglement. Int. J. Mod. Phys. D 2014, 23, 1450043. [Google Scholar] [CrossRef]
- Hartle, J.B.; Hawking, S.W. Wave function of the Universe. Phys. Rev. D 1983, 28, 2960–2975. [Google Scholar] [CrossRef]
- Robles-Pérez, S.; Alonso-Serrano, A.; Bastos, C.; Bertolami, O. Vacuum decay in an interacting multiverse. Phys. Lett. B 2016, 759, 328–335. [Google Scholar] [CrossRef]
- Ijjas, A.; Steinhardt, P.J.; Loeb, A. Inflationary paradigm in trouble after Planck2013. Phys. Lett. B 2013, 723, 261–266. [Google Scholar] [CrossRef]
- Scardigli, F.; Gruber, C.; Chen, P. Black hole remnants in the early universe. Phys. Rev. D 2011, 83, 063507. [Google Scholar] [CrossRef]
- Bouhmadi-Lopez, M.; Chen, P.; Huang, Y.C.; Lin, Y.H. Slow-roll inflation preceded by a topological defect phase à la Chaplygin gas. Phys. Rev. D 2013, 87, 103513. [Google Scholar] [CrossRef]
- Kanno, S. Cosmological implications of quantum entanglement in the multiverse. Phys. Lett. B 2015, 751, 316–320. [Google Scholar] [CrossRef]
- Bousso, R.; Harlow, R.; Senatore, L. Inflation after false vacuum decay: New evidence from BICEP2. J. Cosmol. Astropart. Phys. 2014, 2014, 019. [Google Scholar] [CrossRef]
- Bousso, R.; Harlow, R.; Senatore, L. Inflation after false vacuum decay: Observational prospects after planck. Phys. Rev. D 2015, 91, 083527. [Google Scholar] [CrossRef]
- Garriga, J.; Vilenkin, A.; Zhang, J. Black holes and the multiverse. J. Cosmol. Astropart. Phys. 2016, 2016, 064. [Google Scholar] [CrossRef]
- Mersini-Houghton, L. Predictions of the quantum landscape multiverse. Class. Quantum Gravity 2017, 34, 047001. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mersini-Houghton, L. Testing predictions of the quantum landscape multiverse 1: The Starobinsky inflationary potential. J. Cosmol. Astropart. Phys. 2017, 2017, 002. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mersini-Houghton, L. Testing predictions of the quantum landscape multiverse 2: The exponential inflationary potential. J. Cosmol. Astropart. Phys. 2017, 2017, 020. [Google Scholar] [CrossRef]
- Robles-Pérez, S.; Bouhmadi-Lopez, M.; Morais, J.; Krämer, M. Effects of the multiverse in the power spectrum of the CMB. 2017, in press. [Google Scholar]
- Robles-Pérez, S.; Balcerzak, A.; Dąbrowski, M.P.; Krämer, M. Inter-universal entanglement in a cyclic multiverse. Phys. Rev. D 2017, 95, 083505. [Google Scholar] [CrossRef]
- Robles-Pérez, S.J. Creation of entangled universes avoids the big bang singularity. J. Gravity 2014, 2014, 382675. [Google Scholar] [CrossRef]
- Bouhmadi-Lopez, M.; Chen, P.; Liu, Y. Cosmological imprints of a generalized Chaplygin gas model for the early universe. Phys. Rev. D 2011, 84, 023505. [Google Scholar] [CrossRef]
| 1 | Let us add the superscript 3 to the action, the Lagrangian and to the Hamiltonian density of the third quantization procedure. |
| 2 | To our knowledge, this was first done in Ref. [2]. Before that, the multiverse was considered by many physicists to be an exotic proposal deprived of any scientific validation. Still today, there are many scientists that are sceptic about the whole proposal. However, we can now pose new and more precise observable imprints, and more and more groups are working on the search of the imprints of the multiverse [2,3,13,14,15,16,17,18,19,20]. |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robles-Pérez, S.J. Observational Consequences of an Interacting Multiverse. Universe 2017, 3, 49. https://doi.org/10.3390/universe3020049
Robles-Pérez SJ. Observational Consequences of an Interacting Multiverse. Universe. 2017; 3(2):49. https://doi.org/10.3390/universe3020049
Chicago/Turabian StyleRobles-Pérez, Salvador J. 2017. "Observational Consequences of an Interacting Multiverse" Universe 3, no. 2: 49. https://doi.org/10.3390/universe3020049
APA StyleRobles-Pérez, S. J. (2017). Observational Consequences of an Interacting Multiverse. Universe, 3(2), 49. https://doi.org/10.3390/universe3020049





